Tutorial 28: Connectivity

[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]

Authors: Hossein Shahabi, Mansoureh Fahimi, Francois Tadel, Esther Florin, Sergul Aydore, Syed Ashrafulla, Elizabeth Bock, Sylvain Baillet

Contents

  1. Introduction
  2. General terms/considerations for a connectivity analysis
  3. Simulated data (AR model)
  4. Coherence (FFT-based)
  5. Granger Causality
  6. Coherence and envelope (Hilbert/Morlet)
  7. Simulated data (phase synchrony)
  8. Correlation
  9. Phase locking value
  10. Method selection and comparison
  11. Connectivity measures on real data
  12. Granger Causality - Mathematical Background
  13. Additional documentation

Introduction

During the past few years, the research focus in brain imaging moved from localizing functional regions to understanding how different regions interact together. It is now widely accepted that some of the brain functions are not supported by isolated regions but rather by a dense network of nodes interacting in various ways.

Brain networks (connectivity) is a recently developed field of neuroscience which investigates interactions among regions of this vital organ. These networks can be identified using a wide range of connectivity measures applied on neurophysiological signals, either in time or frequency domain. The knowledge provides a comprehensive view of brain functions and mechanisms.

This module of Brainstorm tries to facilitate the computation of brain networks and the representation of their corresponding graphs. Figure 1 illustrates a general framework to analyze brain networks. Preprocessing and source localization tasks for neural data are thoroughly described in previous sections of this tutorial. The connectivity module is designed to carry out remained steps, including the computation of connectivity measures, and statistical analysis and visualizations of networks.

[ATTACH]

General terms/considerations for a connectivity analysis

Sensors vs sources: The connectivity analysis can be performed either on sensor data (like EEG, MEG signals) or reconstructed sources (voxels/scouts).

Nature of the signals: The selection of connectivity method depends on the nature of the data. Some approaches are more suitable for spontaneous data (resting state) while others work better with task data (trials).

Point-based connectivity vs. full network: Most of the connectivity functions in this toolbox have the option to either compute the connectivity between one point (channel) and the rest of the network (1 x N) or the entire network (N x N). While the later calculates the graph thoroughly, the first option enjoys a faster computation and it is more useful when you are interested in the connectivity of an ROI with the other regions of the brain.

Temporal resolution: Connectivity networks can be computed in two ways; static and dynamic. Time-varying networks can present the dynamics of brain networks. In contrast, the static graphs illustrate a general perspective of brain connectivity which is helpful in specific conditions. Users need to decide which type of network is more informative for their study.

Time-frequency transformation: Many connectivity measures use a time-frequency transformation to transfer the data to the frequency domain. These approaches include short time Fourier transform, Hilbert transform, and Morlet wavelet.

Output data structure: Consequently, computed connectivity matrices in this toolbox have up to four dimensions; channels x channels x frequency bands x time. Also, when dealing with trials and several files, each file has that 4-D structure.

Simulated data (AR model)

In order to compare different connectivity measures, we use simulated data with known ground truth. Three channels are

\begin{eqnarray*} x_{1}(n) & = & a_{1}x_{1}(n-1) + \cdots + a_{k}x_{1}(n-k) + e_{1}(n) \\ x_{2}(n) & = & a_{1}x_{2}(n-1) + \cdots + a_{k}x_{2}(n-k) + e_{2}(n) \\ x_{3}(n) & = & a_{1}x_{3}(n-1) + \cdots + a_{k}x_{3}(n-k) + b_{1}x_{2}(n-1) + \cdots + b_{r}x_{2}(n-r) + e_{3}(n) \\ \end{eqnarray*}

where a1,...,an are coefficients of an all-pass filter and b1,...,bn are coefficients for a lowpass filter which describes the transfer function from channel 2 to channel 3. One can take the Fourier trnasform from these equations and rearrange them in a matrix form. Based on this model, we generated signals and tested the available connectivity measures. This dataset is available here.

\begin{eqnarray*} A(f)X(f) & = & E(f) \\ define \quad H(f) & = & A^{-1}(f) \quad Transfer \quad function\\ X(f) & = & H(f)E(f) \\ \end{eqnarray*}

[ATTACH]

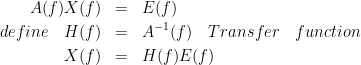
TODO : explain the figure

Coherence (FFT-based)

The coherence is a statistical measure which computes the relation between two signals, like x(t) and y(t), in the frequency domain. The magnitiude-squared coherence is,

\begin{eqnarray*} C_{xy}(f) &=& \frac{\left |S_{xy}(f) \right |^{2}}{S_{xx}(f)S_{yy}(f)} \\ S_{xy}(f) &:& Cross-spectral \quad density \\ S_{xx}(f) \quad and \quad S_{yy}(f) &:& Auto-spectral \quad density \\ \end{eqnarray*}

The coherence function uses the Fourier transform to compute the spectral densities. A related measure which alleviates the problem of volume conduction is the lagged-coherence (ref).

\begin{eqnarray*} LC_{xy}(f) = \frac{Im \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ Re\left ( S_{xy}(f) \right ) \right ]^{2} }} \\ \end{eqnarray*}

TODO : explain the elememts of the equation

[ATTACH]

In general, after running the connectivity processes, you can find a multi-dimensional matrix of connectivity in the database. In order to represent this matrix, there are several options.

Right click on the file and select Power spectrum and Display as image These two figures are plotted here. The left figure shows the Coherence values in all analyzed frequencies. Another figure displays the Transfer matrix between channels for the selected frequency bin.

[ATTACH]

[ATTACH]


Similarly, we can run this process and select "imaginary coherence". which gives us the following representation,

[ATTACH]

[ATTACH]

Granger Causality

Granger Causality (GC) is a method of functional connectivity, adapted by Clive Granger in the 1960s, but later refined by John Geweke in the form that is used today. Granger Causality is originally formulated in economics but has caught the attention of the neuroscience community in recent years. Before this, neuroscience traditionally relied on stimulation or lesioning a part of the nervous system to study its effect on another part. However, Granger Causality made it possible to estimate the statistical influence without requiring direct intervention (ref: wiener-granger causality a well-established methodology).

Granger Causality is a measure of linear dependence, which tests whether the variance of error for a linear autoregressive model estimation of a signal (A) can be reduced when adding a linear model estimation of a second signal (B). If this is true, signal B has a Granger Causal effect on the first signal A, i.e., independent information of the past of B improves the prediction of A above and beyond the information contained in the past of A alone. The term independent is emphasized because it creates some interesting properties for GC, such as that it is invariant under rescaling of A and B, as well as the addition of a multiple of A to B. The measure of Granger Causality is nonnegative, and zero when there is no Granger causality(Geweke, 1982).

The main advantage of Granger Causality is that it is an asymmetrical measure, in that it can dissociate between A->B versus B->A. It is important to note however that though the directionality of Granger Causality is a step closer towards measuring effective connectivity compared to symmetrical measures, it should still not be confused with “true causality”. Effective connectivity estimates the effective mechanism generating the observed data (model-based approach), whereas GC is a measure of causal effect based on prediction, i.e., how well the model is improved when taking variables into account that are interacting (data-driven approach) (Barrett and Barnett, 2013). The difference with causality is best illustrated when there are more variables interacting in a system than those considered in the model. For example, if a variable C is causing both A and B, but with a smaller delay for B than for A, then a GC measure between A and B would show a non-zero GC for B->A, even though B is not truly causing A (Bressler and Seth, 2011).

The complete formulation of this method is discussed in the advanced section. Here, we apply the Granger causality and its spectral version on the simulated data.

[ATTACH]

Input options:

Estimator options:

Output options:

[ATTACH]

Spectral Granger causality

[ATTACH]

[ATTACH]

Coherence and envelope (Hilbert/Morlet)

This process

[ATTACH]

[ATTACH]

Simulated data (phase synchrony)

Correlation

The correlation is the basic approach to show the dependence or association among two random variables or MEG/EEG signals. While this method has been widely used in electrophysiology, it should not be considered as the best technique for finding the connectivity matrices. The correlation by its nature fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals.

[ATTACH]

Phase locking value



Method selection and comparison

We can have a comparison between different connectivity functions. The following table briefly does this job.

[ATTACH]

Comparing different approaches with the ground truth we find out that the HCorr function works slightly better than other coherence functions.

[ATTACH]

Connectivity measures on real data

In this section we will show how to use the Brainstorm connectivity tools on real data.

Experimental Setep and data recording:

For this part we will use the LFP monkey data described in Bresslers et al (1993), these data are widely used over the last past years in many studies.

The original data could be found in this link: http://www.ccs.fau.edu/~bressler/Data/Nakamura/LFP/Prepro/LFP.html

These recordings were made using 51um diameter bipolar electrodes sepetated by 2.5mm in macaque monkeys. For our analysis we have selected the monkey U0001f649 named GE. Voltage are recorded at 200Hz sampling rate. The signals are recorded from a total of 15 electrode pairs in the right hemisphere. The location of the electrodes are shown in this figure. Voltage are recorded at 200Hz sampling rate.

[ATTACH] [ATTACH]

On the left, a schem of the monkey brain area, on the right, the locations of 15 electrode pairs in the right hemisphere (reproduced from Aydore et al. (2013) and Bresslers et al (1993).)

In these experiments the monkey was trained to depress a lever and wait for a visual stimulus that informs the monkey to either let go the lever (release) or keep the lever down (nogo, not release the lever). The visual stimulus is presented with four dots on a screen. The dots forms either diagonal line or a shape of diamond. For our analysis in this tutorial, we select a dataset with a diagonal line as the 'NOGO' condition and the diamond as the 'GO' condition.

For more details about the experement please refer to Bresslers et al (1993).

Importing and analysing data within brainstorm:

For our case, we imported and adapted the data to the brainstorm format, you can download the data here todo--> (add the link here).

Voltage are on recorded at 200Hz sampling rate. After pooling and ordering the dataset together, we select 480 trials for each condition.

Defining the lever initial descent to be at time t = 0ms. Each trial last 600ms, the stimulus was given 100ms after the lever was depressed, and last for 100ms. On go trials, a water reward was provided 500 ms after stimulus onset if the hand was lifted within 500ms. On the nogo trials, the lever was depressed for 500ms.

In this analysis we will focuse mainly in two time window. The early answer for t [100, 250 ms] in which we expect a visual activation on the occipital area (striate and prestriate areas).

We will also show some analysis on the late answer, for t [250, 450 ms] in which we expect an activation/connectivity between the striate and motor cortex in the GO condition and no or less activation for the NOGO condition.

Process of computation :

For all the connectivity meaures, we will compute the connectivity matrix (NxN) for all he trials and for the both conditions (GO snd NOGO), then we will average the all the connectivity measure for each condition. Afterward we will analyse the average matrix between the condition.

Step 1 : Drag and drop all the trials for both condition in Process1.

Step 2 : Run process1 and select the desired connectivity measure menu, choose the desired parameters (see bellow) and start the computation.

Step 3 : Average the connectivity measure for all trial bellonging the same condition.

To free space in your hard disc and in order to be able to compute other connectivity meaure, you can/should remove the previous individual connectivity for each trial. To do so, keep the 'time freq' in process1, click Run and choose : File>Delete File>Delete selected Files and then click on run.

. [ATTACH]

Phase Locking Value (PLV):

We compute the PLV. We select the two groupes of files in the the process 1, then hit Run, select Connectivity then Phase Locking Value NxN. Choose time window between 100 to 250ms. 

Keep the other options as they are, select the Magnitude and choose the option 'Save individual resulys (one file per input file)' and finaly click on Run.

. [ATTACH]

This could take some times according to your computer and the size of your data.

Now, in order to have one measure for each condition, we need to average all the connectivity measure across trials. We do this from the Brainstorm Process1 window, select 'Process time-freq' (the third icone). Then click on run and select : Average->Average Files, select the option : By trial group (folder average) with the function Arithmetic average. This will compute the average connectivity PLV value for the Go and NoGo stimulus.

Early answer t ϵ [100-250 ms]:

Right click on the connectivity file and select the first option > Display as graph [NxN]. We display bth for the GO (left figure) and NOGO (right figure) conditions.

[ATTACH] [ATTACH]

Coherence:

We use the same data as previous, and we will compute the coherence. We will try to show similar results as shown in the Bresslers et al.

Correlation:

/!\ End of edit conflict

Advanced

Granger Causality - Mathematical Background

[ATTACH]



Practical issues about GC:

Temporal resolution: the high time resolution offered by MEG/EEG and intracranial EEG allows for a very powerful application of GC and also offers the important advantage of spectral analysis.

Stationarity: the GC methods described so far are all based on AR models, and therefore assume stationarity of the signal (constant auto-correlation over time). However, neuroscience data, especially task-based data such as event-related potentials are mostly nonstationary. There are two possible approaches to solve this problem. The first is to apply methods such as differencing, filtering, and smoothing to make the data stationary (see a recommendation for time domain GC). Dynamical changes in the connectivity profile cannot be detected with the first approach. The second approach is to turn to versions of GC that have been adapted for nonstationary data, either by using a non-parametric estimation of GC or through measures of time-varying GC, which estimate dynamic parameters with adaptive or short-time window methods (Bressler and Seth, 2011).

Number of variables: Granger causality is very time-consuming in the multivariate case for many variables (O(m^2) where m represents the number of variables). Since each connection pair results in two values, there will also be a large number of statistical comparisons that need to be controlled for. When performing GC in the spectral domain, this number increases even more as statistical tests have to be performed per frequency. Therefore, it is usually recommended to select a limited number of ROIs or electrodes based on some hypothesis found in previous literature, or on some initial processing with a more simple and less computationally heavy measure of connectivity.

Pre-processing: The influence of pre-processing steps such as filtering and smoothing on GC estimates is a crucial issue. Studies have generally suggested to limit filtering only for artifact removal or to improve the stationarity of the data but cautioned against band-pass filtering to isolate causal influence within a specific frequency band (Barnett and Seth, 2011).

Volume Conduction: Granger causality can be performed both in the scalp domain or in the source domain. Though spectral domain GC generally does not incorporate present values of the signals in the model, it is still not immune from spurious connectivity measures due to volume conduction (for a discussion see (Steen et al., 2016)). Therefore, it is recommended to reduce the problem of signal mixing using additional processing steps such as performing source localization and doing connectivity in the source domain.

Data length: because of the extent of parameters that need to be estimated, the number of data points should be sufficient for a good fit of the model. This is especially true for windowing approaches, where data is cut into smaller epochs. A rule of thumb is that the number of estimated parameters should be at least (~10) several times smaller than the number of data points.

Additional documentation

References

Articles

Forum discussions







Feedback: Comments, bug reports, suggestions, questions
Email address (if you expect an answer):


Tutorials/Connectivity (last edited 2019-08-10 04:39:09 by TakfarinasMedani)