Tutorial 13: Artifact cleaning with SSP
Authors: Francois Tadel, Elizabeth Bock, John C Mosher, Sylvain Baillet
As previously said, the frequency filters are not adapted to remove artifacts that are transient or overlapping in frequency domain with the brain signals of interest. Other approaches exist to correct for these artifacts, based on the spatial signature of the artifacts.
If an event is very reproducible and occurs always at the same location (eg. eye blinks and heartbeats), the sensors will always record the same values when it occurs. We can identify the topographies corresponding to this artifact (ie. the spatial distributions of values at one time point) and remove them from the recordings. This spatial decomposition is the basic idea behind two widely used approaches: the SSP (Signal-Space Projection) and ICA (Independent Component Analysis) methods.
This introduction tutorial will focus on the SSP approach, as it is a lot simpler and faster but still very efficient for removing blinks and heartbeats from MEG recordings. The interface for running ICA decompositions is very similar and will be described in an advanced tutorial.
Contents
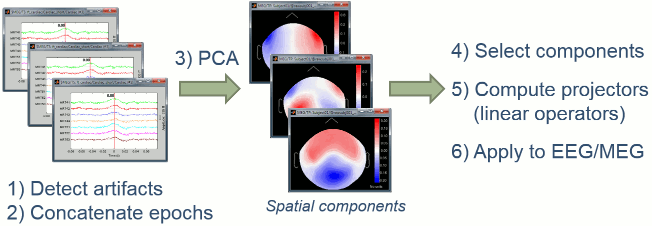
Overview
The general SSP objective is to identify the sensor topographies that are typical of a specific artifact, then to create spatial projectors to remove the contributions of these topographies from the recordings.
- We start by identifying many examples of the artifact we are trying to remove. This is what we've been doing in the previous tutorial with the creation of the "cardiac" and "blink" events.
- We extract a short time window around each of these event markers and concatenate in time all the small blocks of recordings.
- We run a principle components analysis (PCA) on the concatenated artifacts in order to get a decomposition in various spatial components (number of components = number of sensors).
- If it works well, we can find in the first few principal components some topographies that are very specific of the type of artifact we are targeting. We select these components to remove.
- We compute a linear projector for each spatial component to remove and save them in the database (in the "Link to raw file"). They are not immediately applied to the recordings.
- Whenever some recordings are read from this file, the SSP projectors are applied on the fly to remove the artifact contributions. This approach is fast and memory efficient.
Note that these tools are available on continuous files only ("Link to raw file") and cannot be applied to recordings that have already been imported in the database.
The order matters
This procedure has to be repeated separately for each artifact type. The order in which you process the artifacts matters, because for removing the second artifact we typically use the recordings cleaned with the first set of SSP projectors. We have to decide which one to process first.
It works best if each artifact is defined precisely and as independently as possible from the other artifacts. If the two artifacts happen simultaneously, the SSP projectors calculated for the blink may contain some of the heartbeat topography and vice versa. When trying to remove the second artifact, we might not be able to clearly isolate it anymore.
Because the heart beats every second or so, there is a high chance that when the subject blinks there is a heartbeat not too far away in the recordings. Therefore a significant number of the blinks will be contaminated with heartbeats. But we have usually a lot of "clean" heartbeats, we can start by removing these ones. To correctly isolate these two common artifacts, we recommend the following procedure:
- Remove the markers "cardiac" that are occurring during a blink (done in the previous tutorial),
Compute the cardiac SSP (with no eye movements, because we removed the co-occurring events),
Compute the blink SSP (with no heartbeats, because they've already been taken care of).
If you have multiple modalities recorded simultaneously, for example MEG and EEG, you should run this entire procedure twice, once for the EEG only and once for the MEG only. You will always get better results if you process the different types of sensors separately. Same thing when processing Elekta-Neuromag recordings: separately process the magnetometers (MEG MAG) and the gradiometers (MEG GRAD).
SSP: Heartbeats
Double-click on the link to show the MEG sensors for Run #01.
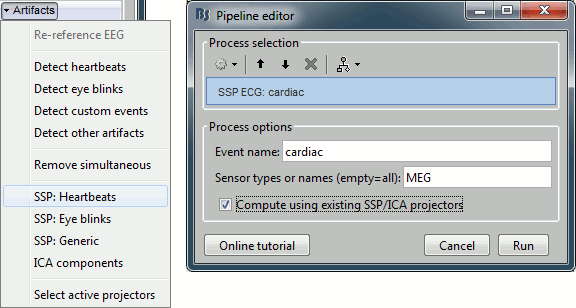
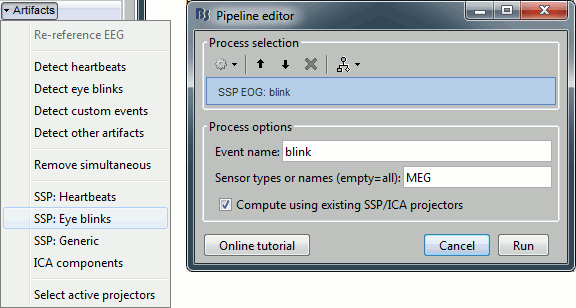
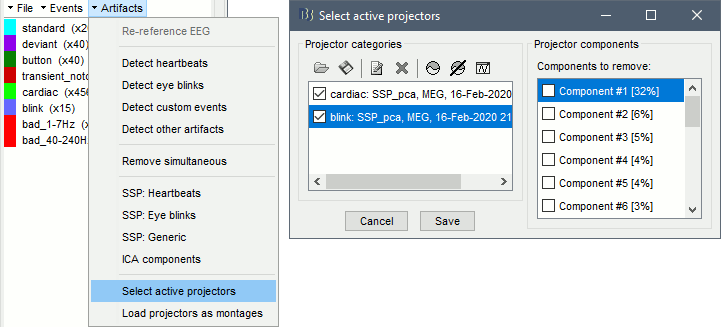
In the Record tab, select the menu: "Artifacts > SSP: Heartbeats".
Event name: Name of the event to use to calculate the projectors, enter "cardiac".
Sensor types: Type of sensors for which the projection should be calculated ("MEG"). Note that you will always get better results if you process the different types of sensors separately.
Compute using existing SSP projectors: You have the option to calculate the projectors from the raw recordings, or from the recordings filtered with the previously computed SSP projectors.
Unless you have a good reason for not considering the existing projectors, you should select this option. Then if the results are not satisfying, try again with the option disabled.
For this step it doesn't make any difference because there are not projectors yet in the file.
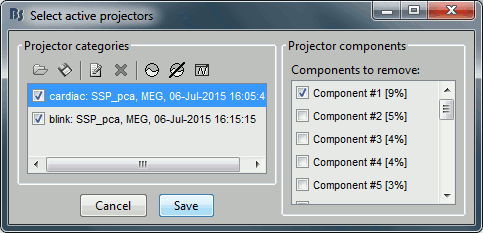
After the computation is done, a new figure is displayed, that lets you select the active projectors.
On the left: The projector categories where each row represents the result of an execution of this process (usually one for each sensor type and each artifact).
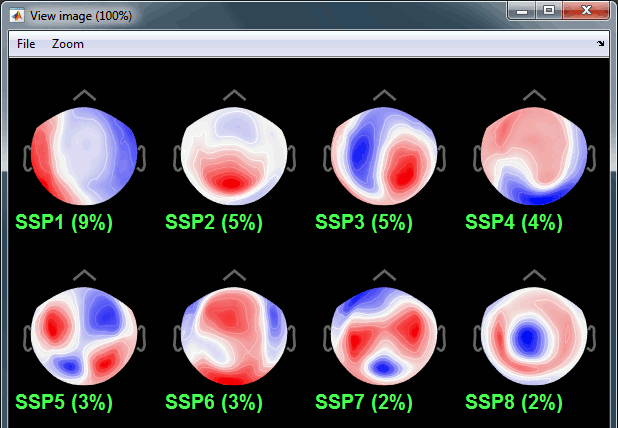
On the right: The spatial components returned by the PCA decomposition. The percentage indicated between brackets is the singular value for this each component, normalized for this decomposition (percentage = Si / sum(Si), see technical details at the end of this page).
Percentage: More practically, it indicates the amount of signal that was captured by the component during the decomposition. The higher it is, the more the component is representative of the artifact recordings that were used to calculate it. In the good cases, you would typically see one to three components with values that are significantly higher than the others.
- When a component is selected, it means that it is removed from the recordings. A spatial projector is computed and applied to the recordings on the fly when reading from the continuous file.
Default selection: The software selects the first component and leaves the others unselected. This selection is arbitrary and doesn't mean the cleaning is correct, you should always manually review the components that you want to remove.

Evaluate the components
The percentage indicated for the first value (9%) is much higher than the following ones (5%, 5%, 4%, 3%...), this could indicate that it targets relatively well the cardiac artifact. Let's investigate this.
Click on the first component, then click on the toolbar button [Display component topography]. This menu shows the spatial distribution of the sensor values for this component. Note that you don't have to select the component (ie. check the box) to display it. This topography seems to correspond to a strong dipolar activity located relatively far from the sensor array, it matches the type of artifact we expect from the heart activity.

The second button "Display component topography [No magnetic interpolation]" produces the same figure but without the reinterpolation of the magnetic fields that is typically applied to the MEG recordings in Brainstorm, it may help understand some difficult cases. This magnetic interpolation will be detailed later in the introduction tutorials.
You can display multiple components in the same figure: select them at the same time in the list (holding the Shift/Ctrl/Cmd button of your keyboard) and then click on the button "Display topography". No other strong components looks like it could be related with the heartbeats.
The last button in the toolbar [Display component time series], opens a figure that represents the evolution of the contribution of this component over time. The higher the amplitude, the more present the selected topography in the recordings. Click on it to show the component #1, then display the ECG signal at the same time (right-click on the file > ECG > Display time series).
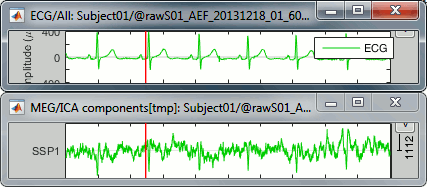
We observe that the "SSP1" trace correlates relatively well with the ECG trace, in the sense that we captured most the ECG peaks with this component. However, the component seems also to capture much more signal than just the heartbeats: many alpha oscillations and some of the ocular activity. The example below shows a blink in the EOG, ECG and SSP component #1.
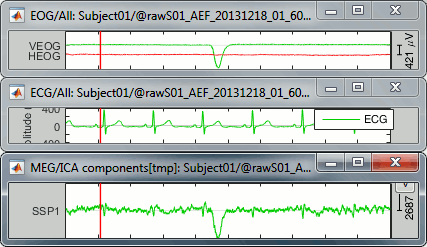
If you remove this component from the recordings, you can expect to see most of the artifacts related with the cardiac activity to go away, but you will also remove additional signal elements that were not really well identified. The job is done but it causes some unwanted side effects.
- It is in general possible to refine the SSP decomposition by going back to the selection of "cardiac" markers that we used to compute it. You could look at all the ECG peaks individually and remove the markers located in segments of recordings that are noisier or that contain a lot of alpha activity (~10Hz). You would need to delete this SSP decomposition and run again the same process.
Alternatively, or if you don't manage to extract a clean cardiac component with a PCA/SSP decomposition, you could try to run an ICA decomposition instead. You might be able to get better results, but it comes with significant computation and manual exploration times. Note that for some subjects, the cardiac artifact is not very strong and could be simply ignored in the analysis.
Evaluate the correction
The topography of the component #1 looks like it represents the heart activity and its temporal evolution shows peaks where we identified heartbeats. It is therefore a good candidate for removal, we just need to make sure the signals look good after the correction before validating this choice.
- Show the left-temporal MEG sensors (CTF LT) and select/unselect the first SSP component.
- Repeat this for different time windows, to make sure that the cardiac peaks in the MEG sensors really disappear when the projector #1 is selected and that the rest is not altered too much.
No correction:

Cardiac component #1 removed:

In this example we will consider that the current decomposition is good enough.
Make sure you select the component #1, then click on [Save] to validate the modifications.After this window is closed, you can always open it again from the Record tab with the menu Artifacts > Select active projectors. At this stage of the analysis, you can modify the list of projectors applied to the recordings at any time.
SSP: Eye blinks
Let's try the same thing with the eye blinks.
Select the process "Artifacts > SSP: Eye blinks"
Run it on the event type "blink", that indicates the peaks of the VEOG signal.
Select the option "Compute using existing projectors" (if this step doesn't seem to work correctly, try again without selecting this option).
You see now a new category of projectors. Based on the distribution of values, this first component is most likely a good representation of the artifact we are trying to remove. The second one could be a good candidate as well.

Select the first three components and display their topographies:

Component #1: Most likely a blink,
Component #2: Probably a saccade (another type of eye movement),
- Component #3: Not related with the eye movements (maybe related with the alpha activity).
As a side note, if you had not selected the option "Compute using existing SSP/ICA projectors", you would have obtained the projectors below, which correspond to the topography of the artifact in the original signals (without considering the cardiac projector). It is normal if the topographies we obtain after removing the cardiac peaks are slightly different, this is because they are computed on the different subspace of the signals. The relative singular values is smaller after the cardiac correction, maybe because the recordings we used to compute it already contained some eye movements.

Display the times series for these three components, together with the EOG signals. You have to uncheck temporarily the component #1 to be able to display its signal. When it is checked, it is removed from the signal therefore it corresponds to a flat trace.
The figure below shows the EOG and SSP values between 318s and 324s. The SSP1 trace matches the blink observed in VEOG and SSP2 matches the saccade observed in HEOG.

Left-temporal MEG signals when there is no component selected:
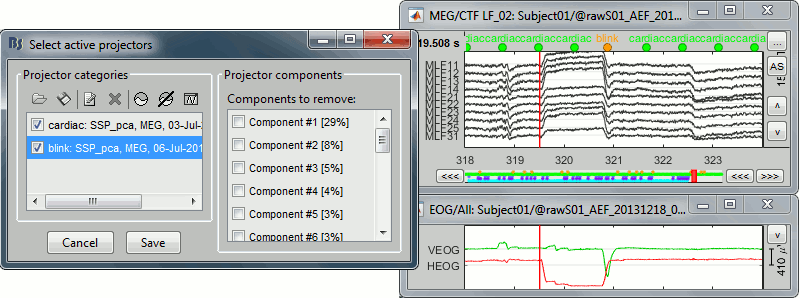
With only the component #2 selected (saccade):

With components #1 and #2 selected (blink + saccade):

Keep the components #1 and #2 selected and click on [Save] to validate your changes.
Run #02
Reproduce the same operations on Run #02:
- Close everything with the [X] button at the top-right corner of the Brainstorm window.
Open the MEG recordings for run AEF #02 (double-click on the file link).
Artifacts > SSP: Heartbeats: Event name "cardiac", sensors "MEG", use existing SSP projectors.
Select component #1, click on [Save].
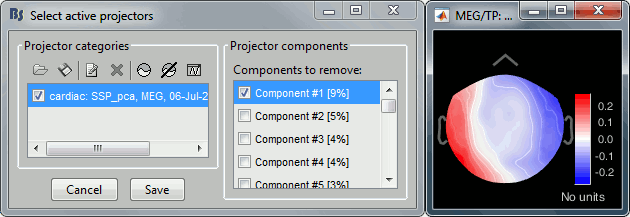
Artifacts > SSP: Eye blinks: Event name "blink", sensors "MEG", use existing SSP projectors.
Select component #1, click on [Save].

- Note that in this second session, the representation of the saccade was not as clear as in the first file. The distribution of the percentage values does not show any clear component other from the blink one, and the topographies are not as clear. In general, the saccade processing requires a separate step, we will illustrate this in the next tutorial.
Note for beginners
Everything below is advanced documentation, you can skip it for now.
SSP: Generic
The calculation of the SSP for the heartbeats and the eye blinks are shortcuts to a more generic process "Artifacts > SSP: Generic". You may need this process if the standard parameters do not work of if you want to use this technique to remove other types of artifacts.
Time window: What segment of the file you want to consider.
Event name: Markers that are used to characterize the artifact. If you don't specify any event name, it will use the entire time window as the input of the PCA decomposition.
Event window: Time segment to consider before and after each event marker. We want this time window to be longer than the artifact effect itself, in order to have a large number of time samples representative of a normal brain activity. This helps the PCA decomposition to separate the artifact from the ongoing brain activity.
Frequency band: Definition of the band-pass filter that is applied to the recordings before calculating the projector. Usually you would use the same frequency band as we used for the detection, but you may want to try to refine this parameter if the results are not satisfying.
Sensor types or names: List of sensor names or types for which the SSP projectors are calculated. You can get better results if you process one sensor type at a time.
Compute using existing SSP/ICA projectors: Same as in the heartbeats/blinks processes.
Save averaged artifact in the database: If you check this option with an event name selected, the process will save the average of all the artifact epochs (event marker + event window) before and after the application of the first component of the SSP decomposition. This is illustrated in the next section.
Method to calculate the projector:
PCA: What was described until now: SVD decomposition to extract spatial components.
Average: Uses only one spatial component, the average of the time samples at which the selected events occur. This has no effect if there are no events selected.

Averaged artifact
One efficient way of representing the impact of this artifact correction is to epoch the recordings around the artifacts before and after the correction and compute the average of these epochs.
- Run the process "SSP: Generic" with:
- The default blink options: event "blink", [-200,+200]ms, [1.5-15]Hz.
The option "Computing existing SSP/ICA projectors" disabled.
The option "Save averaged artifact in the database" selected.
- The option panel should look like the screen capture in the previous section.
Look at the topography of the first component. You can notice that the percentage value is higher than what we got previously, and that the topography looks different than previously.

- This difference comes from the fact that this time we did not use the cardiac SSP to compute the blink SSP ("Compute existing SSP" disabled). This could indicate that there is some form of cross-contamination of the "blink" and "cardiac" events that we designed here. The origin of the common signals between the different segments of artifact is sometimes due to important alpha waves (around 10Hz) that are present for most of the recordings. It don't matter much, you just have to remember that the computation order matters and that you can try variations of the suggested workflow to fit better your recordings.
- Otherwise, the difference between this topography and the previous one could be only due to the fact that they represent the artifact in different subspaces (in the first case, one dimension has already been removed). Even if the two artifacts were completely independant (the two removed dimensions are orthogonal), the topographies would look slightly different.
You should see now two additional files in your database. They are both the average of the 19 blinks identified in the recordings, [-200,+200]ms around the "blink" events. The top row shows the average before the SSP correction, the bottom row the same average but recomputed after removing the first component of the decomposition. The artifact is gone.

Delete this new category, and make sure you get back to the previous settings (first component of both "cardiac" and "blink" selected). Click on [Save] to validate this modification.
Troubleshooting
You have calculated your SSP projectors as indicated here but you don't get any good results. No matter what you do, the topographies don't look like the targeted artifact. You can try the following:
- Review one by one the events indicating the artifacts, remove the ones that are less clear or that occur close to another artifact.
- Select or unselect the option "Compute using existing SSP".
- Change the order in which you compute the projectors.
- Use the process "SSP: Generic" and modify some parameters:
- Use a narrower frequency band: especially the EOG, if the projectors capture some of the alpha oscillations, you can limit the frequency band to [1.5 - 9] Hz.
- Reduce or increase the time window around the peak of the artifact.
- Change the method: Average / SSP.
- If you have multiple acquisition runs, you may try to use all the artifacts from all the runs rather than processing the files one by one. For that, use the Process2 tab instead of Process1. Put the "Link to raw file" of all the runs on both sides, Files A (what is used to compute the SSP) and Files B (where the SSP are applied).
Always look at what this procedure gives you in output. Most of the time, the artifact cleaning will be an iterative process where you will need several experiments to adjust the options and the order of the different steps in order to get optimal results.
SSP Theory
The Signal-Space Projection (SSP) is one approach to rejection of external disturbances. Here is a short description of the method by Matti Hämäläinen, from the MNE 2.7 reference manual, section 4.16.
Unlike many other noise-cancellation approaches, SSP does not require additional reference sensors to record the disturbance fields. Instead, SSP relies on the fact that the magnetic field distributions generated by the sources in the brain have spatial distributions sufficiently different from these generated by external noise sources. Furthermore, it is implicitly assumed that the linear space spanned by the significant external noise patterns has a low dimension.
Without loss of generality we can always decompose any n-channel measurement b(t) into its signal and noise components as:
b(t) = bs(t) + bn(t)
Further, if we know that bn(t) is well characterized by a few field patterns b1...bm, we can express the disturbance as
bn(t) = Ucn(t) + e(t) ,
where the columns of U constitute an orthonormal basis for b1...bm, cn(t) is an m-component column vector, and the error term e(t) is small and does not exhibit any consistent spatial distributions over time, i.e., Ce = E{eeT} = I. Subsequently, we will call the column space of U the noise subspace. The basic idea of SSP is that we can actually find a small basis set b1...bm such that the conditions described above are satisfied. We can now construct the orthogonal complement operator
P⊥ = I - UUT
and apply it to b(t) yielding
b(t) ≈ P⊥bs(t) ,
since P⊥bn(t) = P⊥Ucn(t) ≈ 0. The projection operator P⊥ is called the signal-space projection operator and generally provides considerable rejection of noise, suppressing external disturbances by a factor of 10 or more. The effectiveness of SSP depends on two factors:
The basis set b1...bm should be able to characterize the disturbance field patterns completely and
The angles between the noise subspace space spanned by b1...bm and the signal vectors bs(t) should be as close to π/2 as possible.
If the first requirement is not satisfied, some noise will leak through because P⊥bn(t) ≠ 0. If the any of the brain signal vectors bs(t) is close to the noise subspace not only the noise but also the signal will be attenuated by the application of P⊥ and, consequently, there might by little gain in signal-to-noise ratio.
Since the signal-space projection modifies the signal vectors originating in the brain, it is necessary to apply the projection to the forward solution in the course of inverse computations.
SSP Algorithm
The logic of the SSP computation is the following:
- Take a small time window around each marker to capture the full effect of the artifact, plus some clean brain signals before and after. The default time window is [-200,+200]ms for eye blinks, and [-40,+40]ms for the heartbeats.
- Filter the signals in a frequency band of interest, in which the artifact is the most visible (in practice, we extract a segment long enough so that it can be filtered properly, and cut it after filtering).
Concatenate all these time blocks into a big matrix A = [b1, ..., bm]
Compute the singular value decomposition of this matrix A: [U,S,V] = svd(A, 'econ')
The singular vectors Ui with the highest singular values Si are an orthonormal basis of the artifact subspace that we want to subtract from the recordings. The software selects by default the vector with the highest eigenvalue. Then it is possible to redefine interactively the selected components.
Calculate the projection operator: P⊥i = I - UiUiT
Apply this projection on the MEG or EEG recordings F: F = P⊥iF
The process has to be repeated separately several times for each sensor type and each artifact.
Steps #1 to #5 are done by the processes "Artifact > SSP" in the Record tab: the results, the vectors Ui, are saved in the channel file (field ChannelMat.Projector(i).Components).
Steps #6 and #7 are calculated on the fly when reading a block of recordings from the continuous file: when using the raw viewer, running a process a process on the continuous file, or importing epochs in the database.
Step #8 is the manual control of the process. Take some time to understand what you are trying to remove and how to do it. Never trust blindly any fully automated artifact cleaning algorithm, always check manually what is removed from the recordings, and do not give up if the first results are not satisfying.
Extract the time series
It could be useful to save the SSP or ICA time series in a new file for further processing. Here is one solution to get there:
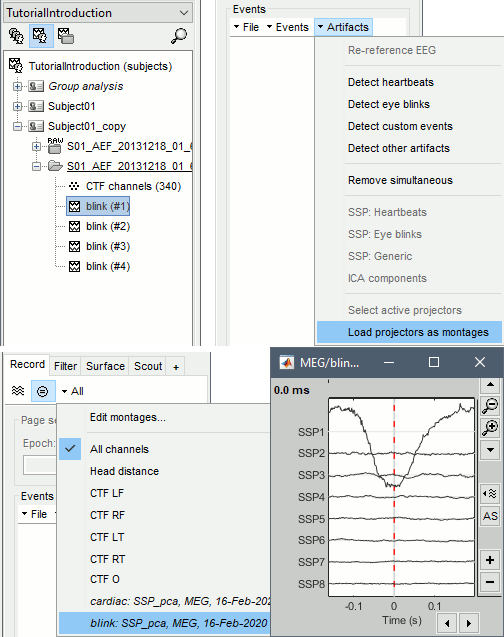
First, make sure you do not remove the components you are interested in: open the continuous recordings, Record tab > Artifacts > Select active projectors, unselect the components you want to study, so that they are kept in the imported data.
Import the segments of recordings of interest from the continuous file: select the option Apply SSP/ICA projectors, otherwise the projectors would be discarded from the new channel file in the imported folder.

To review the SSP/ICA time series (optional): open the recordings you just imported, and select the menu Artifacts > Load projector as montages in the Record tab. The projectors are made available in the montage menu.
To create a new file with the SSP/ICA time series in the database: select the file you imported in Process1 and run the process Standardize > Apply montage, with the option Create new folders selected.

On the hard drive
The projectors are saved in the channel file associated with the recordings. This means that they will be shared by all the files that share the same channel file. As a consequence, you cannot share the channel files between acquisition runs if you are planning to use different SSP projectors for different runs.
You can find them in the field ChannelMat.Projector (array of structures):
Comment: String representing the projector in the window "Select active projectors".
Components: [Nsensors x Ncomponents], each column is one spatial component.
CompMask: [1 x Ncomponents], Indicates if each component is selected or not (0 or 1).
Status: 0=Category not selected, 1=Category selected, 2=Projectors already applied to the file.
SingVal: [1 x Ncomponents], Singular values of the SVD decomposition for each component.

Additional documentation
Articles
- C. D. Tesche, M. A. Uusitalo, R. J. Ilmoniemi, M. Huotilainen, M. Kajola, and O. Salonen, "Signal-space projections of MEG data characterize both distributed and well-localized neuronal sources," Electroencephalogr Clin Neurophysiol, vol. 95, pp. 189-200, 1995.
- M. A. Uusitalo and R. J. Ilmoniemi, "Signal-space projection method for separating MEG or EEG into components," Med Biol Eng Comput, vol. 35, pp. 135-40, 1997.
Tutorials and forum discussions
Tutorial: SSP cookbook
Additional SSP examples can be found in the tutorials in section Other analysis scenarios.