Tutorial 21: Noise and data covariance matrices
Authors: Francois Tadel, Elizabeth Bock, John C Mosher, Richard Leahy, Sylvain Baillet
Modeling and measuring certain characteristics of the noise contaminating the data is beneficial to source estimation. For instance, minimum norm estimators can integrate second-order sample statistics of sensor noise (summarized into a noise covariance matrix, see below). Beamformers further require similar sample statistics for the data portion of interest (summarized into a data covariance matrix). This first section of this tutorial explains how to obtain a noise covariance estimate from MEG empty room recordings.
Contents
Noise covariance
Instrumental noise ("sensor noise") can be readily captured in MEG using two or more minutes of empty room measurements. We encourage the use of noise recordings collected the same day as the subject's recordings (if possible just before the session) and pre-processed in the same manner (with same sampling rate and same frequency filters applied) as the participant data. In this study we have already prepared a 2-min segment of noise recordings that we will use to estimate noise covariance sample statistics.
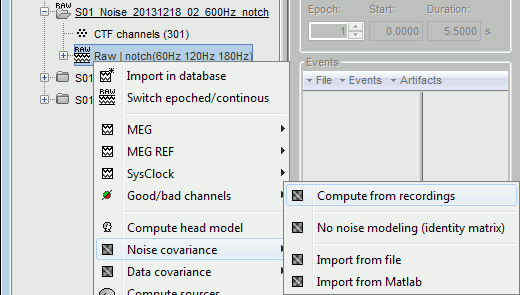
Right-click on the entry for noise recordings > Noise covariance. Available menus:
Compute from recordings: Use the selected recordings to estimate noise covariance statistics.
No noise modeling: Use an identity matrix as noise covariance. This option is useful when no noise recording is available (e.g. ongoing EEG without any baseline of no interest).
Import from file: Use noise covariance statistics available from another source (e.g., obtained using the MNE software.)
Import from Matlab: Import any [Nchannels x Nchannels] matrix as noise covariance matrix from the Matlab workspace.
Select the menu Noise covariance > Compute from recordings. Available options:
Files: The top part of this window shows a summary of the files that have been selected to estimate the noise: 1 file of 120s at 600Hz. Total number of time samples in selected file: 72,000. We can also choose to use only a portion of this file, with the option "baseline". The large continuous files are split in blocks of a maximum of 10,000 samples that are then processed as different files.
Remove DC offset: All the selected blocks of data are baseline corrected and concatenated to form a large matrix "F". There are two options for baseline correction:
Block by block: The average value of each channel is subtracted from each block before concatenating files together. Let Fi contain data from block #i:
F = Concatenate[Fi - mean(Fi)].Global: The average value of each channel is removed after concatenation (same correction for all blocks): F = Concatenate[Fi] - mean(Concatenate[Fi]).
The sample noise covariance is computed from F: NoiseCov = F * F' / Nsamples
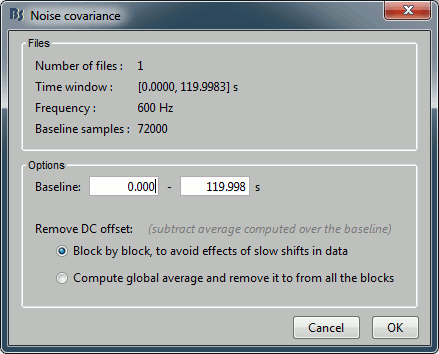
For this tutorial, keep the default options and click on [OK].
- One new file is created and appears under the noise data folder, next to the channel file. The corresponding contextual menus are:
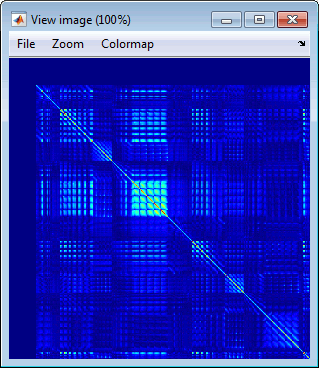
Display as image: Opens a display of the noise covariance matrix as an indexed image (same as double-click on file). This can be useful to quickly control the quality of the recordings: for instance, noisier channels appear as rows/columns marked in red.
Copy to other folders: Copy the file obtained to all the other folders of the same subject, to avoid re-computing the noise covariance statistics again for each folder from the same session.
Copy to other subjects: Copy this file to all the folders of all the subjects in the protocol.
You can also copy a noise covariance file to another folder just like any other file:
Right-click > File > Copy/Paste, or keyboard shortcuts Ctrl+C/Ctrl+V.
Right-click on the the noise covariance file > Copy to other folders: We need this file in the two folders where the epochs were imported before we compute the respective source models.
Variations on how to estimate sample noise covariance
The sample noise covariance matrix is straightforward to obtain. Brainstorm's interface features a lot of flexibility to select the files and time windows used to calculate the sample statistics. You need to have a clear understanding of the concept of "noise" to pick the best possible option. We support the notion that noise covariance accounts for contaminants that remain present in the data after preprocessing is complete. Hence it is not meant to account for eye blinks, heartbeats, muscle artifacts, flat or bad channels and noisy segments: all of these need to be taken care of during previous preprocessing steps, as show in previous tutorial sections. The noise covariance entry is to account for remaining and stationary instrumental, sensor and environmental noise components. For this reason, the ideal scenario is to use segments of recordings that contain exclusively this type of contaminant, or segments of recordings deemed not to contain any of brain signals of interest. This section is advanced reading material that can be used as a reference in a different experimental context.
The case of MEG
From empty-room recordings: actual noise measurements (due to the instrument, environment) using empty-room conditions (no subject under the MEG helmet) are possible in MEG. We recommend you obtain 2 to more minutes of empty-room data right before bringing the subject in the MEG room, or right after the experiment is finished.
You can verify quantitatively how stable and reproducible is the noise covariance estimated (e.g., during the day/week). The MEG system may be located in a "quiet environment", allowing that you re-use the same noise recordings and therefore, noise covariance matrix, for all runs and subjects acquired on the same day.
From resting-state segments: When studying evoked responses (aka event-related responses), you may want to collect a few minutes of recordings where the subject is resting, i.e. not performing the task. Using these segments to obtain the noise covariance estimates implies that resting brain activity will be assumed as "noise", which we know now is not the case. We therefore encourage MEG users to acquire short empty-room runs instead.
From pre-stimulus baseline: Using concatenated pre-stimulation baseline segments from individual trials is in principle similar to the previous scenario, hence has similar limitations: regions prominently active during pre-stimulation baseline will tend to be attenuated by source analysis.
The case of EEG
It is less straightforward to estimate sensor noise from EEG data, because the electrodes need to be attached to a conductive medium (i.e. the scalp) to produce signals. Therefore only the last two options shown above in the MEG section are possible in EEG:
resting baseline and pre-stimulation baseline.
EEG noise levels depend on the quality of the electrode connection with the skin. It varies considerably between subjects, and during acquisition. Indeed, the conductive gel/paste/solution used for contact tends to dry up, which affects impedance. The electrode cap/locations can also move slightly, depending on how cooperative the participants. To account for variable noise levels between subjects, it is therefore preferrable to use one channel file per subject, because it allows the definition of one noise covariance entry per participant. In some specific cases, if the quality of the recordings varies a lot over time, it is preferrable to segment long recordings into shorter runs, and obtain different noise covariance matrices for each.
EEG in resting-state conditions
If the target brain activity to your experiment is resting, resting segments cannot be used to obtain noise statistics. For MEG, use empty-room measurements as explained above. For EEG, there are possible options: use sensor variance estimates, or avoid estimating empirical noise statistics.
Option #1: Calculate noise covariance over a long segment of resting recordings, but save only the diagonal elements, i.e. the variance measured at each sensor. This option is available in Brainstorm's advanced options of source computation: select the option "Diagonal noise covariance".
Option #2: Select "No noise modeling" in the contextual menu. This option uses the identity matrix as noise covariance matrix, and therefore assumes equal, unit variance of noise on every sensor. In inverse modeling, this is equivalent to assuming that noise is homoskedastic, and equivalent on all sensors. With this latter option, if data quality is not even on all electrodes, a higher noise level on some sensors may be explained with stronger, spurious source activity.
Epilepsy
Interictal spikes are often considered as events of interest in epilepsy studies. In that respect, they can be considered as a form of brain activity evoked by the epileptogenic process, very much like a stimulus-related response. For this reason, one shall be cautious about how to define noise conditions from ongoing EEG or MEG recordings to study epilepsy. Defining a segment of time adjacent to the spike as "background noise" is certainly not justified. In practice, however, one often uses a data segment clear from visible interictal activity. As discussed above, MEG has the additional, preferred option of using empty-room data as a baseline - an option not available with EEG.
The same options as above are available to the epilepsy researcher:
Option #1a: Estimate noise covariance statistics from blocks of recordings away from the peak of any identified interictal spike, and keep only the diagonal (the variance of each sensor time series). This option is available in Brainstorm's advanced options of source computation: select the option "Diagonal noise covariance".
Option #1b: If a large period of time clear of visible interictal events is available, use this latter to estimate the full noise covariance array.
Option #2(MEG): Use empty-room data as baseline.
Option #3: Select "No noise modeling" in the popup menu (identity matrix, unit variance of noise on every sensor).
Recommendations
Long noise recordings: In order to obtain a more accurate estimation of the noise covariance, a sufficiently large number of time samples is required: at least N*(N+1)/2 samples, (N is the number of sensors.) This amounts to 40s of data for CTF275 recordings at 1000Hz, or 20s for 128-channel EEG at 500Hz. Remember to always use as much data as possible to estimate noise covariance statistics.
Do not use signal averages: For this reason, you should never compute the noise covariance matrix from averaged responses. If you want to import recordings that you have fully pre-processed with another program, we recommend you import the individual trials and use them to estimate noise covariance. If you can only import the averaged responses in Brainstorm, please be aware that you may under estimate noise levels and bias source results.
Using one block: If you want to use a segment of "quiet" recordings in a continuous file: right-click on the continuous file > Noise covariance > Compute from recordings, then copy the noise covariance to the other folders. This is the case described in this tutorial.
Use single trials: If you want to use the pre-stimulation baseline from single trials, first import the trials in the database, then select all the groups of imported trials at once, right-click on one of them > Noise covariance > Compute from recordings, and finally copy the file to the other folders.
Using multiple continuous blocks: This is similar to the single trial case. Import in the database all the blocks you consider as quiet resting baselines, then select all the imported blocks in the database explorer > Noise covariance > Compute from recordings.
Data covariance
Beamforming source mapping further requires the estimation of data covariance statistics. The LCMV beamformer uses an estimated data covariance matrix to compute spatial filters that define the beamformer. It is important that this covariance matrix contains contributions from all sources that contribute to the data over the time window to be analyzed (signal + noise).
We have found, as have others, that it is important to use a relatively long time window for robust beamformer performance. This also helps to avoid numerical instability when inverting the data covariance, as required in computing the beamformer kernel matrix. Our recommendations:
Evoked responses: Use a window that spans prestim through the end of the response of interest, with a minimum of 500ms total duration.
Spontaneous data: Use the full time window to be analyzed, with a minimum of 30s of data.
The procedure to compute the data covariance is very similar to the noise covariance:
For run#01, select all the trials, right-click > Data covariance > Compute from recordings.
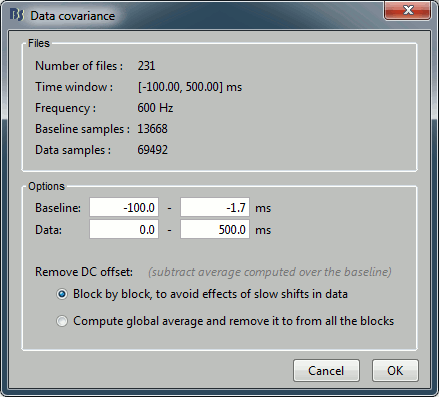
We need to specify two time windows:
Baseline: Pre-stimulus time, used for DC offset correction (subtracts the baseline mean).
Data: Time segment of interest (let's use all the time available post-stimulus in this tutorial example).
Repeat the same steps for run#02.
On the hard drive
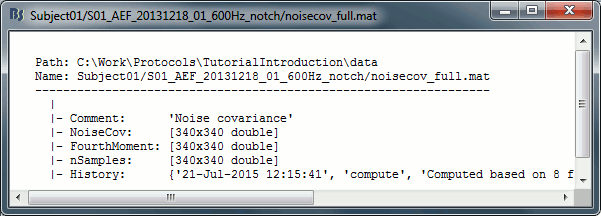
Right-click on any noise covariance file > File > View file contents:
Structure of the noise/data covariance files: noisecov_*.mat / ndatacov_*.mat
Comment: String displayed in the database explorer to represent this file.
NoiseCov: [nChannels x nChannels] noise covariance: F * F' ./ (nSamples-1)
Unknown values are set to zero.FourthMoment: [nChannels x nChannels] fourth order moments: F.^2 * F'.^2 ./ (nSamples-1)
nSamples: [nChannels x nChannels] number of time samples that were used for each pair of sensors. This is not necessarily the same value everywhere, some channels can be declared as bad only for a few trials.
Related functions
process_noisecov.m: Function for process "Sources > Compute covariance (noise or data)"
bst_noisecov.m: Computes the data/noise covariance matrices.
panel_noisecov.m: Options panel.
Additional documentation
Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718
Forum: Data covariance and number of trials: https://neuroimage.usc.edu/forums/t/34094