Phase-amplitude coupling

This tutorial introduces the concept of phase-amplitude coupling (PAC) and the metrics used in Brainstorm to estimate it. Those tools are illustrated on three types of data: simulated recordings, rat intra-cranial recordings and MEG signals.

Contents

  1. Phase-amplitude coupling (CURRENTLY BEING UPDATED - UNFINISHED)
  2. Simulated recordings
  3. Rat recordings
  4. MEG recordings (CURRENTLY BEING UPDATED - UNFINISHED)

Phase-amplitude coupling (CURRENTLY BEING UPDATED - UNFINISHED)

Introduction

The oscillatory activity in multiple frequency bands is observed in different levels of organization from micro-scale to meso-scale and macro-scale. Studies have been shown that brain functions are achieved with simultaneous oscillations in different frequency bands [Schutter and Knyazev, 2012]. Classical studies in this field were only focused on rhythms in each of these frequency bands, and it has been reported that these rhythms are linked to perception and cognition [Cohen, 2008]. However, it is revealed that not only examining brain activity in each single frequency band, but also the relation and interaction between oscillations in different bands, can be informative in understanding brain function. Thus, this concept increasingly receives interest especially in the field of cognitive neuroscience. This interaction between several oscillations is also known as cross-frequency coupling (CFC).

Two forms of recognized CFC in brain rhythms are: phase amplitude coupling (PAC), and phase-phase coupling (PPC). In the first type, which is also called nested oscillations, the phase of the lower frequency oscillation (nesting) drives the power of the coupled higher frequency oscillation (nested), that results in synchronization of amplitude envelope of faster rhythms with the phase of slower rhythms. The second form is amplitude independent phase locking between n cycles of high frequency oscillation and m cycles of low frequency one. That's why it is also called n:m phase synchrony [Palva et al., 2005].

Among these two types, phase amplitude coupling received more interests. It has been shown that behavioral tasks can modulate the phase amplitude coupling [Voytek et al., 2010], and also it is potentially involved in sensory integration, memory process, and attentional selection [Lisman and Idiart, 1995, Lisman, 2005, Schroeder and Lakatos, 2009]. This coupling is observed in several brain regions including hippocampus, basal ganglia, and neocortex; and these observations are reported in rats, mice, sheep, and monkeys, as well as humans [Tort et al., 2010].

Following figure shows a schematic of phase amplitude coupling. In the top signal, we have sum of a fast and slow oscillation where the power of fast oscillation's envelope changes with the phase of slower oscillation, which is a sample of PAC. The bottom signal shows only the fast oscillation and the variation in its power. As it is obvious from comparison of two signals, the fast rhythm's power is always maximum, at a certain phase of slower oscillation, this phase is called coupling phase.

schematic.jpg

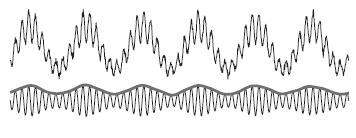
Measures of cross frequency phase amplitude coupling can monitor the relationship between the activities that modulate low frequency oscillations like sensory or motor inputs, and the local cortical activities such as local computations that are correlated to amplitude of higher frequency oscillation [Canolty and Knight, 2010].

All these interesting features of this coupling, resulted in proposing several methods for its measuring. Each of these methods has limitations and advantages in comparison to others, and can be used for a particular purpose; that's why no preferred standard method has been chosen for this estimation yet [Tort et al., 2010]. One of these methods which is implemented in brainstorm is called Mean Vector Length (MVL), proposed by Canolty et al. (2006). This method, and the step by step instruction of using it is described in this section of the tutorial.

A measure of PAC: Mean Vector Length (Modulation Index)

Canolty et al. (2006) pointed out that a time series defined in the complex plane by A_f_A x exp(i \phi_f_p) could be used to extract a phase-amplitude coupling measure. In this formula A_f_A is the envelope of fast oscillation, and \phi_f_p is the phase of slow oscillation.

Therefore, after filtering in fast and slow oscillation, and extracting the phase of slow, and the amplitude of fast rhytm; each instantaneous fast oscillation amplitude point is represented by the length of the complex vector, whereas the theta phase of the time point is represented by the vector angle (see following figure).

mvl_step3.jpg mvl_steps.jpg

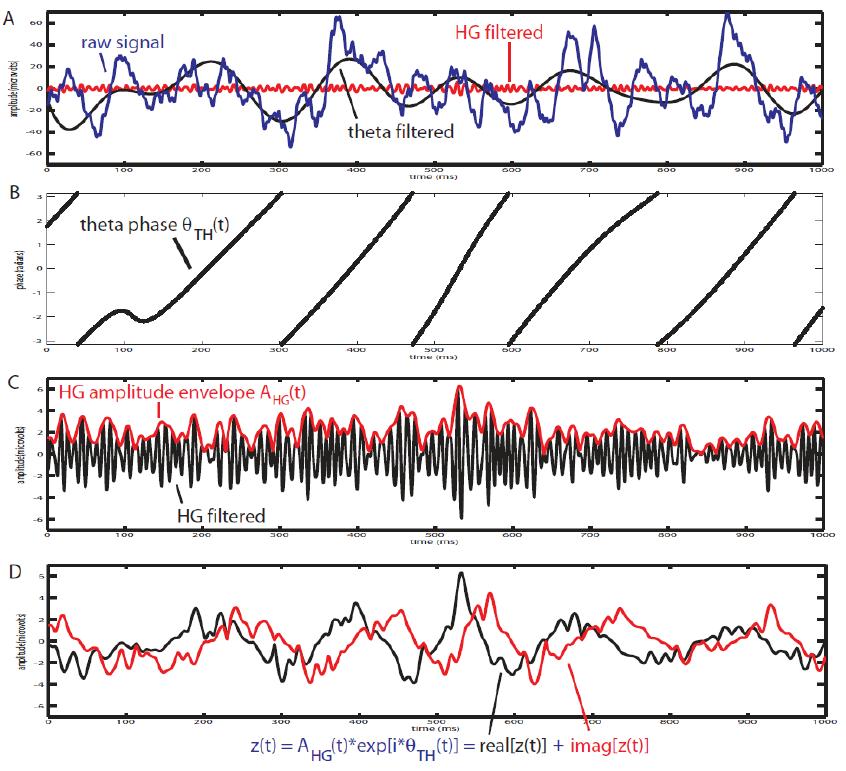
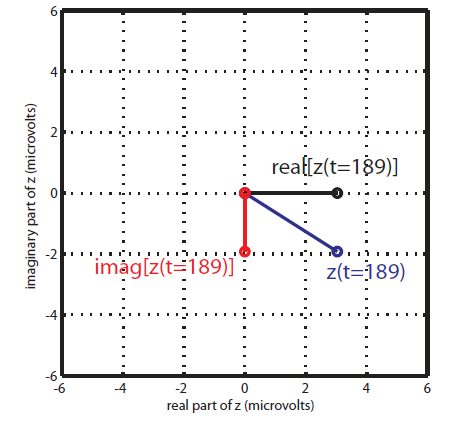
In the case of an absence of phase-amplitude coupling, the plot of the .... time series in the complex plane is characterized by a roughly uniform circular density of vector points, symmetric around zero, because the AfA values are on average the same for all phases .... If there is modulation of the f_A amplitude by the f_P phase, this means that A_f_A is higher at certain phases than others. This higher amplitude for certain angles will lead to a “bump” in the complex plane plot of the ... time series, leading to loss of symmetry around zero. This loss of symmetry can be inferred by measuring the length of the vector obtained from the mean over all points in the complex plane. It is thus assumed that a symmetric distribution as it occurs during lack of coupling leads to a small mean vector length (because the points in the different phases would cancel each other), whereas the existence of coupling leads to a larger mean vector length [Tort et al. 2010]. For more detail read [Canolty et al, 2006].

References:

Canolty, R. T., Edwards, E., Dalal, S. S., Soltani, M., Nagarajan, S. S., Kirsch, H. E., Berger, M. S., Barbaro, N. M., & Knight, R. T. (2006).High gamma power is phase-locked to theta oscillations in human neocortex. science, 313(5793), 1626-1628.

Palva, J. M., Palva, S., & Kaila, K. (2005). Phase synchrony among neuronal oscillations in the human cortex. The Journal of Neuroscience, 25(15), 3962-3972.

Schutter, D. J., & Knyazev, G. G. (2012). Cross-frequency coupling of brain oscillations in studying motivation and emotion. Motivation and emotion, 36(1), 46-54.

Tort, A. B., Komorowski, R., Eichenbaum, H., & Kopell, N. (2010). Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. Journal of neurophysiology, 104(2), 1195-1210.

Simulated recordings

Step-by-step instructions with as many screen captures as possible: generation and analysis of the signals.

Generation of simulated data

To generate the simulated data, follow the steps below:

Analysis of simulated data

Rat recordings

How to download the data.

Step-by-step instructions to analyze the recordings.

MEG recordings (CURRENTLY BEING UPDATED - UNFINISHED)

Step-by-step instructions to analyze the wMNE source signals for Phase Amplitude Coupling.

In order to do this part of the tutorial you will need to get the file sample_resting.zip from the Download page.

Preparation of the anatomy, basic pre-processing and source modeling will be only mentioned briefly and will be similar to the continuous recordings tutorials found here: Continuous Recordings Tutorial

Step 1: Pre-processing

The basc pre-processing steps will be outlined briefly here. If you you require more information than the overview provided here, detailed description and guidance for all the steps can be found in the Continuous Recordings tutorial or within the tutorials for the '12 Easy steps for Brainstorm', all of which are available from this page: Tutorials

Before doing Phase amplitude coupling analysis we need the pre-processed files to analyze. We need to:

First steps

Anatomy

[ATTACH]

You now need to define the fiducial points

Functional data

Pre-Processing

All data should be pre-processed and checked for artifacts prior to doing analyses such as PAC (including marking bad segments, and correcting for artifacts such as eye blinks and heartbeats with SSPs). For the purposes of this tutorial, we will artifact correct with SSPs but will not go through marking out bad sections. When using your own data reviewing the raw data for bad sections and using clean data is of the utmost importance.

SSPs for cardiac and eye artifact. Signal Source Projection (SSPs) are a method in brainstorm for projection away stereotyped artifacts (such as eye blinks and heartbeats) out of the functional data.

[ATTACH]

Regarding sin removal: PAC analysis involves examining a very wide band of frequencies, often the examining the entire range of 2Hz - 150Hz or more. This band contains the frequencies contaminated by line noise, of either 50 or 60 Hz and their harmonics. Brainstorm offers tools to remove line noise from functional data.

Here we will not do sin removal for time efficiency and also because it is not required for accurate PAC analysis.

The PAC function looks for high frequencies occuring specifically certain phases of low signals such that the ubiquitous nature of line contamination effectively cancels it out for being identified as PAC. (Similarly, doing sin removal results in no 60 Hz anywhere, such that the function also identifies no PAC).

To demonstrate that we can safely proceed without sin removal, consider the following PAC maps performed on the same time series with the only difference being line noise removal on one data set. The time series on the left is the raw signal and the time series on the right had sin removal performed (60Hz and 120Hz).

[ATTACH]

Best practice regarding line noise removal and PAC estimates is: ???

Importing

Once the data is pre-processed and ready for further analysis we will now import the data into Brainstorm, project the sources and do the PAC analysis

[ATTACH]

Note: importing this long recording will create a new large file (~3 gb) and may take a couple minutes.

Project Sources

The imported file should have saved as a new condition in our tree in the brainstorm database. At this point we still have the sensor data and now want to project the data into source space. We will need a head model and noise covariance matrix (as well as the imported anatomy) in order to do this.

Head Model

Noise covariance: In the original zip download folder there is an empty room recording from when this data was collected. It is labelled XXXX

[ATTACH]

We are now ready to run the PAC analysis.

Step 2: Using the PAC Function - the Basics

Once you have the sources projected onto the anatomy proceed with the following instructions to use the PAC function on the source data.

The PAC function in Brainstorm is not time resolved, but will analyze any given time series for any stable occurence of PAC over any time segment you give it. This can be done at the sensor or source level for and EEG or MEG data. Here we will analyze the source data, by giving the function the time series of the vertices of our projected data.

The Function

[ATTACH]

Process Options

Once you click on 'Phase-amplitude coupling' you should get an options box with the following options.

[ATTACH]

We will first demonstrate the process by computed the PAC for a single vertice (a single time series in source space). This will allow us to examine what the PAC process does and visualize the result.

[ATTACH]

[ATTACH]

[ATTACH]


The full PAC comodulograms contain a lot of information, especially considering that we have this amount of information for every time series.

You need not save the full PAC maps when doing this analysis - the MaxPAC function offers the option to save only the values at the maxPAC - at the frequency pairing with the highest coupling strength. This examines the time series for the maximally coupled pairing and then saves only the results related to that value. It is no quicker, but saves much smaller files.

To demonstrate this, we can re-run the same PAC analysis on the same time series, but unselect the 'Save full PAC maps' options. (You can do this if you wish, but if it is a long computation on your system you can look at the result below - it is simply another representation of the same data in the 'Full' file).

Using the maxPAC in this manner saves nothing that can be visualized, and double clicking on the resultant file simply opens the file contents, which contains the 4 values of interest computed by the maxPAC function.


[ATTACH]


If you are unfamiliar with these tables, it is the 'File Contents' table available for every file in the Brainstorm database by right clicking - file - view file contents.It contains path and name of the actual file on the computer as well as some summary information of everything in the file.

Relevant MaxPAC information in File Contents

This is a much more efficient way of saving and representing a small part of the data and pulling out the main mode of PAC in any time series. The caveat is (as we can see in the example map of vertex # 224) that pulling out only the strongest pair may not be particularly representative of the overall PAC in the time series. In this special case, where the difference in coupling strength between f-low of 11.47 and 8.30 is likely to be statistically insignificant it may be somewhat arbitrary which pair is picked.

The vertex used here is something of an anomaly in that most of the time there is a much more obvious single pairing apparent in the PAC maps. When doing PAC analysis you should consider the relevance and importance of finding only the maxPAC pair for your hypothesis and guide your analysis accordingly.

Step 3: Verifying with Canolty Maps

Canolty maps are a type of Time Frequency decomposition that offer another way to visualize the data and serve as a complimentary tool to visualize and assess Phase-Amplitude Coupling. Currently there are no significance tests in Brainstorm that can give a measure if PAC is significant in a given time series, but the Canolty maps provide an important way to verify and corroborate the results of the PAC process.

Canolty maps are a kind of time frequency decomposition in which the zero point of the map is lined up to the trough of a low frequency of interest. Conceptually, it lines up the data to a specific low frequency so as to visualize what happens in the power spectrum related to the phase of the low frequency. More concretely, it filters the data to extract the low frequency of interest, marks each trough as an 'event', extracts a time window around each 'event' and averages over all of them. The colormap of the Canolty map represents power in relation to the mean power. By representing a time frequency map in relation to a low frequency, we can visualize whether the power of any high frequencies fluctuates systematically with the phase of the low frequency (basically - we can visualize PAC). If there is PAC present, we should see quite stereotyped stripes of the power of certain high frequencies changing consistently with the phase of the low frequency. If there is no PAC there will be no discernable pattern (the map will just look like a 'mess').

Canolty maps are named after the author of the paper in which they were published, entitled 'High gamma power is phase-locked to theta oscillations in human neocortex' by Canolty & Knight which appeared in Science in 2006.

The Function

The Canolty Map's function is also found in the Frequency tab from the process functions.

[ATTACH]

There are two ways to use Canolty maps - you can manually input a low frequency of interest or you can give it the maxPAC file and it will take the low frequency at the maxPAC value.

We will continue by doing the Process2 version to compliment our maxPAC results.

[ATTACH]

[ATTACH]


When you click on the Canolty Maps (process2) function you should get a an options box like this.

[ATTACH]

Process Options

The only difference in the Process1 version of Canolty Maps is the additional required field of Nesting Frequency. In this case you can enter in any low frequency of interest with which to compute the Canolty Map(s).

[ATTACH]

[ATTACH]

[ATTACH]

[ATTACH]

[ATTACH]

[ATTACH]

[ATTACH]

/!\ Edit conflict - other version:

/!\ Edit conflict - your version:

/!\ End of edit conflict

You may remember that in the PAC comodulogram for vertice 224 the maxPAC value was at 11.47 Hz but that there was also other areas of high PAC, including an almost equal coupling intensity at 8.3 Hz. Canolty maps only portray information relevant to the low frequency used to create the map - therefore we cannot make any conclusions about PAC at low Freq = 8.3 with the Canolty map we have made with low Freq = 11.47 Hz.

We will now examinethe PAC at lowFreq = 8.3 with a new Canolty map using the Process1 version. Since 8.3 Hz is not the low frequency at the maxPAC pairing in the maxPAC pair we cannot examine this by giving the maxPAC file, we must manually specify it as a low frequency of interest.

[ATTACH]

[ATTACH]

[ATTACH]


[ATTACH]


An alternative check we can use Canolty maps is to verify that in the case where the PAC function indicates very low levels of Phase-amplitude coupling, that the Canolty map function also corroborates this.

[ATTACH]

[ATTACH]

You should notice that the Process1 version of canolty maps can be done on any time series without ever doing the exhaustive PAC process. However, since Canolty maps only use one low frequency of interest, this is not a very efficient approach (unless you have a specific frequency of interest, such as in a frequency tagging paradigm).

Step 4: 'Advanced' PAC analysis

By now you should have a pretty good idea of how to use the PAC process, what it gives out and how to check these results with the complementary Canolty maps process. The 'advanced' aspect is not a question of increased difficulty but simply of increased scale. We have been working with a single time series here. It is likely that PAC analysis you perform will want to look at much larger sets of data.

This basically comes down to filling in the 'Source indices' option for the PAC process. Option for this:

Options for reducing computation time

When you run a file with multiple time series and open it (with full PAC maps) it will open the map of the first time series, in the same way as if you only had one. In the Brainstorm window there is a 'Selected data' option to go to any time series of interest. You can also scroll through the maps using the up and down arrows on the keyboard.

[ATTACH]

The same things all apply for using the Canolty process.

Experiment as you want using the PAC function with inputs of multiple time series.

Tutorials/TutPac (last edited 2014-01-17 21:58:41 by jamy)