Phase-amplitude coupling
Authors: Soheila Samiee, Thomas Donoghue, Francois Tadel, Sylvain Baillet
This tutorial introduces the concept of phase-amplitude coupling (PAC) and the metrics used in Brainstorm to estimate it. Those tools are illustrated first on simulated recordings. In separate tutorials, we illustrate how to use them on resting-state MEG recordings and rat intra-cranial signals.
Introduction
Phase-amplitude coupling
The oscillatory activity in multiple frequency bands is observed in different levels of organization from micro-scale to meso-scale and macro-scale. Studies have been shown that brain functions are achieved with simultaneous oscillations in different frequency bands [Schutter and Knyazev, 2012]. Classical studies in this field were only focused on rhythms in each of these frequency bands, and it has been reported that these rhythms are linked to perception and cognition [Cohen, 2008]. However, it is revealed that not only examining brain activity in each single frequency band, but also the relation and interaction between oscillations in different bands, can be informative in understanding brain function. Thus, this concept increasingly received interest especially in the field of cognitive neuroscience. This interaction between several oscillations is also known as cross-frequency coupling (CFC).
Two forms of recognized CFC in brain rhythms are: phase amplitude coupling (PAC), and phase-phase coupling (PPC). In the first type, which is also called nested oscillations, the phase of the lower frequency oscillation (nesting) drives the power of the coupled higher frequency oscillation (nested), that results in synchronization of amplitude envelope of faster rhythms with the phase of slower rhythms. The second form is amplitude independent phase locking between n cycles of high frequency oscillation and m cycles of low frequency one. That's why it is also called n:m phase synchrony [Palva et al., 2005].
Among these two types, phase-amplitude coupling received more interests. It has been shown that behavioral tasks can modulate the phase amplitude coupling [Voytek et al., 2010], and also it is potentially involved in sensory integration, memory process, and attentional selection [Lisman and Idiart, 1995, Lisman, 2005, Schroeder and Lakatos, 2009]. This coupling is observed in several brain regions including hippocampus, basal ganglia, and neocortex; and these observations are reported in rats, mice, sheep, and monkeys, as well as humans [Tort et al., 2010].
Following figure shows a schematic of phase amplitude coupling. In the top signal, we have the sum of a fast and slow oscillations, where the power of fast oscillation's envelope changes with the phase of the slower oscillation, which is a sample of PAC. The bottom signal shows only the fast oscillation and the variation in its power. As it is obvious from comparison of two signals, the fast rhythm's power is always maximum, at a certain phase of slower oscillation, this phase is called coupling phase.
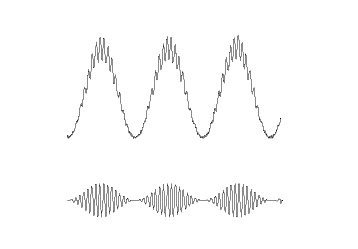
Measures of cross frequency phase amplitude coupling can monitor the relationship between the activities that modulate low frequency oscillations like sensory or motor inputs, and the local cortical activities such as local computations that are correlated to amplitude of higher frequency oscillation [Canolty and Knight, 2010].
All these interesting features of this coupling resulted in proposing several methods for its measuring. Each of these methods has certain limitations and also advantages over the others, and can be used for a particular purpose; that's why no preferred standard method has been chosen for this estimation yet [Tort et al., 2010]. One of these methods, which is implemented in Brainstorm, is called Mean Vector Length (MVL), proposed by Canolty et al. (2006). This method and the step by step instruction of using it is described in this section of the tutorial.
A measure of PAC: Mean Vector Length (Modulation Index)
Canolty et al. (2006) pointed out that a time series defined in the complex plane by 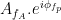 could be used to extract a phase-amplitude coupling measure. In this formula
could be used to extract a phase-amplitude coupling measure. In this formula 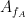 is the envelope of fast oscillation, and
is the envelope of fast oscillation, and 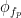 is the phase of slow oscillation.
is the phase of slow oscillation.
Therefore, after filtering in fast and slow oscillation, and extracting the phase of slow, and the amplitude of fast rhytm; each instantaneous fast oscillation amplitude component in time is represented by the length of the complex vector, whereas the slow oscillation phase of the same time point is represented by the vector angle (see following figure).
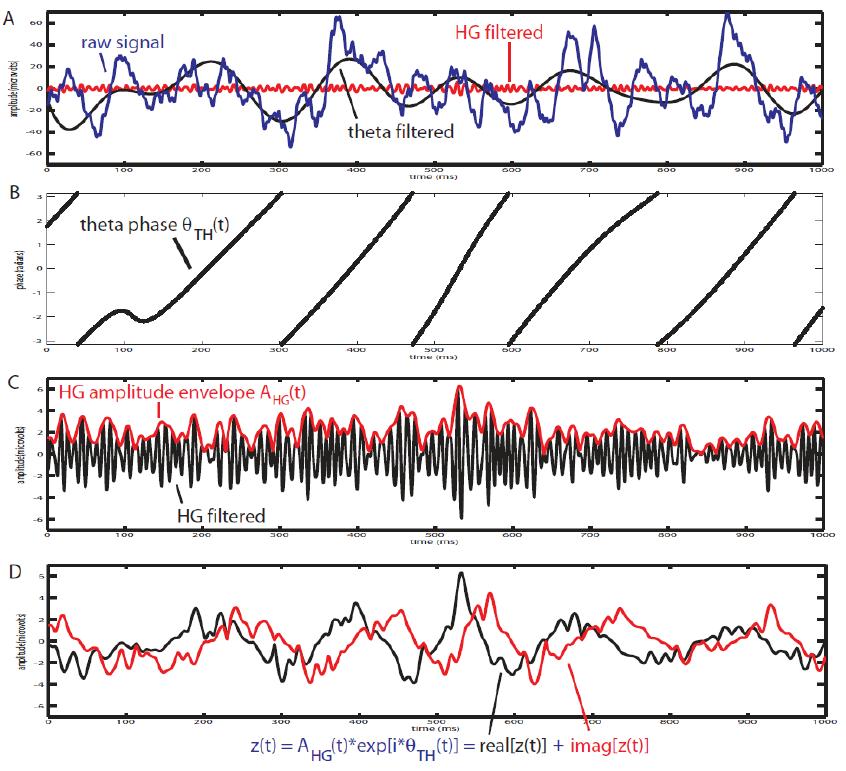
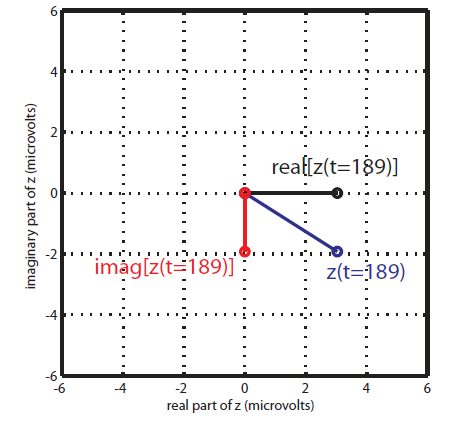
At the absence of phase-amplitude coupling, the plot of the 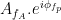 time series in the complex plane is characterized by a roughly uniform circular density of vector points, symmetric around zero, because the
time series in the complex plane is characterized by a roughly uniform circular density of vector points, symmetric around zero, because the 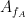 values (averaged over cycles of slow oscillation) are approximately the same for all phases. If there is modulation of the
values (averaged over cycles of slow oscillation) are approximately the same for all phases. If there is modulation of the 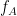 amplitude by the
amplitude by the  phase, the
phase, the 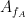 would be higher at certain phases than others. This higher amplitude for certain angles will lead to a “bump” in the polar plot of the
would be higher at certain phases than others. This higher amplitude for certain angles will lead to a “bump” in the polar plot of the 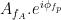 , leading to loss of symmetry around zero. This loss of symmetry can be inferred by measuring the length of the vector obtained from the mean over all points in the complex plane. It is thus assumed that a symmetric distribution as it occurs during lack of coupling leads to a small mean vector length (because the points in the different phases would cancel each other), whereas the existence of coupling leads to a larger mean vector length [Tort et al. 2010]. For more detail read [Canolty et al, 2006].
, leading to loss of symmetry around zero. This loss of symmetry can be inferred by measuring the length of the vector obtained from the mean over all points in the complex plane. It is thus assumed that a symmetric distribution as it occurs during lack of coupling leads to a small mean vector length (because the points in the different phases would cancel each other), whereas the existence of coupling leads to a larger mean vector length [Tort et al. 2010]. For more detail read [Canolty et al, 2006].
References
Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, Berger MS, Barbaro NM, Knight RT (2006). High gamma power is phase-locked to theta oscillations in human neocortex, Science, 313(5793), 1626-1628.
Canolty RT, Knight RT (2010). The functional role of cross-frequency coupling. Trends in cognitive sciences, 14(11), 506-515
Cohen MX (2008). Assessing transient cross-frequency coupling in EEG data. Journal of neuroscience methods, 168(2), 494-499.
Palva JM, Palva S, Kaila K (2005). Phase synchrony among neuronal oscillations in the human cortex. The Journal of Neuroscience, 25(15), 3962-3972.
Schutter DJ, Knyazev GG(2012). Cross-frequency coupling of brain oscillations in studying motivation and emotion. Motivation and emotion, 36(1), 46-54.
Tort AB, Komorowski R, Eichenbaum H, Kopell N (2010). Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. Journal of neurophysiology, 104(2), 1195-1210.
Voytek B, Canolty RT, Shestyuk A, Crone NE, Parvizi J, Knight RT (2010). Shifts in gamma phase–amplitude coupling frequency from theta to alpha over posterior cortex during visual tasks.Frontiers in human neuroscience, 4.
Simulate signals
You can generate a synthesized data containing cross-frequency phase-amplitude coupling, with your preferred parameters. The model used for data generation is a simple method introduced in [Tort et al. 2010]. In this section, we generate a dataset of synthesized signal and analyze it with available phase-amplitude coupling estimation tool in brainstorm.
Select the menu File > Create new protocol > "TutorialPac" and select the options:
"Yes, use protocol's default anatomy",
"No, use one channel file per condition".
Right-click on the TutorialPac folder > New subject > Subject01
In the Process1 tab, leave the file list empty and click on the button [Run]
Select the process "Simulate > Simulate PAC signals".
Set all the parameters as follows:
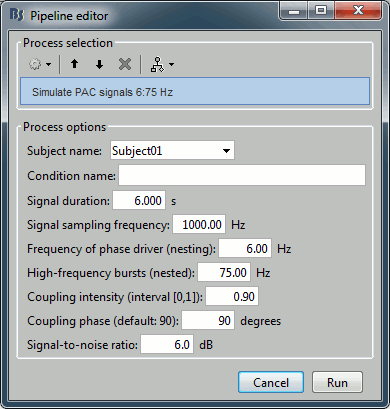
After running the process, you'll get a synthesized data file:
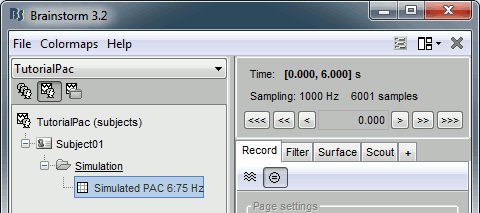
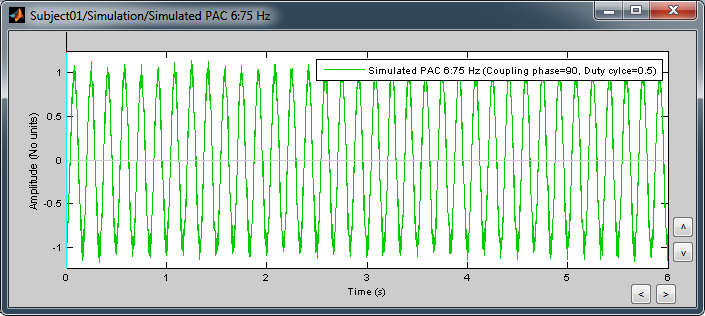
Double-click on it to display the generated signal:
Process options
Subject name: Specify in which subject the simulated file is saved.
Condition name: Specify the folder in which the file is saved (default: "Simulation").
Signal sampling frequency: Sampling frequency of the simulated signal in Hz.
Nested and nesting frequency: Definition of the phase-amplitude coupling.
Coupling intensity: Value between 0 and 1 which determines how coupled the two oscillations are.
Coupling phase: Phase of slow oscillation (phase driver) where we have the maximum envelope of fast oscillation (high frequency bursts). For example, if
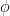 =90 degree, the maximum coupling happens in the peaks of slow oscillation.
=90 degree, the maximum coupling happens in the peaks of slow oscillation. Signal-to-noise ratio: Determines the power of the noise that will be added to the pure coupled oscillations. This noise composed of two parts: a component with 1/f spectrum which simulate the background brains activity, and a white noise which represents the noise of data recording.
PAC estimation
To extract the phase-amplitude coupling from this signal:
Drag the simulated file to the Process1 tab:
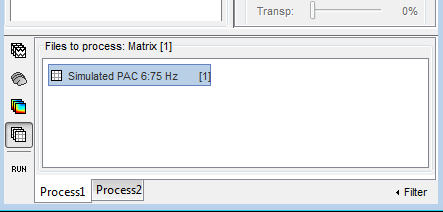
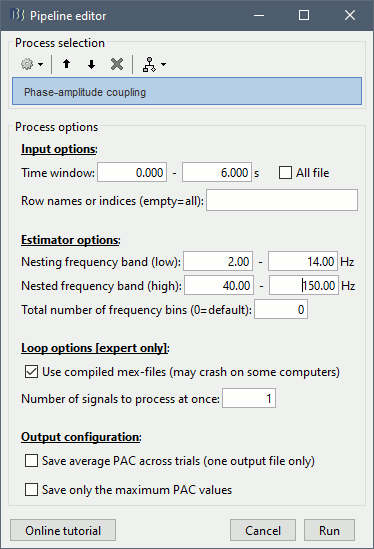
Select the process "Frequency > Phase-amplitude coupling"
Set the parameters as follows:
The PAC map calculated from your simulated signal is saved in a new file.
![[ATTACH] [ATTACH]](/moin_static198/brainstorm1/img/attach.png)
- This coupling map, also known as comodulogram, shows the cross-frequency coupling in frequency domain. The pseudo color of the map indicates the level of coupling between each pair of low and high frequencies. The abscissa represents the frequencies analyzed as phase frequency, while the frequencies for amplitude are represented in the ordinate axis.
Here, in this example, there is a bump around 6-8 Hz for the phase and 70-85 Hz for the amplitude, which contains the pair that we initially used for synthesizing the data.The parameters of the point with maximum coupling intensity in the map will be shown in the title of the figure. These parameters are the maximum pac level, and the corresponding
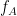 and
and 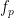 , which are 0.3, 6.14 Hz, and 80.18, respectively Hz in this case.
, which are 0.3, 6.14 Hz, and 80.18, respectively Hz in this case.
Process options
Input options:
Time window: The time segment of the input file to be analyzed for PAC.
Row names or indices: The name of channels to be processed in the case of input files containing multiple signals. If empty, it will process all the signals in the file.
Estimator options:
Nesting frequency band (low): Frequencies to consider for slow oscillation (frequency for phase)
- Can be a wide exploratory range (2-30Hz) or a smaller specific range (theta: 4-8Hz)
Nested frequency band (high): Freq to consider for high freq bursts (frequency for amplitude)
- Can be a wide exploratory range (40-250 Hz) or a smaller specific range (low gamma: 40-80Hz)
- Note: Nested frequencies can only be as high as your sampling rate has the resolution to yield
Loop options: Should be left at default options unless you know how to use them.
Parallel processing toolbox: PAC analysis of each time series (of a vertex or sensor) is independent of the PAC analysis of every other time series. This function is done with a loop and each iteration of the loop is independent of the one previously. The parallel processing toolbox uses a parfor loop in which multiple time series can be processed in parallel. You can consider this option only if you have a lot of RAM available in your computer.
Use mex-files: Compiled mex-files are available for running this process and contribute to speeding up the computation time.
Number of signals to process at once: The file that is given to the function is processed in blocks of signals, and this option signifies how many signals are in each block. Increasing this value can make the process a bit faster but requires a large amounts of memory.
Output options:
Save average PAC across trials: If this box is selected and multiple files have been given to the process, then the process will save the average PAC across all trials in a new file.
- Be careful with this option: although it is offered, averaging over frequencies (such as is required to do this) can be problematic and results from this option should be interpreted carefully.
Save only the maximum PAC value: If this option is selected then only the frequency pair with the maximum PAC coupling is saved for each signal in input (maxPAC), instead of the full PAC comodulogram. The default option is to save all the PAC values for each and every frequency pairing for each and every signal.
- Saving the full PAC maps entails saving a matrix of [Nsignals x 1 x Nfa x Nfp], this will very quickly create very large files. Check this option if the files generated are too large to display, save or process on your computer.
- The maxPAC is not a very stable estimator of the most significant frequency pairing in the comodulograms, so it can be usefull to save all the values for a visual inspection of the full PAC maps.
File contents
The files saved by this process have the same structure as the time-frequency files, with an additional "sPAC" field. To review its contents, right-click on the PAC file > File > View file contents.
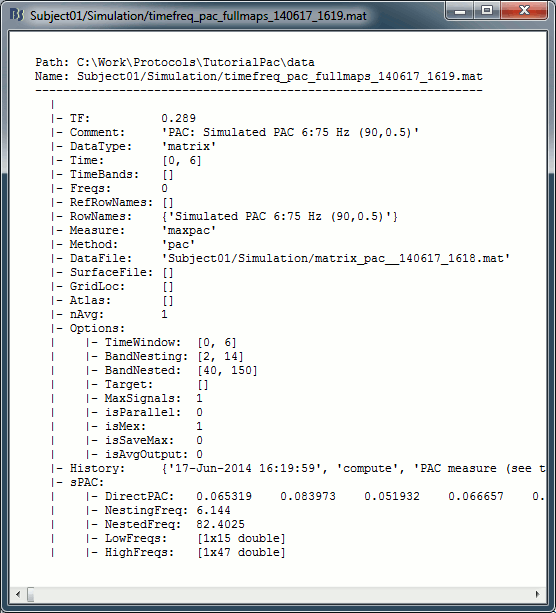
Some of the relevent fields in the maxPAC files:
TF: [Nsignals x 1 x 1], Coupling strength of the maximally coupled frequency pairing (maxPAC)
Options: All the parameters that were given to the process
sPAC: All the additional information related to the output of the PAC function
DirectPAC: [Nsignals x Ntime x Nlow x Nhigh], PAC values for all the frequency pairings
NestingFreq: [Nsignals x 1], Low frequency at the maxPAC
NestedFreq: [Nsignals x 1], High frequency at the maxPAC
LowFreqs: [Nlow x 1], List of low frequencies used for the DirectPAC matrix
HighFreqs: [Nhigh x 1], List of high frequencies used for the DirectPAC matrix
Recommendations
PAC estimation using the MVL algorithm
In order to have a reliable result from this method it is required to use a signal which length is at least ten cycles of the slowest oscillation in your low oscillation band.
Considering this point is more important in analysis of real databases, where the noise level (and/or background brain activity) can be higher than synthesized data, and the coupling intensity can be low. Thus, if you want to examine the coupling for slow oscillations in [2, 14] Hz, it would be better to use a signal with minimum length of 10 cycles of the slowest oscillation, which would be 10 x 0.5 = 5 S.