Deviation maps

Authors: Pauline Amrouche, Raymundo Cassani

This tutorial introduces the implementation of the computation of deviation maps in Brainstorm. This tutorial is based on the results from five subjects of the OMEGA tutorial, as such, before proceeding, please complete the OMEGA tutorial as we will build on its results.

Introduction

Electrophysiology recordings have been used to estimate the brain activity, this is to say source estimation or source mapping. Source mapping have been explored to identify and describe abnormal brain activity patterns in patients with specific clinical phenotypes compared to healthy controls.Normative modelling helps define the healthy range of certain biomarkers and map individual differences at the single-subject level—a concept known as deviation maps.

Several studies have explored the potential of electrophysiology recordings to identify and describe abnormal activity patterns in patients with specific clinical phenotypes compared to healthy controls. Normative modelling has been used to define the healthy range of certain biomarkers and map individual differences at the single-subject level, a concept to which we refer as deviation maps. This approach has been applied in refractory epilepsy using scalp EEG in Janiukstyte et al., 2023 and in identifying new biomarkers for mild traumatic brain injury (mTBI) using MEG in Itälinna et al., 2023 for instance.

In this tutorial, we will create dummy deviation maps from the MEG spectral features of five subjects from the OMEGA tutorial. Four subjects will serve as the reference population, against which the fifth subject will be compared.

Pre-processing

Extract spectral features

Deviation maps can be derived from any statistic defined on a common spatial scale across subjects. In this example, we will extract a feature from the power spectrum computed for each vertex of the cortical surface. The feature is the standard deviation of the power spectrum computed on overlapping short time windows, with the final power for a given frequency bin being the standard deviation of power across all time windows. Additionally, the mean or the coefficient of variation (standard deviation/mean) of the power across time windows can also be analysed. Note that the mean of the power spectra is by definition the power spectrum density (PSD) computed with the the Welch method.

For this tutorial, we will compute the standard deviation of the power spectrum across time windows to illustrate to show how to use the Compute PSD features process. We will use only the first 100 s of the recordings as it is faster and should lead to similar results. Then we project those results from each individual cortex into on the common anatomy. Total processing time is around 6 minutes.

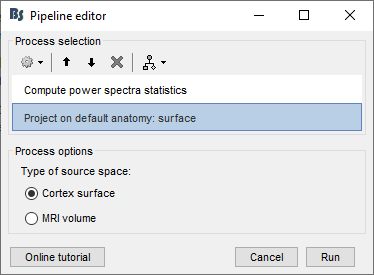
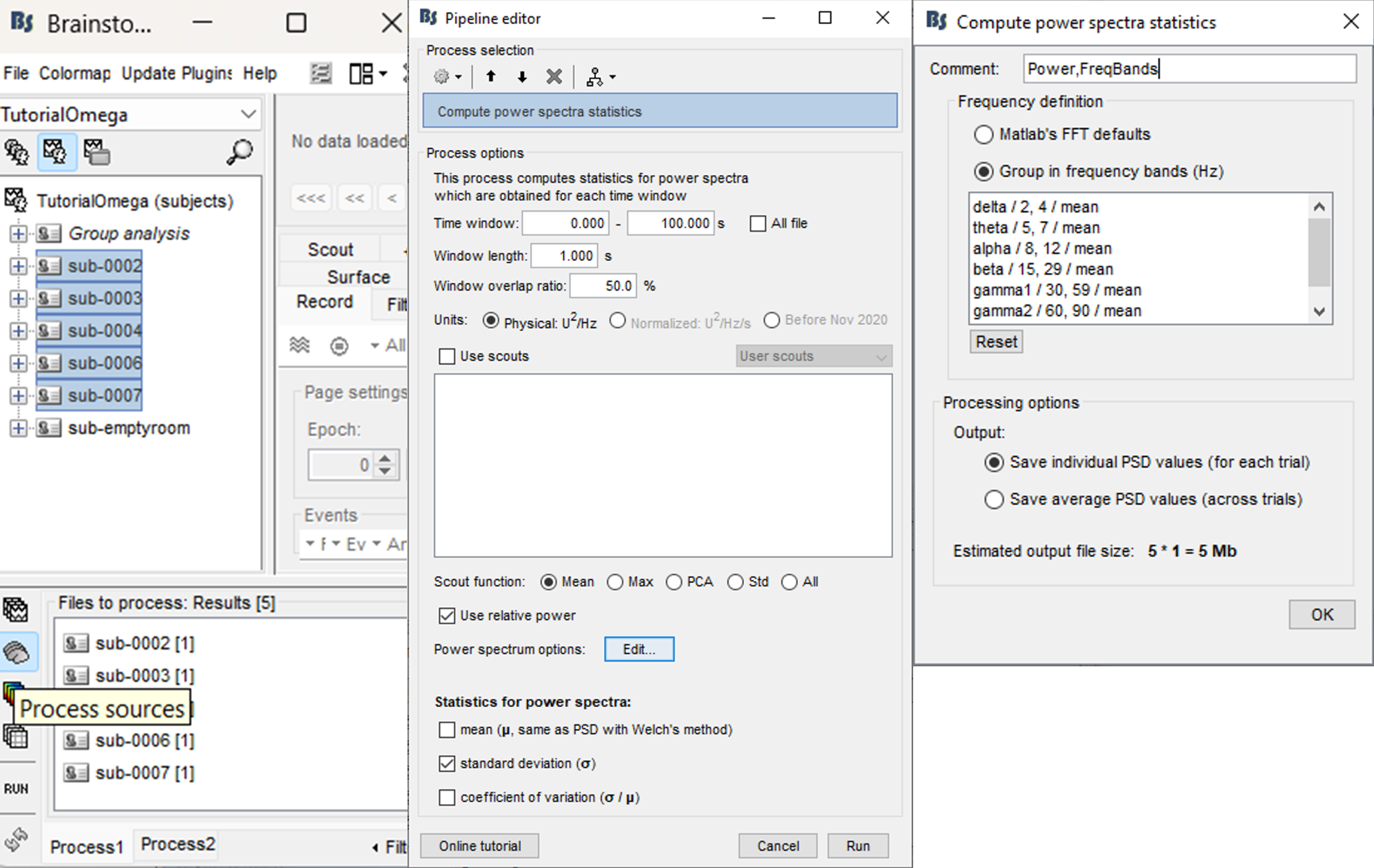
• Drag-and-drop the five subjects (not sub-emptyroom) into the Process1 box and click the [Process sources] button. You should have one file selected per subject.

• Select process: Frequency > Compute PSD features: 0-100s, 1s, 50% overlap, Physical, Extract std, Use relative power, Edit…, Group in frequency bands, Save individual

  • Time window, window length, window overlap ratio, units, scouts, scout function: these options are the same as in the Frequency > Power spectrum density (Welch) process. Link

  • Extract mean: Whether to extract mean feature (across time windows), this is to say the PSD.

  • Extract std: Whether to extract standard deviation (across time windows).

  • Extract varcoef: Whether to extract coefficient of variation (std/mean).

  • Use relative power: Check to consider the relative power (Power frequency bin / Total power) for each window instead of the raw power of the frequency bin.

  • The process returns 1 to 3 files depending on the number of features extracted.

    

• Add process: Sources>Project on default anatomy: Cortex surface.

  • 

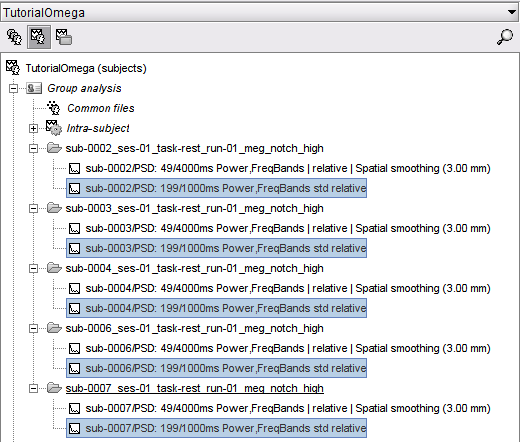
Once the processing is complete, you should see the one PSD file for the extracted PSD feature for each Subject folder in the Group analysis Subject

• 

Deviation maps process

For each of the computed PSD files (standard deviation of power), there is a value for each vertex in the cortical surface and each frequency bin, thus the next step it to create a normative distribution from the values of the reference population (4 subjects in this example). For the subject outside this reference population, we calculate the z-score for the same feature relative to the normative distribution. When considering a given deviation level (d), if the subject's value falls outside the d/2​ and 1−d/2​ quantile interval in the empirical distribution. For example, for example a deviation level of 0.05 leads to the quantiles at 2.5% and 97.5% of the reference distribution. If the feature value falls outside of those quantiles, we flag the (vertex-frequency) point as deviant. This process is repeated for every vertex and frequency, creating the deviation map.

We will now compute the deviation map for subject sub-0002 compared to the reference population (all other subjects).

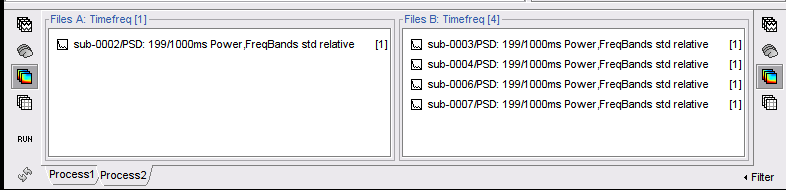
• Click on the Process2 tab

• Drag-and-drop the file sub-0002/PSD: 199/1000ms Power,FreqBands std relative to the FilesA side of the Process2 tab. Which is located ion the Subject Group analysis in the sub-0002_... folder.

• Similar to the step above, drag-and-drop the files sub-000X/PSD: 199/1000ms Power,FreqBands std relative for the remaining four subjects (sub-0003, sub-0004, sub-0006 and sub-0007) to the FilesB side of the Process2 tab.

  • 

• Select process: Test>Compare (A) to normative PSDs (B) :

  • Use log10 values: Whether log10 values of the feature are used. Uncheck

  • Deviation level: 0.5

  • Assume normal distribution of residuals: whether consider the quantiles of a normal distribution rather than the quantiles of the empirical distribution. Uncheck.

  • Test for normality of residuals: If checked will output in the Brainstorm report the ratio of distributions for which the normality hypothesis can be rejected according to Shapiro-Wilk test. If the ratio is too high then the distributions should not be assumed normal.

  • Frequency definition: Definition of the frequency bands, either the same as the input, frequency range or frequency bands defined by the user. Select Same as input

    

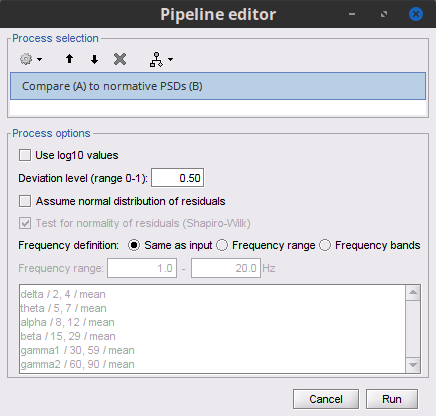
• Run the process.

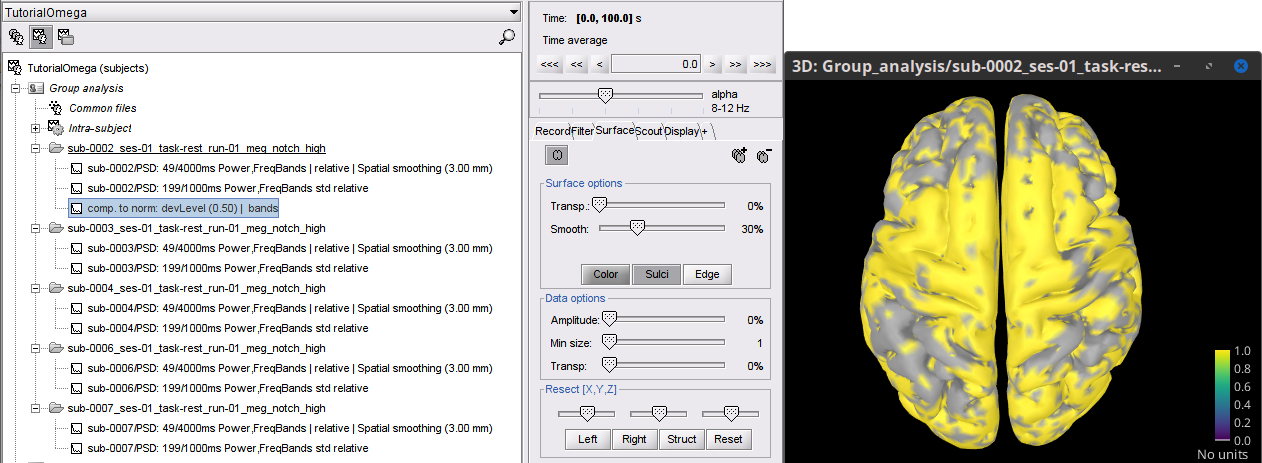
As result there will be a new PSD file: comp. to norm: devLevel (0.50) |  bands in the sub-0002_... folder.

• Open the file "comp. to norm: devLevel (0.50)| bands" for "comparison to normative, deviation level of 0.5, frequency bins by bands". This is the dummy deviation map for sub-0002, every vertex with value 1 falls outsite of the desired quantiles of the normative distribution.

Additional documentation

• V. Janiukstyte et al., ‘Normative brain mapping using scalp EEG and potential clinical application’, Sci Rep, vol. 13, no. 1, p. 13442, Aug. 2023, doi: 10.1038/s41598-023-39700-7.

• V. Itälinna, H. Kaltiainen, N. Forss, M. Liljeström, and L. Parkkonen, ‘Using normative modeling and machine learning for detecting mild traumatic brain injury from magnetoencephalography data’, PLOS Computational Biology, vol. 19, no. 11, p. e1011613, Nov. 2023, doi: 10.1371/journal.pcbi.1011613.

Tutorials

• Tutorial: Source estimation

• Tutorial: Power spectrum

• Tutorial: Omega tutorial

• Tutorial: Statistics