Functional connectivity: Phase Transfer Entropy

Bugs
1

Dear Experts,
I am a junior user of Brainstorm (BTW, congratulations for the tool).
I am inferring the functional connectivity in sources space with the Phase Transfer Entropy (PTE) NxN method using EEG data recorded during sleep.
The source activities, due to the computational complexity of the problem, is averaged before the PTE calculation in 148 scouts with Destrieux parcellation (scoutfunc=mean; scouttime=before). Since I don't have the MRI of the subjects I'm employing an MRI template. For this reason I'm using sources on the cortical surface with unconstrained orientation.

I tried 2 options, normalized PTE and non-normalized PTE but I'm having some trouble interpreting the results I get from the normalized PTE.

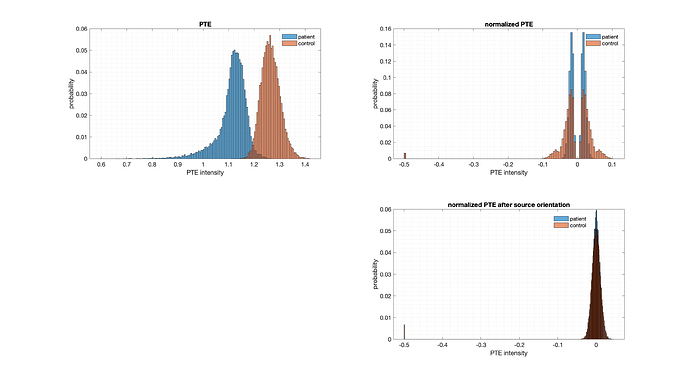
In the Figure attached I plotted an histogram of the obtained non-normalized (top-left) and normalized (top-right) PTE values of 1 control and 1 patient.

Figure
Figure2840×1568 149 KB

Since the graph on the right seemed strange to me I tried to invert the order in which the 2 operations of matrix normalization and source orientation are performed.

So instead of normalizing the PTE matrix (1483 x 1483) and then orienting the sources (absmax function) to get a normalized PTE matrix (148 x 148) I perform first the orientation (snippet 1) and only after the normalization (snippet 2).

Snippet 1 (bst_connectivity.m, line #620)

% Dimension #1
if isUnconstrA
[R, sInputA.GridAtlas, sInputA.RowNames] = bst_source_orient(, sInputA.nComponents, sInputA.GridAtlas, R, UnconstrFunc, sInputA.DataType, sInputA.RowNames);
end
% Dimension #2
if isUnconstrB
R = exchanges(R, [2 1 3 4]);
[R, sInputB.GridAtlas, sInputB.RowNames] = bst_source_orient(, sInputB.nComponents, sInputB.GridAtlas, R, UnconstrFunc, sInputB.DataType, sInputB.RowNames);
R = permutations(R, [2 1 3 4]);
end

Snippet 2 (PhaseTE_MF.m, line #142)

%% Compute dPTE
tmp = triu(PTE) + tril(PTE)';
dPTE = [triu(PTE./tmp,1) + tril(PTE./tmp',-1)];

The result by reversing the operations is shown in Figure (bottom-right)

which seems more interpretable to me.

What do you think? In the case of sources with unconstrained orientation, shouldn't one first orient and only then normalize?

Thank you very much for your support.

Kind regards

Max

2

@Sylvain?

3

Hi Max:

Just for me to understand better: did you apply source orientation after averaging time series across the atlas parcels? If yes, then the orientation is not informative. As a side note, averaging sources across parcels is computationally effective for PTE NxN computations but will be detrimental to sensitivity to higher-frequency components, which will average to zero across the relatively large surface areas of the parcels.

I would recommend to 1) extract source orientations 2) average across parcels and 3) compute PTE / normalized PTE. Alternatively, 2) could be computing exhaustively across all sources and then average PTE values across parcels, if computationally tractable.

I hope this helps.

4

Thank you Sylvain for your prompt response.
Yes, I applied the source orientation after averaging time series across the atlas parcels.
Although, for the sake of clarity, the plots attached above refer to the PTE in the frequency range 1-4 Hz and already at low frequencies one can notice a strange response.

I will try the two options you suggested. The 2. proposal is computationally too expensive even on a cluster. For this case I have to reduce the size of the matrices.

Thank you!

Best regards

Max

1 Like