How can we compute the primary and volume current contributions?
Hi François do you know how?
Some have computed with his software but he put is as excutable script I am not able to see the code.
This is why your community is very good and also helpful because it is open and every one can see the code
Thank you
@John_Mosher @Sylvain @tmedani @juangpc
please do have an answer?
Referencing our paper here: https://neuroimage.usc.edu/paperspdf/IEEEBME99.pdf
Table 1, the EEG and MEG "infinity" models are the contributions of the primary current to the sensor measurement. These models assume no boundaries (infinitely far away), and thus the primary current is the only term. The basic formulas can be seen in eqs (7) and (8) for a single dipole.
However, we are generally not interested in just the contribution of the primary current but rather the total current. Because current MUST be conserved, and the head is bounded, then solutions to the total field can be found as a function of the primary current.
Eq (3) reveals that the magnetic field is the combination of the primary and secondary currents, with the secondary contribution found in the right hand term. Similarly, the eeg potential is shown in (5), which is a more complicated expression of the primary and secondary currents, yielding a difficult formula to be solved, generally numerically.
In a spherical model, the solutions can be found analytically. Eq (10) represents the total magnetic field as a function of strictly the primary current. The secondary currents are absolutely included, but they are now hidden in the overall formula. Compare (10) with (7). So one way to back out just the contribution of the secondary current would be to subtract (7) from (10).
The ultimate contribution of Table 1 was to show that every case of MEG and EEG could be reduced down to a single linear kernel that transfers the primary current into a calculation of the total field or potential.
So in Brainstorm, our head models always calculate the contribution of the total current, both EEG and MEG as a function of just the primary current. We do this current dipole by current dipole in the source grid, for each channel, yielding the "gain matrix" found in the head model.
- John
Thank you @John_Mosher for your reply
so if I want to compute the TP ratio indicated above in the image what should I do?
![]()
so as I understand that t is the gain matrix,
and what about p?
and also v?
how can I get it?
does brainstorm also provide it?
do you know a toolbox that provide them?
I don't believe we calculate eq (7) directly in the brainstorm code, but it should be relatively straightforward for you to program that simple formula for your particular interest. The sensor location and orientations are found in the Channel structure. After you calculate the head model (that is done correctly for the total current), the dipole locations of the source grid can be found in the Head Model structure. Calculate (7) for your particular question, to arrive at the solution for the primary. The contribution from the volume is total - primary.
I don't have a code handy that creates the primary component by itself, but I encourage you to try programming it yourself.
- JOhn
As a follow up to this question of primary and secondary currents and their ratios, you could do the following exercise, using the spherical head model in Brainstorm, to demonstrate the role of primary and secondary currents, without the need to program the primary model. You will need to adjust the dipole orientation or the sensor orientations.
Let's put a dipole on the z-axis ("upward" axis), in a hemispherical array of MEG sensors, spherical head centered on 0,0,0. (See our conference paper https://neuroimage.usc.edu/paperspdf/error_92.pdf or the full journal paper https://www.sciencedirect.com/science/article/abs/pii/001346949390043U where we discuss such theoretical arrays.)
P = scalar magnetic field at the MEG sensor due to the contribution of the primary current.
V = scalar magnetic field at the MEG sensor due to the contribution of the volume current.
T = scalar magnetic field at the MEG sensor due to the contribution of the total current.
From your reference:
Eq(12) is the ratio T/P
Eq(13) is the ratio P/V
-
Regardless of the sensor orientations, orient the dipole upwards (z orientation), i.e. a radial dipole in a perfect sphere. Then P = V, but T = 0, since V exactly cancels P. The total field is exactly zero everywhere, regardless of sensor location or orientation, because volume current contributions exactly cancel primary current contributions. So your Eq(12) is identically 0, and Eq(13) is identically 1.
-
Now orient the dipole in the x-direction (i.e. a tangential dipole). Now orient all of the MEG sensors in the radial direction. In this special well-known configuration (radial sensors outside a perfect sphere), the volume currents contribute absolutely nothing to the radial field, so T = P, and V = 0. So (12) = 1, and (13) is undefined.
-
For the same dipole and the exact same MEG sensor locations as in 2), simply orient all MEG sensors in the x-direction. Now the primary current contributes exactly nothing (because the dipole is also oriented in the x-direction), and the total field is just due to the volume currents. So (12) is undefined, and (13) = 0.
Any other orientation of the MEG sensors is a variation of these two extremes. The Sarvas model used in Brainstorm (eq (10) of the above reference paper https://neuroimage.usc.edu/paperspdf/IEEEBME99.pdf) calculates the magnetic field for any arbitrarily oriented MEG sensor outside of a sphere, which is always due to the total current field.
If you want to study the vector magnetic field (not just the scalar magnetic field in the direction of the MEG sensor), duplicate each sensor location to be actually three collocated sensors, oriented in the three x, y, and z directions. The head model calculation now gives you the vector magnetic field at each point outside the head, due to the total current flowing in the sphere.
But I'm uncertain as to what additional insights you hope to gain by attempting to parse out volume from primary in this external vector field.
How can I compute BEM matrix that maps surface potentials to secondary B fields, ?
For questions relative to OpenMEEG, I recommend you contact the OpenMEEG developers:
https://openmeeg.github.io/contact.html
@Alexandre @mclerc @papadop
Hi @Francois
I contacted the developerof openmeeg:
Alexandre said:
yes you can do this with openmeeg
https://openmeeg.github.io/tutorial.html#om-gain
you would need to zero either of the matrices Source2MEGMat or Head2MEGMat
see the note
you read the matrix in matlab, put only zeros and save it back using om_xxx functions in brainstorm
Alex
Infact in BST when I compute the forward model with openmeeg everything goes automatically so how can I read the Source2MEGMat or Head2MEGMat matrix in matlab
wher I donot know how to get them, and I donot know how to access the om_xxx functions in brainstorm as I am a user interface
can you help more in the steps please?
How can I zero either of the matrices Source2MEGMat or Head2MEGMat?
and save it back using om_xxx functions in brainstorm?
konowing that it seems that the om function is .exe
![]()
Thank you
Hi,
In order to access these files you need to put a break point on the
bst_openmeeg.m
function, then run it step by step, and check the outputs files in the .brainstorm/tmp folder,
you will find all the relative files related to this computation.
You will probably find the files that Alexandre pointed to.
Regarding the functions with om_xxxx, I think some of them are on
brainstorm3\external\openmeeg
but you can find more functions within the fieldtrip toolbox,
in the folder " \fieldtrip\external\openmeeg "
I hope this can help you.
Best,
Takfarinas
Thank you Tmedani, checking the .brainstorm/tmp folder I have
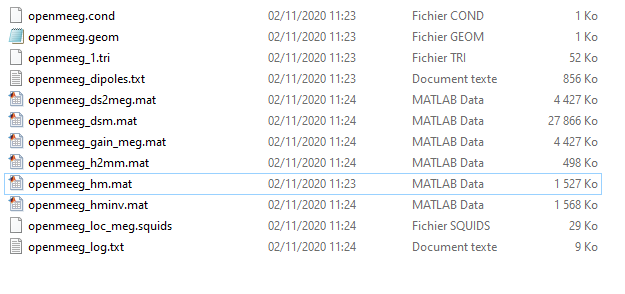
do you mean the I should find the matrices Source2MEGMat or Head2MEGMat here? if yes do you know what is it? and do you know how can I save it back using om_xxx functions in brainstorm as @Alexandre said? does the saving should be by reading it from .brainstorm/tmp folder,?
Thank you again
Head2MEGMat = openmeeg_h2mm.mat
Not sure about the other one, check in bst_openmeeg.m and the openmeeg doc.
Ok, thanks.
I solved it, like the below I think
I add those lines before res = om_call...
but Alexendre said either Source2MEGMat or Head2MEGMat,
this what I didnot understand it theoretically, 1)do you have a clue?
- Is the below correct?
load(h2mmfile);
linop = zeros(size(linop));
save(h2mmfile, 'linop');
res = om_call('om_gain -MEG', ['"' hminvfile '" "' dsmfile '" "' h2mmfile '" "' ds2megfile '"'], meggain_file, 'Assembling MEG leadfield...');
This is a specific to OpenMEEG, please try to discuss this with them.
Don't hesitate to post your conclusions here for future users.
Thanks
