Local minima problem

Discussions
, ,
#1

Good evening!
Reading about source localization it comes the local minima problem, but I can't figure out the local minima concept in eeg source localization

Can anyone please help me to understand (or suggest some stuff about this topic) What Is local minima and why it Is a huge problem in eeg source analysis??

Thanks in Advance!

#2

Hello,

Could you be more specific as to what you're referring to? Perhaps it's to the fact that some minimization procedures are not guaranteed to find the global minimum, but can "get stuck" in a local minimum. This is a general concept that may or may not apply to various source localization algorithms. It's difficult to say more without knowing the context of your question.

Best,
Marc

#3

Hi!
thanks for your reply,
well for me the issue is just that:

what is "to get stuck in local minima"?

I understand that it is something that is just for dipole localization (I think), and in many papers appears the statment that Local minima is a problem to avoid, but I can not understand what is the local minima problem in dipole source localization and why is it a problem, I was trying to find out more information about that but I can't find it.

So I ashemmed but I think I need to get the concept, in simply words or in some examples, by the way, how the BS software overcomes this issue (local minima)?

#4

I guess the issue you are referring to is related with iterative dipole fitting of single dipoles.
When trying to find the electric dipole that explains the best the EEG/MEG, most algorithms do the following:

  • Start by initializing the dipole position and orientation at a random position in the brain
  • Move a bit the dipole and change a bit the orientation in various directions, and then select the new dipole that gives the best results, ie. which minimize the residuals (EEG recordings - simulated EEG explained by the dipole)
  • This is done repeatedly until the algorithm does not manage to improve the solution anymore.
  • Good case: the final dipole explains the best the recordings, and probably indicates where the activity comes from in the brain.
  • Bad case: the algorithm converge to a "local minimum", but there is actually another position in the brain where the dipole would have explained better the recordings (the "global minimum"). This position could have been found by initializing the algorithm in a different way, with a different initial dipole position.

This algorithm corresponds to what is done by the FieldTrip dipole fitting (process "Sources > FieldTrip: ft_dipolefitting" in Brainstorm).

Single dipole fitting algorithms have lots of issues, this is one of the reason for which we recommend using distributed source models instead. If you are interested in using Brainstorm or reading more about this, you can find documentation here:
https://neuroimage.usc.edu/brainstorm/Tutorials/SourceEstimation
https://neuroimage.usc.edu/brainstorm/Tutorials#Background_readings

#5

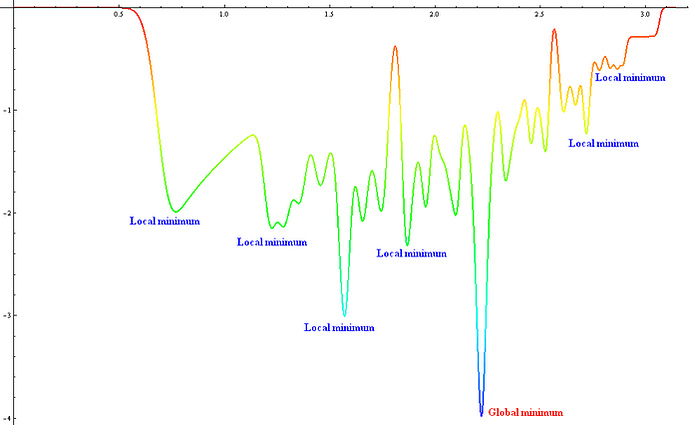
If it helps, in the simplest terms a local minima is a point which is lower than the surrounding area of the function, but which is not the lowest point in the entire function. The global minimum is the lowest point in the entire function and is what you want to find. You can visualize this in the image below.

Minima%20example
Minima%20example692×427 44.1 KB

There can be any number of local minima, and algorithms which search for the global minimum will sometimes locate a local and call it the global. This can happen for a number of reasons which you will find vary by the nature of the function and the style of the algorithm you use. When this occurs, it is bad because your algorithm had misidentified the global minimum and given you the wrong point to work with. Both the location and the level or value of the minimum are wrong and give erroneous results. One way of attempting to overcome this is to run your algorithm multiple times, with a different starting point each time. This increases the chance that it will find the global rather than getting stuck in a local.

http://www.benfrederickson.com/numerical-optimization/
This site gives a good visual example of this. Click on the function to move the starting point and you will see that starting on the right side of this function causes it to settle, or "get stuck," in the local minima rather than the global. There are multidimensional examples if you keep scrolling. You can also visualize how adjusting your expansion and contraction rates affects the algorithm as well.

Hope this helps!

1 Like
#6

Really Thank you to Both of you!!!
Thank you a lot, I understand it now!

You two are good teachers.

1 Like