Noise covariance matrix in BST

Discussions
1

Dear All,

I have a discusion with someone about noise covariance matrix, he said:

You can specify the noise level in brainstorm by specifying noise covariance matrix (S). If you want to just consider sensor noise (with uniform noise across sensors) then you can specify the noise covariance matrix to be S = sigma^2 I, where I is the Nsensors x Nsensors identity matrix and sigma^2 is the noise variance. For example, for OPMs sigma^2 would be (6 fT)^2, if you consider just unit bandwidth (the noise variance is sigma^2 = (6fT/sqrt(Hz))^2 * 1 Hz).

So as I understand to do it in brainstorm I should do:

  1. Noise covariane ---> compute from recordings
  2. Export it to matlab (name it noise_cov)
  3. Our sensor have a noise variance of: s2 = (6e-15)^2;
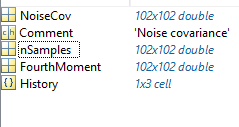
    Then noise_cov.NoiseCov = s2*eye(size(gain,1)); Is this true?

The noise_cov matrix contain several matrix, I just need to update the NoiseCov?
image

The other part of his sentence I did not understand it:
, if you consider just unit bandwidth (the noise variance is sigma^2 = (6fT/sqrt(Hz))^2 * 1 Hz).
do you have explanation for it? does what I did above is enough? and what is the application for if we want to consider a unit bandwidth, and how ?

Thanks in advance!

2

Then noise_cov.NoiseCov = s2*eye(size(gain,1)); Is this true?

This looks OK.

The noise_cov matrix contain several matrix, I just need to update the NoiseCov?

Set the matrices nSamples and FourthMoment to [], this will prevent any misuse of these values.
This would be only used if you were using the advanced option "Automatic shrinkage" in the source estimation options.

, if you consider just unit bandwidth (the noise variance is sigma^2 = (6fT/sqrt(Hz))^2 * 1 Hz).
do you have explanation for it? does what I did above is enough? and what is the application for if we want to consider a unit bandwidth, and how ?

I don't know. What you need in the noise covariance file is a broadband value.
You'd better ask directly the people how told you what to do, it looks like they know exactly what you should do.