Hello,
i know this is probably more a bug of either nirstorm or MEM, but since I am starting to question my sanity, I. thought I could come ask my question here:
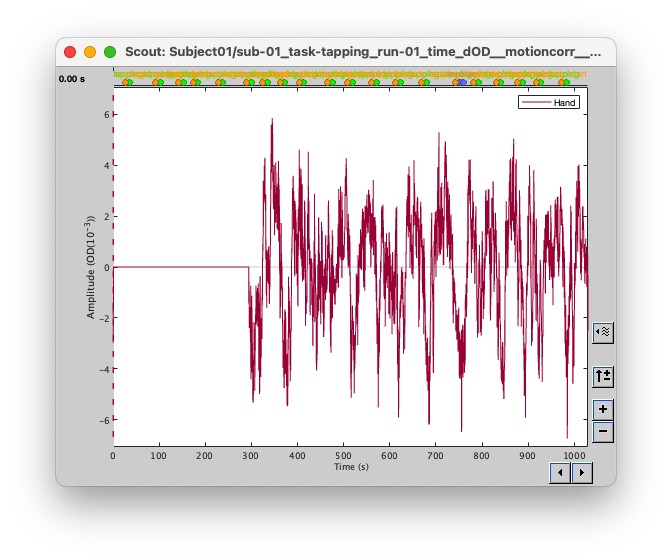
TLDR: I am trying to localize 1000s of a signal using MEM, and for some reason, the 300s at the beginning of the signal are exactly 0.
Solved here: Stange bug when saving MEM results - #2 by edelaire
Long version:
I have 1000s of nirs signal, and I want to localize using MEM or MNE. But for some reason, the beginning of the file doesn't get localized and is set to exactly zeros; which makes no sense!
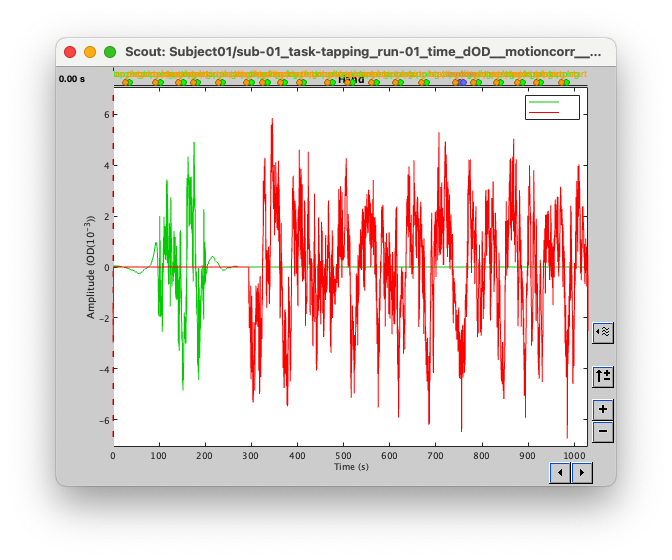
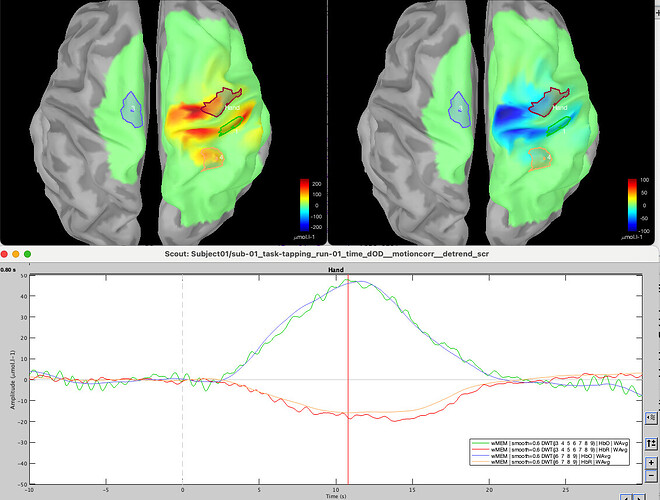
I tried to localize only part of the signal (between 100s and 200s) and then I got the signal:
But when I tried to localize the entire recording then: the beginning is forced to 0. After reading back the entire code 4 times, trying some voodoo magic, i just tried to put a breakpoint after the computation of MEM and before the saving in the database (here: nirstorm/bst_plugin/inverse/process_nst_cmem.m at master · Nirstorm/nirstorm · GitHub)
and to my surprise: The signal is there. I ploted the average over a specific roi using
idx = cortex.Atlas(1).Scouts(2).Vertices;
figure; plot(OPTIONS.DataTime, mean(grid_amp(idx,:)))
but if i then look at the file in the database, not signal is there between 0 and 300s
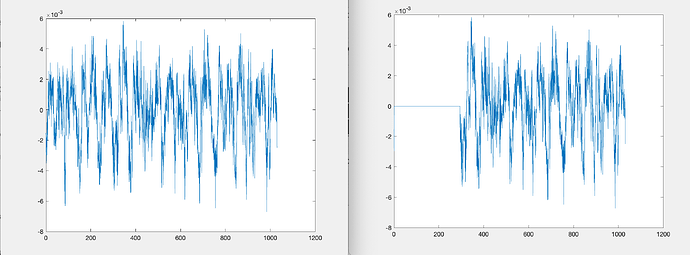
Left is if I plot the signal at the breakpoint before saving in Brainstorm, right is if I take the file from Brainstorm database. it should be exactly the same (and it is at the end).
edit: So I put a breakpoint here: just after the saving in the brainstorm database and the results doesn't make sense at all. nirstorm/bst_plugin/inverse/process_nst_cmem.m at master · Nirstorm/nirstorm · GitHub
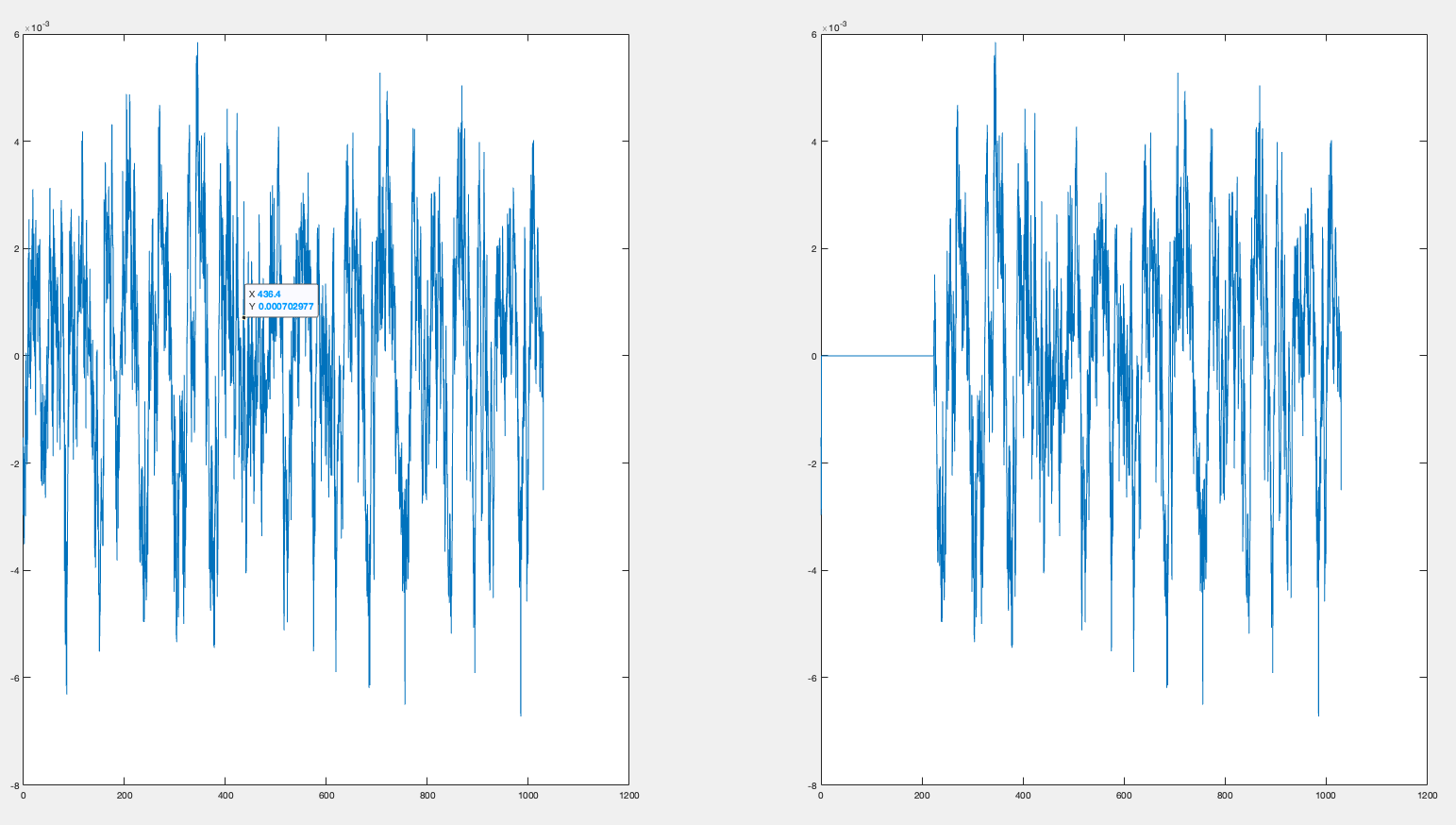
I used the following code to compare what we are trying to save with what is save and the beginning of the file just get chopped of. I don't understand why.
sCortex = in_tess(head_model.SurfaceFile);
idx = sCortex.Atlas(1).Scouts(2).Vertices;
sDataNew = in_bst_results(ResultFile);
figure;
subplot(121);
plot(time, mean(data(idx,:)))
subplot(122);
plot(time, mean(sDataNew.ImageGridAmp(idx,:)))
Resulting in :
If you have any ideas, I would really appreciate it !
Thanks a lot,
Edouard