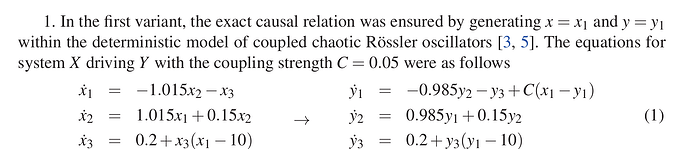Hello everyone,
I’m looking to set up a simulation in EEG and would like some insights on the best approach. Specifically, I want to generate EEG signals using different modeling techniques, to see what is the result of these changes which I am going to impose! The approach that I’m considering is:
Deterministic Model with Coupled Chaotic Rössler Oscillators:
In the first variant, the exact causal relation was ensured by generating x = x1 and y = y1 within the deterministic model of coupled chaotic Rössler oscillators. The equations for system X driving Y with the coupling strength C = 0.05 were as follows:
x1 = -1.015x2-x3
x2 = 1.015x1 +0.15x2
x3 = 0.2+x3(x1-10)
У1 = −0.985y2 − y3+C(x1 −y1)
y2 = 0.985y1 +0.15у2 (1)
y3 = 0.2+y3(y1-10)
and I am not sure what shoud I do with the rest of other electrodes, as temporal side (at this moment!).
Please give me hints,
where should I start and which steps should I take? to generate data which can be fed to the brianstorm software as a correct input!
Just let you know, I have prior experience with brainstorm, and any given direction would be acknowledged in the final manuscripts which I intended to do spontaneously by myself.
I am waiting for your directions!
Amir
Ping @dboutet, do you have some pointers on this topic?
In the coding part, you can use the process Simulate > Simulate generic signals, in there you can call your function to generate the EEG data as the variable Data
1 Like
Hi,
For the pure modelling aspect, it would be helpful to have a bit more information about what you are doing and trying to achieve with the modelling first if you're ok with sharing some details. Here are some important questions:
- Are the x and y variables representing EEG sensors or brain regions/parcels? Is the output of your model a sensor time series or a neurophysiological measure (or at least an analog of it)?
- Do you have a forward model if simulating sensors and aiming to compare it with empirical sensor data, or an inverse model if simulating sources and aiming to compare it with empirical source-space data?
- Do you aim to model the whole brain or just some specific subset/network?
- Do you have synthetic or empirical structural connectivity matrix (from DWI, or tracers for non-human primates) to provide a "baseline" connectivity between the nodes/units/ROIs in your model? Or are you looking to infer the connectivity weights (e.g., DCM-like analysis).
Without the above information it's hard to give advice on what to do since it's going to be conditional on the answers to those questions. However, here are some generic statements that you might find helpful:
- You cannot really model the sensors directly to study deterministic coupling since the sensor signals have overlapping information from the biological system that induced them. You can however study deterministic coupling by modelling neural sources and passing the simulations through a forward model to generate EEG sensor data and analyse that.
- True neural sources don't operate in a vacuum; the whole brain operates as a multi-scale (sometimes sparsely) interconnected system. However, we cannot model everything, so we need to narrow down on the specific subset of interest and basically account for everything else using some tricks. Sometimes the trick is as simple as including some additive white noise as input (e.g., to account for some un-modelled sensory input to a cortical model). Just need to find the trick that is context and objective appropriate.
Hopefully this reply was useful and not overly verbose.
Dominic
1 Like
Thank you in advance for your detailed questions, and I would be happy to reply.
Response to 1: X and Y are example representative of sensors which they are representing the recorded time series format. In this step, I do not consider them to be representative of a special disease condition.
Response to 2: Currently, I just want t do forward modeling (with OpenMEEG BEM) and all my aim is to do it with the simulation level without comparing the empirical data.
Although later might based on the obtained data series, later I would prefer to be more focused on short time simulation like 1 second maximum with the hope to develop the mismatch negativity like responses, and consequently to compare them.
Response to 3: the whole brain activity
Response to 4: I am going to make these synthetic data series and based on the fact some causality inference models allow me to get the brain regions “time scouts” based on some parcillation of anatomical atlas. Then, see, how algorithms in the brain level simulation could decipher the sensor level grand truth. And to refer your question, I think I would do more connectivity weights.
My hypothesis is that , if I have a data which I know its causality on the sensor level, if I do forward modeling , would I find a coherent story or not? Still I am not sure for the inverse modeling what should I do (might I did not study enough), although if I can gave like this:
simulated data (what I would give) → forward modeling → brain cortex time series → inverse modeling → get the time series data again (what I would get)
based on this plan I would be able to see in this process, the grand truth of causality in the data that I feed, still remains the same causality relationship?!
To keep up with your generic guid, please let me know, where should I start? I do not have any idea! I would follow any direction! And appreciate your time for elaboration.
best,
Amir
Hi,
So, if I understand this correctly (correct me if I'm wrong), you want to simulate sensor time series, then use a source localization model on the simulated time series to have simulated source time series, and finally project your simulated source time series back into the sensors and see what you get back out of this process. Is that correct?
If that's the case, I think you'll find that with most source localization approaches you will get exactly the sensor time series back since most of them boil down to estimating the entries of a linear transformation matrix based on some model of the head-sensor physical system. This would be true regardless of the dynamical model used, what it represents or how it behaves, since the source localization models are mostly concerned about the head position and sometimes head anatomy. I'm not sure if some EEG source localization models behave much differently (I mostly work with MEG), but as far as I know this is also what you'd expect from most EEG source models since the main difference from MEG comes from how the head model is derived, not how the projection is derived.
Hope this helps,
Dominic