Before source reconstruction, the EEG data I imported was expressed as amplitude in uV, but after source reconstruction, I found that the magnitude of the time series was 10^-9,Is the unit of the data after source reconstruction current density? Is it still possible to convert to amplitude?
Hi @YYingH1213, welcome to the Brainstorm Forum,
The units on the source reconstruction depend on the method that was used. This is because some methods implement normalization. Check the info in this link:
https://neuroimage.usc.edu/brainstorm/Tutorials/SourceEstimation#MN_imaging_variants
Thank you for your reply. I use sLORETA. In this case, the signal unit after source reconstruction is A-m. The original signal is expressed in amplitude, and the source reconstruction is expressed in current density. In this case, there will be a problem, because we are performing synchronous coupling analysis on multimodal EEG and EMG signals, and EMG signals are expressed in amplitude. In this case, can we directly use the EEG and EMG signals after source reconstruction for coupling analysis (such as coherence, Granger causality, and phase-locked value)?
Thank you for your reply. I use sLORETA. In this case, the signal unit after source reconstruction is A-m. The original signal is expressed in amplitude, and the source reconstruction is expressed in current density. In this case, there will be a problem, because we are performing synchronous coupling analysis on multimodal EEG and EMG signals, and EMG signals are expressed in amplitude. In this case, can we directly use the EEG and EMG signals after source reconstruction for coupling analysis (such as coherence, Granger causality, and phase-locked value)?
Is there a way to convert source signals expressed as current density after traceability into EEG signals expressed as amplitude
It seems there is confusion on the nature of the signals.
EEG signals capture the difference of potential (voltage) between two points on the scalp, and it is measured in [Volt]. These signals are in the sensor space (so there is a time series for each sensor).
Once sources are estimated, they are not any more a difference of potential, they are brain activity, or electrical currents (actually current densities) in the brain, they can be [Ampere*m]. These signals are in the source space, thus, there is one time series per vertex in your source space if sources are constrained. Otherwise, If you are working with unconstrained sources there are three time series per vertex). See this post for details on why [Ampere*m] are the units for current density:
This should not a problem, the connectivity metric will compute between time series, regardless of their units. Moreover, most of connectivity metrics are not affected by the scale of the signals. You can check this tutorial where coherence between EMG and sources is computed:
https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence
But in this case, the amplitude squared coherence function, as the name implies, is the square of the calculated signal amplitude to represent the self-spectrum of the signal, but the signal, if the signal is represented by the current source density, is the square of the current source density still the self-spectrum of the signal?
In the name magnitude squared coherence, the squared part makes reference that the magnitude of the coherence is squared.
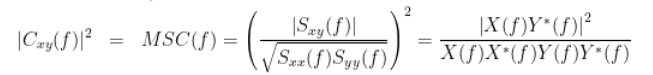
https://neuroimage.usc.edu/brainstorm/Tutorials/Connectivity#Coherence
Computing connectivity with current densities should not be a problem.
@John_Mosher, can you provide some input in here?
Thank you for your reply, could you please give me some help if I use the unconstrained sources approach to source reconstruction?
This makes reference to the Dipole orientation parameter that was used when estimating sources:
https://neuroimage.usc.edu/brainstorm/Tutorials/SourceEstimation#Source_estimation_options