Missing unit of Global Field Power

[RenataKoch]

Hello,

I have used the Cluster function for Power to generate the global field power of 59 EEG electrodes, but when I view the results (image below), there is no unit, only scale. Is the base unit µV or V, or something else?

[Raymundo.Cassani]

Hi @RenataKoch,

The units for the Power cluster function will be [V²] for EEG, and [T²] for MEG.

Being x of the shape [nSensors, nSamples], the Power function returns the average across sensors of the square of the all the signals: mean(x.^2, 1)

GFP is computed as the standard deviation across sensors: std(x, 1, 1)

The results between power function and GFS.^2 are very similar or event identical as the mean of all the sensor values at a given time point is zero most of the time. If average reference is used, power and GFP.^2 are the same.

Global Field Power Calculation Difference

After checking the literature, the most standard definition of the GFP is the standard deviation across sensors: Global field power and topographic similarity | SpringerLink Glossary — MNE 1.2.dev0 documentation [Eeglablist] get global field power of ERP data Brainstorm was computing a RMS measure instead (sqrt(sum(x.^2)), and then normalizing by the maximum for display (brainstorm3/figure_timeseries.m at master · brainstorm-tools/brainstorm3 · GitHub). The results is usually very similar or …

[mcp0228]

Hello @Raymundo.Cassani,
My apologies for opening up an old conversation. I just have a question about the mathematics behind the claim that GFP and power are equal when average reference is used.
The "std" function used to compute GFP is defined by Matlab from this documentation with the formula shown below. And the power cluster function is defined by "power = E(x.^2)/N" (formula 3).

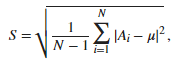
The mean of all the sensor values is most of the time close to zero or IS equal to zero in the case of EEG with an average reference. Therefore in the Matlab "std" formula, the variable "µ" will be 0 (formula 1 and 2). However, I still do not see how GFP and power functions could be equal when average reference is used as the power function does not have a square root and is divided by "N" not "N-1".

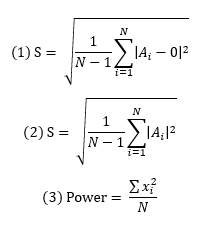
Would you mind providing a mathematical explanation for this?

[Raymundo.Cassani]

Thanks for point the mistake in the reply. If the signals are zero mean The Power cluster is very close to the GFP.^2 or the variance across sensors. RMS in fact is the one that is similar to GFP.

@Raymundo.Cassani

If average reference is used, power and GFP.^2 are the same.

This is true in Brainstorm as GFS is computed with std(x,1,1), where the first 1 indicates that the standard deviation is normalized with N not with N-1

This was mentioned also in a previous post:
Global Field Power Calculation Difference

---

P.S. I checked my notes, and indeed, "variance" is the term I was comparing with power.

[mcp0228]

Thank you for the prompt reply Raymundo, understood!