|
Size: 4070
Comment:
|
Size: 3872
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| BrainSync is an orthogonal transformation that allows direct comparison of resting fMRI (rfMRI) time series across subjects. For this purpose, we exploit the geometry of the rfMRI signal space to conjecture the existence of anorthogonal transformation that synchronizes fMRI time series across ses-sions and subjects. The method is based on the observation that rfMRIdata exhibit similar connectivity patterns across subjects, as reflected inthe pairwise correlations between different brain regions. The orthogonal transformation that performs the synchronization is unique, invertible, efficient to compute, and preserves the connectivity structure of theoriginal data for all subjects. Similarly to image registration, where wespatially align the anatomical brain images, this synchronization of brain signals across a population or within subject across sessions facilitates longitudinal and cross-sectional studies of rfMRI data. | BrainSync is an orthogonal transformation that allows comparison of resting fMRI (rfMRI) time series across subjects. For this purpose, we exploit the geometry of the rfMRI signal space to conjecture the existence of anorthogonal transformation that synchronizes fMRI time series across sessions andsubjects. The method is based on the observation that rfMRI data exhibit similar connectivity patterns across subjects, as reflected in the pairwise correlations between different brain regions. The orthogonal transformation that performs the synchronization is unique, invertible, efficient to compute, and preserves the connectivity structure of theoriginal data for all subjects. Similarly to image registration, where we spatially align the anatomical brain images, this synchronization of brain signals across a population or within subject across sessions facilitates longitudinal and cross-sectional studies of rfMRI data. |
| Line 15: | Line 15: |
| The input is assumed to be two time x vertices datasets, one is denoted as subject and second as target. It is highly recommened that the input is normalized to have unit varaince. If not, BrainSync will throw a warning and do the normalization internally. Before returning the outputs, the means for each time series will be added back and varaince rescaled back to its original value. However, we recommend doing the normalization using the function normalize_data.m. | The input is assumed to be two time x vertices datasets, one is denoted as subject and second as target. It is highly recommened that the input is normalized to have unit varaince. Please use the functions provided below before applying BrainSync as follows. |
| Line 36: | Line 36: |
| The python source code for BrainSync can be downloaded here. | The python source code for BrainSync can be downloaded below. |
| Line 38: | Line 38: |
| [[http://neuroimage.usc.edu/neuro/Resources/BrainSync?action=AttachFile&do=get&target=brainsync.py|Download]] | '''[[http://neuroimage.usc.edu/neuro/Resources/BrainSync?action=AttachFile&do=get&target=brainsync.py|Download]]''' |
| Line 45: | Line 45: |
| sub = normalizeData(sub) # Do the data normalization for subject brain ref = normalizeData(ref) # Do the data normalization for the reference brain |
sub, _, _ = normalizeData(sub) # Do the data normalization for subject brain ref, _, _ = normalizeData(ref) # Do the data normalization for the reference brain |
BrainSync
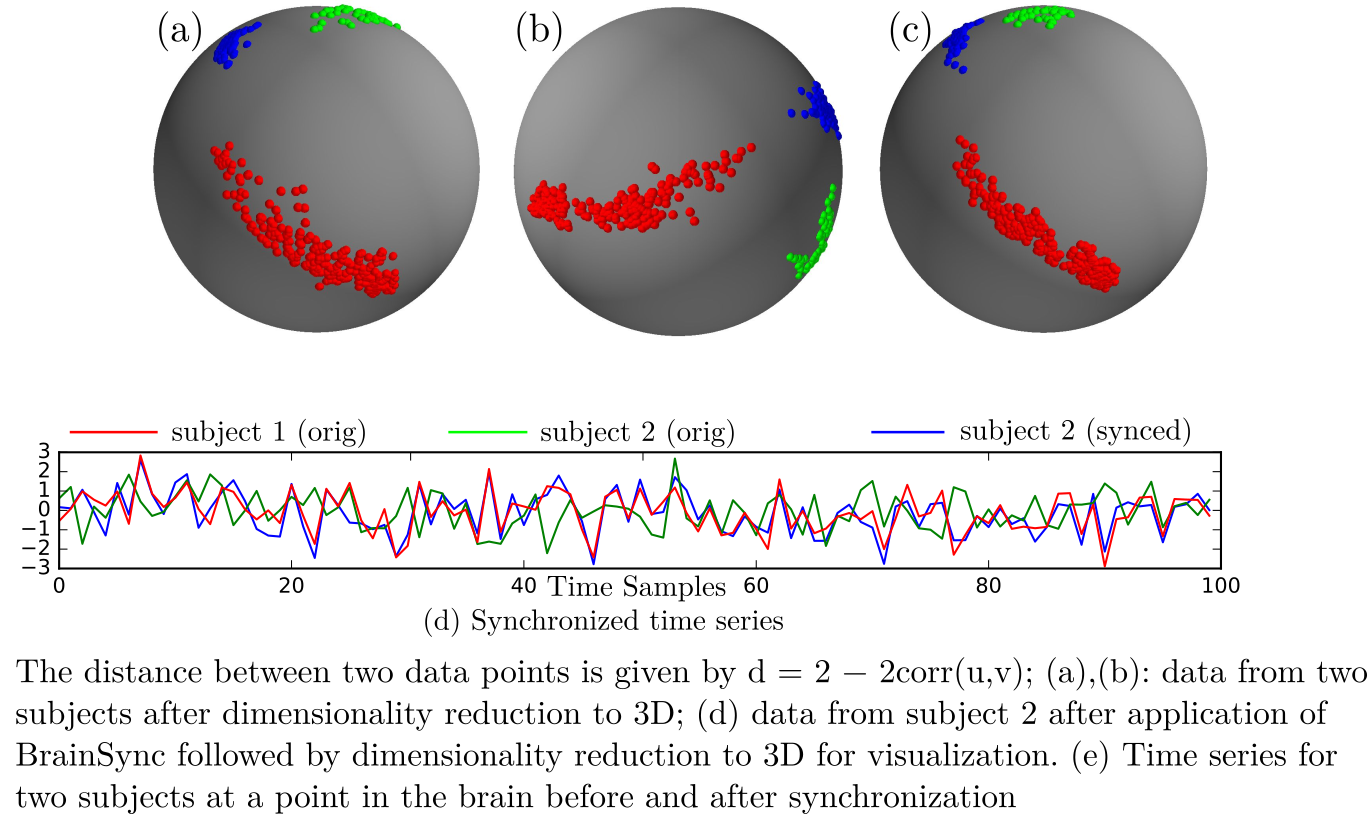
BrainSync is an orthogonal transformation that allows comparison of resting fMRI (rfMRI) time series across subjects. For this purpose, we exploit the geometry of the rfMRI signal space to conjecture the existence of anorthogonal transformation that synchronizes fMRI time series across sessions andsubjects. The method is based on the observation that rfMRI data exhibit similar connectivity patterns across subjects, as reflected in the pairwise correlations between different brain regions. The orthogonal transformation that performs the synchronization is unique, invertible, efficient to compute, and preserves the connectivity structure of theoriginal data for all subjects. Similarly to image registration, where we spatially align the anatomical brain images, this synchronization of brain signals across a population or within subject across sessions facilitates longitudinal and cross-sectional studies of rfMRI data.
The BrainSync concept is illustrated below:
Please refer to our publications below for detailed explanation and examples.
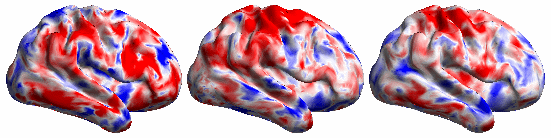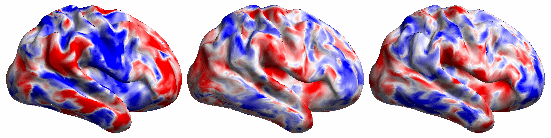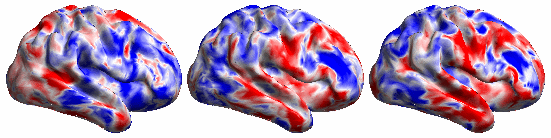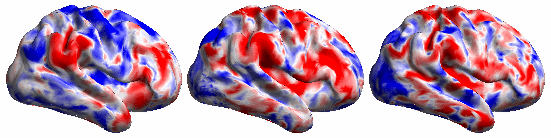
The following video shows the rfMRI signal of a (left) subject brain; (middle) a reference brain and (right) synced subject.
Software
The input is assumed to be two time x vertices datasets, one is denoted as subject and second as target. It is highly recommened that the input is normalized to have unit varaince. Please use the functions provided below before applying BrainSync as follows.
Matlab
The matlab source code for BrainSync can be downloaded below.
As an input we assume data matrices (Time x Vertices) of two scans, referred to as sub and ref. First the data should be normalized to 0 mean and unit variance by running:
sub = normalizeData(sub) % Do the data normalization for subject brain ref = normalizeData(ref) % Do the data normalization for the reference brain
and then the data can be synchronized using the following code.
% subSynced is the synched data for the subject and % O is the associated orthogonal transform [subSynced, O] = brainSync(ref, sub)
Python
The python source code for BrainSync can be downloaded below.
As an input we assume data as numpy arrays (Time x Vertices) of two scans, referred to as sub and ref. First the data should be normalized to 0 mean and unit variance by running:
from brainsync import brainSync, normalizeData sub, _, _ = normalizeData(sub) # Do the data normalization for subject brain ref, _, _ = normalizeData(ref) # Do the data normalization for the reference brain
and then the data can be synchronized using the following code.
# subSynced is the synched data for the subject and # O is the associated orthogonal transform subSynced, O = brainSync(ref, sub)