Gain matrix computation including subcortical structures

gianmarcoduma · September 29, 2021, 9:14am

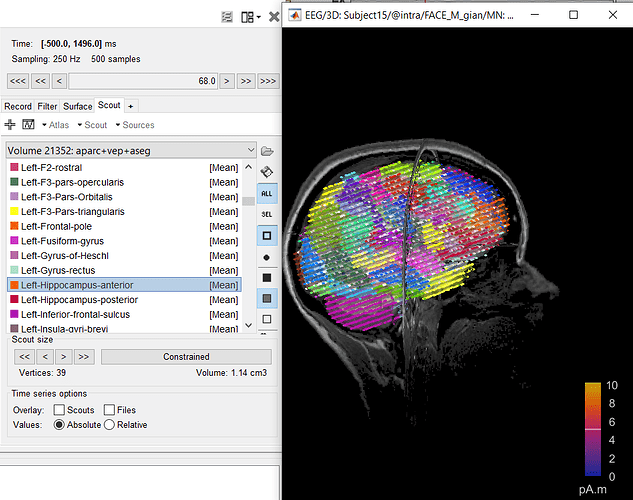
Dear everyone I need your suggestion to understand if what I'm doing is correct. My purpose is to include in the BEM model also the subcortical structures as caudate, hippocampus, amigdala, etc.. I generated the surface of each of this elements with freesurfer, and I can correctly import them in brainstorm. The position in the cortex seems to be correct, in fact they are inserted inside the cortex, and you can see them only if you increase the transparency (I attach the figure with hippocampus divided into anterior and posterior). I already read the tutorials about the deep brain structures, and it suggests to use mixed surface with volume for the deep brain areas. However I wanted to use surface since after the gain matrix computation I need work on it in order to reduce the gain matrix to an atlas based matrix obtaining number of areas x electrodes, instead number of vertices x elec. For me it is easier to do that with surface, since I know which vertex belongs to a specific region of the atlas. So my question is this, if I can correctly insert the surface of the deep brain structure in the cortex, will the computation of the Gain Matrix be correct? I tried to compute the BEM with this new cortex and I obtained a gain matrix with the correct number of vertices including also the subcortical areas, but I wanted to know how reliable this could be, and if what I did can be considered reasonable. Thanks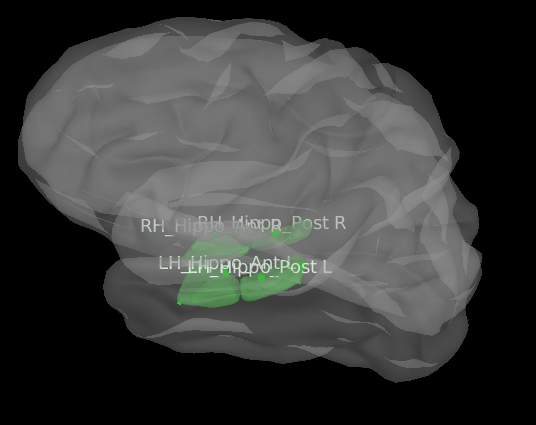 Screenshot from 2021-09-29 11-10-57

Francois · September 29, 2021, 10:32am

I already read the tutorials about the deep brain structures, and it suggests to use mixed surface with volume for the deep brain areas.

The type of constrains recommended depend on the structure. For the hippocampus, the authors estimated that the best was to use the surface with orientations constrained to the cortex normal.

For me it is easier to do that with surface, since I know which vertex belongs to a specific region of the atlas.

You can also get the indices of the rows in the head model for each structure referenced in the Structure atlas. See function bst_convert_indices.m

However I wanted to use surface since after the gain matrix computation I need work on it in order to reduce the gain matrix to an atlas based matrix obtaining number of areas x electrodes, instead number of vertices x elec.

The simplest approach would be to compute a volume head model, and create volume scouts for each of your ROIs of interest. You can use the ASEG volume parcellation imported from FreeSurfer directly to create the scouts you need. (if you don't see the ASEG atlas available as a parcellation file in the anatomy: update Brainstorm and import the anatomy again)
https://neuroimage.usc.edu/brainstorm/Tutorials/TutVolSource#Volume_atlases

gianmarcoduma · September 29, 2021, 2:14pm

Thanks!!
I have a question about the scouts that may seem offtopic but it's related to the VEP atlas we are trying to use. The VEP atlas splits the hippocampus in two (anterior and posterior) by following the eigendirection of the that region. When I split the hippocampus manually with 'subdivide selected scout' function in the gui < fixed numeber = 2, I had a similar results to those of the VEP. I checked the code and I am not sure I have understood how Brainstorm cuts in two a selected scout. The k-means line is commented, and the code uses the Surf.VertConn structure to divide the scout. Do you think that this two approaches are different?

Francois · October 1, 2021, 8:48am

The Brainstorm algorithm for subdividing scouts in has a random initialization. If you get similar results, it's probably only by chance. I don't think you can expect to use this reliably on multiple subjects.

gianmarcoduma · October 8, 2021, 1:42pm

Hi Francois, I'm trying to compute the gain matrix including subcortical areas by setting everything in the volume space as you suggested me. We have a volume segmentation of the VEP atlas, made with freesurfer. The file it's named vep+aseg.mgz. I can import it in brainstorm. However, when I import the volume atlas there is a problem. I only see the segmented regions named 'Unkwown' in the scouts section and they are not separatd in different colors. Indeed in freesurfer to see correctly all the areas I need to upload a specific lookup table. I think that brainstorm automatically upload the Freesurfer lookup table which I think it's encapsulated in the file, but in my case it is not correct. I need to import the VEP lookup table and attach it to this atlas. Do you think that this could be possible to do it in brainstorm? If not, what I could do?
Thanks

Francois · October 12, 2021, 10:06am

Could you please share these files: T1.mgz + vep+aseg.mgz + lookup table
(zip them, upload the .zip somewhere and post the download link here)
Thanks

gianmarcoduma · October 12, 2021, 11:12am

I was not able to upload the files directly here, but you should be able to find them at the following link. I think that once you try to download I need to give you the permission. I put some limitation due to possible privacy reasons, so that only those I allow to can download these files.
Thanks
https://drive.google.com/drive/folders/16QPAVPjCbEUGci8ZWqConrHGNcuNhwWM?usp=sharing

gianmarcoduma · October 12, 2021, 5:23pm

Hi Francois, I'm sorry if I'm bothering you so much. It's that we are trying to create a gain matrix using also the subcortical structures for the EEG, and it is more complicated than the I thought. At the moment I'm trying different approaches, using the subcortical as constrained, unconstrained and also the set modelling option 'loose' , considering both surfaces and volume. The results of the forward solution gives the Gain matrix and the GridOrient matrix, which provides the direction of the dipoles. From what I have understood from the code is that when I compute it as a volume the GridOrient value of those specific areas will 0. So when I run the bst_gain_orient to obtain a gain matrix the contribution of that specific subcortical areas will be zero, is that rigth? Unless I set those region as db, and the function dba_get_model will assume random direction of the dipoles, of specific cortical areas like amygdala, putamen, etc and normal direction for the areas set as surfaces. It is that correct?

Francois · October 13, 2021, 8:18am

We have a volume segmentation of the VEP atlas, made with freesurfer. The file it's named vep+aseg.mgz.

To import the file vep+aseg.mgz: right-click on the subject anatomy folder > Import MRI > File format: Volume atlas (subject space).

Answer YES to the question related to the orientation of the volume.
IGNORE co-registration
NO reslice

Because the file contains the tag aseg, it is going to use the labels defined in function mri_getlabels_freesurfer.m:

github.com

brainstorm-tools/brainstorm3/blob/master/toolbox/anatomy/mri_getlabels_freesurfer.m

function Labels = mri_getlabels_freesurfer()
% ATLAS     : FreeSurfer ASEG + Desikan-Killiany (2006) + Destrieux (2010)
% REFERENCE : https://surfer.nmr.mgh.harvard.edu/fswiki/FsTutorial/AnatomicalROI/FreeSurferColorLUT

% @=============================================================================
% This function is part of the Brainstorm software:
% https://neuroimage.usc.edu/brainstorm
% 
% Copyright (c) University of Southern California & McGill University
% This software is distributed under the terms of the GNU General Public License
% as published by the Free Software Foundation. Further details on the GPLv3
% license can be found at http://www.gnu.org/copyleft/gpl.html.
% 
% FOR RESEARCH PURPOSES ONLY. THE SOFTWARE IS PROVIDED "AS IS," AND THE
% UNIVERSITY OF SOUTHERN CALIFORNIA AND ITS COLLABORATORS DO NOT MAKE ANY
% WARRANTY, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO WARRANTIES OF
% MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE, NOR DO THEY ASSUME ANY
% LIABILITY OR RESPONSIBILITY FOR THE USE OF THIS SOFTWARE.
%
% For more information type "brainstorm license" at command prompt.

This file has been truncated. show original

The problem is that the volume contains lots of labels that are not defined in this function, as this is not the standard FreeSurfer LUT: FsTutorial/AnatomicalROI/FreeSurferColorLUT - Free Surfer Wiki

If you rename the file and remove the aseg tag (eg. vep.mgz), it would be imported without the FS labels, which leads to: no labels and random colors. Not what you want either.

The two solutions I could see:

You edit the function mri_getlabels_freesurfer.m locally (put it in your .brainstorm/process function so that it doesn't get erased at the next Brainstorm update) and add the missing labels.
You create a file vep+aseg.csv with the CAT12 syntax in the same folder: it would be used as the labels file instead of the default ASEG labels.

Example:

ROIid;ROIabbr;ROIname;ROIcolor
1;lPreCG;Left Precentral gyrus;203 142 203
2;rPreCG;Right Precentral gyrus;203 142 203

Francois · October 13, 2021, 8:30am

I'm not sure how useful all these options are. It seems to me that it adds more complexity than benefits, as compare to using simple surface or volume head models... but you're welcome to give us your feedback after testing all these.

From what I have understood from the code is that when I compute it as a volume the GridOrient value of those specific areas will 0. So when I run the bst_gain_orient to obtain a gain matrix the contribution of that specific subcortical areas will be zero, is that rigth?

In mixed head models: GridOrient is set to zero for the regions with unconstrained orientations (the field is left completely empty in the case of a volume head model).

In bst_gain_orient.m the values of GridOrient are not used in the case of unconstrained/loos orientations (GridAtlas.Scouts(iScout).Region(3) = 'U' or 'L').

github.com

brainstorm-tools/brainstorm3/blob/master/toolbox/forward/bst_gain_orient.m#L62


      
                  if isempty(iGrid)

                      continue;

                  end

                  % Get correpsonding row indices based on the type of region (constrained or unconstrained)

                  switch (GridAtlas.Scouts(iScout).Region(3))

                      case 'C'

                          % Create a sparse block diagonal matrix for orientations

                          GridOrientBlock = blk_diag(GridOrient(iGrid,:)', 1);

                          % Apply the orientation to the Gain matrix

                          GainBlocks{end+1} = Gain(:,iGridGain) * GridOrientBlock;

                      case {'U','L'}

                          GainBlocks{end+1} = Gain(:,iGridGain);

                      otherwise

                          error(['Invalid region "' GridAtlas.Scouts(iScout).Region '"']);

                  end

              end

              % Concatenate the blocks

              Gain = cat(2, GainBlocks{:});

          end

Unless I set those region as db, and the function dba_get_model will assume random direction of the dipoles, of specific cortical areas like amygdala, putamen, etc and normal direction for the areas set as surfaces.

I'm not sure what you mean here. You always define explicitly the orientation constrains you want (with DBA it uses a predefined set of recommended constrains). Random orientation is never assumed.

gianmarcoduma · October 13, 2021, 12:59pm

Thanks, that really helped me! I have been able to import the VEP volume with the correct LUT. I have modified the mri_getlabels_freesurfer.m to include also the VEP LUT

gianmarcoduma · October 13, 2021, 1:54pm

I'm sorry I have assumed erroneously that in the bold part of the code:

function [SrcLoc, SrcOri, sScout, iVertModif] = dba_get_model( sScout, sCortex )
% Get the grid of source points (position+orientation) for a given brain region.
%
% Yohan Attal, Francois Tadel - HM-TC project 2013

% Vertex indices
iVert = sScout.Vertices;
% If soome vertices are removed from the original scout, the modified version is saved in this variable
iVertModif = [];
% Check depending on the region name
switch sScout.Label
case {'Accumbens L','LAcc','Accumbens R','RAcc'}
regionType = 'vol';
regionOrient = 'random';

You were setting random orientation for the dipole for the volume part. Indeed the values of the volume uncostrined subcortical areas in the GridOrient is 0. So when I do bst_gain_orient obvioulsy the values of the volume areas will be zero in the gain matrix. In order to have an oriented gain matrix without zeros, a possible idea would be to have random for each dipole in the volume, so that when reorienting the gain matrix the contribution of the random dipoles direction in the volume, should cancel out, resulting in a minimum contribution of the subcortical areas.
At the moment we simulate with neural mass/field model the time series of the activity in a specific region or vertex. In a neural mass model let's image we have 162 areas (VEP atlas). We then multiply the oriented gain matrix ( electrode X ROI ) with the simulated signal (ROI x Time), if in the oriented gain matrix we find zeros, the resulted simulated signal at the electrode level will results in 0 contribution of the subcortical areas, while if we randomize the direction the contribution still remains little, but is not zero.

This was the general idea, however I think it's a long story to discuss on the forum. You helped me a lot as usual, I'll keep you updated with the results we will obtain.
Thanks again for your help