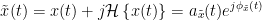Connectivity
Authors: Hossein Shahabi, Raymundo Cassani, Takfarinas Medani, François Tadel, Sylvain Baillet
Brain functions (e.g., in cognition, behavior and perception) stem from the coordinated activity of multiple regions. Brain connectivity investigates how these different regions (or nodes) interact as a network. Depending on which connectivity characteristic is studied, a distinction is made between structural (fiber pathways), functional (non-directed statistical associations) and effective (causal interactions) connectivity between regions. Effective connectivity is often referred as directed functional connectivity. In this tutorial we will see how to compute different connectivity metrics for non-directed and directed functional analyses using Brainstorm, first with simulated data and later with real data.
We encourage the interested reader to learn more about the specific aspects of electrophysiology for studying human connectomics.
Contents
Introduction
Definitions
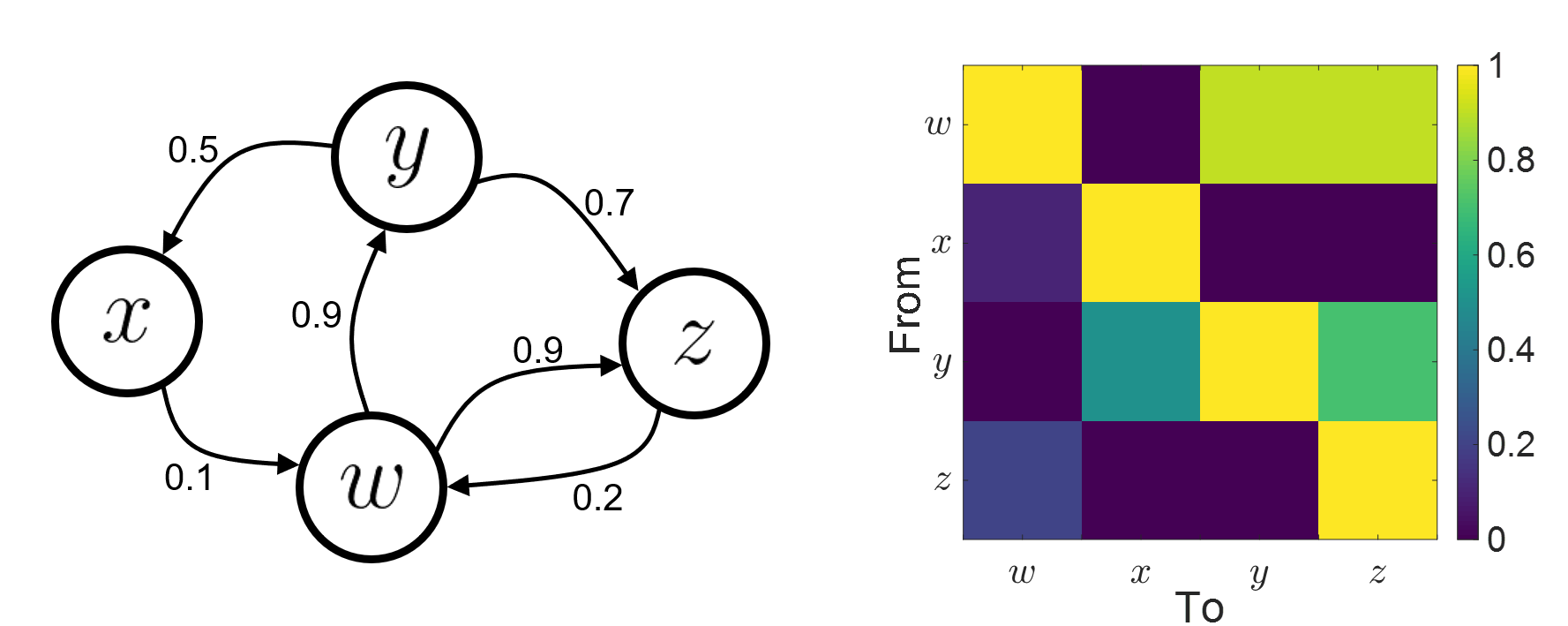
Connectivity analyses are commonly performed by computing a bivariate measure between pairs of regional time series of interest. The outcome (a.k.a connectome) can be presented as a connectivity graph (left image), where each region is represented as a node (x, y, z,...), and the values of the connectivity metric shown next to the edge linking between two nodes. The connectome can also be represented by a connectivity matrix, a.k.a. adjacency matrix (right image).
Sensors or sources: The signals used for connectivity analyses can be from sensor data (EEG/MEG signals) or from source time seriess (voxels or scouts).
Directed vs. non-directed: The direction of the interaction between signals (as statistical causation) can be measured with directed metrics. Non-directed metrics produce symmetrical connectivity graphs/matrices as connectivity "from Signal  to Signal
to Signal 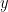 " is identical to connectivity "from Signal
" is identical to connectivity "from Signal 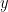 to Signal
to Signal  ".
".
Experimental condition: Depending on the neuroscience question, connectivity analyses can be performed on resting-state (spontaneous) or task (e.g., trials) data.
Full vs. ROI connectivity: In a full connectivity analysis, the connectivity metric is computed for all the possible node pairs at all N brain locations (noted N×N here). Alternatively, ROI connectivity is performed between one node of interest (a.k.a. a seed, e.g., one brain region or a behavioral marker) and N other regions (1×N approach).
Time-frequency transformations: Some connectivity metrics rely on a time-frequency representation of the signals. These latter are obtained with approaches such as the short-time Fourier transform, Hilbert transform, and Morlet wavelets.
Just as in other areas of electrophysiology studies, connectivity analyses need to be guided by mechanistic hypotheses concerning the expected effects.
Sensor-level
Sensor connectivity analyses present two important limitations:
Their anatomical interpretation is limited and ambiguous.
Sensor data is severely corrupted by field spread and volume conduction. Hence, activity from one single brain area is detected at multiple, often distant, sensor locations, which may be wrongly interpreted as network connections.
Source-level
Source connectivity analyses are neuroanatomically interpretable and can be derived across participants, following spatial normalization and registration.
It is recommended to verify that the outcomes of sensor and source connectivity analyses are compatible with one another (Lai et al., 2018).
NxN analyses
Whole-brain connectivity analysess at the typical resolution of cortical surfaces in Brainstorm involve thousands of source locations, making the N×N) derivations impractical. For instance, 15000 cortical vertices would yield a connectivity matrix of 15000x15000x8 bytes = 1.6Gb. If unconstrained cortical sources are used and coherence is computed across 50 frequency bins, the memory allocation increases to 45000X45000x50 = 754 Gb per participant/condition/trial/etc. Reducing the N (via e.g., cortical parcellations, ROIs) is therefore essential.
Regions of interest
Scouts are Brainstorm ROIs can be defined in multiple ways depending on study priors of all sorts, and other considerations such as the source estimation method, experimental task, and data available (Schhoffen and Gross, 2009). ROIs can be defined via:
Study priors from the literature, working hypotheses,
Association with a non-neuronal signal,
Signal strength, ROIs as regions with strongest activity in an experimental condition,
Whole-braincortical parcellation to reduce N.
Whole-brain connectivity analyses may be exposed to the issue of circular analysis (Kriegeskorte et al., 2009).
The optimal selection of ROIs to perform source connectivity analysis is still an open question.
Requirements
Please note that this is an advanced tutorial, it assumes that that you have already followed all the introduction tutorials. For readability, most of the interface details are omitted, you must be familiar with the Brainstorm software in order to reproduce the computations illustrated below.
This tutorial is mostly based on simulated data, and independent from the other tutorials. Only one part at the end uses the results of the introduction tutorials (auditory oddball dataset), in order to illustrate how to apply the connectivity processes to real MEG recordings.
Let's start by creating a new protocol in the Brainstorm database:
Select the menu File > Create new protocol > "TutorialConnectivity" and select the options:
Yes, use protocol's default anatomy,
No, use one channel file per condition.
Right-click on the TutorialConnectivity folder > New subject > Subject01
Simulated data
To compare different connectivity metrics, we use simulated data with known ground truth using a multivariate autoregressive (MVAR) model. This model consist in three signals in a way that:
Signal 1: Components at 10 and 25 Hz with a dominant peak at 25 Hz (beta band).
Signal 2: Same components, but dominant peak is at 10 Hz (alpha band).
Signal 3: Similar power for both components (10 and 25 Hz).
Signal 1>>Signal 3: Signal 3 is influenced by Signal 1, with a peak at 25 Hz.
Simulation process:
In the Process1 tab, leave the file list empty and click on the button [Run]
Select process: Simulate > Simulate AR signals.
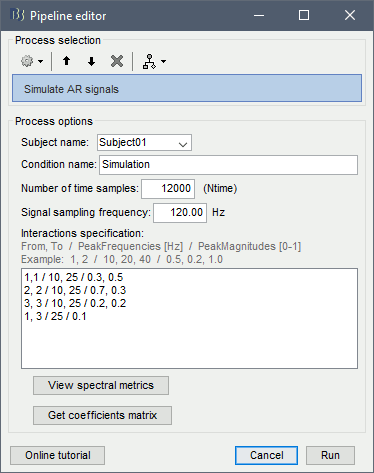
Process options:
Subject name: Target subject for the simulated signals. Select Subject01.
Condition name: Target folder for the simulated signals. Set to Simulation.
Number of time samples: Duration of signals, in samples. Set to 12 000.
Sampling frequency: Fs for the simulated signals. Set to 120 Hz.
Interaction specifications: Spectral parameters for the interaction between signals in the MVAR model, given as: From, To / Peak frequencies [Hz] / Peak relative magnitudes [0-1]
Set to:1, 1 / 10, 25 / 0.3, 0.5 2, 2 / 10, 25 / 0.7, 0.3 3, 3 / 10, 25 / 0.2, 0.2 1, 3 / 25 / 0.1
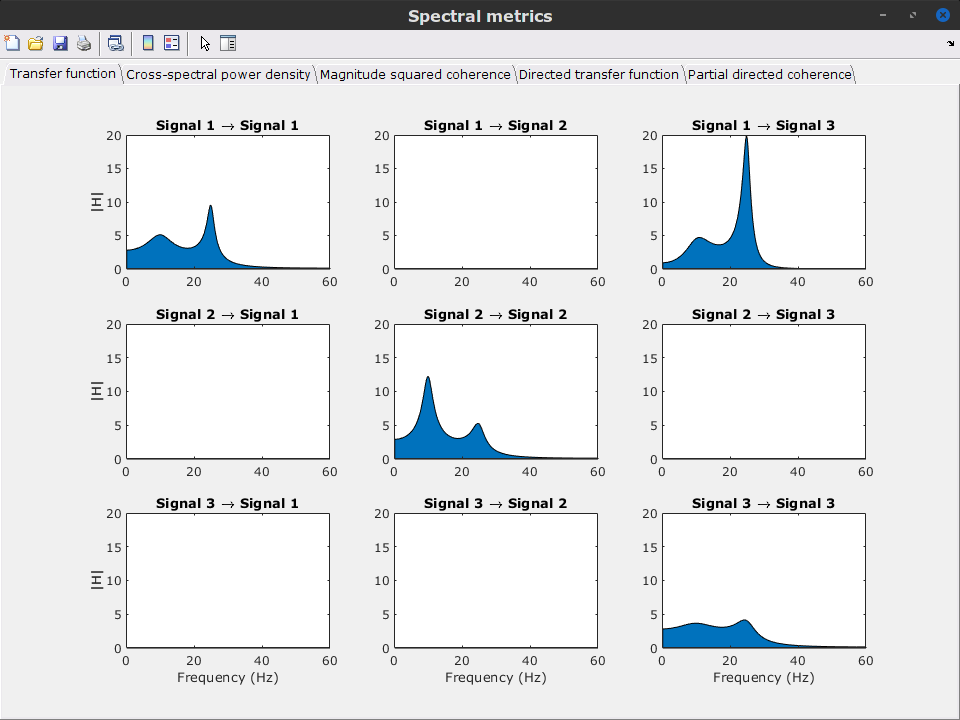
View spectral metrics: Display spectral metrics related to the MVAR process: transfer function, cross-spectral power density, magnitude square coherence, directed transfer function (DTF) and partial directed coherence (PDC). The transfer function,
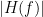 , contains information about the relationships between signals and their spectral characteristics; it is non-symmetric, so it allows for finding causal dependencies. The auto-transfer function (diagonal elements in the image) correspond to the power spectrum of the signals. The off-diagonal terms represent the interactions between different signals. Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values.
, contains information about the relationships between signals and their spectral characteristics; it is non-symmetric, so it allows for finding causal dependencies. The auto-transfer function (diagonal elements in the image) correspond to the power spectrum of the signals. The off-diagonal terms represent the interactions between different signals. Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values.
Get coefficients matrix: Shows the coefficients related to the MVAR model. These coefficients can be used in the process Simulate > Simulate AR signals (ARfit) to simulate the same model.
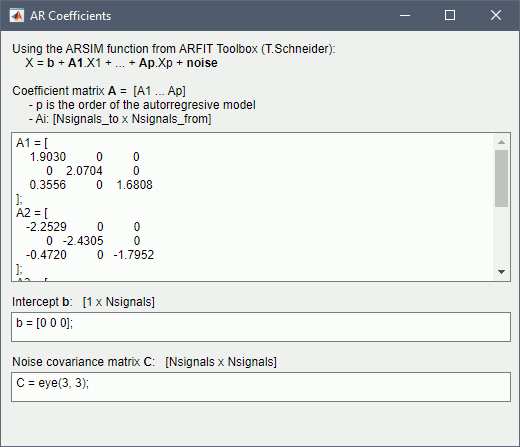
Execution:
Click Run to simulate the signals described by the MVAR model.
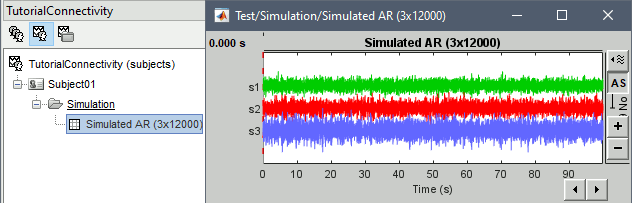
In the next sections we will compute different connectivity metrics for these simulated signals. As such, place the simulated data in the Process1 tab, click on [Run] (
 ) to open the Pipeline editor, and select the connectivity metric.
) to open the Pipeline editor, and select the connectivity metric.
This tutorial illustrates only the computation full connectivity graphs (Process 1: NxN). It is however possible to compute the connectivity between 1 signal and the other signals in the same file (Process1: 1xN), or between signals from two different files (Process2: AxB). These options will be illustrated at the end of the tutorial.
Credits:
This process relies on the ARSIM function from the ARFit toolbox:
https://github.com/tapios/arfitNeumaier A, Schneider T
Estimation of parameters and eigenmodes of multivariate autoregressive models
ACM Transactions on Mathematical Software, 2001Schneider T, Neumaier A
Algorithm 808: ARfit – A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models
ACM Transactions on Mathematical Software, 2001
Correlation
Correlation is a non-directed connectivity metric that can be used to show similarity, dependence or association among two random variables or signals. While this metric has been widely used in electrophysiology, it should not be considered the best technique to evaluate connectivity. Due to its nature, correlation fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals.
Process options
Process Connectivity > Correlation NxN:
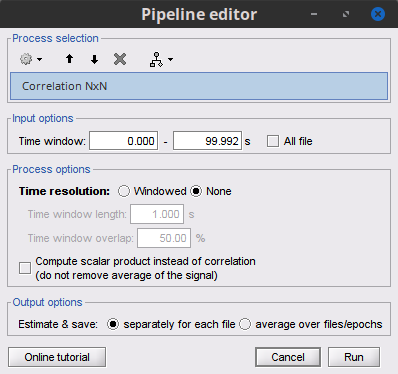
Time window: Segment of the signal used for the connectivity analysis. Select: All file.
Compute scalar product: If unchecked, the mean of the signals is subtracted before computing the correlation. Uncheck it.
Output options: Select Save individual results.
Result visualization
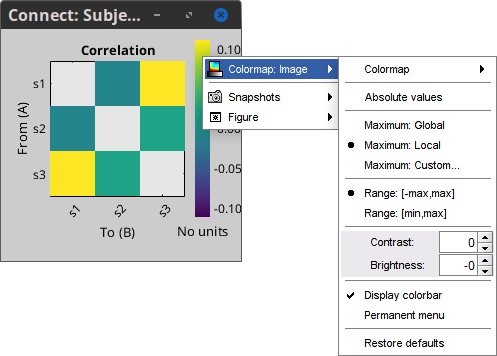
The results are stored as a N×N connectivity file, icon
 . Right-click to see its display options:
. Right-click to see its display options:
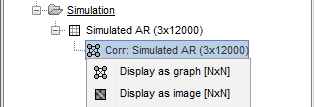
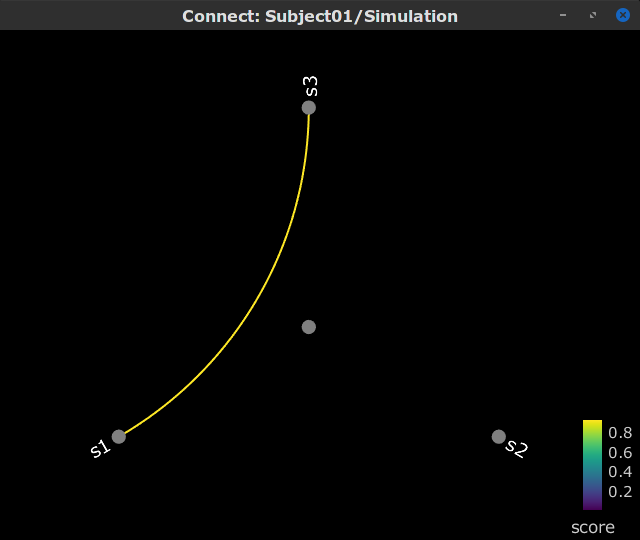
Display as graph: Plots the connectivity graph using a chord diagram where the color of the edges shows the connectivity metric value. See the connectivity graph tutorial for a detailed explanation of the options of this visualization.
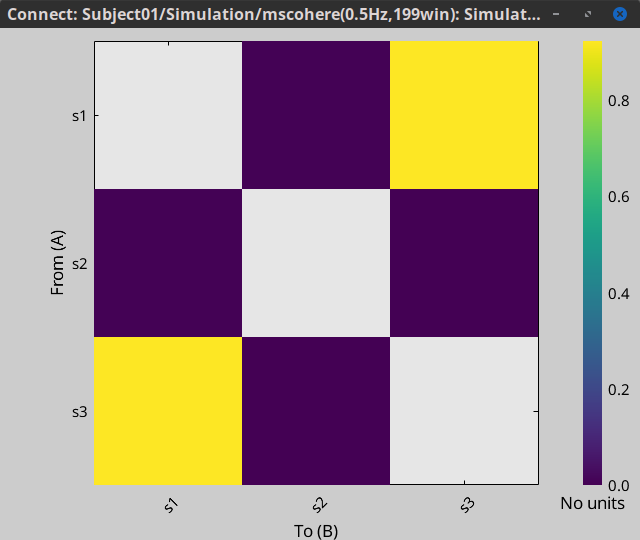
Display as image: Plots the adjacency matrix for the connectivity file.
Display fibers:Additional option available for source connectivity results when a fiber track surface is available, as shown here.
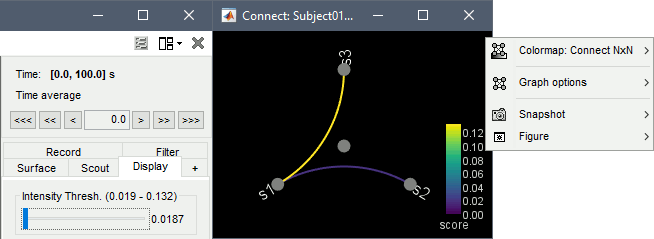
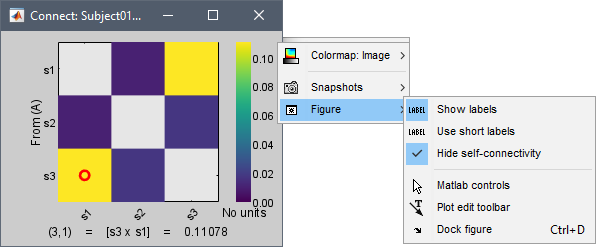
Display options:
Diagonal values: The value of the connectivity metric between a signal and itself is plotted as zero so that it doesn't force scaling the colormap to 1 if the other values are much smaller.
Labels: Click on the figure to see the signal names and connectivity values as the image legend. In order to see the labels corresponding to each column and row: right-click on the figure > Figure > Show labels. If your signal names are very long, try the option Use short labels.
Colormap: By default, the NxN colormap is configured to display the absolute values of the connectivity measures. As in the general case, correlation values can be positive or negative, you need to check this option carefully. If you expect to see negative values, make sure to change the colormap configuration: right-click on the figure > Colormap > Uncheck Absolute values.
Coherence
Coherency or complex coherence, 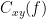 , is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Its magnitude square coherence (MSC),
, is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Its magnitude square coherence (MSC), 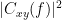 , often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals
, often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals 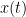 and
and 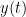 , with spectra
, with spectra 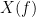 and
and 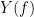 , the MSC is defined as:
, the MSC is defined as:
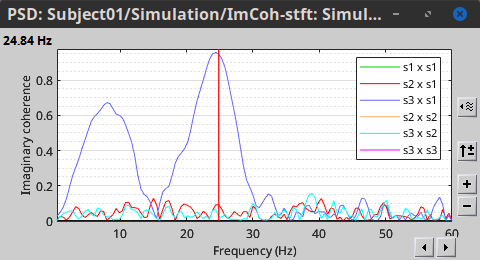
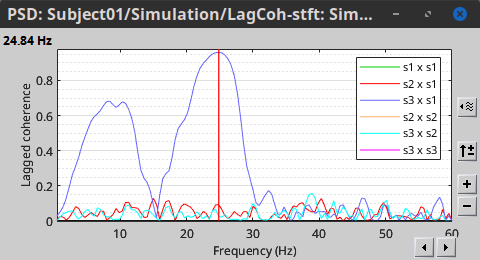
Two related measures, which alleviate the problem of volume conduction, are imaginary coherence (Nolte et al., 2004), 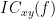 , and the lagged coherence (Pascual-Maqui, 2007),
, and the lagged coherence (Pascual-Maqui, 2007), 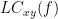 , which are defined as:
, which are defined as:
where 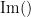 and
and 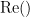 describe the imaginary and real parts of a complex number.
describe the imaginary and real parts of a complex number.
To calculate coherence values in Brainstorm, select the process.
Process options
Process Connectivity > Coherence NxN:
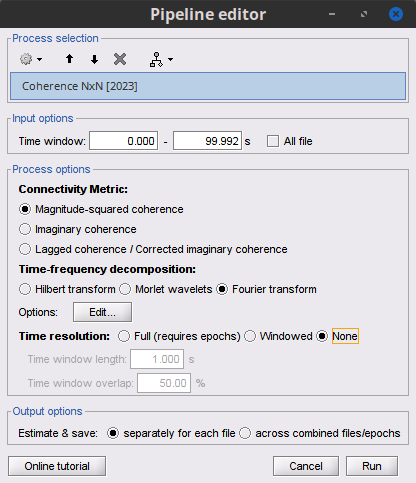
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Remove evoked response: If checked, removes the average of all the files in input (the "trials") from each file, before computing the connectivity measure. Meaningful only in the context of ERP/ERF analyses. Uncheck it.
Process options: Different measures. Select: Magnitude squared coherence.
Window length: Duration in seconds for the spectrum estimation. Set to: 1s.
Overlap: Percentage of overlap between consecutive windows. Set to: 50%.
Highest frequency: After the computation, removes all the frequencies above this threshold, mostly for visualization purposes. It should be <= Fs/2. Set to: 60 Hz.
Output options: Select: Save individual results.
Result visualization
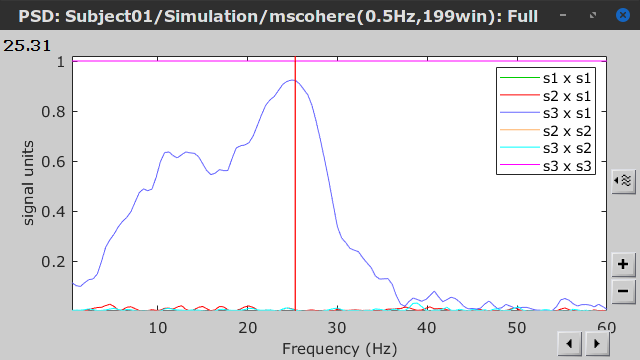
Coherence is a function of frequency, as such, for each frequency point there is a connectivity graph and a connectivity matrix. Right-click on the coherence result file to see its display options:
Display as graph: Plot the connectivity graph at a given frequency point.
Display as image: Plot the connectivity matrix at a given frequency point.
Power spectrum: Plot coherence as a function of frequency for all the possible node pairs.
Open the 3 representations. These representations are linked such as by clicking on the spectral representation of the coherence, we change the frequency that is displayed in the connectivity graph and matrix. This frequency can be also changed in the Time panel.
|
|
|
|
|
|
In the same way, we can compute the other types of coherence. The figure below presents the spectra for the imaginary coherence (left) and the lagged coherence (right). Both, imaginary and lagged coherence aim to address the volume conduction problem, although they present small differences.
|
|
|
Granger causality
Granger causality (GC) is a method of directed functional connectivity, which is base on the Wiener-Granger causality methodology. GC is a measure of linear dependence, which tests whether the prediction of signal 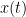 (using a linear autoregressive model) is improved by adding signal
(using a linear autoregressive model) is improved by adding signal 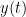 (also using a linear autoregressive model). If this is true, signal
(also using a linear autoregressive model). If this is true, signal 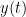 has a Granger causal effect on the first signal. In other words, independent information of the past of signal
has a Granger causal effect on the first signal. In other words, independent information of the past of signal 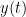 improves the prediction of signal
improves the prediction of signal 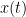 obtained with the past of signal
obtained with the past of signal 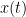 alone. GC is nonnegative, and zero when there is no Granger causality. As only the past of the signals is considered, the GC metric is directional. The term independent is emphasized because it creates some interesting properties for GC, such as, that it's invariant under rescaling of
alone. GC is nonnegative, and zero when there is no Granger causality. As only the past of the signals is considered, the GC metric is directional. The term independent is emphasized because it creates some interesting properties for GC, such as, that it's invariant under rescaling of 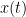 and
and 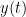 , as well as the addition of a multiple of
, as well as the addition of a multiple of 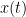 to <<latex($$y(t)$$).
to <<latex($$y(t)$$).
See Granger causality - mathematical background for a complete formulation of the method.
Despite the name, Granger causality indicates directionality but not true causality.
For example, if a variable 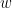 is causing both
is causing both  and
and 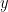 , but with a smaller delay for
, but with a smaller delay for 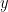 than for
than for  , then the GC measure between
, then the GC measure between  and
and 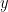 would show a non-zero GC for
would show a non-zero GC for 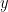 -->
-->  , even though
, even though 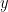 is not truly causing
is not truly causing  (Bressler and Seth, 2011).
(Bressler and Seth, 2011).
Process options
Process Connectivity > Bivariate Granger causality NxN
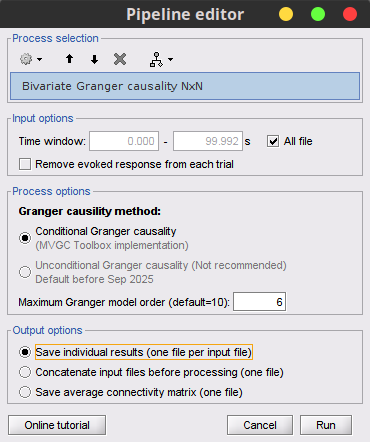
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Remove evoked response: If checked, removes the average of all the files in input (the "trials") from each file, before computing the connectivity measure. Meaningful only in the context of ERP/ERF analyses. It is recommended by some authors as it meets the zero-mean stationarity requirement (improves stationarity of the system). However, the problem with this approach is that it does not account for trial-to-trial variability. For a discussion see (Wang et al., 2008). Uncheck it.
Maximum Granger model order: The most common criteria used to define the order of the model are the Akaike’s information criterion, the Bayesian-Schwartz’s criterion, and the Hannan-Quinn criterion. Too low orders may lack the necessary details, while too big orders tend to create spurious values of connectivity. While our simulated signals were created with a model of 4, here we used as model order of 6 for a decent connectivity result.
Output options: Select Save individual results.
Result visualization
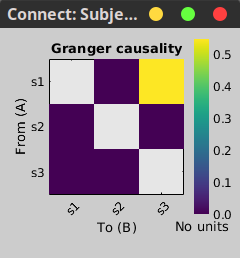
In the connectivity graph (left) the directionality is shown with an arrow head at the center for the arc connecting nodes. As GC metric is not symmetric, the connectivity matrix (right) is not symmetric. The upper right element of this matrix shows there is a signal flow from signal 1 to signal 3.
|
|
|
Spectral Granger causality
GC lacks of resolution in the frequency domain, as such, the spectral Granger causality was developed (Dhamala et al., 2008).
Process options
Process: Connectivity > Bivariate Granger causality NxN.
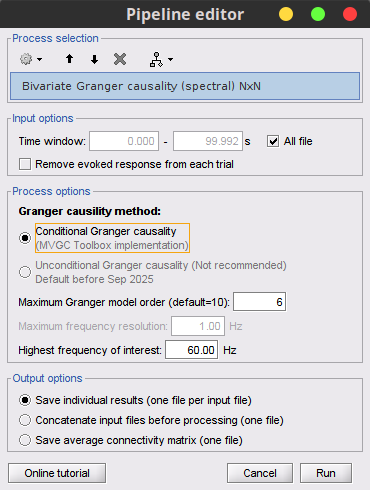
With respect to GC, spectral GC presents two extra parameters:Maximum frequency resolution: Width of frequency bins in PSD estimation. Set to 1 Hz.
Highest frequency: After the computation, removes all the frequencies above this threshold, mostly for visualization purposes. It should be <= Fs/2. Set to: 60 Hz.
Result visualization
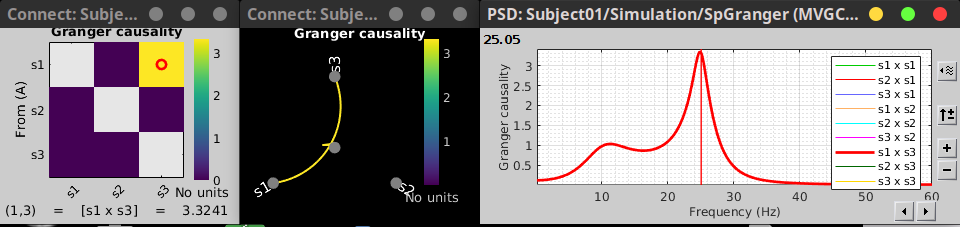
As with coherence, spectral GC can be plotted as a function of frequency. The plot below clearly shows a peak around 25 Hz for the interaction from signal 1 to signal 3, as expected.
Envelope correlation
In the time-frequency tutorial the Morlet wavelets and Hilbert transform were introduced as methods to decompose signals in the time-frequency (TF) domain. The result of this TF transformation can be seen as a set of narrowband complex signals, which are analytic signals.
The analytic signal, 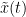 , is a complex signal uniquely associated to a real signal,
, is a complex signal uniquely associated to a real signal, 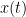 , that has been useful in signal processing due to its characteristics, more specifically, its module
, that has been useful in signal processing due to its characteristics, more specifically, its module 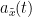 , and phase
, and phase 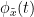 , correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the associated real signal
, correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the associated real signal 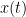 . The real part of
. The real part of 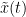 is its associated real signal
is its associated real signal 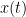 , and the imaginary part is the Hilbert transform of the same real signal
, and the imaginary part is the Hilbert transform of the same real signal 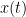 .
.
The instantaneous amplitude (or envelope) of these band analytic signals can be used to carry out pairwise connectivity analysis with metrics such as correlation and coherence (including lagged coherence).
In computing the envelope correlation, an optional step is to orthogonalize the envelopes by removing their real part of coherence before the correlation (Hipp et al., 2012). This orthogonalization process alleviates the effect of volume conduction in MEG/EEG signals.
Process options
Process: Connectivity > Envelope Correlation N×N [2020]
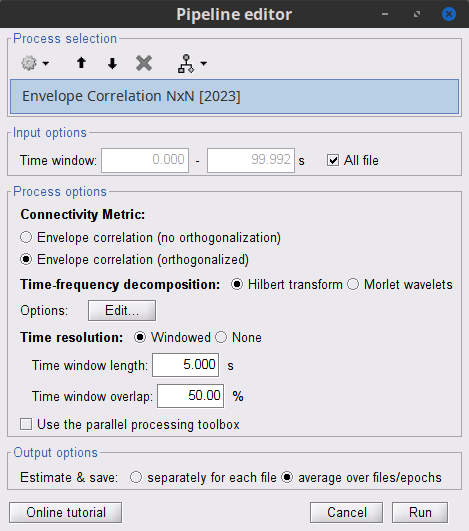
Time window: Segment of the signal used for the connectivity analysis. Select: All file.
Remove evoked response: If checked, removes the average of all the files in input (the "trials") from each file, before computing the connectivity measure. Meaningful only in the context of ERP/ERF analyses. Uncheck it.
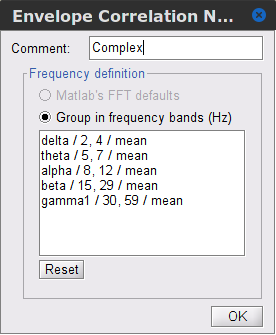
Time-frequency transformation method: Either Hilbert transform or Morlet wavelets. Each of this methods requires additional parameters that are found in an external panel that opens by clicking on Edit. See the time-frequency tutorial. In this example, the sampling frequency of the signals being 120Hz, make sure you remove the "gamma2" band.
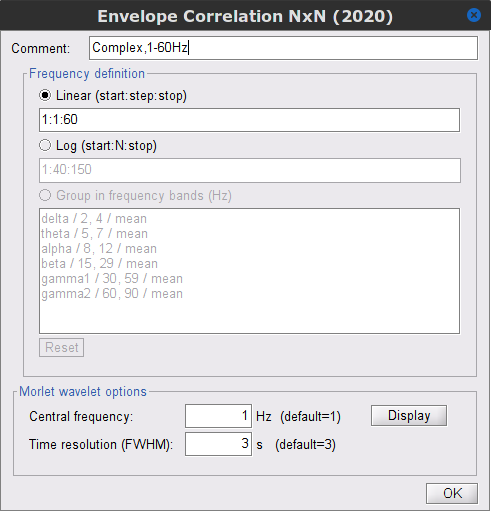
Signal splitting: This process has the capability of splitting the input data into several blocks for performing time-frequency transformation, and then merging them to build a single file. This feature helps to save a huge amount of memory and, at the same time, avoids breaking a long-time recording to short-time signals, which makes inconsistency in dynamic network representation of spontaneous data. The maximum number of blocks which can be specified is 20. Set to 1.
Connectivity measure: This is the connectivity metric that will be used with the envelopes. Select Envelope correlation (orthogonalized).
Time resolution: If Dynamic is selected, connectivity is saved for each window of analysis. If Static is selected, the connectivity results from all the windows are averaged. Select Dynamic.
Estimation window length: Duration in milliseconds to compute the connectivity measure. Set to 5000 ms
Sliding window overlap: Percentage of overlap between consecutive windows to compute the connectivity measure. Set to 50%.
Use the parallel processing toolbox: Enables the use of the parallel processing toolbox in Matlab to accelerate the computational procedure. Uncheck it.
Output configuration: Generally, the above calculation results in a 4-D matrix, where dimensions represent channels (1st and 2nd dimensions), time points (3rd dimension), and frequency (4th dimension). In the case that we analyze event-related data, we have also several files (trials). However, due to the poor signal-to-noise ratio of a single trial, an individual realization of connectivity matrices for each of them is not in our interests. Consequently, we need to average connectivity matrices among all trials of a specific event. The second option of this part performs this averaging.
Result visualization
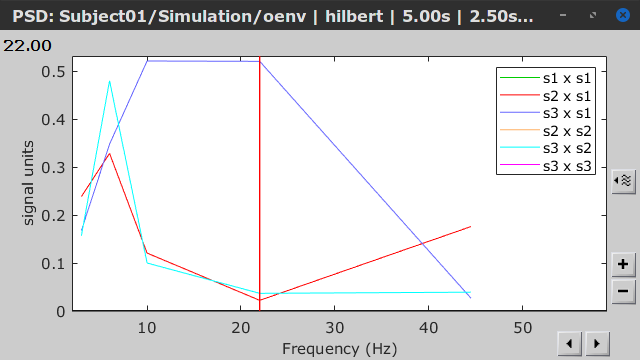
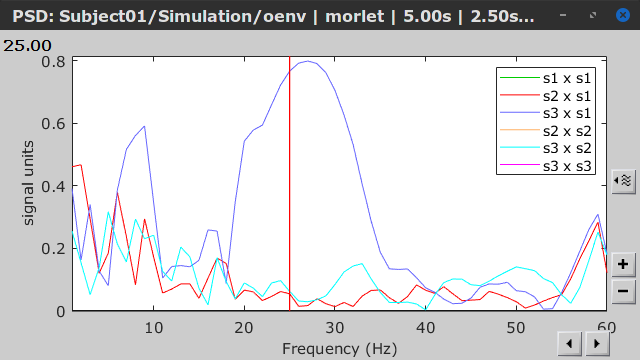
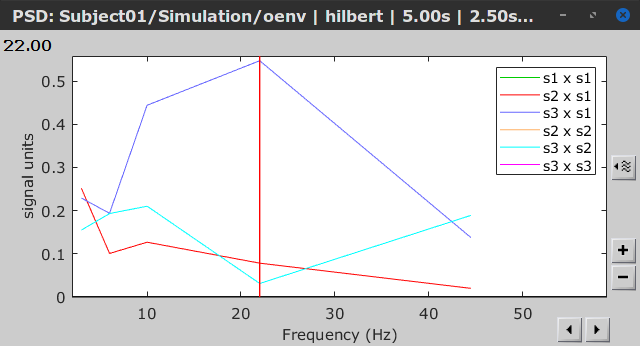
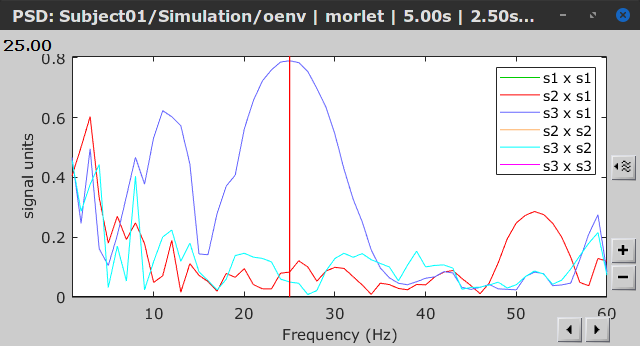
Similar to the results from coherence and spectral Granger causality, the envelope correlation can be plotted as a function of frequency, and as a function of time if the Time resolution option is set to Dynamic. Below, the results obtained with the Hilbert transform (left) and with Morlet wavelet (right) for the first 5-s window (top) and the 5-s last window (bottom).
|
First 5-s window |
|
|
Last 5-s window |
|
Phase locking value
An alternative class of connectivity metrics considers only the relative instantaneous phase between the two signals, i.e., phase-locking or synchronization (Tass et al., 1998). Phase locking is a fundamental concept in dynamical systems that has been used in control systems (the phase-locked loop) and in the analysis of nonlinear, chaotic and non-stationary systems. Since the brain is a nonlinear dynamical system, phase locking is an appropriate approach to quantifying connectivity. A more pragmatic argument for its use in studies of LFPs, EEG, and MEG is that it is robust to fluctuations in amplitude that may contain less information about interactions than does the relative phase (Lachaux et al., 1999; Mormann et al., 2000).
The most commonly used phase connectivity metric is the phase-locking value (PLV), which is defined as the length of the average vector of many unit vectors whose phase angle corresponds to the phase difference between two signals (Tass et al., 1998). If the distribution of the phase difference between the two signals is uniform, the length of such an average vector will be zero. Conversely, if the phases of the two signals are strongly coupled, the length of the average vector will approach unity. For event-related studies, we would expect the phase difference across trials to be uniform distributed unless the phase is locked to the stimulus. In that case, we may have nonuniform marginals which could in principle lead to indications of phase locking between two signals. Considering a pair of narrow-band analytic signals 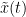 and
and 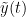 , obtained from the TF transformation using the Hilbert transform:
, obtained from the TF transformation using the Hilbert transform:
![\begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*} \begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_34340c3731fe7904b2885462bc74b6a893456cc5_p1.png)
with:
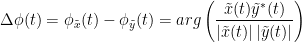
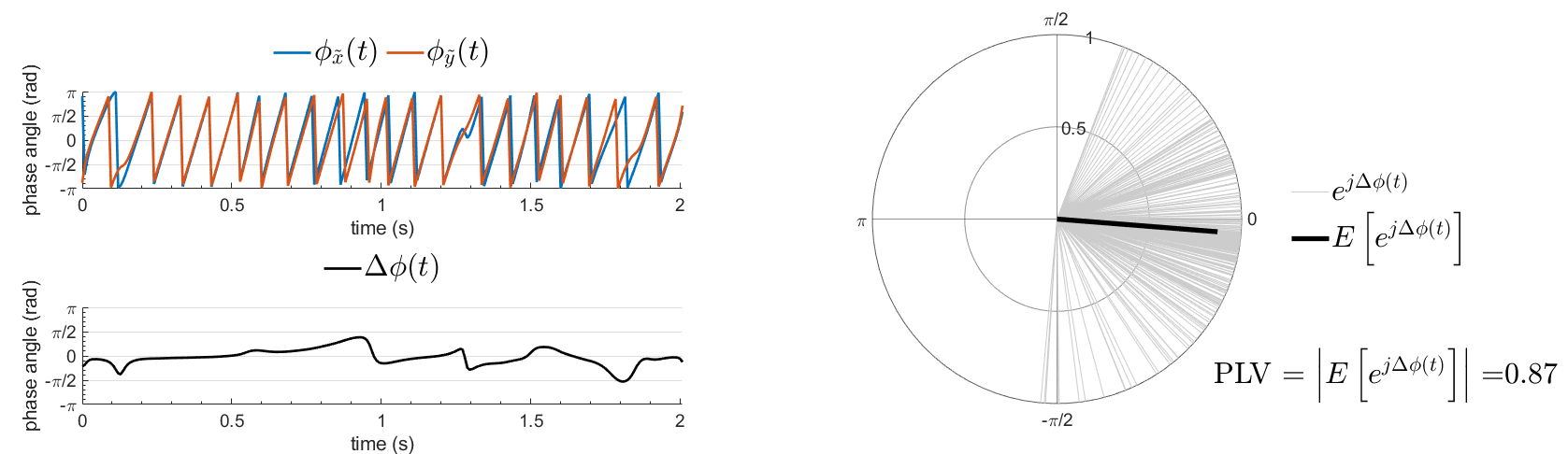
Process options
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Frequency bands: Used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial. In this example, the sampling frequency of the signals being 120Hz, make sure you remove the "gamma2" band.
Keep time information: Computes PLV across trials, thus the result is a PLV time series for each frequency band.
Measure: How the resulting vector is reported. Select Magnitude.
Output options: Select Save individual results.
Result visualization
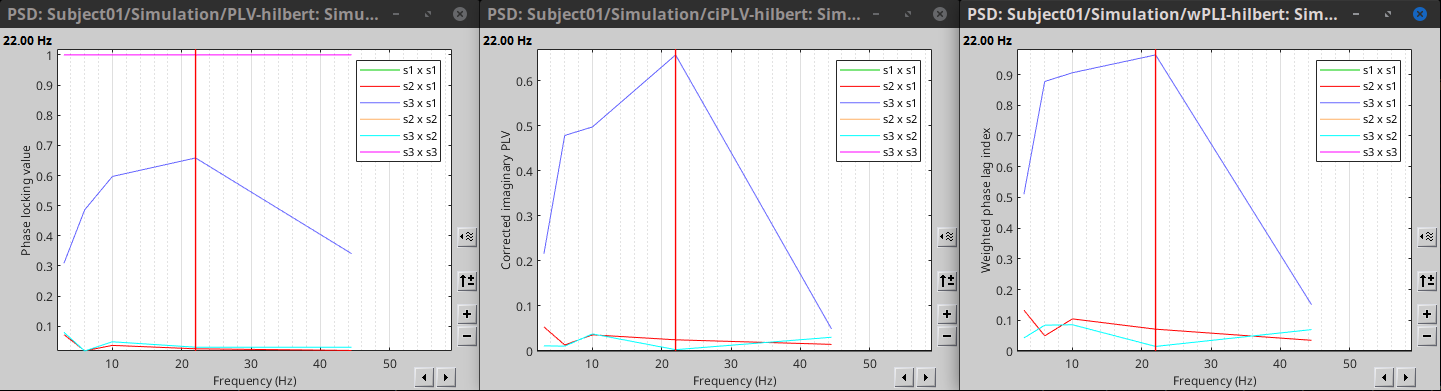
PLV is frequency resolved, and it was computed for the delta, theta, alpha, beta and gamma bands. With the simulated data, we expect a higher PLV value in the beta band (15 to 29 Hz), between signal 1 and signal 3. This result is seen as a peak at 22 Hz (center of beta band) shown in PLV as a function of frequency.
Phase transfer entropy
Phase transfer entropy (PTE) is a directed connectivity metric that quantifies the transfer entropy (TE) between two instantaneous phase time series (Lobier et al., 2014). Similar to GC, TE estimates whether including the past of both source and target time-series influences the ability to predict the future of the target time-series. In PTE, if a phase signal 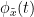 causes the signal
causes the signal 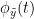 , the mutual information, between
, the mutual information, between 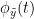 and the past of
and the past of 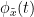 i.e.
i.e. 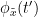 is larger than the mutual information of
is larger than the mutual information of 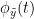 , the past of
, the past of 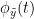 i.e.
i.e. 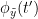 and
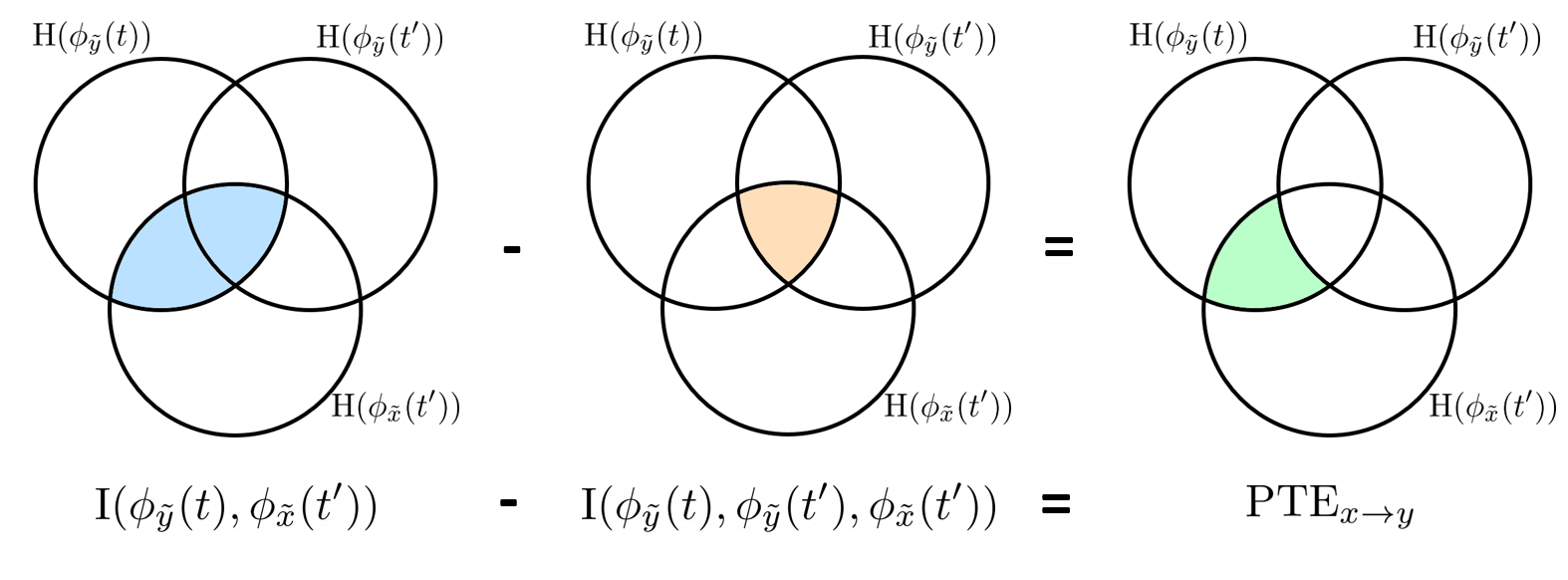
and 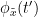 . This relationship can be seen on the Venn diagram below, where
. This relationship can be seen on the Venn diagram below, where 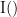 and
and  , indicate mutual information and the individual entropies respectively. Lastly, PTE cannot be negative, and its magnitude does not have a meaningful upper bound.
, indicate mutual information and the individual entropies respectively. Lastly, PTE cannot be negative, and its magnitude does not have a meaningful upper bound.
Process options
Process: Connectivity > Phase Transfer Entropy NxN
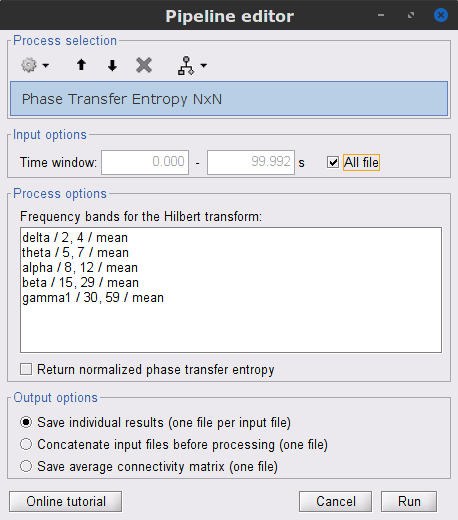
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Frequency bands: Used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial. In this example, the sampling frequency of the signals being 120Hz, make sure you remove the "gamma2" band.
Return normalized phase transfer entropy: Divides the each directional PTE value between two signals by the sum of both directional PTE values for those two signals.
Result visualization
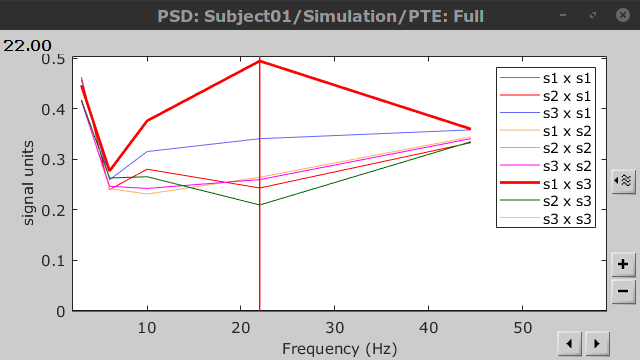
PTE was computed for the delta, theta, alpha, beta and gamma bands. With the simulated data, we expect a higher PTE value in the beta band, From signal 1 To signal 3, as PTE is directed metric. This is confirmed with a peak at 22 Hz (center of beta band) shown in PTE frequency representation.
 .
.
Method selection and comparison
The following table list the available connectivity metrics in Brainstorm and their description.
Metric |
Directionality |
Domain |
1×N |
N×N |
Time resolved |
Process |
Info |
Correlation |
Non-directed |
Time |
✅ |
✅ |
✅ |
bst_corrn.m |
|
Coherence |
Non-directed |
Frequency |
✅ |
✅ |
✅ |
bst_cohn.m |
|
Granger causality |
Directed |
Time |
✅ |
✅ |
❌ |
bst_granger.m |
|
Spectral Granger causality |
Directed |
Frequency |
✅ |
✅ |
❌ |
bst_granger_spectral.m |
|
Envelope Correlation (2020) |
Non-directed |
T-F |
✅ |
✅ |
✅ |
bst_henv.m |
|
Phase locking value |
Non-directed |
Phase |
✅ |
✅ |
❌ |
bst_connectivity.m |
|
Phase transfer entropy |
Directed |
Phase |
❌ |
✅ |
❌ |
PhaseTE_MF.m |
Real data: Auditory dataset [TODO]
TODO: Rewrite this section with coherence on scouts, with single trials.
--
In this section we will use the results obtained in the introduction tutorials. The goal here is only to illustrate the interface of these tools on real data, as the results are not particularly interesting. The corticomuscular coherence tutorial provides more complete and meaninful guidelines for computing connectivity measures on real MEG recordings.
Let's go back to our auditory oddball dataset, available in the protocol TutorialIntroduction if you have followed the introduction tutorials. As the stimulus is played on both ears, we expect to observe highly correlated activity in the primary auditory cortices, in both experimental conditions (standard and deviant beeps), around 0 to 150 ms after the stimulus due to auditory evoked responses at 50 and 100 ms (M50, M100).
In the rest of this section, correlation is computed on the scouts time series of the average response for the standard and deviant conditions. On practice connectivity metrics are computed trial-wise and the results are aggregated. An example of this approach can be seen in the corticomuscular coherence tutorial.
In the Scouts tutorial, we have created 4 scouts for these regions of interest: A1L and A1R for the left and right primary cortices respectively, IFGL for the left inferior frontal gyrus, and M1L for the left primary motor cortex.
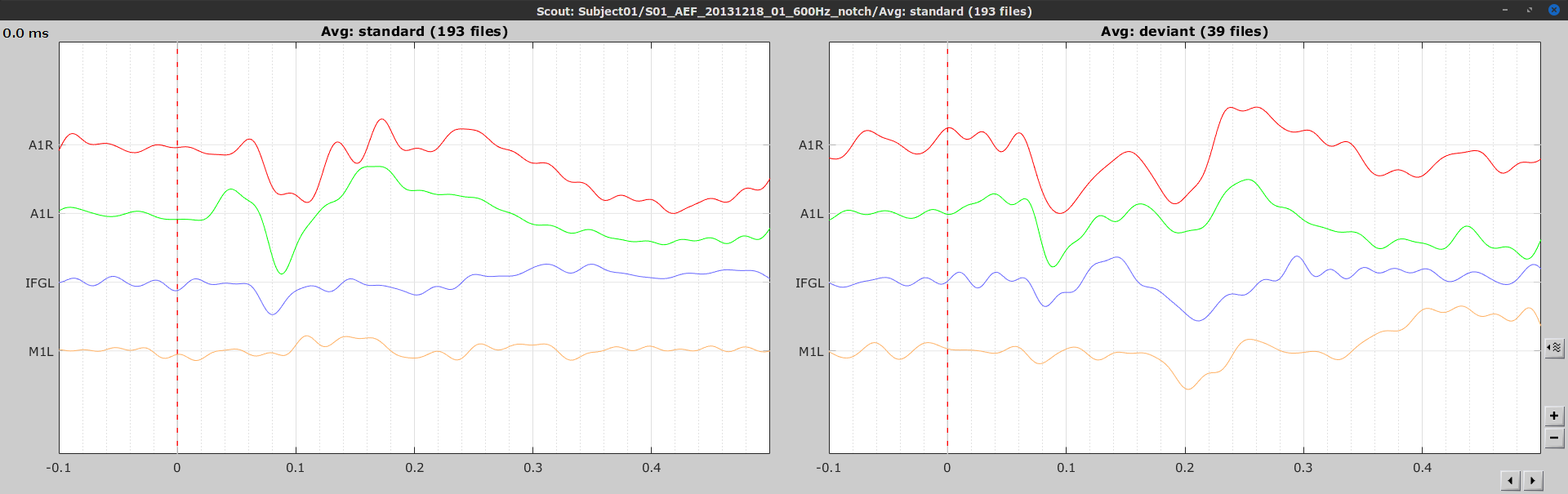
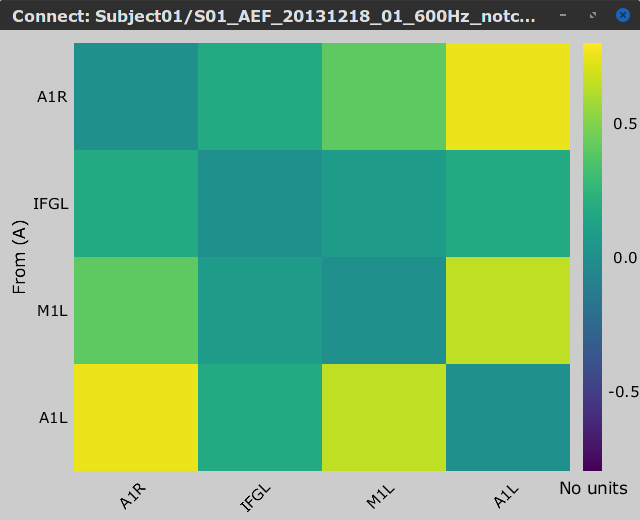
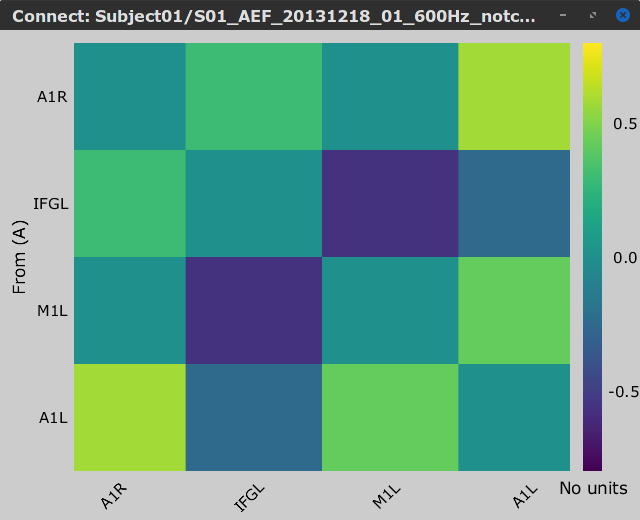
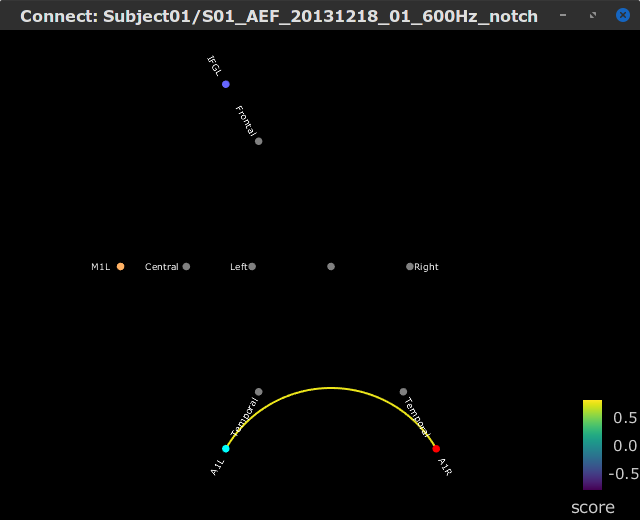
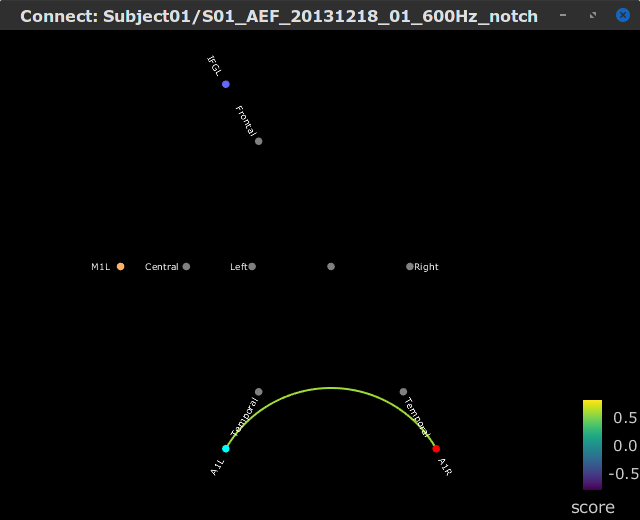
Let's compute source-domain correlation for standard and deviant conditions for the Run #1: S01_AEF_20131218_01_600Hz_notch data.
Drag and drop the source files associated to the average standard response (Avg: standard (193 files)) and the average deviant response (Avg: deviant (193 files)) within the Process1 tab, select the option 'source process' (
 ), and click on the [Run] button.
), and click on the [Run] button. Add a the process, Connectivity > Correlation NxN. Set the time window from 0 to 150 ms. Check the Use scouts option, and select User scouts as atlas in the drop menu. Set the Scout function to Mean, for When to apply the scout function select Before. And select Save individual results (one file per input). Finally click on [Run].
Display the connectivity matrices as Image (top) and as Graph (bottom). Adjust the colormaps to show signed values (no absolute), and set the a custom range from -0.8 to 0.8. Lastly, adjust the Intensity threshold for the graph to the maximum (around 0.7), so only the strongest correlations are kept, mainly, between scouts in the left and right auditory cortices.
Standard |
|
Deviant |
|
|
|
|
|
|
In this early response period, we appreciate that the correlation matrices for the standard ann deviant response are quite similar, and the strongest correlation happens between the scouts on the primary auditory cortices; just as expected.
On the hard drive
File name
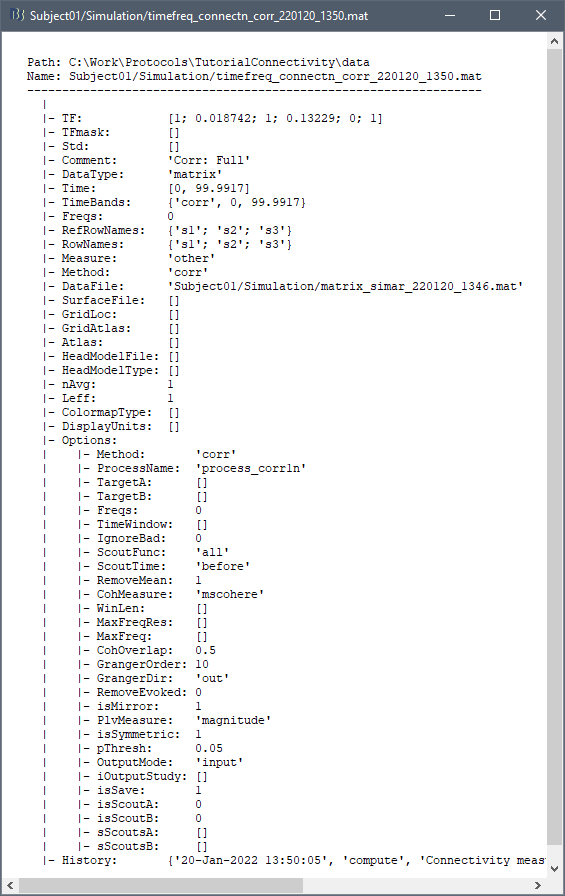
The connectivity file structure is an extension of the time-frequency structure. The file names start with timefreq_, followed by connect1 (1xN) or connectn (NxN or AxB), the connectivity method and a time stamp. Example: timefreq_connectn_corr_220120_1350.mat.
File structure
Right click on of the first connectivity file computed here > File > View file contents.
The data structure is the same as for the time-frequency files. Only the fields that some specificity related with the connectivity analysis are documented here.
TF: [Nr x Ntime x Nfreq] matrix containing all the connectivity values. The connectivity matrix R computed in bst_connectivity.m between two sets of signals A and B, is optimized and saved in the TF variable. The size of the R matrix is [Na x Nb x Ntime x Nfreq]. The relation between Na x Nb and Nr depends on the type of optimization in the file. See details below.
RefRowNames: Cell-array of strings {Na x 1}. Labels of the rows of the connectivity matrix R (Y axis in the image display, with the label From). In the case of a AxB process, these labels are the names of the signals extracted from the first list of files (FilesA).
RowNames: Cell-array of strings {Nb x 1}. Labels of the columns of the connectivity matrix R (X axis in the image display, with the label To). In the case of a AxB process, these labels are the names of the signals extracted from the second list of files (FilesB).
Freqs: Double [1 x Nfreq] for a simple list of frequencies; or cell-array {Nfreq x 3} if using frequency bands, where each line represents a band {'band_name', 'frequency definition', 'function'}
Time: [1,Ntime] for time-resolved files; [1,2] for files with no data dimension (e.g. correlation). When no time is available, this variable describes the time segment from which the connectivity measure was computed.
Options.isSymmetric: Boolean indicating whether the matrix R saved in the TF field is symmetric (e.g. NxN correlation or coherence) or not (e.g. Granger causality). If the R matrix is symmetric, it is saved in a compressed format, with only the values from lower triangular matrix.
Connectivity matrix encoding
Let's consider the structure TfMat, loaded from a connectivity file, for example by right-clicking on the file > File > Export to Matlab. The connectivity matrix R can be obtained with function GetConnectMatrix. The size of R is [Na x Nb x Ntime x Nfreq].
R = bst_memory('GetConnectMatrix', TfMat);If the matrix is not symmetrical (ie. not compressed): for each time and frequency, the list of values from the first dimension of the TF variable are reshaped into a 2D matrix: [Na x Nb].
If the matrix is symmetrical and compressed: only the lower triangular matrix is saved in the TF variable. The full matrix is first reconstructed with function process_compress_sym>Expand, then reshaped into [Na x Nb].
Saving the connectivity matrix R back in the TF variable is possible by reshaping to [Nx1] (R(:)) and then compressing again the matrix:
TfMat.TF = process_compress_sym('Compress', R(:));
Additional documentation
Related tutorials
Articles
Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M.
Identifying true brain interaction from EEG data using the imaginary part of coherency.
Clinical Neurophysiology. 2004 Oct;115(10):2292–307.Pascual-Marqui RD.
Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions.
arXiv preprint arXiv:0706.1776. 2007 Jun 12.Bressler SL, Seth AK.
Wiener–Granger causality: a well established methodology.
Neuroimage. 2011 Sep 15;58(2):323-9.Dhamala M, Rangarajan G, Ding M.
Estimating Granger causality from Fourier and wavelet transforms of time series data.
Physical review letters. 2008 Jan 10;100(1):018701.Hipp JF, Hawellek DJ, Corbetta M, Siegel M, Engel AK.
Large-scale cortical correlation structure of spontaneous oscillatory activity.
Nature neuroscience. 2012 Jun;15(6):884-90.Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, et al.
Detection of n : m Phase Locking from Noisy Data: Application to Magnetoencephalography.
Phys Rev Lett. 1998 Oct 12;81(15):3291–4.Lobier M, Siebenhühner F, Palva S, Palva JM.
Phase transfer entropy: a novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions.
Neuroimage. 2014 Jan 15;85:853-72.Barzegaran E, Knyazeva MG.
Functional connectivity analysis in EEG source space: The choice of method
Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105.Lai M, Demuru M, Hillebrand A, Fraschini M.
A comparison between scalp- and source-reconstructed EEG networks.
Sci Rep. 2018 Dec;8(1):12269.Schoffelen J-M, Gross J.
Source connectivity analysis with MEG and EEG.
Hum Brain Mapp. 2009 Jun;30(6):1857–65.Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI.
Circular analysis in systems neuroscience: the dangers of double dipping.
Nat Neurosci. 2009 May;12(5):535–40.
Forum discussions
Granger causality: https://neuroimage.usc.edu/forums/t/12506
Coherence on single trials: https://neuroimage.usc.edu/forums/t/22726
TODO
Brainstorm group
- Statistics: What tests do we recommend? Parametric or only non-parametric?
Using parametric tests requires values that are following a normal distributions:
https://neuroimage.usc.edu/brainstorm/Tutorials/Statistics#Parametric_Student.27s_t-testYou have to validate carefully for this normality hypothesis first:
https:/neuroimage.usc.edu/brainstorm/Tutorials/Statistics#Histograms
- Envelope correlation:
- Remove old processes: Amplitude envelope correlation?
- Write process_henv1.m (1xN) and process_henv2.m (AxB)
Test scout/before: https://neuroimage.usc.edu/forums/t/problem-with-time-dynamic-envelope-correlation/21542/6
- Granger:
- 1xN vs Nx1 / in vs out
- Do we want to have the same dimensions to compute subtraction in-out?
- If we do, we need to remove the xlabel (To) and ylabel (From)
Raymundo, Sylvain
- Read data: Can we find something more meaningful than what we compute in the example in the dataset? A full connectome in a task vs. baseline maybe?
Remove option: scout before/after? otherwise it must be discussed in the tutorial
- Before: First it computes the average of the sources time series by scout (Ns scouts), then computes the connectivity matrix (Ns x Ns). This connectivity matrix contains zero values on the diagonal, and is saved directly as the output file.
- After: First it estimates the connectivity between all the possible sources in all the Ns scouts. For simplicity, let's consider the scouts have number of vertices Nv: There are Ns*Nv sources, the connectivity matrix [Ns*Nv x Ns*Nv] matrix contains zeros on the diagonal. Then the scout function is applied to the connectivity values by pair of scouts: computes Ns*Ns times the average of Nv*Nv values. Each average of these Nv*Nv values, corresponding to the connectivity value for a pair of scouts, has very little chance to be zero (even if there are zeros on the diagonal). The final connectivity measure saved to the output file for a scout with itself is usually not zero.
- Add memory and computation time considerations
How to choose the best parameters. ex : plv better with 100 samples & narrow bands (?)
- Section on unconstrained sources:
- Explain what happens with and without scouts.
- Comments about PCA
- Mention that it is possibly easier with constrained sources?
Francois
Update section "Real data" after decided what to do with the Scout:before/after option
- Finish tutorial script
- Add tutorial script to this page
- New measures:
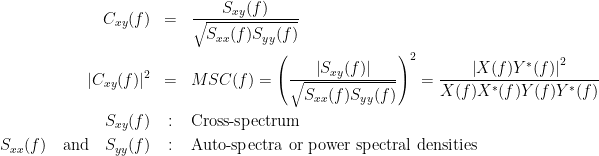
![\begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*} \begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_697a31e2ea80e1d7e07fbd14e43c910e44e14e3c_p1.png)