Tutorial 20: Head modelling
Authors: Francois Tadel, Elizabeth Bock, John C Mosher, Richard Leahy, Sylvain Baillet
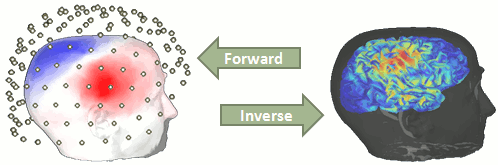
The following tutorials describe how cerebral currents can be estimated from the MEG/EEG recordings we have processed so far. To achieve this, we need to consider two distinct modeling problems: the modeling of the electromagnetic properties of the head and of the sensor array (a.k.a. head model or forward model), and the estimation of the brain sources which have produced the data, according to the head model in question. That second step is known as source modeling or solving an inverse problem. It requires that forward modeling of head tissues and sensor characteristics is completed first. This tutorial explains how to compute a head model for the subject of the auditory oddball experiment.
Contents
Why estimating sources?
Reconstructing the activity of the brain from MEG or EEG recordings involves several sophisticated steps. Athough Brainstorm simplifies the procedures required, it is important to understand whether source modeling is essential to answer the neuroscience question which brought you to collect data in the first place.
If one of your primary objectives is to identify and map the regions of the brain involved in a specific stimulus response or behaviour, source estimation can help address this aspect. Empirical interpretations of sensor topographies can inform where brain generators might be located: which hemisphere, what broad aspect of the anatomy (e.g., frontal vs. posterior regions). Source estimation improves anatomical resolution further from the interpreration of sensor patterns. The spatial resolution of MEG and EEG depends on source depth, the orientation of the current flow, and overall SNR: still, a sub-centimeter spatial resolution can be expected in ideal conditions, especially when contrasting source maps between conditions or groups.
Source mapping is a form of spatial deconvolution of sensor data. In EEG in particular, scalp topographies are very smooth and it is common that contributions from distant brain regions overlap over large clusters of electrodes. Moving to the source space can help separating active regions.
In MEG, source maps can be a great asset to alleviate some issues that are specific to the modality. Indeed in MEG and contrarily to EEG, the head of the participant is not fixed with respect to sensor locations. Hence data sensor topographies depend on the position of the subject's head. Therefore, between two runs of acquisition, or between subjects with different head shapes and sizes and positions under the helmet, the same MEG sensors may pick up signals from different parts of the brain. This problem does not exist in EEG, where electrodes are attached to the head and arranged according to standard positions.
Another important point to consider when interpreting MEG sensor maps and that can be solved by working in the MEG source space instead, is that MEG manufacturers use different types of sensor technology (e.g., magnetometers vs. gradiometers; axial vs. tangential gradiometers, etc. yielding different physical measures). This is not an issue with EEG, with essentially one sensor type (electrodes, dry or active, all measuring Volts).
Nevertheless, if your neuroscience question can be solved by measuring signal latencies over broad regions, or other aspects which do not depend crucially on anatomical localization (such as global signal properties integrated over all or clusters of sensors), source modeling might not be required. To sort out this question will influence the time and computational resources required for data analysis (source analysis multiplies the needs in terms of disk storage, RAM and CPU performance).
The origins of MEG/EEG signals
To better understand how forward and inverse modelling work, we need to have a basic understanding of the physiological origins of MEG/EEG signals. Note that, as always with modeling, we need to deal with various degrees of approximation.
Overall, it is assumed that most of - but not exclusively - the MEG/EEG signals are generated by postsynaptic activity of ensembles of cortical pyramidal neurons of the cerebral cortex. The reason is essentially in the morphology and mass effect of these cells, which present elongated shapes, and are grouped in large assemblies of cells oriented in a similar manner along the cortex. Mass effects of close-to-simulatenous changes in post-synaptic potentials across the cell group add up in time and space. These effects can conveniently be modeled at a mesoscopic spatial scale with electric dipoles distributed along the cortical mantle (green arrows in figure below). Note that there is growing evidence that MEG and EEG are also sensitive to deeper, cortical and subcortical structures, including brain nuclei and the cerebellum. Brainstorm features advanced models of these structures, as an option to your analysis. The emphasis in this tutorial is on cortical source models, for simplicity.
The primary and volume currents generated by current dipoles create differences in electrical potentials and magnetic fields that can be detected outside the head. They can be measured with electrodes placed on the skin (EEG, with respect to a reference) or very sensitive magnetic detectors (MEG).
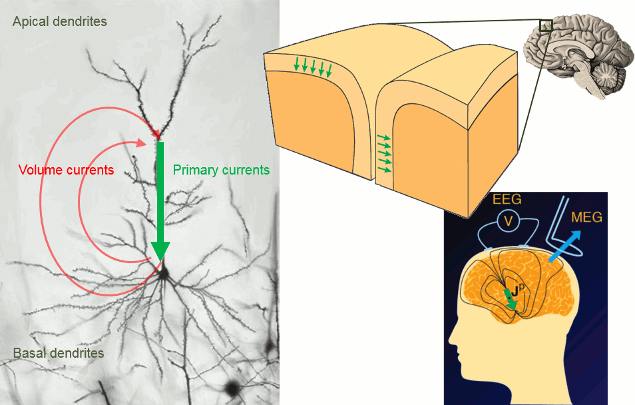
- Matti Hamalainen, 2007
Source models
Dipole fitting vs distributed models
MEG/EEG source estimation consists in modeling brain activity with current dipoles. A current dipole is a convenient model equivalent to the net post-synaptic electrophysiological activity of local assemblies of neurons. Two main approaches have been explored for source MEG/EEG estimation: dipole fitting methods - where the position and amplitude of one to a few equivalent current dipoles (ECD) are estimated over relatively short time windows - and distributed models - where the location (and typically, the orientation) of a large number dipoles is fixed; the dipoles sample a spatial grid covering the entire brain volume or the cortical surface - requiring estimation of the amplitude of a vast sample of dipoles in a fixed grid at each time point.
Equivalent dipole fitting approaches are quite straightforward and can be adequate when the number of brain regions expected to be active is small (typically less than 3). Therefore, it is most adequate for responses at early post-stimulus latencies. They cannot generalize to capture complex dynamics over extended period of time (epochs) and the associated estimation techniques are quite sensitive to initial conditions (how many dipoles to fit? where does the search start? etc). Our strategy in Brainstorm is to promote distributed source models, which are less user-dependent, can generalize to all experimental conditions, and yield time-resolved image volumes that can be processed in many different, powerful ways (group statistics, spatial segmentation, use of regions fo interest, correspondence with fMRI, etc.)
Source constraints
When opting for distributed source models, the positions and orientations of the elementary dipoles that will define the "voxel" grid of the source images produced need to be defined. This set of dipoles is called the source space. By default, Brainstorm constrains the source space to the cortex, where signal-to-noise and sensitivity is maximum in MEG/EEG. Note however that more complete models that include subcortical structures and the cerebellum are available in Brainstorm. Therefore, one decision you need to make before proceeding with source imaging is whether more complete source spaces are required to answer your neuroscience question.
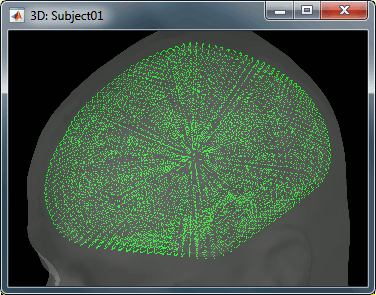
For this tutorial, we use the simple approach where current dipoles are automatically assigned to each of the vertices of the cortical surface (see the nodes in the grey mesh in the leftmost image below). When importing the anatomy of the subject, we downsampled the cortex surface to 15,000 vertices.
This default number of 15,000 vertices is empirical. Over the years, our experience seemed to show that it represents a good balance between the representation of the brain circumvolutions, the surface sampling and the amount of data that is generated. Using less vertices makes it difficult to preserve the shape of the brain, using more vertices produces more data without adding to the spatial resolution of the method and may lead to computational memory issues.
Orientation constraints
After defining the locations of the dipoles, we also need to define their orientations. We offer two main approaches: unconstrained dipole orientations or constrained to the normal of the cortex.
In the unconstrained case, three orthogonal dipoles are assigned to each vertex of the cortex surface. This triplet forms a basis to account for local currents flowing in any arbitrary direction. This option corresponds to a source space of 45,000 dipoles (3 orientations x 15000 vertices).
In the constrained case, we assign only one dipole to each vertex and impose its orientation to be normal to the cortex surface. to match the physiological observation that the pyramidal cells are mostly organized perpendicularly to the cortex surface. This has the advantage of limiting the number of dipoles to 15,000 (one per vertex) and making the results much easier to display and process. However, this constraint is sometimes too strong and distorts the reconstruction.
In the Brainstorm workflow, this orientation constraint is offered as an option of the inverse model and will be discussed in the following introduction tutorials. Technically, we always start by the computation of the forward model for the full grid of dipoles without orientation restrictions (45,000 dipoles). The orientation constraint is applied just before estimating the sources. We do not have to make this decision now.
Fully unconstrained
The spatial constraint of imposing all the dipoles to be on the cortical surface might also be too restrictive in some cases, because our model is then not able to correctly represent the activity in deeper brain structures or in the cerebellum. Therefore we also offer an option to use the entire brain volume as our source space (the green dots below represent dipoles locations in volume model). This produces results that can be better or worse depending on the data, but in all the cases much more difficult to review. Volume and mixed head volumes are discussed in the advanced tutorials about source modeling.
Forward problem
The first step of the source reconstruction consists in computing a model that explains how the electric currents or the magnetic fields flow from the electric generators in the brain (source space) through the different tissues of the head (mostly brain, CSF, skull and skin), to finally reach the sensors.
The question of building a model that connects the values we observe outside of the head (MEG/EEG) to the electric activity of the cortical dipoles in the brain is called forward problem.
The model we obtain after solving this problem is called head model in Brainstorm, but can also be referred to as forward model, leadfield matrix or gain matrix.
In this tutorial we will use the default source space: the low-resolution cortex surface with 15,000 vertices, as the support of 45,000 dipoles. We will use indifferently the terms dipole and source.
What we expect to get at the end of this process is a matrix [Nsensors x Nsources].
Available methods for MEG forward modeling
Single sphere: The head is considered as a homogeneous sphere.
Overlapping spheres: Refines the previous model by fitting one local sphere for each sensor.
OpenMEEG BEM: Symmetric Boundary Element Method from the open-source software OpenMEEG. Described in an advanced tutorial: BEM head model.
Models recommended for each modality
MEG: Overlapping spheres.
The magnetic fields are not affected too much by the heterogeneity of the tissues of the head. There is no real need for modeling the head with too much detail.EEG: OpenMEEG BEM.
The electric currents are strongly affected by jumps between very conductive tissues (brain, CSF, skin) and an insulant medium (the skull). A realistic head model is advised for integrating the properties of the skull correctly. When computing a BEM model is not an option, for instance if OpenMEEG crashes for unknown reasons, the Berg's three-layer sphere can be an acceptable option.sEEG/ECoG: The OpenMEEG BEM option is the only one available.
Computation
The forward models are related with the anatomy of the subject and the description of the sensors, therefore the menus associated to its computation are attached to the channel file.
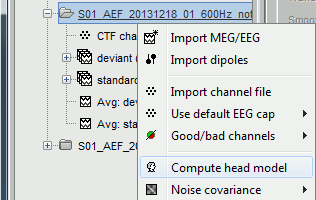
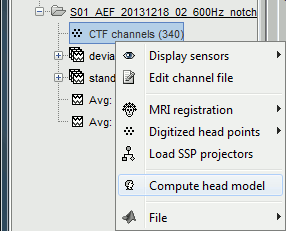
In the imported Run#01, right-click on the channel file or the folder > Compute head model.
Keep the default options selected: Source space=Cortex, Forward model=Overlapping spheres.
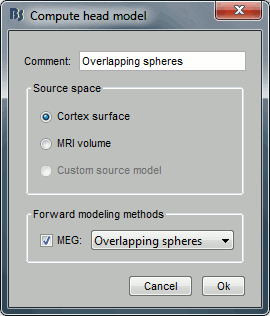
You obtain one new file in the database. It is always saved in the same folder as the channel file.
There is not much you can do with this file except for using it for estimating sources. This will be the purpose of the following tutorials.Right-click on the new head model > Check spheres. This window shows the spheres that were estimated. You can check them by following the indications written in green at the bottom of the window: use left/right arrows. At each step, the current sensor marker is displayed in red, and the sphere you see is its local estimation of the inner skull shape.
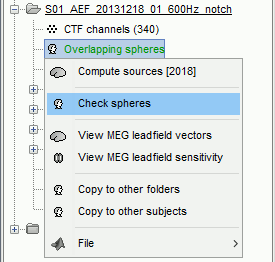
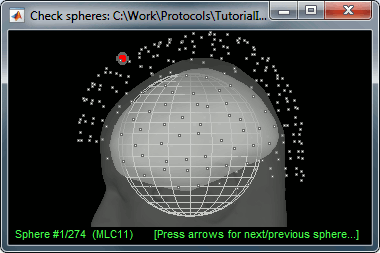
This algorithm is supposed to use the inner skull surface from the subject, but we usually do not have this information. In this case, a pseudo-innerskull is reconstructed using a dilated version of the cortex envelope.
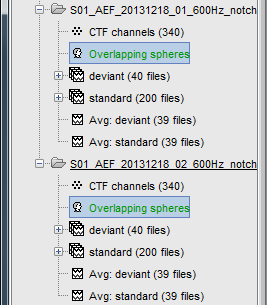
Repeat the same operation for the other file. We have two different acquisition runs with two different relative position of the head and the sensors, therefore we need to compute two different head models.
In the imported Run#02, right-click on the channel file > Compute head model.
Database explorer
Additional considerations about the management of the head model files.
If you have multiple head models computed in the same folder, you would see one displayed in green and the others in black. The one in green is selected as the default head model, it will be used for all the following computation steps. To change the default selection, double-click on another head model file (or right-click > Set as default head model).
You can use the database explorer for batching the computation of the head model. The menu "Compute head model" is available in popup menus in the database explorer at all the levels. It is applied recursively to all the folders contained in the node(s) you selected.
On the hard drive
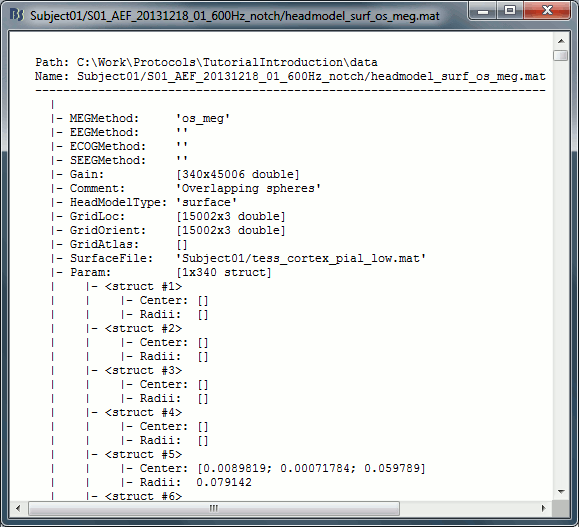
Right-click on any head model > File > View file contents:
Structure of the head model files: headmodel_*.mat
MEGMethod: Forward model used for MEG sensors ('os_meg', 'meg_sphere', 'openmeeg' or empty).
EEGMethod: Forward model used for EEG sensors ('eeg_3sphereberg', 'openmeeg' or empty).
ECOGMethod: Forward model used for ECoG sensors ('openmeeg' or empty).
SEEGMethod: Forward model used for sEEG sensors ('openmeeg' or empty).
Gain: Leadfield matrix, [Nsensors x Nsources], equivalent to [Nsensors x 3*Nvertices]
Comment: String displayed in the database explorer to represent this file.
HeadModelType: Type of source space used for this head model ('surface', 'volume', 'mixed').
GridLoc: [Nvertices x 3], (x,y,z) positions of the grid of source points. In the case of a surface head model, it corresponds to a copy of the 'Vertices' matrix from the cortex surface file.
GridOrient: [Nvertices x 3], direction of the normal to the surface for each vertex point (copy of the 'VertNormals' matrix of the cortex surface). Empty in the case of a volume head model.
GridAtlas: In the case of mixed head models, contains a copy of the "Source model options" atlas structure that was used for creating the model.
SurfaceFile: Relative path to the cortex surface file related with this head model.
Param: Description of the sphere that was estimated for each sensor (Center/Radius).
Gain matrix
The Gain matrix stores the leadfield for 3 orientations (x,y,z) at each grid point (p1, p2, ...).
The successive columns of the Gain matrix are: [p1_x, p1_y, p1_z, p2_x, p2_y, p2_z ...]To convert this unconstrained leadfield matrix to a constrained model, where the orientation of each dipole is fixed and normal to the cortex surface:
Export the head model file to the HeadModel structure: Right-click > File > Export to Matlab.
> Gain_constrained = bst_gain_orient(HeadModel.Gain, HeadModel.GridOrient);
The dimension of the output matrix is three times smaller: [Nsensors x Nvertices]
Useful functions
in_headmodel_bst(HeadModelFile, ApplyOrient, FieldsList): Read a head model.
bst_gain_orient(Gain, GridOrient): Apply orientation constraints.
References [TODO]
Huang MX, Mosher JC, Leahy RM (1999)
"A sensor-weighted overlapping-sphere head model and exhaustive head model comparison for MEG," Phys Med Biol, 44:423-440 | pdf
Additional documentation
Tutorial: BEM with OpenMEEG
Tutorial: Volume source estimation
External documentation: Electromagnetic neural source imaging
Forum: Sensor modeling: http://neuroimage.usc.edu/forums/showthread.php?1295
Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718
Forum: EEG and default anatomy: http://neuroimage.usc.edu/forums/showthread.php?1774
Forum: Mixed head models indices: http://neuroimage.usc.edu/forums/showthread.php?1878
Forum: Gain matrix units for EEG: http://neuroimage.usc.edu/forums/showthread.php?1837