Tutorial 22: Source estimation
Authors: Francois Tadel, Elizabeth Bock, Rey R Ramirez, John C Mosher, Richard M Leahy, Sylvain Baillet
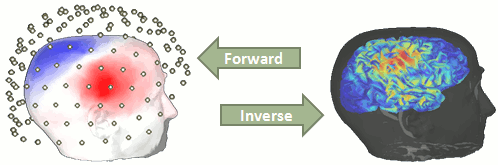
This section describes how to estimate brain activity accounting for scalp recordings.
Contents
- Background
- Source estimation options
- Computing sources for an average
- Display: Cortex surface
- Recommended post-processing steps
- Display: MRI Viewer
- Display: MRI 3D
- Sign of constrained maps
- Unconstrained orientations
- Standardization of source maps
- Delete your experiments
- Computing sources for single trials
- Averaging in source space
- Note for beginners
- Averaging normalized values
- Display: Contact sheets and movies
- Model evaluation
- Advanced options: Minimum norm
- Advanced options: LCMV beamformer
- Advanced options: Dipole modeling
- Combining MEG+EEG for source estimation
- On the hard drive
- Additional documentation
Background
Estimating brain activity at potentially thousands of brain locations (determined by the forward head model) from much fewer sensor locations is a so-called ill-posed inverse problem. One implication is that an infinite number of source activity patterns may explain equivalently well the sensor data. These aspects are explained in detail here and here.
Such ill-posedness is not specific to EEG/MEG. It is quite typical in many other fields of science and engineering.
There is a vast EEG/MEG literature on the question. Brainstorm features three well-documented types of approaches: minimum-norm imaging, beamforming, and dipole modeling.
One common advantage between these approaches is that they are computationally efficient, even on large datasets. The estimates of brain source activity are derived via a linear recombination of sensor recordings. Brainstorm therefore computes a kernel ("a large matrix") conveniently stored in the database and that can be multiplied with sensor data arrays to obtain source time series, at specific brain locations, or across the entire brain.
Below we first describe the options of the minimum-norm imaging approach, then beamformers and dipole modeling. These latter are technically similar.
Source estimation options
Method
Minimum-norm (MN) imaging
- MN imaging estimates the amplitude of brain sources distributed across the brain or constrained to the cortex. The MN solution to the ill-posed EEG/MEG inverse problem is the one that best fits the sensor data with minimum overall amplitude of brain activity.
MN imaging requires the specification of noise statistics via a so-called noise covariance matrix. MEG users can best estimate noise statistics from an empty-room recording. If not available, as in EEG, noise covariance can be derived directly from recordings (e.g., from pre-stim segments, if relevant to the scientific question) or be assumed as uniform across sensors as described below.
Beamforming
- Brainstorm features the well-studied linearly constrained minimum variance (LCMV) beamformer to estimate source activity through a spatial filtering procedure. In lay terms, beamformer scans through all potential brain locations specified in the head model and estimates their respective contributions to sensor data, while attenuating the contributions from other brain regions.
Beamforming is technically similar to MN imaging, although it is more sensitive to approximations of the head model than MN imaging, and requires specific additional inputs. It is also blind to sources at different brain locations, but which time series are highly correlated.
LCMV beamformers require the specification of the data (noise+signal) covariance matrix, estimated directly from the recordings. LCMV source images can either be used as such, or post-processed, with a dipole model fitted at every time point of their largest peak(s). Please refer to the section further below for more detail about beamformers.
Dipole modeling
Brainstorm features a simple localization approach that adjusts the parameters of a single current dipole fitted to the sensor data at each point in time. As mentioned above, a LCMV-type map is first produced, and an equivalent current dipole is fitted at the strongest peak location of that map (more detail here).
Recommended option
- After exploring many, more sophisticated alternatives, our preference is to use simple and robust imaging approaches such as MN imaging or beamforming over single dipole scanning. However, this decision is often a matter of tradition in different resarch groups or subfields.
- Brainstorm enables the convenient comparison of these three approaches on your own data, with all possible sub-options, as detailed below.
MN imaging variants
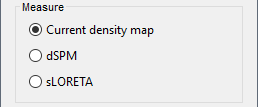
By default, MN imaging estimates the amplitude of brain electrical currents at each grid location determined by the forward head model (i.e., either in volume or on the cortical surface). As discussed here, the currents are expressed in A-m. Brainstorm does not normalize by surface area (A/m, i.e., current surface density) or volume (A/m^2, i.e., current volume density). Nonetheless, we refer to this default setting as yielding a current density map.
Current density map option: implements a L2-minimum norm estimate of brain current. FOr consistency, Brainstorm's method is identical to MNE's. Please refer to the MNE manual (Section 6, "The current estimates") for a technical description. Units are scaled to pA-m.
To further compensate for the inhomogenous sensitivity of EEG/MEG with depth and orientation of the current flow, we recommend that the current density maps obtained with this option be further standardized using a z-score transformation with respect to a specific time segment of no interest (e.g., pre-stimulus baseline) or experimental condition (e.g., resting-state).
Alternatively, such standardization can be achieved directly with respect to global noise and data covariance statistics via the dSPM and sLORETA options.
dSPM [recommended]: the derivations are those of the dynamical Statistical Parametric Mapping approach by Dale et al. (2000), based on the default MN option above and scaled with respect to the noise covariance. The resulting dSPM maps are a set of z-scores. Units: unitless "z".
sLORETA: Standardized LOw Resolution brain Electromagnetic TomogrAphy approach proposed by Pasqual-Marqui (2002).. The default current density maps are normalized with respect to the theoretical data covariance, found as the sum of the noise covariance and a model of brain signal covariance (see original paper for detail). (Note that the sLORETA data covariance is not the empirical data covariance estimated directly from the data, as used in beamformers, but rather the theoretical “statistical” data covariance used in minimum norm estimation). Per Eq 16 and 17 of Pascual-Marqui’s technical details paper, Brainstorm employs sLORETA’s concept of the unitless Resolution Kernell R. Thus the units of Brainstorm’s sLORETA implementation are output in units of A-m, which are the units of the minimum norm source estimation, which pass through the square root of the inverted resolution kernel.
Source model: Dipole orientations [TODO]
The current flow of neural activity at each source localtion is modeled by the orientation of an equivalent current dipole. Brainstorm features the following options to determine this orientation:
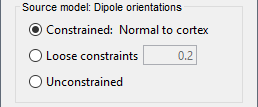
Constrained: Normal to cortex: this option is available only when working with "surface" grid locations (such as the cortical surface). Current dipoles are oriented normally to the cortical surface, to model the orientation of macrocolumns of pyramidal neurons perpendicular to the cortex.
Size of the imaging kernel: [Nvertices x Nchannels].Loose: This option is available only when working with "surface" grid locations (such as the cortical surface). In addition to a dipole normal to cortex as above, two additional dipoles are adeed in the tangential plane at each cortical location. Their amplitude is constrained below a fraction of the main normal dipole's. The recommended values are between 0.1 and 0.6. This option relaxes the constraint of strict orientation to the cortex to account for anatomical and physiological uncertainties.
Size of the imaging kernel: [3*Nvertices x Nchannels].Unconstrained: This option is available for both "surface" and "volume" source grids. There are 3 orthogonal dipoles at each grid location along the x, y, and z ("Cartesian") directions of the coordinate system.
Size of the imaging kernel: [3*Nvertices x Nchannels].Recommended option: The fully constrained option require only one dipole per source grid location, instead of three. Therefore, the source and kernel files are smaller, faster to compute and display. However, when using MRI templates instead of individual anatomy, loose/unconstrained orientation models may account for some of the model uncertainties (see this section).
Sensors

Brainstorm automatically detects the type of sensors (mEg, EEG, etc.) available from the head model selected for source imaging. In the example above, only MEG sensors are available. Select one or all the sensor types available you are interested in.
However, cross-modality calculations -- the fusion between MEG and EEG data to yield a joint source map -- are very sensitive to covariance calculations and head model approximations. As of Spring of 2018, we have also elected to NOT account for cross-covariances between different sensor types. If you wish to obtain a joint, multimodal source model, we recommend that you compute each source map separately and then combine them visually or quantitatively.
Computing sources for an average
We describe here a basic example of how to use Brainstorm to obtain a MN imaging maps of event-related average sensor data.
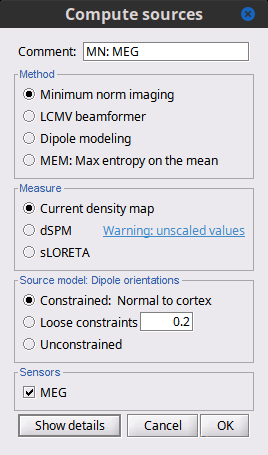
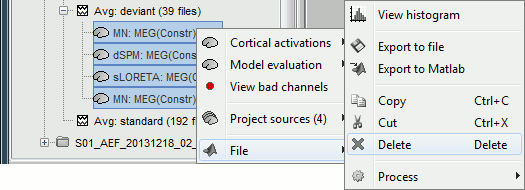
In Run#01, right-click on the average response for the deviant stim > Compute sources [2018].
Select the options: Minimum norm imaging, Current density map, Constrained: Normal to cortex.
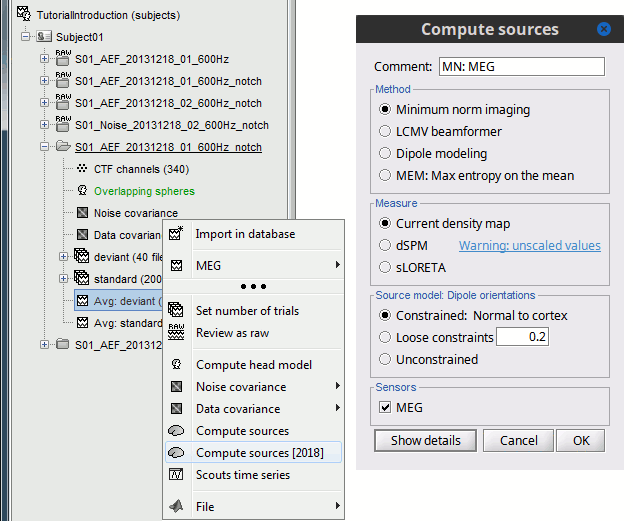
(The other "Compute sources" menu is for legacy options and implementations of the same imaging options.)The outcome of this process is a new dependent file of the sensor data, indicated with a brain icon. The file label (aka "comment") indicates "MN", which stands for "minimum-norm", and "Constr", which stands for "Constrained: normal orientation".
Display: Cortex surface
Right-click on this new source file with the brain icon and select > Cortical activations > Display on cortex.
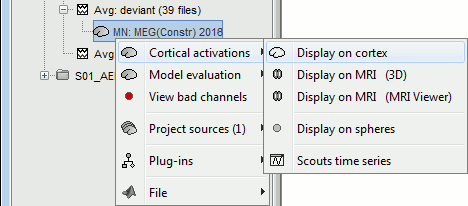
Double-click on the recordings for the deviant average to display the sensor time series alongside their brain source maps.
In the filter tab, add a low-pass filter at 40Hz to smooth the time series a bit.
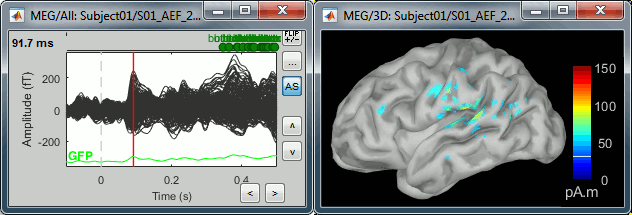
- Note how the display of the sensor and brain map windows are sync'd in time (click anywhere in the white portion of the time series window or use the left/right keyboard arrows to change the time stamp). You can also use all the menus and shortcuts introduced in the anatomy tutorial to use pre-set displays (0-6 keys).
Edit the display properties of the brain map in the Surface tab:
Amplitude: applies a minimum threshold to the source amplitude values displayed. The threshold is defined as a percentage ratio of the maximum amplitude value of the currrent color scale.
Min size: removes the smaller clusters in the source map, which number of source is smaller than the "min size" value entered.
Transparency: changes the opacity of the source map on the cortex surface.
Note that these parameters only adjust the visualization of source maps. They do not have effect on the actual source time series.
A few more words about the amplitude threshold parameter:
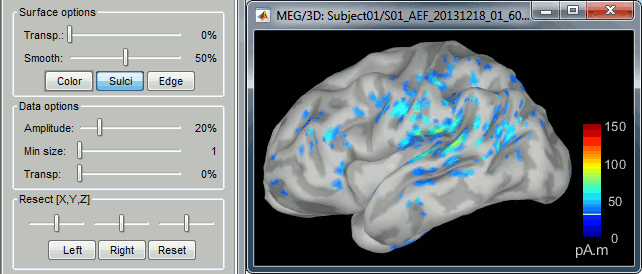
The maximum of the current colorbar depends on the Sources colormap parameters. If "Maximum: Global" is selected, the maximum indicated should be around 150 pA.m in the present dataset. This value represents the maximum of the source map across the entire dataset (across space and time). You can change the colorbar maximum value with the colormap option "Maximum: Custom".
On the screen capture below, the threshold value is set to 20%: only sources with amplitudes greater than 0.20*150 = 30 pA.m are shown.
The threshold value is shown in the colorbar with a horizontal white line.In the current data example, the source map should indicate strong activations around the primary auditory cortex around 91ms, bilaterally.
Recommended post-processing steps
The original source maps may look noisy or patchy. This is due to the strict orientation constraint used in the brain mapping procedure, which emphasizes the sensitivity of brain current strengths to the curvature of the cortex (this effect is more pronounced with MEG than EEG).
Please be cautious not to interpret disconnected colored patches as distinct brain activations without further post processing. The absolute spatial resolution of MEG source mapping is limited (~5-10mm, worse in EEG), although its relative resolution between experimental conditions, hence with post processing, can be much finer (1mm or less, see for instance this retinotopy study).
For now, you may generate smoother versions of the source maps by applying a spatial smoothing process (process "Sources > Spatial smoothing"), or using unconstrained source models, or standardizing source amplitude by applying a z-score transformation with respect to a time period of reference.
Brain maps obtained with dSPM or sLORETA are also standardize, more immune to orientation confounds (see below for more detail).
Display: MRI Viewer
Right-click on the source file for the deviant average > Cortical activations > Display on MRI (MRI Viewer).
See Brainstorm's MRI Viewer detailed tutorial in Sections #2 and #3.
This display shows cortical source activity interpolated in the the MRI volume. Set the amplitude threshold to 0% to visualize the cortex ribbon used onto which source activity is mapped.
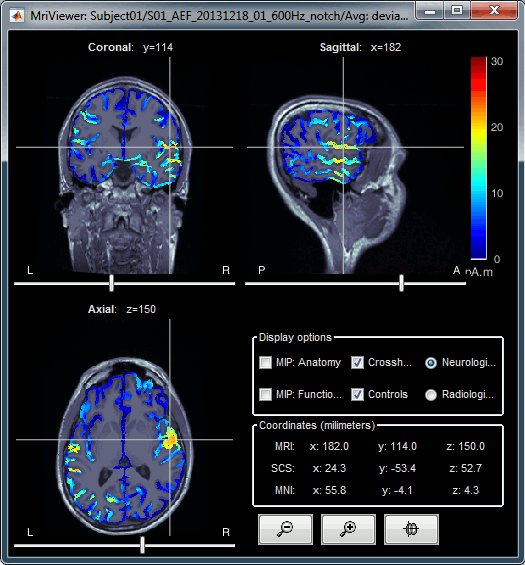
- Visualization parameters:
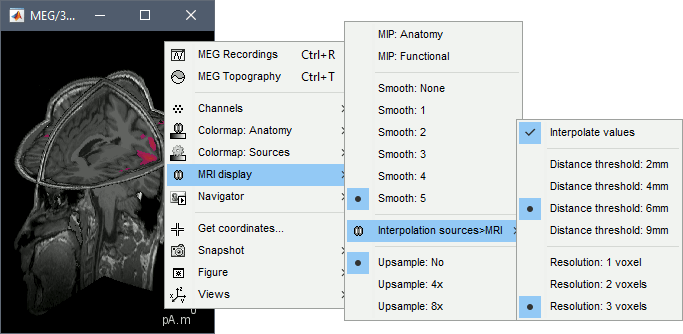
MIP Anatomy: check this box to obtain a "glass brain" view of the structural MRI, across all three spatial dimensions. MIP stands for "Maximum Intensity Projection"
MIP Functional: to obtain a glass brain view of the source map.
Amplitude threshold: in the Surface tab of the main Brainstorm window, to apply a threshold on the source map, as explained for the 3-D cortex view above.
Current time: shows the current time stamp in the data recordings, at the top-right of the main Brainstorm window. You also use the right/left arrows to move in time, or click anywhere in the white area of the sensor time series window.
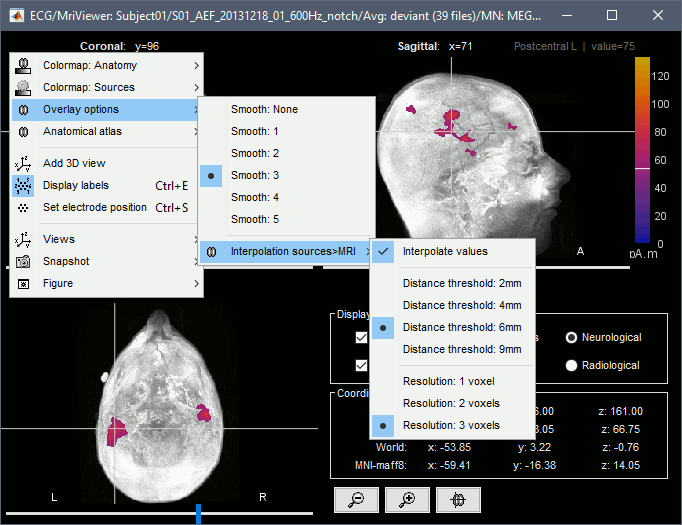
Overlay options: Right-on the figure to get access additional options.
Smooth: Increase this value to smooth the source map further, for visualization purposes. This parameter defines the size of the smoothing kernel, in number of voxels.
Interpolation sources>MRI: Parameters to compute the interpolation on the MRI volume of the source maps, available on a source space of 15000 points located on the cortex surface. This procedure associates to each of the millions of MRI voxels a value computed from these 15000 source values. This menu lets you control some parameters of this interpolation.
Interpolate values: If enabled, performs a distance-weighted interpolation with 3 nearest neighbors (default for source results). If disable, performs a single nearest-neighbor lookup instead (useful to represent integer values that should not be interpolated, such as parcel labels).
Distance threshold: Maximum distance between a colored voxel and a grid point.
Resolution: Spatial resolution of the interpolated source maps. By default, the interpolation computes a source volume downsampled by a factor 3 with respect to the anatomical MRI, in order to make the computation faster. In that case, each colored element has a dimension of 3x3x3 voxels. If a higher resolution is needed (e.g. for displaying SEEG data) this parameter can be lowered to 1 or 2 voxels. Using a 1-voxel resolution requires the computation of 3*3*3=27 times more voxel values than with the default option, leading to much longer computation times.
Display: MRI 3D
Right-click on the source file for the deviant average > Cortical activations > Display on MRI (3D).
We detailed this feature in the previous tutorial sections about MRI and surface visualization.
Keep right mouse button pressed and move the mouse to change the MR slices displayed. You can also use the Resect panel of the Surface tab.
Sign of constrained maps
Source brain maps consist of time series that are complex curves of positive and negative values.
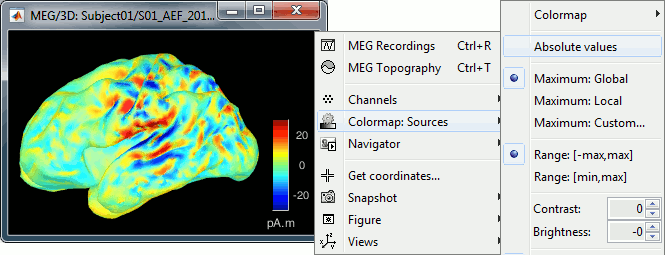
You can visualize how the sign of source amplitudes is distributed across the cortex using the cortical display of sources: set the amplitude threshold to 0%, then make sure the colormap shows relative (i.e., both positive and negative) values. For this, right click over the colorbar Colormap: Sources > uncheck the "Absolute values" option. At any time, you can double-click on the colorbar to reset the colormap options to default values.
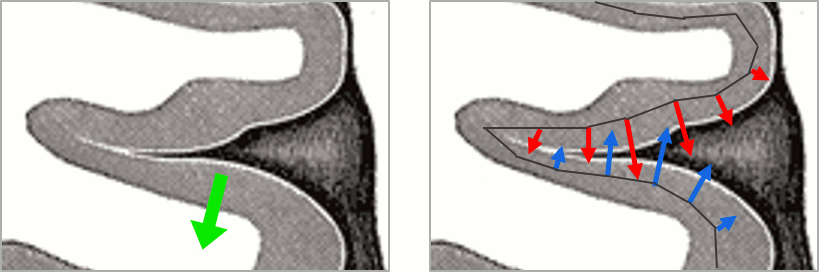
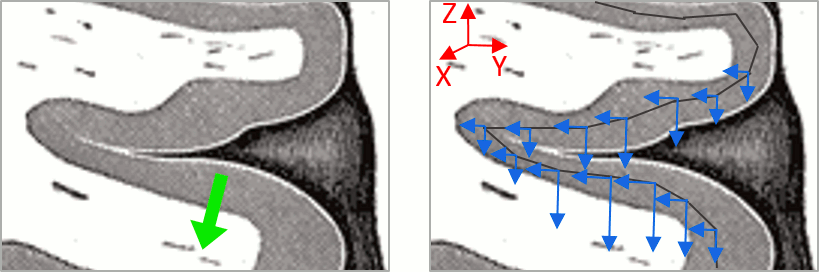
As shown below, a typical brain map will show stripes of positive and negative values, with sign changes around sulcal locations. This is another manifestation of the limited absolute spatial resolution of MEG/EEG source mapping. Sources of opposite sides of sulcus are oriented in opposite directions by default. Source mapping shows they have oppositive signs meaning that the respective neural currents are estimated as flowing in the same direction. We will see later how this sign ambiguity can be managed via either the processing of rectified source time series (if you wish to map source amplitude effects only). It is crucial to preserve the sign though if you are in interested in frequency specific brain activity, such as spectral, time-frequency and connectivity analyses.
More on sign ambiguity: On opposite walls of a sulcus, brain source are very close to each other, with opposite orientations. If the true brain activity sits only on one side of a sulcus as shown below with a green arrow, the MN-imaging brain map lower spatial resolution will spread the estimated currents over multiple nearby locations, shown with the red and blue arrows below, which have opposite default directions that are imposed by anatomy (dipoles pointing outwards the cortical surface). The signs of the current flows will be opposite, with positive values (red arrows) on one side of the sulcus and negative values on the other side (blue arrows).
For visualization purposes, we are mostly interested at this stage in visualizing the magnitude of brain activity, hence the default colormap option "absolute values" being selected.
Unconstrained orientations
The "loose constraints" and "unconstrained" options for source orientations yield 3 time series per brain location (from three orthogonal elementary sources), which increases the dimensionality of the source maps, hence complexify their interpretation, but produces smoother renderings of current flows. We recommend these options when using an MRI template instead of the individual MRI volume of study participants, or when studying subcortical brain structures. Unconstrained maps can subsequently be converted to "flat" maps, i.e. a single orientation per location, which may be needed for some processes.
Here we will illustrate the fully unconstrained case. The procedure for the loose constraints options is similar.
In Run#01, right-click on the trial average of the deviant condition > Compute sources [2018].
Select the options: Minimum norm imaging, Current density map, Unconstrained.Double-click on the source file produced (brain icon, labelled with "Unconstr") and on the corresponding sensor data file. The two brain maps below represent the same file at 91ms, with different colormap options (absolute values on the left, relative values on the right). Explanations below.
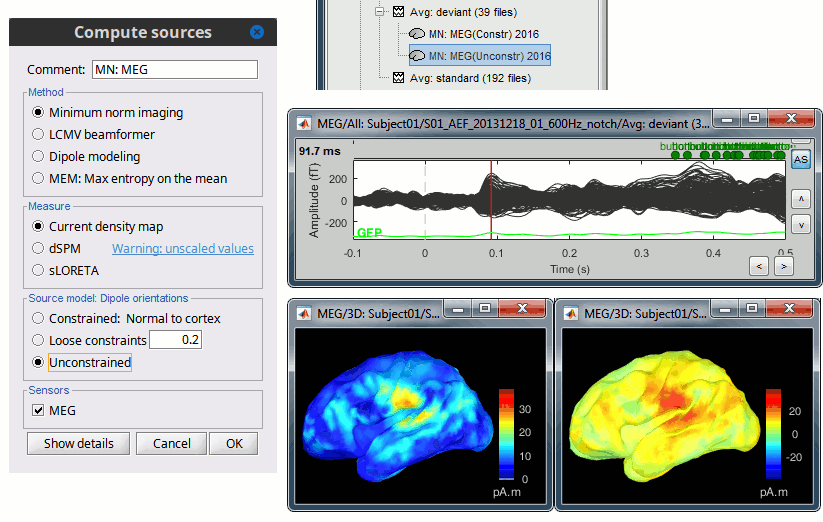
Again, using unconstrained/loose source orientations consists of triplets of dipoles with orthogonal orientations at each cortex location. To display their activity in a visually-meaningful manner, we first need to reduce the dimensions of the source data and color code the outcome. Brainstorm displays the norm of the vectorial sum of the three orientations at each vertex.
S = sqrt(Sx2 + Sy2 + Sz2)
This explains that only positive values are displayed over the source map. Note that the actual full values along each orientation (x,y,z) are signed and can be retrieved from the source file for further derivations (e.g., spectral analyses).
- The unconstrained/loose orientation maps are typically smoother than with the constrained orientation option (but see post-processing steps below) because they are less overly sensitive to changes in the curvature of the cortex.
You may delete the unconstrained source file: we will not use this option further in the introduction tutorials. Please refer to the tutorial EEG and epilepsy for further exploration of this option.
Standardization of source maps
Standardization procedures can compensate some of the bias of MN imaging source maps towards superficial source locations (in both MEG and EEG) and radially oriented current flows (in MEG). It also enables a fairer comparison of brain activity between individuals, based on its relative change with a data segment of reference.
Reference data segments can be extracted from empty-room recordings (MEG), pre-stimulus baseline or resting state data (MEG and EEG).
dSPM and sLORETA proceed to such standardization within their respective source mapping procedures. Brainstorm also features a Z-score normalization process, which enables a versatile definition of the reference data segment.
Source map standardization does not alter the dynamics of the source time series and only scales their respective amplitude changes. The scaling factors are different at each brain location, hence the resulting source maps will look different than the original MN images, but with the same temporal dynamics.
dSPM, sLORETA (embedded standardization)
In Run#01, right-click on the average sensor data of the deviant condition > Compute sources [2018].
Select successively the two normalization options: dSPM, sLORETA, (constrained).
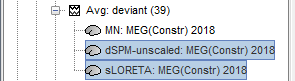
Double-click on all the resulting source files to compare them (screen capture below is at the 143-ms time point):
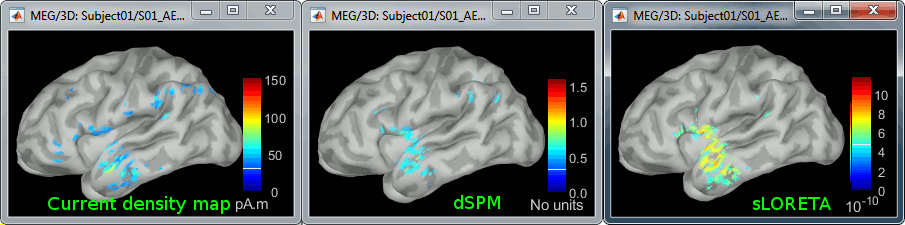
Current density maps (MN imaging): without further standardization, MN imaging tends be biased towards the most superficial gyral crowns (see Z-score procedure below).
dSPM: compensates some of this bias. The amplitude of brain maps are converted to z-scores. You may adjust the z-scores with the number of trials used to obtain the sample average via specific process "Sources > Scale averaged dSPM" (see Averaging normalized values).
sLORETA: the statistics are proper to the method and therefore, are not related to z-scores.
Z-score transformation of brain maps
The Z-transformation of MN imaging brain maps centre source amplitudes around their mean over a reference segment, and scale them with respect to their standard deviation over the same reference segment: Z = (Data - μ) / σ
- The mean and standard deviation parameters are estimated from the data and are specific of each source location. Hence, sources with lower fluctuations over the reference segment (e.g., with less noise, or overall smaller amplitude) will be boosted by the transformation.
In Process1: Select the constrained current density map (file MN: MEG(Constr)).
Run process "Standardize > Baseline normalization", [-100,-1.7]ms, Z-score transformation
Do not select "Use absolute values" as for now, we wish to preserve the sign of source amplitudes.
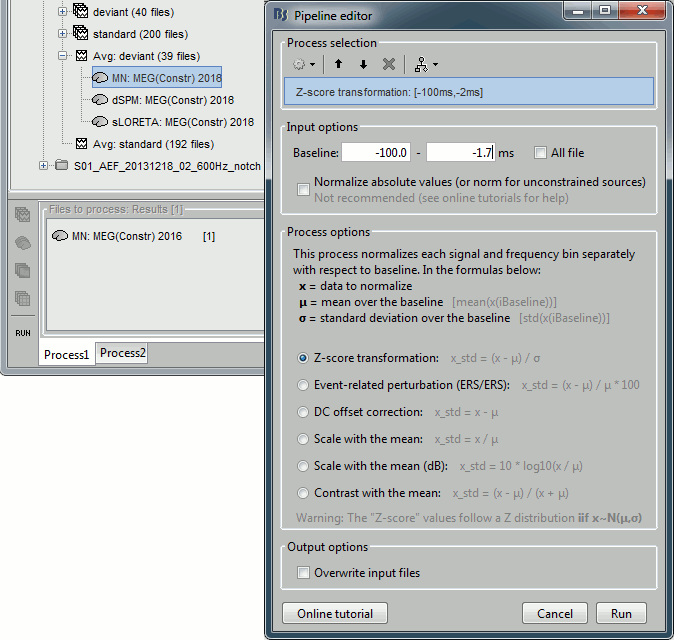
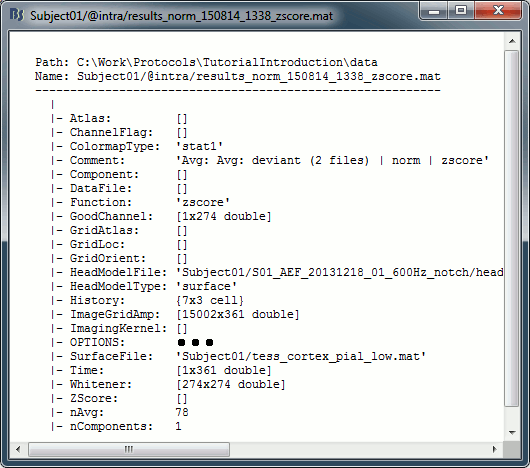
Double-click on the new brain map file (with the "| zscore" tag).
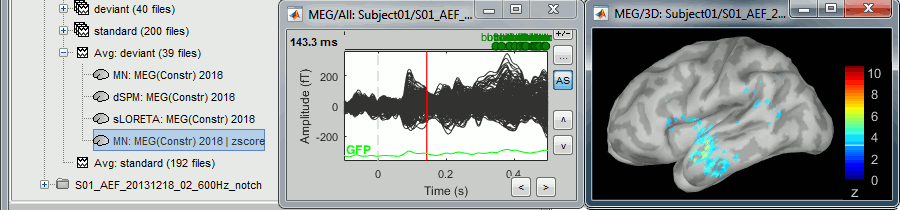
- We can appreciate that the standardized map is now qualitatively similar to dSPM and sLORETA versions.
- A map value of 3 means that the source amplitude at this time point is 3 times above the typical amplitude of that same source during the reference segment.
Please note Brainstorm's online filters do not affect the z-transformed source maps. Using the Filter tab and applying a bandpass filter will update the display all sensor time series and source maps on display, except the z-transormed maps.
If you wish to use a reference segment from another data file (e.g., a resting state recording as reference for the current task recording), use the Process2 process tab by dragging and dropping the reference source map in the Files A list on the left, and the source maps to be standardized in the Files B list on the right.
Recommended options
Use non-standardized current density maps (MN imaging) for:
- Computing imaging kernels shared across single trials.
- Averaging files across several MEG/EEG runs.
- Deriving spectral, time-frequency decompositions, phase-amplitude, or connectivity measures on single trials.
Use standardized maps (dSPM, sLORETA, Z-score) for:
- Producing source maps of trial averages (ERP/ERF).
- Before running a group analysis of source maps.
- Recommended standardization approach:
- dSPM and sLORETA are convenient linear measures which are easy to manipulate with Brainstorm.
- sLORETA maps are spatially smoother but with no direct statistical interpretation without further inference testing.
- dSPM and Z-score maps are statistically interpretable as excursions with respect to a reference data segment (Z-score), or with respect to noise covariance statistics (dSPM).
Delete your experiments
Before we proceed with the rest of the tutorial, please delete the source maps computed so far.
Select all the source files you computed until now and delete them.
Computing sources for single trials
MN imaging models are linear: their respective imaging kernels can be pre-computed from anatomy and sensor locations only, then can be applied at once on long, ongoing or several epoched data segments on the fly. Here we show how to obtain source maps across multiple single trial epochs.
Right-click on the head model or the folder for Run#01 > Compute sources [2018].
Select: Minimum norm imaging, Current density map, Constrained: Normal to cortex
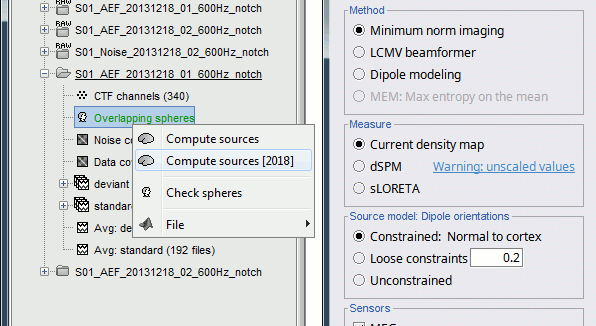
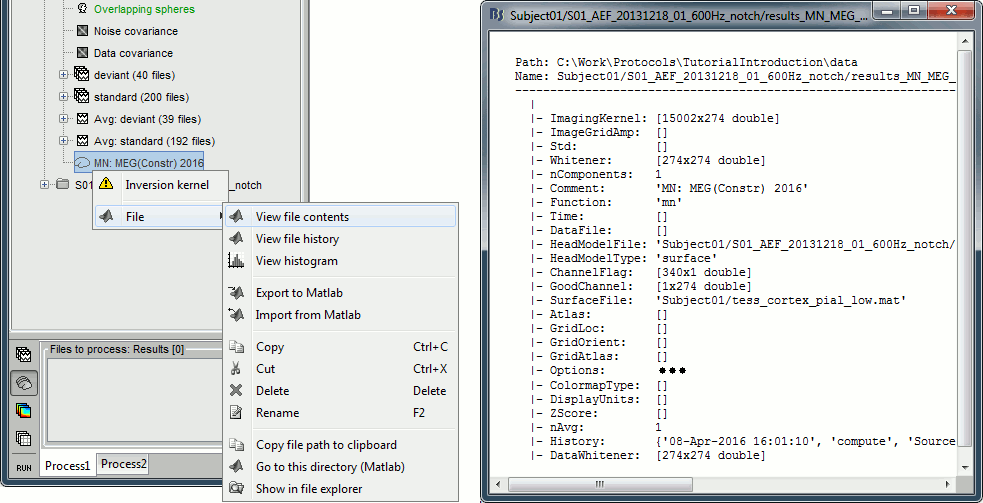
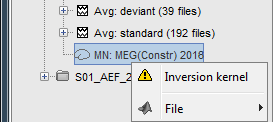
This procedure produces a shared imaging kernel (white brain icon) that is comon to all data files in Run #01. If you right-click on this new file, a warning message pops up that says "Inversion kernel". This file does not contain source maps, only the linear operator (kernel) to convert the sensor data into source maps.
All data files in Run #01 (averages and single epochs) now show a link to a source file (grey brain icon), which is a virtual brain map that is computed on the fly when visualized: Brainstorm multiplies the imaging kernel by the sensor data time series, for greater computational and data storage efficacy. You may now visualize and manipulate these virtual source maps just like the maps we computed above.
Averaging in source space
Computing the average
First compute the same source model for the the second acquisition run.
In Run#02, right-click on the head model or the folder > Compute sources [2018].
Select: Minimum norm imaging, Current density map, Constrained: Normal to cortex
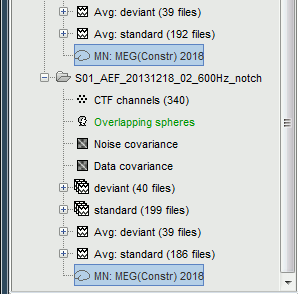
Now we have the source maps available for all the recordings, we can average them in source space across runs. This allows us to average MEG recordings that were recorded with different head positions (in this case Run#01 and Run#02 have different channel files so they could potentially have different head positions preventing the direct averaging at the sensor level).
Thanks to the linearity of the minimum norm model: MN(Average(trials)) = Average(MN(trials))
The two following approaches are equivalent:- Averaging the sources of all the individual trials across runs,
- Averaging the sources for the sensor averages that we already computed for each run.
- We will use the second option: using the sources for the sensor-level averages. It is a lot faster because it needs to read 4 files (one average file per run and per condition) instead of 456 files (total number of good trials in the two runs).
Drag and drop to the Process1 tab the average recordings for Run01 and Run02, then press the [Process sources] button on the left to select the source files instead of the MEG recordings.
Run process "Average > Average files":
Select "By trial group (subject average)" to average together files with similar names.
Select "Arithmetic average" function.
Check "Weighted average" to account for the different numbers of trials in both runs.
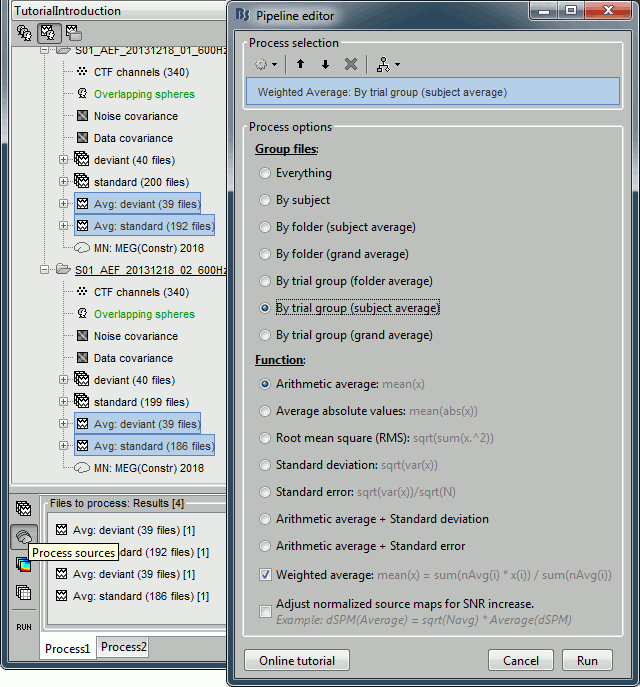
The two averages that are produced (one for each condition) are saved in the folder Intra-subject. This is where all the files computed using information from multiple folders within the same subject are saved. If you prefer to have them somewhere else, you can create new folders and move them there, just like you would do with a regular file explorer.
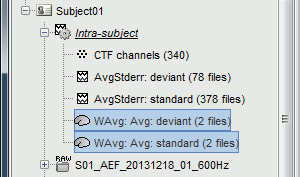
The file comments say "2 files" because they were computed from two averages each (one from each run), but the number of corresponding trials is correctly updated in the file structure.
Right-click on each of them > File > View file contents, and check the Leff field:
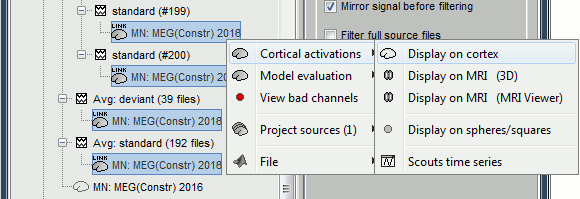
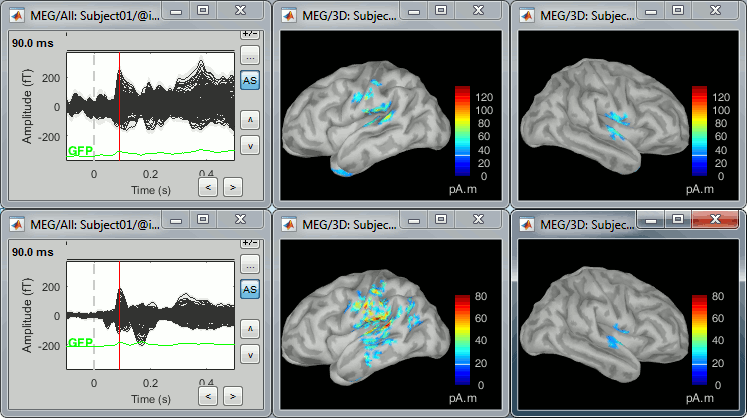
78 trials for the deviant condition, 378 trials for the standard condition.Double-click on the source averages to display them (deviant=top, standard=bottom).
Open the sensor-level averages as a time reference.
Use the predefined view "Left, Right" for looking at the two sides at the same time (shortcut: "7").
Visualization filters
Note that opening the source maps can be very long because of the filters for visualization. Check in the Filter tab, you may have a filter applied with the option "Filter all results" selected. In the case of averaged source maps, the 15,000 source signals are filtered on the fly when you load a source file. This filtering of the full source files can take a significant amount of time, consider unchecking this option if the display is too slow on your computer.
- It was not a problem until now because the source files were saved in the compact form (Kernel*recordings) and the visualization filters were applied on the recordings, then projected to the source space. This fast option is not available anymore with these averages across runs.
- The visualization filters will not be available anymore after we apply a Z-score normalization. If we want to display Z-score source maps that are smoothed in time, we will have to apply explicitly the filters on the file, with the Process1 tab.
Low-pass filter
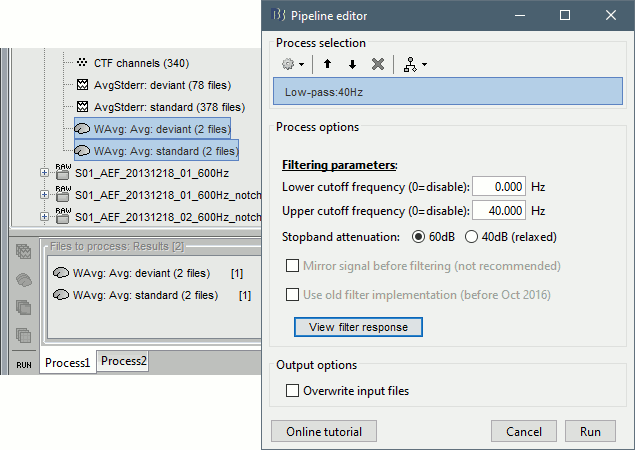
- Clear the Process1 list, then drag and drop the new averages in it.
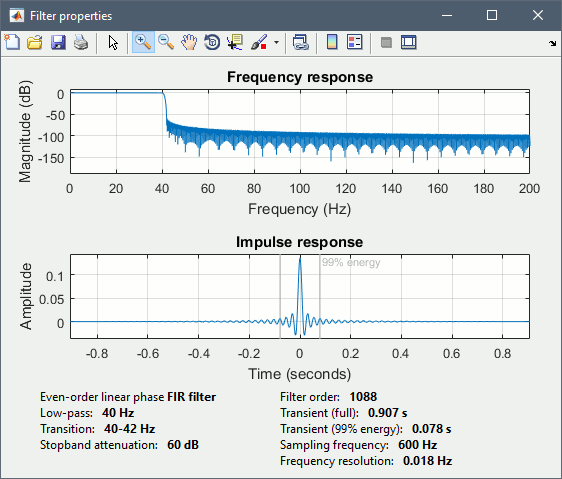
Run process "Pre-process > Band-pass filter": [0,40] Hz
Epochs are too short: Look at the filter response, the expected transient duration is at least 78ms. The first and last 78ms of the average should be discarded after filtering. However, doing this would get rid of almost all the 100ms baseline, which we need for normalization. As mentioned here, we should have been importing longer epochs in order to filter and normalize the averages properly.
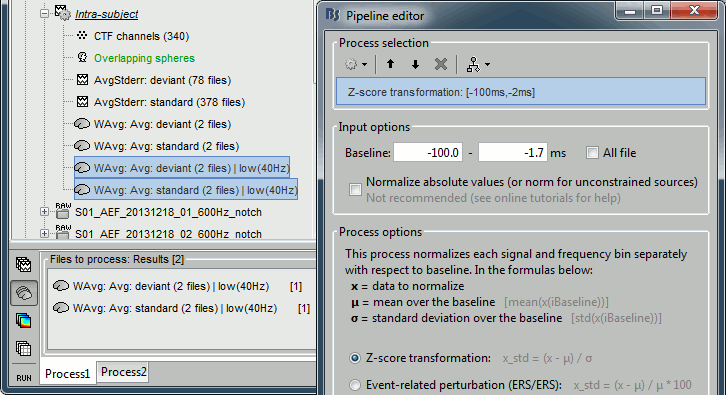
Z-score normalization
- In Process1, select the two filtered averages.
Run process "Standardize > Baseline normalization", baseline=[-100,-1.7]ms, Z-score.
Four new files are accessible in the database: two filtered and two filtered+normalized.
Double-click on the source averages to display them (deviant=top, standard=bottom).
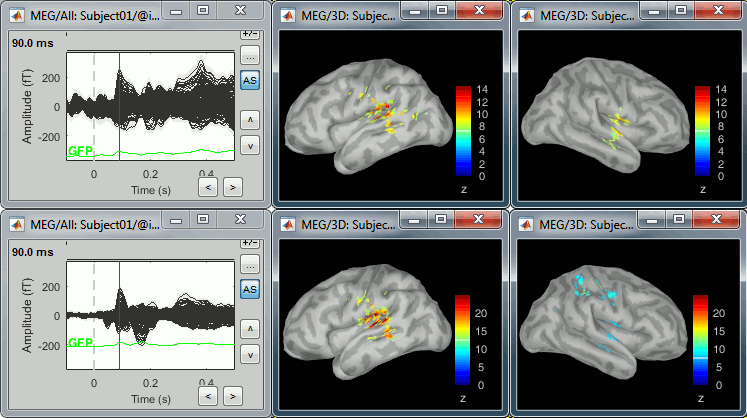
- The Z-score source values at 90ms are higher for the standard condition (~25) than for the deviant condition (~15). We observe this because the two conditions have very different signal-to-noise ratios. The standard condition has about 5x more trials, therefore the standard deviation over the baseline is a lot lower, leading to higher Z-score.
Delete the non-normalized filtered files, we will not use them in the following tutorials.
Note for beginners
Everything below is advanced documentation, you can skip it for now.
Averaging normalized values
Averaging normalized source maps within a single subject requires more attention than averaging current density maps. Since averaging reduces variance, the resulting source maps will have a different statistical distribution than the nominal distribution of the individual maps.
For example, averaging z-score normalized maps will result in maps with variance less than 1. The same holds true for dSPM maps. Assuming independent samples, the variance of an average of N maps drops by 1/N. For this reason, it is generally recommended to select the "Weighted average" option in the ‘Average files’ process when averaging trials or source maps (which performs mean(x) = (N1*sum(x1(i)) + N2*sum(x2(i)) + …)/ (N1+N2+…) ) in order to keep track of the number of samples and the actual variance of averaged statistical maps.
dSPM
- An averaged dSPM map has variance equal to 1/N (and thus standard deviation equal to 1/sqrt(N)). Therefore one could multiply the averaged dSPM map by sqrt(N) in order to maintain variance 1 under the null hypothesis. In previous versions of Brainstorm, this was done automatically when visualizing the files, and when averaging source maps with the option "Adjust normalized source maps for SNR increase". To simplify the interface and make the interpretation of maps more intuitive and consistent with other cases (min-norm, z-scored), we now dropped this option. Thus averaging dSPM maps now results in maps with variance less than 1, and is consistent with handling min-norm, z-scored and sLORETA maps.
Ajusting an averaged dSPM file by this sqrt(N) factor is still possible manually, eg. in order to visualize cortical maps that can be interpreted as Z values. Select the average dSPM files in Process1 and run process "Sources > Scale averaged dSPM". This should be used only for visualization and interpretation, scaled dSPM should never be averaged or used for any other statistical analysis.
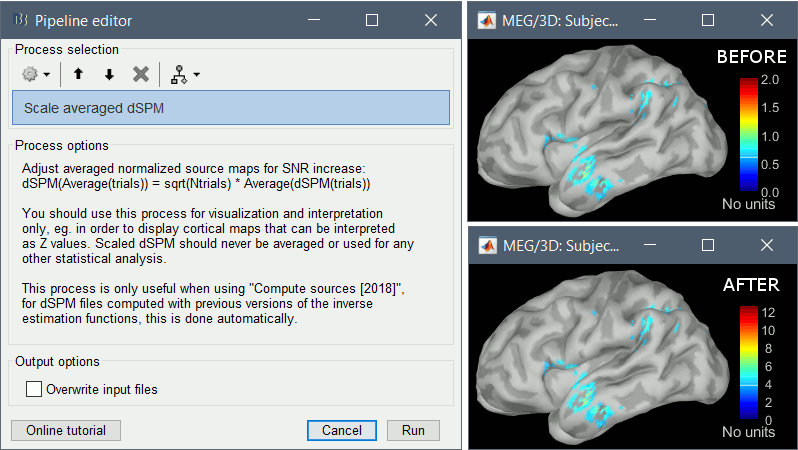
Z-score
- The same SNR issues arise while averaging Z-scores: the average of the Z-scores is lower than the Z-score of the average.
When computing averages at the subject level: Always avoid averaging Z-score maps.
Average the current density maps, then normalize.
sLORETA
- This normalization is not based on the SNR of signal, but rather on the spatial smoothness of the maps. Managing these maps is similar to min-norm maps: the variance of the individual maps is not explicitly modeled or known analytically.
- As in other cases, sLORETA(Average(trials)) = Average(sLORETA(trials)), and this relationship is guaranteed to hold with averaging uneven number of samples when using the option "Weighted average".
Display: Contact sheets and movies
A good way to represent what is happening in time is to generate contact sheets or videos. Right-click on any figure and go to the menu Snapshot to check out all the possible options. For a nicer result, take some time to adjust the size of the figure, the amplitude threshold and the colormap options (hiding the colorbar can be a good option for contact sheets).
A time stamp is added to the captured figure. The size of the text font is fixed, so if you want it to be readable in the contact sheet, you should make you figure very small before starting the capture. The screen captures below where produced with the colormap "hot".
Contact sheet: Right-click on any figure > Snapshot > Time contact sheet: Figure

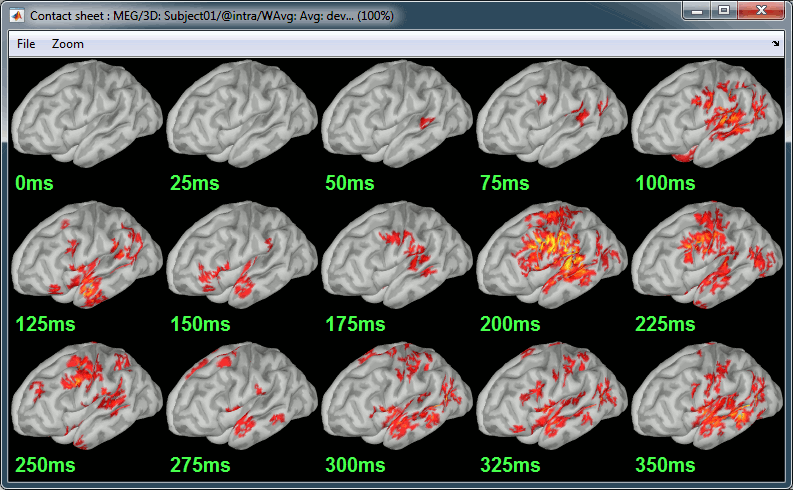
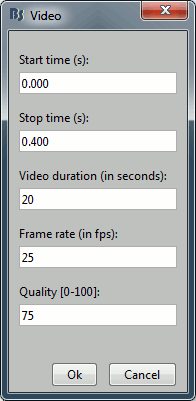
Movies: Right-click on any figure > Snapshot > Movie (time): All figures
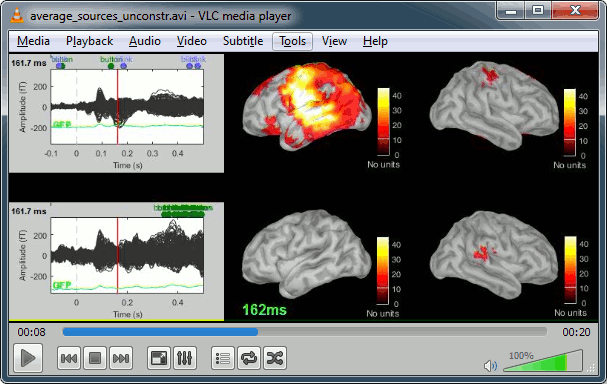
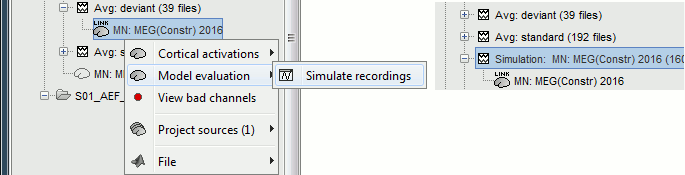
Model evaluation
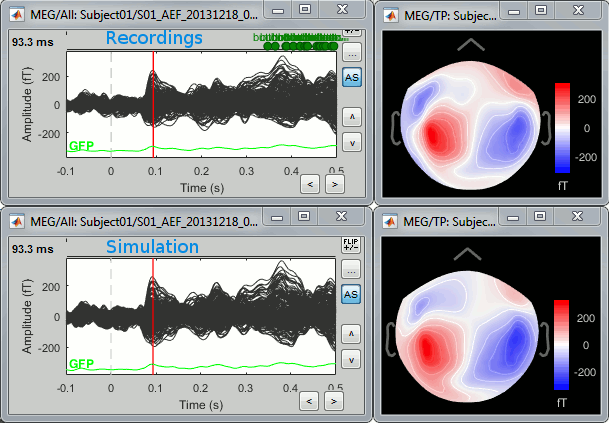
One way to evaluate the accuracy of the source reconstruction if to simulate recordings using the estimated source maps. This is done simply by multiplying the source time series with the forward model:
MEG_simulated [Nmeg x Ntime] = Forward_model [Nmeg x Nsources] * MN_sources [Nsources x Ntime]
Then you can compare visually the original MEG recordings with the simulated ones. More formally, you can compute an error measure from the residuals (recordings - simulated).
To simulate MEG recordings from a minimum norm source model, right-click on the source file, then select the menu "Model evaluation > Simulate recordings".
Open side-by-side the original and simulated MEG recordings for the same condition:
Advanced options: Minimum norm
Right-click on the deviant average for Run#01 > Compute sources [2018].
Click on the button [Show details] to bring up all the advanced minimum norm options.
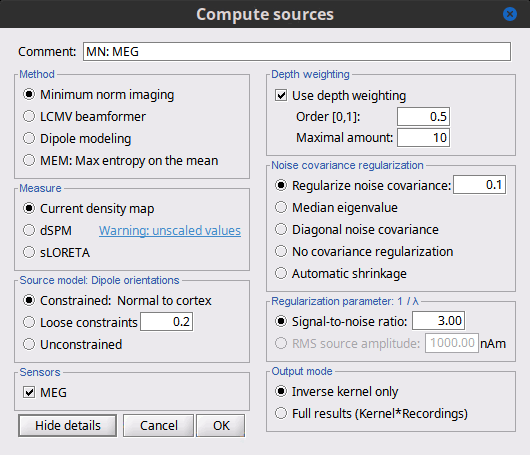
Depth weighting
Briefly, the use of various depth weightings was far more debated in the 1990s, before the introduction of MNE normalization via dSPM, sLORETA, and other "z-scoring" methods, which mostly cancel the effects of depth weighting (put another way, after normalization min norm results tend to look quite similar whether depth weighting is used or not).
By modifying the source covariance model at each point in the source grid, deeper sources are "boosted" to increase their signal strength relative to the shallower dipoles; otherwise, the resulting MNE current density maps are too dominated by the shallower sources. If using dSPM or sLORETA, little difference in using depth weighting should be noted. To understand how to set these parameters, please refer to the MNE manual. (options --depth, --weightexp and --weightlimit).
Noise covariance regularization [TODO]
MNE and dipole modeling are best done with an accurate model of the noise covariance, which is generally computed from experimental data. As such, these estimates are themselves prone to errors that arise from relatively too few data points, weak sensors, and strange data dependencies that can cause the eigenspectrum of the covariance matrix to be illconditioned (i.e. a large eigenvalue spread or matrix condition number). In Brainstorm, we provide several means to "stabilize" or "regularize" the noise covariance matrix, so that source estimation calculations are more robust to small errors.
Regularize noise covariance: The L2 matrix norm is defined as the largest eigenvalue of its eigenspectrum. This option adds to the covariance matrix a diagonal matrix whos entries are a fraction of the matrix norm. The default is 0.1, such that covariance matrix is stabilized by adding to it an identity matrix that is scaled to 10% of the largest eigenvalue.
Median eigenvalue: The eigenspectrum of MEG data can often span many decades, due to highly colored spatial noise, but this broad spectrum is generally confined to the first several modes only. Thus the L2 norm is many times greater than the majority of the eigenvalues, and it is difficult to prescribe a conventional regularization parameter. Instability in the inverse is dominated by defects found in the smallest eigenvalues. This approach stabilizes the eigenspectrum by replicating the median (middle) eigenvalue for the remainder of the small eigenvalues.
Diagonal noise covariance: Deficiencies in the eigenspectrum often arise from numerical inter-dependencies found among the channels, particularly in covariance matrices computed from relatively short sequences of data. One common method of stabilization is to simply take the diagonal of the covariance matrix and zero-out the cross-covariances. Each channel is therefore modeled as independent of the other channels. The eigenspectrum is now simply the (sorted) diagonal values.
No covariance regularization: We simply use the noise covariance matrix as computed or provided by the user.
Automatic shrinkage: Stabilization method of Ledoit and Wolf (2004), still under testing in the Brainstorm environment. Basically tries to estimate a good tradeoff between no regularization and diagonal regularization, using a "shrinkage" factor. See Brainstorm code "bst_inverse_linear_2018.m" for notes and details.
Recommended option: This author (Mosher) votes for the median eigenvalue as being generally effective. The other options are useful for comparing with other software packages that generally employ similar regularization methods. [TODO]
Regularization parameter [TODO]
In minimum norm estimates, as mentioned above in the comparisons among methods, the data covariance matrix is essentially synthesized by adding the noise covariance matrix to a modeled signal covariance matrix. The signal covariance matrix is generated by passing the source prior through the forward model. The source prior is in turn prescribed by the source model orientation and the depth weighting.
A final regularization parameter, however, determines how much weight the signal model should be given relative to the noise model, i.e. the "signal to noise ratio" (SNR). In Brainstorm, we follow the definition of SNR as first defined in the original MNE software of Hamalainen. The signal covariance matrix is "whitened" by the noise covariance matrix, such that the whitened eigenspectrum has elements in terms of SNR (power). We find the mean of this spectrum, then take the square root to yield the average SNR (amplitude). The default in MNE and in Brainstorm is "3", i.e. the average SNR (power) is 9.
Signal-to-noise ratio: Use SNR of 3 as the classic recommendation, as discussed above.
RMS source amplitude: An alternative definition of SNR, but still under test and may be dropped. [TODO]
Output mode
As mentioned above, these methods create a convenient linear imaging kernel that is "tall" in the number of elemental dipoles (one or three per grid point) and "wide" only in the number of sensors. At subsequent visualization time, we efficiently multiply the kernel with the data matrix to compute the min norm images.
For some custom purposes, however, a user may find it convenient to pre-multiply the data matrix and generate the full source estimation matrix. This would only be recommended in small data sets, since the full results can become quite large.
Kernel only: Saves only the linear inverse operator, a model that converts sensor values into source values. The size of this matrix is: number of sources (15000) x number of MEG sensors (274). The multiplication with the recordings is done on the fly by Brainstorm in a transparent way. For long recordings or numerous epochs, this form of compact storage helps saving a lot of disk space and computation time, and it speeds up significantly the display. Always select this option when possible.
Full results: Saves in one big matrix the values of all the sources (15,000) for all the time samples (361). The size in memory of such a matrix is about 45Mb for 600ms of recordings. This is still reasonable, so you may use this option in this case. But if you need to process longer recordings, you may face "Out of memory" errors in Matlab, or fill your hard drive quickly.
- Full results [15000x361] = Inverse kernel [15000x274] * Recordings [274x361]
Advanced options: LCMV beamformer
As mentioned in the introduction above, two other methods can be selected for source estimation, a beamformer and dipole modeling. In this section, we review the options for the beamformer. On top of the noise covariance matrix, you need to estimate a data covariance matrix in order to enable the option "LCMV beamformer" in the interface.
Note that pre-whitening with the noise covariance matrix has not yet been implemented for the LCMV beamformer, and only the data covariance is used in the current version. The noise covariance has no impact on the LCMV beamformer results. However, if there is no noise covariance file available in the database, the "Compute sources" interface returns an error: to go around this limitation, you may select the "No noise modeling (identity matrix)" option in the contextual menu for the noise covariance.
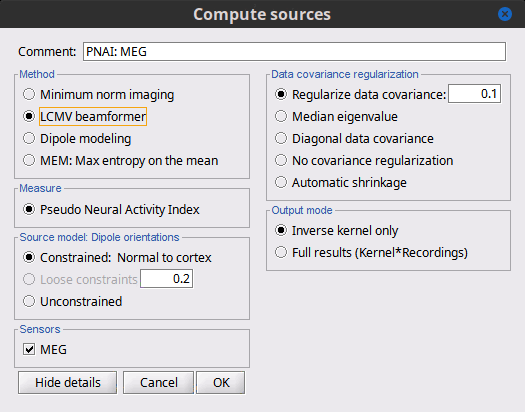
Measure
The only option "Pseudo Neural Activity Index" (PNAI), is named after the definition of the Neural Activity Index (NAI). We have modified Van Veen’s definition to rely strictly on the data covariance, without need for a separate noise covariance matrix, but the basic premise is the same as in dSPM, sLORETA, and other normalizations. Viewing the resulting "map," in an identical manner to that with MNE, dSPM, and sLORETA described above, reveals possibly multiple sources as peaks in the map. Note that PNAI scores are unitless, because they correspond to standardized statistical fluctuations of neural currents. In this way, PNAI scores are analogous to z-scoring.
Dipole orientations
We recommend you choose "unconstrained" and let the later Dipole scanning process, which finds the best fitting dipole at each time point, optimize the orientation with respect to the data.
Data covariance regularization
Same definitions as in MNE, only applied to the data covariance matrix, rather than the noise covariance matrix. Our recommendation is to use median eigenvalue.
Advanced options: Dipole modeling
Dipole modeling fits a single dipole at each potential source location to produce a dipole scanning map. This map can be viewed as a indication of how well, and where, the dipole fits at each time point. However, we recommend using the subsequent best-dipole fitting routine (dipole scanning) to determine the final location and orientation of the dipole (one per time point). Please note that this function does not fit multiple simultaneous dipoles.
Although not widely recognized, dipole modeling and beamforming are more alike than they are different – when comparing the inverse operators required to compute the dipole scanning map (dipole modeling) and the beamformer output map (LCMV), we see that they differ only in that the former uses an inverse noise covariance matrix while the latter replaces this with the inverse of the data covariance.
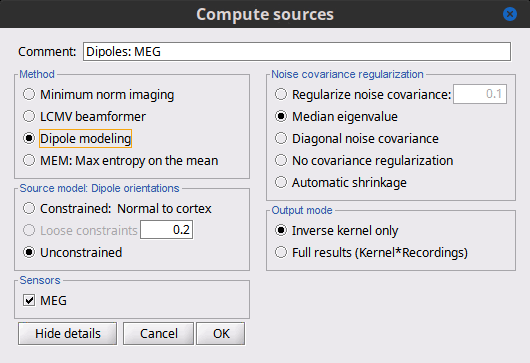
Measure
This field is now missing, but the resulting imaging kernel file is directly analogous to the PNAI result from LCMV beamforming. The user can display this scanning measure just as with the LCMV case, where again the normalization and units are a form of z-scoring.
Dipole orientations
Use "unconstrained source" modeling and let the process "dipole scanning" optimize the orientation of the dipole for every time instance.
Noise covariance regularization
Similarly, use "median eigenvalue".
The tutorial "MEG current phantom (Elekta)" demonstrates dipole modeling of 32 individual dipoles under realistic experimental noise conditions.
Combining MEG+EEG for source estimation
Magnetoencephalography and EEG sensor data can be processed jointly to produce combined source estimates. Joint processing presents unique challenges because EEG and MEG use head models that exhibit differing sensitivities to modeling errors, which can in turn lead to inconsistencies between EEG and MEG with respect to the (common) source model. In practice joint processing is relatively rare (Baillet et al., 1999). However, these data are complementary, which means that joint processing can potentially yield insights that cannot be seen with either modality alone.
For example, in the evoked responses in the data set used here, the first peak over the occipital areas is observed in MEG (90 ms) slightly before EEG (110 ms). This delay is too large to be caused by acquisition imprecisions. This indicates that we are not capturing the same brain processes with the two modalities, possibly because the orientation and type of activity in the underlying cortical sources is different.
MEG and EEG have different sensitivities to source orientation and depth. Given the challenges of joint processing, our advice is to first look at the source reconstructions for the two modalities separately before trying to use any type of fusion technique.
On the hard drive
Constrained shared kernel
Right-click on a shared inverse file in the database explorer > File > View file contents.
Structure of the source files: results_*.mat
Mandatory fields:
ImagingKernel: Linear inverse operator that must be multiplied by the recordings in order to get the full source time series. If defined, ImageGridAmp must be empty.
- Size for constrained sources [Nsources x Nchannels]
- Size for unconstrained sources [3xNsources x Nchannels]. Order of sources: source1.x, source1.y, source1.z, ... sourceN.z)
ImageGridAmp: Full source time series, in Amper.meter. If this field is defined, ImagingKernel must be empty. If you want this field to be set instead of ImagingKernel, make sure you select the advanced option Full results when estimating the sources.
- Size for constrained sources [Nsources x Ntime]
- Size for unconstrained sources [3xNsources x Ntime]. Order of sources: source1.x, source1.y, source1.z, ... sourceN.z)
Time: [1 x Ntime] Time values for each sample recorded in F, in seconds.
nComponents: Number of dipoles per grid point: 1=Constrained, 3=Unconstrained, 0=Mixed. In the case of mixed head models, the atlas GridAtlas documents region by region how the list of grid points matches the list of dipoles.
Function: Type of values currently saved in the file: 'mn', 'mnp', 'dspm', 'dspm2018', 'dspm2018sc', 'sloreta', 'lcmv', 'lcmvp', 'lcmvnai', 'lcmvpow', 'gls', 'glsp', 'glsfit', 'glschi', 'zscore', 'ersd'...
HeadModelType: Type of source space used for this head model ('surface', 'volume', 'mixed').
HeadModelFile: Relative path to the head model used to compute the sources.
SurfaceFile: Relative path to the cortex surface file related with this head model.
Atlas: Used only by the process "Sources > Downsample to atlas".
GridLoc: [Nvertices x 3], (x,y,z) positions of the grid of source points. In the case of a surface head model, it is empty and you read directly the positions from the surface file.
GridOrient: [Nvertices x 3], direction of the normal to the surface for each vertex point (copy of the 'VertNormals' matrix of the cortex surface). Empty in the case of a volume head model or unconstrained sources.
GridAtlas: Atlas "Source model" used with mixed source models.
GoodChannel: [1 x Nchannels] Array of channel indices used to estimate the sources.
DataFile: Relative path to the recordings file for which the sources where computed. If this field is set, the source file appears as a dependent of the DataFile.
Comment: String displayed in the database explorer to represent this file.
History: Operations performed on the file since it was create (menu "View file history").
Optional fields:
Options: Structure that contains all the options of the inverse calculation. This is saved in the file only for bookkeeping.
Whitener: Noise covariance whitener computed in bst_inverse_linear_2018.m
DataWhitener: Data covariance whitener computed in bst_inverse_linear_2018.m
SourceDecompVa: [3 x Nsources] Concatenated right singular vectors from the SVD decomposition of the whitened leadfield for each source (only for unconstrained sources).
SourceDecompSa: [3 x Nvertices] Vector diagonal of the singular values from the SVD decomposition of the whitened leadfield for each source (only for unconstrained sources).
Std: For averaged files, number of trials that were used to compute this file.
DisplayUnits: String, force the display of this file using a specific type of units.
ChannelFlag: [Nchannels x 1] Copy of the ChannelFlag field from the original data file.
Leff: Effective number of averages. For averaged files, number of trials that were used to compute this file. For source files that are attached to a data file, we use the Leff field from the data file.
Full source maps
In Intra-subject, right-click on one of the normalized averages > File > View file contents.
This file has the same structure as a shared inverse kernel, with the following differences:
It contains the full time series (ImageGridAmp) instead of an inverse operator (ImagingKernel).
The Z-score process updated the field Function ('mn' => 'zscore')
Source links
- The links are not real files on the hard drive, if you select the menu "View file contents" for any of them it would display the structure of the corresponding shared kernel.
They are saved in the database as strings with a specific structure: "link|kernel_file|data_file". This string associates a shared inverse operator with some recordings. The two files have to be available to load the this file. All the functions in Brainstorm are equipped to reconstruct the full source matrix dynamically.
Filename tags
_KERNEL_: Indicates that the file contains only an inverse kernel, it needs to be associated with recordings to be opened.
Useful functions
in_bst_results(ResultsFile, LoadFull, FieldsList): Load a source file and optionally reconstruct the full source time series on the fly (ImagingKernel * recordings).
in_bst(FileName, TimeBounds, LoadFull): Load any Brainstorm data file with the possibility to load only a specific part of the file.
bst_process('LoadInputFile', FileName, Target, TimeWindow, OPTIONS): The most high-level function for reading data files, can compute scout values on the fly.
Additional documentation
Articles
Minimum norm: Baillet S, Mosher JC, Leahy RM
Electromagnetic brain mapping, IEEE SP MAG 2001.dSPM: Dale AM, Liu AK, Fischl BR, Buckner RL, Belliveau JW, Lewine JD, Halgren E
Dynamic statistical parametric mapping: combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron 2000 Apr, 26(1):55-67sLORETA: Pascual-Marqui RD
Standardized low-resolution brain electromagnetic tomography (sLORETA): technical details, Methods Find Exp Clin Pharmacol 2002, 24 Suppl D:5-12LCMV Beamformer:
Jaiswal A, Nenonen J, Stenroos M, Gramfort A, Dalal SS, Westner BU, Litvak V, Mosher JC, Schoffelen JM, Witton C, Oostenveld R,
Comparison of beamformer implementations for MEG source localization,
Neuroimage. 2020 Aug 1, 216: 116797
Westner BU, Dalal SS, Gramfort A, Litvak V, Mosher JC, Oostenveld R, Schoffelen JM
A unified view on beamformers for M/EEG source reconstruction,
NeuroImage. 2022 Feb 1;246:118789
Tutorials
Tutorial: Volume source estimation
Tutorial: Deep cerebral structures
Tutorial: Computing and displaying dipoles
Tutorial: Dipole fitting with FieldTrip
Tutorial: Maximum Entropy on the Mean (MEM)
Forum discussions
Forum: Minimum norm units (pA.m): http://neuroimage.usc.edu/forums/showthread.php?1246
Forum: Imaging resolution kernels: http://neuroimage.usc.edu/forums/showthread.php?1298
Forum: Spatial smoothing: http://neuroimage.usc.edu/forums/showthread.php?1409
Forum: Units for dSPM/sLORETA: http://neuroimage.usc.edu/forums/showthread.php?1535
Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718
Forum: Sign of the MNE values: http://neuroimage.usc.edu/forums/showthread.php?1649
Forum: Combine MEG+EEG: https://neuroimage.usc.edu/forums/t/1684
Forum: Combine mag+gradiometers: http://neuroimage.usc.edu/forums/showthread.php?1900
Forum: Combine EEG+fMRI: http://neuroimage.usc.edu/forums/showthread.php?2679
Forum: Residual ocular artifacts: http://neuroimage.usc.edu/forums/showthread.php?1272
Forum: Dipole fitting: http://neuroimage.usc.edu/forums/showthread.php?2400
Forum: Dipole scanning and goodness of fit: https://neuroimage.usc.edu/forums/t/33645
Forum: Simulate recordings from sources: http://neuroimage.usc.edu/forums/showthread.php?2563
Forum: Simulate recordings from simulated signals: https://neuroimage.usc.edu/forums/t/2421
Forum: Pre-whitening: https://neuroimage.usc.edu/forums/t/10459
Forum: Adjustment of SNR option: https://neuroimage.usc.edu/forums/t/36817
Forum: LCMV beamformer and noise covariance: https://neuroimage.usc.edu/forums/t/30943
Forum: Debugging weird sLORETA results: https://neuroimage.usc.edu/forums/t/21265
Forum: Subset of sensors: https://neuroimage.usc.edu/forums/t/26496