Best: Brain Entropy in space and time
Authors: Zerouali Y, Lacourse K, Chowdhury R, Hedrich T, Afnan J, Delaire E, Lina JM, Grova C.
Are you interested in estimating the spatial extent of EEG/MEG sources?
Are you interested in localizing oscillatory patterns?
Are you interested in localizing synchronous cortical sources?

This tutorial introduces the toolbox BEst – "Brain Entropy in space and time" that implements several EEG/MEG source localization techniques within the “Maximum Entropy on the Mean (MEM)” framework. These methods are particularly dedicated to estimate accurately the source of EEG/MEG generators together with their spatial extent along the cortical surface. Assessing the spatial extent of the sources might be very important in some application context, and notably when localizing spontaneous epileptic discharges. We also proposed two other extensions of the MEM framework within the time frequency domain dedicated to localize oscillatory patterns in specific frequency bands and synchronous sources.
Contents
Introduction
BEst toolbox is the result of a collaborative work between two research teams:
|
LATIS Lab directed by Dr. Jean Marc Lina, Prof. in Electrical Engineering Dpt at Ecole de Technologie Supérieure, Montréal. Main students involved: Younes Zerouali and Karine Lacourse |
|
Multimodal Functional Imaging Lab directed by Dr. Christophe Grova, Prof. in Biomedical Engineering Dpt and Neurology and Neurosurgery Dpt, Mcgill University and Concordia University, PERFORM centre / School of Health, Montréal, QC, Canada. Main students involved: Rasheda Chowdhury, Tanguy Hedrich, Jawata Afnan and Edouard Delaire |
The package proposes three methods:
cMEM: Standard MEM with stable clustering source localization in the time-domain. The originality of this method is its ability to recover to the spatial extent of the underlying sources. To do so, the solution is estimated using a unique, but optimal, parcelization of the cortex as spatial prior. These parcels are estimated assuming brain activity to be spatially stable. (Chowdhury et al. Plos One 2013)
wMEM: wavelet based MEM dedicated to perform source localization of oscillatory patterns in the time-frequency domain. The data and the solution are expressed in a discrete wavelet expansion. The spatial prior is a parcelization of the cortex specific to each time-frequency piece of the data (Lina et al. IEEE TBME 2012).
rMEM: ridge MEM dedicated to localize cortical sources exhibiting synchrony. Continuous complex-valued wavelet analysis of the data allows detection data segments exhibiting synchrony between sensors. rMEM consists in localizing the generators of these detected synchrony patterns (Zerouali et al. IEEE TBME 2013).
See below for more information on the BEst license and the associated publications.
Principle of the “Maximum Entropy on the Mean”
The MEM solver relies on a probabilistic (Bayesian) approach where inference on the current source intensities is estimated from the informational content in the data (notion of maximum of entropy): “The maximum entropy distribution is uniquely determined as the one which is maximally noncommittal with regard to missing information” (E.T. Jaynes, Information and statistical mechanics, Phys. Rev. 106(4), 1957). The first applications of MEM in electromagnetic source localization were proposed by Clarke and Janday (The solution of biomagnetic inverse problem by maximum statistical entropy, Inv. Problem 5, 1989). A concomitant work entitled “if realistic neurophysiological constraints are imposed, then maximum entropy is the most probable solution of the EEG inverse problem” (Inv. Problem 6, 1990) was published by Rice.
The main contribution of our group consists in the prior model that we consider within the MEM regularization framework. It started with the idea of describing brain activity as being organized by cortical parcels, each parcel having the possibility of being active or not, whereas MEM offers the possibility to estimate a contrast of current density within each active parcel. This idea was first introduced within the classical MEM framework by Amblard et al. (Biomagnetic source detection by Maximum Entropy and Graphical Models, IEEE TBME, 2004), using notably data-driven approaches to estimate the cortical parcels (Lapalme et al., Data-driven parceling and entropic inference in MEG, NeuroImage, 2006). The use of such a spatial model within the MEM framework is the key idea allowing MEM to be sensitive to the spatial extent of the sources along the cortical surface (Grova et al. Evaluation of EEG localization methods using realistic simulations of interictal spikes. Neuroimage 2006). The most recent development consists in the extension of MEM within the time frequency domain in order to localize oscillatory and synchronous generators.
Best toolbox offers three different kind of information to be localized on the cortex: generators with time series stable within parcels; generators of oscillatory patterns and generators of synchrony.
Install BEst toolbox
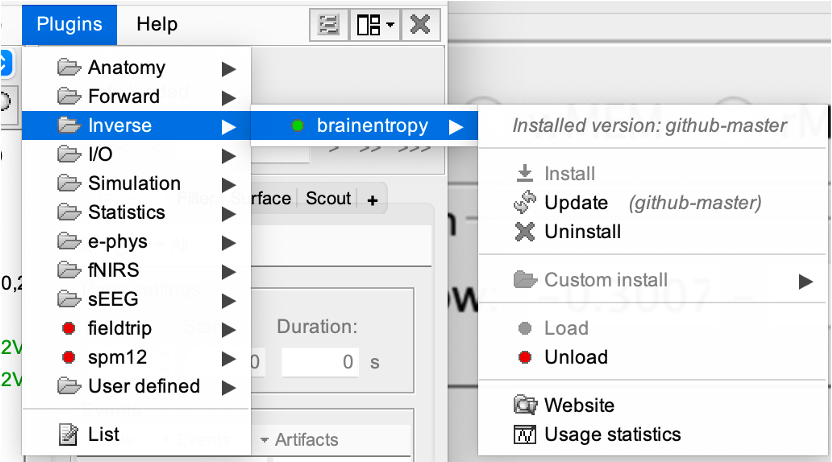
You can install the BEst toolbox from Brainstorm directly. For that, go to Plug-ins > inverse > brainentropy. Or, the plugin will install automatically once you call one of the processes for the first time.
Dataset and preliminary steps
This tutorial describes an example of how to use cMEM and wMEM to localize a map of event-related average sensor data. We used the same dataset used in Tutorial 22 entitled source estimation. The dataset can be obtained by downloading the Brainstorm dataset used in the introductory tutorials.
The detailed information about this database for source localization is provided in the following link: https://neuroimage.usc.edu/brainstorm/DatasetIntroduction
Brainstorm database
This dataset corresponds to the standard Auditory stimulation dataset provided in Brainstorm:sample_introduction.zip in https://neuroimage.usc.edu/bst/download.php.
To use this dataset, following steps should be done to prepare the data for localization in Brainstorm starting tutorials (2-16).
If all the steps were followed until Tutorial 16, an average of 39 deviant trials will be obtained.
Switch to the “Anatomy” view of this protocol, right click on the Subject01> Generate BEM surfaces using the default parameters.
Switch to the “Functional data” view; right click on the Subject01> Compute head model.
- Select OPENMEEG BEM, click Ok
- Set the conductivity of the Brain layer to 0.33, click Ok.
Right click on Subject01 > Noise covariance > No noise covariance. Unlike the other methods proposed in Brainstorm, MEM does not require prior calculation of a noise covariance matrix. This matrix can be estimated using a physiological baseline signal that can either be part of the data to be localized or a different piece of data. In some circumstances, the noise covariance matrix can be estimated from empty room data.
Launch BEst
- Go to the “Functional data (sorted by subject)” view
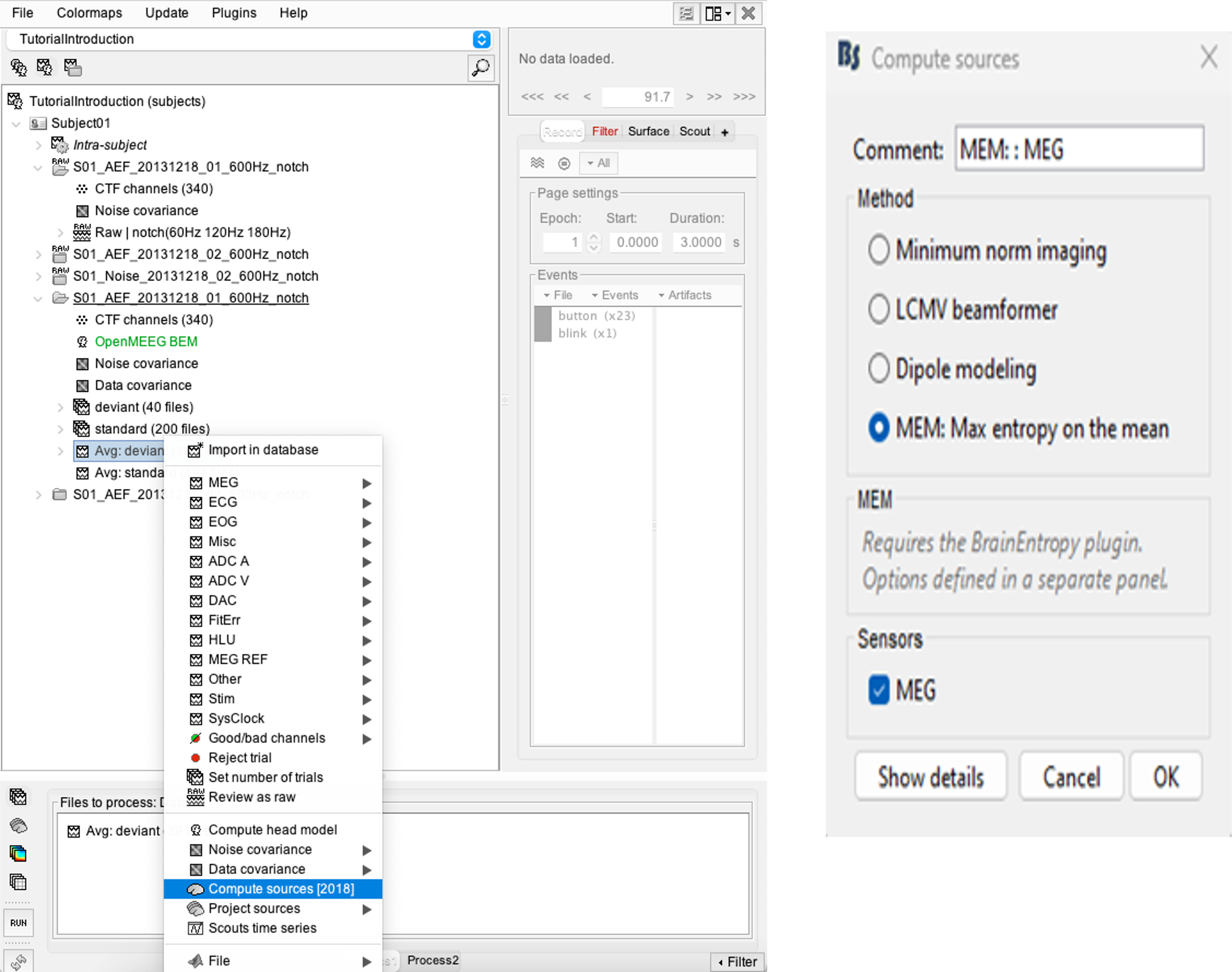
Right-click on the data average > Compute sources > MEM: Max Entropy on the mean > Ok. It is recommended that you customize the comment field so as to avoid confusion when performing multiple localizations for a given dataset.
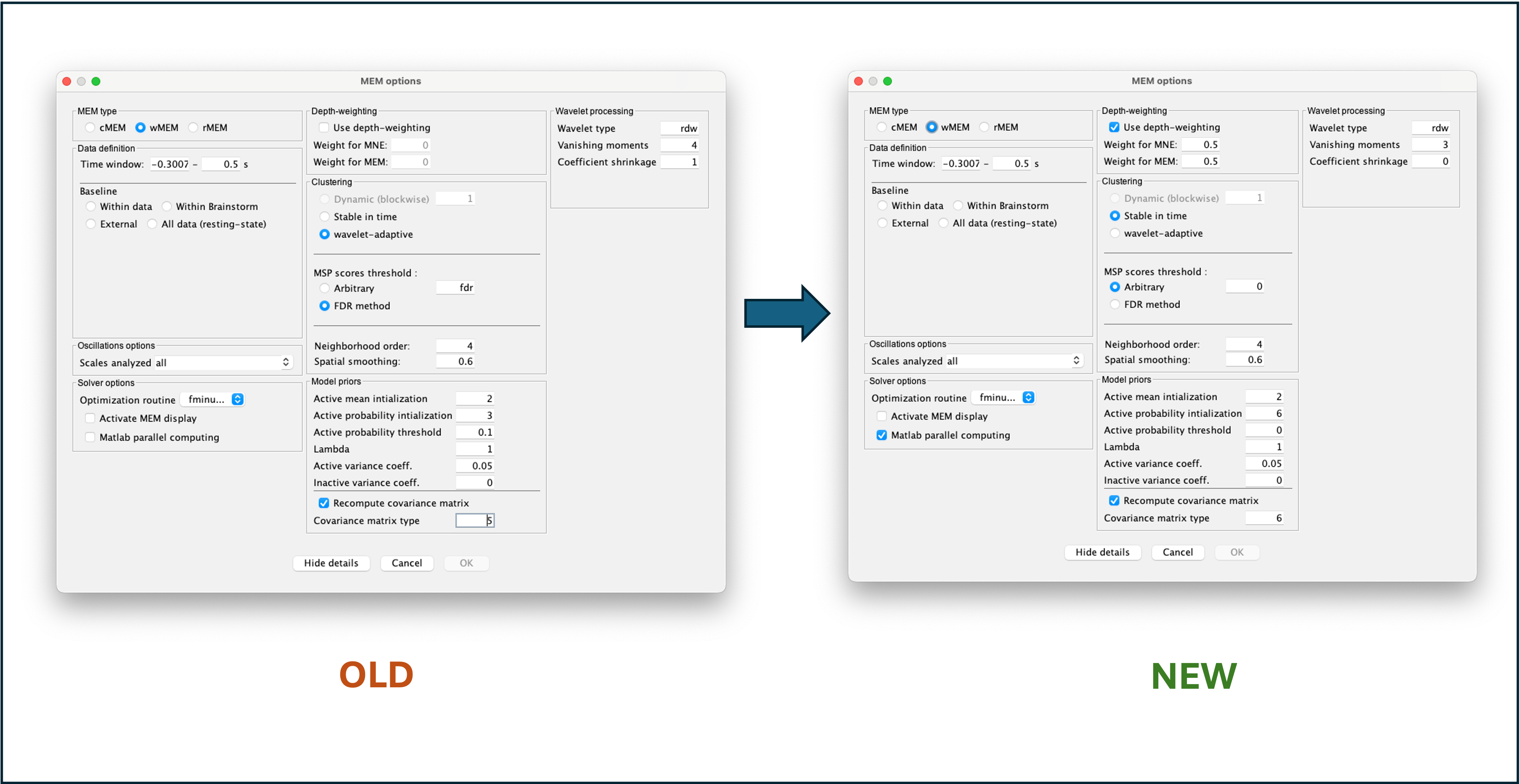
From July 2024, and version 3.0.0 of BEst, the default option of MEM changed. In particular, MEM is now using a depth-weighting of 0.5 by default. To continue to use the previous setting, consult the section Change of default parameters.
Warning: please take note that the " MEM: Max entropy on the mean" option is disabled when using a volumic head model. Please use a head model based on the cortical surface instead (right-click on the condition > Compute head model > Cortex surface).
The MEM option panel appears. You have the choice between 3 methods. cMEM is the standard MEM in the time domain. wMEM focuses on the oscillatory patterns by computing MEM in the wavelet domain. rMEM is dedicated in finding synchronous sources using continuous wavelets.
- Select the MEM method (cMEM: time series representation, wMEM: time-scale representation, or rMEM: wavelet representation). Define the data time window and the baseline data while keeping other parameters at default values. Then hit Ok.
cMEM
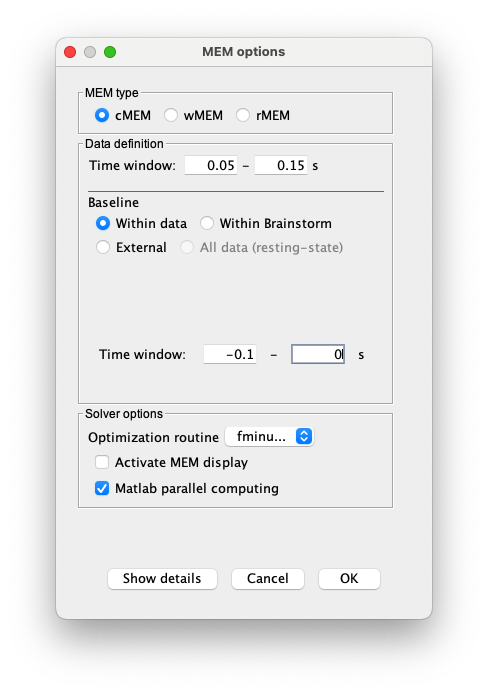
You have clicked on cMEM. The panel then displays all the principals parameters associated with this method. Avanced user can access to more subtle parameters by clicking on the button Show details. The ‘OK’ will be then available once all mandatory parameters have been specified.
The principals parameters for the methods are:
- Data definition:
This corresponds to the window of the data that will be localized
Selection of a specific time window may be useful for long data epochs (default: localize whole data window).
Suggested time window for this dataset: 0.05 to 0.15 s.
- Baseline
Three choices are available for baseline definition. cMEM will consider such a baseline to estimate the noise covariance matrix in the sensor space.
○ Within data: the baseline is a time window to be selected within the recordings.
○ Within Brainstorm: this option allows you to find a specific baseline present in the protocol, if you type the name. For example, if your baseline is named ‘Baseline’, type ‘Baseline’ and click on find.
○ External: the user can import baseline data from a file using brainstorm import tools.
In any case, the user can define a time window for the baseline
Suggested baseline for this dataset: within data, with interval -0.1 to 0 s.
All other parameters can be kept with their default values:
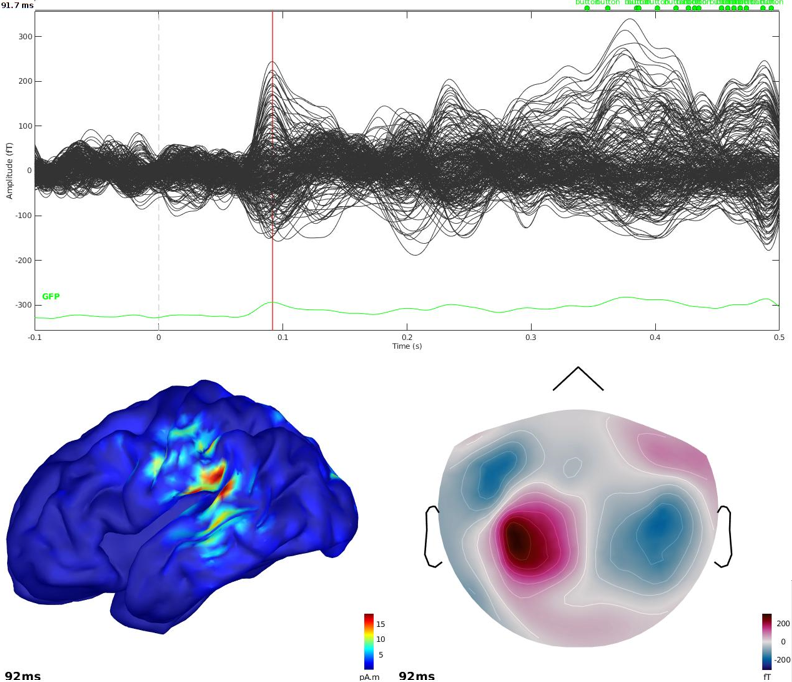
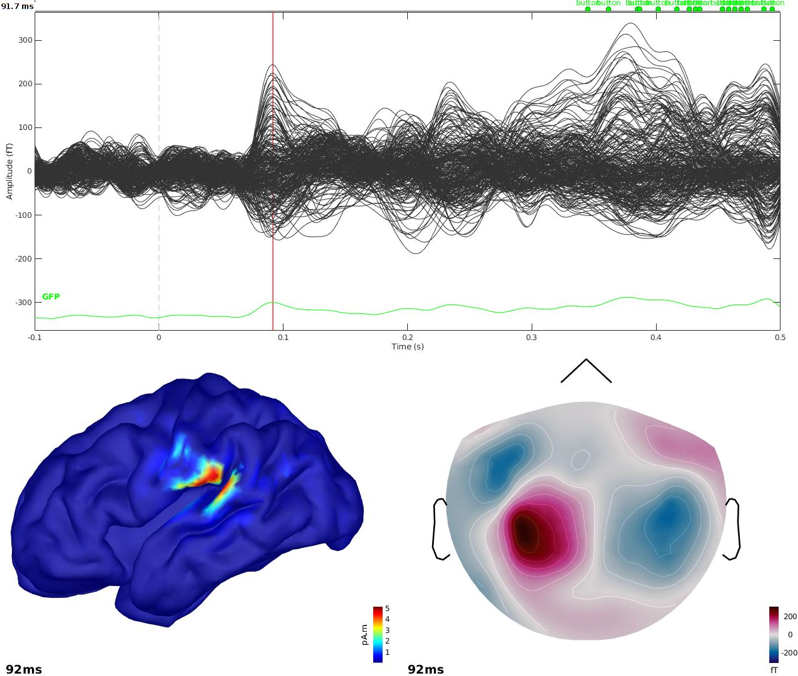
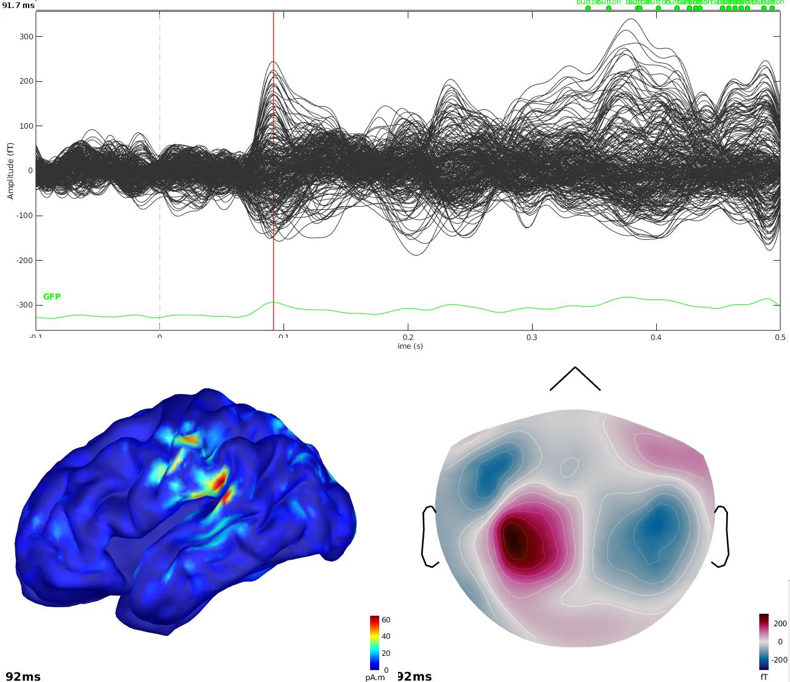
4. Hitting Ok will launch cMEM estimation. At the end, a new results file appears in the database under the appropriate dataset. Simply double-click it to visualize.
We suggest to look at the sources around t = 91.7 ms.
wMEM
You have clicked on wMEM. The panel then displays all the parameters associated with this method.
Principle: The data is decomposed following a discrete multiresolution scheme using real Daubechies wavelets. The time-scale plane can then be threshold to keep only significant coefficients, up to a fraction of total signal power.
wMEM then localizes the sources associated to each wavelet coefficient of the time-scale plane, thus yielding an estimation of wavelet coefficients for each source. As we keep only significant oscillatory modes from the time-scale planes, this method efficiently targets the oscillating neural sources. Interestingly, the Daubechies wavelets have a stable inverse transform, which allows us to recover efficiently the time course associated to each source.
With the BEst_tutorial_auditory_stimulation, we propose the following first experiment (similar to cMEM previous experiment)
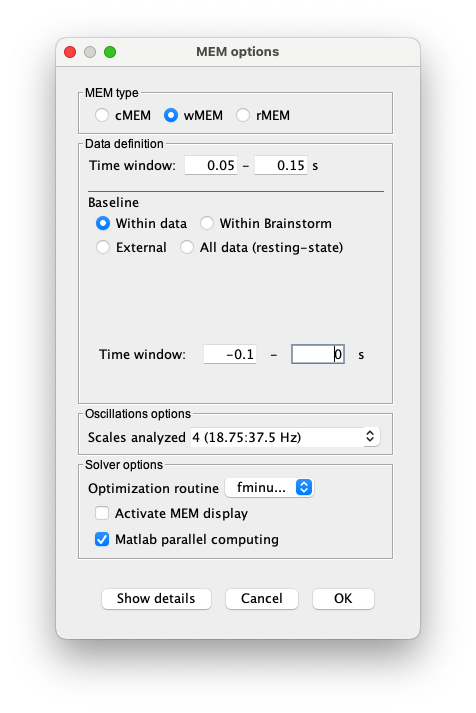
1. Selection of a specific time window may be useful to localize specific time-frequency components of the recordings (default: localize whole data window). Suggested time window for this dataset: 0.05 to 0.15 s.
2. Four choices are available for baseline definition. wMEM will consider such a baseline to estimate the noise covariance matrix in the sensor space.
○ Within data: the baseline is a time window to be selected within the recordings.
○ Within Brainstorm: this option allows you to find a specific baseline present in the protocol, if you type the name. For example, if your baseline is named ‘Baseline’, type ‘Baseline’ and click on find .
○ External: the user can import baseline data from a file using brainstorm import tools.
○ All data (resting state): This option is usefull for resting state data when no clear baseline can be selected and works by generating surrogate data by reshufling the signal within a slidding windows and computing a noise covariance matrix for eahc window. (recommended window lengh for EEG/MEG: 1 seconds).
Suggested baseline for this dataset: within data, with interval -1 to 0 s
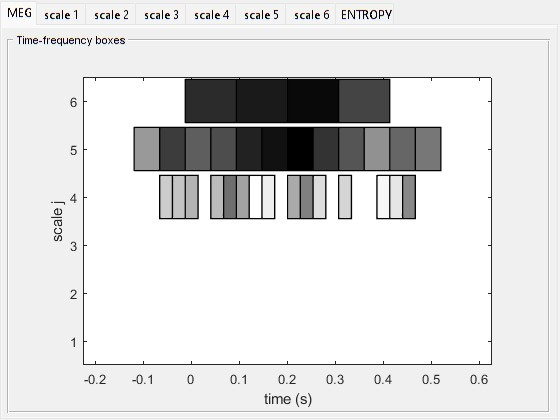
3. Selection of scales to be localized. Suggested scale = 4 (corresponding to frequency band: 18.75 to 37.5 Hz).
This figure, that you can get by selecting MEM display in the ‘expert parameters’ column, shows the global Multi-Resolution power (mean wavelet power over all MEG sensors). Each box corresponds to a wavelet at some scale (index j) and located in time. The scale ( j ) increases with the inverse of the frequency: the lower is j, the faster the local oscillation. The darker is a box, the more power is associated with it. As expected, the evoked response recruits high frequencies between 0 and 0.2 s. With the above scale selected (j = 4, frequency: 18.75-37.5 Hz), we pick only a piece of the oscillation that composes the response in this particular time window.
5. Hitting Ok will launch the wMEM method. At the end, a new result file appears in the database under the appropriate dataset. Simply double-click it to visualize.
You will notice on the command window that 4 time-frequency boxes have been used (at scale j = 4 i.e. oscillations in the 18.75-37.5 Hz frequency band, peak of the wavelet located at 0.020 seconds). This oscillation is part of the short duration oscillatory pattern occurring at 91.7 msec.
Other suggestions:
- run the wMEM with the same parameters as before but with scale = 5;
- run the wMEM with the same parameters as before but with the scale = all. Then, you will combine all the boxes (8 boxes in all) that are above the time window you have selected:
License
BEst is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version. BEst is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should receive a copy of the GNU General Public License along with BEst. If not, get it here.
minFunc. Schmidt M. see license
References
The references to be acknowledged for each method are:
cMEM with stable clustering. MEG source localization of spatially extended generators of epileptic activity: comparing entropic and hierarchical bayesian approaches. Chowdhury RA, Lina JM, Kobayashi E, Grova C. PLoS One. 2013;8(2):e55969
wMEM. Wavelet-based localization of oscillatory sources from magnetoencephalography data. Lina J, Chowdhury R, Lemay E, Kobayashi E, Grova C. IEEE Trans Biomed Eng. 2012 Mar 6.
Additional technical references:
MEM. Biomagnetic source detection by maximum entropy and graphical models. Amblard C, Lapalme E, Lina JM. IEEE Trans Biomed Eng. 2004 Mar;51(3):427-42.
MEM and Parcelization: Data-driven parceling and entropic inference in MEG. Lapalme E, Lina JM, Mattout J. Neuroimage. 2006 Mar;30(1):160-71.
MSP. Multivariate source prelocalization (MSP): use of functionally informed basis functions for better conditioning the MEG inverse problem. Mattout J, Pélégrini-Issac M, Garnero L, Benali H. Neuroimage. 2005 Jun;26(2):356-73.
Validation and applications:
Evaluation of EEG localization methods using realistic simulations of interictal spikes. Grova C, Daunizeau J, Lina JM, Bénar CG, Benali H, Gotman J. Neuroimage. 2006 Feb 1;29(3):734-53.
Concordance between distributed EEG source localization and simultaneous EEG-fMRI studies of epileptic spikes. Grova C, Daunizeau J, Kobayashi E, Bagshaw AP, Lina JM, Dubeau F, Gotman J. Neuroimage. 2008 Jan 15;39(2):755-74
Spatial correlation of hemodynamic changes related to interictal epileptic discharges with electric and magnetic source imaging. Heers M, Hedrich T, An D, Dubeau F, Gotman J, Grova C, Kobayashi E. Hum Brain Mapp. 2014 Feb 24.
Optimal eye-gaze fixation position for face-related neural responses. Zerouali Y, Lina JM, Jemel B. PLoS One. 2013 Jun 6;8(6):e60128.
Oscillatory activity in parietal and dorsolateral prefrontal cortex during retention in visual short-term memory: additive effects of spatial attention and memory load. Grimault S, Robitaille N, Grova C, Lina JM, Dubarry AS, Jolicoeur P. Hum Brain Mapp. 2009 Oct;30(10):3378-92.
* Afnan, Jawata, et al. "Validating MEG source imaging of resting state oscillatory patterns with an intracranial EEG atlas." Neuroimage 274 (2023): 120158.
* Afnan, Jawata, et al. "EEG/MEG source imaging of deep brain activity within the maximum entropy on the mean framework: Simulations and validation in epilepsy." Human Brain Mapping 45.10 (2024): e26720.
(advanced) Expert MEM Parameters
General
Depth-weighting
Weight parameter applied for the estimation of the source covariance of MNE and MEM. We recommmend to keep the two parameters equal. Default value: 0.5
Clustering
- The major prior of the MEM is that cortical activity is compartmented into discrete parcels. The activity of a given source within a patch is thus linked to the activity of its neighbors. This step is thus important for the MEM approach and we propose some strategies to optimize it, depending on the type of activity we target for source localization. All these approaches are data-driven and consist mainly in two steps: sources scoring and labelling.
Source scoring: MSP
We first attribute a score to each source indicating its probability of explaining a segment of data. These scores are estimated using the multivariate source prelocalisation technique - MSP (Mattout et al. Neuroimage 2005). The MSP proceeds by computing a signal space projector using the SVD of the normalized data segment. The leadfields of each source are then normalized and projected on that space. The L2 norm of that projection thus gives a probability-like index between 0 and 1 weighting the contribution of each source to the data.
The MSP quantifies the probability for each source to explain some variability in a data segment. Implicitly, we expect MSP scores to discriminate active regions from inactive ones in relation to the analyzed data window. MSP aims at identifying good candidate dipolar sources contributing to the localization, with great sensitivity, but relatively low specificity. In this regard, the size of the data window on which MSP is applied is an important issue. If it is too short, the variability to be explained is low and all sources will have low scores. On the opposite, if it is too large, all sources will have high MSP scores. We thus propose three strategies to obtain appropriate MSP scores distributions:
Stable in time [ recommended ]
- Dynamic (blockwise)
- Wavelet-adaptative
Source labelling: spatial clustering
The aim of this step is to group cortical sources into spatially homogenous cortical parcels based on their MSP scores. The clustering algorithm selects the sources with maximal MSP score, which are considered as seed points. The parcels are then constructed using a region growing algorithm starting from those seed points. It proceeds as follows:
- Select the source with maximal MSP score: it is the first seed point
- Select all the sources around the seed point to form a cluster. The size of the cluster is determined by the neighborhood order value
- Amongst the other sources, we select the source with maximal MSP score, which will be the next seed point
- We repeat steps 2-3 until all the sources belong to a cluster
MSP scores threshold
It is possible to apply a threshold on the MSP scores before applying the spatial clustering. All the sources that have MSP score below this threshold are then excluded and will not be part of any cluster and of the reconstructed sources. The threshold can be set arbitrarily from 0 to 1, 0 excluding none of the sources.
The MSP threshold can also be derived from the baseline using a FDR criterion (Lina et al. IEEE TBME 2012).
We recommend to use a threshold of 0, excluding none of the sources.
Neighborhood order
The neighborhood order determines the size of the parcels in the spatial clustering. The neighborhood order relates to the number of maximal spatial connections along the geodesic cortical surface between an element of a cluster and the seed of this cluster. Therefore, the higher the neighborhood order, the larger the cluster and the lower the number of parcels. (Chowdhury et al. Plos One 2013, page 3)
Spatial smoothing
We can apply a spatial smoothing constraint (LORETA like) within each parcel during the MEM regularization. The parameter of smoothing can vary from 0 (no spatial smoothing) to 1 (high spatial diffusion inside the parcels). (Chowdhury et al. Plos One 2013, page 3 & 4, Harrison et al. Neuroimage 2007)
Model prior
For the definition of the MEM prior model i.e., spatial clustering, the distribution of source intensities within each active parcel are modeled using a Gaussian distribution with a mean (mk) and a variance (Σk). The proposed prior model consists in using a hidden variable tuning the active state of each parcel. The probability of every parcel for being active has to be initialized as well (αk). The parameters of the active parcels can be initialized using different ways.
- Active mean initialization (default choice, 2): Initialization of source intensity within each parcel.
- 1: mean of the source intensities computed by the weighted minimum norm scores of the sources within each parcel (mk = mean(Jmn)),
- 2: null initialization (mk = 0) [Default],
- 3: mean of the source intensities computed with a cluster-based version of the weighted minimum norm,
- 4: L-curve optimized minimum norm estimate.
- Active probability initialization (default choice, 3): Initialization of the probability of the parcels being active (αk).
- 1: mean of MSP scores of the sources within each parcel,
- 2: max of MSP scores of the sources within each parcel,
- 3: median of MSP scores of the sources within each parcel, [default for cMEM]
- 4: all parcels initialized at 0.5,
- 5: all parcels initialized at 1,
- 6: % of MNE energy within each parcel. [default for wMEM]
* Active probability threshold (default choice, 0): Parcels with sub-threshold initial probability are turned off. Parcels that are turned off cannot be part of the MEM solution.
* Lambda (default choice, 1): Initial sensor’s weights vector.
- 0: all sensors initialized at 0,
- 1: random weights
* Active variance coefficient (default choice, 0.05): model of variance of the active state. By default, variance is set to 5% of the mean of the square of the minimum norm estimate in each parcel. This proportion can be changed by setting active variance coefficient to desired value between 0 and 1.
- Inactive variance coefficient (default choice, 0): model of variance of the inactive state.
- Recompute covariance matrix: If this option is checked, a new covariance matrix will be recomputed instead of using the sensors covariance matrix already computed in brainstorm.
- Use Empty room noise: This option is available when there is empty room noise available in the database. If you want this option to be available, the Brainstorm protocol must contain a dataset named “emptyroom”. The panel will look for “emptyroom” in the following order: 1) in the same study as the dataset to be localized, 2) in the subject node, 3) in the default subject node.
* Covariance matrix type (default choice, 2): Only relevant if Recompute covariance matrix is checked.
- 0: identity matrix,
- 1: diagonal matrix, all sensors have same variance,
- 2: diagonal matrix,
- 3: full matrix
- 4: wavelet-based estimation of the noise. We compute the discrete wavelet transform of the data and estimate the noise from the finest scale, j=1. Note that the shrinkage is applied if selected. The matrix is diagonal.
- 5: wavelet-based estimation of the noise. We compute the discrete wavelet transform of the data and estimate the noise from the finest scale, j=1. Note that the shrinkage is applied if selected. Unique value along the diagonal, which is the average of the diagonal terms
- 6: (default)wavelet-based estimation of the noise. We compute the discrete wavelet transform of the data and estimate the noise from the finest scale, j=2. Note that the shrinkage is applied if selected. The matrix is diagonal.
If there exists an emptyroom datasets and the option “Use emptyroom” is selected, the wMEM computes a scale-specific covariance matrix and a scale-dependent shrinkage (if selected). In this case, only options 4 and 5 are available and take a different meaning:
- 4: diagonal scale-specific covariance matrix – different values along the diagonal
- 5: (default – forced if neither 4 nor 5) diagonal scale-specific covariance matrix – unique value along the diagonal, which is the average of the diagonal terms
Solver options
* Optimization routine (default, fminunc): Optimization routine used for the MEM. Two toolboxes are available:
- fminunc: Unconstrained optimization, part of the matlab optimization toolbox,
- minFunc: Unconstrained optimization, copyright Mark Schmidt (selected when the optimization toolbox is not available).
Option specific to wMEM
Wavelet Processing
- Wavelet type: RDW - Discrete Wavelet transform (Real Daubechies) used for wMEM
- Vanishing moments (default, 4): Number of vanishing moments of the wavelet. This parameter shapes the impulse response function of the wavelet. The larger this number, the more de-correlated are the coefficients, but the lower is the spectral resolution
- Coefficient shrinkage (default, 1): Only relevant if Wavelet type is set to RDW. Indicates if the coefficients of the time-scale plane must be shrinked, used for data reduction.
Option specific to rMEM
* Wavelet type: CWT - Continuous wavelet transform used for rMEM * Decomposition levels (default, 128): Number of decomposition levels.
Wavelet Processing
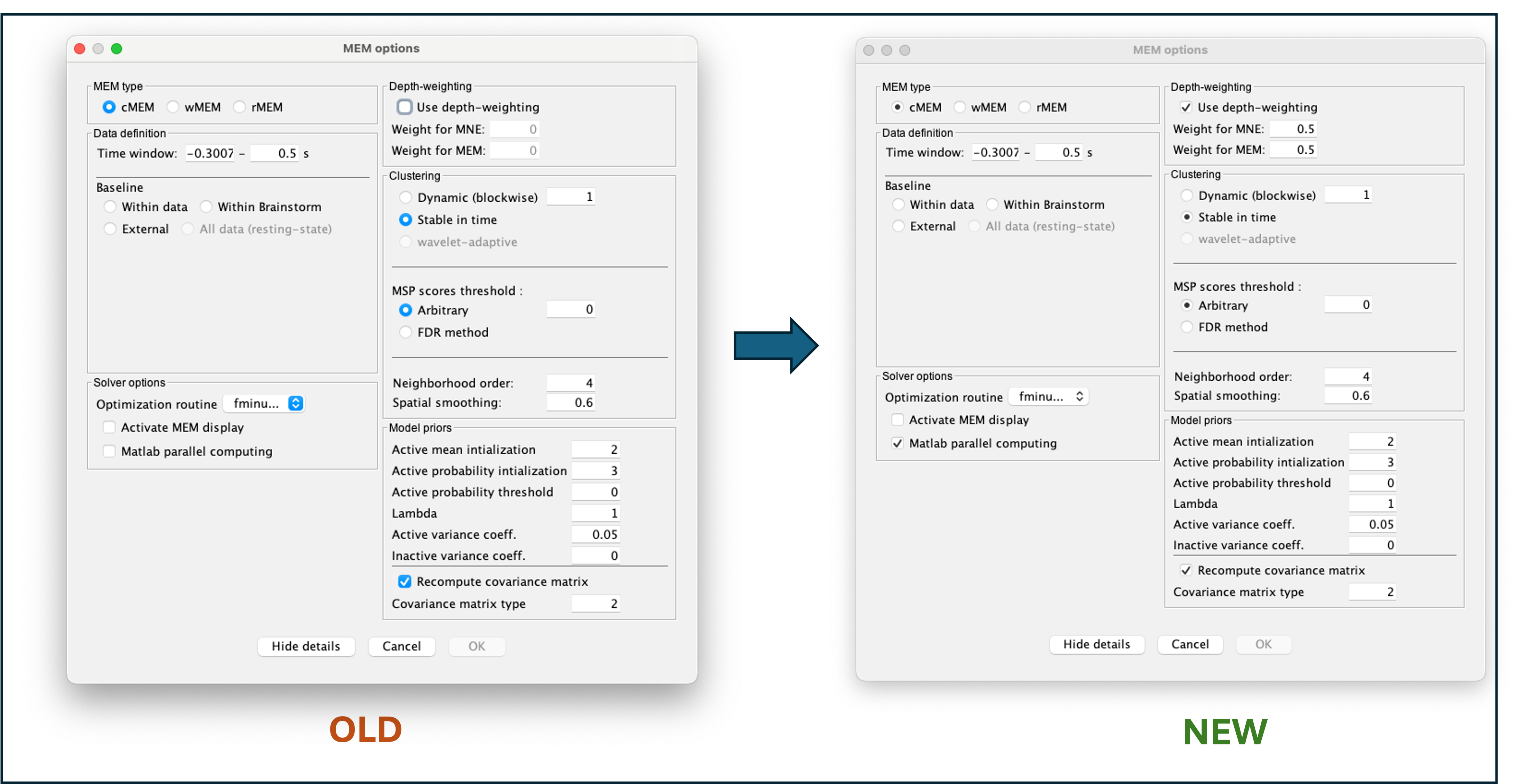
(Advanced) Change of default parameters (v3.0.0)
Since version 3.0.0 of BEst, the default parameters of cMEM and wMEM changed. To replicate previous results, use the export mode and enter the previous default parameters. We strongly recommend using the new default value.
cMEM
In the new version of cMEM, the depth-weighting parameter is now set to 0.5 for both MNE and MEM (previously 0). This change is to be more aligned with the default parameter used by Brainstorm for MNE.
wMEM
Similar to cMEM, the depth-weighting parameter is now set to 0.5 for both MNE and MEM (previously 0). This change is to be more aligned with the default parameter used by Brainstorm for MNE.
Additionally, the default method for the parcellation of the cortex is now 'stable in time' instead of 'wavelet-adaptative'. This means that the same parcellation of the cortex is now used for every time-frequency box instead of having a specific parcellation per time-frequency box.