|
Size: 24921
Comment:
|
← Revision 185 as of 2019-04-03 17:55:59 ⇥
Size: 26328
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| __'''Warning'''__: The developments described below have been abandonned. Please refer to the [[https://neuroimage.usc.edu/brainstorm/Tutorials/SourceEstimation?highlight=%28beamformer%29#Advanced_options:_LCMV_beamformer|source estimation tutorial]]. ... |
|
| Line 2: | Line 6: |
| ==== [TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE] ==== ''Authors: Hui-Ling Chan, Francois Tadel, Sylvain Baillet'' |
''Authors: Hui-Ling Chan, Francois Tadel, Sylvain Baillet '' |
| Line 7: | Line 10: |
| We are going to use the protocol '''!TutorialRaw''' created in the [[http://neuroimage.usc.edu/brainstorm/Tutorials#Processing_continuous_recordings|introduction tutorials]]. If you have not followed these tutorials yet, please do it now. | '''IMPORTANT''': The LCMV beamformer is now part of the main Brainstorm distribution. We recommend you refer instead to the new documentation in the introduction tutorials: [[Tutorials/SourceEstimation|Source estimation]]. |
| Line 11: | Line 14: |
| == Installation == This tutorial requires you download the two processes below and copy them to your personal process folder ($HOME/.brainstorm/process): * [[attachment:process_beamformer_lcmv.m]] * [[attachment:process_beamformer_mcb.m]] |
|
| Line 12: | Line 21: |
| Beamforming methods scan each targeted source position <<latex($\bf r$)>> and estimate the spatial filter <<latex(${\bf w}_{\bf r,q}$)>>. By multiplying with the MEG recordings <<latex(${\bf m}(t)$)>>, the spatial filter <<latex(${\bf w}_{\bf r,q}$)>> outputs the temporal waveform <<latex($y_{\bf r,q}(t)$)>> of the dipole source at that position with the dipole orientation <<latex($\bf q$)>> as below: | Beamforming methods scan each targeted source position <<latex($\bf r$)>> and estimate the spatial filter <<latex(${\bf w}_{\bf r,q}$)>>. By multiplying with the MEG recordings <<latex(${\bf m}(t)$)>>, the spatial filter <<latex(${\bf w}_{\bf r,q}$)>> outputs the temporal waveform <<latex($y_{\bf r,q}(t)$)>> of the dipole source at that position with the dipole orientation <<latex($\bf q$)>> as below: |
| Line 18: | Line 27: |
| ==== Vector-type beamformer ==== For each position <<latex($\mathbf{r}$)>>, three orthogonal spatial filters <<latex($\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$)>> are computed by applying the unit-gain constraint as well as the minimum norm and minimum variance criteria as below [Liu and Van Veen, 1992; Van Veen et al., 1997]: |
=== Vector-type beamformer === For each position <<latex($\mathbf{r}$)>>, three orthogonal spatial filters <<latex($\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$)>> are computed by applying the unit-gain constraint as well as the minimum norm and minimum variance criteria as below [Liu and Van Veen, 1992; Van Veen et al., 1997]: |
| Line 25: | Line 34: |
| ==== Scalar-type beamformer ==== For each position <<latex($\mathbf{r}$)>>, the source orientation <<latex($\mathbf{q}$)>> is first estimated to enable the spatial filter to output the source activity with maximum power or fitting some other criteria. The dipole orientation can be obtained by exhaustive search, non-linear search [Robinson and Vrba, 1999], or analytical solution [Chen et al., 2006]. The estimated dipole orientation <<latex($\hat{\mathbf{q}}$)>> is then applied to calculate the spatial filter as follows [Robinson and Vrba, 1999]: |
=== Scalar-type beamformer === For each position <<latex($\mathbf{r}$)>>, the source orientation <<latex($\mathbf{q}$)>> is first estimated to enable the spatial filter to output the source activity with maximum power or fitting some other criteria. The dipole orientation can be obtained by exhaustive search, non-linear search [Robinson and Vrba, 1999], or analytical solution [Chen et al., 2006]. The estimated dipole orientation <<latex($\hat{\mathbf{q}}$)>> is then applied to calculate the spatial filter as follows [Robinson and Vrba, 1999]: |
| Line 28: | Line 37: |
| <<latex($ \hat{\mathbf{w}}_{\mathbf{r,q}}=(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\hat{\bf{q}}\left(\hat{\bf q}^{\rm T}\mathbf{L}_\mathbf{r}^{\rm T}(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\hat{\bf q}\right)^{-1} \enspace.$)>> | <<latex($ \hat{\mathbf{w}}_{\mathbf{r,q}}=(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\hat{\bf{q}}\left(\hat{\bf q}^{\rm T}\mathbf{L}_\mathbf{r}^{\rm T}(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\hat{\bf q}\right)^{-1} \enspace.$)>> |
| Line 31: | Line 40: |
| LCMV stands for '''linearly-constrained minimum variance'''. LCMV beamformer is vector-type beamformer [Van Veen et al., 1997]. For each position <<latex($\mathbf{r}$)>>, this method calculates the neural activity index, which is interpreted as the estimate of source to noise variance. | LCMV stands for''' linearly-constrained minimum variance'''. LCMV beamformer is vector-type beamformer [Van Veen et al., 1997]. For each position <<latex($\mathbf{r}$)>>, this method calculates the neural activity index, which is interpreted as the estimate of source to noise variance. |
| Line 33: | Line 42: |
| ==== Neural activity index ==== For each position <<latex($\mathbf{r}$)>>, the variance of source activity during active state <<latex($T_{\rm a}$)>> is calculated as follows [Liu and Van Veen, 1992; Van Veen et al., 1997]: |
=== Neural activity index === For each position <<latex($\mathbf{r}$)>>, the variance of source activity during active state <<latex($T_{\rm a}$)>> is calculated as follows [Liu and Van Veen, 1992; Van Veen et al., 1997]: |
| Line 36: | Line 45: |
| <<latex($ \rm{Var}_{\rm a}(\bf r) =\rm{trace} \left \{{\bf W}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf W}_{\bf r}\right \} \enspace, $)>> | <<latex($ \rm{Var}_{\rm a}(\bf r) =\rm{trace} \left \{{\bf W}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf W}_{\bf r}\right \} \enspace, $)>> |
| Line 40: | Line 49: |
| <<latex($ \rm{Var}_{\rm a}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $)>> | <<latex($ \rm{Var}_{\rm a}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $)>> |
| Line 44: | Line 53: |
| <<latex($ \rm{Var}_{\rm a}(\bf r) = \lambda_1 \left \{{\bf W}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf W}_{\bf r}\right \}\enspace, $)>> | <<latex($ \rm{Var}_{\rm a}(\bf r) = \lambda_1 \left \{{\bf W}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf W}_{\bf r}\right \}\enspace, $)>> |
| Line 48: | Line 57: |
| <<latex($ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $)>> | <<latex($ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $)>> |
| Line 52: | Line 61: |
| When the location <<latex($\mathbf{r}$)>> is far from sensors, the elements of lead field matrix <<latex($\mathbf{L}_{\bf r}$)>> are small. So the elements of <<latex($\mathbf{W}_{\bf r}$)>> are generally large and the estimated variance for the deep source becomes large. When the location <<latex($\mathbf{r}$)>> is close to sensors, the elements of lead field matrix <<latex($\mathbf{L}_{\bf r}$)>> are large. It results in small values of the elements of <<latex($\mathbf{W}_{\bf r}$)>> and small estimated variance for the superficial source. To reduce the effect caused by the depth of source location, the estimated source variance <<latex($\rm{Var}_{\rm a}(\bf r)$)>> is normalized by the noise variance <<latex($\rm{Var}_{\rm c}(\bf r)$)>> as follows: | When the location <<latex($\mathbf{r}$)>> is far from sensors, the elements of lead field matrix <<latex($\mathbf{L}_{\bf r}$)>> are small. So the elements of <<latex($\mathbf{W}_{\bf r}$)>> are generally large and the estimated variance for the deep source becomes large. When the location <<latex($\mathbf{r}$)>> is close to sensors, the elements of lead field matrix <<latex($\mathbf{L}_{\bf r}$)>> are large. It results in small values of the elements of <<latex($\mathbf{W}_{\bf r}$)>> and small estimated variance for the superficial source. To reduce the effect caused by the depth of source location, the estimated source variance <<latex($\rm{Var}_{\rm a}(\bf r)$)>> is normalized by the noise variance <<latex($\rm{Var}_{\rm c}(\bf r)$)>> as follows: |
| Line 54: | Line 63: |
| <<latex($ \rm{Var}_{\rm N}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $)>> | <<latex($ \rm{Var}_{\rm N}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $)>> |
| Line 58: | Line 67: |
| <<latex($ \rm{Var}_{\rm N}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $)>> | <<latex($ \rm{Var}_{\rm N}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $)>> |
| Line 62: | Line 71: |
| ==== LCMV process ==== 1. Drag and drop all of the epochs in ''Subject01 / right / right | timeoffset (98 files)'' into ''Process1''. . 1. Click on [RUN] and select the process "'''Sources > Beamformer: LCMV'''".<<BR>>Configure the options as follows:<<BR>><<BR>> {{attachment:process_lcmv.gif||height="423",width="313"}} 1. With this window you can select the method you want to use to estimate the source variance and noise variance, the time window of active state, the regularization parameter, and the sensors you are going to use for this estimation. You can edit the following options: |
=== LCMV process === 1. Drag and drop all of the epochs in ''Subject01 / right / right | timeoffset (98 files)'' into Process1. 1. Click on [RUN] and select the process "'''Sources > Beamformer: LCMV'''".<<BR>>Configure the options as follows:<<BR>><<BR>> {{attachment:LCMV_parameter_setting_right.png|LCMV_options.png}} <<BR>> 1. With this window you can select the method you want to use to estimate the source variance and noise variance, the time window of active state, the regularization parameter, and the sensors you are going to use for this estimation. You can edit the following options:<<BR>><<BR>> |
| Line 69: | Line 76: |
| * '''Method''': | * '''Method''':<<BR>> |
| Line 72: | Line 79: |
| * '''Constrained''': The dipole orientation for each vertex is set to the normal vector to the cortex surface (not available for volume head models). This method may give less smooth results than the unconstrained methods. | * '''Constrained''' '''(normal to cortex)''': The dipole orientation for each vertex is set to the normal vector to the cortex surface (not available for volume head models). This method may give less smooth results than the unconstrained methods. |
| Line 74: | Line 81: |
| * '''Time range of interest''': Total time period over which we want to calculate the neural activity index. * '''Active window size''': Defines the duration of the active state. The active window is slided all along the time range of interest. A large active window size is recommended, at least larger than the number of sensors in number of time samples. * '''Temporal resolution''': Defines the time lapse between two estimations of the neural activity index. * If this "active size window" or "temporal resolution" are '''set to zero''', the active window size is set to the entire time range of interest. The temporal resolution becomes irrelevant because only one neural activity index will be estimated. * If there are multiple active state windows, the time label of the neural activity index will be set as the middle time of each active state window, that is, <<latex($t_1,t_2,t_3,\ldots,t_{N-1},t_{N}$)>> in the following figure. You are going to obtain the spatiotemporal dynamics of neural activity index bewteen <<latex($t_1$)>> and <<latex($t_N$)>>. <<BR>><<BR>> {{attachment:slidingwindow.png||height="219",width="437"}} * '''Regularization parameter''': This value will be multiplied with the maximum eigenvalue of the covariance matrix computed from the recordings during ''Time range of interest''. A larger value of regularization parameter would give smoother results. Large regularization parameter value is more suitable for noisy data. When analyzing simulation data sets, the regularization parameter value can be reduced. * '''Sensors type''': Modalities that are used for the reconstruction. Here we only have one type of MEG sensors, so nothing to change. |
* '''Time range of interest''': Total time period over which we want to calculate the neural activity index. * '''Active window size''': Defines the duration of the active state. The active window is slided all along the time range of interest. A large active window size is recommended, at least larger than the number of sensors in number of time samples. * '''Temporal resolution''': Defines the time lapse between two estimations of the neural activity index. If this "''active size window''" or "''temporal resolution''" are set to '''zero''', the active window size is set to the entire time range of interest. The ''temporal resolution'' becomes irrelevant because only one neural activity index will be estimated. If there are multiple active state windows, the time label of the neural activity index will be set as the middle time of each active state window, that is, <<latex($t_1,t_2,t_3,\ldots,t_{N-1},t_{N}$)>> in the following figure. You are going to obtain the spatiotemporal dynamics of neural activity index bewteen <<latex($t_1$)>> and <<latex($t_N$)>>. <<BR>><<BR>> {{attachment:slidingwindow.png||width="542",height="273"}} * '''Regularization parameter''': This value will be multiplied with the maximum eigenvalue of the covariance matrix computed from the recordings during Time range of interest. A larger value of regularization parameter would give smoother results. Large regularization parameter value is more suitable for noisy data. When analyzing simulation data sets, the regularization parameter value can be reduced. * '''Sensors type''': Modalities that are used for the reconstruction. Here we only have one type of MEG sensors, so nothing to change. |
| Line 83: | Line 87: |
| 1. Two new files are available in the database explorer.<<BR>> * '''right: LCMV (Unconstr/svd, 0-296ms)''': This file saves the neural activity index for every dipole position. <<BR>><<BR>> {{attachment:LCMV_results_list_svd_source.png}}<<BR>> <<BR>> Double click on this file. Right click on anywhere of the pop-out window. From the pop-out menu, select ''Colormap:Sources > Maximum: Custom...''. Set ''Minimum'' to be '''1.2''' and ''Maximum'' to be '''2.0'''. Click ''Ok''. <<BR>> <<BR>> {{attachment:Colormaplimit.png}} <<BR>><<BR>> Set the time to be anytime between 0 and 295.8 ms. Then click ''Surface'' tab on the right panel of database explorer. Set ''Data options > Amplitude'' to be '''50%'''. <<BR>><<BR>> {{attachment:LCMV_results_svdtrace_map.png}} <<BR>><<BR>>The maps of neural activity index estimated using ''Unconstrained (trace)'' and ''Unconstrained (max sigular value)'' are shown in the left and right figures, respectively. Both maps display strong activations in the left sensory area. * '''right: LCMV/filter (Unconstr/svd,0-296ms)''': This file saves the three spatial filters along the x, y, and z directions for each dipole position. These spatial filters are normalized by the standard deviation of noise. Note that there is one spatial filter for each dipole location if the method'' Cortically Constrained ''is used. <<BR>><<BR>> {{attachment:LCMV_results_list_svd_filter.png}}<<BR>> 1. Explore spatiotemporal dynamics of sources in right condition <<BR>><<BR>> {{attachment:DatabaseExpoloreRightAvgEig.png||height="286",width="267"}} <<BR>> * 17.5 ms (left): S1 left * 37.5 ms (middle): S1 left * 75 ms (right): bilateral S2 <<BR>><<BR>> {{attachment:RightEig17p5.png||height="183",width="209"}} {{attachment:RightEig37p5.png||height="183",width="211"}} {{attachment:RightEig75.png||height="179",width="209"}} <<BR>><<BR>> 1. Explore spatiotemporal dynamics of sources in left condition <<BR>><<BR>> {{attachment:DatabaseExplorerLeftAvgEig.png||height="308",width="292"}} <<BR>> * 18.3 ms (top-left): S1 right * 34.1 ms (top-right): S1 right * 60 ms (bottom-left): S2 right * 75.8 ms (bottom-right): bilateral S2 <<BR>><<BR>> {{attachment:LeftEig18p3.png||height="188",width="209"}} {{attachment:LeftEig34p1.png||height="190",width="209"}} <<BR>><<BR>> {{attachment:LeftEig60.png||height="189",width="208"}} {{attachment:LeftEig75p8.png||height="188",width="208"}} <<BR>><<BR>> |
1. Two new files are available in the database explorer.<<BR>><<BR>> * '''right: LCMV (Unconstr/svd, 5-296ms)''': This file saves the neural activity index for every dipole position. <<BR>><<BR>> {{attachment:LCMV_right_svd.png|LCMV_results_list_svd_source.png}} <<BR>> <<BR>> Double click on this file. Right click on anywhere of the pop-out window. From the pop-out menu, select'' Colormap:Sources > Maximum: Custom...''. Set Minimum to be '''1.2''' and Maximum to be '''2.0'''. Click Ok. <<BR>> <<BR>> {{attachment:Colormaplimit.png}} <<BR>><<BR>> Set the time to be anytime between 0 and 296 ms. Then click ''Surface'' tab on the right panel of database explorer. Set ''Data options > Amplitude'' to be '''50%''' and ''Data options > Min Size'' to be '''5'''. <<BR>><<BR>> {{attachment:LCMV_right_NAImap.png||width="572",height="213"}} <<BR>><<BR>>The maps of neural activity index estimated using ''Unconstrained'' ''(max sigular value)'', ''Unconstrained (trace)'', and ''Constrained (normal to cortex)'' are shown from left to right. All maps display strong activations in the left primary somatosensory area (S1). * '''right: LCMV/filter (Unconstr/svd, 5-296ms)''': This file saves the three spatial filters along the x, y, and z directions for each dipole position. These spatial filters are normalized by the standard deviation of noise. Note that there is one spatial filter for each dipole location if the method ''Cortically Constrained ''(normal to cortex) is used. <<BR>><<BR>> {{attachment:LCMV_right_svd_filter.png|LCMV_results_list_svd_filter.png}} <<BR>> 1. Explore spatiotemporal dynamics of anatomically constrained beamformer outputs in the right condition. <<BR>><<BR>> {{attachment:DatabaseExploreRightAvgConstr.png}} <<BR>><<BR>>Double click on this file. Set the time to be '''15.8 ms''', '''30 ms''', or '''60 ms'''. Right click on anywhere of the pop-out window. From the pop-out menu, select ''Colormap:Sources > Maximum: Local...''. Then click ''Surface'' tab on the right panel of database explorer. Set ''Data options > Amplitude'' to be '''70%''' and ''Data options > Min Size'' to be '''5'''.<<BR>><<BR>> * '''16 ms''' (left): left S1 * '''30 ms''' (middle): left S1 * '''60 ms '''(right): left S2 <<BR>><<BR>> {{attachment:LCMV_right_constr_16ms.png||width="204",height="200"}} {{attachment:LCMV_right_constr_30ms.png||width="206",height="200"}} {{attachment:LCMV_right_constr_60ms.png||width="205",height="200"}} <<BR>><<BR>> * '''70 ms''': bilateral S2 <<BR>><<BR>> Set the time to be 70 ms. Then click ''Surface'' tab on the right panel of database explorer. Set'' Data options > Amplitude'' to be '''41%''' and ''Data options > Min Size'' to be '''5'''. <<BR>><<BR>> {{attachment:LCMV_right_constr_70ms.png||width="614",height="228"}} <<BR>><<BR>> 1. Explore spatiotemporal dynamics of anatomically constrained beamformer outputs in the right condition. <<BR>><<BR>> {{attachment:LCMV_left_Constr_filter.png}} <<BR>><<BR>>Double click on this file. Set the time to be '''20 ms''', '''30 ms''', or '''60 ms'''. Right click on anywhere of the pop-out window. From the pop-out menu, select ''Colormap:Sources > Maximum: Local..''.. Then click ''Surface'' tab on the right panel of database explorer. Set ''Data options > Amplitude'' to be '''60%''' and ''Data options > Min Size'' to be '''5'''. <<BR>><<BR>> * '''20 ms''' (left): right S1 * '''30 ms''' (middle): right S1 * '''60 ms''' (right): right S2 <<BR>><<BR>> {{attachment:LCMV_left_constr_20ms.png||width="166",height="184"}} {{attachment:LCMV_left_constr_30ms.png||width="163",height="183"}} {{attachment:LCMV_left_constr_60ms.png||width="163",height="182"}} <<BR>><<BR>> * '''73.3 ms''': bilateral S2. Set the time to be '''73.3 ms'''. Then click ''Surface'' tab on the right panel of database explorer. Set ''Data options > Amplitude'' to be '''45%''' and ''Data options > Min Size'' to be '''5'''. <<BR>><<BR>> {{attachment:LCMV_left_constr_73.3ms.png}} <<BR>><<BR>> |
| Line 98: | Line 102: |
| Maximum constrast beamformer (MCB) is scalar-type beamformer [Chen et al., 2006]. For each position <<latex(\bf r)>>, it provides an analytical solution of dipole orientation <<latex(\bf q)>>, which maximizes the constrast of beamformer outputs between active state and control state as bellow: | Maximum constrast beamformer (MCB) is scalar-type beamformer [Chen et al., 2006]. For each position <<latex(\bf r)>>, it provides an analytical solution of dipole orientation <<latex(\bf q)>>, which maximizes the constrast of beamformer outputs between active state and control state as bellow: |
| Line 100: | Line 104: |
| <<latex($\hat{\bf q}=\arg \max_{\bf q} \rm{Var}_{\rm N}(\bf r) = \arg \max_{\bf q} \bf{w}_{\bf{r,q}}^{\rm T} {\bf C}_{\rm a} \bf{w}_{\bf{r,q}} \left(\bf{w}_{\bf{r,q}}^{\rm T} {\bf C}_{\rm c} \bf{w}_{\bf{r,q}} \right)^{-1}\enspace,$)>> | <<latex($\hat{\bf q}=\arg \max_{\bf q} \rm{Var}_{\rm N}(\bf r) = \arg \max_{\bf q} \bf{w}_{\bf{r,q}}^{\rm T} {\bf C}_{\rm a} \bf{w}_{\bf{r,q}} \left(\bf{w}_{\bf{r,q}}^{\rm T} {\bf C}_{\rm c} \bf{w}_{\bf{r,q}} \right)^{-1}\enspace,$)>> |
| Line 102: | Line 106: |
| where <<latex(${\bf C}_{\rm a}$)>> is the covariance matrix computed from the measurements during active state and <<latex(${\bf C}_{\rm c}$)>> is the covariance matrix computed from the measurements during control state. | where <<latex(${\bf C}_{\rm a}$)>> is the covariance matrix computed from the measurements during active state and <<latex(${\bf C}_{\rm c}$)>> is the covariance matrix computed from the measurements during control state. |
| Line 104: | Line 108: |
| ==== Solution of dipole orientation ==== | === Solution of dipole orientation === |
| Line 107: | Line 111: |
| <<latex($ \mathbf{w}_{\mathbf{r,q}}=(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\bf{q}\left({\bf q}^{\rm T}\mathbf{L}_\mathbf{r}^{\rm T}(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}{\bf q}\right)^{-1} = {\bf A}_{\bf r}{\bf q}\left( {\bf q}^{\rm T}{\bf B_{r}q}\right)^{-1}\enspace,$)>> | <<latex($ \mathbf{w}_{\mathbf{r,q}}=(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\bf{q}\left({\bf q}^{\rm T}\mathbf{L}_\mathbf{r}^{\rm T}(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}{\bf q}\right)^{-1} = {\bf A}_{\bf r}{\bf q}\left( {\bf q}^{\rm T}{\bf B_{r}q}\right)^{-1}\enspace,$)>> |
| Line 111: | Line 115: |
| <<latex($ \rm{Var}_{\rm N}(\bf r) = {\bf q}^{\rm T}{\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf A}_{\bf r}{\bf q} \left({\bf q}^{\rm T}{\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf A}_{\bf r}{\bf q} \right)^{-1}={\bf q}^{\rm T}{\bf P}_{\bf r}{\bf q} \left({\bf q}^{\rm T}{\bf Q}_{\bf r}{\bf q} \right)^{-1}\enspace,$)>> | <<latex($ \rm{Var}_{\rm N}(\bf r) = {\bf q}^{\rm T}{\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf A}_{\bf r}{\bf q} \left({\bf q}^{\rm T}{\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf A}_{\bf r}{\bf q} \right)^{-1}={\bf q}^{\rm T}{\bf P}_{\bf r}{\bf q} \left({\bf q}^{\rm T}{\bf Q}_{\bf r}{\bf q} \right)^{-1}\enspace,$)>> |
| Line 113: | Line 117: |
| where both of the 3-by-3 matrices <<latex(${\bf P}_{\bf r} = {\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf A}_{\bf r}$)>> and <<latex(${\bf Q}_{\bf r}={\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf A}_{\bf r}$)>> does not depend on the dipole orientation <<latex($\bf q$)>>. The solution of dipole orientation <<latex($\hat{\bf q}$)>> is the eigenvector corresponding to the maximum eigenvalue of the matrix <<latex(${\bf Q}_{\bf r}^{-1}{\bf P}_{\bf r}$)>>. | where both of the 3-by-3 matrices <<latex(${\bf P}_{\bf r} = {\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf A}_{\bf r}$)>> and <<latex(${\bf Q}_{\bf r}={\bf A}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf A}_{\bf r}$)>> does not depend on the dipole orientation <<latex($\bf q$)>>. The solution of dipole orientation <<latex($\hat{\bf q}$)>> is the eigenvector corresponding to the maximum eigenvalue of the matrix <<latex(${\bf Q}_{\bf r}^{-1}{\bf P}_{\bf r}$)>>. |
| Line 115: | Line 119: |
| ==== Statistical mapping ==== | === Statistical mapping === |
| Line 118: | Line 122: |
| <<latex(${\rm F}({\bf r},t)=\hat{{\bf w}}_{\bf{r,q}}^{\rm T} {\bf C}_{T_t}\hat{\bf{w}}_{\bf{r,q}} \left(\hat{\bf{w}}_{\bf{r,q}}^{\rm T} {\bf C}_{\rm c} \hat{\bf{w}}_{\bf{r,q}} \right)^{-1} \enspace,$)>> | <<latex(${\rm F}({\bf r},t)=\hat{{\bf w}}_{\bf{r,q}}^{\rm T} {\bf C}_{T_t}\hat{\bf{w}}_{\bf{r,q}} \left(\hat{\bf{w}}_{\bf{r,q}}^{\rm T} {\bf C}_{\rm c} \hat{\bf{w}}_{\bf{r,q}} \right)^{-1} \enspace,$)>> |
| Line 120: | Line 124: |
| where <<latex(${\bf C}_{T_t}=\sum_{T_t}{\|{\bf m}(t)-(\sum_{T_t}{{\bf m}(t)/N_{\rm T}}) \|^{2}}/(N_{\rm T}-1)$)>> is the covariance matrix computed from the measurements during window <<latex($T_t$)>>, <<latex($N_{\rm T}$)>> is the size of <<latex($T_t$)>>, and the range of <<latex($T_t$)>> is <<latex($t \pm 0.5N_{\rm T}$)>> . <<latex($T_t$)>> is a segment of active state <<latex($T_{\rm a}$)>>. The meaning of F-statistic is the same as the normalized variance <<latex($\rm{Var}_{\rm N}(\bf r)$)>> used in LCMV beamforming method. | where <<latex(${\bf C}_{T_t}=\sum_{T_t}{\|{\bf m}(t)-(\sum_{T_t}{{\bf m}(t)/N_{\rm T}}) \|^{2}}/(N_{\rm T}-1)$)>> is the covariance matrix computed from the measurements during window <<latex($T_t$)>>, <<latex($N_{\rm T}$)>> is the size of <<latex($T_t$)>>, and the range of <<latex($T_t$)>> is <<latex($t \pm 0.5N_{\rm T}$)>> . <<latex($T_t$)>> is a segment of active state <<latex($T_{\rm a}$)>>. The meaning of F-statistic is the same as the normalized variance <<latex($\rm{Var}_{\rm N}(\bf r)$)>> used in LCMV beamforming method. |
| Line 122: | Line 126: |
| If the number of <<latex($N_{\rm T}$)>> is small, the peak of temporal dynamics of F-statistic value may shift. In this case, it is more appropriate to replace the covariance matrix <<latex(${\bf C}_{T_t}$)>> with | If the number of <<latex($N_{\rm T}$)>> is small, the peak of temporal dynamics of F-statistic value may shift. In this case, it is more appropriate to replace the covariance matrix <<latex(${\bf C}_{T_t}$)>> with |
| Line 132: | Line 136: |
| ==== MCB process ==== 1. Drag and drop all of the epochs in ''Subject01 / right / right | timeoffset (98 files)'' into ''Process1''. 1. Click on [RUN] and select the process "'''Sources > Maximum Contrast Beamformer'''". <<BR>><<BR>> {{attachment:MCBPipelineEditorFmap2.png}} 1. With this window you can select the dipole orientation you want to use, the time window of active state, the window size you are going to use for the computation of F-statistics, the regularization parameter, and the sensors you are going to use for this estimation. You can edit the following options: |
=== MCB process === 1. Drag and drop all of the epochs in ''Subject01 / right / right | timeoffset (98 files)'' into Process1. 1. Click on [RUN] and select the process "''Sources > Maximum Contrast Beamformer''". <<BR>><<BR>> {{attachment:MCBPipelineEditorFmap2.png}} <<BR>><<BR>>With this window you can select the dipole orientation you want to use, the time window of active state, the window size you are going to use for the computation of F-statistics, the regularization parameter, and the sensors you are going to use for this estimation. You can edit the following options:<<BR>> |
| Line 139: | Line 140: |
| * '''Dipole orientation''': Please select ''Unconstrained'', which calculates the dipole orientation using the maximum contrast criterion. The method ''Cortially Constrained'' uses the orientation of cortical surface as dipole orientation. Note that the method'' Cortially Constrained ''is only available when the Head Model provides the orientation for each grid location. The unconstrained method may give more smooth results than the cortically constrained method. * '''Time windows''': Three parameters have to be set: ''Time range of active window'','' F statistic window size'', and ''Temporal resolution''. The dipole orientation and spatial filter is estimated using the variance of source activity during active state <<latex($T_a$)>>. ''F-statistic window size'' defines the length of the window for the computation of F-statistics, that is, <<latex($N_{\rm T}$)>>. The time window for computing F-statistics is going to be slided in ''Time range of active state'' with the interval set to be ''Temporal resolution''. If there are more than one F-statistic windows, the time label of the F statistics will be set as the middle time of each window, that is, <<latex($t_1,t_2,t_3,\ldots,t_{N-1},t_{N}$)>> in the following figure. And you will obtain the spatiotemporal F-statistics bewteen <<latex($t_1$)>> and <<latex($t_N$)>>.<<BR>><<BR>> {{attachment:MCBSlidingWindow.png||height="250",width="498"}} * '''Regularization parameter''': This value will be multiplied with the maximum eigenvalue of the covariance matrix computed from the recordings during ''Time range of interest''. The larger value of regularization parameter may give the more smooth results. * '''Sensors type''': Modalities that are used for the reconstruction. Here we only have one type of MEG sensors, so nothing to change. * '''Method for F statistic computation''': Please select ''Variance (use user define baseline) / Variance'' to compute F-statistic values''. ''The other two methods are ''Power / Variance and Variance (use user defined baseline) / Variance''. When the methiod'' Variance (use user defined baseline) / Variance ''is selected, the field of ''Baseline time window for F-ststistic calculation'' must be given. In this example, we set the baseline to be '''-104.2''' to '''-10''' ms. * Click on [Run]. 1. Two new files are available in the database explorer. * '''right:MCB: !SpatilFilter(Unconstr)|0.0_295.8ms''': This file saved the spatial filter for each grid point. The spatial filters are normalized using the standard deviation of beamformer outpouts during control state. <<BR>><<BR>> {{attachment:MCBSF.png}} * '''right:MCB: F-statistics var(b)/var(Unconstr)|0.0_295.8ms''': This file saved the F-statistic value for each grid point during 0-295.8 ms. <<BR>><<BR>> {{attachment:MCBDatabaseExplorerFmaps.png||height="296",width="364"}} <<BR>><<BR>> Double click on this file. Set the time to be anytime between 0 and 295.8 ms. Then click ''Surface'' tab on the right panel of database explorer. Set Data options > Amplitude to be '''95%'''. <<BR>><<BR>> {{attachment:MCBFmaps3Methods.png||height="207",width="587"}} <<BR>><<BR>>From left to right, the figures display the F statistics computed using ''Power / Variance, Variance / Variance, and Variance (use user defined baseline) / Variance''. The baseline used in this example was set to be '''-104.2 '''~''' -10''' ms. 1. Process ''Subject01 / left / left | timeoffset (101 files)'' using the same procedure. <<BR>><<BR>> {{attachment:MCBFmapsleft.png||height="207",width="602"}} <<BR>><<BR>>From left to right, the figures display the F statistics computed using ''Power / Variance, Variance / Variance, and Variance (use user defined baseline) / Variance''. The baseline used in this example was set to be '''-104.2 ~ -10''' ms. <<BR>><<BR>> 1. Process ''Subject01 / right / right | timeoffset (98 files)'' using the following parameter values to obtain the spatiotemporal dynamics of F-statistics.<<BR>><<BR>> {{attachment:MCBPipelineEditorFDynamics2.png}} <<BR>><<BR>>Two new files are available in Database explorer: * '''right:MCB: !SpatilFilter(Unconstr)|0.0_295.8ms''': This file saves the spatial filter for each grid points. The filename shows the time range used to compute spatial filters, that is, 0.0 to 295.8 ms in this case. * '''right:MCB: F-statistics var(b)/var(Unconstr)|10.0_290.0ms(ws:20.0ms,tr:10.0ms,bs:-104.2_-10.0ms)''': This file saved the spatiotemporal dynamics of F-statistics between 10.0 and 290.0 ms. The abbreviations for ''F-statistics window size,temporal resolution, ''and'' baseline'' is ''ws, tr, ''and'' bs''. Click on this file. Choose ''Surface'' tab and set ''Data options > Amplitude'' to be '''50'''%. Right click on the pop-out window. Select ''Snapshot > Time contact sheet: Figure''.''<<BR>><<BR>> {{attachment:MCBSnapshotSettting.png}} <<BR>><<BR>>''In this window, set ''Start time (ms)'' to be '''10''', ''End time (ms)'' to be '''290''', and ''Number of snapshots'' to be '''29'''. Click on ''Ok''.You will obtain the following figures. <<BR>><<BR>> {{attachment:MCBFdynamicsRight.png||height="397",width="514"}} <<BR>><<BR>>These figures display the F-statistics maps between 10 ms and 290 ms with 10-ms time interval. The baseline used in this example is set to be -104.2 ~ -10 ms. 1. Process "Subject01 / left / left | timeoffset (101 files)" with the same parameter values used in the previous step to obtain the spatiotemporal dynamics of F-statistics. <<BR>><<BR>> {{attachment:MCBFdynamicsLeft.png||height="334",width="540"}} == Beamformer-based correlation/coherence imaging == ==== Dynamic imaging of coherent sources (DICS) ==== [Under construction] ==== Spatiotemporal imaging of linearly-related source components (SILSC) ==== [Under construction] |
* '''Dipole orientation''': Please select ''Unconstrained'', which calculates the dipole orientation using the maximum contrast criterion. The method ''Constrained (normal to cortex) ''uses the orientation of cortical surface as dipole orientation. Note that the method ''Constrained (normal to cortex)'' is only available when the Head Model provides the orientation for each grid location. The unconstrained method may give more smooth results than the cortically constrained method. * '''Time windows''': Three parameters have to be set: ''Time range of active window'', ''F statistic window size'', and ''Temporal resolution''. The dipole orientation and spatial filter is estimated using the variance of source activity during active state <<latex($T_a$)>>. ''F-statistic window size'' defines the length of the window for the computation of F-statistics, that is, <<latex($N_{\rm T}$)>>. The time window for computing F-statistics is going to be slided in ''Time range of active state'' with the interval set to be ''Temporal resolution''. If there are more than one F-statistic windows, the time label of the F statistics will be set as the middle time of each window, that is, <<latex($t_1,t_2,t_3,\ldots,t_{N-1},t_{N}$)>> in the following figure. And you will obtain the spatiotemporal F-statistics bewteen <<latex($t_1$)>> and <<latex($t_N$)>>.<<BR>><<BR>> {{attachment:MCBSlidingWindow.png||width="582",height="292"}} * '''Regularization parameter''': This value will be multiplied with the maximum eigenvalue of the covariance matrix computed from the recordings during Time range of interest. The larger value of regularization parameter may give the more smooth results. * '''Sensors type''': Modalities that are used for the reconstruction. Here we only have one type of MEG sensors, so nothing to change. * '''Method for F statistic computation''': The default is set to be ''Variance (use user define baseline) / Variance'' to compute F-statistic values. The other two methods are ''Power / Variance'' and ''Variance / Variance''. When the methiod ''Variance (use user defined baseline) / Variance'' is selected, the field of ''Baseline time window for F-ststistic calculation'' must be given. In this example, we set the baseline to be -104.2 to -10 ms. 1. Click on [Run]. Two new files are available in the database explorer. * '''right:MCB: SpatilFilter(Unconstr)|0.0_295.8ms''': This file saved the spatial filter for each grid point. The spatial filters are normalized using the standard deviation of beamformer outpouts during control state. <<BR>><<BR>> {{attachment:MCBSF.png}} * '''right:MCB: F-statistics var(b)/var(Unconstr)|0.0_295.8ms''': This file saved the F-statistic value for each grid point during 0-295.8 ms. <<BR>><<BR>> {{attachment:MCBDatabaseExplorerFmaps.png}} <<BR>><<BR>> Double click on this file. Set the time to be anytime between 0 and 295.8 ms. Then click ''Surface'' tab on the right panel of database explorer. Set ''Data options > Amplitude'' to be '''95%'''. <<BR>><<BR>> {{attachment:MCBFmaps3Methods.png||width="617",height="219"}} <<BR>><<BR>>From left to right, the figures display the F statistics computed using Power / Variance, Variance / Variance, and Variance (use user defined baseline) / Variance. The baseline used in this example was set to be -104.2 ~ -10 ms. 1. Process Subject01 / left / left | timeoffset (101 files) using the same procedure. <<BR>><<BR>> {{attachment:MCBFmapsleft.png||width="596",height="205"}} <<BR>><<BR>>From left to right, the figures display the F statistics computed using ''Power / Variance'', ''Variance / Variance'', and ''Variance (use user defined baseline) / Variance''. The'' baseline'' used in this example was set to be '''-104.2 ~ -10 ms'''. <<BR>><<BR>> 1. Process Subject01 / right / right | timeoffset (98 files) using the following parameter values to obtain the spatiotemporal dynamics of F-statistics.<<BR>><<BR>> {{attachment:MCBPipelineEditorFDynamics2.png}} <<BR>><<BR>>Two new files are available in Database explorer: * '''right:MCB: SpatilFilter(Unconstr)|0.0_295.8ms''': This file saves the spatial filter for each grid points. The filename shows the time range used to compute spatial filters, that is, 0.0 to 295.8 ms in this case. * '''right:MCB: F-statistics var(b)/var(Unconstr)|10.0_290.0ms(ws:20.0ms,tr:10.0ms,bs:-104.2_-10.0ms)''': This file saved the spatiotemporal dynamics of F-statistics between''' 10.0''' and '''290.0 ms'''. The abbreviations for F-statistics window size, temporal resolution, and baseline is ''ws'', ''tr'', and ''bs''. Click on this file. Choose ''Surface'' tab and set ''Data options > Amplitude'' to be '''50%'''. Right click on the pop-out window. Select ''Snapshot > Time contact sheet: Figure.''<<BR>><<BR>> {{attachment:MCBSnapshotSettting.png}} <<BR>><<BR>>In this window, set ''Start time (ms)'' to be '''10''', ''End time (ms)'' to be '''290''', and ''Number of snapshots'' to be '''29'''. Click on Ok. You will obtain the following figures. <<BR>><<BR>> {{attachment:MCBFdynamicsRight.png||width="783",height="604"}} <<BR>><<BR>>These figures display the F-statistics maps between 10 ms and 290 ms with 10-ms time interval. The baseline used in this example is set to be -104.2 ~ -10 ms. 1. Process "''Subject01 / left / left | timeoffset (101 files)''" with the same parameter values used in the previous step to obtain the spatiotemporal dynamics of F-statistics. <<BR>><<BR>> {{attachment:MCBFdynamicsLeft.png||width="796",height="494"}} |
| Line 166: | Line 155: |
| 1. Liu TC and Van Veen BD, (1992) <<BR>> [[http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=120801&tag=1|Multiple window based minimum variance spectrum estimation for multidimensional random fields]] <<BR>> IEEE Transactions on Signal Processing, 40(3): 578-589 1. Van Veen BD, Van Drongelen W, Yuchtman M, Suzuki A (1997)<<BR>>[[http://www.ncbi.nlm.nih.gov/pubmed/9282479|Localization of brain electrical activity via linearly constrained minimum variance spatial filtering]]<<BR>>IEEE Transactions on Biomedical Engineering 44(9): 867-880. 1. Gross J, Kujala J, Hamalainen M, Timmermann L, Schnitzler A, Salmelin R (2001) <<BR>> [[http://www.pnas.org/cgi/pmidlookup?view=long&pmid=11209067|Dynamic imaging of coherent sources: Studying neural interactions in the human brain]] <<BR>> Proc Natl Acad Sci U S A 98(2): 694-699. 1. Robinson SE and Vrba J (1999) <<BR>>''Functional neuroimaging by synthetic aperture magnetometry''<<BR>>Recent Advances in Biomagnetism. Tohoku University Press 1999: 302-305. 1. Chen YS, Cheng CY, Hsieh JC, Chen LF (2006)<<BR>>[[http://www.ncbi.nlm.nih.gov/pubmed/16941832|Maximum contrast beamformer for electromagnetic mapping of brain activity]]<<BR>>IEEE Transactions on Biomedical Engineering 53(9): 1765-1774. |
1. Liu TC and Van Veen BD, (1992) <<BR>> Multiple window based minimum variance spectrum estimation for multidimensional random fields <<BR>> IEEE Transactions on Signal Processing, 40(3): 578-589 1. Van Veen BD, Van Drongelen W, Yuchtman M, Suzuki A (1997)<<BR>>Localization of brain electrical activity via linearly constrained minimum variance spatial filtering<<BR>>IEEE Transactions on Biomedical Engineering 44(9): 867-880. 1. Gross J, Kujala J, Hamalainen M, Timmermann L, Schnitzler A, Salmelin R (2001) <<BR>> Dynamic imaging of coherent sources: Studying neural interactions in the human brain <<BR>> Proc Natl Acad Sci U S A 98(2): 694-699. 1. Robinson SE and Vrba J (1999) <<BR>>Functional neuroimaging by synthetic aperture magnetometry<<BR>>Recent Advances in Biomagnetism. Tohoku University Press 1999: 302-305. 1. Chen YS, Cheng CY, Hsieh JC, Chen LF (2006)<<BR>>Maximum contrast beamformer for electromagnetic mapping of brain activity<<BR>>IEEE Transactions on Biomedical Engineering 53(9): 1765-1774. |
| Line 172: | Line 161: |
| == Feedback == |
Warning: The developments described below have been abandonned. Please refer to the source estimation tutorial.
...
Beamforming methods
Authors: Hui-Ling Chan, Francois Tadel, Sylvain Baillet
The estimation of source distribution is an important step to understand the brain activity from EEG and MEG data. Dipole fitting, minimum norm estimation and beamformer are three commonly used methods. It has been proved that beamforming methods provide good spatial resolution. This tutorial will show how to apply beamforming methods to MEG data and obtain the statistic map of source activation.
IMPORTANT: The LCMV beamformer is now part of the main Brainstorm distribution. We recommend you refer instead to the new documentation in the introduction tutorials: Source estimation.
Installation
This tutorial requires you download the two processes below and copy them to your personal process folder ($HOME/.brainstorm/process):
Introduction
Beamforming methods scan each targeted source position 
and estimate the spatial filter 
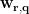. By multiplying with the MEG recordings 
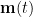, the spatial filter 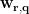outputs the temporal waveform 
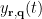of the dipole source at that position with the dipole orientation 
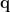as below:
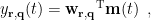
where 'T' indicates the transpose of a matrix or vector. The beamforming spatial filter can be vector-type or scalar-type.
Vector-type beamformer
For each position 
, three orthogonal spatial filters ![$\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_2d3ac467d26334f39241546468515832d42349b6_p1.png "$\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$")
are computed by applying the unit-gain constraint as well as the minimum norm and minimum variance criteria as below [Liu and Van Veen, 1992; Van Veen et al., 1997]:
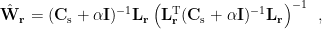
where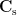 
is the covariance matrix of MEG recordings during window 
, 
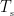is the identity matrix,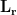 
is the gain matrix for the dipole located at position 
, and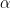 
is the regularization parameter which compromises the minimum norm and minimum variance criteria.
Scalar-type beamformer
For each position , the source orientation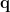 
is first estimated to enable the spatial filter to output the source activity with maximum power or fitting some other criteria. The dipole orientation can be obtained by exhaustive search, non-linear search [Robinson and Vrba, 1999], or analytical solution [Chen et al., 2006]. The estimated dipole orientation 
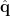is then applied to calculate the spatial filter as follows [Robinson and Vrba, 1999]:
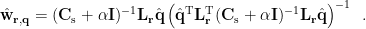
LCMV beamformer
LCMV stands for linearly-constrained minimum variance. LCMV beamformer is vector-type beamformer [Van Veen et al., 1997]. For each position , this method calculates the neural activity index, which is interpreted as the estimate of source to noise variance.
Neural activity index
For each position , the variance of source activity during active state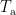 
is calculated as follows [Liu and Van Veen, 1992; Van Veen et al., 1997]:
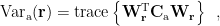
or
![$ \rm{Var}_{\rm a}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_c51fec46af184e9d1d52b84223372b5eec451b54_p1.png "$ \rm{Var}_{\rm a}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $")
where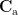 
is the covariance matrix computed from MEG recordings during active state 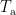. Alternatively, the variance of beamformer outpout along the dominant direction can be calculated by using the singular value decomposition [Gross et al., 2001]:
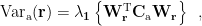
or
![$ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_7ffb424c314741d9890b9a605a93cab8f598943b_p1.png "$ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} \enspace, $")
where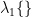 
indicates the maximum eigenvalue of the expression in braces.
When the location is far from sensors, the elements of lead field matrix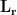 
are small. So the elements of 
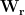are generally large and the estimated variance for the deep source becomes large. When the location is close to sensors, the elements of lead field matrix 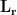are large. It results in small values of the elements of 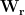and small estimated variance for the superficial source. To reduce the effect caused by the depth of source location, the estimated source variance 
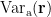is normalized by the noise variance 
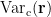as follows:
![$ \rm{Var}_{\rm N}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_ca0f463fd01656bbacba2d78248876ab006d764c_p1.png "$ \rm{Var}_{\rm N}(\bf r) =\rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \rm{trace} \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $")
or
![$ \rm{Var}_{\rm N}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_c9bfb5b5902444d064f8462f3fb4066c57610edb_p1.png "$ \rm{Var}_{\rm N}(\bf r) =\lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}^{-1}{\bf L}_{\bf r}]^{-1}\right \} / \lambda_1 \left \{[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}^{-1}{\bf L}_{\bf r}]^{-1}\right \}\enspace, $")
where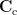 
is the covariance matrix computed from MEG recordings during control state 
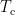. The normalized variance 
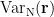is called neural activity index (NAI). In the Brainstorm, the noise covariance will be used as the covariance matrix for control state. Please refer to Tutorial 7: Noise covariance matrix for the details of noise covariance computation.
LCMV process
Drag and drop all of the epochs in Subject01 / right / right | timeoffset (98 files) into Process1.
Click on [RUN] and select the process "Sources > Beamformer: LCMV".
Configure the options as follows:
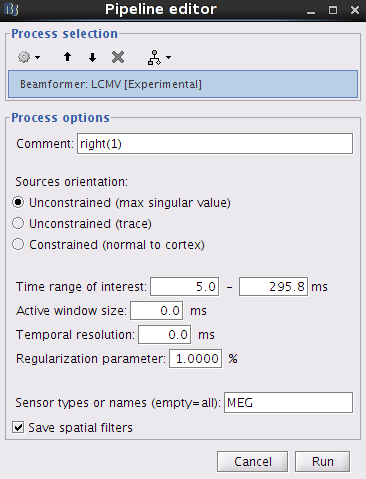
With this window you can select the method you want to use to estimate the source variance and noise variance, the time window of active state, the regularization parameter, and the sensors you are going to use for this estimation. You can edit the following options:
Comment: This field contains what is going to be displayed in the database explorer.
Method:
Unconstrained (max singular value): Calculates the variances of source activity and noise by using the maximum singular value.
Unconstrained (trace): Calculates the variances by using the trace.
Constrained (normal to cortex): The dipole orientation for each vertex is set to the normal vector to the cortex surface (not available for volume head models). This method may give less smooth results than the unconstrained methods.
Time window of active state: The neural activity index is computed using the source activity variance during the active state
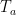. Time range of interest: Total time period over which we want to calculate the neural activity index.
Active window size: Defines the duration of the active state. The active window is slided all along the time range of interest. A large active window size is recommended, at least larger than the number of sensors in number of time samples.
Temporal resolution: Defines the time lapse between two estimations of the neural activity index. If this "active size window" or "temporal resolution" are set to zero, the active window size is set to the entire time range of interest. The temporal resolution becomes irrelevant because only one neural activity index will be estimated. If there are multiple active state windows, the time label of the neural activity index will be set as the middle time of each active state window, that is,
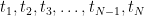in the following figure. You are going to obtain the spatiotemporal dynamics of neural activity index bewteen 
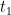and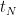 
.
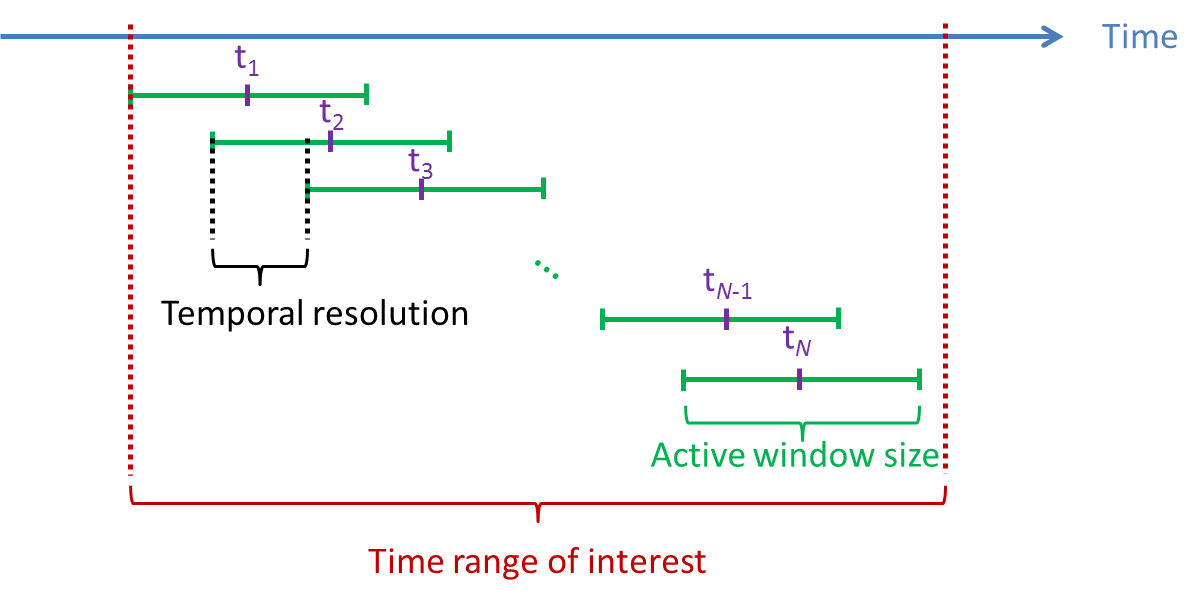
Regularization parameter: This value will be multiplied with the maximum eigenvalue of the covariance matrix computed from the recordings during Time range of interest. A larger value of regularization parameter would give smoother results. Large regularization parameter value is more suitable for noisy data. When analyzing simulation data sets, the regularization parameter value can be reduced.
Sensors type: Modalities that are used for the reconstruction. Here we only have one type of MEG sensors, so nothing to change.
Save spatial filters: Check this option if you want to save the spatial filters. Checking this option if you want to observe the temporal profile of source or compute functional connectivity. Note that the amplitudes of these temporal profiles are not meaningful because the spatial filter is caluclated for one voxel at a time without the holistic consideration on whole brain activity. So, the amplitude of beamformer outpout can not represent the source amplitude and the relationship of the amplitude between each grid point is meaningless. However, the beamformer outpouts can further be used to calculate correlation or coherence between each region because these two estimations include the normalization of amplitude and thus the ampltidue of source waveforms doesn't effect the results.
Two new files are available in the database explorer.
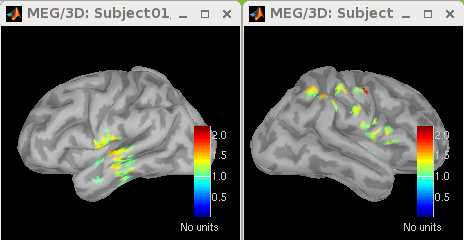
right: LCMV (Unconstr/svd, 5-296ms): This file saves the neural activity index for every dipole position.
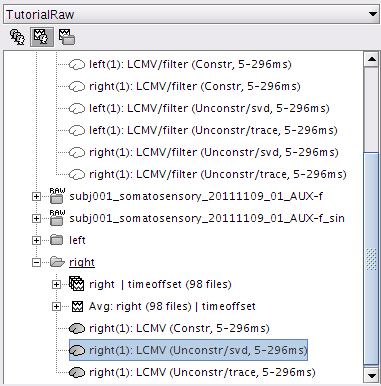
Double click on this file. Right click on anywhere of the pop-out window. From the pop-out menu, select Colormap:Sources > Maximum: Custom.... Set Minimum to be 1.2 and Maximum to be 2.0. Click Ok.
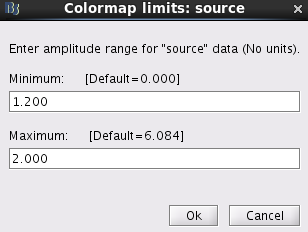
Set the time to be anytime between 0 and 296 ms. Then click Surface tab on the right panel of database explorer. Set Data options > Amplitude to be 50% and Data options > Min Size to be 5.
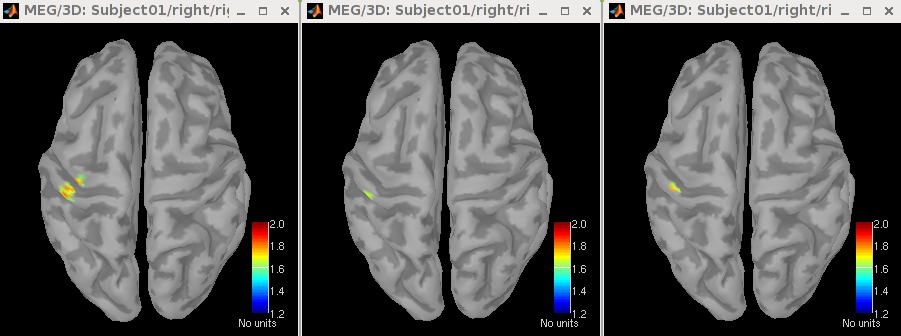
The maps of neural activity index estimated using Unconstrained (max sigular value), Unconstrained (trace), and Constrained (normal to cortex) are shown from left to right. All maps display strong activations in the left primary somatosensory area (S1).right: LCMV/filter (Unconstr/svd, 5-296ms): This file saves the three spatial filters along the x, y, and z directions for each dipole position. These spatial filters are normalized by the standard deviation of noise. Note that there is one spatial filter for each dipole location if the method Cortically Constrained (normal to cortex) is used.
Explore spatiotemporal dynamics of anatomically constrained beamformer outputs in the right condition.
Double click on this file. Set the time to be 15.8 ms, 30 ms, or 60 ms. Right click on anywhere of the pop-out window. From the pop-out menu, select Colormap:Sources > Maximum: Local.... Then click Surface tab on the right panel of database explorer. Set Data options > Amplitude to be 70% and Data options > Min Size to be 5.
16 ms (left): left S1
30 ms (middle): left S1
60 ms (right): left S2
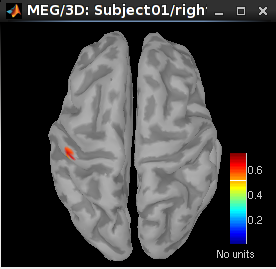
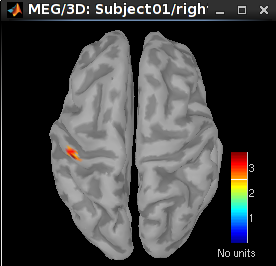
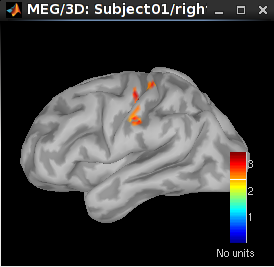
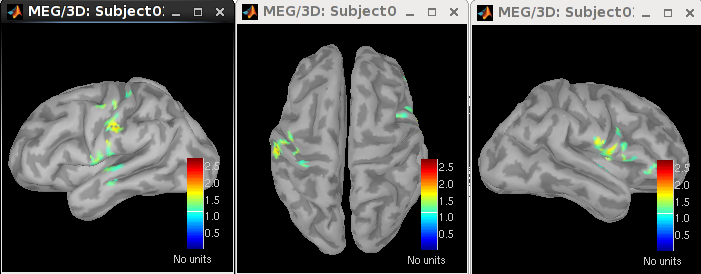
70 ms: bilateral S2
Set the time to be 70 ms. Then click Surface tab on the right panel of database explorer. Set Data options > Amplitude to be 41% and Data options > Min Size to be 5.
Explore spatiotemporal dynamics of anatomically constrained beamformer outputs in the right condition.
Double click on this file. Set the time to be 20 ms, 30 ms, or 60 ms. Right click on anywhere of the pop-out window. From the pop-out menu, select Colormap:Sources > Maximum: Local.... Then click Surface tab on the right panel of database explorer. Set Data options > Amplitude to be 60% and Data options > Min Size to be 5.
20 ms (left): right S1
30 ms (middle): right S1
60 ms (right): right S2
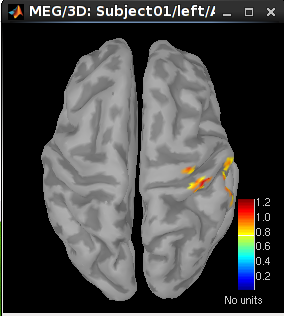
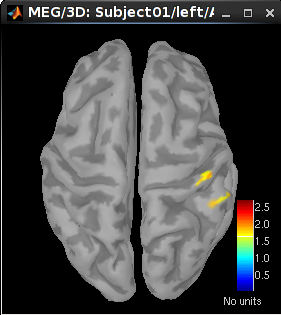
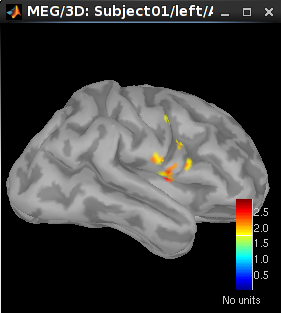
73.3 ms: bilateral S2. Set the time to be 73.3 ms. Then click Surface tab on the right panel of database explorer. Set Data options > Amplitude to be 45% and Data options > Min Size to be 5.
Maximum constrast beamformer
Maximum constrast beamformer (MCB) is scalar-type beamformer [Chen et al., 2006]. For each position 
, it provides an analytical solution of dipole orientation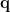 
, which maximizes the constrast of beamformer outputs between active state and control state as bellow:
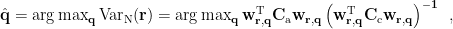
where 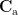is the covariance matrix computed from the measurements during active state and 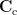is the covariance matrix computed from the measurements during control state.
Solution of dipole orientation
The solution of spatial filter can be rewritten as
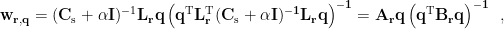
where both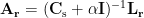 
and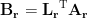 
depend only on the dipole location . Then the objective function for obtaining the dipole orientation 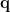can be rewritten as
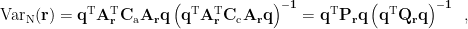
where both of the 3-by-3 matrices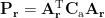 
and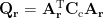 
does not depend on the dipole orientation 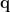. The solution of dipole orientation 
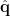is the eigenvector corresponding to the maximum eigenvalue of the matrix 
.
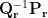Statistical mapping
After obtaining the dipole orientation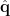 
and the spatial filter 
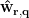for dipole position , the F-statistic value at time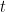 
can be obtained using the following formula:
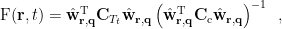
where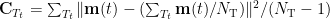 
is the covariance matrix computed from the measurements during window 
, 
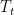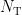is the size of 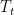, and the range of 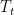is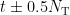 
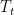. is a segment of active state 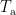. The meaning of F-statistic is the same as the normalized variance 
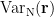used in LCMV beamforming method.
If the number of 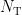is small, the peak of temporal dynamics of F-statistic value may shift. In this case, it is more appropriate to replace the covariance matrix 
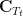with
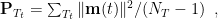
or
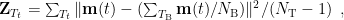
where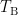 
represents the window of baseline and its size is 
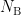. When 
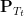is used, the F-statistic value represents the estimate of source power to noise variance.
MCB process
Drag and drop all of the epochs in Subject01 / right / right | timeoffset (98 files) into Process1.
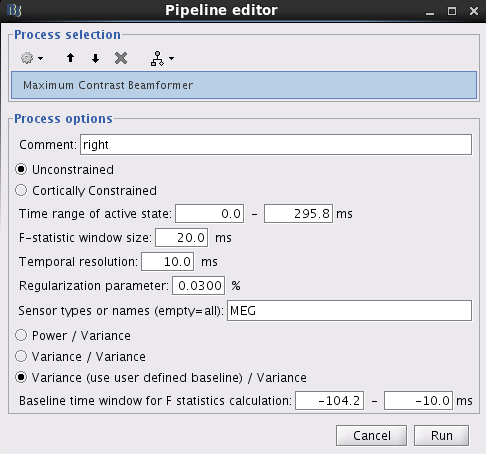
Click on [RUN] and select the process "Sources > Maximum Contrast Beamformer".
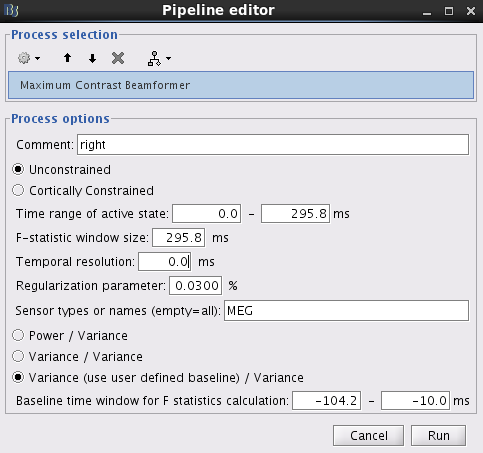
With this window you can select the dipole orientation you want to use, the time window of active state, the window size you are going to use for the computation of F-statistics, the regularization parameter, and the sensors you are going to use for this estimation. You can edit the following options:
Comment: This field contains what is going to be displayed in the database explorer.
Dipole orientation: Please select Unconstrained, which calculates the dipole orientation using the maximum contrast criterion. The method Constrained (normal to cortex) uses the orientation of cortical surface as dipole orientation. Note that the method Constrained (normal to cortex) is only available when the Head Model provides the orientation for each grid location. The unconstrained method may give more smooth results than the cortically constrained method.
Time windows: Three parameters have to be set: Time range of active window, F statistic window size, and Temporal resolution. The dipole orientation and spatial filter is estimated using the variance of source activity during active state
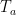. F-statistic window size defines the length of the window for the computation of F-statistics, that is, 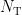. The time window for computing F-statistics is going to be slided in Time range of active state with the interval set to be Temporal resolution. If there are more than one F-statistic windows, the time label of the F statistics will be set as the middle time of each window, that is, 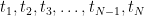in the following figure. And you will obtain the spatiotemporal F-statistics bewteen 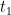and .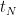
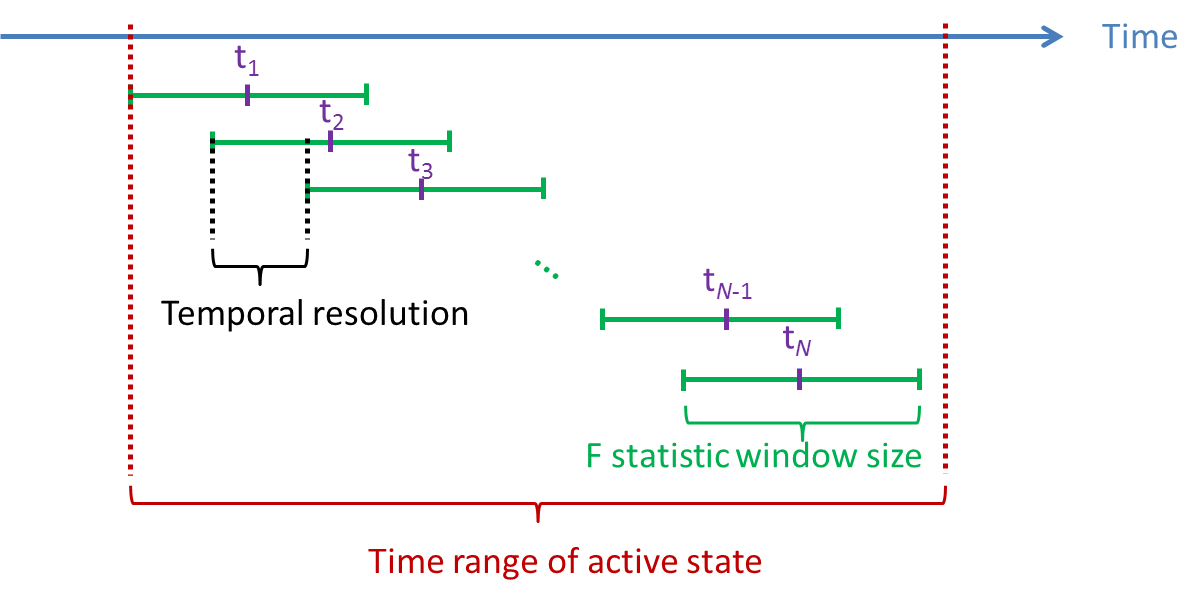
Regularization parameter: This value will be multiplied with the maximum eigenvalue of the covariance matrix computed from the recordings during Time range of interest. The larger value of regularization parameter may give the more smooth results.
Sensors type: Modalities that are used for the reconstruction. Here we only have one type of MEG sensors, so nothing to change.
Method for F statistic computation: The default is set to be Variance (use user define baseline) / Variance to compute F-statistic values. The other two methods are Power / Variance and Variance / Variance. When the methiod Variance (use user defined baseline) / Variance is selected, the field of Baseline time window for F-ststistic calculation must be given. In this example, we set the baseline to be -104.2 to -10 ms.
- Click on [Run]. Two new files are available in the database explorer.
right:MCB: SpatilFilter(Unconstr)|0.0_295.8ms: This file saved the spatial filter for each grid point. The spatial filters are normalized using the standard deviation of beamformer outpouts during control state.
right:MCB: F-statistics var(b)/var(Unconstr)|0.0_295.8ms: This file saved the F-statistic value for each grid point during 0-295.8 ms.
Double click on this file. Set the time to be anytime between 0 and 295.8 ms. Then click Surface tab on the right panel of database explorer. Set Data options > Amplitude to be 95%.
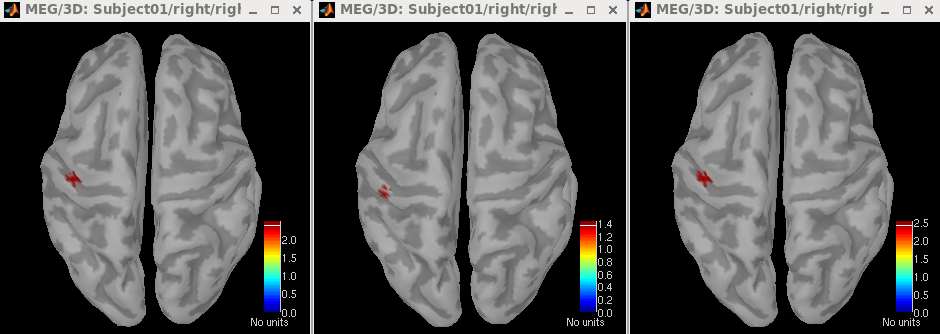
From left to right, the figures display the F statistics computed using Power / Variance, Variance / Variance, and Variance (use user defined baseline) / Variance. The baseline used in this example was set to be -104.2 ~ -10 ms.
Process Subject01 / left / left | timeoffset (101 files) using the same procedure.
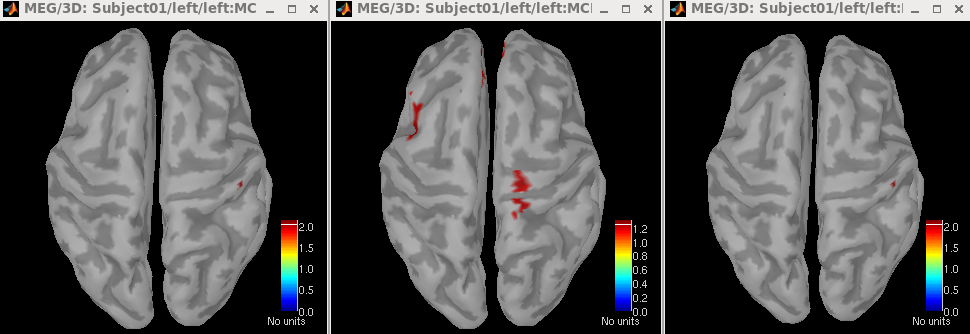
From left to right, the figures display the F statistics computed using Power / Variance, Variance / Variance, and Variance (use user defined baseline) / Variance. The baseline used in this example was set to be -104.2 ~ -10 ms.
Process Subject01 / right / right | timeoffset (98 files) using the following parameter values to obtain the spatiotemporal dynamics of F-statistics.
Two new files are available in Database explorer:right:MCB: SpatilFilter(Unconstr)|0.0_295.8ms: This file saves the spatial filter for each grid points. The filename shows the time range used to compute spatial filters, that is, 0.0 to 295.8 ms in this case.
right:MCB: F-statistics var(b)/var(Unconstr)|10.0_290.0ms(ws:20.0ms,tr:10.0ms,bs:-104.2_-10.0ms): This file saved the spatiotemporal dynamics of F-statistics between 10.0 and 290.0 ms. The abbreviations for F-statistics window size, temporal resolution, and baseline is ws, tr, and bs. Click on this file. Choose Surface tab and set Data options > Amplitude to be 50%. Right click on the pop-out window. Select Snapshot > Time contact sheet: Figure.
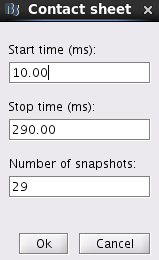
In this window, set Start time (ms) to be 10, End time (ms) to be 290, and Number of snapshots to be 29. Click on Ok. You will obtain the following figures.
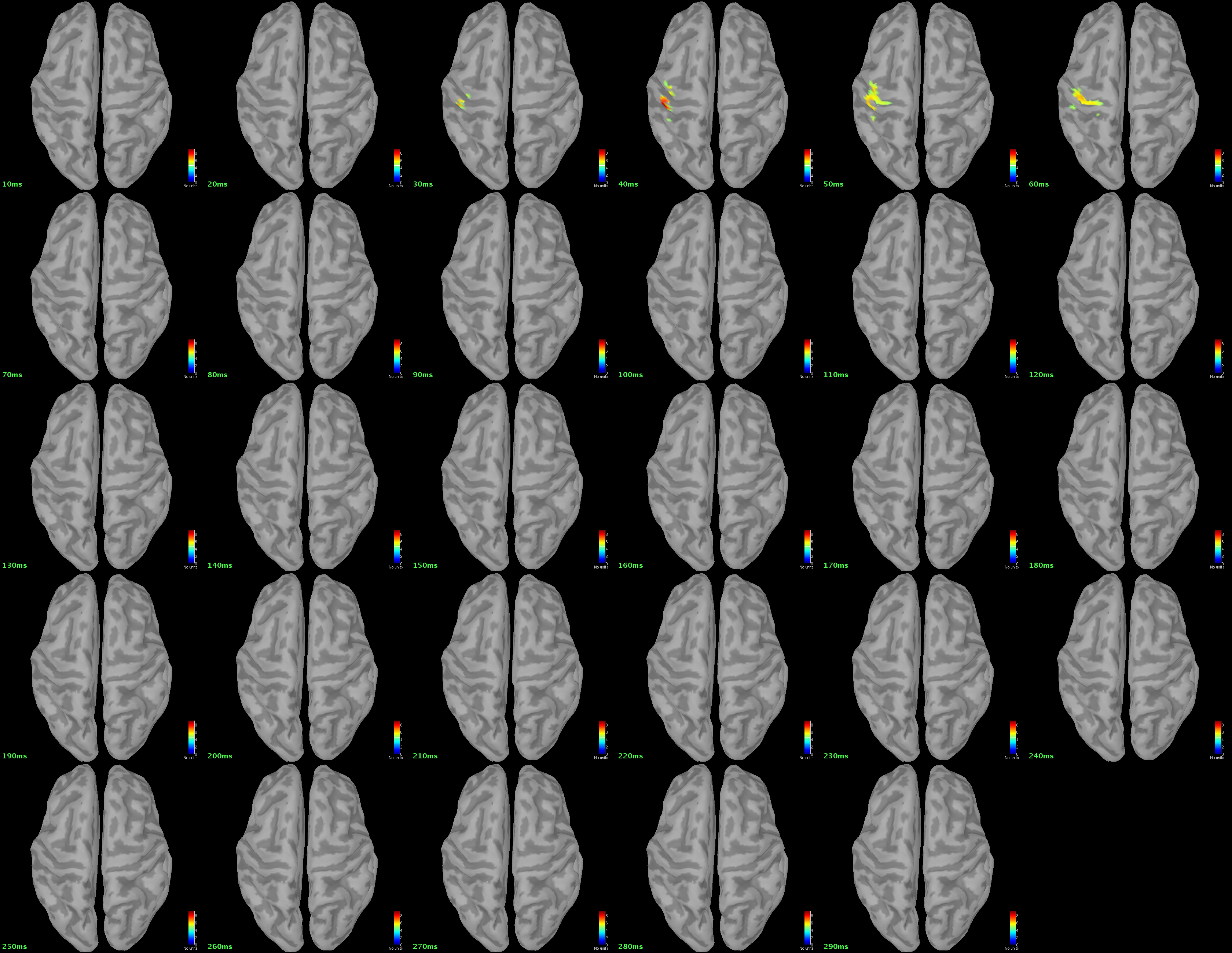
These figures display the F-statistics maps between 10 ms and 290 ms with 10-ms time interval. The baseline used in this example is set to be -104.2 ~ -10 ms.
Process "Subject01 / left / left | timeoffset (101 files)" with the same parameter values used in the previous step to obtain the spatiotemporal dynamics of F-statistics.
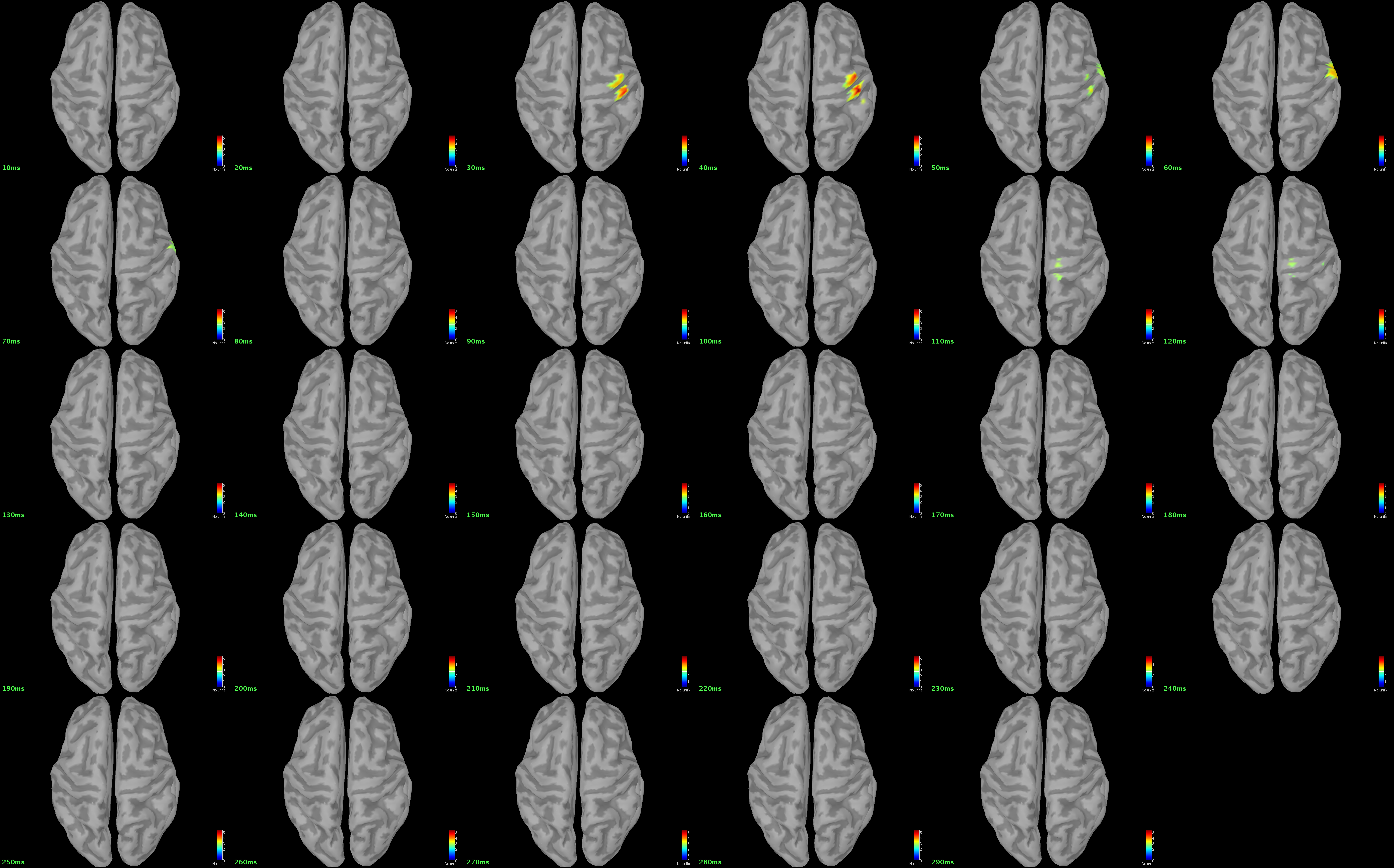
References
Liu TC and Van Veen BD, (1992)
Multiple window based minimum variance spectrum estimation for multidimensional random fields
IEEE Transactions on Signal Processing, 40(3): 578-589Van Veen BD, Van Drongelen W, Yuchtman M, Suzuki A (1997)
Localization of brain electrical activity via linearly constrained minimum variance spatial filtering
IEEE Transactions on Biomedical Engineering 44(9): 867-880.Gross J, Kujala J, Hamalainen M, Timmermann L, Schnitzler A, Salmelin R (2001)
Dynamic imaging of coherent sources: Studying neural interactions in the human brain
Proc Natl Acad Sci U S A 98(2): 694-699.Robinson SE and Vrba J (1999)
Functional neuroimaging by synthetic aperture magnetometry
Recent Advances in Biomagnetism. Tohoku University Press 1999: 302-305.Chen YS, Cheng CY, Hsieh JC, Chen LF (2006)
Maximum contrast beamformer for electromagnetic mapping of brain activity
IEEE Transactions on Biomedical Engineering 53(9): 1765-1774.