|
Size: 14568
Comment:
|
Size: 14767
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 94: | Line 94: |
| where <<latex(${\bf C}_{T_t}=\sum_{T_t}{\|{\bf m}(t)-(\sum_{T_t}{{\bf m}(t)/N_T}) \|^{2}}/N_T$)>> is the covariance matrix computed from the measurements during window <<latex($T_t$)>>. If the size of window <<latex($T_t$)>> is small, the peak of temporal dynamics of F-statistic value may shift. In this case, it is more appropriate to replace the covariance matrix <<latex(${\bf C}_{T_t}$)>> with | where <<latex(${\bf C}_{T_t}=\sum_{T_t}{\|{\bf m}(t)-(\sum_{T_t}{{\bf m}(t)/N_T}) \|^{2}}/(N_T-1)$)>> is the covariance matrix computed from the measurements during window <<latex($T_t$)>> and <<latex($N_T$)>> is the size of <<latex($T_t$)>>. If <<latex($N_T$)>> is small, the peak of temporal dynamics of F-statistic value may shift. In this case, it is more appropriate to replace the covariance matrix <<latex(${\bf C}_{T_t}$)>> with |
| Line 96: | Line 96: |
| <<latex(${\bf P}_{T_t}=\sum_{T_t}{\|{\bf m}(t)\|^{2}}/N_T\enspace,$)>> | <<latex(${\bf P}_{T_t}=\sum_{T_t}{\|{\bf m}(t)\|^{2}}/(N_T-1)\enspace,$)>> |
| Line 100: | Line 100: |
| <<latex(${\bf Z}_{T_t}=\sum_{T_t}{\|{\bf m}(t)-(\sum_{T_B}{{\bf m}(t)/N_B}) \|^{2}}/N_T\enspace,$)>> | <<latex(${\bf Z}_{T_t}=\sum_{T_t}{\|{\bf m}(t)-(\sum_{T_{\rm B}}{{\bf m}(t)/N_{\rm B}}) \|^{2}}/(N_T-1)\enspace,$)>> where <<latex($T_{\rm B}$)>> represetns the window of baseline and <<latex($N_{\rm B}$)>> is the length of window <<latex($T_{\rm B}$)>>. |
Beamforming methods
Authors: Hui-Ling Chan, Francois Tadel, Sylvain Baillet
The estimation of source distribution is an important step to understand the brain activity from EEG and MEG data. Dipole fitting, minimum norm estimation and beamformer are three commonly used methods. It has been proved that beamforming methods provide good spatial resolution. This tutorial will show how to apply beamforming methods to MEG data and obtain the statistic map of source activation.
We are going to use the protocol TutorialRaw created in the introduction tutorials. If you have not followed these tutorials yet, please do it now.
Contents
Introduction
Beamforming methods scan each targeted source position  and estimate the spatial filter
and estimate the spatial filter 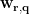 . By multiplying with the MEG recordings
. By multiplying with the MEG recordings 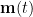 , the spatial filter
, the spatial filter 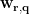 outputs the temporal waveform
outputs the temporal waveform 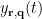 of the dipole source at that position with the dipole orientation
of the dipole source at that position with the dipole orientation 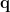 as below:
as below:
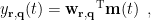
where 'T' indicates the transpose of a matrix or vector. The beamforming spatial filter can be vector-type or scalar-type.
Vector-type beamformer
For each position  , three orthogonal spatial filters
, three orthogonal spatial filters ![$\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$ $\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_2d3ac467d26334f39241546468515832d42349b6_p1.png) are computed by applying the unit-gain constraint as well as the minimum norm and minimum variance criteria as below [Van Veen et al., 1997]:
are computed by applying the unit-gain constraint as well as the minimum norm and minimum variance criteria as below [Van Veen et al., 1997]:
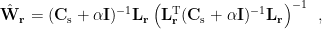
where 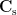 is the covariance matrix of MEG recordings during window
is the covariance matrix of MEG recordings during window 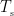 ,
,  is the identity matrix,
is the identity matrix, 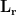 is the gain matrix for the dipole located at position
is the gain matrix for the dipole located at position  , and
, and 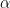 is the regularization parameter which compromises the minimum norm and minimum variance criteria.
is the regularization parameter which compromises the minimum norm and minimum variance criteria.
Scalar-type beamformer
For each position  , the source orientation
, the source orientation 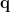 is first estimated to enable the spatial filter to output the source activity with maximum power or fitting some other criteria. The dipole orientation can be obtained by exhaustive search [Vrba and Robinson, 2000] or analytical solution [Chen et al., 2006]. The estimated dipole orientation
is first estimated to enable the spatial filter to output the source activity with maximum power or fitting some other criteria. The dipole orientation can be obtained by exhaustive search [Vrba and Robinson, 2000] or analytical solution [Chen et al., 2006]. The estimated dipole orientation 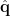 is then applied to calculate the spatial filter as follows [Vrba and Robinson, 2000]:
is then applied to calculate the spatial filter as follows [Vrba and Robinson, 2000]:

LCMV beamformer
LCMV stands for linearly-constrained minimum variance. LCMV beamformer is vector-type beamformer. For each position  , this method calculates the neural activity index, which is interpreted as the estimate of source to noise variance.
, this method calculates the neural activity index, which is interpreted as the estimate of source to noise variance.
Neural activity index
For each position  , the variance of source activity during active state
, the variance of source activity during active state 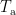 is calculated as follows:
is calculated as follows:
![$ \rm{Var}_{\rm a}(\bf r) =trace \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $ $ \rm{Var}_{\rm a}(\bf r) =trace \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_cb2e09fb09a948bd8f3590a5fb5ec78b3f485b92_p1.png)
or
![$ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $ $ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_a4850818772e2ccb0091762ad12b2ea377c4bd92_p1.png)
where 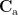 is the covariance matrix computed from MEG recordings during active state
is the covariance matrix computed from MEG recordings during active state 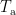 and
and 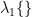 indicates the maximum eigenvalue of the expression in braces.
indicates the maximum eigenvalue of the expression in braces.
When the location  is far from sensors, the elements of lead field matrix
is far from sensors, the elements of lead field matrix 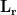 are small. So the elements of
are small. So the elements of ![$\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$ $\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_6f70bec44ed33947d8956368ab78866325802ce0_p1.png) are generally large and the estimated variance for the deep source becomes large. When the location
are generally large and the estimated variance for the deep source becomes large. When the location  is close to sensors, the elements of lead field matrix
is close to sensors, the elements of lead field matrix 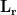 are large. It results in small values of the elements of
are large. It results in small values of the elements of ![$\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$ $\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_6f70bec44ed33947d8956368ab78866325802ce0_p1.png) and small estimated variance for the superficial source. To reduce the effect caused by the depth of source location, the estimated source variance
and small estimated variance for the superficial source. To reduce the effect caused by the depth of source location, the estimated source variance 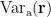 is normalized by the noise variance
is normalized by the noise variance 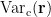 as follows:
as follows:
![$ \rm{Var}_{\rm N}(\bf r) =\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \} / \rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $ $ \rm{Var}_{\rm N}(\bf r) =\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \} / \rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_9dc2071036c085e508246a6f349dce3d1cdaff8b_p1.png)
or
![$ \rm{Var}_{\rm N}(\bf r) =\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \} / \lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $ $ \rm{Var}_{\rm N}(\bf r) =\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \} / \lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_dceaf91650d673f53184c138b87d9a91e8d53899_p1.png)
where 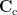 is the covariance matrix computed from MEG recordings during control state
is the covariance matrix computed from MEG recordings during control state 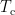 . The normalized variance
. The normalized variance 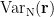 is called neural activity index (NAI).
is called neural activity index (NAI).
LCMV process
Drag and drop all of the epochs in Subject01 / right / right | timeoffset (98 files) into Process1.
Click on [RUN] and select the process "Sources > LCMV Beamformer".
Select Sources > LCMV Beamformer in Pipeline editor.
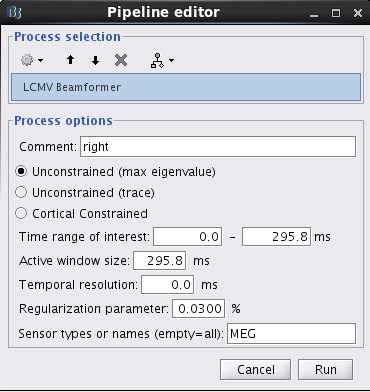
With this window you can select the method you want to use to estimate the source variance and noise variance, the time window of active state, and the sensors you are going to use for this estimation. You can edit the following options:
Comment: This field contains what is going to be displayed in the database explorer.
Method: Please select Unconstrained (max eigenvalue) or Unconstrained (trace). The method Unconstrained (max eigenvalue) calculates the variances of source activity and noise by using the maximum eigenvalue. The method Unconstrained (trace) calculates the variances of source activity and noise by using trace. The method Cortial Constrained use the orientation of cortical surface as dipole orientation. Note that the method Cortial Constrained is only available when the Head Model provides the orientation for each grid location. The unconstrained methods may give more smooth results than the cortical constrained method.
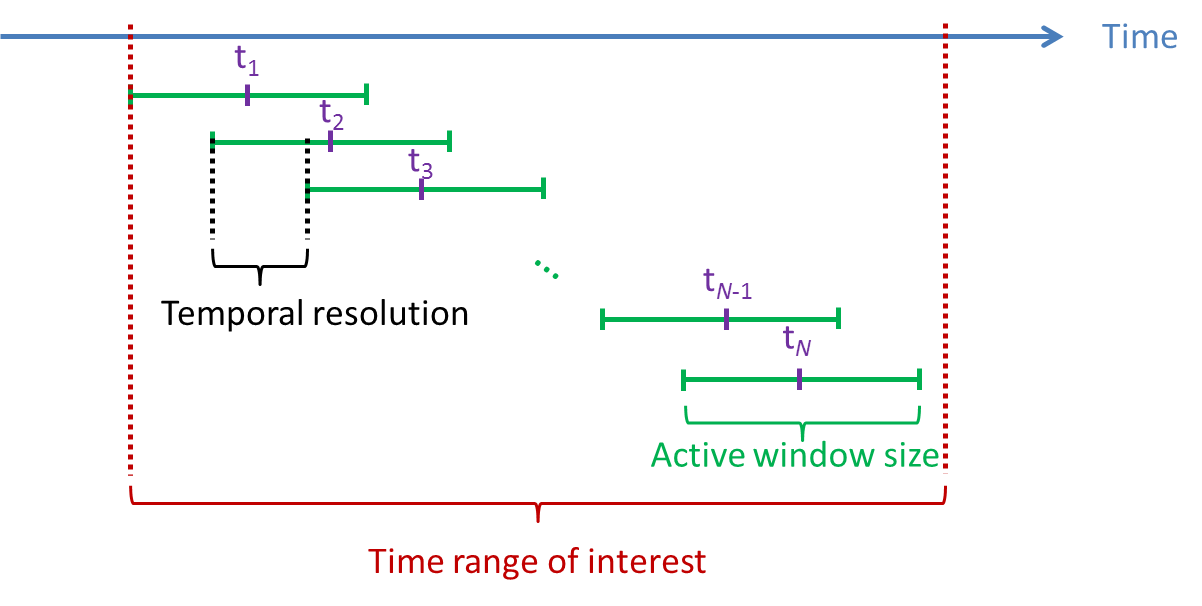
Time window of active state: Three parameters have to be set: Time range of interest, Active window size, and Temporal resolution. The neural activity index is computed using the variance of source activity during active state
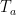 . Active window size defines the duration of active state. Large active window size (at least larger than the number of sensors) is recommended. The time window of active state is going to be slided in Time range of interest with the interval set to be Temporal resolution. If there are multiple active state windows, the time label of the neural activity index will be set as the middle time of each active state window, that is,
. Active window size defines the duration of active state. Large active window size (at least larger than the number of sensors) is recommended. The time window of active state is going to be slided in Time range of interest with the interval set to be Temporal resolution. If there are multiple active state windows, the time label of the neural activity index will be set as the middle time of each active state window, that is, 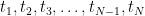 in the following figure.
in the following figure.
Regularization parameter: This value will be multiplied with the maximum eigenvalue of the covariance matrix computed from the recordings during Time range of interest. The larger value of regularization parameter may give the more smooth results.
Sensors type: Modalities that are used for the reconstruction. Here we only have one type of MEG sensors, so nothing to change.
Click on Run.
Two new files are available in the database explorer.
right: LCMV: spatial filter(Unconstr)|0.0_295.8ms: This file saves the three orthogonal spatial filters for each dipole position. These spatial filters are normalized by the variance of noise. Note that there is one spatial filter for each dipole location if the method Cortically Constrained is used.
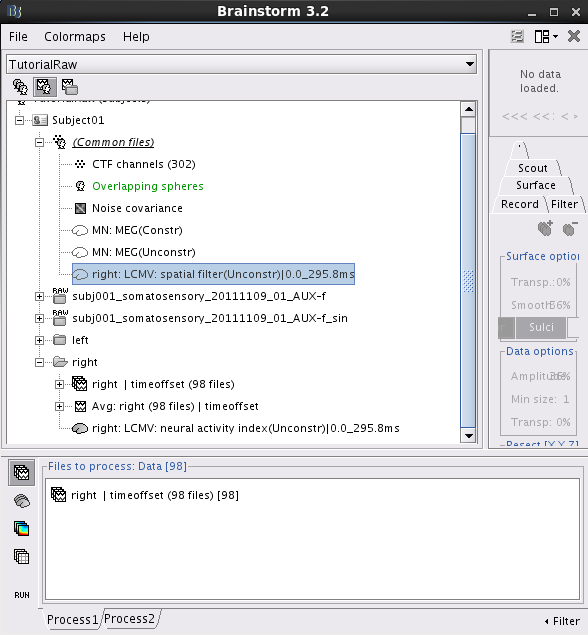
right: LCMV: neural activity index(Unconstr)|0.0_295.8ms: This file saves the neural activity index for every dipole position.
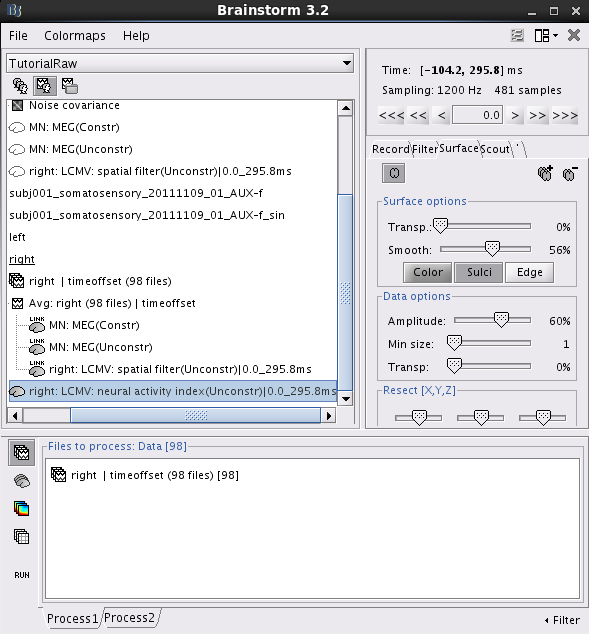
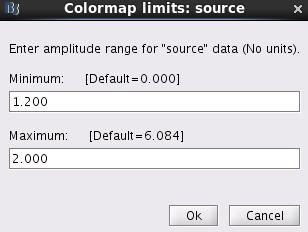
Double click on this file. Right click on anywhere of the pop-out window. From the pop-out menu, select Colormap:Sources > Maximum: Custom.... Set Minimum to be 1.2 and Maximum to be 2.0. Click Ok.
Set the time to be anytime between 0 and 295.8 ms. Then click Surface tab on the right panel of database explorer. Set Data options > Amplitude to be 50%.
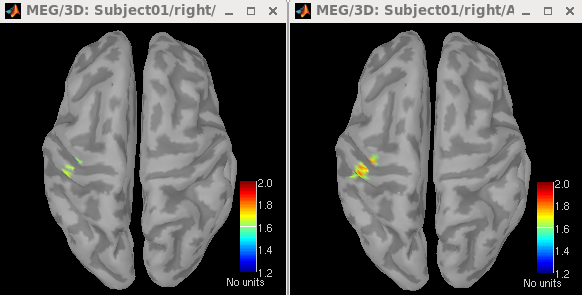
The maps of neural activity index estimated using Unconstrained (trace) and Unconstrained (max eigenvalue) are shown in the left and right figures, respectively. Both maps display strong activations in the left sensory area.
Maximum constrast beamformer (MCB)
Maximum constrast beamformer (MCB) is scalar-type beamformer. For each position  , it provides an analytical solution of dipole orientation
, it provides an analytical solution of dipole orientation 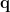 , which maximizes the constrast of beamformer outputs between active state and control state as bellow:
, which maximizes the constrast of beamformer outputs between active state and control state as bellow:
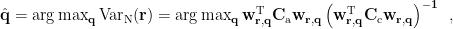
where 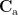 is the covariance matrix computed from the measurements during active state and
is the covariance matrix computed from the measurements during active state and 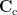 is the covariance matrix computed from the measurements during control state.
is the covariance matrix computed from the measurements during control state.
Solution of dipole orientation
The solution of spatial filter can be rewritten as
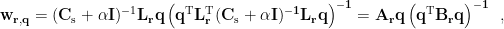
where both 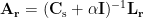 and
and 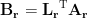 depend only on the dipole location
depend only on the dipole location  . Then the objective function for obtaining the dipole orientation
. Then the objective function for obtaining the dipole orientation 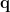 can be rewritten as
can be rewritten as
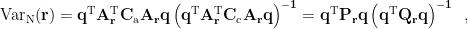
where both of the 3-by-3 matrices  and
and 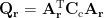 does not depend on the dipole orientation
does not depend on the dipole orientation 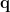 . The solution of dipole orientation
. The solution of dipole orientation 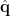 is the eigenvector corresponding to the maximum eigenvalue of the matrix
is the eigenvector corresponding to the maximum eigenvalue of the matrix 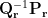 .
.
Statistical mapping
After obtaining the dipole orientation 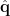 and the spatial filter
and the spatial filter 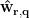 for dipole position
for dipole position  , the F-statistic value at time
, the F-statistic value at time 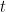 can be obtained using the following formula:
can be obtained using the following formula:
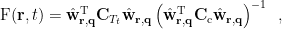
where  is the covariance matrix computed from the measurements during window
is the covariance matrix computed from the measurements during window 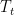 and
and 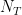 is the size of
is the size of 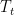 . If
. If 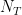 is small, the peak of temporal dynamics of F-statistic value may shift. In this case, it is more appropriate to replace the covariance matrix
is small, the peak of temporal dynamics of F-statistic value may shift. In this case, it is more appropriate to replace the covariance matrix  with
with
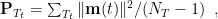
or
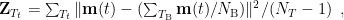
where 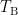 represetns the window of baseline and
represetns the window of baseline and 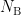 is the length of window
is the length of window 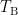 .
.
MCB process
[Under construction]
Beamformer-based correlation/coherence imaging
Dynamic imaging of coherent sources (DICS)
[Under construction]
Spatiotemporal imaging of linearly-related source components (SILSC)
[Under construction]
References
Van Veen BD, Van Drongelen W, Yuchtman M, Suzuki A (1997)
Localization of brain electrical activity via linearly constrained minimum variance spatial filtering
IEEE Transactions on Biomedical Engineering 44(9): 867-880.Vrba J, Robinson SE (2000)
Differences between synthetic aperture magnetometry (SAM) and linear beamformers
Biomag 2000: 681-684.Chen YS, Cheng CY, Hsieh JC, Chen LF (2006)
Maximum contrast beamformer for electromagnetic mapping of brain activity
IEEE Transactions on Biomedical Engineering 53(9): 1765-1774.
Feedback
