|
Size: 1192
Comment:
|
Size: 6024
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| ''Authors: Hui-Ling Chan'' | ''Authors: Hui-Ling Chan, Francois Tadel''', '''Sylvain Baillet'' |
| Line 6: | Line 6: |
| We are going to use the protocol '''TutorialRaw''' created in the previous tutorial [[Tutorials/TutRawAvg]]. If you have not followed this tutorial yet, please do it now. | We are going to use the protocol '''!TutorialRaw''' created in the previous tutorial [[Tutorials/TutRawAvg|Epoching and Averaging]]. If you have not followed this tutorial yet, please do it now. |
| Line 11: | Line 11: |
| Beamfoming methods are | Beamfoming methods scan each targeted voxel/vertex position <<latex($\bf r$)>> and estimate the spatial filter <<latex(${\bf w}_{\bf r,q}$)>>. By multiplying with the MEG recordings <<latex(${\bf m}(t)$)>>, the spatial filter <<latex(${\bf w}_{\bf r,q}$)>> outputs the temporal waveform <<latex($y_{\bf r,q}(t)$)>> of the dipole source at that position with the dipole orientation <<latex($\bf q$)>> as below: |
| Line 13: | Line 13: |
| ==== Spatial filter ==== Text |
<<latex($ y_{\bf r,\bf q}(t) = {{\bf w}_{\bf r,\bf q}}^{\rm T}{\bf m}(t)\enspace, $)>> |
| Line 16: | Line 15: |
| ==== Section 2 ==== Text |
where 'T' indicates the transpose of a matrix or vector. The beamforming spatial filter can be vector type or scalar type. |
| Line 19: | Line 17: |
| == Linearly-constrained minimum variance beamformer (LCMV) == ==== Section 1 ==== Text |
==== Vector-type beamformer ==== For each position <<latex($\mathbf{r}$)>>, three orthogonal spatial filters <<latex($\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$)>> are computed by applying the unit-gain constraint as well as the minimum norm and minimum variance criteria as below: |
| Line 23: | Line 20: |
| ==== Section 2 ==== | <<latex($ \hat{\mathbf{W}}_{\mathbf r}=(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\left(\mathbf{L}_\mathbf{r}^{\rm T}(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\right)^{-1} \enspace,$)>> where <<latex(${\bf C}_{\rm s}$)>> is the covariance matrix of MEG recordings during window <<latex($T_{\rm_s}$)>>, <<latex($\mathbf{I}$)>> is the identity matrix, <<latex($\mathbf{L}_{\mathbf{r}}$)>> is the gain matrix for the dipole located at position <<latex($\bf{r}$)>>, and <<latex($\alpha$)>> is the regularization parameter which compromises the minimum norm and minimum variance criteria. ==== Scalar-type beamformer ==== For each position <<latex($\mathbf{r}$)>>, the source orientation <<latex($\mathbf{q}$)>> is first estimated to enable the spatial filter to output the source activity with maxmum power or fitting some other criteria.The estiamted dipole orientation <<latex($\hat{\mathbf{q}}$)>> is then applied to calculate the spatial filter as follows: <<latex($ \hat{\mathbf{w}}_{\mathbf{r,q}}=(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\hat{\bf{q}}\left(\mathbf{L}_\mathbf{r}^{\rm T}\hat{\bf q}(\mathbf{C}_{\rm s}+\alpha\mathbf{I})^{-1}\mathbf{L}_\mathbf{r}\hat{\bf q}\right)^{-1} \enspace.$)>> == Linearly-constrained minimum variance (LCMV) beamformer == LCMV beamformer is vector-type beamformer. For each position <<latex($\mathbf{r}$)>>, this method calculates the neural activity index, which is interpreted as the estimate of source to noise variance. ==== Neural activity index ==== For each position <<latex($\mathbf{r}$)>>, the variance of source activity during active state <<latex($T_{\rm a}$)>> is calculated as follows: <<latex($ \rm{Var}_{\rm a}(\bf r) =trace \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $)>> or <<latex($ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $)>> where <<latex(${\bf C}_{\rm a}$)>> is the covariance matrix computed from MEG recordings during active state <<latex($T_{\rm a}$)>> and <<latex($\lambda_1\{\}$)>> indicates the maximum eigenvalue of the expression in braces. When the location <<latex($\mathbf{r}$)>> is far from sensors, the elements of lead field matrix <<latex($\mathbf{L}_{\bf r}$)>> are small. So the elements of <<latex($\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$)>> are generally large and the estimated variance for the deep source becomes large. When the location <<latex($\mathbf{r}$)>> is close to sensors, the elements of lead field matrix <<latex($\mathbf{L}_{\bf r}$)>> are large. It results in small values of the elements of <<latex($\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$)>> and small estimated variance for the superficial source. To reduce the effect caused by the depth of source location, the estimated source variance <<latex($\rm{Var}_{\rm a}(\bf r)$)>> is normalized by the noise variance <<latex($\rm{Var}_{\rm c}(\bf r)$)>> as follows: <<latex($ \rm{Var}_{\rm N}(\bf r) =\frac{\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}}{\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}}\enspace, $)>> or <<latex($ \rm{Var}_{\rm N}(\bf r) =\frac{\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}}{\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}}\enspace, $)>> where <<latex(${\bf C}_{\rm c}$)>> is the covariance matrix computed from MEG recordings during control state <<latex($T_{\rm c}$)>>. The normalized variance <<latex($ \rm{Var}_{\rm N}(\bf r)$)>> is called neural activity index (NAI). ==== Example ==== {{attachment:anat.gif}} |
Beamforming methods
Authors: Hui-Ling Chan, Francois Tadel, Sylvain Baillet
The estimation of source distribtion is an important step to understand the brain activity from EEG and MEG data. Dipole fitting, minimum norm estimation, and beamformer are three commonly used methods. It has been proved that beamforming methods provide good spatial resolution. This tutorial will show how to apply beamforming methods to MEG data and obtain the statistic map of source activation.
We are going to use the protocol TutorialRaw created in the previous tutorial ?Epoching and Averaging. If you have not followed this tutorial yet, please do it now.
Contents
Introduction
Beamfoming methods scan each targeted voxel/vertex position 
and estimate the spatial filter 
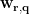. By multiplying with the MEG recordings 
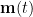, the spatial filter 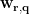outputs the temporal waveform 
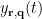of the dipole source at that position with the dipole orientation 
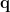as below:
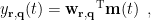
where 'T' indicates the transpose of a matrix or vector. The beamforming spatial filter can be vector type or scalar type.
Vector-type beamformer
For each position 
, three orthogonal spatial filters ![$\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_2d3ac467d26334f39241546468515832d42349b6_p1.png "$\mathbf{W}_{\mathbf{r}}=\left[\mathbf{w}_{\mathbf{r},\mathbf{q}_x},\mathbf{w}_{\mathbf{r},\mathbf{q}_y},\mathbf{w}_{\mathbf{r},\mathbf{q}_z}\right]$")
are computed by applying the unit-gain constraint as well as the minimum norm and minimum variance criteria as below:
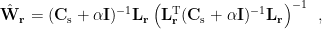
where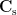 
is the covariance matrix of MEG recordings during window 
, 
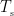is the identity matrix,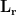 
is the gain matrix for the dipole located at position 
, and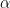 
is the regularization parameter which compromises the minimum norm and minimum variance criteria.
Scalar-type beamformer
For each position , the source orientation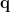 
is first estimated to enable the spatial filter to output the source activity with maxmum power or fitting some other criteria.The estiamted dipole orientation 
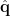is then applied to calculate the spatial filter as follows:
Linearly-constrained minimum variance (LCMV) beamformer
LCMV beamformer is vector-type beamformer. For each position , this method calculates the neural activity index, which is interpreted as the estimate of source to noise variance.
Neural activity index
For each position , the variance of source activity during active state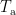 
is calculated as follows:
![$ \rm{Var}_{\rm a}(\bf r) =trace \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_cb2e09fb09a948bd8f3590a5fb5ec78b3f485b92_p1.png "$ \rm{Var}_{\rm a}(\bf r) =trace \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $")
or
![$ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_a4850818772e2ccb0091762ad12b2ea377c4bd92_p1.png "$ \rm{Var}_{\rm a}(\bf r) =\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}\enspace, $")
where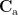 
is the covariance matrix computed from MEG recordings during active state 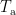and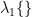 
indicates the maximum eigenvalue of the expression in braces.
When the location is far from sensors, the elements of lead field matrix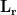 
are small. So the elements of ![$\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_6f70bec44ed33947d8956368ab78866325802ce0_p1.png "$\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}$")
are generally large and the estimated variance for the deep source becomes large. When the location is close to sensors, the elements of lead field matrix 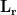are large. It results in small values of the elements of and small estimated variance for the superficial source. To reduce the effect caused by the depth of source location, the estimated source variance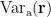 
is normalized by the noise variance 
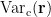as follows:
![$ \rm{Var}_{\rm N}(\bf r) =\frac{\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}}{\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_3daae73b23ee47f5968097f0fc12301d0b864f30_p1.png "$ \rm{Var}_{\rm N}(\bf r) =\frac{\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}}{\rm{trace} \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}}\enspace, $")
or
![$ \rm{Var}_{\rm N}(\bf r) =\frac{\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}}{\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}}\enspace, $](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=get&target=latex_511814276cf57828c3dcb343ee8f32abe3a78038_p1.png "$ \rm{Var}_{\rm N}(\bf r) =\frac{\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm a}{\bf L}_{\bf r}\right]^{-1}\right \}}{\lambda_1 \left \{\left[{\bf L}_{\bf r}^{\rm T}{\bf C}_{\rm c}{\bf L}_{\bf r}\right]^{-1}\right \}}\enspace, $")
where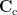 
is the covariance matrix computed from MEG recordings during control state 
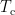. The normalized variance 
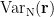is called neural activity index (NAI).
Example
![[ATTACH]](/brainstorm/Tutorials/Beamformers?action=AttachFile&do=upload_form&ticket=0067f35898.15be836a69f7093a3ec5445e8afdd84982122860&target=anat.gif "[ATTACH]"){kind=small}
Text
Maximum constrast beamformer (MCB)
Section 1
Text
Section 2
Text
Beamformer-based correlation/coherence imaging
Dynamic imaging of coherent sources (DICS)
Text
Spatiotemporal imaging of linearly-related source components (SILSC)
Text