|
Size: 3545
Comment:
|
Size: 62255
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| = Tutorial 27: Connectivity = | <<HTML(<style>.backtick {font-size: 16px;}</style>)>><<HTML(<style>abbr {font-weight: bold;}</style>)>> <<HTML(<style>em strong {font-weight: normal; font-style: normal; padding: 2px; border-radius: 5px; background-color: #EEE; color: #111;}</style>)>> = Tutorial 28: Connectivity = |
| Line 4: | Line 6: |
| ''Authors: Francois Tadel, Esther Florin, Sergul Aydore, Syed Ashrafulla, Elizabeth Bock, Sylvain Baillet'' During the past few years, the research focus in brain imaging moved from localizing functional regions to understanding how different regions interact together. It is now widely accepted that some of the brain functions are not supported by isolated regions but rather by a dense network of nodes interacting in various ways. In order to quantify the amount of information exchanged between regions, experts in signal processing developed metrics to compare signals recorded in these different regions. These inter-regional measures can help us explore the brain dynamics by understanding if two regions are activated synchroneously during a task (functional connectivity) or linked by causal interactions (effective connectivity). This tutorial introduces the measures and display tools available in Brainstorm to explore this inter-regional connectivity. |
''Authors: Hossein Shahabi, Mansoureh Fahimi, Francois Tadel, Esther Florin, Sergul Aydore, Syed Ashrafulla, Takfarinas Medani, Elizabeth Bock, Sylvain Baillet'' Cognitive and perceptual functions are the result of coordinated activity of functionally specialized regions in the brain. [[http://www.scholarpedia.org/article/Brain_connectivity|Brain connectivity]] investigates how these different regions (or nodes) interact as a network, with the goal of having a better understanding of how the brain processes information. Depending on which connectivity characteristic is studied, a distinction is made between '''structural''' (fiber pathways), '''functional''' (non-directed statistical dependency) and '''effective''' (causal interaction) connectivity between regions. Effective connectivity is often referred as directed functional connectivity. In this tutorial we will see how to compute different connectivity metrics for non-directed and directed functional analyses in Brainstorm, first with simulated data and later with real data. <<FootNote(This is a note)>> |
| Line 12: | Line 12: |
| == Connectivity processes == In the Process1 and Process2 tabs, the menu "Connectivity" contains the following options: * Correlation * Coherence (Imaginary coherence and Magnitude-squared coherence) * Granger causality * Granger causality (spectral) * Phase-locking value (PLV) Each of these metrics offer several variations: * '''[1xN]''': Connectivity between one signal and all the other signals in the same set of signals <<BR>> (ie. one sensor and all the other sensors in the same file, one source and all the other sources, etc). The output file has the same dimensions as the input files and can be visualized in a similar way. * '''[NxN]''': Connectivity between all the possible pairs of signals in the input files (recordings, source maps or scouts). The output file is full connectivity matrix [Nsignals x Nsignals x Ntime x Nfreq]. * '''[AxB]''': The Process2 tabs offers more flexibilty. You can select different types of files in the two lists FilesA and FilesB. For example, by selecting recordings in FilesA and sources in FilesB, you can compute the connectivity between one sensor and all the sources. {{attachment:process_list.gif||height="375",width="710"}} == Simulate auto-regressive signals == Process: Simulate > Simulate AR signals Process: Simulate > Simulate AR signals (random) == Example 1: Correlation sensor-sources == * In Process1, select == Example 2: Coherence scout-scout == == Method: Correlation == == Method: Coherence == == Method: Granger causality == == Method: Phase locking value == == Unconstrained sources == Describe how the three orientations are handled. |
== General considerations in connectivity analysis == '''Sensors or sources:''' Connectivity analysis can be performed on sensor data (EEG/MEG signals) or on reconstructed sources (voxels or scouts). '''Recording condition:''' While connectivity analysis can be performed on resting-state (spontaneous) and event-related (trials) recordings, the appropriate connectivity method depends on the recording condition. '''Point-based connectivity vs. full network:''' Connectivity can be computed between one node (aka seed) and the rest of the nodes in the network (1×N approach), or between all the possible node pairs in the network (N×N approach). While the later calculates the detailed connectivity graph, the 1×N approach is faster to compute and it is more useful when you are interested in the connectivity of a specific ROI wrt other regions of the brain. '''Temporal resolution:''' Connectivity networks can be computed in two ways; static and dynamic. Time-varying networks can present the dynamics of brain networks. In contrast, the static graphs illustrate a general perspective of brain connectivity which is helpful in specific conditions. Users need to decide which type of network is more informative for their study. '''Time-frequency transformation: ''' Many connectivity methods rely on the [[Tutorials/TimeFrequency|time-frequency representation]] of the data. These approaches include short time Fourier transform, Hilbert transform, and Morlet wavelet. /* {{attachment:GeneralFlowConn.png||width="700",height="230"}} */ /* {{attachment:SimSignals1.PNG||width="550",height="400"}} */ == Simulated data (MAR model) == To compare different connectivity metrics, we use simulated data with known ground truth. Consider three channels constructed using the following multivariate autoregressive (MAR) process of 4th order. {{{#!latex \begin{eqnarray*} x_1(n) & = & \sum_{k=1}^{4} A_{(1,1,k)}x_1(n-k) + e_1(n) \\ x_2(n) & = & \sum_{k=1}^{4} A_{(2,2,k)}x_2(n-k) + e_2(n) \\ x_3(n) & = & \sum_{k=1}^{4} A_{(3,3,k)}x_3(n-k) + \sum_{k=1}^{d} A_{(1,3,k)}x_1(n-k) + e_3(n)\\ \end{eqnarray*} }}} where <<latex($$A_{(i,i,:)}$$)>> with <<latex($$i = 1, 2 \textrm{ and } 3$$)>> are coefficients of 4th order all-pole filters. These coefficients were calculated in a way that the first channel has a dominant peak in the beta band (25 Hz), the second channel shows the highest power in the alpha band (10 Hz), and the third channel a similar level of energy in both bands. Additionally, the signal in the third channel is influenced by the signal in first channel by the filter <<latex($$A_{(1,3,:)}$$)>>. For a MAR model, the transfer function (or frequency response) is defined as: {{{#!latex $$H_{i,j}(f) = \frac{1}{A_{i,j}(f)}$$\\ }}} {{attachment:TransferMatrix3_AR3.png||width="550",height="400"}} The diagonal elements show the auto-transfer function, which in our specific case is the spectrum of the signals. The off-diagonal terms represent the interactions between different signals. Here, we see the transfer function from channel 1 to channel 3. These transfer functions are our connectivity ground of truth. The simulated data and scripts to generate it can be found '''here'''. {{{#!wiki comment/dotted This seems beyond the goal of the tutorial: Besides the original transfer functions, we can compute the [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Directed_Transfer_Function|directed transfer function (DTF)]] and [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Partial_Directed_Coherence|partial directed coherence (PDC)]]. {{attachment:Directed transfer function_AR3.png|Directed transfer function_AR3.png|width="550",height="400"}} {{attachment:Partial Directed Coherence_AR3.png|Partial Directed Coherence_AR3.png|width="550",height="400"}} }}} == Correlation == [[https://en.wikipedia.org/wiki/Correlation_and_dependence|Correlation]] is a non-directed connectivity metric that can be used to show similarity, dependence or association among two random variables or MEG/EEG signals. While this metric has been widely used in electrophysiology, it should not be considered the best technique to evaluate connectivity. The correlation metric by its nature fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals. * Put the Simulated data in the '''''Process1''''' tab. * Click on '''''[Run]''''' ( {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconRun.gif}} ) to open the Pipeline editor. * Add the '''''Connectivity » Correlation NxN''''' process with the following options and run it. * '''Time window''': Select the entire signal. * '''Sensor types or names''': Leave it empty. * '''Include bad channels''': Check it. * '''Process options''': Uncheck it so the means will be subtracted before computing the correlation. * '''Output configuration''': Select Save individual results. <<BR>> {{attachment:guiCorr1n.png||width="400"}} <<BR>> * After running a N×N connectivity process, the result are stored as a N×N connectivity file (with the icon {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconConnectN.gif}} ). Right-click on this file to see its display options: * '''Display as graph''': plots the connectivity graph using a [[https://en.wikipedia.org/wiki/Chord_diagram|chord diagram]] where the color of the edges shows the connectivity metric value. * '''Display as image''': plots the [[https://en.wikipedia.org/wiki/Adjacency_matrix|adjacent matrix]] for the connectivity file. <<BR>><<BR>> {{attachment:imageConnectN.png||width="700"}} <<BR>> {{{#!wiki note For '''non-directed connectivity metrics''', the metric value " from Signal <<latex($$i$$)>> to Signal <<latex($$j$$)>> " is equal to the metric value " from Signal <<latex($$j$$)>> to Signal <<latex($$i$$)>> ". }}} {{{#!wiki note In '''Display as image''', the value of the connectivity metric between a signal and itself plotted as '''zero''' so that it doesn't force scaling the colormap to 1 if the other values are much smaller. }}} == Coherence == Coherency or complex coherence, <<latex($$C_{xy}(f)$$)>>, is a complex-valued metric that measures of the linear relationship of two signals in the frequency domain. And, its magnitude square coherence (MSC), <<latex($$C^2_{xy}(f)$$)>>, often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals <<latex($$x(t)$$)>> and <<latex($$y(t)$$)>>, with spectra <<latex($$X(f)$$)>> and <<latex($$Y(f)$$)>>, the MSC is defined as: . {{{#!latex \begin{eqnarray*} C^2_{xy}(f) &=& \left(\frac{\left |S_{xy}(f) \right |}{\sqrt{ S_{xx}(f)S_{yy}(f) }}\right)^2 = \frac{\left |X(f)Y^*(f) \right |^{2}}{X(f)X^*(f)Y(f)Y^*(f)} \\ S_{xy}(f) &:& \textrm{Cross-spectrum} \\ S_{xx}(f) \quad \textrm{and} \quad S_{yy}(f) &:& \textrm{Auto-spectra or power spectral densities} \\ \end{eqnarray*} }}} Two related measures, which alleviate the problem of volume conduction, are [[www.|imaginary coherence]], <<latex($IC_{xy}(f)$)>>, and the [[www.|lagged coherence]], <<latex($LC_{xy}(f)$)>>, which are defined as: . {{{#!latex \begin{eqnarray*} IC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \qquad \qquad \qquad \qquad LC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\ \end{eqnarray*} }}} where <<latex($$\mathrm{Im}$$)>> and <<latex($$\mathrm{Re}$$)>> describe the imaginary and real parts of the cross spectrum. To calculate coherence values in Brainstorm: * Put the Simulated data in the '''''Process1''''' tab. * Click on '''''[Run]''''' ( {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconRun.gif}} ) to open the Pipeline editor. * Add the '''''Connectivity » Coherence NxN''''' process with the following options and run it. * '''Time window''': Select the entire signal. * '''Sensor types or names''': Leave it empty. * '''Include bad channels''': Check it. * '''Process options''': Uncheck it so the means will be subtracted before computing the correlation. * '''Output configuration''': Select Save individual results. <<BR>> {{attachment:guiCorr1n.png||width="400"}} <<BR>> {{attachment:CohProcess_Aug19.PNG||width="350",height="400"}} * Set the options as follows: * '''Time window''': Select the entire signal. * '''Removing evoked response''': Check this box to remove the averaged evoked response from the individual trials. * '''Measure''': You can select either the "Magnitude-Squared" coherence or the "Imaginary" coherence. we first select the former one. * '''Maximum frequency resolution''': This value characterizes the distance between frequency bins. Smaller values give higher resolutions but probably noisier. * '''Highest frequency of interest''': It specifies the highest frequency which should be analyzed. Here, we selected Fs/2 = 125 Hz to have the coherence in all frequencies. * '''Output configuration''': Select one file per input file. In general, after running the connectivity processes, you can find a multi-dimensional matrix of connectivity in the database. In order to represent this matrix, there are several options. Right-click on the file and select '''Power spectrum''' and '''Display as image.''' These two figures are plotted here. The left figure shows the Coherence values in all analyzed frequencies. Another figure displays the Transfer matrix between channels for the selected frequency bin. {{attachment:CohResults1_Aug19.PNG||width="670",height="350"}} <<BR>><<BR>><<BR>> Similarly, we can compute the "imaginary coherence": {{attachment:StatCoherence_Process_lc.PNG||width="350",height="400"}} <<BR>><<BR>> And the "lagged coherence": {{attachment:StatCoherence-Results_lc.PNG||width="650",height="300"}} <<BR>><<BR>> We see the last two measures are similar but have different values in several frequencies. However, both imaginary and lagged coherence are more accurate than coherence. == Granger Causality == Granger Causality (GC) is a method of functional connectivity, adapted by Clive Granger in the 1960s, but later refined by John Geweke in the form that is used today. Granger Causality is originally formulated in economics but has caught the attention of the neuroscience community in recent years. Before this, neuroscience traditionally relied on stimulation or lesioning a part of the nervous system to study its effect on another part. However, Granger Causality made it possible to estimate the statistical influence without requiring direct intervention (ref: wiener-granger causality a well-established methodology). <<BR>><<BR>> Granger Causality is a measure of linear dependence, which tests whether the variance of error for a linear autoregressive model estimation of a signal (A) can be reduced when adding a linear model estimation of a second signal (B). If this is true, signal B has a Granger Causal effect on the first signal A, i.e., independent information of the past of B improves the prediction of A above and beyond the information contained in the past of A alone. The term independent is emphasized because it creates some interesting properties for GC, such as that it is invariant under rescaling of A and B, as well as the addition of a multiple of A to B. The measure of Granger Causality is nonnegative, and zero when there is no Granger causality(Geweke, 1982). <<BR>><<BR>> The main advantage of Granger Causality is that it is an asymmetrical measure, in that it can dissociate between A->B versus B->A. It is important to note however that though the directionality of Granger Causality is a step closer towards measuring effective connectivity compared to symmetrical measures, it should still not be confused with “true causality”. Effective connectivity estimates the effective mechanism generating the observed data (model-based approach), whereas GC is a measure of causal effect based on prediction, i.e., how well the model is improved when taking variables into account that are interacting (data-driven approach) (Barrett and Barnett, 2013). The difference with causality is best illustrated when there are more variables interacting in a system than those considered in the model. For example, if a variable C is causing both A and B, but with a smaller delay for B than for A, then a GC measure between A and B would show a non-zero GC for B->A, even though B is not truly causing A (Bressler and Seth, 2011). The complete formulation of this method is discussed in the advanced section. Here, we apply the Granger causality and its spectral version on the simulated data. * Put the Simulated data in the Process1 tab. * Click on [Run] to open the Pipeline editor. * Run the process: '''Connectivity > Bivariate Granger causality NxN ''' <<BR>><<BR>> {{attachment:StatGranger_Process.PNG||width="350",height="400"}} <<BR>><<BR>> '''Input options: ''' * '''Time window:''' specifies the time window you want to use for your model. * '''Remove evoked response from each trial:''' this option refers to subtracting the average of phase-locked activity (ERP) from each individual trial. Presently some studies measure interdependency of ongoing brain activity by removing the average event-related potential from each trial. It is also recommended by some as it meets the zero-mean stationarity requirement (improves stationarity of the system). However, the problem with this approach is that it does not account for trial-to-trial variability (For a discussion see (Wang et al., 2008) '''''todo-> link to paper'''''). '''Estimator options: ''' * '''Model order:''' Selection of model order is a critical issue and is typically evaluated from criteria derived from information theory. Several criteria have been proposed, of which the most used are Akaike’s information criterion, the Bayesian-Schwartz’s criterion, and the Hannan-Quinn criterion (Koichi and Antonio, 2014 '''''link'''''). Model fitting quality crucially depends on the proper model order selection. Too low orders may lack the necessary details, while too big orders tend to create spurious values of connectivity. Note that in our simulated example even though the simulation was created with an underlying model of 4, a Granger model order of '''''6''''' was selected with decent resulting connectivity. '''Output options: ''' * '''Save individual results (one file per input file):''' option to save GC estimates on several files separately. * '''Concatenate input files before processing (one file):''' option to save GC estimates on several files as one concatenated matrix. By running the process function, the Granger causality can be displayed in a matrix. <<BR>><<BR>> {{attachment:GrangerMatrixRes2.png||width="350",height="350"}} <<BR>><<BR>> <<BR>><<BR>> The upper right element of this matrix shows there is a signal flow from channel 1 to channel 3. However, the Granger function by itself cannot represent the transfer function (frequency spectrum). To do that, we need to run the Spectral Granger causality. {{attachment:GrangerSpecProcess3.png||width="350",height="400"}} <<BR>><<BR>> Here, is that process similar to the previous function with two extra options. These include the frequency resolution and maximum frequency of interest which was discussed previously in the Coherence process. As a result, the power spectrum of the transfer function is depicted: <<BR>><<BR>> {{attachment:SpecResultGranger2.png||width="400",height="350"}} <<BR>><<BR>> <<BR>><<BR>> It shows a clear peak at 25 Hz, as expected. == Coherence and envelope Correlation by Hilbert transform and Morlet wavelets == In chapter 24, the Morlet wavelets and Hilbert transform were fully introduced and examined as tools to decompose signals in the time-frequency domain. This representation can be used for computing the coherence and related measures as well. Besides the lagged and Imaginary Coherence, which were discussed earlier in this tutorial, a measure named "envelope correlation" was found in 2010 '''(ref)'''. This method work based on the pairwise orthogonalization of signals, removing their real part of coherence, and computing the correlation between the orthogonalized parts. The entire process alleviates the effect of volume conduction in MEEG signals. This method has shown to work well on resting-state MEG. In late 2019, we launched our newly designed process called "HCoh". This process and its corresponding functions compute the Coherence, lagged-coherence, and envelope correlation using the Hilbert transform and Morlet wavelets. By splitting the signals and employing the Parallel processing toolbox (if applicable and available), it is capable of analyzing long recordings and a high number of channels in an efficient time. The complete mathematical background about this process is presented in the "advanced" section. The general framework can be simplified as {{attachment:FlowChartHCorr.png||width="850",height="170"}} <<BR>><<BR>> Now, we are ready to start working with this process. * Put the Simulated data in the Process1 tab. * Click on [Run] to open the Pipeline editor. * Run the process: '''Connectivity > HCoh NxN ''' <<BR>><<BR>> {{attachment:DynHCorr_Process.PNG||width="400",height="550"}} * '''Input Options:''' The time range of the input signal can be specified here. Also, bad channels and the evoked response of trials can be discarded, if appropriate. * '''Time-frequency transformation method:''' The method for this transformation (Hilbert transform or Morlet Wavelets) should be selected. Additionally, this analysis needs further inputs, e.g. frequency ranges, number of bins, and Morlet parameters, which can be defined by an external panel as depicted in Figure 4 (By clicking on “Edit”). A complete description regarding time-frequency transformation can be found here. In the context of connectivity study, we must analyze complex output values of these functions, so two other options (power and magnitude) are disabled on the bottom of this panel. * '''Signal splitting:''' This process has the capability of splitting the input data into several blocks for performing time-frequency transformation, and then merging them to build a single file. This feature helps to save a huge amount of memory and, at the same time, avoid breaking a long-time recording to short-time signals, which makes inconsistency in dynamic network representation of spontaneous data. The maximum number of blocks which can be specified is 20. * '''Connectivity measure:''' Here, three major and widely used coherence based measures of brain connectivity can be computed. Next, desired parameters for windowing, i.e. window length and overlap, should be determined. Please note that these values are usually defined based on the nature of data, the purpose of the study, and the selected connectivity measure. * '''Parallel processing:''' This feature, which is only applicable for envelope correlation, employs the parallel processing toolbox in Matlab to accelerate the computational procedure. As described in the advanced section of this tutorial, envelope correlation utilizes a pairwise orthogonalization approach to attenuate the cross-talk between signals. This process requires heavy computation, especially for a large number of channels, however, using Parallel Processing Toolbox, the software distributes calculations on several CPU threads. The maximum number of pools varies on each computer and it is dependent on the CPU. * '''Output configuration:''' Generally, the above calculation results in a 4-D matrix, where dimensions represent channels (1st and 2nd dimensions), time points (3rd dimension), and frequency (4th dimension). In the case that we analyze event-related data, we have also several files (trials). However, due to poor signal to noise ratio of a single trial, an individual realization of connectivity matrices for each of them is not in our interests. Consequently, we need to average connectivity matrices among all trials of a specific event. The second option of this part performs this averaging. == Phase locking value == An alternative class of measures considers only the relative phase through the computation of a phase locking value between the two signals (Tass et al., 1998). Phase locking is a fundamental concept in dynamical systems that has been used in control systems (the phase-locked loop) and in the analysis of nonlinear, chaotic and non-stationary systems. Since the brain is a nonlinear dynamical system, phase locking is an appropriate approach to quantifying interaction. A more pragmatic argument for its use in studies of LFPs (local field potentials), EEG and MEG is that it is robust to fluctuations in amplitude that may contain less information about interactions than does the relative phase (Lachaux et al., 1999; Mormann et al., 2000). The most commonly used phase interaction measure is the Phase Locking Value (PLV), the absolute value of the mean phase difference between the two signals expressed as a complex unit-length vector (Lachaux et al., 1999; Mormann et al., 2000). If the marginal distributions for the two signals are uniform and the signals are independent then the relative phase will also have a uniform distribution and the will be zero. Conversely, if the phases of the two signals are strongly coupled then the PLV will approach unity. For event-related studies, we would expect the marginal to be uniform across trials unless the phase is locked to a stimulus. In that case, we may have nonuniform marginals which could in principle lead to false indications of phase locking. Phase synchronization between two narrow-band signals is frequently characterized by the Phase Locking Value (PLV). Consider a pair of real signals s1(t) and s2(t), that have been band-pass filtered to a frequency range of interest. Analytic signals can be obtained from s1(t) and s2(t) using the Hilbert transform: {{{ }}} Using analytical signals, the relative phase between z1(t) and z2(t) can be computed as, {{{ }}} The instantaneous PLV is {{{ }}} <<BR>> == Correlation == The correlation is the basic approach to show the dependence or association among two random variables or MEG/EEG signals. While this method has been widely used in electrophysiology, it should not be considered as the best technique for finding the connectivity matrices. The correlation by its nature fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals. * Put the Simulated data in the Process1 tab. * Click on [Run] to open the Pipeline editor. * Run the process: '''Connectivity > Correlation NxN ''' <<BR>> {{attachment:StatCorrelation_Process.PNG||width="350",height="350"}} * Set the options as follows: * '''Time window''': Select the entire signal. * '''Estimator options''': leave the box unchecked so the means will be subtracted before computing the correlation. * '''Output configuration''': Select one file per input. == Method selection and comparison == We can have a comparison between different connectivity functions. The following table briefly does this job. {{attachment:TableComparison.PNG||width="700",height="400"}} Comparing different approaches with the ground truth we find out that the HCorr function works slightly better than other coherence functions. {{attachment:Coh13_AR3.png||width="600",height="350"}} == Connectivity measures on real data : LFP data == In this section we will show how to use the Brainstorm connectivity tools on real data. '''LFP data recorded on monkey __Experimental Setup and data recording:__'''__ __ For this part we will use the Local Field Potential (LFP) monkey data described in [[https://www.nature.com/articles/366153a0.pdf|Bresslers et al (1993)]], these data are widely used over the last past years in many studies. The original data could be found in this [[http://www.ccs.fau.edu/~bressler/Data/Nakamura/LFP/Prepro/LFP.html|link]], more information on the data organization is explained [[http://www.ccs.fau.edu/~bressler/Data/Nakamura/LFP/Info/Data.htm|here]] and also [[http://www.ccs.fau.edu/~bressler/Data/Nakamura/LFP/Info/Codes.htm|here]]. These recordings were made using 15 surface-to-depth bipolar electrodes, separated by 2.5mm, implanted in the cerebral hemisphere contralateral to the monkey's prefered hand.For our analysis in this tutorial, we have selected the monkey named GE. The data are recorded from 6 main areas of the right cortex (Straite, Prestriate, Parietal, Somato, Motor, and frontal cortex). The approximative locations of the 15 electrodes are shown in this figure. The are digitazed at 200sample per second (200Hz). {{attachment:GE_brain.png||width="390",height="200"}} {{attachment:GE_electrodePosition.png||width="300",height="200"}} On the left, a scheme of the monkey brain area, on the right, the locations of 15 electrode pairs in the right hemisphere (reproduced from [[https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3674231/|Aydore et al (2013)]] and [[https://www.nature.com/articles/366153a0.pdf|Bresslers et al (1993)]]). In these experiments, the monkey was trained to depress a lever and wait for a visual stimulus that informs the monkey to either let go the lever (release/GO) or keep the lever down (not release/NOGO). The visual stimulus is presented with four dots arranged as a left (or right) slanted line or diamand on a display screen. (The dots form either a shape of a diagonal line or a shape of a diamond.) For our analysis in this tutorial, we select a dataset with a diagonal line as the 'NOGO' stimulus and the diamond as the 'GO'. For more details about the experiment please refer to [[https://www.nature.com/articles/366153a0.pdf|Bresslers et al (1993)]] and to this [[http://www.ccs.fau.edu/~bressler/Data/Nakamura/LFP/Prepro/LFP.html|page]]. '''__Importing and analyzing data within brainstorm:__'''__ __ For our case, we imported and adapted the data to the brainstorm format, you can download a sample of the data [[attachment:BstConnectivityTutoMonkeyData_less_online.zip|here]]'''. ''(todo >this sample contains only 50 epochs per condition, the full data should uploaded asap) '' ''' Voltage is in uV and was recorded at 200Hz sampling rate. After pooling and ordering the dataset together, we randomly select 480 trials for each condition (GO and NOGO) with only one conctingency for condition (only one kind of stimulation for each condition). '''__Timeline explanation__ ''' Defining the lever initial descent to be at time t = 0ms. Each trial lasts 600ms, the stimulus was given 100ms after the lever was depressed, and last for 100ms. On GO trials, a water reward was provided 500 ms after stimulus onset only if the hand was lifted within the 500ms. On the NOGO trials, the lever was depressed for 500ms. In the following figure, we show the time line of the averaged response for the 480 epochs for the GO condition. The blue line is at '''t = 0ms''' begening of the recording, the green line is the stimulus onset at '''t = 100ms''', the orange line is the mean time of the response onset in the case of the GO condition (release the lever), the red line is the time cursor, set at '''t = 250ms''', time that we choose to separate between '''''early response''''' and '''''late response''''' in this tutorial. ---- . {{attachment:lfpTimeLine.png||width="680",height="400"}} ---- . In this analysis, we will focus mainly on two windows. The '''''early response''''' for '''''t ϵ[100, 250 ms]''''' in which we expect a visual activation on the occipital area (striate and prestriate areas, group of electrodes 1 to 6). We will also show some analysis on the '''late response''', for '''''t ϵ [250, 450 ms]''''' in which we expect an activation/connectivity between the striate and motor cortex in the GO condition and no or less activation for the NOGO condition. '''__Process of computation: __ ''' For most of the connectivity measures, we will use the following steps : First we compute the the connectivity value between one pair of electrode (or scouts) for each trial (time serie), in this case we have 480 trials for each condition, therefore we will compute 480 values for each pair of electrods. After that we will average the connectivity over all the trails and we will get the average value for the pair of electrodes. As explained in the previous sections, Brainstorm offers two options, the NxN (matrix) or 1xN (vector) measures, whre N is the number of channel. * Step 1 : Drag and drop all the trials for both condition in Process1 tab. * Step 2 : Click on [Run] to open the Pipeline editor. Select the desired connectivity measure, choose the desired parameters (see bellow) and click on Run the computation. . After running the connectivity processes, you can find a multi-dimensional matrix of connectivity in the database. This matrix (or vector) is computed for each trial. But in this case s=we need to average all these data. * Step 3 : Average the connectivity measure for all trial bellonging the same condition. . On the Process1, select the option 'time freq' process, and click on Run. Select the process "Average > Average files". Select the options: By trial group (folder), Arithmetic average, Keep all the event markers, then lunch to computation. . An average of the connectivity measure is computed and appeares in the Brainstorm database window. '''__Remove intermediate data :__ ''' To free space in your hard disc and in order to be able to compute other connectivity meaure, you can/should remove the previous individual connectivity for each trial. To do so, keep the 'time freq' in process1, click Run and choose : File>Delete File>Delete selected Files and then click on run. This process will delet the individual data for each trial. {{attachment:DeleteFiles.png||width="380",height="250"}} === Phase Locking Value (PLV) === We select the two groupes of files in the the process 1 (drag and drop), then hit Run, select Connectivity then Phase Locking Value NxN. Choose time window between 100 to 250ms (for early analysis and later 250 to 450 ms for the late response). For Hilbert transform, we select bands from 12 to 60 Hz as shown in the fugure. The PLV is more accurate on short frequency band and to pretend for significant value we recommend to use time windows with more than 100 samples (it's not the cqse in this data). For the remaining, keep the other options as they are, select the Magnitude and choose the option 'Save individual results (one file per input file)' and finaly click on Run. {{attachment:PLV_EarlyAnswerWithERP.png||width="380",height="650"}} This could take some times according to your computer and the size of your data. Now, in order to have one measure for each condition, we need to average all the connectivity measure across trials. We do this from the Brainstorm Process1 window, select 'Process time-freq' (the third icone). Then click on run and select : Average->Average Files, select the option : By trial group (folder average) with the function Arithmetic average. This will compute the average connectivity PLV matrix for the Go and NoGo stimulus. In order to represent this matrix, there are several options. Right click on the connectivity file and select the first option > Display as graph [NxN]. We display both figures for the GO (left figure) and NOGO (right figure) conditions. As explained above, we will focus on the early response in which we expect high connectivity measures on the striate and prestriate areas. For the late response, we expect high measures on/between the occipital and motor cortex du to the eventual hand movements.. '''__Early response__ t ϵ [100-250 ms]: ''' The first option to display the results is: select the connectivity file in the database, right-click and then choose the first option "Display as a graph" From the brainstorm control panel "Display", we can tune the value of the frequency band from the cursor. Same options are available for the connectivity threshold and for the distance filtring. * '''Intensity threshold: '''You can play with the cursor of threshold in order to show more or less connectivity between the nodes. * '''Distance filtering: '''set a limit physical distance between two nodes (electrodes in this example). * '''Frequency band selection: '''Some of the method compute the connectivity within the frequency band, as the PLV, in this case, you have to select the band with a cursor For these data we don't have the exact location of the electrode on the cortex, we build an approximation of the location, therefore we will set the distance filtering to zero in this case. For the following figure, we choose 0mm, band1, threshold 0.844. {{attachment:plv_early_go_band1.PNG||width="345",height="240"}} {{attachment:plv_early_nogo_band1.PNG||width="345",height="240"}} As we expected, the results show high connectivity value (PLV) between the striate and prestriate area. The strength of the measures is almost the same for both conditions, however, we observe some difference on the electrodes between the Line and the Diamond, this is probably due to the difference on the shape (patern) of the [[https://www.physiology.org/doi/pdf/10.1152/jn.1996.75.1.481|visual stimuli]]. We will also display the connectivity matrix as an image, either by selecting the measure and press 'Enter' or Right-click on the connectivity file and select the first option > Display as an image [NxN] {{attachment:plv_early_go_band1_image_ncm.PNG||width="345",height="240"}} {{attachment:plv_early_nogo_band1_image_ncm.PNG||width="345",height="240"}} As we saw before, the highest values are between the electrodes 2, 3, 4, 5, and 6 which are in the occipital cortex. To highlight the difference between the two conditions, we can use the Process2 and compute the difference between the two images. ''(Further methods for statistics are under development)'' From the Process2 bar, we can compute the difference between the images in order to highlight the main difference between the two condition. To do that, you jus drag the associated connectivity file for the condition one to the Files A and the condition two to the files B, then click on run, select Difference, then one of the proposed options, in this tutorial we selected the 'Normalized: A-B/A+B'. {{attachment:plv_early_go_band1_image-plv_early_nogo_band1_image_ncm.PNG||width="690",height="450"}} The resulted image shows the highest difference in the connectivity is between the electrodes (2,6) and (3,6), this is exactely the difference that we observed in the previous graphes, which is mainly the difference between the two conditions. There is also diference in the paires (1,14), (8,14) and (11,14), which involves the visuql, the motor and the frontal cortexes, probably due to the preparation to the decision making, and prepare to activate or inhibite the action of the hand. '''__Late response __t ϵ [250-450 ms] : ''' distance filtering : 0mm, band1, threshold 0.644 {{attachment:plv_late_go_band1.PNG||width="345",height="240"}} {{attachment:plv_late_nogo_band1.PNG||width="345",height="240"}} In this late response, also as we expected, we see higher value in the GO condition then the NOGO condition. Also we observe a connexion between the striate to motot cortex, this connection is related to the mouvmenet of the hand to release the lever. These results show also the connection between the striat/prestiriate to the frontal regions since this later is involved in the selection of actions based on perceptual cues and reward values as shown in this [[https://www.sciencedirect.com/science/article/pii/S2352154614000278|paper]]. These connectivity results are highly correlated to the ones observed within the previous publications [[https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3674231/|Aydore et al. (2013)]] and [[https://www.nature.com/articles/366153a0.pdf|Bresslers et al (1993)]]. We should also notice that is in this process, the difference in the result is related to the implementation methods, the selected time windows and the sample data size and choice (here we picked randomly 480 samples from each condition). As in previous, we will visualize the results as an image for the difference between the two conditions. Of course, ultimately statistical analysis of these maps is required to make scientific inferences from your data. {{attachment:plv_late_go_band1_image-plv_late_nogo_band1_image_ncm.PNG||width="690",height="450"}} From this matrix, we can check pixels by pixels the different values and combinations of electrodes, we notice a slight difference between the electrodes (1,4), (2,4), (1,8), (2,9), (2,10), (4,8), (7,8) but also it shows the highest value between (3,9) and (9,14) wich is related to the connection between the visual cortex to the motor cortex and to the frontal cortex. '''__Remove the ERP from the signal:__ ''' As explained in the previous sections, some connectivity measures can be estimated without the the ERP, this option brings the signals to a slightly more stationary state [Wang and al] If we choose the option that remove the ERP from each trial before computing the connectivity, we end up with these results ('''''todo : ''remove the erp is not available on bst for plv for now''') : '''__Early response__''' t ϵ [100-250 ms] : Parameters : 0mm, band1, threshold 0.75 {{attachment:PLVnoERP_early_go_band1.PNG||width="345",height="240"}} {{attachment:PLVnoERP_early_nogo_band1.PNG||width="345",height="240"}} '''__Late response__ t ϵ [250-450 ms] ''': Parameters :0mm, band1, threshold 0.666 {{attachment:PLVnoERP_late_go_band1_bis.PNG||width="345",height="240"}} {{attachment:PLVnoERP_late_nogo_band1.PNG||width="345",height="240"}} We observe coherent results with this option. For the early response, a new connextion in the cortex motor between the node (10,11) is highlighted. For the late response, more connextion value are visible in the cas of GO condition. === Coherence (COH) === We use the same data as previous, and we will compute the coherence. We will try to show similar results as shown in the [[https://www.nature.com/articles/366153a0.pdf|Bresslers et al (1993)]] in which high value of coherence are observed between the striate and motor cortex areas for the GO condition within the freauency band 12-25 Hz. '''__Early response__ t ϵ [100-250 ms] ''': Parameters : 0mm, band2, threshold 0.5, with the ERP {{attachment:COH_early_go_band2.PNG||width="345",height="260"}} {{attachment:COH_early_nogo_band2.PNG||width="345",height="260"}} For both conditions, we observe similar value. '''__Late response__ t ϵ [250-450 ms] ''': Parameters : 0mm, band2, threshold 0.35, with the ERP {{attachment:COH_late_go_band2.PNG||width="345",height="260"}} {{attachment:COH_late_nogo_band2.PNG||width="345",height="260"}} As expected, in this case, high value of the coherence are observed for the GO condition (>0,6) wherease for the NOGO condition this value is less than 0,4. We noticed also connection between the visual striate and prestriate to the motor cortex in the GO condition. '''Results without the ERP : __Early respinse__ t ϵ [100-250 ms] ''': Parameters : 0mm, band1, threshold 0.35, {{attachment:COHnoERP_early_go_band1.PNG||width="345",height="240"}} {{attachment:COHnoERP_early_nogo_band1.PNG||width="345",height="240"}} '''__Late response__ t ϵ [250-450 ms] ''': Parameters : 0mm, band1, threshold 0.66 {{attachment:COHnoERP_late_go_band1.PNG||width="345",height="240"}} {{attachment:COHnoERP_late_nogo_band1.PNG||width="345",height="240"}} === Correlation (COR) === We use the same data as previous, and we will compute the correlation. As explained before, the correlation is the basic and simple method to observe interaction between region. '''__Late response__ t ϵ [250-450 ms] : ''' Parameters : 0mm, threshold 0.7, with the ERP {{attachment:CORR_late_go_band1.PNG||width="345",height="240"}} {{attachment:CORR_late_nogo_band1.PNG||width="345",height="240"}} Parameters : 0mm, threshold 0.63, without the ERP {{attachment:CORRnoERP_late_go_band1.PNG||width="345",height="240"}} {{attachment:CORRnoERP_late_nogo_band1.PNG||width="345",height="240"}} === Spectral Granger Causality (SGC) === '''__Early response__ t ϵ [100-250 ms] : ''' Parameters : 0mm, threshold 2.5, band1 12.5, with the ERP {{attachment:SGC_early_go_band1.PNG||width="345",height="240"}} {{attachment:SGC_early_nogo_band1.PNG||width="345",height="240"}} In this example, we see that reciprocal causal influences existe between the electrodes of the striate (1,2,3) and the prestriate(4,5,6). We can also see that the the channel 1 initiates the exchange, and physiologically, the striate cortex precedes prestriate cortex in the anatomical organisation of the visual system. '''__Late response__ t ϵ [250-450 ms] : ''' Parameters : 0mm, threshold 0.315, band1 12.5, with ERP {{attachment:SGC_late_go_band1.PNG||width="345",height="240"}} {{attachment:SGC_late_nogo_band1.PNG||width="345",height="240"}} '''__Early response__ t ϵ [100-250 ms] : ''' Parameters : 0mm, threshold 2.5, band1 12.5, without ERP {{attachment:SGC_early_go_band1.PNG||width="345",height="240"}} {{attachment:SGC_early_nogo_band1.PNG||width="345",height="240"}} '''__Late response__ t ϵ [250-400 ms] : ''' Parameters : 0mm, threshold 0.315, band1 12.5 {{attachment:SGC_late_go_band1.PNG||width="345",height="240"}} {{attachment:SGC_late_nogo_band1.PNG||width="345",height="240"}} Early response: without ERP ---- . distance filtering : 0mm, threshold ~0.5, band1 12.5 {{attachment:SGCnoERP_early_go_band1.PNG||width="345",height="240"}} {{attachment:SGCnoERP_early_nogo_band1.PNG||width="345",height="240"}} ---- . '''Late response: '''without ERP ---- . distance filtering: 0mm, threshold 0.315, band1 12.5 {{attachment:SGC_late_go_band1.PNG||width="345",height="240"}} {{attachment:SGC_late_nogo_band1.PNG||width="345",height="240"}} Early response: without ERP . distance filtering : 0mm, threshold ~0.5, band1 12.5 {{attachment:SGCnoERP_early_go_band1.PNG||width="345",height="240"}} {{attachment:SGCnoERP_early_nogo_band1.PNG||width="345",height="240"}} Late response: without ERP ---- . distance filtering : 0mm, threshold ~0.27, band1 12.5 {{attachment:SGCnoERP_late_go_band1.PNG||width="345",height="240"}} {{attachment:SGCnoERP_late_nogo_band1.PNG||width="345",height="240"}} === Phase Transfer Entropy (PTE) === early with erp 0,1, b1. 0mm ...not relevant > recheck ---- == TODO : Connectivity measure on real data : MEG/EEG data == {{attachment:SGCnoERP_early_go_band1.PNG||width="345",height="240"}} {{attachment:SGCnoERP_early_nogo_band1.PNG||width="345",height="240"}} Late response: without ERP . distance filtering : 0mm, threshold ~0.27, band1 12.5 {{attachment:SGCnoERP_late_go_band1.PNG||width="345",height="240"}} {{attachment:SGCnoERP_late_nogo_band1.PNG||width="345",height="240"}} === Phase Transfer Entropy (PTE) === early with erp 0,1, b1. 0mm ...not relevant > recheck == TODO : Connectivity measure on real data : MEG/EEG data == For all the brain imaging experiments, it is highly recommended to have a clear hypothesis to test before starting the analysis of the recordings. With this auditory oddball experiment, we would like to explore the temporal dynamics of the auditory network, the deviant detection, and the motor response. According to the literature, we expect to observe at least the following effects: * Bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). * Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. * Decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). * '''The''' first response peak (91ms), the sources with high amplitudes are located around the primary auditory cortex, bilaterally, which is what we are expecting for auditory stimulation. * For this experiment we will focus on the beta high and gamma frequency, as shown here https://brainworksneurotherapy.com/what-are-brainwaves, "Beta is a ‘fast’ activity, present when we are alert, attentive, engaged in problem-solving, judgment, decision making, or focused mental activity." * 1 dataset: * '''S01_AEF_20131218_02_600Hz.ds''': Run #2, 360s, 200 standard + 40 deviants For this data we select three main time windows to compute the connectivity: '''time 1 : 0-150 ms''' : we expect the bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). '''time 2 : 100-300 ms''': Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. '''time 3 : 300-550 ms''' : Frontal regions activation related to the decision making and '''motor'''preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. === Sources level === Connectivity is computed at the source points (dipole) or at a defined brain region also called scouts. The signal used art this level is obtained from the inverse problem process, in which each source-level node (dipole) is assigned with an activation value at each time point. Therefore, we can compute the connectivity matrix between all pairs of the node. This process is possible only of the inverse problem is computed '''(ref to tuto here). ''' To run this in brainstorm, you need to drag and drop the source files within the process1 tab, select the option 'source process' click on the Run button, then you can select the connectivity measure that you want to perform. As in the previous section, we can compute the source connectivity matrix for each trail, then average overall trial. However, this process is time and memory consuming. For each trial, a matrix of 15002x15002 elements is computed and saved in the hard disc (~0.9 Go per trial). In the case of the unconstrained source, the size is 45006x45006. {{attachment:connectivitySourceSpace.png||width="500",height="400"}} This is obviously a very large number and it does not really make sense. Therefore, the strategy is to reduce the dimensionality of the source space and adopt a parcellation scheme, in other terms we will use the scouts. Instead, to compute the connectivity value values between two dipoles, we will use a set of dipoles pairs that belong to a given area in the cortex. Although the choice of the optimal parcellation scheme for the source space is not easy. The optimal choice is to choose a parcellation based on anatomy, for example the Brodmann parcellation [[http://www.nature.com/nature/journal/v536/n7615/full/nature18933.html|here]]. In brainstorm these atlases are imported in Brainstorm as scouts (cortical regions of interest), and saved directly in the surface files as explained in this tutorial [[https://neuroimage.usc.edu/brainstorm/Tutorials/LabelFreeSurfer?highlight=(parcellation)#Cortical_parcellations|here]]. In this tutorial, we will use the scouts " Destrieux atlas'''" (following figure)''' {{attachment:destrieuxScouts.png||width="500",height="400"}} To select this atlas, from the connectivity menu, you have to check the box 'use scouts', select the scout function 'mean' and apply the function 'Before', save individual results. In this tutorial, we select the correlation as example, the same process is expected for the other methods. {{attachment:processConnectivityScouts.png||width="300",height="400"}} For more detail for these options please refer to this [[https://neuroimage.usc.edu/forums/t/choosing-scout-function-before-or-after/2454|thread]] The following matrix is the solution that we obtain with these scouts with the size of 148x148 for this atlas (~400 Ko) {{attachment:connectivityScoutDistrieux.png||width="500",height="400"}} For this data we select three main time windows to compute the connectivity: time 1 : 0-150 ms : we expect the bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). time 2 : 100-300 ms : Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. time 3 : 300-550 ms : Frontal regions activation related to the decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. ---- === Coherence === === Correlation === For this data we select three main time windows to compute the connectivity: time 1 : 0-150 ms : we expect the bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). time 2 : 100-300 ms : Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. time 3 : 300-550 ms : Frontal regions activation related to the decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. ---- . '''For the time 1,''' We find high correlation value in both hemisphere on the temporal areas. This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas. Corresponding to the name of the areas here time 3 : 300-550 ms : Frontal regions activation related to the decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. ==== Coherence ==== ==== Correlation ==== '''For the time 1,''' We find high correlation value in both hemisphere on the temporal areas. This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas. Corresponding to: name of the areas here Similar results are observed either for the deviant and standard sounds. {{attachment:MatrixDeviantCorDestrieuxTime1.PNG||width="500",height="400"}} {{attachment:GraphDeviantCorDestrieuxTime1.PNG||width="600",height="400"}} '''For the time 3, ''' ---- === PLV === This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas. Corresponding to: name of the areas here Similar results are observed either for the deviant and standard sounds. {{attachment:MatrixDeviantCorDestrieuxTime1.PNG||width="500",height="400"}} {{attachment:GraphDeviantCorDestrieuxTime1.PNG||width="600",height="400"}} '''For the time 3, ''' ==== PLV ==== ---- . {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} {{attachment:GraphDeviantPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} } {{attachment:GraphDevianPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} === TODO : Sensors level === Connectivity is computed at the sensors or the electrodes levels from the recorded time series. === PLV === {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} {{attachment:GraphDeviantPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. ---- . {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} } {{attachment:GraphDevianPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} === TODO : Sensors level === Connectivity is computed at the sensors or the electrodes levels from the recorded time series. === PLV === {{attachment:GraphStandardPlvMEGBandbetaHzTime3_All.PNG||width="345",height="300"}} {{attachment:GraphDevianPlvMEGBandbetaHzTime3_all.PNG||width="345",height="300"}} Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. ---- . {{attachment:GraphStandardPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} {{attachment:GraphDevianPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} '''<<TAG(Advanced)>> ''' ''TODO : discuss '' ''- Explain or give more information about the methods and how to choose the best parameters'' ex: plv better with 100 samples & narrow bands Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. {{attachment:GraphStandardPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} {{attachment:GraphDevianPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} ''TODO : discuss'' ''- Explain or give more information about the methods and how to choose the best parameters'' ex : plv better with 100 samples & narrow bands ''- Explain the choice either with ERP or without, and why (link to the cited paper, can't find it)'' ''- Show/add other relevant measures of statistics to separate the two conditions'' ''- Add the option : checkbox remove the erp for PLV and CORR and PTE'' ''- ...'' '''<<TAG(Advanced)>> ''' == Granger Causality - Mathematical Background == ''' {{attachment:GC_Math_Time2.PNG||width="700",height="450"}} <<BR>><<BR>> '''Practical issues about GC: '''Temporal resolution: '''the high time resolution offered by MEG/EEG and intracranial EEG allows for a very powerful application of GC and also offers the important advantage of spectral analysis. <<BR>><<BR>> '''Stationarity: '''the GC methods described so far are all based on AR models, and therefore assume stationarity of the signal (constant auto-correlation over time). However, neuroscience data, especially task-based data such as event-related potentials are mostly nonstationary. There are two possible approaches to solve this problem. The first is to apply methods such as differencing, filtering, and smoothing to make the data stationary (see a recommendation for time domain GC). Dynamical changes in the connectivity profile cannot be detected with the first approach. The second approach is to turn to versions of GC that have been adapted for nonstationary data, either by using a non-parametric estimation of GC or through measures of time-varying GC, which estimate dynamic parameters with adaptive or short-time window methods (Bressler and Seth, 2011). <<BR>><<BR>> '''Number of variables:''' Granger causality is very time-consuming in the multivariate case for many variables (O(m^2) where m represents the number of variables). Since each connection pair results in two values, there will also be a large number of statistical comparisons that need to be controlled for. When performing GC in the spectral domain, this number increases even more as statistical tests have to be performed per frequency. Therefore, it is usually recommended to select a limited number of ROIs or electrodes based on some hypothesis found in previous literature, or on some initial processing with a more simple and less computationally heavy measure of connectivity. <<BR>><<BR>> '''Pre-processing: '''The influence of pre-processing steps such as filtering and smoothing on GC estimates is a crucial issue. Studies have generally suggested to limit filtering only for artifact removal or to improve the stationarity of the data but cautioned against band-pass filtering to isolate causal influence within a specific frequency band (Barnett and Seth, 2011). <<BR>><<BR>> '''Volume Conduction: '''Granger causality can be performed both in the scalp domain or in the source domain. Though spectral domain GC generally does not incorporate present values of the signals in the model, it is still not immune from spurious connectivity measures due to volume conduction (for a discussion see (Steen et al., 2016)). Therefore, it is recommended to reduce the problem of signal mixing using additional processing steps such as performing source localization and doing connectivity in the source domain. <<BR>><<BR>> '''Data length: '''because of the extent of parameters that need to be estimated, the number of data points should be sufficient for a good fit of the model. This is especially true for windowing approaches, where data is cut into smaller epochs. A rule of thumb is that the number of estimated parameters should be at least (~10) several times smaller than the number of data points. <<BR>><<BR>> == Sections to add == * Discuss option concatenate vs. average for the estimation of coherence on single trials: https://neuroimage.usc.edu/forums/t/difference-between-averaging-coherence-and-concatenate/22726/4 * Discuss pValues computed for the various methods |
| Line 46: | Line 694: |
| Document the file tags Document how to extract the connect matrix How to input your own connect matrix |
'''TODO''': Document data storage. |
| Line 53: | Line 697: |
| * Forum: Connectivity matrix storage:[[http://neuroimage.usc.edu/forums/showthread.php?1796-How-the-Corr-matix-is-saved|http://neuroimage.usc.edu/forums/showthread.php?1796]] * Forum: Comparing coherence values: http://neuroimage.usc.edu/forums/showthread.php?1556 * Forum: Reading NxN PLV matrix: http://neuroimage.usc.edu/forums/showthread.php?1681-PLV-NxN-Read-matrix |
==== References ==== ==== Articles ==== * Lagged-Coherence: Pascual-Marqui RD. [[https://arxiv.org/pdf/0706.1776|Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions]], arXiv preprint arXiv:0706.1776. 2007 Jun 12. * Phase transfer entropy: Lobier M, Siebenhühner F, Palva S, Palva JM [[http://www.sciencedirect.com/science/article/pii/S1053811913009191|Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions]], NeuroImage 2014, 85:853-872 * Barzegaran E, Knyazeva MG. [[https://doi.org/10.1371/journal.pone.0181105|Functional connectivity analysis in EEG source space: The choice of method]] Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105. ==== Forum discussions ==== * Connectivity matrix storage:[[http://neuroimage.usc.edu/forums/showthread.php?1796-How-the-Corr-matix-is-saved|http://neuroimage.usc.edu/forums/showthread.php?1796]] * Comparing coherence values: http://neuroimage.usc.edu/forums/showthread.php?1556 * Reading NxN PLV matrix: http://neuroimage.usc.edu/forums/t/pte-how-is-the-connectivity-matrix-stored/4618/2 * Export multiple PLV matrices: https://neuroimage.usc.edu/forums/t/export-multiple-plv-matrices/2014/4 * Scout function and connectivity: http://neuroimage.usc.edu/forums/showthread.php?2843 * Unconstrained sources and connectivity: http://neuroimage.usc.edu/forums/t/problem-with-surfaces-vs-volumes/3261 * Digonal values: http://neuroimage.usc.edu/forums/t/choosing-scout-function-before-or-after/2454/2 * Connectivity pipeline: https://neuroimage.usc.edu/forums/t/help-for-connectivity-pipeline/12558/4 * Ongoing developments: https://neuroimage.usc.edu/forums/t/connectivity-tutorial-and-methods-development-on-bst/12223/3 * Granger causality: https://neuroimage.usc.edu/forums/t/is-granger-causality-analysis-a-linear-operation/12506/12 * Amplitude Envelope Correlation: * https://neuroimage.usc.edu/forums/t/problem-with-time-dynamic-envelope-correlation/21542/9 * https://github.com/brainstorm-tools/brainstorm3/issues/142 |
| Line 59: | Line 722: |
| <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/Statistics&next=Tutorials/Scripting")>> | <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/GroupAnalysis&next=Tutorials/Scripting")>> |
Tutorial 28: Connectivity
[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]
Authors: Hossein Shahabi, Mansoureh Fahimi, Francois Tadel, Esther Florin, Sergul Aydore, Syed Ashrafulla, Takfarinas Medani, Elizabeth Bock, Sylvain Baillet
Cognitive and perceptual functions are the result of coordinated activity of functionally specialized regions in the brain. Brain connectivity investigates how these different regions (or nodes) interact as a network, with the goal of having a better understanding of how the brain processes information. Depending on which connectivity characteristic is studied, a distinction is made between structural (fiber pathways), functional (non-directed statistical dependency) and effective (causal interaction) connectivity between regions. Effective connectivity is often referred as directed functional connectivity. In this tutorial we will see how to compute different connectivity metrics for non-directed and directed functional analyses in Brainstorm, first with simulated data and later with real data. 1
Contents
- General considerations in connectivity analysis
- Simulated data (MAR model)
- Correlation
- Coherence
- Granger Causality
- Coherence and envelope Correlation by Hilbert transform and Morlet wavelets
- Phase locking value
- Correlation
- Method selection and comparison
- Connectivity measures on real data : LFP data
- TODO : Connectivity measure on real data : MEG/EEG data
- TODO : Connectivity measure on real data : MEG/EEG data
- Granger Causality - Mathematical Background
- Sections to add
- On the hard drive
- Additional documentation
General considerations in connectivity analysis
Sensors or sources: Connectivity analysis can be performed on sensor data (EEG/MEG signals) or on reconstructed sources (voxels or scouts).
Recording condition: While connectivity analysis can be performed on resting-state (spontaneous) and event-related (trials) recordings, the appropriate connectivity method depends on the recording condition.
Point-based connectivity vs. full network: Connectivity can be computed between one node (aka seed) and the rest of the nodes in the network (1×N approach), or between all the possible node pairs in the network (N×N approach). While the later calculates the detailed connectivity graph, the 1×N approach is faster to compute and it is more useful when you are interested in the connectivity of a specific ROI wrt other regions of the brain.
Temporal resolution: Connectivity networks can be computed in two ways; static and dynamic. Time-varying networks can present the dynamics of brain networks. In contrast, the static graphs illustrate a general perspective of brain connectivity which is helpful in specific conditions. Users need to decide which type of network is more informative for their study.
Time-frequency transformation: Many connectivity methods rely on the time-frequency representation of the data. These approaches include short time Fourier transform, Hilbert transform, and Morlet wavelet.
Simulated data (MAR model)
To compare different connectivity metrics, we use simulated data with known ground truth. Consider three channels constructed using the following multivariate autoregressive (MAR) process of 4th order.

where 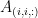 with
with 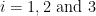 are coefficients of 4th order all-pole filters. These coefficients were calculated in a way that the first channel has a dominant peak in the beta band (25 Hz), the second channel shows the highest power in the alpha band (10 Hz), and the third channel a similar level of energy in both bands. Additionally, the signal in the third channel is influenced by the signal in first channel by the filter
are coefficients of 4th order all-pole filters. These coefficients were calculated in a way that the first channel has a dominant peak in the beta band (25 Hz), the second channel shows the highest power in the alpha band (10 Hz), and the third channel a similar level of energy in both bands. Additionally, the signal in the third channel is influenced by the signal in first channel by the filter  . For a MAR model, the transfer function (or frequency response) is defined as:
. For a MAR model, the transfer function (or frequency response) is defined as:
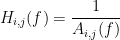
The diagonal elements show the auto-transfer function, which in our specific case is the spectrum of the signals. The off-diagonal terms represent the interactions between different signals. Here, we see the transfer function from channel 1 to channel 3. These transfer functions are our connectivity ground of truth.
The simulated data and scripts to generate it can be found here.
Correlation
Correlation is a non-directed connectivity metric that can be used to show similarity, dependence or association among two random variables or MEG/EEG signals. While this metric has been widely used in electrophysiology, it should not be considered the best technique to evaluate connectivity. The correlation metric by its nature fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals.
Put the Simulated data in the Process1 tab.
Click on [Run] (
 ) to open the Pipeline editor.
) to open the Pipeline editor. Add the Connectivity » Correlation NxN process with the following options and run it.
Time window: Select the entire signal.
Sensor types or names: Leave it empty.
Include bad channels: Check it.
Process options: Uncheck it so the means will be subtracted before computing the correlation.
Output configuration: Select Save individual results.
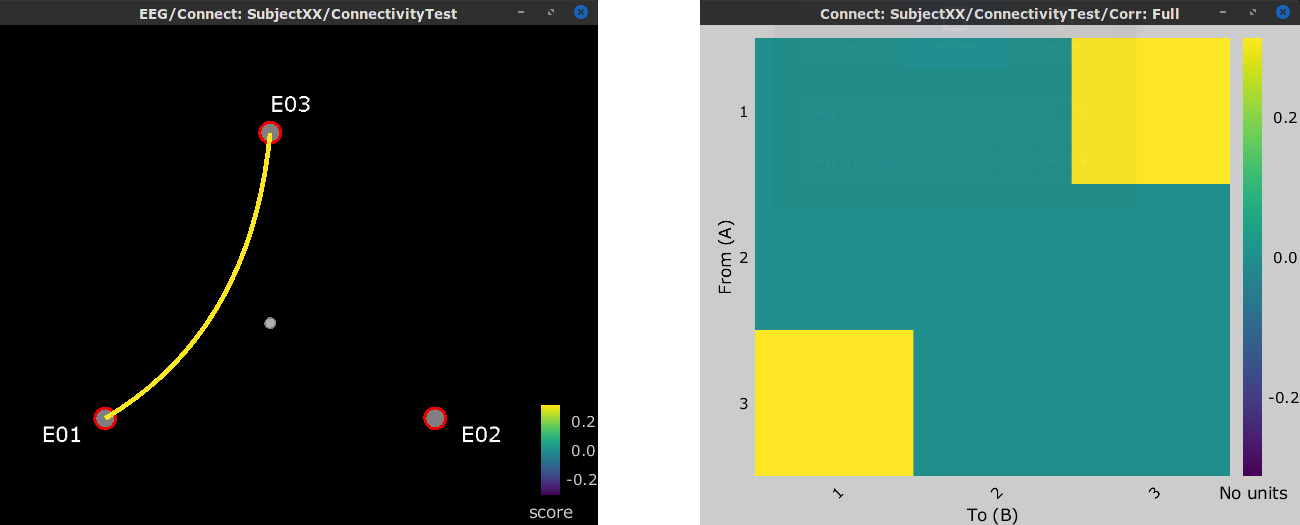
After running a N×N connectivity process, the result are stored as a N×N connectivity file (with the icon
 ). Right-click on this file to see its display options:
). Right-click on this file to see its display options: Display as graph: plots the connectivity graph using a chord diagram where the color of the edges shows the connectivity metric value.
Display as image: plots the adjacent matrix for the connectivity file.
For non-directed connectivity metrics, the metric value " from Signal  to Signal
to Signal  " is equal to the metric value " from Signal
" is equal to the metric value " from Signal  to Signal
to Signal  ".
".
In Display as image, the value of the connectivity metric between a signal and itself plotted as zero so that it doesn't force scaling the colormap to 1 if the other values are much smaller.
Coherence
Coherency or complex coherence, 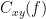 , is a complex-valued metric that measures of the linear relationship of two signals in the frequency domain. And, its magnitude square coherence (MSC),
, is a complex-valued metric that measures of the linear relationship of two signals in the frequency domain. And, its magnitude square coherence (MSC),  , often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals
, often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals 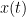 and
and 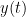 , with spectra
, with spectra 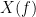 and
and 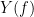 , the MSC is defined as:
, the MSC is defined as:
Two related measures, which alleviate the problem of volume conduction, are ?imaginary coherence, 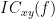 , and the ?lagged coherence,
, and the ?lagged coherence, 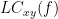 , which are defined as:
, which are defined as:
where  and
and  describe the imaginary and real parts of the cross spectrum.
describe the imaginary and real parts of the cross spectrum.
To calculate coherence values in Brainstorm:
Put the Simulated data in the Process1 tab.
Click on [Run] (
 ) to open the Pipeline editor.
) to open the Pipeline editor. Add the Connectivity » Coherence NxN process with the following options and run it.
Time window: Select the entire signal.
Sensor types or names: Leave it empty.
Include bad channels: Check it.
Process options: Uncheck it so the means will be subtracted before computing the correlation.
Output configuration: Select Save individual results.
- Set the options as follows:
Time window: Select the entire signal.
Removing evoked response: Check this box to remove the averaged evoked response from the individual trials.
Measure: You can select either the "Magnitude-Squared" coherence or the "Imaginary" coherence. we first select the former one.
Maximum frequency resolution: This value characterizes the distance between frequency bins. Smaller values give higher resolutions but probably noisier.
Highest frequency of interest: It specifies the highest frequency which should be analyzed. Here, we selected Fs/2 = 125 Hz to have the coherence in all frequencies.
Output configuration: Select one file per input file.
In general, after running the connectivity processes, you can find a multi-dimensional matrix of connectivity in the database. In order to represent this matrix, there are several options.
Right-click on the file and select Power spectrum and Display as image. These two figures are plotted here. The left figure shows the Coherence values in all analyzed frequencies. Another figure displays the Transfer matrix between channels for the selected frequency bin.
Similarly, we can compute the "imaginary coherence":
We see the last two measures are similar but have different values in several frequencies. However, both imaginary and lagged coherence are more accurate than coherence.
Granger Causality
Granger Causality (GC) is a method of functional connectivity, adapted by Clive Granger in the 1960s, but later refined by John Geweke in the form that is used today. Granger Causality is originally formulated in economics but has caught the attention of the neuroscience community in recent years. Before this, neuroscience traditionally relied on stimulation or lesioning a part of the nervous system to study its effect on another part. However, Granger Causality made it possible to estimate the statistical influence without requiring direct intervention (ref: wiener-granger causality a well-established methodology).
Granger Causality is a measure of linear dependence, which tests whether the variance of error for a linear autoregressive model estimation of a signal (A) can be reduced when adding a linear model estimation of a second signal (B). If this is true, signal B has a Granger Causal effect on the first signal A, i.e., independent information of the past of B improves the prediction of A above and beyond the information contained in the past of A alone. The term independent is emphasized because it creates some interesting properties for GC, such as that it is invariant under rescaling of A and B, as well as the addition of a multiple of A to B. The measure of Granger Causality is nonnegative, and zero when there is no Granger causality(Geweke, 1982).
The main advantage of Granger Causality is that it is an asymmetrical measure, in that it can dissociate between A->B versus B->A. It is important to note however that though the directionality of Granger Causality is a step closer towards measuring effective connectivity compared to symmetrical measures, it should still not be confused with “true causality”. Effective connectivity estimates the effective mechanism generating the observed data (model-based approach), whereas GC is a measure of causal effect based on prediction, i.e., how well the model is improved when taking variables into account that are interacting (data-driven approach) (Barrett and Barnett, 2013). The difference with causality is best illustrated when there are more variables interacting in a system than those considered in the model. For example, if a variable C is causing both A and B, but with a smaller delay for B than for A, then a GC measure between A and B would show a non-zero GC for B->A, even though B is not truly causing A (Bressler and Seth, 2011).
The complete formulation of this method is discussed in the advanced section. Here, we apply the Granger causality and its spectral version on the simulated data.
- Put the Simulated data in the Process1 tab.
- Click on [Run] to open the Pipeline editor.
Run the process: Connectivity > Bivariate Granger causality NxN
Input options:
Time window: specifies the time window you want to use for your model.
Remove evoked response from each trial: this option refers to subtracting the average of phase-locked activity (ERP) from each individual trial. Presently some studies measure interdependency of ongoing brain activity by removing the average event-related potential from each trial. It is also recommended by some as it meets the zero-mean stationarity requirement (improves stationarity of the system). However, the problem with this approach is that it does not account for trial-to-trial variability (For a discussion see (Wang et al., 2008) todo-> link to paper).
Estimator options:
Model order: Selection of model order is a critical issue and is typically evaluated from criteria derived from information theory. Several criteria have been proposed, of which the most used are Akaike’s information criterion, the Bayesian-Schwartz’s criterion, and the Hannan-Quinn criterion (Koichi and Antonio, 2014 link). Model fitting quality crucially depends on the proper model order selection. Too low orders may lack the necessary details, while too big orders tend to create spurious values of connectivity. Note that in our simulated example even though the simulation was created with an underlying model of 4, a Granger model order of 6 was selected with decent resulting connectivity.
Output options:
Save individual results (one file per input file): option to save GC estimates on several files separately.
Concatenate input files before processing (one file): option to save GC estimates on several files as one concatenated matrix.
By running the process function, the Granger causality can be displayed in a matrix.
The upper right element of this matrix shows there is a signal flow from channel 1 to channel 3. However, the Granger function by itself cannot represent the transfer function (frequency spectrum).
To do that, we need to run the Spectral Granger causality. ![]()
Here, is that process similar to the previous function with two extra options. These include the frequency resolution and maximum frequency of interest which was discussed previously in the Coherence process. As a result, the power spectrum of the transfer function is depicted:
It shows a clear peak at 25 Hz, as expected.
Coherence and envelope Correlation by Hilbert transform and Morlet wavelets
In chapter 24, the Morlet wavelets and Hilbert transform were fully introduced and examined as tools to decompose signals in the time-frequency domain. This representation can be used for computing the coherence and related measures as well.
Besides the lagged and Imaginary Coherence, which were discussed earlier in this tutorial, a measure named "envelope correlation" was found in 2010 (ref). This method work based on the pairwise orthogonalization of signals, removing their real part of coherence, and computing the correlation between the orthogonalized parts. The entire process alleviates the effect of volume conduction in MEEG signals. This method has shown to work well on resting-state MEG.
In late 2019, we launched our newly designed process called "HCoh". This process and its corresponding functions compute the Coherence, lagged-coherence, and envelope correlation using the Hilbert transform and Morlet wavelets. By splitting the signals and employing the Parallel processing toolbox (if applicable and available), it is capable of analyzing long recordings and a high number of channels in an efficient time.
The complete mathematical background about this process is presented in the "advanced" section. The general framework can be simplified as
Now, we are ready to start working with this process.
- Put the Simulated data in the Process1 tab.
- Click on [Run] to open the Pipeline editor.
Run the process: Connectivity > HCoh NxN
Input Options: The time range of the input signal can be specified here. Also, bad channels and the evoked response of trials can be discarded, if appropriate.
Time-frequency transformation method: The method for this transformation (Hilbert transform or Morlet Wavelets) should be selected. Additionally, this analysis needs further inputs, e.g. frequency ranges, number of bins, and Morlet parameters, which can be defined by an external panel as depicted in Figure 4 (By clicking on “Edit”). A complete description regarding time-frequency transformation can be found here. In the context of connectivity study, we must analyze complex output values of these functions, so two other options (power and magnitude) are disabled on the bottom of this panel.
Signal splitting: This process has the capability of splitting the input data into several blocks for performing time-frequency transformation, and then merging them to build a single file. This feature helps to save a huge amount of memory and, at the same time, avoid breaking a long-time recording to short-time signals, which makes inconsistency in dynamic network representation of spontaneous data. The maximum number of blocks which can be specified is 20.
Connectivity measure: Here, three major and widely used coherence based measures of brain connectivity can be computed. Next, desired parameters for windowing, i.e. window length and overlap, should be determined. Please note that these values are usually defined based on the nature of data, the purpose of the study, and the selected connectivity measure.
Parallel processing: This feature, which is only applicable for envelope correlation, employs the parallel processing toolbox in Matlab to accelerate the computational procedure. As described in the advanced section of this tutorial, envelope correlation utilizes a pairwise orthogonalization approach to attenuate the cross-talk between signals. This process requires heavy computation, especially for a large number of channels, however, using Parallel Processing Toolbox, the software distributes calculations on several CPU threads. The maximum number of pools varies on each computer and it is dependent on the CPU.
Output configuration: Generally, the above calculation results in a 4-D matrix, where dimensions represent channels (1st and 2nd dimensions), time points (3rd dimension), and frequency (4th dimension). In the case that we analyze event-related data, we have also several files (trials). However, due to poor signal to noise ratio of a single trial, an individual realization of connectivity matrices for each of them is not in our interests. Consequently, we need to average connectivity matrices among all trials of a specific event. The second option of this part performs this averaging.
Phase locking value
An alternative class of measures considers only the relative phase through the computation of a phase locking value between the two signals (Tass et al., 1998). Phase locking is a fundamental concept in dynamical systems that has been used in control systems (the phase-locked loop) and in the analysis of nonlinear, chaotic and non-stationary systems. Since the brain is a nonlinear dynamical system, phase locking is an appropriate approach to quantifying interaction. A more pragmatic argument for its use in studies of LFPs (local field potentials), EEG and MEG is that it is robust to fluctuations in amplitude that may contain less information about interactions than does the relative phase (Lachaux et al., 1999; Mormann et al., 2000).
The most commonly used phase interaction measure is the Phase Locking Value (PLV), the absolute value of the mean phase difference between the two signals expressed as a complex unit-length vector (Lachaux et al., 1999; Mormann et al., 2000). If the marginal distributions for the two signals are uniform and the signals are independent then the relative phase will also have a uniform distribution and the will be zero. Conversely, if the phases of the two signals are strongly coupled then the PLV will approach unity. For event-related studies, we would expect the marginal to be uniform across trials unless the phase is locked to a stimulus. In that case, we may have nonuniform marginals which could in principle lead to false indications of phase locking.
Phase synchronization between two narrow-band signals is frequently characterized by the Phase Locking Value (PLV). Consider a pair of real signals s1(t) and s2(t), that have been band-pass filtered to a frequency range of interest. Analytic signals can be obtained from s1(t) and s2(t) using the Hilbert transform:
Using analytical signals, the relative phase between z1(t) and z2(t) can be computed as,
The instantaneous PLV is
Correlation
The correlation is the basic approach to show the dependence or association among two random variables or MEG/EEG signals. While this method has been widely used in electrophysiology, it should not be considered as the best technique for finding the connectivity matrices. The correlation by its nature fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals.
- Put the Simulated data in the Process1 tab.
- Click on [Run] to open the Pipeline editor.
Run the process: Connectivity > Correlation NxN
- Set the options as follows:
Time window: Select the entire signal.
Estimator options: leave the box unchecked so the means will be subtracted before computing the correlation.
Output configuration: Select one file per input.
Method selection and comparison
We can have a comparison between different connectivity functions. The following table briefly does this job.
Comparing different approaches with the ground truth we find out that the HCorr function works slightly better than other coherence functions.
Connectivity measures on real data : LFP data
In this section we will show how to use the Brainstorm connectivity tools on real data.
LFP data recorded on monkey Experimental Setup and data recording:
For this part we will use the Local Field Potential (LFP) monkey data described in Bresslers et al (1993), these data are widely used over the last past years in many studies.
The original data could be found in this link, more information on the data organization is explained here and also here.
These recordings were made using 15 surface-to-depth bipolar electrodes, separated by 2.5mm, implanted in the cerebral hemisphere contralateral to the monkey's prefered hand.For our analysis in this tutorial, we have selected the monkey named GE.
The data are recorded from 6 main areas of the right cortex (Straite, Prestriate, Parietal, Somato, Motor, and frontal cortex). The approximative locations of the 15 electrodes are shown in this figure. The are digitazed at 200sample per second (200Hz).
On the left, a scheme of the monkey brain area, on the right, the locations of 15 electrode pairs in the right hemisphere (reproduced from Aydore et al (2013) and Bresslers et al (1993)).
In these experiments, the monkey was trained to depress a lever and wait for a visual stimulus that informs the monkey to either let go the lever (release/GO) or keep the lever down (not release/NOGO). The visual stimulus is presented with four dots arranged as a left (or right) slanted line or diamand on a display screen. (The dots form either a shape of a diagonal line or a shape of a diamond.)
For our analysis in this tutorial, we select a dataset with a diagonal line as the 'NOGO' stimulus and the diamond as the 'GO'.
For more details about the experiment please refer to Bresslers et al (1993) and to this page.
Importing and analyzing data within brainstorm:
For our case, we imported and adapted the data to the brainstorm format, you can download a sample of the data here. (todo >this sample contains only 50 epochs per condition, the full data should uploaded asap)
Voltage is in uV and was recorded at 200Hz sampling rate. After pooling and ordering the dataset together, we randomly select 480 trials for each condition (GO and NOGO) with only one conctingency for condition (only one kind of stimulation for each condition).
Timeline explanation
Defining the lever initial descent to be at time t = 0ms. Each trial lasts 600ms, the stimulus was given 100ms after the lever was depressed, and last for 100ms. On GO trials, a water reward was provided 500 ms after stimulus onset only if the hand was lifted within the 500ms. On the NOGO trials, the lever was depressed for 500ms.
In the following figure, we show the time line of the averaged response for the 480 epochs for the GO condition. The blue line is at t = 0ms begening of the recording, the green line is the stimulus onset at t = 100ms, the orange line is the mean time of the response onset in the case of the GO condition (release the lever), the red line is the time cursor, set at t = 250ms, time that we choose to separate between early response and late response in this tutorial.
In this analysis, we will focus mainly on two windows. The early response for t ϵ[100, 250 ms] in which we expect a visual activation on the occipital area (striate and prestriate areas, group of electrodes 1 to 6). We will also show some analysis on the late response, for t ϵ [250, 450 ms] in which we expect an activation/connectivity between the striate and motor cortex in the GO condition and no or less activation for the NOGO condition.
Process of computation:
For most of the connectivity measures, we will use the following steps :
First we compute the the connectivity value between one pair of electrode (or scouts) for each trial (time serie), in this case we have 480 trials for each condition, therefore we will compute 480 values for each pair of electrods. After that we will average the connectivity over all the trails and we will get the average value for the pair of electrodes. As explained in the previous sections, Brainstorm offers two options, the NxN (matrix) or 1xN (vector) measures, whre N is the number of channel.
- Step 1 : Drag and drop all the trials for both condition in Process1 tab.
- Step 2 : Click on [Run] to open the Pipeline editor. Select the desired connectivity measure, choose the desired parameters (see bellow) and click on Run the computation.
- After running the connectivity processes, you can find a multi-dimensional matrix of connectivity in the database. This matrix (or vector) is computed for each trial. But in this case s=we need to average all these data.
- Step 3 : Average the connectivity measure for all trial bellonging the same condition.
On the Process1, select the option 'time freq' process, and click on Run. Select the process "Average > Average files". Select the options: By trial group (folder), Arithmetic average, Keep all the event markers, then lunch to computation.
- An average of the connectivity measure is computed and appeares in the Brainstorm database window.
Remove intermediate data :
To free space in your hard disc and in order to be able to compute other connectivity meaure, you can/should remove the previous individual connectivity for each trial. To do so, keep the 'time freq' in process1, click Run and choose : File>Delete File>Delete selected Files and then click on run. This process will delet the individual data for each trial.
Phase Locking Value (PLV)
We select the two groupes of files in the the process 1 (drag and drop), then hit Run, select Connectivity then Phase Locking Value NxN. Choose time window between 100 to 250ms (for early analysis and later 250 to 450 ms for the late response).
For Hilbert transform, we select bands from 12 to 60 Hz as shown in the fugure. The PLV is more accurate on short frequency band and to pretend for significant value we recommend to use time windows with more than 100 samples (it's not the cqse in this data).
For the remaining, keep the other options as they are, select the Magnitude and choose the option 'Save individual results (one file per input file)' and finaly click on Run.
This could take some times according to your computer and the size of your data.
Now, in order to have one measure for each condition, we need to average all the connectivity measure across trials. We do this from the Brainstorm Process1 window, select 'Process time-freq' (the third icone). Then click on run and select : Average->Average Files, select the option : By trial group (folder average) with the function Arithmetic average. This will compute the average connectivity PLV matrix for the Go and NoGo stimulus.
In order to represent this matrix, there are several options.
Right click on the connectivity file and select the first option > Display as graph [NxN]. We display both figures for the GO (left figure) and NOGO (right figure) conditions.
As explained above, we will focus on the early response in which we expect high connectivity measures on the striate and prestriate areas. For the late response, we expect high measures on/between the occipital and motor cortex du to the eventual hand movements..
Early response t ϵ [100-250 ms]:
The first option to display the results is: select the connectivity file in the database, right-click and then choose the first option "Display as a graph" From the brainstorm control panel "Display", we can tune the value of the frequency band from the cursor. Same options are available for the connectivity threshold and for the distance filtring.
Intensity threshold: You can play with the cursor of threshold in order to show more or less connectivity between the nodes.
Distance filtering: set a limit physical distance between two nodes (electrodes in this example).
Frequency band selection: Some of the method compute the connectivity within the frequency band, as the PLV, in this case, you have to select the band with a cursor
For these data we don't have the exact location of the electrode on the cortex, we build an approximation of the location, therefore we will set the distance filtering to zero in this case.
For the following figure, we choose 0mm, band1, threshold 0.844.
As we expected, the results show high connectivity value (PLV) between the striate and prestriate area. The strength of the measures is almost the same for both conditions, however, we observe some difference on the electrodes between the Line and the Diamond, this is probably due to the difference on the shape (patern) of the visual stimuli.
We will also display the connectivity matrix as an image, either by selecting the measure and press 'Enter' or Right-click on the connectivity file and select the first option > Display as an image [NxN]
As we saw before, the highest values are between the electrodes 2, 3, 4, 5, and 6 which are in the occipital cortex.
To highlight the difference between the two conditions, we can use the Process2 and compute the difference between the two images. (Further methods for statistics are under development)
From the Process2 bar, we can compute the difference between the images in order to highlight the main difference between the two condition. To do that, you jus drag the associated connectivity file for the condition one to the Files A and the condition two to the files B, then click on run, select Difference, then one of the proposed options, in this tutorial we selected the 'Normalized: A-B/A+B'. ![]()
The resulted image shows the highest difference in the connectivity is between the electrodes (2,6) and (3,6), this is exactely the difference that we observed in the previous graphes, which is mainly the difference between the two conditions. There is also diference in the paires (1,14), (8,14) and (11,14), which involves the visuql, the motor and the frontal cortexes, probably due to the preparation to the decision making, and prepare to activate or inhibite the action of the hand.
Late response t ϵ [250-450 ms] :
distance filtering : 0mm, band1, threshold 0.644
In this late response, also as we expected, we see higher value in the GO condition then the NOGO condition. Also we observe a connexion between the striate to motot cortex, this connection is related to the mouvmenet of the hand to release the lever.
These results show also the connection between the striat/prestiriate to the frontal regions since this later is involved in the selection of actions based on perceptual cues and reward values as shown in this paper.
These connectivity results are highly correlated to the ones observed within the previous publications Aydore et al. (2013) and Bresslers et al (1993). We should also notice that is in this process, the difference in the result is related to the implementation methods, the selected time windows and the sample data size and choice (here we picked randomly 480 samples from each condition).
As in previous, we will visualize the results as an image for the difference between the two conditions.
Of course, ultimately statistical analysis of these maps is required to make scientific inferences from your data.
From this matrix, we can check pixels by pixels the different values and combinations of electrodes, we notice a slight difference between the electrodes (1,4), (2,4), (1,8), (2,9), (2,10), (4,8), (7,8) but also it shows the highest value between (3,9) and (9,14) wich is related to the connection between the visual cortex to the motor cortex and to the frontal cortex.
Remove the ERP from the signal:
As explained in the previous sections, some connectivity measures can be estimated without the the ERP, this option brings the signals to a slightly more stationary state [Wang and al]
If we choose the option that remove the ERP from each trial before computing the connectivity, we end up with these results (todo : remove the erp is not available on bst for plv for now) :
Early response t ϵ [100-250 ms] :
Parameters : 0mm, band1, threshold 0.75
Late response t ϵ [250-450 ms] :
Parameters :0mm, band1, threshold 0.666
We observe coherent results with this option. For the early response, a new connextion in the cortex motor between the node (10,11) is highlighted. For the late response, more connextion value are visible in the cas of GO condition.
Coherence (COH)
We use the same data as previous, and we will compute the coherence. We will try to show similar results as shown in the Bresslers et al (1993) in which high value of coherence are observed between the striate and motor cortex areas for the GO condition within the freauency band 12-25 Hz.
Early response t ϵ [100-250 ms] :
Parameters : 0mm, band2, threshold 0.5, with the ERP
For both conditions, we observe similar value.
Late response t ϵ [250-450 ms] :
Parameters : 0mm, band2, threshold 0.35, with the ERP
As expected, in this case, high value of the coherence are observed for the GO condition (>0,6) wherease for the NOGO condition this value is less than 0,4. We noticed also connection between the visual striate and prestriate to the motor cortex in the GO condition.
Results without the ERP : Early respinse t ϵ [100-250 ms] :
Parameters : 0mm, band1, threshold 0.35,
Late response t ϵ [250-450 ms] :
Parameters : 0mm, band1, threshold 0.66
Correlation (COR)
We use the same data as previous, and we will compute the correlation. As explained before, the correlation is the basic and simple method to observe interaction between region.
Late response t ϵ [250-450 ms] :
Parameters : 0mm, threshold 0.7, with the ERP
Parameters : 0mm, threshold 0.63, without the ERP
Spectral Granger Causality (SGC)
Early response t ϵ [100-250 ms] :
Parameters : 0mm, threshold 2.5, band1 12.5, with the ERP
In this example, we see that reciprocal causal influences existe between the electrodes of the striate (1,2,3) and the prestriate(4,5,6). We can also see that the the channel 1 initiates the exchange, and physiologically, the striate cortex precedes prestriate cortex in the anatomical organisation of the visual system.
Late response t ϵ [250-450 ms] :
Parameters : 0mm, threshold 0.315, band1 12.5, with ERP
Early response t ϵ [100-250 ms] :
Parameters : 0mm, threshold 2.5, band1 12.5, without ERP
Late response t ϵ [250-400 ms] :
Parameters : 0mm, threshold 0.315, band1 12.5
Early response: without ERP
- distance filtering : 0mm, threshold ~0.5, band1 12.5
Late response: without ERP
- distance filtering: 0mm, threshold 0.315, band1 12.5
Early response: without ERP
- distance filtering : 0mm, threshold ~0.5, band1 12.5
Late response: without ERP
- distance filtering : 0mm, threshold ~0.27, band1 12.5
Phase Transfer Entropy (PTE)
early with erp 0,1, b1. 0mm ...not relevant > recheck
TODO : Connectivity measure on real data : MEG/EEG data
Late response: without ERP
- distance filtering : 0mm, threshold ~0.27, band1 12.5
Phase Transfer Entropy (PTE)
early with erp 0,1, b1. 0mm ...not relevant > recheck
TODO : Connectivity measure on real data : MEG/EEG data
For all the brain imaging experiments, it is highly recommended to have a clear hypothesis to test before starting the analysis of the recordings. With this auditory oddball experiment, we would like to explore the temporal dynamics of the auditory network, the deviant detection, and the motor response. According to the literature, we expect to observe at least the following effects:
Bilateral response in the primary auditory cortex (P50, N100), in both experimental conditions (standard and deviant beeps).
Bilateral activity in the inferior frontal gyrus and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only.
Decision making and motor preparation, for the deviant beeps only (after 300ms).
The first response peak (91ms), the sources with high amplitudes are located around the primary auditory cortex, bilaterally, which is what we are expecting for auditory stimulation.
For this experiment we will focus on the beta high and gamma frequency, as shown here https://brainworksneurotherapy.com/what-are-brainwaves, "Beta is a ‘fast’ activity, present when we are alert, attentive, engaged in problem-solving, judgment, decision making, or focused mental activity."
- 1 dataset:
S01_AEF_20131218_02_600Hz.ds: Run #2, 360s, 200 standard + 40 deviants
For this data we select three main time windows to compute the connectivity:
time 1 : 0-150 ms : we expect the bilateral response in the primary auditory cortex (P50, N100), in both experimental conditions (standard and deviant beeps).
time 2 : 100-300 ms: Bilateral activity in the inferior frontal gyrus and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only.
time 3 : 300-550 ms : Frontal regions activation related to the decision making and motorpreparation, for the deviant beeps only (after 300ms).
The computation are done here only for the second recording.
Sources level
Connectivity is computed at the source points (dipole) or at a defined brain region also called scouts. The signal used art this level is obtained from the inverse problem process, in which each source-level node (dipole) is assigned with an activation value at each time point.
Therefore, we can compute the connectivity matrix between all pairs of the node. This process is possible only of the inverse problem is computed (ref to tuto here).
To run this in brainstorm, you need to drag and drop the source files within the process1 tab, select the option 'source process' click on the Run button, then you can select the connectivity measure that you want to perform.
As in the previous section, we can compute the source connectivity matrix for each trail, then average overall trial. However, this process is time and memory consuming. For each trial, a matrix of 15002x15002 elements is computed and saved in the hard disc (~0.9 Go per trial). In the case of the unconstrained source, the size is 45006x45006.
This is obviously a very large number and it does not really make sense. Therefore, the strategy is to reduce the dimensionality of the source space and adopt a parcellation scheme, in other terms we will use the scouts. Instead, to compute the connectivity value values between two dipoles, we will use a set of dipoles pairs that belong to a given area in the cortex.
Although the choice of the optimal parcellation scheme for the source space is not easy. The optimal choice is to choose a parcellation based on anatomy, for example the Brodmann parcellation here. In brainstorm these atlases are imported in Brainstorm as scouts (cortical regions of interest), and saved directly in the surface files as explained in this tutorial here.
In this tutorial, we will use the scouts " Destrieux atlas" (following figure) ![]()
To select this atlas, from the connectivity menu, you have to check the box 'use scouts', select the scout function 'mean' and apply the function 'Before', save individual results.
In this tutorial, we select the correlation as example, the same process is expected for the other methods.
For more detail for these options please refer to this thread
The following matrix is the solution that we obtain with these scouts with the size of 148x148 for this atlas (~400 Ko)
For this data we select three main time windows to compute the connectivity:
time 1 : 0-150 ms : we expect the bilateral response in the primary auditory cortex (P50, N100), in both experimental conditions (standard and deviant beeps).
time 2 : 100-300 ms : Bilateral activity in the inferior frontal gyrus and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only.
time 3 : 300-550 ms : Frontal regions activation related to the decision making and motor preparation, for the deviant beeps only (after 300ms).
The computation are done here only for the second recording.
Coherence
Correlation
For this data we select three main time windows to compute the connectivity:
time 1 : 0-150 ms : we expect the bilateral response in the primary auditory cortex (P50, N100), in both experimental conditions (standard and deviant beeps).
time 2 : 100-300 ms : Bilateral activity in the inferior frontal gyrus and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only.
time 3 : 300-550 ms : Frontal regions activation related to the decision making and motor preparation, for the deviant beeps only (after 300ms).
The computation are done here only for the second recording.
For the time 1, We find high correlation value in both hemisphere on the temporal areas.
This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas.
Corresponding to the name of the areas here
time 3 : 300-550 ms : Frontal regions activation related to the decision making and motor preparation, for the deviant beeps only (after 300ms).
The computation are done here only for the second recording.
Coherence
Correlation
For the time 1, We find high correlation value in both hemisphere on the temporal areas.
This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas.
Corresponding to: name of the areas here
Similar results are observed either for the deviant and standard sounds.
For the time 3,
PLV
This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas.
Corresponding to: name of the areas here
Similar results are observed either for the deviant and standard sounds.
For the time 3,
PLV
Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key.
TODO : Sensors level
Connectivity is computed at the sensors or the electrodes levels from the recorded time series.
PLV
Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key.
TODO : Sensors level
Connectivity is computed at the sensors or the electrodes levels from the recorded time series.
PLV
Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key.
TODO : discuss
- Explain or give more information about the methods and how to choose the best parameters
ex: plv better with 100 samples & narrow bands
Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key.
TODO : discuss
- Explain or give more information about the methods and how to choose the best parameters
ex : plv better with 100 samples & narrow bands
- Explain the choice either with ERP or without, and why (link to the cited paper, can't find it)
- Show/add other relevant measures of statistics to separate the two conditions
- Add the option : checkbox remove the erp for PLV and CORR and PTE
- ...
Granger Causality - Mathematical Background
Temporal resolution: the high time resolution offered by MEG/EEG and intracranial EEG allows for a very powerful application of GC and also offers the important advantage of spectral analysis.
Stationarity: the GC methods described so far are all based on AR models, and therefore assume stationarity of the signal (constant auto-correlation over time). However, neuroscience data, especially task-based data such as event-related potentials are mostly nonstationary. There are two possible approaches to solve this problem. The first is to apply methods such as differencing, filtering, and smoothing to make the data stationary (see a recommendation for time domain GC). Dynamical changes in the connectivity profile cannot be detected with the first approach. The second approach is to turn to versions of GC that have been adapted for nonstationary data, either by using a non-parametric estimation of GC or through measures of time-varying GC, which estimate dynamic parameters with adaptive or short-time window methods (Bressler and Seth, 2011).
Number of variables: Granger causality is very time-consuming in the multivariate case for many variables (O(m^2) where m represents the number of variables). Since each connection pair results in two values, there will also be a large number of statistical comparisons that need to be controlled for. When performing GC in the spectral domain, this number increases even more as statistical tests have to be performed per frequency. Therefore, it is usually recommended to select a limited number of ROIs or electrodes based on some hypothesis found in previous literature, or on some initial processing with a more simple and less computationally heavy measure of connectivity.
Pre-processing: The influence of pre-processing steps such as filtering and smoothing on GC estimates is a crucial issue. Studies have generally suggested to limit filtering only for artifact removal or to improve the stationarity of the data but cautioned against band-pass filtering to isolate causal influence within a specific frequency band (Barnett and Seth, 2011).
Volume Conduction: Granger causality can be performed both in the scalp domain or in the source domain. Though spectral domain GC generally does not incorporate present values of the signals in the model, it is still not immune from spurious connectivity measures due to volume conduction (for a discussion see (Steen et al., 2016)). Therefore, it is recommended to reduce the problem of signal mixing using additional processing steps such as performing source localization and doing connectivity in the source domain.
Data length: because of the extent of parameters that need to be estimated, the number of data points should be sufficient for a good fit of the model. This is especially true for windowing approaches, where data is cut into smaller epochs. A rule of thumb is that the number of estimated parameters should be at least (~10) several times smaller than the number of data points.
Sections to add
Discuss option concatenate vs. average for the estimation of coherence on single trials: https://neuroimage.usc.edu/forums/t/difference-between-averaging-coherence-and-concatenate/22726/4
- Discuss pValues computed for the various methods
On the hard drive
TODO: Document data storage.
Additional documentation
References
Articles
Lagged-Coherence: Pascual-Marqui RD. Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions, arXiv preprint arXiv:0706.1776. 2007 Jun 12.
Phase transfer entropy: Lobier M, Siebenhühner F, Palva S, Palva JM Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions, NeuroImage 2014, 85:853-872
Barzegaran E, Knyazeva MG. Functional connectivity analysis in EEG source space: The choice of method Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105.
Forum discussions
Connectivity matrix storage:http://neuroimage.usc.edu/forums/showthread.php?1796
Comparing coherence values: http://neuroimage.usc.edu/forums/showthread.php?1556
Reading NxN PLV matrix: http://neuroimage.usc.edu/forums/t/pte-how-is-the-connectivity-matrix-stored/4618/2
Export multiple PLV matrices: https://neuroimage.usc.edu/forums/t/export-multiple-plv-matrices/2014/4
Scout function and connectivity: http://neuroimage.usc.edu/forums/showthread.php?2843
Unconstrained sources and connectivity: http://neuroimage.usc.edu/forums/t/problem-with-surfaces-vs-volumes/3261
Digonal values: http://neuroimage.usc.edu/forums/t/choosing-scout-function-before-or-after/2454/2
Connectivity pipeline: https://neuroimage.usc.edu/forums/t/help-for-connectivity-pipeline/12558/4
Ongoing developments: https://neuroimage.usc.edu/forums/t/connectivity-tutorial-and-methods-development-on-bst/12223/3
Granger causality: https://neuroimage.usc.edu/forums/t/is-granger-causality-analysis-a-linear-operation/12506/12
Amplitude Envelope Correlation: * https://neuroimage.usc.edu/forums/t/problem-with-time-dynamic-envelope-correlation/21542/9
This is a note (1)


![\begin{eqnarray*}
IC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \qquad \qquad \qquad \qquad LC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*} \begin{eqnarray*}
IC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \qquad \qquad \qquad \qquad LC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_af67140a46334a4b50e13076d33d975708a33e91_p1.png)