|
Size: 20546
Comment:
|
← Revision 53 as of 2019-09-18 15:11:15 ⇥
Size: 16021
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| '''[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE] ''' |
|
| Line 6: | Line 4: |
| In this auditory oddball experiment, we would like to test for the significant differences between the brain response to the deviant beeps and the standard beeps, time sample by time sample. Until now we have been computing measures of the brain activity in time or time-frequency domain. We were able to see clear effects or slight tendencies, but these observations were always dependent on an arbitrary amplitude threshold and the configuration of the colormap. With appropriate statistical tests, we can go beyond these empirical observations and assess what are the significant effects in a more formal way. | In this auditory oddball experiment, we would like to explore what are the significant differences between the brain response to the deviant or standard beeps, time sample by time sample. To do this we will be essentially contrasting the values we obtained for both conditions, and testing if the results are significantly different from zero. |
| Line 8: | Line 6: |
| We are typically interested in comparing different groups of samples. We want to know what is significantly different in the brain responses between two experimental conditions or two groups of subjects. So we will be essentially computing differences and testing if these differences are significantly different from zero. Independently from the type of statistical test you are using, you need to pay attention to the way you prepare the data you want to test. You will find at the end of this page some typical workflows we recommend. |
This tutorial focuses only on the first part of this problem: the contrast. Computing a difference between two condition A and B sounds trivial, but it requires some reflection when it comes to interpreting the sign of the subtraction of two signals oscillating around zero. Several options are available, we will try to explain to which application cases they correspond. The statistical significance will be discussed in the next tutorial. |
| Line 14: | Line 10: |
| == Computing a difference == Before running complicated statistical tests that will take hours of computation, you can start by checking what the difference of the average responses looks like. If in this difference you observe obvious effects that are clearly not what you are expecting, it's not worth moving forward with finer analysis: either the data is not clean enough or your initial hypothesis is wrong. |
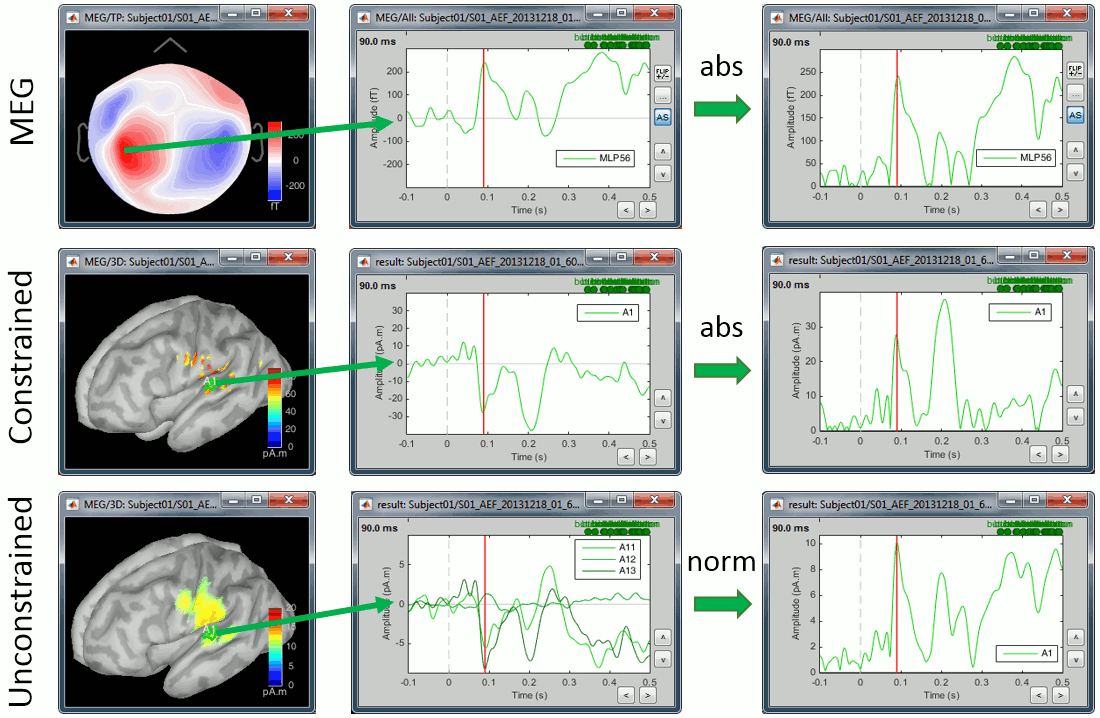
== Sign of the signals == First we need to define on which signals we want to compute the difference: sensor recordings, constrained sources (one signal per grid point) or unconstrained sources (three signals per grid point). For the first two we can compare the signals oscillating around zero or their absolute value, for unconstrained sources we have the additional option to use the norm of the three orientations. |
| Line 17: | Line 13: |
| Computing a difference between condition A and B sounds trivial, but it requires some reflexion when it comes to interpreting the sign of the subtraction of two signals oscillation around zero. We can compute the difference between two conditions in many different ways. | Using the rectified signals (absolute value) gives us an idea of the amount of activity in one particular brain region, but alters the frequency information and therefore cannot be used for time-frequency or connectivity analysis. Additionally, the rectified signals are not always appropriate to detect effects between different experimental conditions, as illustrated in the next section. |
| Line 19: | Line 15: |
| First we need to define on which signals we want to compute the difference: sensor recordings, constrained sources (one signal per grid point) or unconstrained sources (three signals per grid point). For the first two we can compare directly the signals oscillating around zero or their absolute value, for unconstrained sources we have the addional option to compare the norm of the three orientations. | In general, you should not apply an absolute value (or a norm) explicitly to your data. The only application cases for rectified signals are the display of the cortical maps, the comparison of magnitudes between conditions and the group analysis, and in all three cases the absolute value can be applied on the fly. |
| Line 21: | Line 17: |
| {{attachment:diff_signals.gif||height="426",width="653"}} | {{attachment:diff_signals.gif||width="653",height="426"}} |
| Line 23: | Line 19: |
| Using sensor recordings or constrained sources: | Now let's consider the two conditions for each available option. The examples below show the difference (deviant-standard) for one signal only, corresponding to the auditory cortex. The '''operator |x|''' represents the absolute value of x (i.e. the magnitude of x). |
| Line 25: | Line 21: |
| * Non-rectified (the sign of the difference is ambiguous): * Difference of the average current density maps: avg(A) - avg(B) * Difference of the Z-score: zscore(avg(deviant)) - zscore(avg(standard)) * Rectified (removing the ambiguity of the sign): * Difference of the absolute values of the averages: abs(avg(A)) - abs(avg(B)) * Difference of the Z-score on absolute values: zscore(avg(A)) - zscore(avg(B)) * Rectified difference of the averages: (avg(A) - avg(B)) * sign(svg(B)) |
== MEG/EEG sensor == We always observe important differences between (A-B) and (|A|-|B|). In the absolute case the amplitude of the difference is not representative of the distance between the green curve (deviant) and the red curve (standard). In general, the sign of the signal recorded by any MEG or EEG sensor is meaningful and we need to keep it in the analysis to account for the differences between conditions.<<BR>>'''Never use an absolute value on sensor data'''. |
| Line 33: | Line 24: |
| Using unconstrained sources (three orientations per grid point): | {{attachment:diff_sensors.gif||width="549",height="289"}} |
| Line 35: | Line 26: |
| * Difference of the absolute values of the averages: norm(avg(A)) - norm(avg(B)) * Difference of the Z-score: zscore(norm(avg(A))) - zscore(norm(avg(B))) |
== Constrained sources == We also observe important differences between (A-B) and (|A|-|B|). At 175ms, we reach the highest distance between the red and green curves, but it corresponds to a zero in the rectified difference. {{attachment:diff_constr.gif||width="549",height="289"}} '''(A-B)''': Correct amplitude, ambiguous sign. * This measure represents better the distance between the two conditions curves. However, its sign is ambiguous and cannot be used to claim that "the brain response is stronger in condition A than in condition B" (|A|>|B|, cases a/b/e in the table below) or "is stronger in condition B than in condition A" (|B|>|A|, cases c/d). As illustrated in the [[http://neuroimage.usc.edu/brainstorm/Tutorials/SourceEstimation#Sign_of_constrained_minimum_norm_values|source estimation tutorial]], the sign of the current density maps depends on the orientation of the source. <<BR>><<BR>> {{attachment:diff_sign_table.gif||width="327",height="113"}} * This is an appropriate measure to use when the polarity of the signal is important to you, for example when suppression of a negative peak (A-B<0) would be viewed differently than suppression of a positive peak (A-B>0) or a polarity change (sign(A) different from sign(B)). * Suppression of positive signals from A to B (case a) produces the same value as an increase in the negative signal from A to B (case d). Similarly cases b and c will produce the same value. For this reason interpretation of the results requires that you also examine the actual polarities of the two signals at locations in time and space where significant effects are detected. '''|A|-|B|''': Ambiguous amplitude, meaningful sign. * This measure is insensitive to polarity so not adapted to represent the distance between the two conditions, but its sign is meaningful. * The sign indicates the direction of magnitude change and avoids the ambiguity encountered in the earlier measure (case a vs case d) but cannot differentiate between suppression of positive and negative signals (cases a and b). * This measure will avoid the confound due to the ambiguity of the sign of the constrained sources, but will also be less sensitive to cases in which differences in response involve differences in polarity and/or latency than the former measure (e.g. case e in the above table). ==== Conclusion: Which one should you use? ==== * '''(A-B)''': To detect when and where the signals are different. * '''(|A|-|B|)''': When studying one particular effect, if you are interested to know which condition generates a larger response at a specific time point. It is meaningful only if you already know that A and B have the same sign. * '''(|A|^2^-|B|^2^)''': Difference of power, same properties as the difference of magnitude, but maybe more common measure than the absolute value. Many statistics exist for amplitude and power, but not for rectified signals. == Unconstrained sources == The exact same observations apply to the unconstrained sources, using the norm of the three orientations instead of the absolute values. X and Y represent the source vectors with three components each (x,y,z) for conditions A and B. '''Norm(X-Y)''': This measure will detect vector differences between the two signals which can occur if the magnitude and/or orientation changes. It differs from (Norm(X)-Norm(Y)) in being sensitive to changes in apparent source orientation, but cannot differentiate increases from decreases in amplitude. '''Norm(X)-Norm(Y)''': This is the unconstrained equivalent to |A|-|B|, i.e. it will produce a signed value that reflects increases or decreases in magnitude from A to B and should be interpreted similarly. Unlike Norm(X-Y) it is not sensitive to rotation of the source from A to B unless there is an accompanying amplitude change. But on the other hand, because the value is signed, we can differentiate between increases and decreases in amplitude. {{attachment:diff_unconstr.gif||width="679",height="424"}} == Source normalization == The examples above only show minimum norm current density maps that haven't been normalized. The same logic applies to normalized source values, as long as you do not rectify the signals during the computation of the normalization. As a reminder, you should normalize the source maps if you are intending to compare different subjects, it will help bringing them to the same range of values. The list below shows the valid operations for the Z-score normalization, but the same is applicable for dSPM, sLORETA and MNp. Constrained sources: * '''Zscore(A) - Zscore(B)''': Correct amplitude, ambiguous sign. * '''abs(Zscore(A)) - abs(Zscore(B))''': Ambiguous amplitude, meaningful sign. Unconstrained sources: * '''norm(Zscore(A) - Zscore(B))''': Correct amplitude, no sign. * '''norm(Zscore(A)) - norm(Zscore(B))''': Ambiguous amplitude, meaningful sign. Always avoid using the following measures: * Z-score(abs(sources)) * Z-score(norm(sources)) |
| Line 39: | Line 78: |
| Before running complicated statistical tests that will take hours of computation, you can start by checking what the difference of the average responses looks like. If in this difference you cannot observe the effects you are expecting, it's not worth moving forward with finer analysis: the recordings are not clean enough, you don't have enough data or your initial hypothesis is wrong. ==== Absolute difference: |A|-|B| ==== |
|
| Line 43: | Line 85: |
| * Run the process "'''Difference > Difference A-B'''".<<BR>>Select the option "'''Use absolute values'''", which will convert the unconstrained source maps (three dipoles at each cortex location) into a flat cortical map by taking the norm of the three dipole orientations before computing the difference.<<BR>><<BR>> {{attachment:diff_process.gif||height="311",width="478"}} | * Run the process "'''Difference > Difference A-B'''", select the option "'''Use absolute values'''". <<BR>>Do not run the computation now, we will add more steps.<<BR>><<BR>> {{attachment:diff_process_abs.gif||width="497",height="350"}} |
| Line 45: | Line 87: |
| * Rename the new file in "Deviant-Standard", double-click on it and explore it in time. <<BR>><<BR>> {{attachment:diff_contact.gif||height="307",width="638"}} * We are looking at the difference (Deviant-Standard) so positive/red regions indicate higher activity levels for the deviant beeps, and negative/blue regions higher activity for the standard beeps. |
* Add process: "'''File > Set comment'''", New comment = "'''deviant|abs - standard|abs'''" * Add process: "'''Pre-process > Band-pass filter'''", Low-pass: '''0-40Hz''', '''Overwrite'''.<<BR>><<BR>> {{attachment:diff_abs_comment.gif||width="301",height="209"}} {{attachment:diff_abs_lowpass.gif||width="278",height="376"}} * '''Epochs are too short''': As already mentioned in the [[http://neuroimage.usc.edu/brainstorm/Tutorials/SourceEstimation#Low-pass_filter|Source estimation]] and [[http://neuroimage.usc.edu/brainstorm/Tutorials/Epoching#Epoch_length|Epoching]] tutorials, the epochs we imported are too short for filtering properly below 40Hz. If you are reproducing these steps on your own recordings, make sure you work with longer time segments. * Add process: "'''Standardize > Baseline normalization'''", Baseline='''[-100,-1.7]ms''', Method='''Z-score''' <<BR>><<BR>> {{attachment:diff_abs_zscore.gif||width="302",height="336"}} * Run the script, then double-click on the filtered file and explore it in time. This is a cortex map, with positive and negative values. It should be displayed using a colormap that shows relative values (right-click > Colormap > Uncheck the option "Absolute values"). <<BR>><<BR>> {{attachment:diff_contact_abs.gif||width="670",height="297"}} * We are looking at the rectified difference (abs(deviant)-abs(standard)) so positive/red regions indicate higher activity levels for the deviant beeps, and negative/blue regions higher activity for the standard beeps. |
| Line 48: | Line 98: |
| * '''P50''': Maybe a stronger response in the primary auditory cortex for the standard condition. * '''MMN '''(125ms): Stronger response for the deviant (left temporal, inferior frontal). |
* '''50ms''': Stronger auditory response in the standard condition. * '''MMN '''(125ms): Stronger response for the deviant (left temporal, left inferior frontal). |
| Line 51: | Line 101: |
| * '''175ms''': Stronger response in the motor regions for the standard condition (motor inihibition). * '''After 200ms''': Stronger response in the deviant condition. |
* '''175ms''': Stronger response in the motor regions for the standard condition (motor inhibition). * '''After 200ms''': Stronger response in the deviant condition (motor preparation and movement). * Plot the time series for scout A1L (relative and absolute values).<<BR>>The relevant information here is the sign of the difference (option Values:Relative).<<BR>><<BR>> {{attachment:diff_scout_abs.gif||width="602",height="144"}} ==== Relative difference: (A-B) ==== * Recall the last analysis pipeline: menu '''File > Reload last pipeline'''. * In the process '''Difference''': '''Unselect''' the option "Use absolute values". * In the process '''Set comment''': Change the comment to "'''deviant - standard'''". <<BR>><<BR>> {{attachment:diff_rel_process.gif||width="301",height="274"}} {{attachment:diff_rel_comment.gif||width="300",height="254"}} * Run the script and open the filtered difference.<<BR>>Change the colormap definition to show only '''positive values''' (right-click > Colormap: Stat2 > Uncheck: Absolute values) and use a different colormap ("hot" or "jet"). The sign of the relative difference is not meaningful, it depends mostly on the orientation of the dipoles on the cortex.<<BR>><<BR>> {{attachment:diff_contact_rel.gif||width="651",height="298"}} * We can see with much more contrast the areas and times where the two conditions are different, but we lose the ability to say which one is stronger. It is the measure we will use in most cases when computing statistical tests between conditions. * Plot the time series for scout A1L (relative values and absolute). <<BR>>We observe the peak of difference where we were observing a zero with the absolute difference.<<BR>><<BR>> {{attachment:diff_scout_rel.gif||width="600",height="143"}} |
| Line 55: | Line 114: |
| Another process can compute the average and the difference at the same time. We are going to compute the difference of all the trials from both runs at the sensor level. This is usually not recommended because the subject might have moved between the runs. Averaging the recordings across runs is not accurate but can give a good first approximation, in order to make sure we are on the right tracks. | Another process can compute the average and the difference at the same time. We are going to compute the difference of all the trials from both runs at the sensor level. As discussed in the previous tutorials, this is usually not recommended because the subject might have moved between the runs. Averaging MEG recordings across runs is not accurate but can give a good first approximation, in order to make sure we are on the right tracks. It is acceptable here because the movements of the subjects are negligible between the two runs. |
| Line 57: | Line 116: |
| * In Process2, select all the '''deviant trials''' (Files A) and all the '''standard trials''' (Files B). * Run the process "'''Test > Difference of means'''", select the option "'''Arithmetic average'''". <<BR>><<BR>> {{attachment:diff_mean_process.gif||height="341",width="419"}} * Rename the new file in "Deviant-Standard", double-click on it to display it. The difference deviant-standard does not show anymore the early responses (P50, P100) but emphasizes the difference in the later process (MMN/P200 and P300). <<BR>><<BR>> {{attachment:diff_mean_ts.gif||height="164",width="608"}} |
* In Process2, select the following files:<<BR>>Files A: all the '''deviant trials''' from both runs (~80 files)<<BR>>Files B: '''all the standard trials''' from each run (~400 files). * Select the process "'''File > Uniform number of files'''", with the default number of files and the option "Uniform". This will select the same number of files from FilesA and FilesB. The list with the larger number of files (FilesB) is sampled uniformly to get the same number of files on both sides. <<BR>>This step is not necessary here, but it's a good time to illustrate it, in case you need it someday. <<BR>><<BR>> {{attachment:select2_process.gif||width="440",height="427"}} * Add the process "'''Test > Difference of means'''", select the option "'''Arithmetic average'''". <<BR>>The option "weighted average" has no importance because we are averaging only single trials.<<BR>><<BR>> {{attachment:diff_mean_process.gif||width="310",height="358"}} * Run the pipeline. Double-click on the new difference to display it. The difference does not show anymore the early responses (P50, P100) which are similar for the two conditions, but emphasizes the difference in the later process (MMN/P200 and P300). <<BR>><<BR>> {{attachment:diff_mean_ts.gif||width="668",height="167"}} <<BR>>'''Left''': Average of 80 deviant trials.<<BR>>'''Center''': Average of 80 standard trials.<<BR>>'''Right''': Difference of the two, computed in this process. |
| Line 61: | Line 121: |
| == Parametric Student's t-test [TODO] == Using a t-test instead of the difference of the two averages, we can reproduce similar results but with a significance level attached to each value. Parametric method require the values tested to follow a Gaussian distribution. Some sets of data could be considered as Gaussian (example: screen capture of the histogram of the values recorded by one sensor at one time point), some are not (example: histogram ABS(values) at one point). |
== Time-frequency == In the case of time-frequency maps there is no sign ambiguity of the values, so computing a difference is slightly simpler. There are two possible cases: difference between power maps or between normalized maps (eg. ERS/ERD). |
| Line 64: | Line 124: |
| '''WARNING''': This parametric t-test is valid only for '''constrained '''sources. In the case of unconstrained sources, the norm of the three orientations is used, which breaks the hypothesis of the tested values following a Gaussian distribution. This test is now illustrated on unconstrained sources, but this will change when we figure out the correct parametric test to apply on unconstrained sources. | '''Original time-frequency maps''' |
| Line 66: | Line 126: |
| * In the Process2 tab, select the following files: * Files A: All the deviant trials, with the '''[Process sources]''' button selected. * Files B: All the standard trials, with the '''[Process sources]''' button selected. * Run the process "'''Test > Student's t-test'''", Equal variance, '''Absolute value of average'''.<<BR>>This option will convert the unconstrained source maps (three dipoles at each cortex location) into a flat cortical map by taking the norm of the three dipole orientations before computing the difference. <<BR>><<BR>> {{attachment:ttest_process.gif||height="516",width="477"}} * Double-click on the new file for displaying it. With the new tab "Stat" you can control the p-value threshold and the correction you want to apply for multiple comparisons. <<BR>><<BR>> {{attachment:ttest_file.gif||height="243",width="492"}} * Set the options in the Stat tab: p-value threshold: '''0.05''', Multiple comparisons: '''Uncorrected'''. <<BR>>What we see in this figure are the t-values corresponding to p-values under the threshold. We can make similar observations than with the difference of means, but without the arbitrary amplitude threshold (this slider is now disabled in the Surface tab). If at a given time point a vertex is red in this view, the mean of the deviant condition is significantly higher than the standard conditions (p<0.05).<<BR>><<BR>> {{attachment:ttest_contact.gif||height="303",width="512"}} * This approach considers each time sample and each surface vertex separately. This means that we have done Nvertices*Ntime = 15002*361 = 5415722 t-tests. The threshold at p<0.05 controls correctly for false positives at one point but not for the entire cortex. We need to correct the p-values for '''multiple comparisons'''. The logic of two types of corrections available in the Stat tab (FDR and Bonferroni) is explained in [[http://scan.oxfordjournals.org/content/4/4/417.full|Bennett et al (2009)]]. * Select the correction for multiple comparison "'''False discovery rate (FDR)'''". You will see that a lot less elementrs survive this new threshold. In the Matlab command window, you can see the average corrected p-value, that replace for each vertex the original p-threshold (0.05):<<BR>>BST> Average corrected p-threshold: 0.000315138 (FDR, Ntests=5415722) * From the Scout tab, you can also plot the scouts time series and get in this way a summary of what is happening in your regions of interest. Positive peaks indicate the latencies when '''at least one vertex''' of the scout has a value that is significantly higher in the deviant condition. The values that are shown are the averaged t-values in the scout. <<BR>><<BR>> {{attachment:ttest_scouts.gif||height="169",width="620"}} |
* The power of the TF maps are only positive values, so you can simply compute the difference between the power maps, it will give you all the interesting information. * Use the difference of the power: power(TF(A)) - power(TF(B)) * This is what you would use for computing statistics within a subject. |
| Line 76: | Line 130: |
| == FieldTrip: Non-parametric cluster-based statistic [TODO] == We have the possibility to call some of the FieldTrip functions from the Brainstorm environment. For this, you need first to [[http://www.fieldtriptoolbox.org/download|install the FieldTrip toolbox]] on your computer and [[http://www.fieldtriptoolbox.org/faq/should_i_add_fieldtrip_with_all_subdirectories_to_my_matlab_path|add it to your Matlab path]]. |
'''Normalized time-frequency maps''' |
| Line 79: | Line 132: |
| For a complete description of non-parametric cluster-based statistics in FieldTrip, read the following article: [[http://www.sciencedirect.com/science/article/pii/S0165027007001707|Maris & Oostendveld (2007)]]. Additional information can be found on the FieldTrip website: * Tutorial: [[http://www.fieldtriptoolbox.org/tutorial/eventrelatedstatistics|Parametric and non-parametric statistics on event-related fields]] * Tutorial: [[http://www.fieldtriptoolbox.org/tutorial/cluster_permutation_timelock|Cluster-based permutation tests on event related fields]] * Tutorial: [[http://www.fieldtriptoolbox.org/tutorial/cluster_permutation_freq|Cluster-based permutation tests on time-frequency data]] * Tutorial: [[http://www.fieldtriptoolbox.org/faq/how_not_to_interpret_results_from_a_cluster-based_permutation_test|How NOT to interpret results from a cluster-based permutation test]] * Video: [[https://www.youtube.com/watch?v=x0hR-VsHZj8|Statistics using non-parametric randomization techniques]] * Video: [[https://www.youtube.com/watch?v=vOSfabsDUNg|Non-parametric cluster-based statistical testing of MEG/EEG data]] * Functions: [[http://www.fieldtriptoolbox.org/reference/timelockstatistics|ft_timelockstatistics]], [[http://www.fieldtriptoolbox.org/reference/sourcestatistics|ft_sourcestatistics]], [[http://www.fieldtriptoolbox.org/reference/freqstatistics|ft_freqstatistics]] Permuation-based non-parametric statistics are more flexible and do not require to do any assumption on the distribution of the data, but on the other hand they are a lot more complicated to process. Calling FieldTrip's function ft_sourcestatistics requires a lot more memory because all the data has to be loaded at once, and a lot more computation time because the same test is repeated many times. Running this function in the same way as the parametric t-test previously (full cortex, all the trials and all the time points) would require 45000*461*361*8/1024^3 = '''58 Gb of memory''' just to load the data. This is impossible on most computers, we have to give up at least one dimension and run the test only for one time sample or one region of interest. == FieldTrip: Process options [TODO] == Screen captures for the two processes: Description of the process options: The options available here match the options passed to the function ft_sourcestatistics. Cluster correction: Define what a cluster is for the different data types (recordings, surface source maps, volume source models, scouts) Default options: * clusterstatistic = 'maxsum' * method = 'montecarlo' * correcttail = 'prob' == FieldTrip: Example 1 [TODO] == We will run this FieldTrip function first on the scouts time series and then on a short time window. * Keep the same selection in Process2: all the deviant trials in FilesA, all the standard trials in FilesB. * Run process: '''Test > FieldTrip: ft_sourcestatistics''', select the options as illustrated below.<<BR>><<BR>> {{attachment:ft_process_scouts.gif||height="680",width="348"}} * Double-click on the new file to display it: <<BR>><<BR>> * Display on the cortex: see section "Convert statistic results to regular files" below == FieldTrip: Example 2 [TODO] == short time window == Time-frequency files == Both ft_sourcestatistics and ft_freqstatistics are available. Use ft_sourcestatistics if the input files contain full source maps, and ft_freqstatistics for all the other cases (scouts or sensors). == Workflow: Single subject == You want to test for one unique subject what is significantly different between two experimental conditions. You are going to compare the single trials corresponding to each condition directly. <<BR>>This is the case for this tutorial dataset, we want to know what is different between the brain responses to the deviant beep and the standard beep. '''Sensor recordings''': Not advised for MEG with multiple runs, correct for EEG. * '''Parametric t-test''': Correct * Select the option "Arithmetic average: mean(x)". * No restriction on the number of trials. * '''Non-parametric t-test''': Correct * Do not select the option "Test absolute values". * No restriction on the number of trials. * '''Difference of means''': * Select the option "Arithmetic average: mean(x)". * Use the same number of trials for both conditions. '''Constrained source maps''' (one value per vertex): * Use the non-normalized minimum norm maps for all the trials (no Z-score). * '''Parametric t-test''': Incorrect * Select the option "Absolue value of average: abs(mean(x))". * No restriction on the number of trials. * '''Non-parametric t-test''': Correct * Select the option "Test absolute values". * No restriction on the number of trials. * '''Difference of means''': * Select the option "Absolue value of average: abs(mean(x))". * Use the same number of trials for both conditions. '''Unconstrainted source maps''' (three values per vertex): * '''Parametric t-test''': Incorrect * ? * '''Non-parametric t-test''': Correct * ? * '''Difference of means''': * ? '''Time-frequency maps''': * Test the non-normalized time-frequency maps for all the trials (no Z-score or ERS/ERD). * '''Parametric t-test''': ? * No restriction on the number of trials. * '''Non-parametric t-test''': Correct * No restriction on the number of trials. * '''Difference of means''': * Use the same number of trials for both conditions. == Workflow: Group analysis == You have the same two conditions recorded for multiple subjects. '''Sensor recordings''': Strongly discouraged for MEG, correct for EEG. * For each subject: Compute the average of the trials for each condition individually. * Do not apply an absolute value. * Use the same number of trials for all the subjects. * Test the subject averages. * Do no apply an absolute value. '''Source maps (template anatomy)''': * For each subject: Average the non-normalized minimumn norm maps for the trials of each condition. * Use the same number of trials for all the subjects. * If you can't use the same number of trials, you have to correct the Z-score values ['''TODO''']. * Normalize the averages using a Z-score wrt with a baseline. * Select the option: "Use absolue values of source activations" * Select the option: "Dynamic" (does not make any difference but could be faster). * Test the normalized averages across subjects. * Do not apply an absolute value. '''Source maps (individual anatomy)''': * For each subject: Average the non-normalized minimumn norm maps for the trials of each condition. * Use the same number of trials for all the subjects. * If you can't use the same number of trials, you have to correct the Z-score values ['''TODO''']. * Normalize the averages using a Z-score wrt with a baseline. * Select the option: "Use absolue values of source activations" * Select the option: "Dynamic" (does not make any difference but could be faster). * Project the normalized maps on the template anatomy. * Option: Smooth spatially the source maps. * Test the normalized averages across subjects. * Do not apply an absolute value. '''Time-frequency maps''': * For each subject: Compute the average time-frequency decompositions of all the trials for each condition (using the advanced options of the "Morlet wavelets" and "Hilbert transform" processes). * Use the same number of trials for all the subjects. * Normalize the averages wrt with a baseline (Z-score or ERS/ERD). * Test the normalized averages across subjects. * Do no apply an absolute value. == Convert statistic results to regular files [TODO] == * Process: Extract > Apply statistc threshold * Process: Simulate > Simulate recordings from scout [TODO] == Export to SPM == An alternative to running the statical tests in Brainstorm is to export all the data and compute the tests with an external program (R, Matlab, SPM, etc). Multiple menus exist to export files to external file formats (right-click on a file > File > Export to file). Two tutorials explain to export data specifically to SPM: * [[http://neuroimage.usc.edu/brainstorm/ExportSpm8|Export source maps to SPM8]] (volume) * [[http://neuroimage.usc.edu/brainstorm/ExportSpm12|Export source maps to SPM12]] (surface) == On the hard drive [TODO] == Right click one of the first TF file we computed > File > '''View file contents'''. == References == * Bennett CM, Wolford GL, Miller MB, [[http://scan.oxfordjournals.org/content/4/4/417.full|The principled control of false positives in neuroimaging]] <<BR>> Soc Cogn Affect Neurosci (2009), 4(4):417-422. * Maris E, Oostendveld R, [[http://www.sciencedirect.com/science/article/pii/S0165027007001707|Nonparametric statistical testing of EEG- and MEG-data]] <<BR>>J Neurosci Methods (2007), 164(1):177-90. * Maris E, [[http://www.ncbi.nlm.nih.gov/pubmed/22176204|Statistical testing in electrophysiological studies]]<<BR>>Psychophysiology (2012), 49(4):549-65 * Pantazis D, Nichols TE, Baillet S, Leahy RM. [[http://www.sciencedirect.com/science/article/pii/S1053811904005671|A comparison of random field theory and permutation methods for the statistical analysis of MEG data]], Neuroimage (2005), 25(2):383-94. * FieldTrip video: Non-parametric cluster-based statistical testing of MEG/EEG data: <<BR>> https://www.youtube.com/watch?v=vOSfabsDUNg == Additional discussions on the forum == * Forum: Multiple comparisons: http://neuroimage.usc.edu/forums/showthread.php?1297 * Forum: Cluster neighborhoods: [[http://neuroimage.usc.edu/forums/showthread.php?2132-Fieldtrip-statistics|http://neuroimage.usc.edu/forums/showthread.php?2132]] * Forum: Differences FieldTrip-Brainstorm: http://neuroimage.usc.edu/forums/showthread.php?2164 == Delete all your experiments == Before moving to the next tutorial, '''delete '''all the statistic results you computed in this tutorial. It will make it the database structure less confusing for the following tutorials. |
* The values represent deviations with respect with a baseline, they can be positive or negative. Therefore we are in the same configuration as with the sensor data. * Use the difference of the normalized values: Normalize(power(TF(A))) - Normalize(power(TF(B))) * This could be used for comparing visually two averages, or for statistics across subjects. |
Tutorial 25: Difference
Authors: Francois Tadel, Elizabeth Bock, Dimitrios Pantazis, Richard Leahy, Sylvain Baillet
In this auditory oddball experiment, we would like to explore what are the significant differences between the brain response to the deviant or standard beeps, time sample by time sample. To do this we will be essentially contrasting the values we obtained for both conditions, and testing if the results are significantly different from zero.
This tutorial focuses only on the first part of this problem: the contrast. Computing a difference between two condition A and B sounds trivial, but it requires some reflection when it comes to interpreting the sign of the subtraction of two signals oscillating around zero. Several options are available, we will try to explain to which application cases they correspond. The statistical significance will be discussed in the next tutorial.
Contents
Sign of the signals
First we need to define on which signals we want to compute the difference: sensor recordings, constrained sources (one signal per grid point) or unconstrained sources (three signals per grid point). For the first two we can compare the signals oscillating around zero or their absolute value, for unconstrained sources we have the additional option to use the norm of the three orientations.
Using the rectified signals (absolute value) gives us an idea of the amount of activity in one particular brain region, but alters the frequency information and therefore cannot be used for time-frequency or connectivity analysis. Additionally, the rectified signals are not always appropriate to detect effects between different experimental conditions, as illustrated in the next section.
In general, you should not apply an absolute value (or a norm) explicitly to your data. The only application cases for rectified signals are the display of the cortical maps, the comparison of magnitudes between conditions and the group analysis, and in all three cases the absolute value can be applied on the fly.
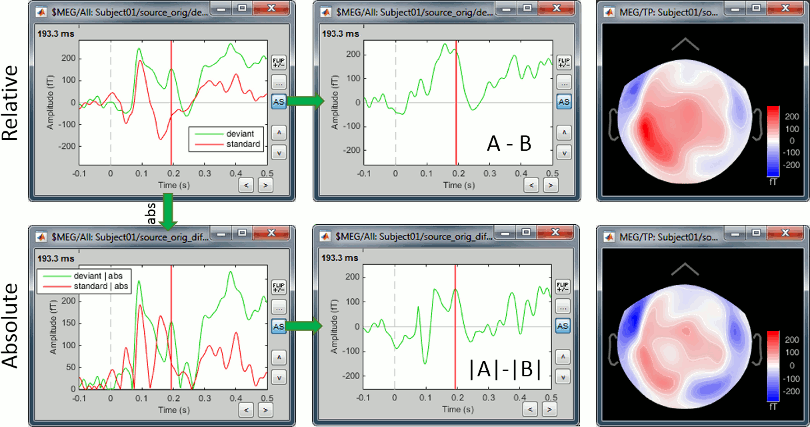
Now let's consider the two conditions for each available option. The examples below show the difference (deviant-standard) for one signal only, corresponding to the auditory cortex. The operator |x| represents the absolute value of x (i.e. the magnitude of x).
MEG/EEG sensor
We always observe important differences between (A-B) and (|A|-|B|). In the absolute case the amplitude of the difference is not representative of the distance between the green curve (deviant) and the red curve (standard). In general, the sign of the signal recorded by any MEG or EEG sensor is meaningful and we need to keep it in the analysis to account for the differences between conditions.
Never use an absolute value on sensor data.
Constrained sources
We also observe important differences between (A-B) and (|A|-|B|). At 175ms, we reach the highest distance between the red and green curves, but it corresponds to a zero in the rectified difference.
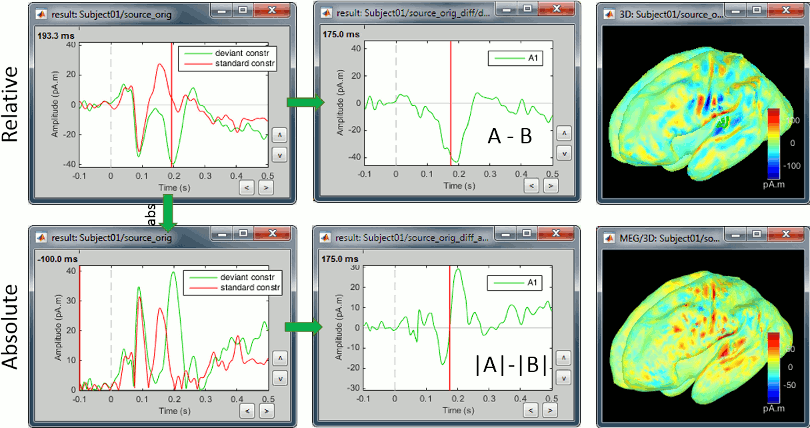
(A-B): Correct amplitude, ambiguous sign.
This measure represents better the distance between the two conditions curves. However, its sign is ambiguous and cannot be used to claim that "the brain response is stronger in condition A than in condition B" (|A|>|B|, cases a/b/e in the table below) or "is stronger in condition B than in condition A" (|B|>|A|, cases c/d). As illustrated in the source estimation tutorial, the sign of the current density maps depends on the orientation of the source.
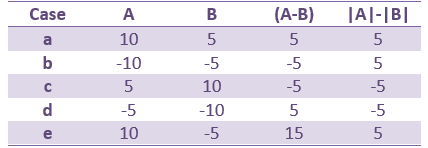
This is an appropriate measure to use when the polarity of the signal is important to you, for example when suppression of a negative peak (A-B<0) would be viewed differently than suppression of a positive peak (A-B>0) or a polarity change (sign(A) different from sign(B)).
- Suppression of positive signals from A to B (case a) produces the same value as an increase in the negative signal from A to B (case d). Similarly cases b and c will produce the same value. For this reason interpretation of the results requires that you also examine the actual polarities of the two signals at locations in time and space where significant effects are detected.
|A|-|B|: Ambiguous amplitude, meaningful sign.
- This measure is insensitive to polarity so not adapted to represent the distance between the two conditions, but its sign is meaningful.
- The sign indicates the direction of magnitude change and avoids the ambiguity encountered in the earlier measure (case a vs case d) but cannot differentiate between suppression of positive and negative signals (cases a and b).
- This measure will avoid the confound due to the ambiguity of the sign of the constrained sources, but will also be less sensitive to cases in which differences in response involve differences in polarity and/or latency than the former measure (e.g. case e in the above table).
Conclusion: Which one should you use?
(A-B): To detect when and where the signals are different.
(|A|-|B|): When studying one particular effect, if you are interested to know which condition generates a larger response at a specific time point. It is meaningful only if you already know that A and B have the same sign.
(|A|2-|B|2): Difference of power, same properties as the difference of magnitude, but maybe more common measure than the absolute value. Many statistics exist for amplitude and power, but not for rectified signals.
Unconstrained sources
The exact same observations apply to the unconstrained sources, using the norm of the three orientations instead of the absolute values. X and Y represent the source vectors with three components each (x,y,z) for conditions A and B.
Norm(X-Y): This measure will detect vector differences between the two signals which can occur if the magnitude and/or orientation changes. It differs from (Norm(X)-Norm(Y)) in being sensitive to changes in apparent source orientation, but cannot differentiate increases from decreases in amplitude.
Norm(X)-Norm(Y): This is the unconstrained equivalent to |A|-|B|, i.e. it will produce a signed value that reflects increases or decreases in magnitude from A to B and should be interpreted similarly. Unlike Norm(X-Y) it is not sensitive to rotation of the source from A to B unless there is an accompanying amplitude change. But on the other hand, because the value is signed, we can differentiate between increases and decreases in amplitude.
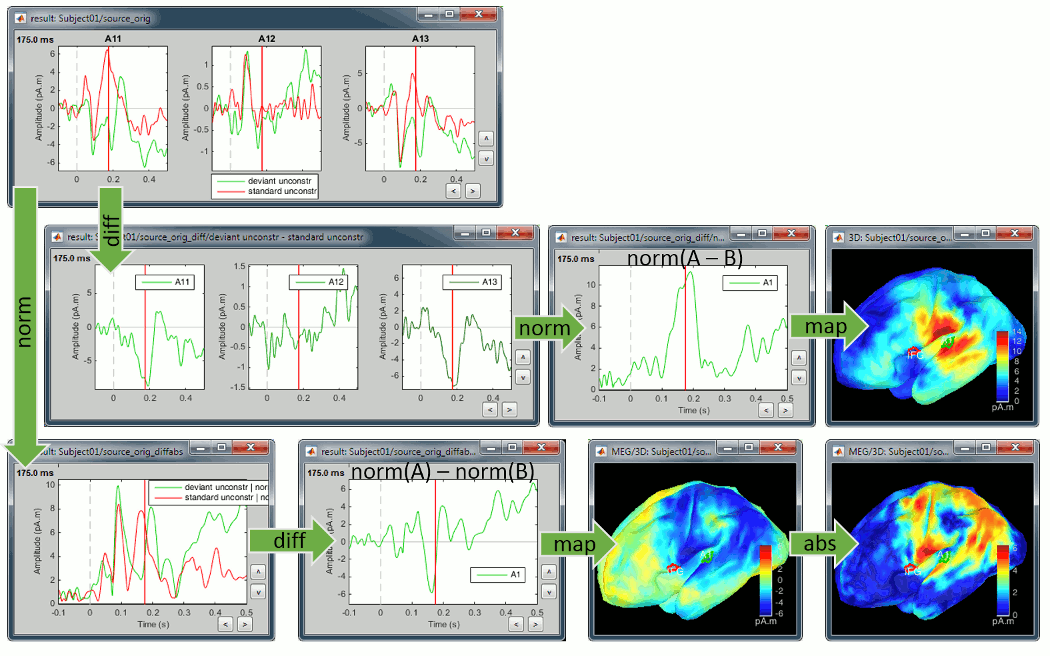
Source normalization
The examples above only show minimum norm current density maps that haven't been normalized. The same logic applies to normalized source values, as long as you do not rectify the signals during the computation of the normalization.
As a reminder, you should normalize the source maps if you are intending to compare different subjects, it will help bringing them to the same range of values. The list below shows the valid operations for the Z-score normalization, but the same is applicable for dSPM, sLORETA and MNp.
Constrained sources:
Zscore(A) - Zscore(B): Correct amplitude, ambiguous sign.
abs(Zscore(A)) - abs(Zscore(B)): Ambiguous amplitude, meaningful sign.
Unconstrained sources:
norm(Zscore(A) - Zscore(B)): Correct amplitude, no sign.
norm(Zscore(A)) - norm(Zscore(B)): Ambiguous amplitude, meaningful sign.
Always avoid using the following measures:
- Z-score(abs(sources))
- Z-score(norm(sources))
Difference deviant-standard
Before running complicated statistical tests that will take hours of computation, you can start by checking what the difference of the average responses looks like. If in this difference you cannot observe the effects you are expecting, it's not worth moving forward with finer analysis: the recordings are not clean enough, you don't have enough data or your initial hypothesis is wrong.
Absolute difference: |A|-|B|
We are going to use the Process2 tab, at the bottom of the Brainstorm figure. It works exactly like the Process1 tab but with two lists of input files, referred to as FilesA (left) and FilesB (right).
In Process2, drag and drop the non-normalized deviant average on the left (FilesA) and the non-normalized standard average on the right (FilesB).
Run the process "Difference > Difference A-B", select the option "Use absolute values".
Do not run the computation now, we will add more steps.
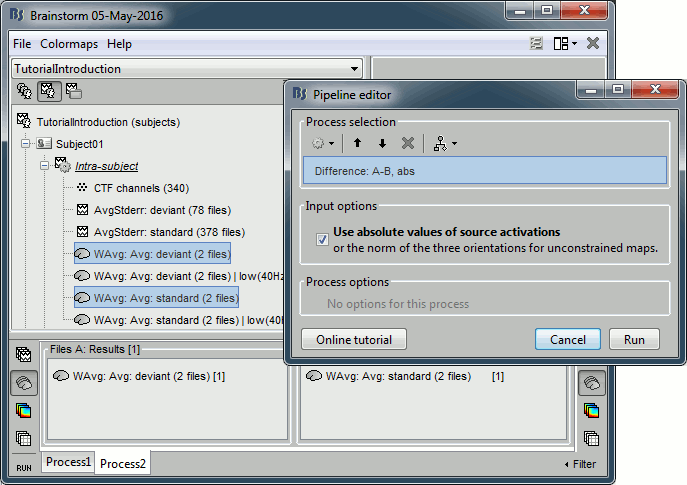
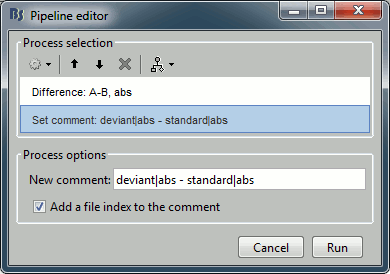
Add process: "File > Set comment", New comment = "deviant|abs - standard|abs"
Add process: "Pre-process > Band-pass filter", Low-pass: 0-40Hz, Overwrite.
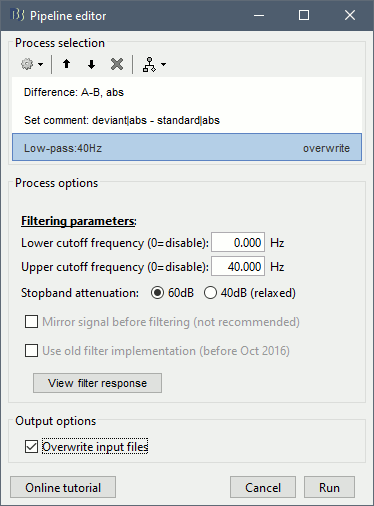
Epochs are too short: As already mentioned in the Source estimation and Epoching tutorials, the epochs we imported are too short for filtering properly below 40Hz. If you are reproducing these steps on your own recordings, make sure you work with longer time segments.
Add process: "Standardize > Baseline normalization", Baseline=[-100,-1.7]ms, Method=Z-score
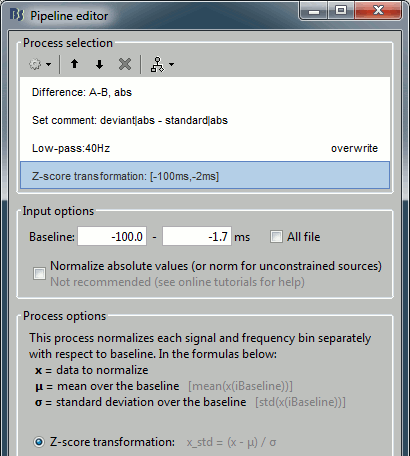
Run the script, then double-click on the filtered file and explore it in time. This is a cortex map, with positive and negative values. It should be displayed using a colormap that shows relative values (right-click > Colormap > Uncheck the option "Absolute values").
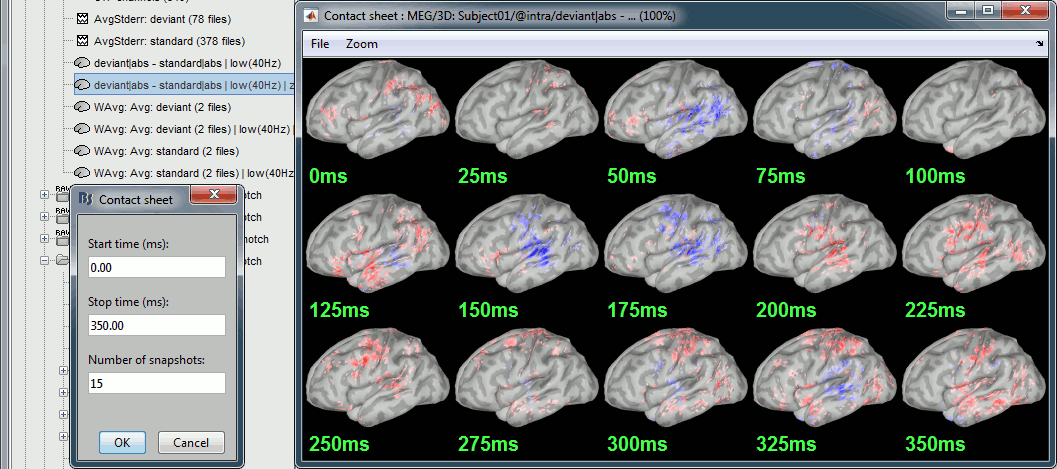
- We are looking at the rectified difference (abs(deviant)-abs(standard)) so positive/red regions indicate higher activity levels for the deviant beeps, and negative/blue regions higher activity for the standard beeps.
Before 50ms: The motor activity in the deviant is probably due to the previous stims.
50ms: Stronger auditory response in the standard condition.
MMN (125ms): Stronger response for the deviant (left temporal, left inferior frontal).
150ms: Stronger response in the auditory system for the standard condition.
175ms: Stronger response in the motor regions for the standard condition (motor inhibition).
After 200ms: Stronger response in the deviant condition (motor preparation and movement).
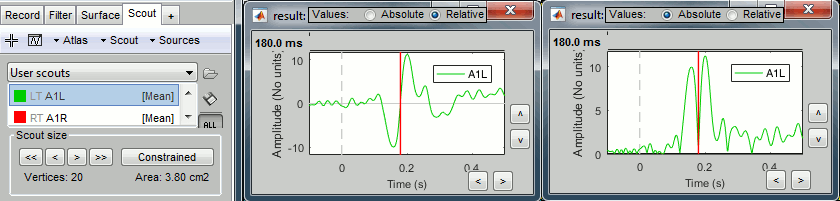
Plot the time series for scout A1L (relative and absolute values).
The relevant information here is the sign of the difference (option Values:Relative).
Relative difference: (A-B)
Recall the last analysis pipeline: menu File > Reload last pipeline.
In the process Difference: Unselect the option "Use absolute values".
In the process Set comment: Change the comment to "deviant - standard".
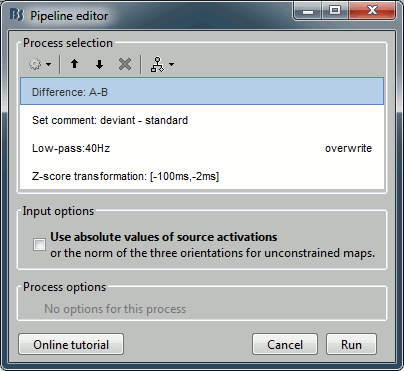
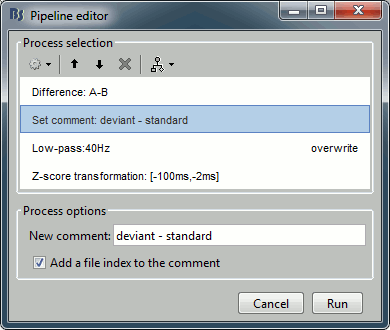
Run the script and open the filtered difference.
Change the colormap definition to show only positive values (right-click > Colormap: Stat2 > Uncheck: Absolute values) and use a different colormap ("hot" or "jet"). The sign of the relative difference is not meaningful, it depends mostly on the orientation of the dipoles on the cortex.
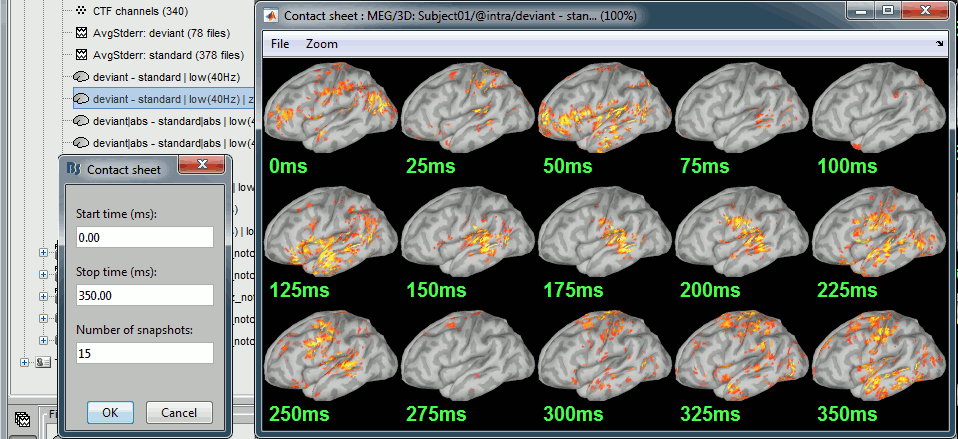
- We can see with much more contrast the areas and times where the two conditions are different, but we lose the ability to say which one is stronger. It is the measure we will use in most cases when computing statistical tests between conditions.
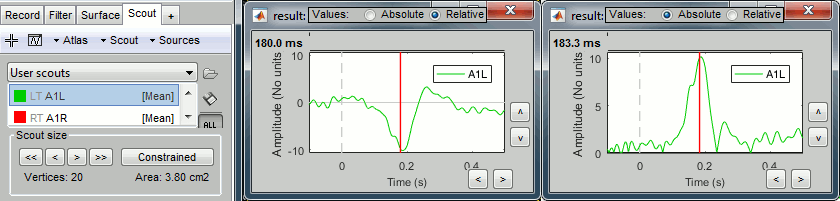
Plot the time series for scout A1L (relative values and absolute).
We observe the peak of difference where we were observing a zero with the absolute difference.
Difference of means
Another process can compute the average and the difference at the same time. We are going to compute the difference of all the trials from both runs at the sensor level. As discussed in the previous tutorials, this is usually not recommended because the subject might have moved between the runs. Averaging MEG recordings across runs is not accurate but can give a good first approximation, in order to make sure we are on the right tracks. It is acceptable here because the movements of the subjects are negligible between the two runs.
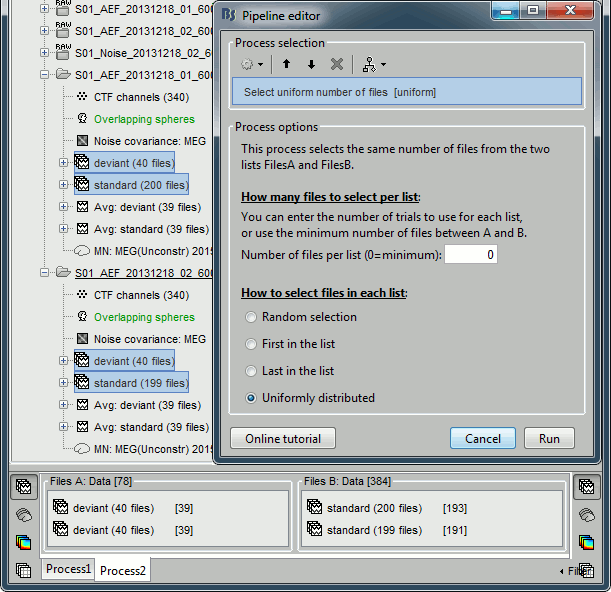
In Process2, select the following files:
Files A: all the deviant trials from both runs (~80 files)
Files B: all the standard trials from each run (~400 files).Select the process "File > Uniform number of files", with the default number of files and the option "Uniform". This will select the same number of files from FilesA and FilesB. The list with the larger number of files (FilesB) is sampled uniformly to get the same number of files on both sides.
This step is not necessary here, but it's a good time to illustrate it, in case you need it someday.
Add the process "Test > Difference of means", select the option "Arithmetic average".
The option "weighted average" has no importance because we are averaging only single trials.
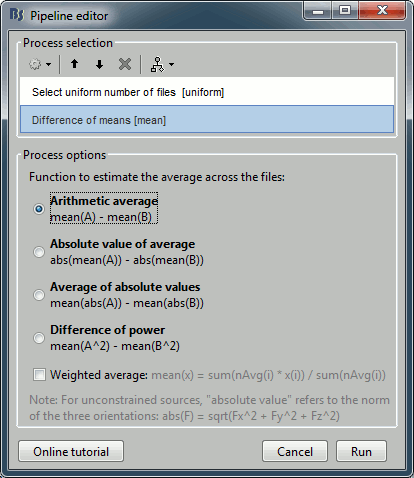
Run the pipeline. Double-click on the new difference to display it. The difference does not show anymore the early responses (P50, P100) which are similar for the two conditions, but emphasizes the difference in the later process (MMN/P200 and P300).
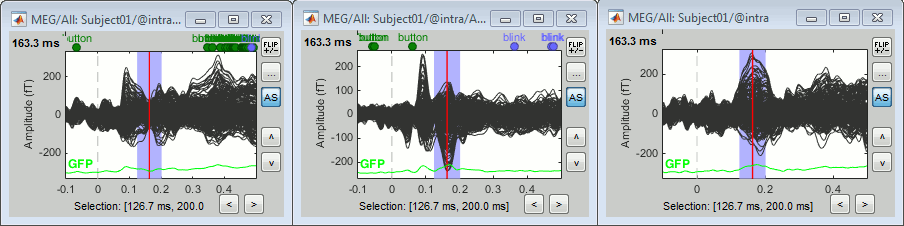
Left: Average of 80 deviant trials.
Center: Average of 80 standard trials.
Right: Difference of the two, computed in this process.
Time-frequency
In the case of time-frequency maps there is no sign ambiguity of the values, so computing a difference is slightly simpler. There are two possible cases: difference between power maps or between normalized maps (eg. ERS/ERD).
Original time-frequency maps
- The power of the TF maps are only positive values, so you can simply compute the difference between the power maps, it will give you all the interesting information.
- Use the difference of the power: power(TF(A)) - power(TF(B))
- This is what you would use for computing statistics within a subject.
Normalized time-frequency maps
- The values represent deviations with respect with a baseline, they can be positive or negative. Therefore we are in the same configuration as with the sensor data.
- Use the difference of the normalized values: Normalize(power(TF(A))) - Normalize(power(TF(B)))
- This could be used for comparing visually two averages, or for statistics across subjects.
