|
Size: 27858
Comment:
|
Size: 27452
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 47: | Line 47: |
| ==== Empty room recordings: 20s ==== | ==== Empty room recordings: 90s ==== |
| Line 51: | Line 51: |
| * From now one, all the pre-processing steps that re-write new continuous files (bandpass filter, sinusoid removal) applied to the resting state MEG recordings should be applied as well to the noise recordings. We will calculate the noise covariance from the noise recordings and then use them to whiten the resting state recordings to estimate the sources. For this operation to be valid, the two datasets must be processed exactly in the same way. The SSP are not a problem as they are applied dynamically to the noise covariance when estimating the sources. | * __Important note__: From now on, all the pre-processing steps that re-write new continuous files (bandpass filter, sinusoid removal) applied to the resting state MEG recordings should be applied as well to the noise recordings. We will calculate the noise covariance from the noise recordings and then use them to whiten the resting state recordings to estimate the sources. For this operation to be valid, the two datasets must be processed exactly in the same way. The SSP are not a problem as they are applied dynamically to the noise covariance when estimating the sources. |
| Line 59: | Line 59: |
| * Double-click on the "Link to raw file" to display the MEG recordings | * Double-click on the "Link to raw file" to display the resting state MEG recordings |
| Line 72: | Line 72: |
| PAC analysis involves examining a wide band of frequencies, often the entire range of 2-150Hz or more. This band contains the frequencies contaminated by line noise, of either 50 or 60Hz and their harmonics. Brainstorm offers tools to remove line noise from functional data and it is most of the time a recommended pre-processing step. However, here we will not run the "Sinusoid removal" process for time efficiency and because it is not required for accurate PAC analysis. The PAC function looks for high frequencies occuring specifically at certain phases of low signals such that the ubiquitous nature of line contamination effectively cancels it out for being identified as PAC. Similarly, running the sinusoid removal results in no 60Hz anywhere, such that the function also identifies no PAC. To demonstrate that we can safely proceed without cleaning for the power line contamination, consider the following PAC maps performed on the same time series with the only difference being line noise removal on one data set (raw data on the left, cleaned for 60Hz and 120Hz on the right). {{attachment:SinCheck.gif||height="168",width="390"}} |
* PAC analysis involves examining a wide band of frequencies, often the entire range of 2-150Hz or more. This band contains the frequencies contaminated by line noise, of either 50 or 60Hz and their harmonics. Brainstorm offers tools to remove line noise from functional data and it is most of the time a recommended pre-processing step. However, here we will not run the "Sinusoid removal" process for time efficiency and because it is not required for accurate PAC analysis. * The PAC function looks for high frequencies occuring specifically at certain phases of low signals such that the ubiquitous nature of line contamination effectively cancels it out for being identified as PAC. Similarly, running the sinusoid removal results in no 60Hz anywhere, such that the function also identifies no PAC. To demonstrate that we can safely proceed without cleaning for the power line contamination, consider the following PAC maps performed on the same time series with the only difference being line noise removal on one data set (raw data on the left, cleaned for 60Hz and 120Hz on the right).<<BR>><<BR>> {{attachment:SinCheck.gif||height="168",width="390"}} |
| Line 79: | Line 76: |
| We need now to calculate a source model for the resting state recordings, using a noise covariance matrix calculated from the noise recordings. |
|
| Line 80: | Line 79: |
| * Right-click on the subject node > Compute head model * Use the overlapping spheres model and keep all of the options at their default values. * SCREEN CAPTURE |
* Right-click on the recordings node ("spontaneous") > Compute head model<<BR>><<BR>> * Use the overlapping spheres model and keep all of the options at their default values.<<BR>><<BR>> * For more information: [[Tutorials/TutHeadModel|Head model tutorial]] |
| Line 85: | Line 86: |
| In the original zip download folder there is an empty room recording from when this data was collected. It is labelled XXXX(TO BE ADDED TO DOWNLOAD) * Right click on 'PACTutorialSubj1', click 'review raw file' and select this file. * Right click on the 'Link to raw file' of the noise recording, go to the 'noise covariance' submenu and click on 'compute from recordings'. * An option box will pop up, within which you should keep all the default values. Click okay to create the noise covariance matrix. This new file should now be available in the tree. Right click on the Noise covariance file and click 'copy to other conditions' to copy this file to all the other conditions where we need it. <<BR>> * Further information as well as the importance and relevance of noise covariance is described here: [[http://neuroimage.usc.edu/brainstorm/Tutorials/TutNoiseCov|Noise Covariance Tutorial]] * You should now have a condition with imported data, a head model and noise covariance that looks like this: {{attachment:importedDB.gif}} * Right click on the raw file again and click 'compute sources'. Use the Minimum norm estimate (wMNE) and keep all the default settings. |
* Right-click on the "Link to raw file" for the noise recordings > Noise covariance > Compute from recordings<<BR>><<BR>> * Leave all the default options and click [OK] * Right-click on the noise covariance file > Copy to other conditions<<BR>><<BR>> * For more information: [[Tutorials/TutNoiseCov|Noise covariance tutorial]] ==== Inverse model ==== * Right-click on the "Link to raw file" * * For more information: [[Tutorials/TutSourceEstimation|Source estimation tutorial]] == Phase amplitude coupling == |
| Line 100: | Line 99: |
| == Phase amplitude coupling == |
Resting state MEG recordings
[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]
Authors: Thomas Donoghue, Soheila Samiee, Elizabeth Bock, Esther Florin, Francois Tadel, Sylvain Baillet
This tutorial explains how to process continuous resting state MEG recordings. It is based on a eyes open resting recordings of one subject recorded at the Montreal Neurological Institute in 2012 with a CTF MEG 275 system. The segmentation of the T1 MRI of the subject was performed using FreeSurfer. This tutorial features a few pre-processing steps and the calculation of phase-amplitude coupling meaures.
Contents
License
This tutorial dataset (MEG and MRI data) remains a property of the MEG Lab, McConnell Brain Imaging Center, Montreal Neurological Institute, McGill University, Canada. Its use and transfer outside the Brainstorm tutorial, e.g. for research purposes, is prohibited without written consent from the MEG Lab.
If you reference this dataset in your publications, please aknowledge its authors (Elizabeth Bock, Esther Florin, Francois Tadel and Sylvain Baillet) and cite Brainstorm as indicated on the website. For questions, please contact us through the forum.
Download and installation
Requirements: You have already followed all the basic tutorials and you have a working copy of Brainstorm installed on your computer.
Go to the Download page of this website, and download the file: sample_resting.zip
Unzip it in a folder that is not in any of the Brainstorm folders (program or database folder).
- Start Brainstorm (Matlab scripts or stand-alone version)
Select the menu File > Create new protocol. Name it "TutorialResting" and select the options:
"No, use individual anatomy",
"No, use one channel file per condition".
Import the anatomy
- Switch to the "anatomy" view.
Right-click on the TutorialResting folder > New subject > Subject02
- Leave the default options you set for the protocol
Right-click on the subject node > Import anatomy folder:
Set the file format: "FreeSurfer folder"
Select the folder: sample_resting/anatomy
- Number of vertices of the cortex surface: 15000 (default value)
- Set the 6 required fiducial points (indicated in MRI coordinates):
- NAS: x=128, y=225, z=135
- LPA: x=54, y=115, z=107
- RPA: x=204, y=115, z=99
- AC: x=133, y=137, z=152
- PC: x=132, y=108, z=150
- IH: x=133, y=163, z=196 (anywhere on the midsagittal plane)
At the end of the process, make sure that the file "cortex_15000V" is selected (downsampled pial surface, that will be used for the source estimation). If it is not, double-click on it to select it as the default cortex surface.
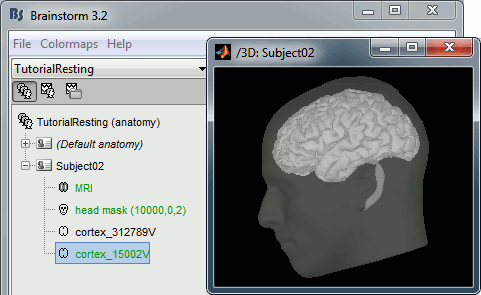
Access the recordings
Resting state recordings: 10min
- The sample_resting download contains two 10 minute resting state runs. We are going to use the first one (run 01).
- Switch to the "functional data" view, the middle button in the toolbar above the database explorer.
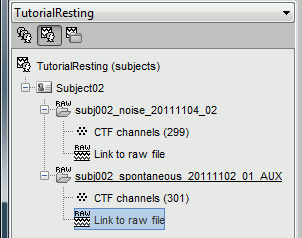
Right click on the Subject02 > Review raw file > Pick the file:
sample_resting/Data/subj002_spontaneous_20111102_01_AUX.dsRefine registration now? YES
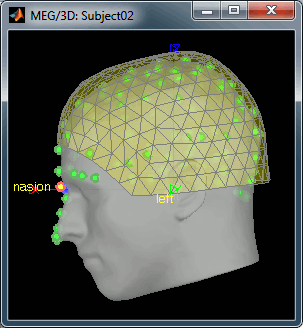
Empty room recordings: 90s
- We are also going to link to the database 20 seconds of empty room measurements that were acquired before the subject entered the MEG room. During the source estimation process, we will use this file to estimate the noise related with the MEG sensors.
Right click on the Subject02 > Review raw file > Pick the file:
sample_resting/Data/subj002_noise_20111104_02.dsIgnore the misplaced MEG helmet you see after the file is link to the database. Those are noise measurements, with no subject in the MEG, so there is no head position in this file. We are not going to use the sensor positions from this file.
Important note: From now on, all the pre-processing steps that re-write new continuous files (bandpass filter, sinusoid removal) applied to the resting state MEG recordings should be applied as well to the noise recordings. We will calculate the noise covariance from the noise recordings and then use them to whiten the resting state recordings to estimate the sources. For this operation to be valid, the two datasets must be processed exactly in the same way. The SSP are not a problem as they are applied dynamically to the noise covariance when estimating the sources.
Pre-processing
All data should be pre-processed and checked for artifacts prior to doing analyses such as PAC (including marking bad segments and correcting for artifacts). For the purposes of this tutorial, we will correct for blinks and heartbeats with SSPs but will not go through marking out bad sections. When using your own data reviewing the raw data for bad segments and using clean data is of the utmost importance.
Heartbeats and eye blinks
Signal Space Projection (SSP) is a method in for projecting away stereotyped artifacts (such as eye blinks and heartbeats) out of the recordings.
- Double-click on the "Link to raw file" to display the resting state MEG recordings
- From the SSP menu in the Record tab, run the automatic detection of the blinks and the heartbeats:
Detect eye blinks: select channel EEG058 (EOG channel), event name "blink"
Detect heartbeats: select channel EEG057 (ECG channel), event name "cardiac"
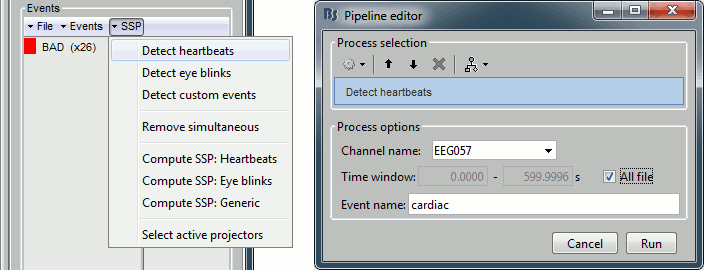
Review the MISC channels and make sure the events detected make sense.
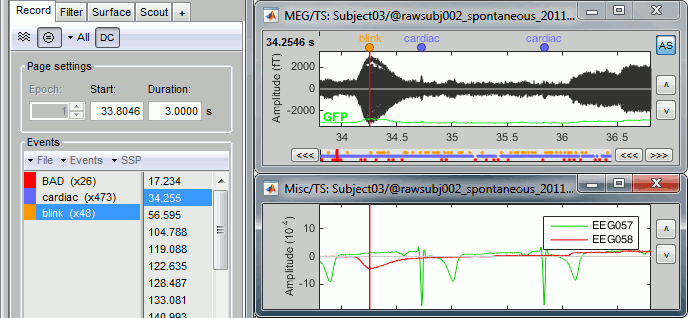
- From the same menu, run the following processes:
Compute SSP: Eyeblinks: Enter event name "blink", sensor types="MEG"
Compute SSP: Heartbeats: Enter event name "cardiac", sensor types="MEG"
The first component of each category should be selected automatically. Leave the default selection as it is but make sure that the corresponding topographies are really representative of blinks and heartbeats.
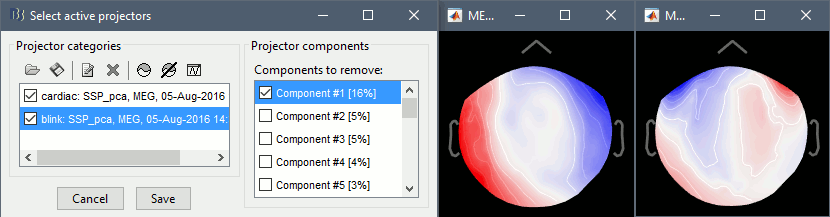
For more information regarding this SSP method, refer to this tutorial: ?Detect and remove artifacts
Power line contamination
- PAC analysis involves examining a wide band of frequencies, often the entire range of 2-150Hz or more. This band contains the frequencies contaminated by line noise, of either 50 or 60Hz and their harmonics. Brainstorm offers tools to remove line noise from functional data and it is most of the time a recommended pre-processing step. However, here we will not run the "Sinusoid removal" process for time efficiency and because it is not required for accurate PAC analysis.
The PAC function looks for high frequencies occuring specifically at certain phases of low signals such that the ubiquitous nature of line contamination effectively cancels it out for being identified as PAC. Similarly, running the sinusoid removal results in no 60Hz anywhere, such that the function also identifies no PAC. To demonstrate that we can safely proceed without cleaning for the power line contamination, consider the following PAC maps performed on the same time series with the only difference being line noise removal on one data set (raw data on the left, cleaned for 60Hz and 120Hz on the right).
![[ATTACH] [ATTACH]](/moin_static198/brainstorm1/img/attach.png)
Source estimation
We need now to calculate a source model for the resting state recordings, using a noise covariance matrix calculated from the noise recordings.
Head model
Right-click on the recordings node ("spontaneous") > Compute head model
Use the overlapping spheres model and keep all of the options at their default values.
For more information: ?Head model tutorial
Noise covariance
Right-click on the "Link to raw file" for the noise recordings > Noise covariance > Compute from recordings
- Leave all the default options and click [OK]
Right-click on the noise covariance file > Copy to other conditions
For more information: ?Noise covariance tutorial
Inverse model
- Right-click on the "Link to raw file"
For more information: ?Source estimation tutorial
Phase amplitude coupling
We are now ready to run the PAC analysis.
Step 2: Using the PAC Function - the Basics
Once you have the sources projected onto the anatomy proceed with the following instructions to use the PAC function on the source data.
This PAC function in Brainstorm is not time resolved, but will analyze any given time series for any stable occurence of PAC over any time segment you give it. This can be done at the sensor or source level for and EEG or MEG data. Here we will analyze the source data, by giving the function the time series of the vertices of our projected data.
The Function
- The function for Phase Amplitude Coupling analysis is found in the frequency menu in the process selection menu.
- Drag and drop the sources file (it should be labelled 'MN: MEG(Constr)') into the dropbox in the process 1 tab. Click on run, go to frequency and click on Phase Amplitude Coupling.
Process Options
Once you click on 'Phase-amplitude coupling' you should get an options box with the following options.
See PAC tutorial for details on those options.
We will first demonstrate the process by computed the PAC for a single vertice (a single time series in source space). This will allow us to examine what the PAC process does and visualize the result.
- In the PAC option box, if the options are not already filled out, fill in time window as the full length of the file (0 - 599.9996) and the frequency options as the wide bands of low: 2 - 30 and high: 40 - 150.
- We are going to arbitrarily compute PAC on source #224. (Vertices in the source data are labelled with numbers). Write '224' in the source indices option.
- Click on run.
- PAC files that are computed will be saved under the file containing the time series from which they were computed under the name 'MaxPAC'.It should look like this in brainstorm.
- Double click on the 'MaxPAC file to open the PAC map - the comodulogram. You should open an interactive graphical representation of the data which looks like this.
- We have this map available because we selected the 'Save Full PAC maps' and can therefore now visualize all the frequencies pairings and their PAC strenghs for each time series.
- The small white circle indicates the PAC pairing with the strongest coupling (the maxPAC pairing) and the results relevant to this pairing that are displayed on the top of the comodulogram.
- MaxPAC: the strength of the coupling
- flow: the low frequency (nesting)
- fhigh: the high frequency (nested)
- coupling phase: the phase of the flow at which the fhigh occurs
- You can click to any frequency pairing and the relevant results will be displayed at the bottom of the comodulogram.This allows you to explore the values represented in the comodulogram. Here I clicked on PAC at around at 9 Hz nesting. We can see that the coupling strength is similar to the coupling at the maxPAC flow of 11.47. This suggests there are two clusters of PAC in this time series, of almost equal occurence.
The full PAC comodulograms contain a lot of information, especially considering that we have this amount of information for every time series (each vertex) if we do this across all sources.
You need not save the full PAC maps when doing this analysis - the MaxPAC function offers the option to save only the values at the maxPAC - at the frequency pairing with the highest coupling strength. This examines the time series for the maximally coupled pairing and then saves only the results related to that value. It is no quicker to compute, but saves much smaller files.
To demonstrate this, we can re-run the same PAC analysis on the same time series, but unselect the 'Save full PAC maps' options. (You can do this if you wish, but if it is a long computation on your system you can look at the result below - it is simply another representation of the same data in the 'Full' file).
Using the maxPAC in this manner saves nothing that can be visualized, and double clicking on the resultant file simply opens the file contents, which contains the 4 values of interest computed by the maxPAC function.
If you are unfamiliar with these tables, it is the 'File Contents' table available for every file in the Brainstorm database by right clicking - file - view file contents. It contains the datapath and name of the actual file on the computer as well as some summary information of everything in the file.
Relevant MaxPAC information in File Contents
- TF: the top line in the table contains the coupling strength(s) of the maximally coupled frequency pairing (maxPAC pair)
- Options: the options struct contains all the parameters that were given to the process
- sPAC: this struct contains all the information related to the PAC function (other than coupling strength saved in TF)
- Nesting Freq: the low frequency at the maxPAC
- Nested Freq: the high frequency at the maxPAC
- PhasePAC: the phase at the maxPAC
- DirectPAC: this holds all the values for all the other pairings to represent the PAC comodulograms
- Empty when full maps are not saved
- Contains a very large matrix when maps are saved
- [Low Freqs]: contains the lowFreqs used
- [High Freqs]: containts the highFreqs used
This is a much more efficient way of saving and representing a small part of the data and pulling out the main mode of PAC in any time series. The caveat is (as we can see in the example map of vertex # 224) that pulling out only the strongest pair may not be particularly representative of the overall PAC in the time series. In this special case, where the difference in coupling strength between f-low of 11.47 and 8.30 is likely to be statistically insignificant it may be somewhat arbitrary which pair is picked.
The vertex used here is something of an anomaly in that most of the time there is a much more obvious single pairing apparent in the PAC maps. When doing PAC analysis you should consider the relevance and importance of finding only the maxPAC pair for your hypothesis and guide your analysis accordingly.
Step 3: Verifying with Canolty Maps
Canolty maps are a type of Time Frequency decomposition that offer another way to visualize the data and serve as a complimentary tool to visualize and assess Phase-Amplitude Coupling. Currently there are no significance tests within Brainstorm that can give a measure if PAC is significant in a given time series, but the Canolty maps provide an important way to verify and corroborate the results of the PAC process.
Canolty maps are a kind of time frequency decomposition in which the zero point of the map is aligned up to the trough of a low frequency of interest. The process lines up the data to a specific low frequency so as to visualize what happens in the power spectrum related to the phase of the low frequency. Specifically, it filters the data to extract the low frequency of interest, marks each trough as an 'event', extracts a time window around each 'event' and averages over all of them. The colormap of the Canolty map represents power in relation to the mean power. By representing a time frequency map in relation to a low frequency, we can visualize whether the power of any high frequencies fluctuates systematically with the phase of the low frequency (basically - we can visualize PAC). If there is PAC present, we should see quite stereotyped stripes of the power of certain high frequencies changing consistently with the phase of the low frequency. If there is no PAC there will be no discernable pattern (the map will just look like a 'mess').
Canolty maps are named after the author of the paper in which they were published, entitled 'High gamma power is phase-locked to theta oscillations in human neocortex' by Canolty & Knight which appeared in Science in 2006.
The Function
The Canolty Map's function is also found in the Frequency tab from the process functions.
There are two ways to use Canolty maps - you can manually input a low frequency of interest or you can give it the maxPAC file and it will take the low frequency at the maxPAC value.
- Process 1 tab - Drop a file of time series into the process one tab and manually select the low-frequency of interest.
- Process 2 tab - Drop a file of time series into File A and the corresponding maxPAC file into File B. This process will make the Canolty maps by finding (for each time series) the low frequency defined in the maxPAC file and use that to create the Canolty map.
We will continue by doing the Process2 version to compliment our maxPAC results.
- Click on the Process2 tab. In the FileA box drop the original time series (the source data file). In the FileB box drop the maxPAC file that we just created for source 224.
- When in the Process2 format, clicking on run will only show the processes available. Canolty maps is still under the frequency tab, but the drop down menu will look a bit different.
When you click on the Canolty Maps (process2) function you should get a an options box like this.
Process Options
Time Window: the time segment from the input file to be used to compute the Canolty map.
Epoch Time: The length of the epochs used.
Source Indices: which time series from the given file to compute the Canolty maps for.
Number of signals to process at once: This process is also done in blocks and this option allows for setting the block size (can be left at the default value).
Save averaged low frequency signals: In order to create the Canolty maps, Brainstorm filters the input time series at the low frequency of interest. This option saves that filtered signal, which can be useful for visualization.
The only difference in the Process1 version of Canolty Maps is the additional required field of Nesting Frequency. In this case you can enter in any low frequency of interest with which to compute the Canolty Map(s).
- Click run and the option box for the Canolty process will pop up. In the case where the given maxPAC file does not include PAC values for all the time series in FileA (such as now, since the maxPAC only contains the PAC values for vertex #224 in FileA) Brainstorm does not automatically determine which time series it has PAC information for and this information has to be given.
- In the 'Source Indices' option write '224' so that it will use the maxPAC for this vertice and compute the Canolty map.
- Canolty maps are saved under the time series file from which they come - similar to the maxPAC. However, if the lowFreq signal is saved the link to this file is saved below. In Brainstorm your database should look something like this.
- Double click on the 'Canolty map' file to open it. You should see the following image. At the top the image the vertice number and low freq are written.
- Here we can see that the Canolty map corroborates what was represented in the maxPAC file. With the data plotted controlling the phase of the low freq (here - 11.47Hz) we can see that the amplitude of the gamma (indicated by the colour) is patterned such that it appears to related to the phase of the low frequency, and as such is phase-amplitude coupling.
- We can also see if the frequencies of the high (nested) frequencies are similar between functions. Similar to our PAC comodulogram, we can see in the Canolty map that the nested frequency is predominantly around 80 Hz, but that we see (less) PAC occuring at other frequencies, such as around 120Hz.
- In the Canolty map itself there is no representation of the low frequency used. It can be useful to visualize the low frequency. The low frequency is accessble through the other link in the brainstorm database. Double click on the file named 'Canolty ERP'. This will open the time series filtered at the low frequency of interest that was used to compute the canolty map.
- It is common for the low frequency to look like this where it appears to fade away further from the 0 point. This is because of some jitter in the signal, and that the low frequency may not be exactly 11.47 Hz, so a filter centered at zero extracts less of signal further away.
- By arranging the Canolty map and Low Frequency file you can get a sense of how the low frequency oscillation and high frequency amplitude relate to each. The time selection on the two is synchronized, so try clicking at particular parts of the low frequency file and examining the power in the Canolty map. You should notice gamma amplitude is low at the peak and trough of the low frequency oscillation and high between them.
- There are other more quantitative ways of verifying the phase of the coupling (such as by using the phase value extracted by the maxPAC function). Canolty maps can be used for visualization purposes, and as converging evidence of the coupling.
You may remember that in the PAC comodulogram for vertice 224 the maxPAC value was at 11.47 Hz but that there was also other areas of high PAC, including an almost equal coupling intensity at 8.3 Hz. Canolty maps only portray information relevant to the low frequency used to create the map - therefore we cannot make any conclusions about PAC at low Freq = 8.3 with the Canolty map we have made with low Freq = 11.47 Hz.
We will now examinethe PAC at lowFreq = 8.3 with a new Canolty map using the Process1 version. Since 8.3 Hz is not the low frequency at the maxPAC pairing in the maxPAC pair we cannot examine this by giving the maxPAC file, we must manually specify it as a low frequency of interest.
- Click on the Process1 tab and drop the source time series.
- Press run, go to frequency and click on the Canolty maps process
- We need to specify the vertice of interest (224) and the low frequency of interest (8.3 Hz). Fill out the option box as follows:
- Press run
- Open the resultant file and you should see the following Canolty map
- Again, we can see that when filtered based on the low frequency of 8.3 Hz the high frequency amplitude changes in a consistent manner in relation to the phase of the low frequency, supporting that there is indeed PAC at a low-freq of 8.3 Hz.
We can also visualize the relation by using the low frequency filtered signal that we saved again.
An alternative use of Canolty maps is to verify that in the case where the PAC function indicates very low levels of Phase-amplitude coupling, that the Canolty map function also corroborates this.
Open the PAC map for vertice #224. Now we want to find a lowFreq where the PAC function did not indicate much coupling.
- Take the lowFreq of 3.57.
- Now use the lowFreq value of 3.57 to create a Canolty map, in the exact same way we did with the low Freq of 8.30, changing only this value in the parameters.
- You should get a Canolty map that looks like this
- Here we can see that the Canolty map displays nothing that looks like consistent coupling between the low frequency of 3.57 Hz and any high frequencies. This is what we expected based on the PAC comodulogram.
You should notice that the Process1 version of canolty maps can be done on any time series without ever doing the exhaustive PAC process. However, since Canolty maps only use one low frequency of interest, this is not a very efficient approach (unless you have a specific frequency of interest, such as in a frequency tagging paradigm).
Step 4: 'Advanced' PAC analysis
By now you should have a pretty good idea of how to use the PAC process, what it gives out and how to check these results with the complementary Canolty maps process. The 'advanced' aspect is not a question of increased difficulty but simply of increased scale. We have been working with a single time series here. It is likely that PAC analysis you perform will want to look at much larger sets of data.
This basically comes down to filling in the 'Source indices' option for the PAC process. Option for this:
- Empty: will perform PAC analysis on all the time series in the file (all sensors or all sources)
- Specify a subset - you can specific single time series or subsets
- Recall that Brainstorm will evaluate what you write in 'Source indices'. This means you can write a single vertex (ex - '224') or a list (ex - '224, 225') and/or something to be evaluated by matlab before being handed to the PAC function (ex. '224:230')
PAC analysis is a very computationally demanding process. Options for reducing computation time include:
- Downsample data
- You can downsample temporally (downsample to a lower sampling rate) or spatially (downsample anatomy to a smaller number of vertices)
- Use shorter time segments
- Use ROIs or scouts to use a smaller number of time series
When you run a file with multiple time series and open it (with full PAC maps) it will open the map of the first time series, in the same way as if you only had one. In the Brainstorm window there is a 'Selected data' option to go to any time series of interest. You can also scroll through the maps using the up and down arrows on the keyboard.
The same things all apply for using the Canolty process.
Experiment as you want using the PAC function with inputs of multiple time series.
Feedback
