Tutorial 22: Source estimation
[CODE]
Note by John 2018/02/16, after many discussions by phone and emails among Sylvain, Richard, Matti, Francois, and myself, the tentative decision is to release the modifications of the bst_inverse_linear_2016 as an updated code called "2018"; I'll leave it to Francois if this should be a new "bst_inverse_linear_2018" code, or simply change the Source Estimation panel to say "2018" using the older name.
The two primary differences between 2016 and 2018 are that (1) 2018 now supports the mixed head model, such that "deep brain analysis" can run with 2018.
(2) The other change to 2016 is an internal change in how noise is regularized. Matti Hamalainen (MNE-Python) and Rey (bst_wmne, our old Source Estimation) both chose the regularizer to be a fraction of the average of each sensor's variance (trace of the noise covariance divided by the number of sensors), which is the same as the average of the eigenvalues. So "0.1" as an input parameter in the "regularization" panel was calculated as 10% of the average variance. I used a different matrix norm, the maximum eigenvalue. Thus the same "0.1" would be 10% of the maximum eigenvalue, and given the large dynamic range of MEG sensors, this is a substantial difference in regularizers between the codes. Thus user's using the same fraction in both methods saw disparate results. We made the decision to change the "reg" option to be nearly the same as Rey's code, to lessen confusion among users switching between codes and platforms. We need to also strengthen the general discussion on the importance of noise regularization.
The new 2018 is "nearly" the same as Rey/Matti, because there is still an open debate on what to do with the cross-correlation terms between modalities. Matti is double checking his codes, but Rey's interpretation/implementation in 2011 was that the cross terms between, say, EEG and MEG, were zero'd out. In Source 2018, I continue this philosophy by doing the same between GRADS and MAGS, which apparently Rey/Matti do keep the cross terms. After conceptual discussions with Richard, we decided to be conservative and zero out the cross terms between all modalities. I have coded 2018 to make this an easily adjustable flag that can be later tested and distributed, if we desire.
Two other fixes in 2018 were made related to the above. (1) 2016 was not regularizing correctly across multiple modalities, by trying to find a single regularizer to the overall matrix. Thus multiple modalities did not work well, since one modality tended to dominate the eigenspectrum and the other modalities were ignored. Each modalitiey is now separately regularized by all of the regularization methods (GRADS and MAGS as well), then recombined back into an overall noise covariance matrix for joint estimation. The open question, discussed above, is whether or not to put the cross terms back between modalities back into this matrix, and we have turned that OFF for now (Feb 2018).
(2) Once the regularizer value "lambda" was selected, I had a bug in that I formed sqrt(eigenvalue)+sqrt(lambda), rather than the correct sqrt(eigenvalue + lambda).
So that users understand that they are running a new version of source estimation that may yield different results from earlier, we decided that it would be better to call this "Source Estimation 2018", rather than e.g. 2016 (fixed).
So the below comments that say "fixed in 2018" reference the above discussion.
John: Drop the option "RMS source amplitude"? As time permits, okay, can be dropped. I discussed this with Richard and Matti. We currently regularize based on an SNR ratio, that's frankly pulled out of the air, e.g. "3". There is another way, based on the physiologic concept of the expected signal strength, such as the "Okada constant" (1 nA-m/mm max possible). But Matti agrees this remains untested. Richard wonders if it's okay to just leave it dormant in the code. Francois would like to clean up the interfaces and codes. So basically, Francois, you're free to remove it for now, we'll return to this alternative in later years, maybe from a different viewpoint.
- The option is not even accessible in the interface: you successively asked me to disable it for the min norm, and then made me hide the entire section "Regularization parameter" for the dipole modelling and the beamformer.
- Can I just remove it from the interface?
- Francois: Update code, tutorials and screen captures accordingly
John, Richard, Sylvain, Matti, Alex: Make the "median eigenvalue" option the default?
Addressed somewhat by 2018 code, but this is still a professional opinion. MEG data in thinly shielded rooms have an enormous dynamic range. Simply taking 10% of the trace average or even 1% of the matrix norm is inadequate to capture properly the truly smaller yet valid eigenvalues. We want regularization to fix deficiently small eigenvalue deep in the tail, but the "reg" option is too crude. In conversation with Matti, for example, he doesn't even use this option with his data, because his mammoth shielded room is that good. So I see no problem in writing that I (Mosher) recommend median eigenvalue, while the code and the user want to try something else.
- John suggests to use the "median eigenvalue" option by default instead of the option "Regularize noise covariance", which as been used for many years.
In this section of the tutorials, John wrote: "Recommended option: This author (Mosher) votes for the median eigenvalue as being generally effective. The other options are useful for comparing with other software packages that generally employ similar regularization methods."
- However this modifies a lot the results: the localization results and the MN amplitudes can be very different. If this is a clear improvement, it's good to promote it. But it cannot be done randomly like this, this has to be discussed (especially with Matti and Alex) and tested.
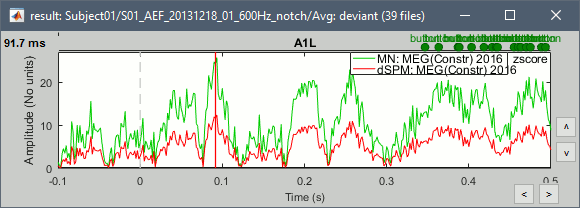
John, Richard, Sylvain: Why are dSPM values 2x lower than Z-score ?
Feb 2018: This remains a bit of a mystery. In separate conversations, Mosher, Hamalainen, and Leahy each think in principle there should be no difference; however, they also acknowledge that the difference may lie in how the cross covariance vs auto-covariance is utilized in either or both. As discussed above, in wide dynamic range such as MEG, there is an enormous difference between using the diagonal values of the noise covariance matrix vs. the full cross-covariance, so does the problem lay here, where one or the other method is not fully exploiting the cross terms? We need a good representative test case to explore.
- The tutorial says "Z-normalized current density maps are also easy to interpret. They represent explicitly a "deviation from experimental baseline" as defined by the user. In contrast, dSPM indicates the deviation from the data that was used to define the noise covariance used in computing the min norm map. "
Therefore should we expect the dSPM values to deviate more from the noise recordings, than the Z-score from the pre-stim baseline? Instead of this we observe much lower values. Is there a scaling issue here?
[ONLINE DOC]
John: Fix all the missing links Feb 2018, working. These were actually Richard's links, so I'm reverse engineering what he was thinking about crosslinking to.
John: Data covariance:
. Feb 2018: I (John) recommend you (Francois) just leave the defaults alone for now. We are working on a new set of papers addressing the beamformers. As Richard has also learned, there is a lot of confusion on how much and what you actually feed a so-called beamformer.
Recommendations moved to the Noise and data covariance tutorial.
- You said: "Our recommendation for evoked responses is to use a window that spans prestim through the end of the response of interest, with a minimum of 500ms total duration. "
- Should I modify the interface (and screen capture of the example) to always include the pre-stim baseline (eg. from -100ms to +500ms, instead of from 0ms to +500ms) ?
Francois: Update the screen capture + code for default selection of the time window
Tutorial: Dipole scanning
John: Unfinished sentence in this section.
Tutorial EEG/Epilepsy
John: Why sLORETA? Feb 2018: sLORETA is a favorite among some of the epilepsy community, particularly Europeans. When processing spikes as single sources, we (Hamalainen and I) do not expect much practical difference between the dSPM and sLORETA. No reason to poke that bear.
