Qualitative comparison of MEG/EEG forward models
[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]
Authors: Takfarinas Medani, Francois Tadel
Contents
Introduction
In this tutorial, we review and compare the forward model computation methods available in Brainstorm.
We apply these methods in a spherical head model and in realistic models, in order to compare the diferent forward solutions in the different scenarios. Our intention is to provide with easy to follow examples so that the reader develops an intuitive interpretation of the properties of different head models.
This is, therefore, a qualitative comparison and not an advanced study. You can find at the end of this page a list of references that investigate deeply and perhaps more rigorously the differents forward models.
At this time, the FEM implementation is available for the EEG and the MEG computation. We will integrate and test soon the FEM for sEEG and ECOG.
Data for the spherical head model
In this part we used the spherical head model distributed by the DUNEeuro team (sphere).
You can directly import and load the following Brainstorm protocol, which already includes previous spherical head model. This protocol can be found here. You need to unzip the files and then load the data as a new protocol.
EEG within a spherical model
The volume conductor or the head model:
The following figure shows on the left the surface model and on right the tetrahedral mesh.
The model has three layers, the brain (inner skull), the outer skull and the scalp.
The source space
For the source space or dipole position, we will use a realistic cortex distributed with the ICBM default subject of brainstorm.
The sensor model
Regarding the electrode's positions, we use the same position defined in this file. The total number of electrodes is 200 regularly distributed on the outer layer.
The forward model
Now, we have all the components of the model, we can start the process to compute the head model. For the EEG, brainstorm offers three methods. We perform these three computations on this model.
3-shell sphere: best-fitting sphere based on the scalp, then OK.
OpenMeeg BEM: use the conductivity 0.33, 0.004 and 0.33, and keep the default options.
DUNEuro FEM: use the default option with the same conductivity value as the previous method.
Qualitative comparison of the methods
In this tutorial, we use the display of the lead field vector to compare visually the performances of the three methods.
Right-click on the head model, and then select 'View lead field vector'. You can select more than the head model in order to overlay the vectors.
In this figure, we show all of these methods and zoom to focus on the vectors.
We can easily see that the three vectors are pointing in the same direction and have the same length.
For more documentations about these lead field vectors, please refer to these pages : (page1, page2)
The computation time
Regarding the computation time:
- 3-shell sphere: less than 30 seconds.
OpenMeeg BEM: ~ 12 minutes.
- DUNEuro FEM: ~ 2 minutes.
Note that the computation time for the FEM and the BEM depends also on the mesh resolution.
This example has 15000 dipoles (x3) and 200 electrodes.
For obtaining a realistic head model, we recommend using either OpenMeeg or DUNEuro. If you have already calculated a 3D mesh descriginb your head model, DUNEuro is faster than OpenMEEG. However OpenMEEG deals with surfaces, which generally speaking are easier to generate.
Duneuro can be used for a more realistic model (more than 3 layers with the complex shape), and can also deal with anisotropic conductivities.
You can generate the FEM mesh if you have the surfaces or the MRI (preferably T1 and T2), this process is explained in this tutorial.
EEG within brainstorm template (3 layers)
In this example, we will present the process of FEM mesh generation from the surface model then highlight the effect of the mesh resolution.
The head model
We will use the default subject, then right-click and generate FEM mesh, and follow the same steps as explained in this section.
We repeated this process four times, and hen we generate four FEM head models with four different values of the 'Max tetrahedral volume'.
Here is a view of the obtained mesh with MaxVol = 10, 1, 0.1 and 0.01 (clockwise order).
Let's give the name V10, V1, V01, and V001 respectively for these head models.
MaxVol: is the maximum volume of the tetrahedral, in this example, we use the CTF coordinate system, therefore MaxVol here is a volume with units of cm3.
The FEM generation time is quite fast, it varies from 15 secondes (V10) to less than 2 minutes (V001).
The source and sensor space
We use a protocol with EEG data, you can reproduce with any protocol with available channels position and EEG recording, this is not important in this tutorial.
For the source space, we use the default cortex with 15000 dipoles. The number of channels is 31, regularly distributed on the scalp surface, the model is shown on this figure.
The forward model & lead field visualisation
Switch to the "functional data" view, right click on the subject => Compute Head model => Duneuro FEM ==> keep the defaults parameters and set the conductivity to 0.33, 0.04 and 0.33.
Repeat the same process for four head models.
The computation time in these models is not expensive, it varies from 1 minute (V10) to 6 minutes(V001).
As in the previous example, we will display the lead field vectors for these head models.
With the FEM, it's known that increasing the mesh increases the accuracy of the solution. Therefore we will use the V001 as a reference solution and we compare the other model to this reference.
From visual checking and for different electrodes configurations(tap H for more help on the figure), we observe that there is less of difference between the V001 and V01. Also, we noticed differences in the model V1 and higher difference in the model V10 (coarse mesh). These basics observations are expected regarding the quality of the mesh.
source estimation
In this section, we perform a source estimation using the previous four head models.
Right-click on the head model ==> compute source [2018] and keep all the parameters as they are.
We repeat the process for the four head models and then we display the results on the cortex. We select a time point to highlight cortical activation.
The name of each figure is displayed on the title bare. We notice that the V01 and V001 have the same range on the scaling (0-300), whereas the V1 and V10 are lower (0-200). V001 and V01 give almost the same regions and are more focal than V1 and V10.
From these observations, we recommend using MaxVol = 0.1 and we set is as the default value for mesh resolution within brainstorm.
Comparaison between the different forward methods
In this section, we compute the forward model using the three available methods (3-shell, OpenMeeg, and DUNEuro). For these three methods, we use the same head model, with the same source and sensor space (as shown in the previous sections). For the Duneuro FEM, we select the head model V01 (the default value for the mesh generation).
Lead field visualisation
the BEM, FEM forward computation in basic model (realistic head model 3 layer) and also within a spherical head model with an analytical solution.
When the forward computation is completed with the three methods, we can display the lead vector.
We can see that the LF arrows of Duneuro and 3-shell are pointing in the same direction. Whereas, for OpenMeeg, there are some outliers (big blue arrows) pointing on wrongs and random directions.
When we check closely the values of the OpenMeeg LF, we notice that the vectors are pointing in the correct direction in most of the source points. The outliers have big value and could not be displayed on the same scale (we are working on that).
These points are some dipoles that are to close to the interface. The OpenMeeg BEM solution is not accurate in these positions. In the literature, similar problems are observed even with the FEM, however, this kind of instability is investigated and Duneuro offers many source models to avoid/minimize these errors.
source estimation
Following the same logic as in the previous section, we perform source localization using the three head model described below.
We select the Minimum norm and we keep the default parameters.
We do the same process, but with sLoreta option :
In this, basic example, we show that all the methods point to the same area with more or less precision.
As said, in this tutorial the objectify is to present how to use these tools.
MEG within a spherical model
In this part of the tutorial, we describe similar approach for the MEG. We will use the data of the PhantomCTF, we recommend you to read the PhantomCTF tutorial for better understanding of this section.
The volume conductor and the source space:
With a similar approach as explained in the introduction tutorial, we can generate the BEM surfaces from the MRI of the phantom. Right-click on the subject ==> Generate BEM surfaces.
This process will generate three surfaces, the inner skull, outer skull, and scalp. We will use these surfaces for the OpenMeeg BEM computation. When these surfaces are available, we can generate the FEM mesh as explained in the previous section. Right-click on the subject, then Generate FEM Mesh, Iso2mesh, MergeMesh and then keep the default options. The following figure shows the BEM and the FEM head model.
From the ICBM head model, we import the cortex and then align it within the phantom as shown in the figure.
The sensor model
We use a similar configuration as explained on the CTF phantom tutorial. The following figure shows the model of the sensor and the head model.
The forward model
For the MEG, brainstorm has four methods.
single sphere: fitting sphere on the cortex, 20 secondes
Overlapping spheres: 30 secondes
OpenMeeg BEM: use only the inner tissue, ~10 minutes,
DUNEuro FEM: use only the inner mesh, ~ 15 min
We use these four methods in this section.
lead field visualisation
We use a similar process to display the lead field vectors.
These figures show the LF arrows, we can easily check the similarity on the different methods.
Brainstorm recommend the use of the Overlapping spheres since it's fast and its shown that the MEG is less affected by the head geometry and the jump on the conductivity.
In this section, we showed the methods available on the brainstorm.
source estimation
For each head model, we estimate the source activation of the cortex. The following figure shows the results.
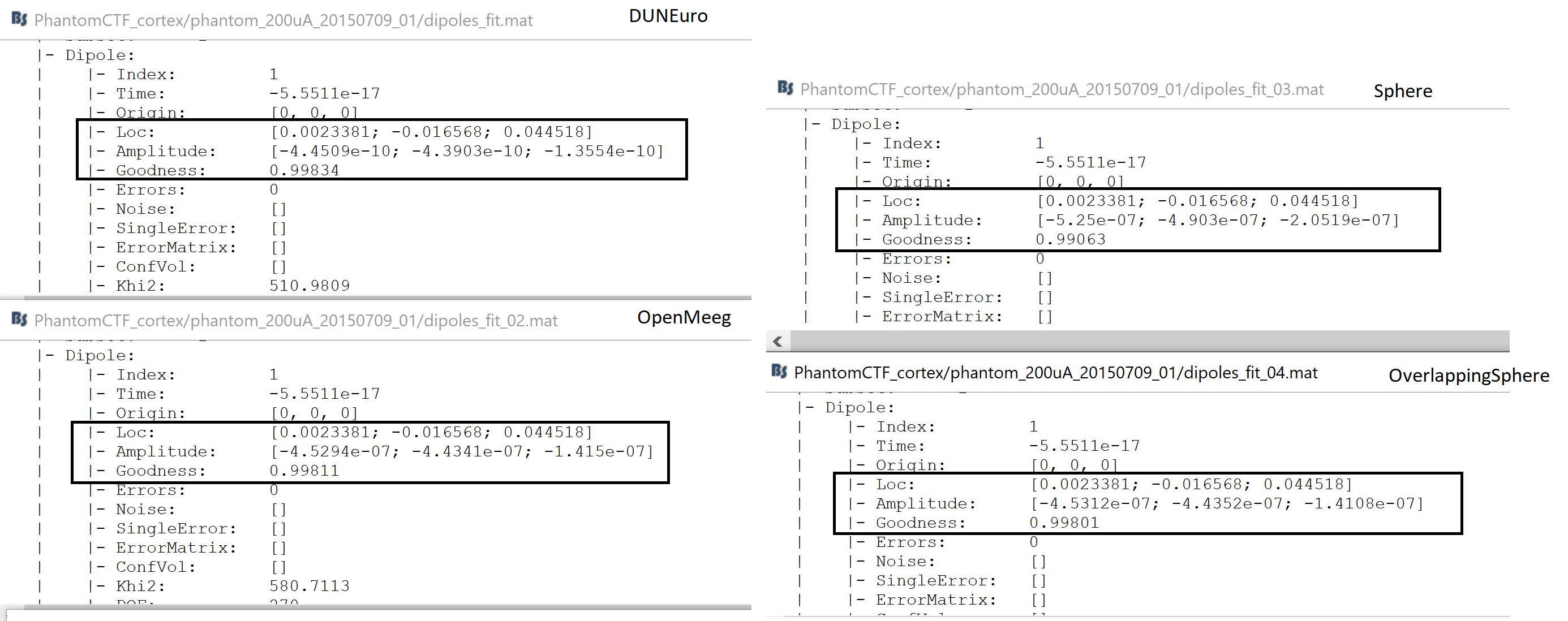
Dipole scan
The following image shows the main results, localization, and orientation, of the fitted dipole.
Note
Check the unit of the MEG ... a factor 1000 is noticed on the final results ... possible solution: either x 1000 the kernel, or /1000 the gain or simply check the input units of the Duneuro.
Application on the introduction tutorial
In this section, we apply the Duneuro computation for the dataset sample of the brainstorm tutorial.
Head model & Forward model
Follow the steps explained on theFEM tutorial the follows the same step to use the Duneuro model to compute the source as explained in this tutorial.
Here is a view of the lead vectors for the two models.
Comparaison of the source localisation
We compute the source using the MN with a constrained source. In this figure, we show the obtained results
These figures show similare activated regions (Gduneuro/100 > computeSource).
Advantages of the FEM
In similar cases, it has shown that the FEM has similar accuracy as the BEM and could be faster {ref: M.Clerc }.
The FEM can be used with a more realistic head model with more than three layers (up to 6 layers). FEM can also include tissue anisotropy.
Ansiotropy model
Head, sensor and source models
In this section, we use the spherical head model, the duneuro model. In order to use the analytical formulation for anisotropy solution, we centered the model. We have also generated a pseudo source space with a shape of the sphere within the inner layer. As electrodes, we have used 200 points regularly distributed on the outer surface.
Anisotropic model Analytical solution VS duneuro solution
In this example, or test, we use the analytical solution (Zhang et al) to compute the solution for a spherical head model where the inner layer is anisotropic. The anisotropy is defined by a different conductivity between the radial and the tangential direction. We use a ratio = radial/tangential. When the ratio is set to 1, in this case, the model is isotropic.
Check the three standard solutions
First, we check the standard solution
Here we see that the three methods have similar results.
Check the analytical solution iso vs aniso ratio 1
then we check the analytical solution of the anisotropy case where we set a ratio to 1
From this figure, we see this when the ratio is set to 1, both implementations, isotropic and anisotropic, lead to the same results.
Check the duneuro iso vs aniso ratio 1
Now we check the duneuro computation using different implementation. The first uses the isotropic model where the conductivity values are specified in the con file as scalar and the mesh is passed with the mesh file. The second uses the anisotropic implementation where the conductivity values are defined in the knw file. In which each mesh element has its own tensor (explain what is a tensor ?). and the mesh is defined in the geo file.
In order to compute the tensor, a new option is added to brainstorm where a tensor is computed on each element and scaled to radial and tangential conductivity. refers to this page for more information.
In the case of the sphere, a simulated tensor is computed, where the ratio and the iso conductivity are known.
Once the tensor is computed we can perform the FEM computation.
Check the the analytical and duneuro
Here is a view for the 4 solutions, analytical with the two versions and the dueneuro with its two versions
From these previous results, it seems that either the analytical implementations and the duneuro implementation yields similar results.
A slight difference appears between the duneuro and the analytical solution is probably due to the mesh resolution and of course, there is always a slight difference between the numerical solution and the analytical reference.
Duneuro vs Analytical solution with ratio > 1
For this example, we have selected a ratio = 5.
Here is a view of the tensors
and here is the result
Here we see that all the vectors are pointing in the same direction for both methods.
We can also see that there is a slight difference between the two solutions, which is similar to what we have seen before. This difference is due to the mesh resolution and natural numerical errors.
Results with volume source space
Check the analytical solution iso vs aniso ratio 1
==== Check the the analytical and duneuro anistropic case====
check here for more information :
https://github.com/brainstorm-tools/brainstorm3/issues/267
===============
