|
Size: 64442
Comment:
|
Size: 15659
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 27: | Line 27: |
| - [[https://simnibs.github.io/simnibs/build/html/index.html|SimNibs]]: this option -recommended for obtaining a realistic model- calls the [[https://simnibs.github.io/simnibs/build/html/documentation/command_line/headreco.html|headreco]] process from SimNIBS toolbox (see the [[https://neuroimage.usc.edu/brainstorm/Tutorials/FemMesh#Additional_Documentation|Additional Documentation]]). It uses the available MRIs for the subject, and then calls SPM and [[http://www.neuro.uni-jena.de/cat/|CAT]] for the segmentation. Finally, the mesh is generated internally by integrated tools (netgen, gmesh and meshfixe). - [[http://www.fieldtriptoolbox.org/|Fieldtrip]]: this option calls FieldTrip's volume segmentation pipeline, based on the segmentation of the MRI then the hexahedral mesh generation. |
- [[https://simnibs.github.io/simnibs/build/html/index.html|SimNibs]]: this option -recommended for obtaining a realistic model- calls the [[https://simnibs.github.io/simnibs/build/html/documentation/command_line/headreco.html|headreco]] process from SimNIBS toolbox (see the [[https://neuroimage.usc.edu/brainstorm/Tutorials/FemMesh#Additional_Documentation|Additional Documentation]]). It uses the available MRIs for the subject, and then calls SPM and [[http://www.neuro.uni-jena.de/cat/|CAT]] for the segmentation. Then the mesh generation is performed internally by integrated tools (netgen, gmesh and meshfixe). - [[http://www.fieldtriptoolbox.org/|Fieldtrip]]: this option calls the volume segmentation function from FieldTrip's pipeline. It generates an hexahedral mesh. |
| Line 33: | Line 33: |
| {{data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAbQAAAHoCAYAAAAheBrKAAAgAElEQVR4Aey9abBtR3kleP90dHSEbcKAp2gDdtlRpkB2YyQdKdAsC3ABjQYQlAbQUWMGWwF22YWppqtM2S6dcskGBBbiPQahAQHx3mVsITS1nibAoHcfqCTLgA02VT/KWKCL3ZMb48qOL3OvzLW/nXs6w73n7P29iPv2kJnflCtzZeY+O/fWoUOHnP1ZDAwDhoF5MXDFFVe4m266yR08eND3JXLOf5dddpl797vfnU3jfDgXOTjvcnz95Ze7yyt/r3e/f+DGXnK66Fo0zzve8Q6n/xaVaeUT3rYExPbPImARsAhYBCwCmxwBIXYjtE2uQbPdImARsAhYBHwErr32WiM0w4JFwCJgEbAIbH4Errv+eiO0za9G88AiYBGwCFgEbIZmGLAIWAQsAhaBQUTAnqENohrNCYuARcAiYBEwQjMMWAQsAhYBi8AgImCENohqNCcsAhYBi4BFwAjNMGARsAhYBCwCg4iAEdogqtGcsAhYBCwCmxcB2RHmscceqzVc0iRP1389CO0b7q6DB71wUSB/h4897pyr3r/rG6K+uB8uKvY8fuywO3jwsPMiKqmruCH27KW+VfjgnHv8mDu89n4sK9bLkrOiujCxFgGLwEIREMJ67/velyW1prQ6pT0JLUcIdZ1OuH/4cF0ZIcVcWp2pi96vs3NRuasuvwl2axv19bwxWpacefVbOYuARWDVEcgRV+5eFztWTmh33XW4mMmROd+4yx286649njFtaue4CXZrG/U11X2v02XJ6aXUMlsELAJ7HAEmMD7va8bKCe3Y49Ip3eX8KqS37nF3zM/a6jqr4v43ZGktLG3KqmVYouSlzsJVvwQX7h+MekQH7h10aQn0sDtGcsOSaSZkJPPwsWNl4qW0pK+w+dhdcUm2JLuhjBA+5HzjrmTzQW+0yM3do5ltSTZ8FZ9abIpuLxrvBhvrYl1rM5ZUg8+V2Eeb7cQiYBEYWgRAZHVLkF387Ulo1LkeROepOrRIKkVH+bhz0lHHR2nSmR0+5h5HhyuP4Ur/Cnk+j/TLgSQiQfhrEGTS4UV8464wG/QzwEShQXxOLuSwASEf7C0/66vRp58XdrGxKBP9YhNKsVE6K2kqtnEZt/AXjpRsYmVFvkXiXbJJZOdkItYhDWaVnwmW08qxZ5vt3CJgERhaBPaB0GhmEKMpnVDL/UhiTG4dynkdOh9dq5G+/7GK9JTF/TJZULms3MIhsjXcoXJ1+rIdehGTzmUSeYcf3SCmpF/b7WWDKApr4+ChoVzhasU/LV9fd/alQXeTzZIGYtW6g7H2v0XAIjDACIDM5MjnfV3tOUNDJ8tqdOeFNL5fLDPKElTssDgdZeSo7zdcZzpHloRlyjAbaJBTLkQ2Kntq9TXI7lqmlA/Lskq/t5N0lcoEJ9JsmPLpciFr8X9bPkrP6Cu0qkENldG6MzKizZIW8SEFtZzCZDtYBCwCg4lAjsBy97o4vEeElmYfadZU11np+03XkobXB/LuCqkFnU1yuGyQiSWx8rJXnb4m2R3LyJIgOnPf6WPw0C4btoaZKWZsTeW0v9Al95vKdfSlg4x6m9MSajn2bLOdWwQsAkOIQBNxNaXV+b4kQis/W8sTiMw60NmKObrjhIn6fsu17/xJv/SU/nkR7kFnixyo96bxjzuafhRy0KUfbzSQQs7Giv/0Q5bDd7m76HWH+GMRzwLKj5LsBhsq+uCwklfJp9JL+uB/WEqOS769ZLDNaeAT3nNUsYfJdrQIWAQGEQFp50Jcdf8kTfJ0/deD0LqKHFg+34GDFAfmm7ljEbAIWAQGFAEjtJbK9LMjLAW25LVki4BFwCJgEdi/CBihVWJPS3/+HTCbnVVCZDcsAhYBi8AaRsAIbQ0rxUyyCFgELAIWgf4RMELrHzMrYRGwCFgELAJrGAEjtDWsFDPJImARsAhYBPpH4Nprr3Vbhw4d6l/SSlgELAIWAYuARWCNInDd9dcboa1RfZgpFgGLgEXAIjBnBGyGNmfgrJhFwCJgEbAIrFcE7BnaetWHWWMRsAhYBCwCc0bACG3OwFkxi4BFwCJgEVivCERC++53v+vsz2JgGDAMGAYMA5uKgRtvvDH8KGRTHTC7rfEZBgwDhgHDgGDACM1mpjYzNwwYBgwDg8CAEZoBeRBAthG6jdANA4YBIzQjNCM0w4BhwDAwCAwYoRmQBwFkG53b6NwwYBgwQjNCM0IzDBgGDAODwIARmgF5EEC20bmNzg0DhgEjNCM0IzTDgGHAMDAIDBihGZAHAWQbndvo3DBgGLjqqqtW82L11//iL9zdd9/tZCuSP/rDP3RvfvOb3a+/4Q3+T87lnqRJHslrYDQwGgYMA4YBw8AiGLj66quXS2hf+tKX3Advusm95Xd+x91www3unnvucV/72tfcd77zHfcP//AP/k/O5Z6kSR7JK2Wk7CLOWFlrDIYBw4BhYLwYWBqhfeMb33CHDx92b3vrW92RI0fcY4895knryD33u4/f8oB7z4e/6P7t2+5x//o/3u3+4MBn3Q2HPutuufUe97Wvfs3nlTJSVmSILAPleEFpdW91bxgwDMyDgaUQ2s7Ojrvmmmvc7bfd5mdiX/ziF93d933Jvfejf+l+9Y/+2r3ojf/FnXnFX7mzXv9X7owrvu5Oee1X3Mm/8og7/XUPuZe88ai76sAR98Bnv+jLigyRJTLnccjKWEMwDBgGDAPjxMDChPYnn/+8u/rtb3cPP/ywn1nd/7lj7oZPf8td8fbvuBe96b+6c379r9w5b/i6e+4b/tyd/fqvurOueNSd+auPuNNe+5A79dXH3EmXP+iedfHn3CnT+93smtvc17/+dS9LZIrsZQJzd3fHzSZbbmtr6rZ3d3vLTuVFhvxN3Gynv5y+Pu3uzNxE9E23e9vcV5flH2dHYPVu9T4EDCxEaDKLEuL55je/6Y4dO+aO/Mlfut+9bte95N/8tZ+NnfOGb3giO+vXvupOe+2j7uRfediddPmX3Emv2nHPedWD7tRf+aI75VWfdydPH3DHv+Je9/QL7nQX/sb/7j7/Jw96mSJ7mTO1REjzEtq2m83CzHF3d9tNPanNJ6sPeIzQrLPpgxfLa3gZKwbmJjR5ziVLgzIzEzK74/Pfcr/xzu+45/3L/+zOfv033PN+/evujF/9ijv51Y+6X/6Nr7jLfu/P3W9e/ZfuN6/+unvlWx515/zag+5ZF93njr/0Xjd55b3uhEvvcidccof7Z+d/2p3+yo+5z37uQS9bdCzrmdqihKZBsj3dm1maEZp1UBp7dm2YMAxUMTA3ocmPN+R5l5DNZ+75mnvDO77tzn79X7rnFsuLZ/zaV9zL/s3X3cfu/Tv32N+Wv2r6ve8791//5u/dTZ/+L+6c193njrvwdnf8xbe5X3z5p92zXnaL+9kXfcyd+YoPuj//87/wOkTXMipPE1qaZRVLiMWS3u72tFhSDPcnxayMbajIwrLgZBKWB4slyel0kmTRkmEkKZ9vy21NZm5nd9flbIp5WTbyi63FOdtn51WwW0wsJoaBYWNgLkKTn9fLLxLl5/cf++Qd7s3v+Y577q//pTvn9X/unvuGr7qzr/gzd9KrHnKfvF8xGfPaf/tH59z33SNf+4475zV3uGde8Cn3Cxd+wh33ko+7Z57/Ufe059/sXv3bN3gdomsZP+nXJJSbYUUyK8hnZxYIabqdnpUlOVsOZJdIJxATyslzr5Q/PHOLpAUCBRlOt13WJqQXxAXZYpO31whtKQMe6+yG3dlZ/Q6/fuciNHlnTH5mf//997t3fvib7iVv/s/uzF/7qjvn9V9xZ1/xqDvjdQ+7yeXH3K2ffZwprHT+/e//N/f3f/8959w/ukO3fdX90xdtu+Mu+Jg77vxt98zzPuKece6H3FPPfp/75KePeF2ic1FAJmIJz71ADPIDDxBTIJQtBwKLRAXyic/OUh6xS+eD7LLcgtDUDDD8wCT86APl2CYtG6QL2YvGxcoPv6FbHVsdjwEDvQlNdvWQF6HlPbP333SLu+Ktf+1O/9U/c2f92p/5Xy+e8bovu9Nee8yd8Movus888DfOue+5+77wNfeH7/2se9Nb73MHDz3k/u7//HsnE7Tvfe8f3fe+933313/zd+7kiw65Z5x32B13/kfcced9yD3j3A+6n33B9e681xzwukTnojuKaEKTCgY5eFKZzNw7LwvLjDlCS+XLZOblYBalZnYgHZ55gbSQpoGmbTr64JWlXzkiva68lmfX1pkZBgwDY8BAb0KTrapkd49HH33U/fsDx9yL3/h1d9prH/GzstNf8yV32muO+l8vTi77nPtfr/6S+40rb3M/f8HH3M+dd4v7p+fd4p72yx91//7gMfeP3/+en6H9f3//ffd//z//r/vlV3/EPf3cD7njzr/ZHXfeTe6Z597onvniG9zPPv/d7sGd/+Rk00nRvUilJEIq/zIxLgFOZu7o4cv8My+QBcgnLu/V/Hxez6JQDnKY0GJeen1gd3tWegWgZFMDoXlysyXHhXCxCKasrBGFYWB9MNCb0GT/Rdmy6iOHPuFe+Xtfc6e/Tt4p+5I7/TU77rRXP+hOedUX3HMu/6w7+bL73bNefrd75ktvd8f7XzDe7k64+DPu5879hLvkXx9x3/rWY+473951f/e3/5d77LG/db943nvdT5z1fveUs9/nnnr2e91Tzz7ofuqcg+7HTrvWveWqm9y9997r935cBDya0LC8GJb80jtlmAFhKRCkBJLCfS4XSarDDE18iPnxo5DinbacTTEvlj2LJUuxywhtfRrTIti0slaPhoHFMdCb0GRTYdmH8W3X3Oye/4Y/daf8yk4xK/uCO+Xyz/l3yiavvM9NXnHEnXjpnf6n+Mdf/Bn3Cy+VXy9+1D3p9JvdG//Dbe7hLz/kvvKVb7jdx3fdnff9qfuxU97hfuKM97ifPOuge4r/O+Cecta73U+eea0756KgU3RbpS9e6RZDi6FhwDAwRAz0JjTZKV9+3fjbv3+TO/21X3anvCq9HH3SZUJk97gTL73bnXjpHe74iz7jf7340/982/3omTe7HzjpBvfi1x12n77lDnfPkfvdQ19+1H3n2992l/7mB90TT/5jPyuTmdlTzz7gnnb2AfdTZ7/b/fQ5B9xxz7/K6xTdQ6wE88k6F8OAYcAwsDgGehOafAJGds1/1b/6gDvlV466ky57wE1eeb878RX3uBMuvdudcMmdnsieccGn3E/98mH3Y2d+yD35tBvdk0+7wb3yX227T37yM+5Tn7zV3XHHEffoI4+6K9/5affjp17tfuq573P/5Hnvcf/kufJ30P3M8w7685953nvcM//51V6n6LZKX7zSLYYWQ8OAYWCIGJib0C7/jQNuMv28O/EVRzyRHX/Jne6Ei2/zS4tPe/5h96NCZKff5H7k9BvcD538fnfZGz/q7rnrLnfLLbe5W2+909177wPu1W+60f3k6e90P/eC69wzXnide8aL6O+F17t/Jn8vuM79Ty+8xgjNPkRqgxnDgGHAMNCIgd6EhiXHK377Gnf8Jfe44y++0z37otvcs19+q/tn53/C/cQ5H3Y/csYH3Y+cLrOy692TTnmfe9pzr3efvPUB98D9n3NHjjzg7r77AffS1x5wTznzWnfcuTe6Z51/o/vF8290z77gJvfsCz7onn3Bze4X5e/8m92zzrvZnXjuH9uSowG5EchDHG2aTzaLMgz0w0BvQsOPQn7vD97ljrvwM+5ZL5O/T7unn/cx92Nn3eyeDCI79f3uSae+1/3Q5IA74xUfcseOPeyOHn3I/enDf+re/B8+4p561jXu2S+52Z3w0g+6yYUfdie97CPupJcdcie/7LD/O+llh92JFx52J750251z0R/7H6LYj0L6Va41BouXYcAwMCYMXHXVVf2+WI2f7V9/44fcSRd9zB330k+5p5/7UfdjZ97knnz6De7Jp13nnnjKe90TTznonnTKQfdDk2vdi177EffQsS/7Xzb+2SOPuItff7175otvcie97MPuORcddqdc/FF36sUfc6dd8gn/d+rFn3CnXPQJ95yXf8Kd+NJPuN/6dzcu5Wf7Y6pY89U6MsOAYWBsGJD3lbcOHTrUeTkHL1Y/8sgj7gX/y3s9mf34mTe5J516nXvSqe93P/yc97gffs4B98ST3+2efOq17sdPf7f7+XPf7175L29wl//WDe7Vb7rJnfby9zuZgQUS+6Q749JPuTMu/bQ749Jb3RmX3OpOv+RWd9rFt7pTL7rVHX/etrv7vp2lvFiNyk3voxWbEre8mBxecuZ9GNM7a1Gm3ymkeh/pbUd+/wzvvbWVmTed/ZlXhpXr3lkuI97zyJinzCL12kdffNezpe0tYk9T2T625uSE8kX/od4llfzx3dGYFrbXK5VTvqc+YP5+JGervhf1KP063yZe9yY03vrqt/63t7kfPeMm98RT3u9nZT988gH3hJOvdU846Rr3xJOv8S9FP+2cA+5p5xx0P/2897pnXyDPym52z77gsJ+JnXHpLe6MSz/jzrj0dnfGpXe4My69051xyZ3u9EvudKddfKc75aI73fMvuc5961t/4/7dW96y8NZXUkEAGra2wr0ZbT6sK5LBz+c637zXYhP0r0K+tqurjq75tPxVXa/Knq5yu+bT/s9bjuXMI2OeMqyz73lXfSFfdfu4vvr65Ne26es+siQvfMDHgivX2ApPkUbKJ2SYiKvufl+72vJjc4hVD5rb7FhVem9CE0OwOfFtt93unv68t7onnHTQ/fDJ73ZPmFzjfmjyTveEyTvck05+p/sfz7zWv1N21itvcgduuN3d8um73adu/az79d8/4p7zciGz2wKJXXq3O+OSe9zp/u9ed/rF97rTLr7HHX/eXe4DN9/udyZZ5ubETGZdAhvAFsDH513K9s0TZo8J6H3Ld8nf1Yeu+broXEaeVdnTVW7XfNrXecuxnHlkzFOGdfY976qva76++pvya536uqlsLi2UF1IK2+ilVZ/iuoXQJpPwFQ8QS5ixTtxkUia6nO5F7oHQ+vaBi+jcy7JzERp/PuYNb5y5/+HZ73A/NPlj94MnvsP94IlXuydMrnY/cso73VPOusb97C+/x737+tvdfUeOuM/ceoc7ctcR9/kvPORe9Jrb3KkX3e3OuPged/rF97nTLnrAnfbyz7pTXiZ/D7iTL/ysO/fy6923v/1t/6mapXw+xoOsvI+jDnacjtOejQx+PueyfD+BOyxJADyYHWLrLNyvykEjka9iT9xsexa/sSZlAEqRgwYhMsryIWPHzXwjSbZEW0kuy/Gy6KsC3l5su4WGWiyl5HwI5ev1hm/EqYbv5aW60fUQbA4+1NuTynNMtSxO6yr38OOHiy+UFzb4zwKF+mF/crra4p2rNx9DivVkNgtY2ME38yaus96d9OmjUDfrgyvBHeLD/pRjkmZzyNu1TSR/y9jJyeE2UNZfxVUoLzIVjnU7qZuhTacBT7xV3mTmZjUfDU76CH+0BZ74iX5B2mTZ/mDnO6+kbzMW/VslH9mr0xAffR/fY8zZKHbt5d+BAwf6PUODcfjA51e/+lX3Sxf+W/ffPett7gdOeLv7wRPe5p540tvdT5z2DvdT51zrjnvx+93HP/1Z97kHPu/uvvt+d999n3OPPPyoe8nrbnXPeVkgslNe9jl38ku/4E6Sv5fI3xfd5MUfdV966M/cHbff7pb2gU/pIKjC4EvuGAFPHchMnXO5Un4BWgFU5EFlgwACKKozMekQI3BAKoXNeO4Q0z2giwbl8yZ5klfy+TI1tkQgkhzYK0f2KV1T5+I73KQTZUHosDPdl45U+5fKw2bkTzpDnrw9zeXrZDXdr+hBLHWMi/rRfubtpo+4UrybdaVYh86K45DiWOeLlo184b62J8kLONt7XCGOsC/XVpBWxm7edvir6yNd6xg0+1yVRySpBmSVTn8r1GW0P377UHQWg794L2EaOsNAqXw/1FPyPU9o5TKcB7JxZHnRftVfsv1SLuZrsB3y9+I41wxNDJMvVV9zzTXu4Ycfdkfuuced/OK3uP/+WX/ofvCEP3JPOvlt7iln/rH72ecfdE9/wfvdm/7gNvfIw4+4rzz6qPv6177qPnj4fnfyBbc4ENnkgi+6E88/6o4/76g7/twdd8KLPuM+dev9Tn54IjpE1zKCEYIfQFsnD5UaZlHcgVTPWUao6CJPMbJGA5V8Od0C0thoC1CXymQ70ATQnM5gN43icra0yIVfLL+LD7Gc11mNc16e6hQwwvWdPtLysY+NqZgt8swNtni7M7JK6ToeRcwqsdT51HWdrorfVK7OB3+fOhOWwefwow23yOdtJP1t14320eCkTU4v/Rn8oK1o39uuobctH6fX+QxZyVfBJ0gQKxLlPgDEi7JBT/j2IepsOgsrMNIX5IhLyoKIBJPoI1Ae18gjcqIPhCGWg37H+6LwLvIgC7Kj/aW2hPZZ/y1HlNur49yEJgbu7Oy4q9/+dvfNb37THbnnXnfKi9/sfuD4q9yPPOft7mlnX+Oe/oL3umedd4M7/iUfctM3fcpd+c473G/+3q3u1Jd+3J184QN+Vnbi+Q+6Z5+74571wmPuF17wkJv8z59wH/3UfV6myBYdywoGZg5cmSw7gIABWu1IGfilsqqT8PGhr12zbJRLjVQaQyIqpGtdTdc5+ZBTsUXZquWinL6f0wEfUEaOuXz+vtab6bh0+VBn1XrQ+eQ698e2sCzO28VPr0/br6/JH9ZVkU/l2L6STSKLOiOWwefero56Ib9SnuzRftbZB1no+Hwn2iAH+bX87DX5g3LAWR/bUTaro8HWNp+TvERocq8UC+9DmgHClmB/QWjehi0XnqeFfqeO0LxOJpO2T13V6GcbRWbQF0iSCVLng/24r4kO6ZDhB4OEX6Sv+rgQoYlxf/L5z3tSk5maLD++4nW/637mrJl76lnXume88H3u+Jfc5E5++WE3ufBj7vjzP+FOfIk8O7vfz85kZvbsFx9zP/+Ch9wzn/sFd+5lN7ov/6ev+FmfkJnIXnYAEHAmNQGw/MrQpxWVEEBd7Uh1g4J9dfcFAFL5ADL0cqPxetWyoMjVMpuuIb8OaCKvbEsiUC23zifoyPmAMsHuMFrVtmg9kFfJJw23pR6CnvISJtuA87o6RXqSo+ORRsLIm7efyvWym7FVpyvN4ENHwmX66+3sB3X2dXUEWXJcDq7In6Kjz+GstQ7IdraxT7kuPiPPIjM0sQ+EgkcUTYQm+aNeIrRy2WJpswOhYYCPX1sGjBXkVlM+9FtlIm/6luPObvn5LdfJKs4XJjQxSmZRsjR4+223+S2qPvrxW9xLL/9dNzn3be6El9zoTr7oo+70Sz7lzrz0Dnfmpfe40y96wD3nwi+6E8475k544f/hnv8vrnc3fvgOX1ZkiKxlzsx04FKlFFNmdJ5Yy5YlrMnUTYtZEzcGPme5fB+kGZas0tJbWW9qwAASL3ElEkz5WIforlwDhFiCkx8u8KguLo8UPwoofiyg5bBfusHV+cBlkm1pSUI6p5yesjyMXLF8U64HkdtsTyjPtqRGW5XF+brK5Xzanzpd1Xwq/pl68zGkusv9KESe6fp8HXDLvrbao0ghW0dkW+rUlV9KDmxo0+99KsWkRxuo0Skym+tO2V7Sn8OV5E/4Rtstk7BKjz8kSvLQPlEu2Jj8Rcyi7V5nSC/hTZYii19O+rYG+9UsCX0N9EG/2I/yGGDqeq+7D0LM2Qj79+q4FEITY+U5l/x4421vfas7cuSIe+yxx9yxLz3k/uBt73ev/NU/cC+69D+6X7rw7e6XLrzGPf9fXOMues217ndmH3Sf+8JDPq+UkbIiY1nPzPYqiKYnv9xncbG4GAYMA3uJgaURGoyWn9fLO2Nv+Z3fcTfccIN/h0w+CCrfUJPPzsifnMs9+fK15JG8UmYZP82HHXa0hmQYMAwYBsaFgaUTGgAkO4rINlmy96NsKiy79Mv3zORPzuWepEkeyYtydhwXAK2+rb4NA4aBZWFgZYS2LANNjoHdMGAYMAwYBrpgwAit5ufeXYJneayRGQYMA4aB9cHA3DuFWCWuTyVaXVhdGAYMA4aB7/qvsvT6fIwFzRqOYcAwYBgwDKwjBmzJcQOXHPV7PH2AFd4tqb7nIjK6yg35yu/Y4L2WrrY02dFVxn7k8+/xxPeJ8nFc1K4u9bBO8etir44Jl+FznW9dr+exmcvwuby/hXe81tXfTbHLCG0fCY1B3Qcw85bTOrQcfa3z41rnC51reoEc+VZ11PpXpUfL9X7Gl/DLL+LqvItc75d/89o8j71chs/ntaGu3KpkzyOXy5TP81vf1flk9+tnx0ZoRmgu7TjRrZPmxiiNS1+vusHttT74I7MzjKRXacMqZcOXZR7nsZfL8Pky7RJZq5I9j1wuw+feTtl5JbP93bLjMXR5oyO0MJsIy2W8nZAHFbaL8dvLYJPiopOfTR22t0Gn1laGv+9U2hYmLlnRsh12mc/YoPVouwFS0YGlv0qDEblR78RdebT++178rSn2FXoqsqkxIq3Jd+8PbVGEMrNMjPX2Ppcdrtqt4yP1pOMAe8J3zbp/Yy75XB5FR5trvinHOMPWUCJL4yDKp3qvq1/klWPUz580ysZvOfiFbl0fEueqLdjCrDxAqubDFk7lfNClj+WYVutYD8xyGPexo1ijbmAbcLJNexDuhc88+9d+23X9jEzHZlSEFkCbGkLY1yzfqGSPM+nMUQajp7D3mSI77KmnyrSRARqRbojxWslDJ812c4V620CMUnaSZhSYXbBOPhc50Vcsq/n9+qpLiTFf3Msu5UFaH99RJhtjIkv4GvKn51coj/iEjo/rNT2jQN64+bH3kdIbfa76WZbTjAvYn2JdthH219VvW/ls/PzAQe8d2GwnYpStw8b6CHtwwo98PbHP1XP2kc9hU5TtSRmaXdEAACAASURBVClfnvXyuY67v1ZtbL98DnYmfLHvdm6Elt15RI+CGOx69OdnYzSjiSTDM4vSSK+YbWXKoOFghofNPFm/z1MnT+7TJqO6HADP/m1Pi1mIL5dmF1yWz71+8i13HfXofA2di5dTkEbwv9oJNdmBeuGOppLf6y93BpitVvJq21uuyz4nHU1yYXOqb00omJkXsehYv7DFx5TsbrSF8lXK+bjBlmb8Qjd8y9XHZJIGBlqXvmab+Rx69DHoTfGX9C51rGXDfl03Oh/rR5lV+hxmgQEPrNvOu5OZxGpcM7SGjiPXYCRAGuh83bkMdbgMXJbldVE+BrLX04XQ/K7r0ii23TQS2dRtk9+sk8/bfC3ZU+kk08i8IpN8qvO9UkbJF91h1hJm15X8pAN2duns+vucOtSKDWRzLS7IzlIsqH5yNsEnPrJ+PtflG9PInjrZfJ/Pq/VR7NZOz4EadXO86Jx18Hkupl3quGLDmvoc7Ez4Yt/tvDupjYvQfMNpWnIsjzAFSJUGQY0vpHUoIzOUgpBCw6zOUpKuOnl5uzXY/dKiWmqcTsPyadLRpD+NErXv0KXvN/rUwfeKPIoxdMrR+xaXgbWdKT7c+bXJbkuHfiYguddULqRl6rExFsn+QBbJP9jAR9bP59q29rSMnTXxZ/1ynqsPIRnMZELMkl9hub6KPW2j1pN8IllETF31sBzYCF1dbJC8q/LZYxZ9RMf4w3Y7JsIbFaFJxYdGFZZX9MP30BHSEkxm+VADv1uZMIPxyxz0nTWxRzoAfx/PvnxDLdvQZjcDOtiTOsPKtWosrL/im8oLPSEf2bhF+lQZdDbad9bF595XksH1hQf4koft9mVKcWuyp/wDhCbd8BdHdGZeH9mYvS7Zgx9J1OOA/WRc+vs0O4ctbDefa1ua0nzerJ3lGEGnz19aPg4zCtYR6xudM+efTt20wEq5TNJX52/V1lTHFbtIj6Q1YwV1k2yQMvzHdQMMlu0v6nVOn6P96AMUttgWOy/XjY7H6AiNAxA6e5vmc0zsvL7BeLxkyGWVMZPOGD+EWKWedZE9Nn8l7mEQUCbodamPTbNj1ITmR2573EFtGkDM3jLB+eVAek60yviEWcB4Blxj8xfY8f3QHmEKOod6HBWhxeWQzM/Nh1rB5leZkCweFg/DwHAxMCpCMyAPF8hWt1a3hgHDgBGaegBsjcIahWHAMGAY2EwMGKEZoZV+0WUNeTMbstWb1ZthYGQvVluFW6M3DBgGDAPDxcCoZmiL/orK/xqp+EGJfjFz2Y2E33Npkq3fM2vKq9O66tDl+l4vW8888uYp09XPOtmL1M08uuvsaJI1T5kmefuZtki8OQ583sWfvvm1zFCe3+vs/6rGIr5rezb52git45KjAGa2veuX5xYFcBfADEWH+LpsX+aRN0+ZLvW0Cv/6yGS/+Hw/bJ9Hf1c7c/mWqY9l8XlOr77XN39b+UBOe/e6xqL2a3/289oIrSOhcSXtxYuQewGyvdAhcVu2nnnkzVOG67zpfBWyu8rkfHzeZC+nzVOGy/P5MmWx3LrzZepjWXxep5vv983PZeVcl9fXOv+yr/da37LtZ3nvete73NahQ4dG8cOAUHHYroe2IeLvZ6mtgHK7NJTlFFvm0HexpIx/ATezPBlGX1heqLclgozk5pY5Yz7/Xay8T1zhrJ+3WJI8nCZbVcF33r2B9cUyvEVY0ze58Jmdhhjzsi4+hxL1xHjO4hZKOg1bE+n72ldJx19OZ/Qz409X2VFG6zfLyvVW9823RjtZRzbOacTP9Tx3XKCj2Kap27fHEqZibAjfTe1G+x7Kox3lt6/S750ynv1WbIKnzHZTsO3Kow+62STZ7Oud9uMEfpBff0cQ+qG3tTxiKjqUXfydNh0LL5e2y4r2ZLALm+B/HdYYI9wXQDbsmff7gojdso/XfeADIyU0Ag2CGiorAThUanVLGgEUyAVl4ubDxd51Md1fg7jK+8XJHnGSz+8Vp3YKyMtNnVLZ5mBjTg7yyREy0cAC6RZlfYPI+85yvc1q82PvQ1E+NsQav7UNdTEO+fK2Ve1OdeTtixsYJ3+4DMeEz3M66/1pl91ZXi0Wk1/NdnKcque+7oE1Vc/zxSXZVfVRp6U4cV2Hcltp0+6GdtPFd+9jqVMPgwS0Q5aB8zrbS/dV3UjbR/spyyFf/ICtqIc+5YsBW2lQVtRXzo+SnSXfpZ8hsvaxLfogZY+OW7pOfubqDfbMW4+I3bKP452hFbMEVIyvSH+vTBoMYIxuSmUISAkMulEX4FYzEz9KktlNzpYWuQBCCdQZOcgX/aOtvqpl8757+4pyXb6zpuPQVY8v5xsfRt4Ut0a7kb84IqY1ZTgmtTob4s/x0L6y7JLfbfK20iCpTqYfWMROr4gNyS3pa8LaquJCtngfvA01mNJ5265zuGgoE9pUWTfqplccvY4gx8eXYhflKTvkPvqNUCf9ygfbq/Ub9bXEgnEgZfg6yG7GWi52ZX+CbVp2l2v4sKrj6J+hhRFqGI00V6SM+FJFokIYLG0VmpMPOXIs2aIaidaDcrn7LAf55Oj1U4PksjnbEojhe7fvrHldZH9nPdQBhsFD0ajlfg+723ytxGQLHQ783C11AhV/Guwpya6JgZaHMlxvHDOfvy42NTpy9Rnl1MQSdsR8feNCtmgZkJ0wpVYrdFm6Zl9KuKA8Xh9dcxno1jbVydKxl3qRQSyOLE/rDddhdoiZHMrh2Ke8toX96mq/liH6xRYsJep01gFb56m3EItyPUPeqo6jJzQJLIAWKlZPtYvOLjNVz1VYBRzcyPx5eXSkK7ZsSyJQLRfl6u5DDvIlW5N/AdQFaRS2oRFqUHt5aqmx7jtrSRfL5vNkA+vxI+eisw3382VydvOsOelPerhMKSZSr7U6g/4kr92ekuxK3eflcRkf57hkSvk72MlYCOdVrOE+6rl/XMqddZjtcFzI5gZMsa06vvq6GRdaH2wJdlZw0TOO3hY/gJm6aWZAm2xNsWZMdy9PfvjBC/woE0KXWLTFVmySv1qsLaneUmzyvsCOZR5HS2ihIWKpKpCWrwAPJtxPIAsNH/fDURpLG3gq6SX5xcNsaWRxKQmzBQVk6hwZACy/zqdSftKlfxAQGiJ8TL6nuKR7TDg+XdlXskunlWJAMv0Xtwv96rtx7Fuz3frZAeqq/EMSxCSMcqs62f6sfw1xTLJTHTbJY9/4+YmMiuOydE1sWC6fe5tLcV5OXLxc8n2r17fHuK5TbLLxJczU1ZGUK8coJ7OIYfEjpzpZHDs+Fx1Rj3rOjTTkDz+UCPowYEAeb2dj+WTn1kC/L4g4zYofvyA2yzyOitCWGTiTlX4laLGwWAwdA1hym9fPRcvPq3ds5YzQ6OfbY6t889eIyDDQjgG/GkHPHfvGbNHyffWNOb8RmhFafB9rzA3BfG/v2McWo7Q8mZZK+8Rg0fJ9dFnegF8jNCM0IzTDgGHAMDAIDBihGZAHAWQbodoMyzBgGDBCM0IzQjMMGAYMA4PAgBGaAXkQQLbRuY3ODQOGASM0IzQjNMOAYcAwMAgMGKEZkAcBZBud2+jcMGAYMEIzQjNCMwwYBgwDg8CAEZoBeRBAttG5jc4NA4YBIzQjNCM0w4BhwDAwCAwYoRmQBwFkG53b6NwwYBgwQjNCM0IzDBgGDAODwIARmgF5EEC20bmNzg0DhgEjNCM0IzTDgGHAMDAIDBihGZAHAWQbndvo3DBgGHjXu97ltg4dOmSdmhGbYcAwYBgwDGw0Bq77wAeM0GxkZyM7w4BhwDCw+RiwGZqNyDZ6RGad0OZ3QlaHVofLwoA9QzNCM0IzDBgGDAODwIARmgF5EEBe1gjP5NhswTCwuRgwQjNCM0IzDBgGDAODwMCoCG13d9tNt7bcVulv4mY7u70rc3d76uVMZjuNZXd3d9xswjrn09d31Li7M3MT8XO63WhfX7mWf3NHr1Z3VndDx8BICW3qtnd3XSK4cN2nsrsT2rabFaS3iL4+tkleIzTrvPpixvIbZjYdAyMnNMye+hPavBW/PZXZ2upnaUZo1jnNi1ErZ9jZVAyMm9DUslwkgbgkOXWHH7wyLN3h3mTmdmR2R0uOON+aTFLeIh8DIy0/FjNE6OdyWxM3nU7SsigtGVbsgy16KXW6nWZoLBv5xfaMfWyrnVunZhgwDGwaBkZKaPxMK83OEmHkZ1AgLnluljsHSezMAiFNt9OzuURmWw7P3aK+glxQTp57pfzBlrhcWRBcLDvddrlZX0xXssUmb7sRmj1btB9CGAYGhoGREloxQ4o/2ChII86YwiwMo5NIDsUsrZbQCrIBMUXiohlUieSgr6YcExUItPyDlvCjD+iTtKhTyUZ5pMM3O9oo3DBgGBgKBkZNaFKJIAM/cwEJ0OwlkEogCiaF3Dl+UQiZnvgiaW45JjPRHYmyA6GxzBz4YI8nvMnMHcVSKWZ0tESaK2/3rFMzDBgGNh0Doya0yrKeIjSdzqQCAvGkVZBFltBUGgOmD6HFvFu0RLo9K71yEJclWwjN206kzTbZuXVqhgHDwKZiYKSExs/Q0swpkgZ19iAuv5w3Cc/GmMT4PEdoIMHyUqFa4uwwQxOARfvwA5Xi15KYRQYdednwI9pLPm4qeM1u63gNA4YBxsCoCI0dt3NrCIYBw4BhYFgYMEIb2K98rIEOq4FafVp9Gga6Y8AIzQjNfrpsGDAMGAYGgQEjNAPyIIBso9juo1iLlcVqqBgwQjNCM0IzDBgGDAODwIARmgF5EEAe6ojT/LLZlGGgOwaM0IzQjNAMA4YBw8AgMDA6QsP7WOGdrfSS8iaPgsIL1eH9s75+pJfHy+/m+fiod9XC+27NMfPv3RXv1fW1RefP+dVm79HHH6z9/pzYL+/haT1yHV9Kl3f8sn6nrySU8sZ3Aul9xrg7THOscnZ4W/wL/vn6zMWkVg5e6vc2Bluqtic9Ma2m/sI7lSm/t9XrKPvJ70XWxbvO5mXd7xOnNp3h/c+y3yjTVU+MbQYvkNV2bLJDl83VQbShR/1qubnrrjHIlV32vXe9611u69ChQ9lGvmxl+y0vACI1Prme0QbC+20f628CiU7T1yynzzleAtedUJlEUvy0bB9fRQY6T5/rNr9y9kqZuu/PBT+aOiaQesoTbCjfT/c0SeB6eZ8l0jHQ13XxrMO6Lu9jWNQZ0iaT5D/khzQm9cLH6dRNefcaalOQN88HdKF33uOqdGu5+rrOXp1P109duXnuc7/GenHepX776IXc/ahnbed1H/jAiAhNRpNL7HB1MJd53QQSnaav57UjRxAiy4/2prNi5lNPaFJek+G8tki5Nr/q7GWdYaSaOmg/Q8+MUIOuLSeNXWan8CPM6Cdu4r86HuQg7xZ15KwnDQDqY8U2Np3rGOjrurLe7gzWdXm+xrl8vgj+Q36Im5BXiqWkhTJ5P5sGEJC7qiN8WXYnq+Xq6zp/dD59XVdu0ftcB9DZp3676IfcZce6i26dZ1wztGLXe91YJShhxISReGqgfH8ym8UGHStxexa/gSabD6OT5U6xTn6UMZvG75+JbeE+bAk76qPicmlRDtnCPrIP3AlDJo6wncsira2T5oaDMrzsgW3Boq3KZ5RhWzneSOdjk72SL2ezl1/b0UuspdNOMfc6JjM3ow+zpjoIOIk2F0SZ0wu7JSbYpDrGYid8ZsjL8Z8O2vY4u/Lo4WALlqkobVZT19ADG3VdVnT6NsFELeein9qAX0LF/T6EVpYD2/gY7SF/+rcjzIhDm5HyObk6FmLH3tZHih0PrGBr+A5iiHtj29kh/2raEWIcZBc4jXVdrpfUdgPuQEwR16Ul6/ljDZtWeRzfM7T4fKOhY9me+hFqAEPKFzrQAEqkYcYXRvJ6ZK+BVHRcSn7s7Ol5BEAOcDEIdFrelmbdLA/nTQTR1ElL+WBD0Al5OLK90VZ0/hWf8/GGLD52szfViZSts5PtCp2J+IJltfI352JeEM1WsjnoQKOvxqPUkQkO5AOsxXM98UfOg3zGGXWE+BQRlgkpfhybsh3JPpYteXwMISt2eLvljl6e6fk85Q4v6Ch3jmyDxBG+8X0+j7GEDd6fVC60q2Ysc0whOy93/+oj2hMxk2xBWi5WIa2KBZTJ9R2IgRy5DliW3I8Dq0z9cl6RIzH22JT6USsc0ZZSHSb/2J5Vn4+O0BBQjD78aA677EewhRG6z1NUkq9UavCVCqe0St46+U1lVBrs1rLbruFn+BFMMetTgITsbgSRB2qIRzktdEaYaVYbpba9Kd6wkY919sYGpogm6BOySQQBebGMzIKKTnU6C7NvwUggOfZB/BJ/QV5JZhP5s4/b04nzMy2PsWQXY4vPg/1lUtHp8IePwECauaBO4EMx0CLMle0MnV9OV7in6r2ISa6DZru6+MM64YfGMu6zPi6X0wM7yn6urj4q9vg+gfGU8OPtLTAYfK3mq8ijugv+BlzWxaTsd7V+EdNlxhoxX+VxtIQmQfUdonRgHlzlRulBIfeXRmgZ+RUQps5KA5ZBoNOarut8Y3k4ryMIH4vYcVf9COnlkTrrTUsatFSCZTaKgS9TE2/YyMecvYlM0giUy4RYVX0I94uBjLcJz9NC3npCK74ALoOhwvZkQ04PiGvbTSORTd02YY3rk89TnFPnp9PZVz6PWKd4c7qWHetMlgKjXwmfKBv0Jz9juaJ+ka/uqO1vumZM5eQBD4m42+OU7F1tfVT9CoSTtZX6o2Rfue1U5aW64TIcJy4T89TU7ypizbas6nxUhLZL3w8LFRqWNkJFp2UOBBv3BXRyLzSY6mhJ0hgs+hpyeLSk8+hrLU/S8afTmq7rdEMWH9EhaDslD+JV9wwuNhAQlYww0RH6BtoeN9iaizfbifOcvZhd6WURlNGkGe8XJIZygcDSs7RGQotkj5Fu6KzqYiV266XG6TQs6Yg9XJ98rtNy19GfRqynjh75c7IQS+BB25LKEKFllqRYhz7XMpuuQ1q1nbJMH1u1bJvszPu9J/WhBhKBMGraRIe20xinmjqolJF8/AMosnFZsdY6ua5WcT4uQkOnhaVFWnoLAKOlmNIznnCff6SgK6r12nfqZfltZXSnygDgtDY5db6xPDnPEQTytBEayqfOD526zFymblos87XaWjSy0NDSj3BgBx9z9uJeaamEfpnnO2mqd8gLdiUCQ2cOcm0iNJGB/EJih+O7cKmjhx6flwg+e00di6T3qWvoif4orOv4I7+3Q+kNdZ58yJUN91KeXPwFEz4+xQCnWWeaaWRtyrUjwgwGEdpWfV2yYT/qgzGZjXvRV9S0He0PX9fWQVZPqjuW4WO/hFhrmRz3VZyPitAWDWAghgSAReUNrbyPT6bTWhc/9SxyXewagx1CyhgcjMFf8zGtKO1lLIzQaCmvLfB+pLzGHXab/XuR7keHmRnQXuhu0+Hrb01ta7N9k9PDKN0Ggptch5tiuxFaA6GlZTYsFVqj3BRgm537M0K2uFvc9xMDRmgNhLafFWO6rWMwDBgGDAP9MGCEZoQWfz1pjadf47F4WbwMA+uFASM0IzQjNMOAYcAwMAgMGKEZkAcBZBspr9dI2erD6mM/MDAqQgu/tsIPPMKx70+Jw0/38y9o6gqM7w9VXl5M7zvpMuEdkm7yuWzX9z362M/y5byrDl2u7/Wy9cwjb54yXf2sk71I3cyju86OJlnzlGmSt59pi8Sb48DnXfzpm1/LDOX3rh/T+tf5+sCBAyP6fIx+sdC/OLiaXy5KY8G31hjAON/EbxLB9tyGycsE+bL1zCNvnjJdY7AK2V1lcj4+3w/b59Hf1c5cvmXqY1l8ntOr7/XN31Y+EPNq+jGtW64XtT8nc1n3RjhDS7OfvaoYfqEXOjfxm0Sw3QhtseWkVcSxq0zOx+ddO5R5ytTJXqasOh18f5n6WBafs7668775tRxdXl/r/Mu+3mt9fewfN6HRnmeopKF/kwh+Cinp9+xyy69h9BeWN3jrLwEZp8lWUyjPu0KwvliGv+uV+Z5Ttgy2cCI9Io+XdbEPY9RTlGm2O41s2R9dRmTiL6cz2pzxp80eyI0yWr53pevtssPV76aJzEY7WQf23yxtdbTkuEBHsUqS+9abjhNjKsam43fTtO+hPC3TMQajbbRdG+FMy/J20moPbLvy6IP+I7hoBz6f9DFqMwbk19+0Q712Lg+7V9iPwSZsJVeHNW47uXpDv3r4ccFq8VWDon2Kv7xdF7bPk/j1/RshoRGoSx8xlD3k8hufRgCqTiA2ktK+j6kjQGVIg0AlsSy5D/B6QHjgp73sOC8aR9wXT+14EW0pGk/YW7BqC8v0eZQc2Oz1+UabbOTne9BXsr/Yn47lyrneiNf7UMgGCbG9JRuVDaHhpFk27G0qU7U7lff2xc1s875Chz7mdNb70y67szzqwGATl8U9HDmty7mUW25cKN4ZIsCMP9iW4sR1jTSQQ8ALtSuJCbXnNt+9jyVbApmhnaI8H7vEzttFbYrbOGRVfKG9JHuVj4O81M4hO+dHs/3puX6IbZCp7dFxS9fN9QZ7YF/fekTs2o4jJDRqXAwkAjeCFioWBBjK1YEiVSzJz3wXqlRe9BcEBOBX0iNoCzvi525SY87rTsQIf3Q+jKoANs7n85J9+bKpIUl69IHKdfnmV0U21UWwMa/Hl/Mdmaoj0l+RLWl1MaWRNNeDyOC/NlxkdXaQzTr5PCtPDb50fl8mFxuOLZ/vR1xIv7fX25Cva+1f63WL7/mYlnVLnt5x9D4FOd5GqvcoT/kt92PbmaN8lfhTH9TXfp+f7Mv1EZXYL7PeSDfi1ec4bkIrCEdmGU2VFKbd/QiNy3CFsJ6YZw+/ScT6YRem+5ht4b4HMzVILttENNGvnW7fmBJ9JdkE6kY91JCSzt2wFNrDbq9fZNWUQTxivmImUNJJNlf86SqbZHA8tDzYw/VWyV8XmxoduThHf1cVF7Il6lKzrHJHnzrqir8ki33pVUdKt7apTpa2RepFBok4or5w1PmD3DTDQTkcUQ7HpvKVtJ44EB1ahtwTW7CUqNM53rBxnnqr0w2ZXY7jJjRf2VWi8oGVEV7RkEOFVfNVKpYblZSnpQdURqVMMZLELInTw3l5JgY5OAL0XM7bT7Ygb9N9yKnmLTe0LSwrevkpTYPay5uEhi0y5brum1/aLvYFMQDZsh4/U6qto2Sb6NZ2I97wV+vhMsjj7eyAi7w/eXtKsqnOOAZaHpfxcY5LptThd7CTdcD/5cclLOXF+vN4r7al5GOKU6muKTYpL/lL6c24qCmTWU3xenrG0ZfxA5j0ySS5x3861uxn9/Lkxwr7Mba7FmsNfQFjzPtG9dR2rcuyLXXnIyQ0LE/JkUBRCTQ9IN7wbxJx5TNIyktn7cst+ocSoSEinimWHqjUyLLXlXinJVK2MZWt6sHI1j+wpjryZXzHGco0262fHeTLiEwvlz7muezvvLHffB70UnzIN35uJKNiHwv/g4c58OvrDHFeTlx0XWxNp+FHAcUPGthmn7dkQ8JUUzwq8ampI8nH+vIyk/9h5aZ/HKOezICWbQ0/lAj6QPiS3q18snOV/VhdH8Fx9D4tod44NuFHawnziEvbcVSE1hYMSy+PJC0eFg/DwHwYkA5fk1SfWC5avo+uIeU1QlPLAUOqXPNlvs7I4mZxWwQDfuWCnjv2lbVo+b76hpR/VDuFDKnizBfrdA0D64WBtASelkr71NGi5fvoGmpem6HZDK30wHqoQDe/1qvzt/qw+lgFBozQjNCM0AwDhgHDwCAwYIRmQB4EkFcx2jOZNoswDGwWBozQjNCM0AwDhgHDwCAwMDpCy71XEd5HaXqvI72To0dsuRdwg47ye13xvQ21ZZGWt9fX+l2cvvrDu2jzPQTvqott5PN5ynctM2++eeybV9cmlovtbzJzRx+80k3oXdBN9MdsXq8Z3KgILXS+iWjkWr5ZpjshT1LYgaJ4AbjL98vir5T8y6NVPQJ+rWsvGkSTzqa0VdvWVTfn4/Ou9s1TZl7Zq9TV1aZV5FuGX0HG/O9nLcOGVcTGZK4PqY2L0GgbGwahbih8jfM+3y8LZRKhlXXJzgOrndGwPjmHD9jVnNOb0jjfKs676uZ8fN7VpnnKzCt7lbq62rSKfMvwa1EZi5ZfRVxM5vqQmdTFuAjNz7aqeyPqhsLX6Vy2YUkkFWZjQkzV7VlCmZSXQV+XFvV0+N5TzIvvIdE2UnGWWOwoX/f9ItgUZZFe3s8vzGqxHFv1KZbnT+tkvgnW1S5emsVemFkd8L205U6yj+3WW1/BdzlyPmy+6u8jphlfUD7YhdiEZelo65zxDLppuyX6LlerraRTdqkIy+HBPtRpk30xDbEtYtDt22Uh9pCB719t7+76ZzPhfoqV2IO8vM0Ryh1+PHxbzG/ltbXl2nCMOrHjehHMXtfHqAhNdxbYmoYbluTJLTlKo+PtaHzn4pcl+xGayEDnwpUdGzyWOov9+pCXn8tpe/na51N7yHE66wzxEPu3Wjdi9nnl22azndLDY5YdztPzxpLN4k9vu8JMtqqjep/tgx2o39xzTvYd+QJhsOy8L1IWf2wby4wbW/t6LHf2mClLfKrxDGRWvR/qqdHWztjpWN8gdR6sKLLTviD22v4UmxBffa3L9cUx6sOOCZtjjMXoCA2VjNGudBBoTBgN8oav3GElEkvkxulRtu8I0mxB7mOGkmvoIb1MjFouX/O5Lgu/WI/ODzt1WdwHcUNWikvq4JGXZfO5lg1ZbXYFEsRInsklc16anRVl8L24onPXdsBuf9+XL9dT9J0680YZLfk4JohBYzwzNi1qa8kGZa/I7uIzy0j2oJ4o9hn5kt+XUWksk89ZfhteINuO4yYy1P9oCU0C4EfumU+xIzhy5IYWlxllaQejYdVIU5nUUcZyxeiW5eOc9SQZTaPZfBrkYbkpEXbK8ySyUQAAIABJREFUjzx5PWGG4MvVdK515dt8kHJNdoUOH7OZ9KyR5ZbOa+zzctaW0BIuOI445xjgnhxz97sQkS9LGOX4hTSqb8rXWq4u9kqGyMFfVXcaxOk0lGnCC/LYMcV47LEYFaHtbs9cXCKh7x/VNSYBh07DDAIjR52eyqSOK7d8ooGn5TRdY7YXl5/8slaVsKQzEDu1LNYd0tIyKHecOo3L4Zxl87mk62uUqbPLxwkDBd9hBp9YTvU82Q75IU/6NV3oFKvx0fmqvqcyrBd6cj7qfHwNfcAOy8E56lbnQdlY50QorKPNJsiB/LLPidy8HMJVXkdd7FPc4Fc3u/LlavHSQJ6s187HQ3jjIjTfAGiZpHimoxsrNwCdFjocIqtMowplUp7QoZLezLtoVT1p9JrtDHxng6We9I0pEG5Y1ko2yGje36t5jlX3babQ4ZHtNeVloNDkQxe70Jl7O+n7ZiyXz31cfMdetY/1df9RSOpQK3oy9QyccGzbyrXFM9V18qlMYrjf3Va2Cee19V2DK7GL/ayLPeRj4IgYJb/ydutyXH/8CIBt0GVYl52Ph8S4rkdFaOy4nY8T8GOvdyMBw/2Q24ARGq3xD7mizTfryAQDRmiGgyH3BUZoRmjxof2QgW6+hY7cCM0IbchtwQjNCM0IzTBgGDAMDAIDRmgG5EEAecijTvPNZlWGgW4YMEIzQjNCMwwYBgwDg8CAEZoBeRBAthFstxGsxcniNGQMjIrQ5B0WvNMjlZp7QO7ff1HvWjEAcmU4XZ+H947Suzc6vc91X919ZHfNm4tP7l5XecvKF99bUt/ZqovZMutlXh/qbJtXXlu5Lvr2ui4X0cd1vlNsgtwWg1WlL+JHX5uC3+kdUykf38/LvOPaV/4m5x8VoWnQ4SVX7JogFYldCeoqtUunsIqyIrNJt07T13U29bkfXnwuk3PuXh+Zy8gbfC0PViB3FXGA7EWPe21bm769rstF9Ok6b/Nt0bpqKr+IH01ydVrQI/upykYKidCkH5PvOkr+/YyDtnc/rsdFaLKrBO3xJ+Q1nc3cJO4YkvYPrKuMRQCzSNk2sGrZ+rrOnz73/QBAzV5z9/rIXEbeJl+b0pahexEZe21bm769rstF9Glf9PUi9dK37CJ+9NUl+YOvidBYxl6RK+tcp/NxEZrfvzHMMFLFyxZTARwaKB6oxXfFsP1ObDj07SnM8OIIqigjy5vI3+ubUrL9EBEvAANZM6U73MeWSFtu67I3h0/CwHbegFmVFdlZuzM2+AFAMRKETXyPl3SjrfjciAwmpttxZ/egV23v1SMP9GvfpS5YN5+jTK1uxIu/QYYtrxq+i5aVh3Lwv9g7FDvtMzZy20TxEhJ/didXV41+kR0cixg3GqBwXeb0xPJZDBV1SWnio8iEz2gnsLdNn4+r2tosxS3h/cQr31nBexcsivxcnOEnvs0m33TL9QVd/YA83W69f6ifHnEL8uoILfVnsG9Mx1ERmlQsgO5BUZDG9rQgOenE42xNdbbFt6sCmGq+J0XlAaII5pa9DiW/LIn6DjlDJj7dg590S74SGaflQNabLes7iqrf0W5lQ5BXbkT6Hi/pel8mYXNkkSmdV/QNMRZ/58wDO5Nved91HFCO74fztGQZOq8iNog52YyYQ1a7DWHTX92hsw0si885D0hGy6nLr+1KssqbEKd8qX65LiEfccJgKxsnbC7tsZk2L/byeJnMx7WbPiExbyNjFkQQBwzV9hrbcg3O4Ffyv1zniHOKW2FH0U5TuW5+LCNuOZ3sh/RvsJvvj+V8dISGhoqjVDQ6WxzlXnlEVowGeaZDn4KJJFmMJhlQ3Bj4vElHHfgq5alRN6V5XZQX8pvsRh4cJV7sl5ep7vmY8SBBRp3+Oi3lLisP7PJ2KN84FnxeVybUdeqUJF+MTYPsOnnappx8nYdl+bSCEMLspuhoPb7KdlbKNdiLWEwm1U5P12+wuZwP5XlG2TVOumwnfRl/O+uTsi1YrI2zjmHRrjHT9Eca4HC7WHXcvM3evjIOugx2NFaGeD0+QiuAvi3Pz3jkN5252YRG+ZnGlMBE+YqlJMiSPEKMAvq0PMIjPypbo6MOaJVOgRpeU9o8drMNobEku4O8RFLIm/Jtu2kksqnbLmIuv0RbVh7oDLao0XlDXFCO45UjnK4dZ06etiknX+eBHH+fcJHihWWvckfG5XIyS376uGz5WTFmL6FMtS4htw7LqVwV5+12dNRHcYA9Xeslxa0BiyQ/5U+PCUDc9fXX0Q/C4yJxQwxCnSYcsO3IM9bj+AgtPstIHXQAiMzCGCTSSZZHqAGM5ft1YMdsr9qhVPXyCM/rUMt9ACfLSrYEeU1pKW/yp9VussHnLUak0RbpDNQ9SfN+q2XE6bQ8u1tGHvaXz5Ov1bhwvuq5XnIMWOB8zbKlcyMZfoYFG0JapZ6po2M9fvWgmF2Eeuojp8mORPxCDLAnV7+o51in8dmkKtdrybvwowY70FluOxTTEgElX3S9lOQ0YLE+zjnZyW/I3+u4Rb0eN9RXCdYybRH5x3QcHaFJ5UqDwXo2KlsauAZF6EzSw2dJR8eT+56UbyDxhwX5DtHrkTxYsvCNVOkgMoF9coTuOHKkDlHStWy+RtnOdpMNEi+egYqu3D1vo/cndFy569w97rQlvUse+COx4HNfluLCaXXnSR/qgewnWU2yfZonsUKG/2m1lgP51VlN2bZASn5pi74Ll/TXy2myI6tjMnMfv7Jav01YzmKoIU7J7hCPHHZy+ny5UvvQ8UzXkpfxnsqmPBpnYWZTxJLizHESOUlWiru0365+QN6icYu2+FgnQhM7SsuhmYE4yg79OEpCG3ql5vxDowIZ5vLk7vlyxWwB6bl7SLPjZu1E0acu58UQY6KPPi63bud9/FhG3NbN/3W1xwhtJFtfWaPaLKJZxw7DMDQfhixu88VtnjZghGaE5pdU5gGPldm7hroOsbaOeb76trjNF7d5MG+ENhJCmwccVmbvGqLF2mJtGFgcA0ZoRmg2QzMMGAYMA4PAgBGaAXkQQLbR7eKjW4uhxXDTMWCEZoRmhGYYMAwYBgaBASM0A/IggLzpI0uz32ZHhoHFMWCEZoRmhGYYMAwYBgaBASM0A/IggGyj28VHtxZDi+GmY8AIzQjNCM0wYBgwDAwCA0ZoBuRBAHnTR5Zmv82ODAOLY+Cqq65yW4cOHbJOzYjNMGAYMAwYBjYaA1dffbURmo2MFh8ZWQwthoYBw8B+Y8AIzUZkGz0i2+8GZPqtEzcMrA8GjNCM0IzQDAOGAcPAIDBghGZAHgSQbZS8PqNkqwuri/3CgBGaEZoRmmHAMGAYGAQGjNAMyIMA8n6NCE2vzUYMA+uDASM0IzQjNMOAYcAwMAgM/OYVV9jP9m2EtT4jLKsLqwvDgGFgXgz8zlX2HtogRibzAsDKWedhGDAMDAUDV9mL1QbmoYDZ/DAsGwbGjYHREdru9tRtbW3R39Rt7+463J/MdnrN2HZ3Zm5SyJtu78ay29OgQ+7t7u642USuC127225askHSJm62k8rDnmRrKGsNdtwN1urf6t8wUI+BUS05RvKZbhPxLI/QtiYzt7MbSKkboWmCK65Bkhk7Dcz1YLbYWGwMA+PGwKh+FLIzm/iZWd9ZWFMjiSSpZmn9CK08g1uFnU0+WNq4OwGrf6v/oWBgVD/b52U8TWpIk/uRpCaTuJwoS4LTaSBEvwxYzJ5S3qmb0rJiL0JTMzLYInqydtJMcChAND+sUzUMGAYWxcCoCE2ChdkPnk2BMEAiZUILS4ixzHSbnoeFZ16J0GZupyAmkdGN0KrP8lChUWcx8yvZaYQWl4wRLztaZ2gYMAyMjtAA+kQYBTEVPxYpEVoxC0NekEogqwyh7e4WRDZ1004/CsEzNCw5ln8YIrZCt/7RCPywozViw4BhwDAQMDBaQhMAgCz8LxGXRGhxxkbP1Op/5RgITduiwcl26jS7ts7MMGAYMAyMkNB2ZtP40/hEMsudoQmwQECyrNn8s/38DK3VTltytCVH26rJMGAYqGDgqquuGs/WV0w04RlaWuLLPkObY8lRCG2X3jNrJjR+hhbITxNi1k4jtAqQbYRqsxTDgGHgxhtvHA+hGeAN8IYBw4BhYLgYMEKzabvNdgwDhgHDwCAwYIRmQB4EkG3UPdxRt9Wt1W1XDBihGaEZoRkGDAOGgUFgwAjNgDwIIHcdwVk+G+0bBoaLASM0IzQjNMOAYcAwMAgMGKEZkAcBZBt1D3fUbXVrddsVA6MktPRSdfEeWMt7XeG9suIFbP+OWXp/jQONd9nCu2P8KZh8fi6rz+O7bPQJGclTtQUvZ1e/sSbvwEFuzjak2XHxDoPrZS/iOa++ecuJT5V2w9/0U20obA+XdsLJxcS/F6rwncvX5V7OrzZ7jz7+YPGdQrwPmtqp2I+t7rT+oCvfd2APV2xVV8pL8ULbTDY2x0rbYNf5NnvgwIFxvYeGrakAKAGG3JtR56/Bwo2FzzlfkJtA2SaTy+bOoWcySS9cSz7cl4+BhnMmtNQg2R4+9zIy/rLcnD2bfm/V/q1avo5/V306n77WcrteY5MC3emnDlo6/NQetFyPSUWCOk+f6za/cvZKmVnxQd9QPtkc/EjtiW1JeSV/ypO7n+5xO9V60jXrsfM8aTXFZVQzNDQ2JrOm4CAtgDIAl8+RLkc/A1pFA92euQnJZf3hnBuKblyFzbJPJclgu3HOcnFvSMdV+7dq+bouuurT+fS1ltv1OkcQUtbPUKaz0hfaczKlvCbDXL6u99r8qrOX5YfZFbUhaTeZGWTQteUmk/L3FcMqyMTJIBREh7xM7qwHfRKns0123o/UxkVo/vMu9aNGAU9aMtiKYObGwucMNgBXN1LOH8+FpGjzYjQ2WapE+Zh3J+zgn7sf8tQQGjXGkC/JZrvlHOlhqZT8xnfayNZqWXwpQBpxmk2GWWG4x42V709mMzctRrjR3w6x8TaXbFMxmE29LYhnnX/sS2O9K3koV+cL0r2dWKJeyK9qjHPxAkagP+d3Wzn2iesNMnEEZrXO4DPszbe13OxnVfHvYm+dzT4WmYFgjOt06qbSNniLvMnMzfyXNngAnGZgMb5FGSO0foSF+qw7jo/QMgDNBSc2/Li0xwBNozgum8BJHTs6tChnK86W8FwLnUK4Vp1zLFfVH2zk/CCQ1IBgX842pMmR/U3X5IcnkKrf3mY1iq3I2p56og73k8zQKbJf/WPjbVXy0cHUxZP91udsO+ytl5f3hWVGGQXuutZ5yS8anEB2Xm6VQNgfLxP7jJbsYQylOhZbgU3oxXExQpPnvVVbk30KE+j8JQ5FOfiP1RbGEmzkYzd7y4O+oKNqJ3QLLgIRS56CxOM95UPm+Vnwt5n82Qc7bye/8RFaTUMCWNDhhNkKg7J6jjL6iFGYNDbuUPhcyjRdV9KKTo3vh/OazqiOgIqZDToC2M5yvW0+X7kxS+OtlCvkcccH/+OMrxjF6hEv6+Tz1tgUOivyafCgZWj58BvHtnqvyBMbaHBUJ1/fb7pujBvN3rUtuevoV0NMdLk6/ZDFx24EUcYPyocYlNNWFX/orLM32BIGghVse5IK7R5y5BjLyAd/PcluueksrLqIjEBy3F9ggAnySjLTQLMcD9Zn5+1EhhiNi9CKUZQGLoIRGnQAVgAag7J6jnK5o29A/gvXMhrNl23s3CodUWgM020tD/am+2IPGkrOV9jGdlds6UhokIEOQ/RxHJHubWoggYr+iv/Jv1r5TWVUWsWuOPKXOLfXl7dhJYRW37GVYqz80fGDf/p+03VdXCGLj7CFBzJIB/Ywm8J9HIMNyU/WW9fupCzb3jX+0JmzN9lZHaglfclOyAp2hKVGnIfnaSFvPaHtRgLEM+1kQ1UP9NnRCC3+XF2DIY6o6FeN0jjkV44+DUsxvkOvdmzcqFj27vas8q01aeycn8+lbNO1TvP5vU0y2mO7QkPQ+UMnUeSrsa1kf7aDTA2dOx0ux+fSaSSfy8s33n6vI8kMnQz7Es5T3vx18LVOflOZlMZ2d6l3bRNswICBfSnJzsY12cH1Bpk5koDMcozzcpBX29x23UU/ZAd/q3UQdGAmku+kmbR8fpnltLQ7bTtsbYt/k73oC7CkjLw4atKM9wsco1wgsPQsrZHQsDTZ+K3EVK/QacdupDaqGRpAETrnsMzgl63QmAhsW5Opm2ZG6twBQZ4c0cDiMhjW/alD02WbrnUadHHHGfIwoZFPtT8nTg0PMnHUDbMcp3wji52Cf0aQOrBy2aST82d/FLIT3p3T/leuI7kXPqvZcKqTZLf2D36nUbI8w8vXe05enS+Qmy1DeMim5/wqlrUCtri+k286PmwD+63zVa4z+lkWzhchNJEBYpbzVca/yV74ENusxzDFtFjmhwwcQ8yqmAa5NhGa9zfW59Qdju/C5esVOu1ohFY7SzNwdAPHquMUSC+R4Kr1mfz1qHepB1/3tGS7bnWjZ5HrZp/Zk8fyKGdoBoY8GPY6Ln4ku8ad2l7HY2z6/AxJ/UJ2XWLgsbmmtq1LjNbRDiM028txz2aypaUltUS5jo3DbFqPgY/Vg9VDVwwYoRmh7RmhdQWl5bMOzDBgGJgHA0ZoRmhGaIYBw4BhYBAYMEIzIA8CyPOM5qyMzQIMA8PCgBGaEZoRmmHAMGAYGAQGRkdo/O4QdjIIPx9P7590HbXp91FQjt/tCef8jgm/K5ZeMpayOdsgcz+P7M88dswb3z662EY+7ypjnjJdZet8e6lL696E69gOJjN39MEr3YTeqdwE+83G/Zv1jYrQ9HtPct30HbQ2YKJj2qtvlrXZs0g6fJHvrGk5TWk677Kvu+rmfHze1Z55yswre5W6utq0inzL8CvIKA/0+ti6DBv66LO8+0deudiPi9Boi51cMPrei41nj75Z1te+PvmjL0ZoFULvE8dcXh1bfZ0rs4n3luHXojIWLb+JcTebE6mOi9CKPdj0XnncCOJ5h+9Xxbx78M0yAW3U19O2Uln/ORrstReWPy87fDh818m/G5a29EFDyenlGIaZL5ZSqzt/xPL8KZzMN8b0e2p1dsWtnMTeLluMlbZzSvax3bwNF/zGkfPJNknY4ij6lfEllsW+fxTbWI7qsU88RbaOVbSp5GvGVtIpZXj7J9jQZF9MU1uUXXk0j6Fy7HjpfeKmU/lAJtWHipXYw/pwjnJp26huOEad2DERwNBiMSpC0x1B7ARof73QaPp/lwuNTZbsqufckNHxyzE15jrbGHDz2hZk0271mT3q2GbWmcpSTHynGZ456nLy/AMdI+RwnugDiMjva1fEZy67qnZU9aXno7APdgADoWNP+cq2EzFUfCdSJV9QPsUvyYbuuCEvlWPbfdlsPMOAJB/nFluxb6nXmTYXDs+tFE6Rt+Kz9iVcV2yndsW+wH9tf32sWL6yWe3moW0QmfY3nhiMjtAAbowcpUPjRsDn3RoYNe6iQ2YZ4Zw7CspPHQXs8jr9/dQxIY3l9raNOhf4zh2Klg2dOT1yT2ZJPnaFraUNXhs6Ga2Hr7vaFX804Gc93Nllzmvs87po2y22o+S7L18eeETfKaZ1ccrd17r4GjFojGfGJq8nc7+rrSUblF8iu4sclpHs4QFcIH+dT/LiT6fxNZ+z/K44hg47pngPLRajJTSpSOwlxw2FzyVP03U1LYyc9+ybZarjYXv4POdH9D9+xiLN4CSN/6qy4Gf9t8/qyldlVfViGUwPNkRm6PAxQBA7MiRGceH8JZuk819bQisTKNutY8BpOV+7EJGXyTGj85BG9V1JS/VXqdsMwWpdbH8ujWXyOZdrwgvns/Nyux5iPEZFaMP8ZhnN+KizwTMWLKmFWU3KCzBLZyAj3LrOQvKFNFrqoY5Kp0EuH1k2nyfZ3e3yfrQshbGOOvtwH/EJnWLVDp2PSYP1NPnSlo/ToY9nHRzLoCcQjM6DsvCpj61NNpTlJHLztvilyxA3lpHikXADP3Q+3E9lUj1wXj7nMnJeh+OmMlqGXW8+4Y2L0HyHT0sgeI5TIoI04hSA6wbB13zOjYE7x5AHMwqRTfrp/ZqQj9LUsl2bLdn04jmJX76aTtOXs/k+PceT0XzIu52doYWH8SEPOk2v1xNcve0cJz7XNpeXEtMshe0CUXs7a75dVtFRYx/r6/6jkHxnq32Ra/4r+9CCsRp7WZ7GC+ojkA/qorutHDOc19Y344dwJfaxn3JdtmfJS45sRw2O4UvudRSOp52X8bqp8RgVoW1qJZndw2hsm1KPRgKGt03BqrbTCE2NpHWA7Noa99gwYIRmmN9UzBuhGaGVlsY2Fchm9/I6YSO05cXScLm3sTRCM0IzQjMMGAYMA4PAgBGaAXkQQLaR8N6OhC3eFu91xIARmhGaEZphwDBgGBgEBozQDMiDAPI6jhbNJpvFGAb2FgOjIjR5Rwbv6wjQcg+//btJmXfAAMxcGaTljuE9nPQ+UC5P13t9dXeV2ydfLj65e5C5TP9zMlcVkya759XZtVyTbsRAH4dYB9pHu95bctjEeI+K0HSjDx1HeScD7DhQV5ldO6Vc+UXKirym8jpNX+fs6XsvvNRcJufcvb5yF8m/Cj+1PVqHvtb5667nLVcnD/fHUAfw1Y5Gak0YGBehyQ4MtH+fkNd0NnOTuGNI2huwLmiLdEqLlBV7msrrNH1d50+f+34AoGavuXt9ZC6adxV+apu0Dn2t89ddz1uuTh7uj6EO4KsdjdCaMDAuQttNhJVGtbINEW9NlbZcwgwu7HzOeSZuRt+Vwp56QSa2HSp2oy+21er1vSjZ0oeIFxUYO0SlO9xPercue3N5i63pdiJDVVZkZ+3O2OAHANvlL1rzvayc3LZiZIMsAYuMEOM0W46+Zr41FtP4Uz0ks6k+EEscuY55+yvoyNUb0vIYqN/Wqqkc7An1oWSorbB42Vzyb3odsO92boS1CAZGRWgSKDxH851LQRrb07CMxkuSsfPBhwyL71KF+zXfBhMS0DOYXIcOmZQmtol+6Yy9HbWERrr9XnaKaOtke11U1neSVb8BJm1D8DuRvbfXy0z3OH5RDvlYiZ23n0is4k/+W2NcNxWZLX7BrmR/eq4aiLWIScXutNRa0VmxW+dlmfk6qNpVLgMSCwSs5W9uHbDfdm5ktigGRkdo6HRxlABKRyZEgqPc45E7Zg9CVtyZIviRJIuRNGYIXk5Tx6hG3l6PIkTo0LL0tbar7VrKN9nNer2u3Icm1T3ErLP/FJs+/rBvfA6bu/rl7aWBA8uqO9d26msu15Ym6bBVzvHHMkJME2HpMoLjUrz7YnCf6wA+2zHVv8Vi/liMj9CkwU9mbluenxXLZ77TmM7it7UEULmOxN+vdADlz2lInjDSLy856i9ZN+mQtNwfd3S+PNnSlKbzhutmu1l/Wp5Ny425eyjT2X+yX9vY5A+n8Xlvvwos7OwGv1hW3bm2U19zufa0ah1UyniCyhPaEOpA/LU/i8GyMDA+QvPP0eR5k162kXup4wgdU1oOQ8D1/Triw2yPOzg+F3laVtQhS1g0c4j35ySAnK5Wu8mGQPjqkzLS0TbMJrv7r+uBl9ra03QMW/2iGKIsBjaBiKv68/VWZ1uZpPxKQIE16MOMim1lHdXztCxaKrOhdQA829GIbNkYGB2hSQB9x6UIQ5Z+Ks+//OiYfmxBS465b0WFzgv5Azly5yS6vR75JlpBBqGDQpnie1FEJlzhWpa+1rL5Gnk72002SLzQ6cOe3L02/2EDvk3VdN01Dfk6+0WEJr6wzbkfhcDWXCyRBhvitcQO372j74UhX9ZWsgv5orwSDhORbmodAEN2NEJbNgZGSWjLDuImyNOdZFebfTlF/rl7XeWtcz6e/ayznWLbUOtg3eNu9q03CRuhjWQNf15CG1MD9rMwRd5j8t98Xe/O2uqnvX6M0IzQRvtQXr83x89QrfNo7zwsRhajdcOAEdpICG3dgGf2WGdoGDAMLBsDRmhGaKOdoS27MZk866ANA/uLASM0IzQjNMOAYcAwMAgMGKEZkAcBZBsZ7+/I2OJv8V8HDBihGaEZoRkGDAOGgUFgwAjNgDwIIK/D6NBssFmKYWB/MWCEZoRmhGYYMAwYBgaBASM0A/IggGwj4/0dGVv8Lf7rgAEjNCM0IzTDgGHAMDAIDBihGZAHAeR1GB2aDTZLMQzsLwaM0IzQjNAMA4YBw8AgMGCEZkAeBJBtZLy/I2OLv8V/HTBghGaEZoRmGDAMGAYGgQEjNAPyIIC8DqNDs8FmKYaB/cWAEZoRmhGaYcAwYBgYBAaM0AzIgwCyjYz3d2Rs8bf4rwMGjNCM0IzQDAOGAcPAIDBghGZAHgSQ12F0aDbYLMUwsL8YMEIzQjNCMwwYBgwDg8CAEZoBeRBAtpHx/o6MLf4W/3XAwKgIbXd32023ttyW+ptu75Y69Z3ZpJRnMtsppUvF7e7M3KSQo8vvbk9L5be2pu7w4w+62aSq29symbmd3bIN6wAOs8E6KcOAYWCTMDBSQpu67d1dlwguXEvFbU8D6YCkIjlNt0ukxqTHhBeJjvJvT5N80YGyXG6TQGO2WidnGDAMrCMGRk1oUiGBwCZutrObZl1ERjqPXO/u7oTZ1mTqpjLrohlWF7LqkmcdwWI2WSdmGDAMrDMGRk1oejYFosHsDBWH+5hRoZxch7RAiJI/zui2thzyQw6OWl4sR8SIvHa0DsQwYBgwDHTDwEgJLT3LYvIC0fA9ARJICgTFJKbTJD/k4FkdygGUSOf7Xo4RWmlZF/GyY7fGbHGyOI0dAyMlNHmmVSwbbqXZFYhGExrfj8uN6oclvOwIUKHcFumQNNxnQkMZO1qnZBgwDBgG5sPAiAltN868QEaYbW01PEPDcmMskyFGBiPIi0kS94zQ5gMtx9fOLYaGAcMAMDBuQotktOVAOPwjEQmcuK5CAAAgAElEQVQSSA7kkyMjvrczm/ofmPiyUX6aBcp9zo+KsCVHa5TAgh0NC4aB+TAwakIT0ICw5F0x+Sm/3APh6GdgabmxTFBRxmTmPn5l+R02vdzI8kGS0Q57hmbP0OxFf8OAYWBuDIyK0IQ47M9iYBgwDBgGhokBIzQjOSN5w4BhwDAwCAwYoRmQBwFkG3EPc8Rt9Wr12gcDRmhGaEZohgHDgGFgEBgwQjMgDwLIfUZxltdG/YaBYWLACM0IzQjNMGAYMAwMAgNGaAbkQQDZRtzDHHFbvVq99sHAKAktvU9W7OnY8v5X+MxMePeMzznQ6VM0+X0iJW98X63YNovfQ2NZ/uVutVtJtXx4bw6fu8E7czjWyWY9dt6ts6ir81XFb15985bz2IqbACT8AkvYFQf+Bsyl9zZxn4/+Xc4MhjlP1/OcX5U2zFvRTWbuaOX7g+ndUbG/rn0EXVtO7xYEW8M7qtwXlOOFDRqCnOYYQaYdu7XDLnEaHaFh6yoAT4Ik92bqI58cPG5QfF6Xx8v0H/lMgA5klhoVGqRuWN4+/1malBc2Tujlb21znV2+rP+waVke277p502+L8O3VcvXNnbVp/Ppay236zU2Fqhgs0R6CdtabsDw8j5a2+ZXzl4pMys+zBvKC/EEm0Pby7cH6JpMqulJTkhDXvn0lMQgtHHokI8J18dIx8yul0NqoyI0kAiTWRcgMXD5nMvq+3xdp9c3fAV6aZzSkeAIHb6xNMwkWR/K4NiUhjybfFy1f6uWr2PfVZ/Op6+13K7XOYKQsmHlYFZ8eb2+s9bY7aq3Ll+bX3X2srwwq0wk5dtTZgYJXdNpaIcsI5SZummx2TjyRkKjgWNIq48Ry7Xz5ZCZxHFchLYzczzLyQEpAL9YRigAz8Dlcy6v7zMB5YhLyuqRIl/rUW6Q37ZUkhosbEO5uHwEn3ws0nJJjuRBxCiLPMEflE2Nlu9PZrNqw9+W+IdyIgsdkcjn2QDLSaNqGfFO3Gw2dbBHytT5B//l2FinSh7KsQ3sC9LlGOt8Ib/w1YcUl5xcjk/SjToIS2Rt5dgnxJX9wTnqResMemFvqneUS+llHK4q/tDbZG+ySWKVbPaxyAwQYwx3yjOs1DYLHMoHgYnAvB5ZlSlkhrSkD7bacXnklYvl+AgtA+JcYBisdedcLuQpdzBIr288oXMoEUVsEJJW7hiYYFAm6lCNC/flyPan67Qhc+joyrp8PmmgahRbkbU99WQE/2FX6GSCTKTFxu6XYxOJefKPy0Gpw4ANJeICIdOSrrZJyuX+OF+0qVZeig/7wnKjDNTZPH7Vxjh9CZ3jU9Wf6i1vT+hU2XeRITJzhCVpTQSRMJjvrIOepjSFiQXij1h0szfhzfvv20vVTo6TEDHwnNpwwmeMN57fUVtpigPstmO+nS4Sl/ERGo3ScoELnQeIiRtf9ZzLc0MIBJEai75GuTTqS5sicyfjGyo1kliumF2hscl91o98OOq0nD3ceGO5Qg/bFMoiPsVxuu2fQ05osMA6+TxnK6fXyleEXSqj0mA/jm11qm3yNtT4Apm6TNt1rV+5GCt/2Ndl62d5OO9GEAnfKCfHYGs5bVXxh946e4MtAaPcVoKd1QFjsr9o61I3BQ7QPrguSue+HpPfuTjAXjsun8gQ03ERWvFQW4MbwQidTgAlk00JuKqziWXVfWlkIAKMarXesj4Z+Smi8NepkUCXHDXZsY2cT851GutFXjRYXPMRHYbYnyvrdVDj99cUj4p+SqvkVR0D7GiSodNQxssmeXV1mrVhJYSWr0vRX4pxQ3xKvrXk47jU1RvLwzlsAX5xX47AMi/fldMFx8lP1rvs+ENvzt5kZ5plIX/wo2wn0kox8/3FxM1kSbnAQzk9zdakvNiBmIV8KQ6Qb8fVkZnEdlSEJg5jtMjkIo1OfuXo0wBc3xFWZ2UMaAanvl+5piUyb4fvjNIyCOuGXDRKTyTbs8p31tB4krxgL8rjWLGl0I0YcKeDMvqIxhpkJbuRD/chM3Qy1fhJ/rw9nLdOfvKPZfA57MGR4xr8ZD1N8lJHyL5AbpsfOh3x4TpjWXJejnHeNi6j/W667qIfsoO/1TqQdGCyntDKM59Vxr/JXq9XBoSZFQ7vhxqAQVYlhnoZmQYRlbyVtEBoOh902XH55DY6Qotg5tkQSIx/lkw/nWdA8jkDMnffdww80i8aB37UgM5f5MgMKdfZeRmypFeQEMrqhprTz/aJfF8Wzyw8YWNGmDpPLhM7BTVTDMSAsqnT4Pz8QwptW+t1yTb1gwf8RJo6D8SP/YMfqQOWZ1JTNy2eS7baQHXFvkCuHFtlKBtzceOYgSTa5LINXK9t5XL6WRbOFyE0kSHlgeVVxr/JXvgQ24vHcMK5j3uG7KoxFIJOMy1O5/OSLf49uMNxpprLh/x2XC6pjZLQDETLBVEunqHzTB1BLo/dW3097EeMfd3TQG4/bGjSGUg2kVtTXkvbLIwaodX8Is6AvBiQ/cxhjTs1q9/F6rctflhZaMu3H+kem5nZ2X7YYjqXi0MjNCO07E/c+za00tKSWqLsK8vyL7eRWzwtnmPBgBGaEdpSCG0sDcb8NHIwDKwvBozQjNCM0AwDhgHDwCAwYIRmQB4EkG3UvL6jZqsbq5u9woARmhGaEZphwDBgGBgEBkZFaOF9EHp/aiu9PIsRRPm9oPy7YZK37pdS5fLhZ+vxXSF+9y27Ie98PyXeq/dclq1nHnnzlEHdth3rZIdXEOarmzadSGfdfI70tuM8Zdpk7lf6IvHmOPD5snxZhcxl2dYkZx675ynTZMNepI2Q0FLHFMgnvSsVrim9eNEaL4miQsJ7Nukl3dJ9te0Pf2dtVQBZlVz4heOy9cwjb54ysL/tuArZXWVyPj5vsxnp85RBWX1cpiwtO3e9TH0si89zeue5twqZ89jRt8w8ds9Tpq9dy84/bkKjnRzws3PevUOCHUaLifTkHnZCwBGV4gmx4d2rVQFkVXLhF47L1jOPvHnKwP624ypkd5XJ+fi8zWakz1MGZfVxmbK07Nz1MvWxLD7P6Z3n3ipkzmNH3zLz2D1Pmb52LTv/uAlNtjcqCChHXBJsvasAX4eZWvoybwBA/TJlE0A4DeSKbXs0yXq7aHsovTVT8CUtraK8LH3inPVFeXGLrep3x0Isypux1umRvKVlVnqJlcs0250GEU1lRBf+cjqjn8v47hl/AysjT9fbZYdl+6NUD9iurNFO1oFtvqiusT2Wrw+6r2OJmMixTZ+XVQzurjyat5nrQHBZwVHHb8JpW0L9lGMU6wz+85Z0pFvLYj/ko5uQc+XRB/1HSWGzz0dtX67lT+QhD8rGj3dKrLl9kL+8glOOU8BwlJXBDHR7mzDArsmXk+3LEQ664qOLrCZMsd3rdD5CQis3HlSGr+DM7AqdVAS6gAckiN24i4bnwUWND2WiDgCW8ufS/EyPSAB5cAwNJDW+sG9dWCrVaQG4RZo04kKu6JDPzKMxYraJ8pwPjSQ2zNhZJBtYD+yUY1OZqt203NvhO2ush89zOuv9ST6wPXPJo/iiPNuCezhyWpdzKefrjT5sCozV2Q5dvizhj/V1S0tx4roOcvS329KgzmOZluFhD+vn86otspdikofyfOTyteeqbpi8IIvbXWv7QB8gcgv/WLf3Q2E4h0Ho9vl9/ei9URUpguRLsvu1mzY7+2CK7V+H8xESWtG5+1GNngWka1QOz8jkHjp+pPuOJEM+odGnTkDyayBBhk5DWZAN5/N5iVTzZct+oPF6uUVD3J7yZzHSDunaRr4unav4iR3Q423yDR2DB4o5DRqq8pC/OLZ8Z0308F/oPCGj0EmduLeLrjkeOq0kl8vQuS6Tqzf2ETLb7OQykInZuj+uOi7ax4a6Zlt1PLLXOVxofXQd/C/jea44eplBjreZcBjlUbuaq334OAF/hGHyJxeTqL8hXyMOeBVAzlvw0SiL4qLrFnau83G0hCaVwuSkZ2KoNG5QoYIVYD2Y8g1Ok10TQHJpvjwtsZRsqgEe24v8IJpEzttu6ssXO4lTQ9Z28HXpvKmTo7Sks/iWWg+7xX7vT00Z+BfzxZFyR4Imv70M1aFAfslvlYfTkJ/rTadz/ZRiQ3K5DOeHfG9rV9vr6oL0eXl0zfqjLjXLSphSy9AkpyJ3HluojMjDH8elSxylHNo7jpCFY5IzZ/uos7UhJtAtx0rcqRz7WypTp1Pu17SbRlk1ZVjnOp+PmtAqAKLlgwSwtNzhR9ZU4SFPWBKRafruEr9ZBtDkGl+wO83+QgfKM5KUpsHr5amlxul0GpceKzHhRlU5z+vhOAX9edtydutZaZOviJGvB6m7om6qOoP+UF+pA+4su+J3Xh7bg3qrxLODnVwGNi4/Lgm3MX5bXE/ax5q6ptjo+OrrZlxofbAl2Fnxv2ccvS2+k6/+OlnS8Ld4+0j9BWRyfXo7VMy65GvDQSU+Xkeqs0XbmvYBNq/bcdSEJpXhK5pIqrwclAAheWVUqoETZcQHxjSDU0uRTaDgtLIN+dkf59EPb0OHDjtSRyG2cmefvVaNrWSXTvOjw6qeMNIt7tM3yLw+P2gIac1262cJ+TIi08ulZ5er/O4ZxyPoJYIk3/BcRfIIbuJSYQc7KzpKcV5OXLztbO906qYFoWmbfd6SDQlTFVs1Rui6CRflGKWYet1eRhHDYsWiThbbw+ciJ/ql2iXSvC7vJ/mnr8kfn19fl+JULP/pPOoa+rW9leuM7GRzik/5WV2+3ZT7iHZMaVtg87odR0Vo6xZ8syeNjC0WFou9wACWSvdCl+nYe0wbodFygwFw7wFoMbeY7xUG/KyEVmP2Sq/p2TuMG6EZocXnB9bw9q7hWaz3LtZpeTItJVr89y7+exlrIzQjNCM0w4BhwDAwCAwYoRmQBwHkvRwFmq5hju6tXje/Xo3QjNCM0AwDhgHDwCAwYIRmQB4EkG10vfmja6tDq8NFMWCEZoRmhGYYMAwYBgaBASM0A/IggLzoyM7K2+zAMLD5GDBCM0IzQjMMGAYMA4PAgBGaAXkQQLbR9eaPrq0OrQ4XxYARmhGaEZphwDBgGBgEBozQDMiDAPKiIzsrb7MDw8DmY8AIzQjNCM0wYBgwDAwCA0ZoBuRBANlG15s/urY6tDpcFANGaEZoRmiGAcOAYWAQGDBCMyAPAsiLjuysvM0ODAObjwEjNCM0IzTDgGHAMDAIDBihGZAHAWQbXW/+6Nrq0OpwUQwYoRmhGaEZBgwDhoFBYMAIzYA8CCAvOrKz8jY7MAxsPgaM0IzQjNAMA4YBw8AgMGCEZkAeBJBtdL35o2urQ6vDRTEwKkLb3d12060tt8V/0223uz319yazncbOvSnfzmziZVx2+EE3mygd0DeZuZ3d3YqOJrmLVrCVt07CMGAYGAsGxkloili6EkpTPhDadDsRFu4tQpRjAaL5aZ2uYcAwsCgGjNB6LDmuitAWrUQrbx2BYcAwYBj4rjNC++53K0uOuzszN8EyoRyLGZ0mNMzAeAmzbYZWkb01dYcPXxaXPKOO6TTZwPrV7NJAbB2ZYcAwYBgIGBgnoRFZCQFFEpntuPicbbrtn3VFAlLP2lBmq8i3PQ3PzboT2sTNdsLyJGTJ0iTOQaIgzZhmhFZ5BmmN2Tp0w4BhQDAwTkJTpAASiaRBhBdnX4rQNIGBeDoTGtmQ04/nbkyo1mit0RoGDAOGgXoMGKGpJUcQEwiFwcPEY4RWDyqOmZ1bnAwDhoG9woARmiK0OCPamrrt4if2u9szvzzIhMbEt7u7E3+qv6wZml5yjEujNLPbK5CYHuuQDAOGgU3AgBGaIjSptERqeJ8sPO9iQpN8mKXFZcmtLbc0QuNlTzzPk/fljNDsGVqPX+ZuQidkNhpZLgsDoyK0ZQVtlXI0aa5Sl8m2jsQwYBgYEgaM0NZstGuEZh3MkDoY88XwvJcYMEIzQrMlvDXDwF52AKbLCGdIGDBCs87MCM0wYBgwDAwCA0ZoBuRBAHlIo0zzxWZNhoH5MGCEZoRmhGYYMAwYBgaBASM0A/IggGwj2vlGtBY3i9uQMDBKQuMXof07ZC3vdoX9HYt30fw31dI+jABD3AOS3h/zW2n5jY6r+VFOjiyf7+u03HtvYr/e1SS8R9esU+ux68U6tqY6XEVs59U3b7mAxbSBAL97mWtDAatpcwKOQbBhy2EfVE6T87BpAbc3vA9a3i81yMnr0DLtejF8b0r8RkdoeGmaX4CWezP6jpmuPO4E+Jzz1d3nPHXnTWVzabl7dbK73l+FzK669yLfqv1btXwdo676dD59reV2veadcrhMebCYJxvYMJlUB10hTYiLCS3lC6+1BLkhb14H22Tn4yAzqedRERoaG5NZF7CjAcru+HzOZevuc56686ayubTcvTrZXe+vQmZX3XuRb9X+rVq+jlFXfTqfvtZyu17XEZqfmU1nxVZwebKBDdPppLq6ILvhTKduWkdotEIS5OR1dPXD8g2L7MZFaH75r7kBlJb1sOVUpRGlESMaBBopPglTdx8zxLBkE2zRZTnPZDaLjbtWZmGfdBBb8n21xw/HMlH2dvrGW2WJ0penZR34rb4LlxsIYJCAJSjkYR/EprgvJslk33J2iix0nCKf7c7JjzJmU/99OZQJ96v+IZ5ybKx3JQ/l2Ab2BelyjDZR/Pv7VV7qk/I5uRyfpLvsd1s59onrjX2Sc9SL1hn0wt5U71w+2rCz7aaMDb8nqrQtud8wQyseEQQ5eR2sz86HRVpN9Tk+Qmt5XoZgpUZHnUfrDI06j2Jfxzo5okeWT6RDqOZJe0KGjqNMoJzfyykICZ0Lp4dz+khpzTM9LsMyywRVtgM+6GchFVklP/O+VeyUkTqRWHWpKdlSjmN6NtNURmzP/bHt0SYQvLeJByF5X1hulIFOeB6//KwlfJ8PsvNyq507+yNlm8pV8hb1Bp18XA6h7fqBRAljPk6a0KhdFXWRfKn6zHbaeR7nQ43L+AiNRoS5Sg2dIBpQdZSoGz1kdLlfHv0WOuQ7azwDFMIh0uW0Ol06D1/zOcrLbASdCO7pfMHWcmeRLVfMuECmIq/WzwbfKvopJl4mXdfKpzyVMioNfuPYVu8VeQ2+QKYu03Zd61cuxsofHT/YoO83Xdfphyw+LovQvM4C78AX21g693FImAxp6Zrts/NxERnqe1yEVnzmRXfmCEZo0KGBhKW0VRBatQFWGu0KCQ1LhDoGbIPEg2OB+KDDwTUf0cGJ3FzZKLPGt4r+hg67Vn5TGZXGtrO8unr39pMMX6bGl5JsKqNl6Gu2g2XgvBTjFrkos4y4QhYfYQsPZJAOjNUtWbJNMd6yJFvEs5yeZmsiX/RCZ8hXbU+ww47jI7VREZoAHCNx7tClI5FfOfo0NCo/GlwyoflOqPwsyNtEnVNopGkGFTqOtLym87ddQ17sBNQoV8rXy0h2tHW2IgOdjdZZ1pFksm+hTPKz6bpZfl6GlgebvO+ypNdS7z5fz3rSZdqu6/yScvgrxzjvK/K26dPpXfRDdqi7KpaDzK7P0HYD9vQybCXOeT+DvRiAlokPdtoxYWcMsRgdofkGVyzh4IcMsTOjD3VuTaZuWvysmDtDPmeAdL0fiAFLmuF5jy4L0g3PkLr/KAQ/SGF5OA8/GAl6mczZB5mB+ZjgmVEpTqlT4TJsK4/Ic3762Bedl/YNduZ88OWok/PXJdtq4qjKaP/gR5pRyLPGfL1nbajxBXKzZZRNFb9zfpEexLhSTsllG9jvtnJ19cby5HyphObbXZppsY18Dhu87snMHfU/fjJCQ1zsOLKf7Y+xwnMdwrrEocusb11sNTvGNdK3+t7M+h7lDG1MYF1nQvMzB3oONaZ6MV83s8O0elvvejNCo+cTQwTrOhFaaWnPbxGWlpmGGHvzab07P6uf4dWPEdrACc0a7fAardWp1alhII8BIzQjtPgLOmsk+UZicbG4GAY2AwNGaEZoRmiGAcOAYWAQGDBCMyAPAsg2gt6MEbTVk9XTKjEwKkILP5Cgd8CKvQLDz8fz71kh+E0/ruC0+M4PfRctvHO1UyKOLjqhe7+P7N88tuyFr2wjn3e1d54yXWXrfHupS+vehOv4bqO8a/bglW5SbFS8CbabjftL2CMktGbiqgNkUyeUS8vdq5O9Dveb7G1KW7XtXXVzPj7vat88ZeaVvUpdXW1aRb5l+BVkpN1k+tq5DBv66rT8+0tiHH8jtI5Ljk0NJZeWu8eBX7fzJnub0lbtR1fdnI/Pu9o3T5l5Za9SV1ebVpFvGX4tKmPR8quIi8ncO8IzQouf1Egzt7BEhqXJ/NY6nCf3LSzdsHA97zfLpFFAxqzDt7Vi3p1ivzzaGkm/D3bZYfl+GvxNn19BQ4yySC/2hvR2lbZrqr5bFsvz53cy3xjraldpWRfbdJX8K+/rx3WFraO03bk6jP6X/Euzh+hXxpdY1ttVjm0sN2c8ve28TVvxqSLtkyx1Y5uznE5JwxZWvCyey4v6jmkKV1cezWMoF3vIQFuI38pTsRKdyMsf10W5w48/WHxINMS3DceoEzvuHcHsdaxHSGjUuWzkN8vo22Z6U1d/XUPA3OFLPvqulO8IKV2DMHQqpNd38GEAwB2Ol5P5hhbnibJARGzzXHZV7ajqo8FKh2+zsf+wNxJDxfc0AAjPfpoJPcWa4skxUPUgMkEmsAvEX70vRE4klrMVmzB7nWlzYbYdPsc9TityKJ5kL8c9+Ul5Vey1/dkyFfnK5h44RvzsaIRW+kHDpgJCNzj4wffLI8qC/Nb1m2XU2MWXkh9Nab6DSh2DLou44MhycU9mSdLJ18UL+eTI5fm8ktbRrvijAT+rbCG0QqbMQOKf1Kfcp223tF2wP/hXJqnoe0OMUV772HbdKZ7ep7JNXm7mfldb2X8+hx9d5Ohydb7ofNDRGhsd76JumRibZLMeOx8mqY1whpZGjAA1N4JcB6Ybms/T0hmyTF1eX1fzhs9vYFaQs1PL0NdVmeVlOMmP5SZPTKqzgE4tN1wn++riVVd+UbtYX5ipdCG0ms6/pQ69rwuQBGLQ5jOns38or491eXL3uxCR95Pqn+0JaVTflK+1XCZ2uoxc819Vd8KtTkO5rjhGfjuWYz6keBihZWcQ5dmLVDg3pnCelnZCgyoTJefX5fU15GGkmeuYdJm2ayxLgRTDrKZso8gQ20WvtlfS8Ndkn05DGT6ybD6XPPoa5ers8n5g2cx3mC2E5jvguvpsrsNkX8rHdaNt19fwRd9vug5pVXshK9gUCAZ4QRrKxjonQmnSGWRq4kg2lH1O5ObL+aXLah0kmUlO2c4qFlOZlMZ28zlk4ViLF0XAyG/H1L6HFAsjtEynGhrw/9/eteS6jWNRb6OB3oUL2YtTg3ieDRQacJBJZwtBZvWSWeplD6+Cmva4Bt1A+6Wrp43agRqX1BWPrkiKsiTHps7AEMXP5eXhIQ9J2bI5ojIDA4+9Yl8osIMvd69pY/9ZpvmK/zOsfU7ijtqOx+bY/p4HfccvSchq3ud97MRMyK71pvyL4YWDRMvjg/1YG0r8UqF2fib+uwzrc/67ib3fny4e8In1obah3774ZOvsGY5oebkitgP/TLl+feEZHdrzNkKb+iKm8eW+ok8aTvY34LYDXtl2yn2sLWpfOTBsV9xvW66ML0GosR6GKWi9SY6EWI4QdqAS2+WwJZbTsSQfp2NGnt0GZpvaod0q6TiB3MZguFV+XNsv8pF8vDbnlqqPggbPipYCdaodTiCcQKZyZs385CP5uCa/1rRNQbsBQVuzg2mbkxM5QA5shQMUNAoan42SA+QAOVAFByhoJHIVRN7KCpTt5G6LHEhzgIJGQaOgkQPkADlQBQc2JWj61gRd4cQefrvftpj3w2l+ucbKYLoN+9/hhN/V2PQp91PrnmI7ljeGRSwuVnbNuO73R4X/l5XDLZdm27BkX1rbsXv0DcOxvLcWl+LJtdqxdD1L27u1/qrFn00Jmh1k+qNPfOOCvnEg1cFziD2nrPiTK2/T7H2qPal4fK2U5onFadq1rr5d4c0dJfXmsMA0DJfYTeVZw85SNlM+Lxmf48m12rF0PUvbWxJv2gpHkNsSNHljBLy/T8Tr+O5d80Lf/O7+kiO/m5pD7DllhbS58jbN3k8lvRN7s1ONxU21Ozf/Je3KlcE0DM/xcw07S9mc067SsjmeXKsdS9eztL1SLJkviFUJFtsSNBCssIqUV+P4l9d60oYX2eoOzr+lHfO8aPA/yXSH523qa4f8LkIHwqT/i5JXC4HwakeqLVu3jw/17l79bfD/ZqmyYtvtXE19Tuwf/X+paf0Yh8e3nW39jyxZOBwf3eueulcyxV7vVJhH67ftjL2DMttn6F/79n195VWsf7Rd4f+35D+//IJH00b7QhdL5vVbiovDP5HW1YH/I1f0H2rKvf47H2P93GE74oNiIP9dhhgrfvgaK+SJbZ/Nj7ZknCkuJfzq8In8H12XFulzrEf8615LJpyARRz6Zv1W3HidJjhr47UpQVPyyqBxhG8n8cdjO0mJkOgEZCdg819OKjie9MPy2nE4sDAs6YN7rSMraIX/o2X9d/dQ1k1g4DcImvcrCHvwNcTh8a2EX7zwLzmWvDKhObFBPGfkUSyDH95ve5/EE7DwecLEKb7urEjpJNhiFhYs4b2AaifKA6gv+Bjq7HGmrUMn8mFa20dtvnR9OfvSb2HhhniW+tfHINSF+AVbwBPTPsyvGEbbXsIdxUTHrJTpLU772MXqQSyQP9Y39BvLMExB+67fptGJWK9CSCGrDFi9ShyuzvwOza/ekPRKZl1Nahkd/M6OG3Q4sGAyNqtiVw+sENW+Xm3deI9hW2/sXuLUb7WvVydQ7/7R6ycb59qKCwLZObh72RW07ZX2LZBH/ZJrrp2Kf9df7Yoby6Df1h7ms2n23uaVdMXTpiVuojMAAA6ESURBVHm/wiTfy+s4kEjLcKfUhvPbTfRBhCQOP1n/wAdnC/rU3dv0dlGm9rN459oO9bgFZ4xftm64xz7Itc+1ocXH82bI3Vg7tX289rn0vfHY3A5NB9ijPD9rj9Rc3PFdNxE7AkcGm4uHQePv+3+nIXF+NecnkN7AsmUTdYiN2Adt+brtjgHE0tY1uB/67W0GQVIfwvFsOIIMcY/NsROyY/MIE9FSedQP22Z7H5u4onlakR2kDTAK+I7nDXgO+inSz5345dLAn4FNd3zecixjw/l9JUEL/Q08AT4MMMz4HWzl+FXWPzFexPAPdbbHqgmeSDv4uU0Mtido7USgx0xhkMkzqLBS9hNI6r+cQnxssIhN3e3hRIRhrBd3dC5eJiAYTBIX8sdFK27b5o377XarbX1e3M3fx8jEE9k5ujaao8bj8eh2u+rzEnmwbRi2mPi00Eb1ActoHl3M+MVHuyoHAbG27b3a0b5DHmB9oVzYIQ3z5tLQt9C2aTaE1/0jR/RR26KYDG0PeaR5e/hFeGJt9/I7n+JtF9zGuINtCDgjXhiO1zPgfu/4OZRBv6Uufm4Tg80Jmg4UKxiyYtPnZ0pWP7DhyxbHx+7IK/ZfUW5wtF82UHG0g87VAw+fo3VcIGjis7WN9+pH0u9W0GTg6mSlOMTiJM37DpOdW3GH+6XyqO9j/6cW6ov3mX5xAfvJPuyPYdaVA8FTn2J4ih9oZ+hXDCP1OaRpHdjuVH19HnkbfscRRNBNyrpwgbbk/EMfJJ/LC0d0iF+SJ4n8uXpDGuBh+GV9w3sMB1sxjP3O2h03wv/r5dopafzcJgabFLQtktEO8BgGLo/ZGcbiYmW3FleC5xYw8UJ6bH753y/t0XM4btxC+9nG2xI2CtpGVlucgJcdeMTT4+l2omYRxEl+Wa4Rz3I8KWgUNB6fXMCBrQqaHmOGb5KG586ceMsnXmK1DlYUtAsmM5JxHTISV+JKDpADczhAQaOgcYdGDpAD5EAVHKCgkchVEHnOqo5luSsgB+rgAAWNgkZBIwfIAXKgCg5Q0EjkKojMFXYdK2z2I/txDgcoaBQ0Cho5QA6QA1VwgIJGIldB5DmrOpblroAcqIMDFDQKGgWNHCAHyIEqOEBBI5GrIDJX2HWssNmP7Mc5HKCgUdAoaOQAOUAOVMEBChqJXAWR56zqWJa7AnKgDg5Q0ChoFDRygBwgB6rgAAWNRK6CyFxh17HCZj+yH+dwgIJGQaOgkQPkADlQBQcoaCRyFUSes6pjWe4KyIE6OEBBo6BR0MgBcoAcqIIDFDQSuQoic4Vdxwqb/ch+nMMBChoFjYJGDpAD5EAVHKCgkchVEHnOqo5luSsgB+rgAAWNgkZBIwfIAXKgCg5Q0EjkKojMFXYdK2z2I/txDgcoaBQ0Cho5QA6QA1VwgIJGIldB5DmrOpblroAcqIMDFDQKGgWNHCAHyIEqOEBBI5GrIDJX2HWssNmP7Mc5HKCgUdAoaOQAOUAOVMGBxQVt99PvDT95DMZWIF++fGn4yWNADPP4lPCHGBLDEp6snWeMh1PSVxG0v/z9n81f3/2LnwgGIvZjHSQEen5+5ieBgeBDDOfxgxjOw0/GJzG8DoZjYx3TVxE0EbNv//kvPwYDwYWCdp1BwEVBHmdOxnl8ShaUxPA6GKJgjYUpaEZ01hRiCtr8AcCVMTEsEZtr5KGgzediCYZjIobpFDQK2t0dbZYMAslzjUntXusghteZjMnDPM4lPETBGgtT0ChodzfxlwwCTiTzJxJiSAzXXrCVjOUxEcN0ChoFjYKW+PLJ2oP5e9ovmUgoaBS0tTlawkMUrLHwdxW052+fmsPux+bjtz8u+gLJx5e7Zrfzn/2b3y6yUfrMzPv6Q/Pm62W+Sj1znqGdzw/NoW2rtvnwcJ4kRuenU7Pf7ZvT03i5hwNge3py9XQ+HB6i9T6d9s2u0D4OFG+3zC8pVzII5kzG54dDx6vd7tA8nM/NFOyGbds1O4MZttmH23pG+jnmG9ZXGl4bQ/Sj4w3w13K3365ds285h3Yk7HhpsJT4fnmPJXJYx4xcU7ZtXWP3a2IYw0z8LuEhcsu2AdNK8Smp09ZTel+C4ZiIYfrdCtrz17fNm49eXJYQmzFhW6KO+YIWJn1PMj9wS8lTmk9sn1qxxAGg4f0++KE2fZqI4DBN86SuardEaMVGySCQPKn6cvEWV8QiVy6Vpm3b73cNTuIaL232YRS0gCH6g2Gpb45va2JoscC2Or/dgiFw14sRtPn81Jz2Q+Fx7d8fmoPh3xgutn7r36X3a2I4x+dc2VhaLO5STKaWK8EQBWssfLeChgL0/O235s1+3u4J7cXCNydobiUfJoGpRCrNf3aTi69HiX847AerXDcpHQ7N4d4FTSbb/al5Oo/vYkswVMxOD6dmD3a7+DFBg352GIONkvpTeUomEsmTKj8lHtsq5fDe86sv9i6PO00IoidxcgIguxS9qg9juGB9WmaJ65oYzvE5VzaWFotbAp8SGyUYjokYpt+MoHlRCsdcB919fX3b7PGooo1H0fFi448uO+H5GMqJrV/f/NAdI+HxpOz0gn21IQLZ9yVmF+2gP6nwojs0mXjboxclpAiNHpH1jhNMvrAr2DenUzheix3FeNt29yDHn2GyCaIn8UFk/cpZcVQbfvWtR0Cya1H/3aSvR8iJIycZJCWD4NLJ2PsS2R2gsGhYRKr1V9rhj1x9exXLrm1PZ3dcFouPY+wF1S8U/BFvyreSicPmWRNDWxdiIGkoQHZ3pWUDp1occGElYgfCPoaLrV/rmHtdE8OUzzY+PsbS43B/OvXGqOsP5XP7KELr0Pnk53//3JXRtNKxOoZxCYYoWGPh2xG0jz82u5efes/BvIjsmr64DXdi8ixNxUXL7PZvm1+//dE8i105N2+fsfl7FS55hhfsSZrkc3kSvvTtTnv+N1/QVBzkioLin6/pZIkk6gjY7QRwtxWe7bhJBmyqDRFGtYu2JF6P0NygchNMGEiY1w2ah4OzgxO01uHz7rqdUcoXzV8yCCSP5p961V2D8KZrIwz6uL+AExypIQ75sAq+70sVfOxnaUfMt6ntk/xrY4g+dXjpwhSegQXu9HfE2s4OfxAxK3ZjuCDu6Nfc8JoYDjBruYhtwbDDQMdYhKuKY+w598COKw98jtjTUwwvqGEROxXTEgzHRAzTb0fQ2p2SCo/scvzuqS8aIl6dwLmjxiBWroz7ogmIVOa+vztrxeLlp7beaXZTuzKMny9ogThIJEtIJXeYFFHEhmGXH0jr74fPMbAenIhU3AbpOoHp9fDQPtQOgyVedxBGSbefkkEgeWy5qfceYy9qvbYNsOr7m83b7qyHeVDQ4v2M/qNvGF8avhaG4k+vreYo0bcjLM7Ufyta9pjRTcwgjF05Zz8sRGz9mm+J65oYImboK8YrB8I49wvUQZ7BbjbwK4YPlrfpNk3Sdfyjn6XhEgxRsMbCNyNoOvHr0aCIVk7QUs/NuqPB9tuIufuYffVDrj1fMsKIZXLhRQWtfXAuKy9LMpwkcGLAfBgeklbErE/6ZB54NoQ20YcYufV4Luq/EQxbvmQQSB5b7pJ7nTh7bTP+YZrUgfcY9ml+oXB4CCLo8yQEDfrZ+q++2fiS+2tiaDEQv8OuX/EwOzQQPl8eTyc0PBRCabvFxdZfgk9JnjUxTPmM8akxNsizoqDZnXQJbpinBMMxEcP0mxM0FRJ39OdEBHZkbhfXHhdGjiilbE7AbLoeT+Ku0AqSiFrwJb3zs+Vi94sKmhvwid0WfLHBk36YD0kvBMP72LGgzePu3dFa2G31bLhJP6QhiTWsExuWi9Wj+fVaMggkj+afcj0/nLqfNehglckXfcSw2M7d2zSXv91F6DdCfZ6EoGE/J3yb0j7NuyaGWodeLQaDeziilTI+PXDH8REmZZ8nCGGqz1L1a/zc65oYWozUV4y3OOXyTD9yDAvaXJ0pUVVfxq4lGKJgjYVvRtD0WZffPodjxv6xYBAU3T3hdrtEeAaC1/tSyM49x4v5MihndmwxAbNx8wVNV6ZyjRNOCKQTscMGvuY8JGbchlvh6jFhe7WTeqgnrJLRvkvvJu7WbzlybEXQ91tiEjc7IDsoSgaB5LHlSu51kuh4lftCjXmIrj87QBwwjPV7jHGhgVjk+hnSIkduWEcuvCaGtt4YBq79IFJ9XvSPDPE5Ltp2NoRT7eLJ9pnmjdWvaXOua2KY8tnGe0Hpc2KQB8bclC+F5PjsvzDi61WxvATLEgzHRAzTv6ug2Qm/9vs5gnYJWWotUzIIJE+t7V+iXcRw+Gx2Kq5bxNCK5VTMbP4SDFGwxsIUNL766u4m/pJBIHns4OF9mMSJYcDiUl5sEUMK2hUF49Z3eNyhzZ9EZPLZ4kRy6aSbKkcM53NxixhS0Cho3W/rKGjzJxEKGjFMifS147coaEtjXILh2DEjpvPI8YqCS0HjZLz0hHCpvZKJRPJcan8L5Yjh/PFcgiEK1lh4NUGTyZufIQa7n35vxjqFE0l+oJQMAmJIDNcWVfIwz7ES/EswHJsvMX0VQZNJm580BtgBsbB0Mj95DGK4YRzxy+NXMpEQQ2J4DQ7guJ0bXlzQ5jrE8n+O7uCIETEiB8gBcmDIAQran0NQSBRiQg6QA+TA/XGAgkZB446QHCAHyIEqOEBBI5GrIDJX0/e3mmafsc+W5gAFjYJGQSMHyAFyoAoOUNBI5CqIvPRKj/a4eyAH7o8DFDQKGgWNHCAHyIEqOEBBI5GrIDJX0/e3mmafsc+W5gAFjYJGQSMHyAFyoAoOUNBI5CqIvPRKj/a4eyAH7o8DFDQKGgWNHCAHyIEqOEBBI5GrIDJX0/e3mmafsc+W5gAFjYJGQSMHyAFyoAoOdIL2+fPnhh9iQA6QA5dw4PXr182nT5+aDx8+uHlEwvh59epV8/79+2ga5mO4jxvxmI7H/wGr+TOpARnO/AAAAABJRU5ErkJggg==||font-size="10pt"}} | {{attachment:meshMethods.JPG||width="350"}} |
| Line 53: | Line 53: |
| 1. '''Max tetrahedral volum''' : is the maximum volume of the tetrahedral element in the mesh. '''Pourcentage of the element to keep''': parameter between 0-100%, it used to keep or not the original input surface nodes. | 1. '''Max tetrahedral volum''' : is the maximum volume of the tetrahedral element in the mesh. '''Pourcentage of the element to keep''': parameter between 0-100%, it used to keep or not the original input surface nodes. |
| Line 201: | Line 205: |
| * Website: https://simnibs.github.io/simnibs * Headreco: https://simnibs.github.io/simnibs/build/html/documentation/command_line/headreco.html * Troubleshooting: https://simnibs.github.io/simnibs/build/html/installation/throubleshooting.html |
* Website: https://simnibs.github.io/simnibs * Headreco: https://simnibs.github.io/simnibs/build/html/documentation/command_line/headreco.html * Troubleshooting: https://simnibs.github.io/simnibs/build/html/installation/throubleshooting.html |
Realistic head model: FEM mesh generation
[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]
Authors: Takfarinas Medani
Contents
Introduction
This tutorial presents the methods integrated into Brainstorm, used to generate a FEM mesh.
The FEM mesh is required for the finite element method computation. The FEM computation could be used for most of the known modalities: EEG/MEG forward problem, TMS or TDSC stimulation and for intracranial modalities like sEEG and ECOG.
In this tutorial, we present the different methods available with Brainstorm to generate the FEM mesh and how to use them from the Brainstorm GUI.
New methods are under development and will be released to Brainstorm in the next future.
Mesh tools
Brainstorm integrates a list of open-source tools. These tools are commonly used by the FEM community to generate either tetrahedral or hexahedra mesh.
Here is the list of the available methods in Brainstorm:
- iso2mesh: this option merges the Brainstorm surfaces available for the subject and then generates a tetrahedral mesh.
- Brain2mesh: this option uses the MRI available on the subject, and calls SPM's segmentation routine. The volume will have 5 tissues (white, gray, CSF, skull and skin). After that, it calls iso2mesh (internally) to generate a tetrahedral mesh.
- SimNibs: this option -recommended for obtaining a realistic model- calls the headreco process from SimNIBS toolbox (see the Additional Documentation). It uses the available MRIs for the subject, and then calls SPM and CAT for the segmentation. Then the mesh generation is performed internally by integrated tools (netgen, gmesh and meshfixe).
- Fieldtrip: this option calls the volume segmentation function from FieldTrip's pipeline. It generates an hexahedral mesh.
You can display the full list and a short description by right click on the MRI of the subject and then click the item "Generate FEM mesh".
iso2mesh
iso2mesh is a Matlab /octave-based mesh generation and processing toolbox. It can create 3D tetrahedral finite element (FE) mesh from surfaces, 3D binary and gray-scale volumetric images such as segmented MRI/CT scans.
Requirement
it If iso2mesh is not installed in your computer, Brainstrom will download the last release from this webpage and install it when it is needed. However, you can also download the iso2mesh from the github and add it to your Matlab path.
When and how to use it
iso2mesh is used as the basic option by Brainstorm to generate FEM mesh from surfaces mesh.
Assuming the situation where you have surfaces mesh of your subject available and you have already computed the OpenMeegforward problem. If you want to use the duneuro FEM to compute the forward model, you need to generate the FEM mesh from a similar surface used by OpenMeeg Here is the way to do it :
- Richt-click on the subject: In this way, Brainstorm will load the inner, outer and the head from the subject data. if any of these surfaces is missing, an error will be displayed.
- Select the 'Generate FEM mesh' item,
- Select the iso2mesh option,
- Set the iso2mesh parameters,
- These options are used by the surf2mesh function.
Select either MergeMesh or MergeSurf.
Max tetrahedral volum : is the maximum volume of the tetrahedral element in the mesh. Pourcentage of the element to keep: parameter between 0-100%, it used to keep or not the original input surface nodes.
Also, a full example is explained in this page.
Here is a view of mesh obtained with different values of the Max volume = [10, 1, 0.1, 0.01] with a keep ratio = 100%.
From our tests, a FEM head model with a value of 0,1 for the tetrahedral volume achieves similar results as the OpenMeeg head model computed from the same surfaces. We have also noticed that the result with v = 0,001 is almost similar to v = 0,01.
Increasing the mesh resolution needs more time to generate the mesh, more time to perform the FEM computation and of course more memory to store the mesh in the database.
If intersections are present on the surfaces mesh, the iso2mesh FEM mesh generation fails (tetgen) and an error will be displayed on the screen. If you face this problem, you need to check the surfaces and/or regenerate new surfaces from the MRI.
Other applications
You can also select any surface mesh, or multiple surfaces (with Shift key), on the Brainstorm anatomy windows and then generate tetrahedral mesh by following the same steps explained above.
Here are some examples using only 2 tissues. This option could be useful for investigation of tissues influence on the EEG/MEG on the forward solution or on the source localization, furthermore, this option could be used for analyzing only SEEG within brain volume.
On the left is FEM model obtained from the scalp and outer scalp surface. On the right, the FEM model generated from inner and outer skull.
Brain2mesh
Brain2Mesh is a MATLAB/Octave based 3D mesh generation toolbox dedicated to the creation of high-quality multi-layered brain mesh models.
Requirement
Brain2Mesh is developed by the same team that developed the iso2mesh toolbox. Therefore iso2mesh is required. So if these toolboxes are not available on your computer, Brainstorm will download the last release and install it when it's needed.
You may also need the SPM12 toolbox. Brain2mesh is used only to generate tetrahedral mesh from the segmentation output. Therefore a segmentation of the MRI will be performed by SPM when this option is called.
More parameters will be added in the next version. If you are using this method you can request our support to help you or to add these parameters asap.
When and how to use it
This option is used when you have the individual MRI of the subject either T1 or T1 and T2. As said before, the SPM toolbox is required. The time required for this option is around 1 hour. here is the view of the obtained mesh from a T1 MRI
This option is based on the brain2mesh toolbox, we keep the default options. We will add more flexibility to control these options in the next future. However, if you want to use this option and you need support, we can help... just post your question on the forum or email us.
Fieldtrip
This option call ?the process of fieldtrip MRI segmentation (function ft_volumesegment) and hexahedral mesh generation (ft_meshprepare) develloped by the SimBio team.
Requirement
To use this option, the Fieldtrip and SPM toolbox should be in your matlab.
When and how to use it
This option can be called by two processes, either from the MRI or from any segmented tissue available on the Brainstorm database.
The mesh generation with the method is faster. It converts all the voxels to hexahedral mesh.
Only the hexahedral mesh is available for this method. You can either call this option from the MRI data or from any segmentation data available on the subject. If you call it from the MRI, a segmentation is processed first, then the mesh. If you call from the tissues, only the mesh process will be performed.
Right-click on the MRI (or the tissues), then "Generate FEM Mesh" then select Fieldtrip option. There are two parameters that the user needs to set, the downsampling of the volume and the node shift ratio.
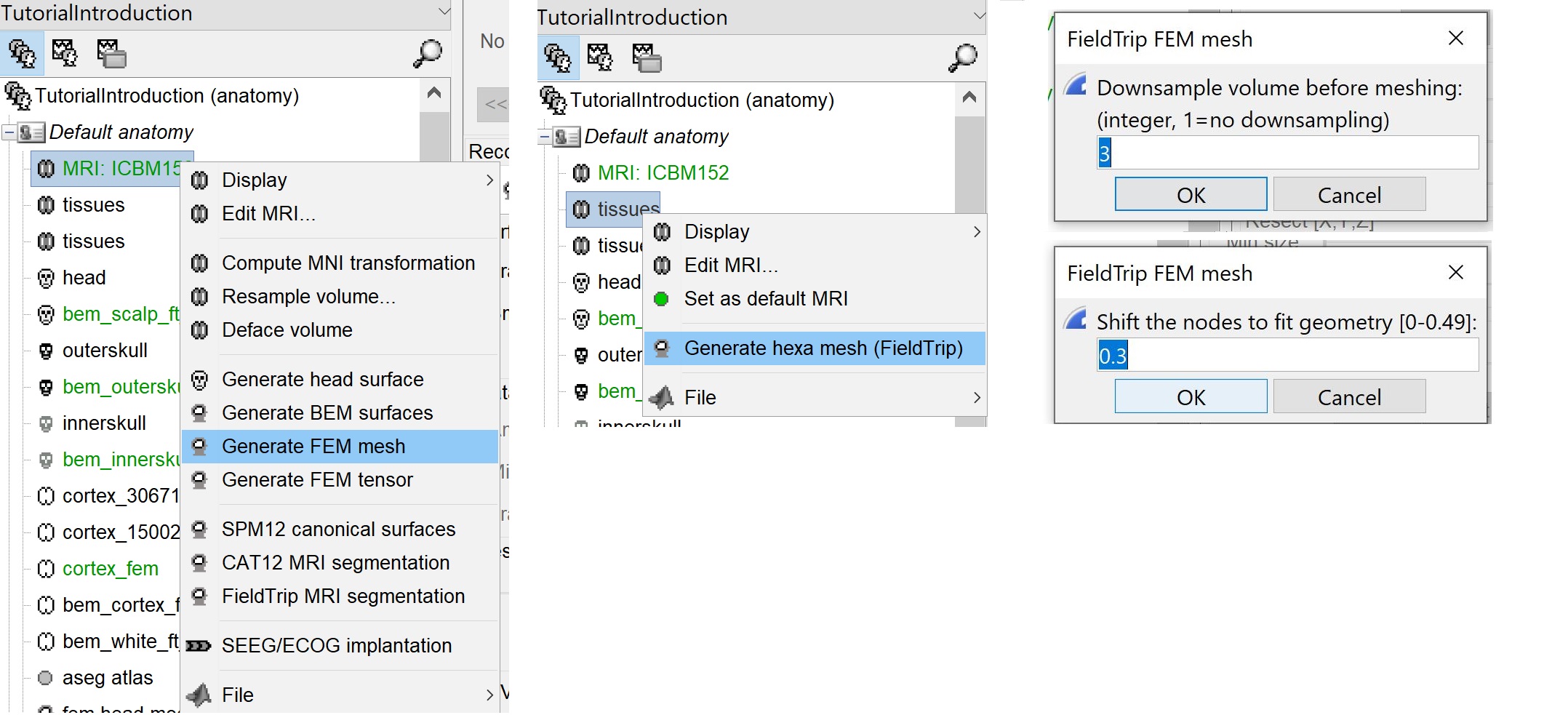
The option "Downsamp volume before meshing" will reduce the number of voxel by this factor.
The "Shift node" option calls the adaptative mesh generation. The process moves the nodes located on the interface either inward or outward in order to fit the geometry as explained here. This figure shows an example (from Fieldtrip webpage), left the unshifted and on the right the shifted.
This method is fast compare to the previous options, the following figures show examples of the mesh obtained with fieldtrip option from the ICBM model.
SimNIBS
SimNIBSsoftware develloped to calculate electric fields caused by Transcranial Electrical Stimulation (TES) and Transcranial Magnetic Stimulation (TMS). From its pipline, Brainstorm integrates the process of the automatic segmentation of MRI images and meshing to create individualized head models. This process is called "headreco and it's explained here.
Requirement
SimNibs is an independent software, Brainstorm call its functions internally therefore you need to install SimNibs and its dependencies. For more details please follow the instructions as explained in this webpage.
To resume, this process calls SPM12 and CAT for the tissue segmentation, then it calls Gmesh and Netgen for the tetrahedral mesh generation. The mesh is checked and repaired by calling the meshfixe process. Depending on your computer performances, this process will take between 2 to 5 hours. We highly recommend closing all other running processes and applications on your computer in order to speed this process.
When and how to use it
Brainstorm can call the main function used for the mesh generation frm the main graphical interface. To create individualized models, SimNIBS require as a T1-weighted image. T2-weighted images are optional, but highly recommended. The main steps used by SimNIBS are explained in this page.
When you have your MRI data available on your subject, follow the same steps are explained above, then select the "SimNibs" method. There is one option related to SimNibs, which is the 'Vertex density' or the number of node per mm2
If you have T1 and T2, you need to call this process by a right-click on the subject in order to include the two datasets, or you can select the T1 and T2 then call the Generate FEM mesh process.
* If there is an MRI file with the string "T2" in the subject anatomy folder, it will use it
- Otherwise, if you select explicitly two MRI files with CTRL+Click, it will use the first one as the T1 and the second one as the T2 (this needs to be documented in the tutorial)
The output head models obtained with this method are represented in the following figure.
The model has 5 layers representing the white matter, gray matter, CSF, skull and scalp.
Roast
comming soon under development and integration.
For more information, please visit: https://www.parralab.org/roast/ and https://github.com/andypotatohy/roast
Brainsuite
BrainSuite is a collection of open source software tools that enable largely automated processing of magnetic resonance images (MRI) of the human brain.
Brainstorm calls Brainsuite tools in order to compute the diffusion tensors from the diffusion wiethed inaging (DWI) data. The diffusion tensor are then converted to conductivity tensors by the linear transformation described by David Tuch et al (ref).
The conductivity tensors are are associated with the FEM mesh of the head model. Where ecah mesh element have it's own tensors.
The tensors are used to represnet the anisotropic conductivity of a tissue. The anisotropy means the change on the conductivity by changing the direction. For more information regarding tensors please refers to this page (add link).
Requirement
Brainsuite is an independant softeware, Brainstoem calls its functions from the core source code, therefore the installation of Brainsuite is required.
Please follow the instructions as explained in this webpage.
Once the instalation is completed, The BrainSuite installation folder must be informed in the Brainstorm preferences (From the Brainsuitrom interface, click on 'File' and then 'Edite preferences').

When and how to use it
[For this version June 2020, only the tetra mesh are supported and tested.]
The brainsuite pipline is used to estimate the anisotropy of the brain tissues. This process is associated with the DUNEuro FEM computation. The conductivity tensors will be assigned to each mesh elements.
In order to use this functionnality the DWI data are required. The Niftii files and the assocaited bvec and bval are required. Further more we assume that you have already generated the FEM mesh from the MRI as explained in the previous sections.
Tissue anisotropy estimation
From Brainstorm, brainsuite is used for the skull stripping, bias field correction and then the diffusion pipline is used to compute the diffusion tensors.
ref to the maon function : likToGit
Brainstorm template
https://github.com/brainstorm-tools/brainstorm3/issues/185#issuecomment-576749612
Level set
comming soon
Additional Documentation
SimNIBS
