|
Size: 17175
Comment:
|
Size: 14395
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| ''Authors: Francois Tadel, John C Mosher, Richard Leahy, Sylvain Baillet'' | ''Authors: Francois Tadel, Elizabeth Bock, John C Mosher, Richard Leahy, Sylvain Baillet'' |
| Line 4: | Line 4: |
| The source estimation methods we use need some metrics computed from the recordings. The minimum norm solution requires an estimation of the noise level in the recordings ('''noise covariance matrix''') and the beamformers need additionally a '''data covariance matrix'''. This tutorial will show first how to compute these files from the recordings, the details that follow can be skipped if you are not interested. | The source estimation methods we use need some metrics computed from the recordings. The minimum norm solution requires an estimation of the noise level in the recordings ('''noise covariance matrix''') and the beamformers additionally need a prototype of the effect we are targeting ('''data covariance matrix'''). This first section of this tutorial shows how to compute a noise covariance matrix from the MEG empty room recordings. The details that follow can be skipped if you are not interested. |
| Line 9: | Line 9: |
| Ideally, we want to represent only the noise of the sensors. In MEG, this is easy to obtain with a few minutes of empty room measurements. The only constrain is to use recordings that have been acquired the same day as the subject's recordings (if possible just before) and pre-processed in the same way (same frequency filters). In this study we have already prepared a segment of 2min of noise recordings, we will estimate the noise covariance based on it. | Ideally, we want to represent only the noise of the sensors. In MEG, this is easy to obtain with a few minutes of empty room measurements. The only constraint is to use noise recordings that have been acquired the same day as the subject's recordings (if possible just before) and pre-processed in the same way (same sampling rate and frequency filters). In this study we have already prepared a segment of 2min of noise recordings, we will estimate the noise covariance based on it. |
| Line 11: | Line 11: |
| * Right-click on the link to the '''noise recordings''' '''> Noise covariance'''. <<BR>><<BR>> {{attachment:noisecov_popup.gif||height="267",width="474"}} * '''Import from file''': Use a matrix that was computed previously using the MNE software. * '''Import from Matlab''': Import from any [nChannels, nChannels] matrix in Matlab workspace. * '''Compute from recordings''': Use the selected recordings to estimate the noise covariance. * '''No noise modeling''': Do not compute the noise covariance matrix from noise recordings. Instead, it creates a file that contains an identity matrix. This is the menu to use when you really don't have access to any noise information, or when you don't have any option to identify this noise (for instance if you are studying ongoing activity with EEG). * Select the menu '''Noise covariance > Compute from recordings''':<<BR>><<BR>> {{attachment:noisecov_options.gif||height="378",width="375"}} * '''Data selection''': The top part of this window shows a summary of the files that have been selected to estimate the noise: 1 file of 120s recorded at 600Hz. Total number of time samples: 72,000.<<BR>>We can chose to use only a part of this file with the option "baseline". The large chunks of continuous files are split in blocks of a maximum of '''10,000 samples''', that are then processed as different files. |
Right-click on the link to the '''noise recordings''' '''> Noise covariance'''. Available menus: |
| Line 19: | Line 13: |
| * '''Remove DC offset''': All the selected blocks of data are baseline corrected and concatenated to form a large matrix "F". There are two options for the baseline correction:<<BR>> '''Block by block''': The average value is subtracted from each block before the concatenation. If Fi is the recordings corresponding to block #i: F = Concatenate[Fi - mean(Fi)].<<BR>>'''Global''': The average value is removed after concatenation (same correction for all blocks). <<BR>>F = Concatenate[Fi] - mean(Concatenate[Fi]). |
* '''Import from file''': Use a matrix that was computed previously using the MNE software. * '''Import from Matlab''': Import from any [nChannels x nChannels] matrix from the Matlab workspace. * '''Compute from recordings''': Use the selected recordings to estimate the noise covariance. * '''No noise modeling''': Use an identity matrix as the noise noise covariance. Useful when you don't have access to noise recordings (eg. ongoing EEG activity or simulations). <<BR>><<BR>> {{attachment:noisecov_popup.gif||height="267",width="474"}} |
| Line 22: | Line 18: |
| Select the menu '''Noise covariance > Compute from recordings'''. Available options: | |
| Line 23: | Line 20: |
| * '''Data selection''': The top part of this window shows a summary of the files that have been selected to estimate the noise: 1 file of 120s at 600Hz. Total number of time samples: 72,000. We can chose to use only a part of this file with the option "baseline". The large chunks of continuous files are split in blocks of a maximum of '''10,000 samples''', that are then processed as different files. | |
| Line 24: | Line 22: |
| * The noise covariance matrix is computed from this concatenated matrix: '''NoiseCov = F * F'''' | * '''Remove DC offset''': All the selected blocks of data are baseline corrected and concatenated to form a large matrix "F". There are two options for the baseline correction:<<BR>>'''Block by block''': The average value is subtracted from each block before the concatenation. <<BR>>If Fi is the recordings corresponding to block #i: F = Concatenate[Fi - mean(Fi)].<<BR>>'''Global''': The average value is removed after concatenation (same correction for all blocks). <<BR>>F = Concatenate[Fi] - mean(Concatenate[Fi]). |
| Line 26: | Line 24: |
| * '''Output''': Compute either a full noise covariance (best option) or just a diagonal matrix (only the variances of the channels). The second option is only useful if you do not have enough time samples to estimate the covariance properly. Just always keep the default selection unless you know exactly what you are doing, Brainstorm detects what the preferred option is for every case. | * The noise covariance is computed from this concatenated matrix: '''NoiseCov = F * F' / Nsamples''' |
| Line 28: | Line 26: |
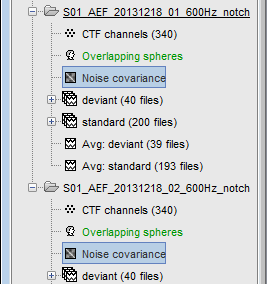
| * Keep the default options and click on ['''OK''']. One new file appears in the noise dataset folder. <<BR>><<BR>> {{attachment:noisecov_file.gif||height="139",width="378"}} {{attachment:noisecov_display.gif||height="170",width="148"}} * '''Display as image''': Shows the noise covariance matrix as an indexed image. This can be useful to quickly check the quality of the recordings. The noisier channels are indicated by red points. You can display the noise covariance for all the sensors at once, or for each sensor type separately. Double-clicking on the file display all the sensors. * '''Copy to other conditions''': Copy this file to all the other folders from the same subject. * '''Copy to other subjects''': Copy this file to all the folders of all the subjects in the protocol. * You can also copy a noise covariance file to another condition/subject just like any other file: using the popup menus File > Copy/Paste, or the keyboard shortcuts Ctrl+C and Ctrl+V. * Right-click on the the noise covariance file > '''Copy to other folders''': We need this file in the two folders where the epochs where imported, in order to estimate the sources for them. <<BR>><<BR>>{{attachment:noisecov_copy.gif}} |
* '''Output''': Compute either a full noise covariance (best option) or just a diagonal matrix (only the variances of the channels). The second option is only useful if you do not have enough time samples to estimate the covariance properly. Always keep the default selection unless you know exactly what you are doing, Brainstorm detects what the preferred option is for every case. <<BR>><<BR>> {{attachment:noisecov_options.gif||height="378",width="375"}} |
| Line 35: | Line 28: |
| == Noise covariance from another dataset == '', but we can also use a baseline of resting recordings. The main problem is in fact to identify segment of recordings that we can consider as "noise", or at least that do not contain any of the brain activity of interest. This tutorial shows how to compute the noise covariance from MEG empty room recordings.'' |
Keep the default options and click on ['''OK''']. |
| Line 38: | Line 30: |
| In order to get a good estimation of the noise, we need much more time samples than what we have in an averaged file. Also, the pre-stimulation baseline might not be a very good estimation of the noise of the sensors. You have several options available to get better results, by using different segments of recordings than the ones that you are analyzing. | * One new file appears in the noise dataset, next to the channel file. Description of the popup menus: |
| Line 40: | Line 32: |
| The only constraint: you need to apply the '''exact same pre-processing operations''' to the recordings you use for the estimation of the noise covariance, and to the recordings for which you are reconstructing the sources: frequency filters, resampling, re-referencing... | * '''Display as image''': Shows the noise covariance matrix as an indexed image. This can be useful to quickly check the quality of the recordings: noisier channels appear in red. You can display the noise covariance for all the sensors at once, or for each sensor type separately. Double-clicking on the file displays all the sensors. * '''Copy to other conditions''': Copy this file to all the other folders of the same subject. * '''Copy to other subjects''': Copy this file to all the folders of all the subjects in the protocol. * You can also copy a noise covariance file to another folder just like any other file: <<BR>>Right-click > File > Copy/Paste, or keyboard shortcuts Ctrl+C/Ctrl+V. <<BR>><<BR>> {{attachment:noisecov_file.gif||height="139",width="378"}} {{attachment:noisecov_display.gif||height="170",width="148"}} |
| Line 42: | Line 37: |
| * '''Use single trials''': If you have the single trials from which the average file was computed, * Create another condition in your subject and import the single trials in it, * Estimate the noise covariance on these single trials only (right-click on the new condition node > Noise covariance > Compute...). Use only the pre-stimulus baseline. * Right-click on the new noise covariance file > Noise covariance > Apply to all conditions. This copies the noise covariance file in the conditions of your averaged files. Alternatively, use the Copy/Paste menus or shortcuts. * '''Use a real baseline''': If you have recorded some resting periods during the experiment, or some empty room measurements, you can use them exactly as in the previous case. * Import the blocks of raw recordings in the database in a new condition * Compute the noise covariance using the entire time window (it is supposed to be noise everywhere) * Copy to other conditions * '''Use the original continuous file''': Same thing as previously, but skipping the import part. You can compute directly the noise covariance from a RAW file: * Right-click on your subject node > Review RAW file. (the management of continuous files in native format is detailed in an advanced tutorial: [[Tutorials/TutRawViewer|Review raw recordings and edit markers]]) * Right-click on Link to raw file > Noise covariance > Compute from recordings. Then select the time window to use as a baseline (subject resting or empty room). * Copy to other conditions. * '''Import from another software''': If you have pre-processed your recordings with the MNE software, you might already have a nice noise covariance matrix available in a ''-cov.fif'' file. Just import it in the average conditions (right-click on condition > Noise covariance > Import from file) |
Right-click on the the noise covariance file > '''Copy to other folders''': We need this file in the two folders where the epochs were imported, in order to estimate the sources for them. |
| Line 56: | Line 39: |
| '''Note for averaged files''': If you import or compute a noise covariance matrix based on a set of RAW recordings (not averaged), and then use it to estimate sources for averaged recordings, you may have to set manually the number of trials that were used to compute the average. | . {{attachment:noisecov_copy.gif||height="225",width="212"}} |
| Line 58: | Line 41: |
| * If you calculate the averages in Brainstorm, you don't have to worry about it, it is done automatically. It is only in the case you have imported in Brainstorm files that were averaged in another software, because the number of averaged trials was probably not saved in the file. * To check if this information is stored in the database: right click on the averaged file for which you want to estimate the sources. Menu ''File > View file contents''. If you see "nAvg = 1", the noise covariance matrix will not be used correctly on that file. To fix this problem: * Right-click on the averaged file > File > Export to Matlab > "data" * In the Matlab command window, type: "data.nAvg = nTrials;" (replace nTrials with the actual number of trials from which the average was computed) * Right-click on the averaged file > File > Import from Matlab > "data" |
<<TAG(Advanced)>> |
| Line 64: | Line 43: |
| == Discussion == Computationally speaking, this noise covariance matrix is very easy to calculate, the Brainstorm interface offers a lot of flexibility to use the files and time windows you want to process. The real difficulty is to define what "noise" means. In your experiment, you want to use segments of recordings that contain only the noise of the sensors if possible, or segments of recordings that do not contain any of the brain signals of interest. This section is not directly useful for the current tutorial, but can be used as a reference for selecting the appropriate method in another experiment. |
== Other scenarios == Computationally speaking, this noise covariance matrix is very easy to calculate, the Brainstorm interface offers a lot of flexibility to select the files and time windows you want to use. The real difficulty is to define what "noise" means. The ideal is to use segments of recordings that contain only the noise of the sensors, or segments of recordings that do not contain any of the brain signals of interest. This section is not directly useful for the current tutorial, but can be used as a reference for selecting the appropriate method in another experiment. |
| Line 68: | Line 47: |
| '''Empty room''': The MEG case is usually easier because we have access to real noise measurements, the MEG room just has to be empty. Record a few minutes right before bringing the subject in the MEG, or after the experiment is done. This would isolate only the noise from the sensors, which is what we are interested in most cases.<<BR>>Additionnally, if you acquire several runs successively, or even several subjects, you can assume that the state of the sensors doesn't change much over the time. Therefore, you can re-use the same noise recordings and noise covariance matrix for several runs and subjects. | '''Empty room''': The MEG case is usually easier because we have access to real noise measurements, the MEG room just has to be empty. Record a few minutes right before bringing the subject in the MEG, or after the experiment is done. This would isolate only the noise from the sensors, which is what we are interested in most cases.<<BR>>If you acquire several runs successively and your MEG system is relatively stable, you can assume that the state of the sensors doesn't change much over the time. Therefore, you can re-use the same noise recordings and noise covariance matrix for several runs and subjects acquired during the same day. |
| Line 70: | Line 49: |
| '''Resting baseline''': Alternatively, when studying evoked responses (aka event-related responses), you can use a few minutes of recordings where the subject is resting, ie. not performing the task. Record those resting segments before or after the experiment, or before/after each run. This approach considers the resting brain activity as "noise", and the sources estimated for the evoked response are going to be preferentially the ones that were not activated during the resting period. | '''Resting baseline''': Alternatively, when studying evoked responses (aka event-related responses), you can use a few minutes of recordings where the subject is resting, ie. not performing the task. Record those resting segments before or after the experiment, or before/after each run. This approach considers the resting brain activity as "noise", the sources estimated for the evoked response are going to be preferentially the ones that were not activated during the resting period. |
| Line 77: | Line 56: |
| The noise level of the electrodes recordings depends primarily on the quality of the connection with the skin, which varies a lot from a subject to another, or even during the acquisition of one single subject. The conductive gel or solution used on the electrodes tends to dry, and the electrode cap can move. Therefore, it is very important to use one channel file per subject, hence one noise covariance per subject. In some specific cases, if the quality of the recordings varies a lot over the time, it can be interesting to split long recordings in different runs, with different noise covariance matrices too. | The noise level of the electrode recordings depends primarily on the quality of the connection with the skin, which varies a lot from a subject to another, or even during the acquisition of one single subject. The conductive gel or solution used on the electrodes tends to dry, and the electrode cap can move. Therefore, it is very important to use one channel file per subject, hence one noise covariance per subject. In some specific cases, if the quality of the recordings varies a lot over the time, it can be interesting to split long recordings in different runs, with different noise covariance matrices too. |
| Line 83: | Line 62: |
| Analyzing a single interictal spike, using either EEG and MEG data, we are faced with a similar problem in defining what is noise. The brain activity before and after the spike can even be very informative about the spike's generation, particularly if it is part of a sequence of interictal activity that precedes ictal (seizure) onset. Defining a segment of time adjacent the spike as "background" may not be practical. In practice, however, we often can find a temporal region of spontaneous brain activity in the recordings that appears adequate for declaring as background, even in the epileptic patient. As discussed above, MEG has the additional option of using empty room data as a baseline, an option not available in EEG. | Analyzing a single interictal spike, using either EEG and MEG data, we are faced with a similar problem in defining what is noise. Even the brain activity before and after the spike can be very informative about the spike's generation, particularly if it is part of a sequence of interictal activity that precedes ictal (seizure) onset. Defining a segment of time adjacent the spike as "background" may not be practical. In practice, however, we can often find a temporal region of spontaneous brain activity in the recordings that appears adequate for declaring as background, even in the epileptic patient. As discussed above, MEG has the additional option of using empty room data as a baseline, an option not available in EEG. |
| Line 87: | Line 66: |
| ==== Forum posts ==== * EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718 |
<<TAG(Advanced)>> |
| Line 90: | Line 68: |
| = From continuous tutorials = === Noise covariance matrix === To estimate the sources properly, we need an estimation of the noise level for each sensor. A good way to do this is to compute the covariance matrix of the concatenation of the baselines from all the trials in both conditions. |
== Recommendations == * '''Long noise recordings''': In order to get a good estimation of the noise covariance, we need a significant number of time samples, at least '''N*(N+1)/2''', where N is the number of sensors. This means about 40s for CTF275 recordings at 1000Hz, or 20s for 128-channel EEG at 500Hz. Always try to use as much data as possible for estimating this noise covariance. * '''Do not import averages''': For this reason, you should never compute the noise covariance matrix from averaged responses. If you want to import recordings that you have fully pre-processed with another program, we recommend you import the individual trials and use them to compute the noise covariance. If you can only import the averaged responses in the Brainstorm database, you have to be aware that you may get poor results in the source estimation. * '''Using one block''': If you want to use a segment of "quiet" recordings in a continuous file: right-click on the continuous file > Noise covariance > Compute from recordings, then copy the noise covariance to the other folders. This is the case described in this tutorial. |
| Line 94: | Line 73: |
| * Select at the same time the two groups of trials (right and left). To do this: hold the Control (or Cmd on Macs) key and click successively on the Right and the Left trial lists. * Right-click on one of them and select: Noise covariance > Compute from recordings. Set the baseline to '''[-104,-5] ms''', to consider as noise everything that happens before the beginning of the stimulation artifact. Leave the other options to the default values. Click on Ok. * This operation computes the noise covariance matrix based on the baseline of all the good trials (199 files). The result is stored in a new file "Noise covariance" in the ''(Common files)'' folder. |
* '''Use single trials''': If you want to use the pre-stimulation baseline of the single trials, first import the trials in the database, then select all the groups of imported trials at once, right-click on one of them > Noise covariance > Compute from recordings, and finally copy the file to the other folders. * '''Using multiple continuous blocks''': This is similar to the single trial case. Import in the database all the blocks you consider as quiet resting baselines, then select all the imported blocks in the database explorer > Noise covariance > Compute from recordings. |
| Line 98: | Line 76: |
| {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutRawAvg?action=AttachFile&do=get&target=noisecov.gif|noisecov.gif|class="attachment"}} | <<TAG(Advanced)>> |
| Line 100: | Line 78: |
| = From auditory = === Noise covariance matrix === * We want to calculate the noise covariance from the empty room measurements and use it for the other runs. * In the '''Noise''' folder, right-click on the Link to raw file > Noise covariance > Compute from recordings. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=noisecov1.gif|noisecov1.gif|height="253",width="392",class="attachment"}} * Keep all the default options and click [OK]. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=noisecov2.gif|noisecov2.gif|height="285",width="291",class="attachment"}} * Right-click on the noise covariance file > Copy to other conditions. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=noisecov3.gif|noisecov3.gif|height="181",width="232",class="attachment"}} * You can double-click on one the copied noise covariance files to check what it looks like: . {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=noisecov4.gif|noisecov4.gif|height="232",width="201",class="attachment"}} * For more information: [[http://neuroimage.usc.edu/brainstorm/Tutorials/TutNoiseCov|Noise covariance tutorial]]. |
== Data covariance matrix [TODO] == The computation of a data covariance matrix is very similar to a noise covariance matrix, except that you need to target the segments of recordings of interest instead of the noise. In the case of an event-related study, you can consider all the recordings in a range of latencies after the stimulation corresponding to the effect you want to localize in the brain. |
| Line 113: | Line 81: |
| == On the heard drive == It contains the [nChannels x nChannels] noise covariance matrix computed. Double-click to display it. |
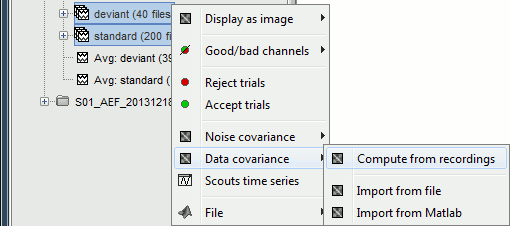
* For '''run#01''', select '''all the trials''', right-click > '''Data covariance > Compute from recordings'''. <<BR>><<BR>> {{attachment:datacov_popup.gif||height="199",width="370"}} * We need to specify the time window of interest in these recordings. If want to image the activity during the primary response, we can for instance consider the segment '''[50,150]ms''' post-stimulus. <<BR>><<BR>> {{attachment:datacov_options.gif||height="356",width="363"}} {{attachment:datacov_timewindow.gif||height="105",width="238"}} * Repeat the operation for '''run#02'''. <<BR>><<BR>> {{attachment:datacov_files.gif||height="238",width="208"}} <<TAG(Advanced)>> == On the hard drive == Right-click on any noise covariance file > File > View file contents: . {{attachment:noisecov_contents.gif||height="175",width="487"}} ==== Structure of the noise/data covariance files: noisecov_*.mat / ndatacov_*.mat ==== * '''Comment''': String displayed in the database explorer to represent this file. * '''NoiseCov''': [nChannels x nChannels] noise covariance: '''F * F' ./ (nSamples-1)'''<<BR>>Unknown values are set to zero. * '''FourthMoment''': [nChannels x nChannels] fourth order moments: '''F.<<HTML(^)>>2 * F'.<<HTML(^)>>2 ./ (nSamples-1) ''' * '''nSamples''': [nChannels x nChannels] number of time samples that were used for each pair of sensors. This is not necessarily the same value everywhere, some channels can be bad only for a few trials. '''Related functions''' * bst_noisecov.m * panel_noisecov.m <<TAG(Advanced)>> == Additional documentation == * Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718 |
Tutorial 21: Noise and data covariance matrices
Authors: Francois Tadel, Elizabeth Bock, John C Mosher, Richard Leahy, Sylvain Baillet
The source estimation methods we use need some metrics computed from the recordings. The minimum norm solution requires an estimation of the noise level in the recordings (noise covariance matrix) and the beamformers additionally need a prototype of the effect we are targeting (data covariance matrix). This first section of this tutorial shows how to compute a noise covariance matrix from the MEG empty room recordings. The details that follow can be skipped if you are not interested.
Contents
Compute the noise covariance
Ideally, we want to represent only the noise of the sensors. In MEG, this is easy to obtain with a few minutes of empty room measurements. The only constraint is to use noise recordings that have been acquired the same day as the subject's recordings (if possible just before) and pre-processed in the same way (same sampling rate and frequency filters). In this study we have already prepared a segment of 2min of noise recordings, we will estimate the noise covariance based on it.
Right-click on the link to the noise recordings > Noise covariance. Available menus:
Import from file: Use a matrix that was computed previously using the MNE software.
Import from Matlab: Import from any [nChannels x nChannels] matrix from the Matlab workspace.
Compute from recordings: Use the selected recordings to estimate the noise covariance.
No noise modeling: Use an identity matrix as the noise noise covariance. Useful when you don't have access to noise recordings (eg. ongoing EEG activity or simulations).
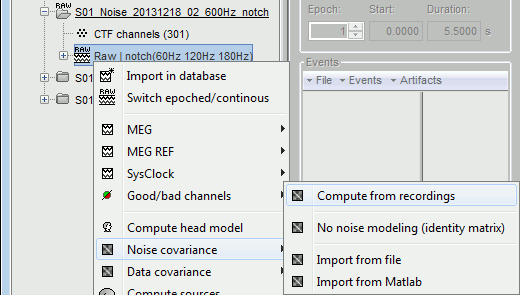
Select the menu Noise covariance > Compute from recordings. Available options:
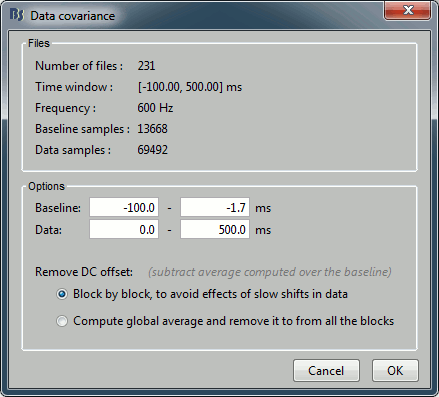
Data selection: The top part of this window shows a summary of the files that have been selected to estimate the noise: 1 file of 120s at 600Hz. Total number of time samples: 72,000. We can chose to use only a part of this file with the option "baseline". The large chunks of continuous files are split in blocks of a maximum of 10,000 samples, that are then processed as different files.
Remove DC offset: All the selected blocks of data are baseline corrected and concatenated to form a large matrix "F". There are two options for the baseline correction:
Block by block: The average value is subtracted from each block before the concatenation.
If Fi is the recordings corresponding to block #i: F = Concatenate[Fi - mean(Fi)].
Global: The average value is removed after concatenation (same correction for all blocks).
F = Concatenate[Fi] - mean(Concatenate[Fi]).The noise covariance is computed from this concatenated matrix: NoiseCov = F * F' / Nsamples
Output: Compute either a full noise covariance (best option) or just a diagonal matrix (only the variances of the channels). The second option is only useful if you do not have enough time samples to estimate the covariance properly. Always keep the default selection unless you know exactly what you are doing, Brainstorm detects what the preferred option is for every case.
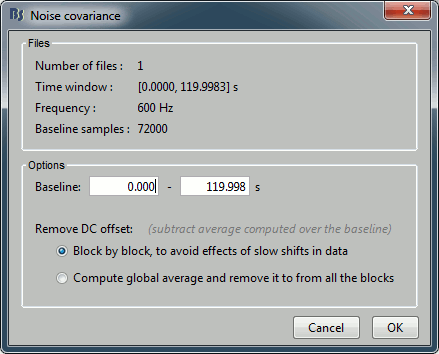
Keep the default options and click on [OK].
- One new file appears in the noise dataset, next to the channel file. Description of the popup menus:
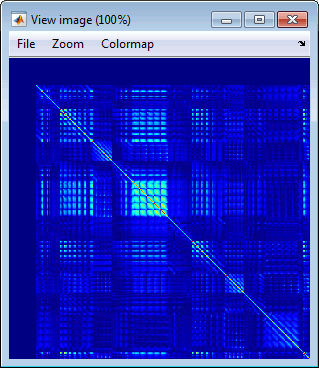
Display as image: Shows the noise covariance matrix as an indexed image. This can be useful to quickly check the quality of the recordings: noisier channels appear in red. You can display the noise covariance for all the sensors at once, or for each sensor type separately. Double-clicking on the file displays all the sensors.
Copy to other conditions: Copy this file to all the other folders of the same subject.
Copy to other subjects: Copy this file to all the folders of all the subjects in the protocol.
You can also copy a noise covariance file to another folder just like any other file:
Right-click > File > Copy/Paste, or keyboard shortcuts Ctrl+C/Ctrl+V.
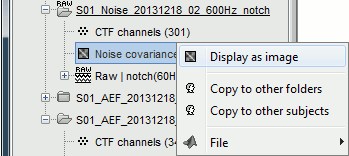
Right-click on the the noise covariance file > Copy to other folders: We need this file in the two folders where the epochs were imported, in order to estimate the sources for them.
Other scenarios
Computationally speaking, this noise covariance matrix is very easy to calculate, the Brainstorm interface offers a lot of flexibility to select the files and time windows you want to use. The real difficulty is to define what "noise" means. The ideal is to use segments of recordings that contain only the noise of the sensors, or segments of recordings that do not contain any of the brain signals of interest. This section is not directly useful for the current tutorial, but can be used as a reference for selecting the appropriate method in another experiment.
MEG
Empty room: The MEG case is usually easier because we have access to real noise measurements, the MEG room just has to be empty. Record a few minutes right before bringing the subject in the MEG, or after the experiment is done. This would isolate only the noise from the sensors, which is what we are interested in most cases.
If you acquire several runs successively and your MEG system is relatively stable, you can assume that the state of the sensors doesn't change much over the time. Therefore, you can re-use the same noise recordings and noise covariance matrix for several runs and subjects acquired during the same day.
Resting baseline: Alternatively, when studying evoked responses (aka event-related responses), you can use a few minutes of recordings where the subject is resting, ie. not performing the task. Record those resting segments before or after the experiment, or before/after each run. This approach considers the resting brain activity as "noise", the sources estimated for the evoked response are going to be preferentially the ones that were not activated during the resting period.
Pre-stimulation baseline: It can also be a valid approach to use the pre-stimulation baseline of the individual trials to estimate the noise covariance. But keep in mind that in this case, everything in your pre-stimulation baseline is going to be attenuated in the source reconstruction, noise and brain activity. Therefore, your stimuli have to be distant enough in time so that the response to a stimulus is not recorded in the "baseline" of the following one. For repetitive stimuli, randomized delays between stimuli can help avoiding expectation effects in the baseline.
EEG
The EEG case is typically more complicated. It is not possible to estimate the noise of the sensors only. Only the two other approaches described for the MEG are still valid:
resting baseline and pre-stimulation baseline.
The noise level of the electrode recordings depends primarily on the quality of the connection with the skin, which varies a lot from a subject to another, or even during the acquisition of one single subject. The conductive gel or solution used on the electrodes tends to dry, and the electrode cap can move. Therefore, it is very important to use one channel file per subject, hence one noise covariance per subject. In some specific cases, if the quality of the recordings varies a lot over the time, it can be interesting to split long recordings in different runs, with different noise covariance matrices too.
EEG and resting state
When studying the resting brain, you cannot use resting recordings as a noise baseline. For MEG the best choice is to use empty room measurements. For EEG, you can chose between two different approaches: using the sensors variance, or not using any noise information.
Option #1: Calculate the covariance over a long segment of the resting recordings, but save only the diagonal, ie. the variance of the sensors. To do so from the interface: just check the box "Diagonal matrix" in the options window.
Option #2: Select "No noise modeling" in the popup menu. This would use an identity matrix instead of a noise covariance matrix (equal, unit variance of noise on every sensor). In the inverse modeling, this is equivalent to the assumption that the noise in the recordings is homoskedastic, and equivalent for all the sensors. The problem with this approach is that an electrode with a higher level of noise is going to be interpreted as a lot of activity in its region of the brain.
Noise and epilepsy
Analyzing a single interictal spike, using either EEG and MEG data, we are faced with a similar problem in defining what is noise. Even the brain activity before and after the spike can be very informative about the spike's generation, particularly if it is part of a sequence of interictal activity that precedes ictal (seizure) onset. Defining a segment of time adjacent the spike as "background" may not be practical. In practice, however, we can often find a temporal region of spontaneous brain activity in the recordings that appears adequate for declaring as background, even in the epileptic patient. As discussed above, MEG has the additional option of using empty room data as a baseline, an option not available in EEG.
We thus have the same options as above:
Option #1a: Compute the noise covariance statistics from blocks of recordings away from the peak of any identified interictal spike, and keep only the diagonal (the variance of the sensors).
Option #1b: If a large period of time is available, calculate the full noise covariance.
Option #2(MEG): Use empty room data as the baseline.
Option #3: Select "No noise modeling" in the popup menu (identity matrix, unit variance of noise on every sensor).
Recommendations
Long noise recordings: In order to get a good estimation of the noise covariance, we need a significant number of time samples, at least N*(N+1)/2, where N is the number of sensors. This means about 40s for CTF275 recordings at 1000Hz, or 20s for 128-channel EEG at 500Hz. Always try to use as much data as possible for estimating this noise covariance.
Do not import averages: For this reason, you should never compute the noise covariance matrix from averaged responses. If you want to import recordings that you have fully pre-processed with another program, we recommend you import the individual trials and use them to compute the noise covariance. If you can only import the averaged responses in the Brainstorm database, you have to be aware that you may get poor results in the source estimation.
Using one block: If you want to use a segment of "quiet" recordings in a continuous file: right-click on the continuous file > Noise covariance > Compute from recordings, then copy the noise covariance to the other folders. This is the case described in this tutorial.
Use single trials: If you want to use the pre-stimulation baseline of the single trials, first import the trials in the database, then select all the groups of imported trials at once, right-click on one of them > Noise covariance > Compute from recordings, and finally copy the file to the other folders.
Using multiple continuous blocks: This is similar to the single trial case. Import in the database all the blocks you consider as quiet resting baselines, then select all the imported blocks in the database explorer > Noise covariance > Compute from recordings.
Data covariance matrix [TODO]
The computation of a data covariance matrix is very similar to a noise covariance matrix, except that you need to target the segments of recordings of interest instead of the noise. In the case of an event-related study, you can consider all the recordings in a range of latencies after the stimulation corresponding to the effect you want to localize in the brain.
For run#01, select all the trials, right-click > Data covariance > Compute from recordings.
We need to specify the time window of interest in these recordings. If want to image the activity during the primary response, we can for instance consider the segment [50,150]ms post-stimulus.
![[ATTACH] [ATTACH]](/moin_static198/brainstorm1/img/attach.png)
Repeat the operation for run#02.
On the hard drive
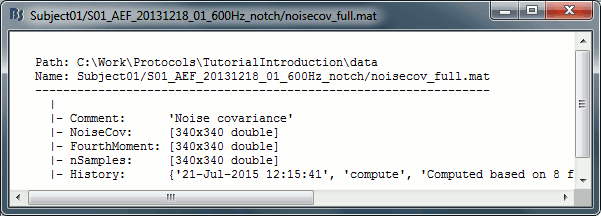
Right-click on any noise covariance file > File > View file contents:
Structure of the noise/data covariance files: noisecov_*.mat / ndatacov_*.mat
Comment: String displayed in the database explorer to represent this file.
NoiseCov: [nChannels x nChannels] noise covariance: F * F' ./ (nSamples-1)
Unknown values are set to zero.FourthMoment: [nChannels x nChannels] fourth order moments: F.^2 * F'.^2 ./ (nSamples-1)
nSamples: [nChannels x nChannels] number of time samples that were used for each pair of sensors. This is not necessarily the same value everywhere, some channels can be bad only for a few trials.
Related functions
- bst_noisecov.m
- panel_noisecov.m
Additional documentation
Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718