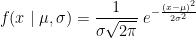|
Size: 8535
Comment:
|
Size: 50205
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| = Tutorial 18: Statistics = ''Authors: Francois Tadel, Dimitrios Pantazis, Elizabeth Bock, Sylvain Baillet'' |
= Tutorial 26: Statistics = '''[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE] ''' ''Authors: Francois Tadel, Elizabeth Bock, Dimitrios Pantazis, Richard Leahy, Sylvain Baillet'' In this auditory oddball experiment, we would like to test for the significant differences between the brain response to the deviant beeps and the standard beeps, time sample by time sample. Until now we have been computing measures of the brain activity in time or time-frequency domain. We were able to see clear effects or slight tendencies, but these observations were always dependent on an arbitrary amplitude threshold and the configuration of the colormap. With appropriate statistical tests, we can go beyond these empirical observations and assess what are the significant effects in a more formal way. |
| Line 6: | Line 10: |
| = From auditory = === Difference deviant-standard === * In the Process2 tab, select the average of the deviant sources (Files A) and the average of the standard sources (Files B). * Run the process "'''Other > Difference A-B'''" {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=average_source_diff.gif|average_source_diff.gif|height="347",width="424",class="attachment"}} * Double-click on the difference to display it, explore it in time. {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=average_source_diff_left.gif|average_source_diff_left.gif|height="252",width="455",class="attachment"}} {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=average_source_diff_right.gif|average_source_diff_right.gif|height="252",width="455",class="attachment"}} * The first observations we can make are the following: * '''P50''': No important difference. * '''N100''': Stronger response in the right auditory system for the deviant condition. * '''MMN '''(125ms): Stronger response for the deviant (left auditory, right temporal/frontal/motor). * '''P200 '''(175ms): Stronger response in the auditory system for the standard condition. * '''After 200ms''': Stronger response in the deviant condition (left auditory, left motor, right auditory, right temporal, right motor, right parietal) * Alternatively, you could calculate the difference of the average of all the "deviant" (80) and all the "standard" (388) trials, using the process "'''Other > Weighted difference'''". It is an attempt to compensate for the difference of number of trials. === Student's t-test === * Using a t-test instead of the difference of the two averages, you can reproduce similar results but with a significance level attached to each value. With this test, we can also use all the trials we have, unlike the difference of the means: The t-test behaves very well with imbalanced designs, we can keep all the standard trials. * In the Process2 tab, select the following files: * Files A: All the deviant trials, with the '''[Process sources]''' button selected. * Files B: All the standard trials, with the '''[Process sources]''' button selected. * Run the process "'''Test > Student's t-test'''", Equal variance, Absolute value of average. {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=ttest_source1.gif|ttest_source1.gif|height="406",width="699",class="attachment"}} * Double-click on the t-test file to open it. Set the options in the Stat tab: * p-value threshold: '''0.05''' * Multiple comparisons: '''FDR''' * Control over dimensions: '''1.Signals''' and '''2.Time''' * Explore the results in time. {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=ttest_source2_left.gif|ttest_source2_left.gif|height="231",width="415",class="attachment"}} {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=ttest_source2_right.gif|ttest_source2_right.gif|height="231",width="415",class="attachment"}} = From CTF = This tutorial introduces the ''Process2 ''tab, which is mainly used to test two different sets of data. This tab works the same way as the ''Process1 ''tab, except that you have to define two sets of files instead of one. This tool will be presented very briefly now, and the results will not have any scientific meaning, because the protocol '' TutorialCTF'' do not contain enough data to perform any interesting statistical test. == Binary processes == The first type of processes you can find in the Process2 panel are binary file-by-file operations. You define a list of files A and a list of files B, with the same number of files in both lists, and you run a process that is going to create one output file for each couple of files (Ai, Bi). The only two process of that type that are available now are: a difference and an average. Let's try the difference, just for illustrating the interface. ==== Files selection ==== Drag and drop the ''Right ''condition in "Files A" list, and the ''Left ''condition in "Files B" list. Select the "recordings" button. Click on Run. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutStat?action=AttachFile&do=get&target=files_sel.gif|files_sel.gif|class="attachment"}} ==== Process selection ==== Select process "Other > Difference A - B" to compute a "file by file" difference between files A and files B. Click on Ok to run the process. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutStat?action=AttachFile&do=get&target=diff.gif|diff.gif|class="attachment"}} ==== Results ==== There where 2 x 2 files in input, there are 2 files in output, in a newly created condition "Right - Left". . {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutStat?action=AttachFile&do=get&target=diff_result.gif|diff_result.gif|class="attachment"}} Now delete this condition before going any further. == Tests == We do not have enough data to illustrate those tests, it will be done soon in another tutorial, based on single trials instead of average recordings. Its works exactly the same way with many files or many subjects: put all the files from condition A in the first list, and all the files from condition B in second list, no matter if they belong to the same subject or not. Then select your process. In the multiple subjects case, the exploration mode "''Functional data (by condition)''" is usually useful to select a given condition for all the subjects. To switch to this mode, click on the third button on top of the database explorer in the main window. === Difference of mean === Calculates separately the average of files A and the average of files B, and the do the subtraction average(A) - average(B). * It gives cortical maps that are similar to the t-tests (following processes), but without the measure of significance of the results. * If there is only one file in each set, it's going to perform the same operation as "Other > Difference A-B" * In the case of sources, there is an extra option to define what type of "Average" function you want to use. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutStat?action=AttachFile&do=get&target=diff_mean.gif|diff_mean.gif|class="attachment"}} === Student's t-test === Get the significant differences between two conditions. * '''Within one subject''': Test a set of individual trials of condition A vs. a set of trials of condition B. * '''Across subjects''': Test a set of subjects for condition A vs. a set of subjects for condition B. Each file (Subject #i, Condition X) is an average response computed across many trials.''' ''' * Same thing as for the difference of means: in the case of source files, there is an extra option to define how to compute the average across the trials. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutStat?action=AttachFile&do=get&target=ttest.gif|ttest.gif|class="attachment"}} === Student's t-test (paired) === For the two previous processes, the number of files in sets A and B do not have to be the same. This one requires to have the same number of samples on both sides. It creates dynamically a new set of files C, where file Ci = (Ai - Bi), and then tests if this set C is equal to zero. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutStat?action=AttachFile&do=get&target=ttest_paired.gif|ttest_paired.gif|class="attachment"}} |
== Random variables == In most cases we are interested in comparing the brain signals recorded for two populations or two experimental conditions A and B. '''A''' and '''B''' are two '''random variables''' for which we have a limited number of repeated measures: multiple trials in the case of a single subject study, or multiple subject averages in the case of a group analysis. To start with, we will consider that each time sample and each signal (source or sensor) is independent: a random variable represents the possible measures for one sensor/source at one specific time point. A random variable can be described with its '''probability distribution''': a function which indicates what are the chances to obtain one specific measure if we run the experiment. By repeating the same experiment many times, we can approximate this function with a discrete histogram of observed measures. {{attachment:stat_distribution.gif||height="205",width="351"}} {{attachment:stat_histogram.gif||height="222",width="330"}} == Histograms == You can plot histograms like this one in Brainstorm, it may help you understand what you can expect from the statistics functions described in the rest of this tutorial. For instance, seeing a histogram computed with only 4 values would discourage you forever from running a group analysis with 4 subjects... ==== Recordings ==== * Let's evaluate the recordings we obtained for sensor '''MLP57''', the channel that was showing the highest value at '''160ms''' in the difference of averages computed in the previous tutorial.<<BR>><<BR>> {{attachment:histogram_channel.gif||height="142",width="459"}} * We are going to extract only one value for each trial we have imported in the database, and save these values in two separate files, one for each condition (standard and deviant). <<BR>>In order to observe more meaningful effects, we will process the trials together from the two acquisition runs. As explained in the previous tutorials ([[http://neuroimage.usc.edu/brainstorm/Tutorials/Averaging#Averaging_across_runs|link]]), this is usually not recommended in MEG analysis, but it can be an acceptable approximation if the subject didn't move between runs. * In Process1, select all the '''deviant trials''' from both runs. <<BR>>Run process '''Extract > Extract values''': <<BR>>Options: Time='''[160,160]ms''', Sensor="'''MLP57'''", Concatenate''' time''' (dimension 2)<<BR>><<BR>> {{attachment:histogram_extract_process.gif||height="264",width="420"}} * Repeat the same operation for all the '''standard trials'''. * You obtain two new files in the folder ''Intra-subject''. If you look inside the files, you can observe that the size of the Value matrix matches the number of trials (78 for deviant, 383 for standard). The matrix is [1 x Ntrials] because we asked to concatenate the extracted values in the 2nd dimension. <<BR>><<BR>> {{attachment:histogram_extract_files.gif||height="139",width="623"}} * To display the distribution of the values in these two files: <<BR>>select them simultaneously, right-click > '''File > View histograms'''. <<BR>><<BR>> {{attachment:histogram_sensor1.gif||height="217",width="674"}} * With the buttons in the toolbar, you can edit the way these distributions are represented: number of bins in the histogram, total number of occurrences (shows taller bars for ''standard'' because it has more values) or density of probability (normalized by the total number of values). <<BR>>In addition, you can plot the '''normal distribution''' corresponding to the mean μ and standard deviation σ computed from the set of values (using Matlab functions ''mean'' and ''std''). * When comparing two sample sets A and B, we try to evaluate if the distributions of the measures are equal or not. In most of the questions we explore in EEG/MEG analysis, the distributions are overlapping a lot. The very sparse sampling of the data (a few tens or hundreds of repeated measures) doesn't help with the task. Some representations will be more convincing than others to estimate the differences between the two conditions. <<BR>><<BR>> {{attachment:histogram_sensor2.gif||height="103",width="330"}} ==== Sources (relative) ==== * We can repeat the same operation at the source level and extract all the values for scout '''A1'''. * In Process1, select all the '''deviant trials''' from both runs. Select button '''[Process sources]'''. <<BR>>Run process '''Extract > Extract scouts time series''': <<BR>>Options: Time='''[160,160]ms''', Scout="'''A1'''", Flip, Concatenate<<BR>><<BR>> {{attachment:histogram_scout1.gif||height="296",width="449"}} * Repeat the same operation for all the '''standard trials'''. * Select the two files > Right-click > File > View histogram.<<BR>><<BR>> {{attachment:histogram_scout2.gif||height="254",width="452"}} * The distributions still look Gaussian, but the variances are now slightly different. You have to pay attention to this information when choosing which parametric t-test to run (see below). ==== Sources (absolute) ==== * In Process1, select the extracted scouts value. Run process "'''Pre-process > Absolute values'''". * Display the histograms of the two rectified files. <<BR>><<BR>> {{attachment:histogram_scout3.gif||height="251",width="487"}} * The rectified source values are definitely '''not''' following a normal distribution, the shape of the histogram has nothing to do with the corresponding Gaussian curves. As a consequence, if you are using rectified source maps, you will not be able to run independent parametric t-tests.<<BR>>Additionally, you may have issues with the detection of some effects (see tutorial [[Tutorials/Difference|Difference]]). ==== Sources (norm) ==== * When processing '''unconstrained '''sources, you are often interested in comparing the norm of the current vector between conditions, rather than the three orientations separately. * To get these values, you can run the process "'''Sources > Unconstrained to flat maps'''" on all the trials of both conditions, then run again the scout values extraction for '''A1/160ms'''. This is the distribution you would get if you use the option "Average of absolute values: mean(abs(x))" in the t-test of averaging processes. <<BR>><<BR>> {{attachment:histogram_scout4.gif||height="99",width="216"}} ==== Time-frequency ==== * Time-frequency power at 55ms / 48Hz, respectively for:<<BR>>1) Sensor MLP57, <<HTML( )>>2) Scout A1, <<HTML( )>>3) Scout A1 (Z-score normalized)<<BR>><<BR>> {{attachment:histogram_tf1.gif||height="100",width="220"}} {{attachment:histogram_tf2.gif||height="100",width="218"}} {{attachment:histogram_tf3.gif||height="100",width="218"}} * None of these sample sets are normally distributed. Independent parametric t-tests don't look like good candidates for testing time-frequency power across trials. ==== Group studies: different distributions ==== * The observations above hold only for the specific dataset we are looking at: '''single subject''' analysis, testing across trials only one frequency, one time sample, one signal. * In the context of a group analysis, we test subject averages between conditions or populations. So we are comparing the distributions of the trial averages, which will tend to be normal when we increase the number of trials ([[https://en.wikipedia.org/wiki/Central_limit_theorem|Central-llimit theorem]]). We will have in many cases less problems to ensure the normal distributions of the sample sets at the group level. * Additionnally, some tricks can help bringing the samples closer to a normal distribution, like averaging in time/space/frequencies, or testing the square root of the data, in the case of time-frequency power. Some solutions are explored in ([[http://www.fil.ion.ucl.ac.uk/spm/doc/papers/sjk_eeg3.pdf|Kiebel, Tallon-Baudry & Friston, HBM 2005]]). == Statistical inference == ==== Hypothesis testing ==== To show that there is a difference between A and B, we can use a statistical hypothesis test. We start by assuming that the two sets are identical then reject this hypothesis. For all the tests we will use here, the logic is similar: * Define a '''null hypothesis''' (H<<HTML(<sub>)>>0<<HTML(</sub>)>>:"A=B") and an alternative hypotheses (eg. H<<HTML(<sub>)>>1<<HTML(</sub>)>>:"A<B"). * Make some assumptions on the samples we have (eg. A and B are independent, A and B follow normal distributions, A and B have equal variances). * Decide which test is appropriate, and state the relevant '''test statistic''' T (eg. Student t-test). * Compute from the measures (A<<HTML(<sub>)>>obs<<HTML(</sub>)>>, B<<HTML(<sub>)>>obs<<HTML(</sub>)>>) the observed value of the test statistic (t<<HTML(<sub>)>>obs<<HTML(</sub>)>>). * Calculate the '''p-value'''. This is the probability, under the null hypothesis, of sampling a test statistic at least as extreme as that which was observed. A value of (p<0.05) for the null hypothesis has to be interpreted as follows: "If the null hypothesis is true, the chance that we find a test statistic as extreme or more extreme than the one observed is less than 5%". * Reject the null hypothesis if and only if the p-value is less than the significance level threshold (<<HTML(α)>>).<<BR>><<BR>> {{attachment:stat_tails.gif||height="322",width="598"}} ==== Evaluation of a test ==== The quality of test can be evaluated based on two criteria: * '''Sensitivity''': True positive rate = power = ability to correctly reject the null hypothesis and control for the false negative rate (type II error rate). A very sensitive test detects a lot of significant effects, but with a lot of false positive. * '''Specificity''': True negative rate = ability to correctly accept the null hypothesis and control for the false positive rate (type I error rate). A very specific test detects only the effects that are clearly non-ambiguous, but can be too conservative and miss a lot of the effects of interest. <<BR>><<BR>> {{attachment:stat_errors.gif||height="167",width="455"}} ==== Different categories of tests ==== Two families of tests can be helpful in our case: parametric and non-parametric tests. * '''Parametric tests''' need some strong assumptions on the probability distributions of A and B then use some well-known properties of these distributions to compare them, based on a few simple parameters (typically the mean and variance). The estimation of these parameters is highly optimized and require very little memory. The examples which will be described here are the Student's t-tests. * '''Non-parametric tests''' do not require any assumption on the distribution of the data. They are therefore more reliable and more generic. On the other hand they are a lot more complicated to process: they require a lot more memory because all the tested data has to be loaded at once, and a lot more computation time because the same test is repeated many times. == Parametric Student's t-test == ==== Assumptions ==== The [[https://en.wikipedia.org/wiki/Student's_t-test|Student's t-test]] is a widely-used parametric test to evaluate the difference between the means of two random variables (two-sample test), or between the mean of one variable and one known value (one-sample test). If the assumptions are correct, the t-statistic follows a [[https://en.wikipedia.org/wiki/Student's_t-distribution|Student's t-distribution]]. . {{attachment:stat_tvalue.gif||height="127",width="490"}} The main assumption for using a t-test is that the random variables involved follow a [[https://en.wikipedia.org/wiki/Normal_distribution|normal distribution]] (mean: μ, standard deviation: σ). The figure below shows a few example of normal distributions. . {{attachment:stat_distrib_normal.gif||height="190",width="298"}} <<latex($$ f(x \; | \; \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi} } \; e^{ -\frac{(x-\mu)^2}{2\sigma^2} } $$)>> ==== t-statistic ==== Depending on the type of data we are testing, we can have different variants for this test: * '''One-sample t-test''' (testing against a known mean μ<<HTML(<sub>)>>0<<HTML(</sub>)>>): <<BR>><<latex($$ t = \frac{\overline{x} - \mu_0}{\sigma/\sqrt{n}} \hspace{40pt} \mathrm{d.f.} = n - 1 $$)>> <<BR>>where <<latex($$\overline{x}$$)>> is the sample mean, σ is the sample standard deviation and ''n'' is the sample size. * '''Dependent t-test''' for paired samples (eg.when testing two conditions across subject). Equivalent to testing the difference of the pairs of samples against zero with a one-sample t-test:<<BR>><<latex($$ t = \frac{\overline{X}_D}{\sigma_D/\sqrt{n}} \hspace{40pt} \mathrm{d.f.} = n - 1 $$)>> <<BR>>where D=A-B, <<latex($$\overline{X}_D$$)>> is the average of D and σ'',,D,,'' its standard deviation. * '''Independent two-sample test, equal variance''' (equal or unequal sample sizes):<<BR>><<latex($$ t = \frac{\bar{X}_A - \bar{X}_B}{s_{X_AX_B} \cdot \sqrt{\frac{1}{n_A}+\frac{1}{n_B}}} \hspace{40pt} s_{X_AX_B} = \sqrt{\frac{(n_A-1)s_{X_A}^2+(n_B-1)s_{X_B}^2}{n_A+n_B-2}} \hspace{40pt} \mathrm{d.f.} = n_A + n_B - 2 $$)>> <<BR>>where <<latex($$s_{X_A}^2$$)>> and <<latex($$s_{X_B}^2$$)>> are the unbiased estimators of the variances of the two samples. * '''Independent two-sample test, u''''''nequal variance''' (Welch's t-test):<<BR>> <<latex($$t = {\overline{X}_A - \overline{X}_B \over s_{\overline{X}_A - \overline{X}_B}} \hspace{40pt}s_{\overline{X}_A - \overline{X}_B} = \sqrt{{s_A^2 \over n_A} + {s_B^2 \over n_B}} \hspace{40pt} \mathrm{d.f.} = \frac{(s_A^2/n_A + s_B^2/n_B)^2}{(s_A^2/n_A)^2/(n_A-1) + (s_B^2/n_B)^2/(n_B-1)} $$)>> <<BR>> where <<latex($$n_A$$)>> and <<latex($$n_B$$)>> are the sample sizes of A and B. ==== p-value ==== Once the t-value is computed (t<<HTML(<sub>)>>obs<<HTML(</sub>)>> in the previous section), we can convert it to a p-value based on the known distributions of the t-statistic. This conversion depends on two factors: the number of degrees of freedom and the tails of the distribution we want to consider. For a two-tailed t-test, the two following commands in Matlab are equivalent and can convert the t-values in p-values. <<BR>>To obtain the p-values for a '''one-tailed t-test''', you can simply '''divide the p-values by 2'''. <<HTML(<BLOCKQUOTE>)>> {{{ p = betainc(df./(df + t.^2), df/2, 0.5); % Without the Statistics toolbox p = 2*(1-tcdf(abs(t),df)); % With the Statistics toolbox }}} <<HTML(</BLOCKQUOTE>)>> The distribution of this function for different numbers of degrees of freedom: . {{attachment:ttest_tcdf.gif||height="177",width="366"}} == Example 1: Parametric t-test on recordings == Parametric t-tests require the values tested to follow a normal distribution. The recordings evaluated in the histograms sections above (MLP57/160ms) show distributions that are matching this assumption relatively well: the shape of the histogram follows the trace of the corresponding normal function, and with very similar variances. It looks reasonable to use a parametric t-test in this case. * In the Process2 tab, select the following files, from '''both runs '''(approximation discussed previously): * Files A: All the '''deviant '''trials, with the [Process recordings] button selected. * Files B: All the '''standard '''trials, with the [Process recordings] button selected. * '''The t-tests work well with unbalanced number of samples''': Unlike the difference of averages, it is better to use all the possible samples you have, even if you have 80 trials in one condition and 400 in the other. * Run the process "'''Test > Parametric t-test'''", Equal variance, Arithmetic average.<<BR>><<BR>> {{attachment:stat_ttest1_process.gif||height="376",width="610"}} * Double-click on the new file for displaying it and add a 2D topography (CTRL+T). The values displayed in the 2D view are the significant t-values. All the sensors that have p-values higher than the significance level threshold (<<HTML(α)>>) are set to zero. * With the new '''Stat tab''' you can control the '''p-value threshold''' and the correction you want to apply for '''multiple comparisons''' (see next section). <<BR>><<BR>> {{attachment:stat_ttest1_file.gif||height="136",width="674"}} == Correction for multiple comparisons == ==== Multiple comparison problem ==== The approach described in this first example performs many tests simultaneously. We test, independently, each MEG sensor and each time sample across the trials, so we run a total of 274*361 = 98914 t-tests. If we select a critical value of 0.05 (p<0.05), it means that we want to see what is significantly different between the conditions while accepting the risk of observing a false positive in 5% of the cases. If we run the test around 100,000 times, we can expect to observe around 5,000 false positives. We need to better control for false positives (type I errors) when dealing with multiple tests. ==== Bonferroni correction ==== The probability to observe at least one false positive, or '''familywise error rate (FWER)''' is almost 1: <<BR>> '''FWER''' = 1 - prob(no significant results) = 1 - (1 - 0.05)^100000 '''~ 1''' A classical way to control the familywise error rate is to replace the p-value threshold with a corrected value, to enforce the expected FWER. The Bonferroni correction sets the significance cut-off at <<latex($$\alpha$$)>>/Ntest. If we set (p <<HTML(≤)>> <<latex($$\alpha$$)>>/Ntest), then we have (FWER <<HTML(≤)>> <<latex($$\alpha$$)>>). Following the previous example:<<BR>>'''FWER''' = 1 - prob(no significant results) = 1 - (1 - 0.05/100000)^100000 '''~ 0.0488 < 0.05''' This works well in a context where all the tests are strictly independent. However, in the case of MEG/EEG recordings, the tests have an important level of dependence: two adjacent sensors or time samples often have similar values. In the case of highly correlated tests, the Bonferroni correction tends too be conservative, leading to a high rate of false negatives. ==== FDR correction ==== The '''false discovery rate (FDR)''' is another way of representing the rate of type I errors in null hypothesis testing when conducting multiple comparisons. It is designed to control the expected proportion of false positives, while the Bonferroni correction controls the probability to have at least one false positive. FDR-controlling procedures have greater power, at the cost of increased rates of Type I errors ([[https://en.wikipedia.org/wiki/False_discovery_rate|Wikipedia]]) In Brainstorm, we implement the Benjamini–Hochberg step-up procedure for FDR correction: * Sort the p-values p(''k'') obtained across all the multiple tests (''k''=1..Ntest). * Find the largest ''k'' such as p(''k'') < ''k'' / Ntest * <<latex($$\alpha$$)>>. * Reject the null hypotheses corresponding to the first ''k'' smallest p-values. ==== In the interface ==== <<HTML(<div style="padding: 0px; float: right;">)>> {{attachment:stat_mcp_gui.gif}} <<HTML(</A></div>)>> You can select interactively the type of correction to apply for multiple comparison while reviewing your statistical results. The checkboxes "Control over dims" allow you to select which are the dimensions that you consider as multiple comparisons (1=sensor, 2=time, 3=not applicable here). If you select all the dimensions, all the values available in the file are considered as the same repeated test, and only one corrected p-threshold is computed for all the time samples and all the sensors. If you select only the first dimension, only the values recorded at the same time sample are considered as repeated tests, the different time points are corrected independently, with one different corrected p-threshold for each time point. When changing these options, a message is displayed in the Matlab command window, showing the number of repeated tests that are considered, and the corrected p-value threshold (or the average if there are multiple corrected p-thresholds, when not all the dimensions are selected): <<HTML(<BLOCKQUOTE>)>> {{{ BST> Average corrected p-threshold: 5.0549e-07 (Bonferroni, Ntests=98914) BST> Average corrected p-threshold: 0.00440939 (FDR, Ntests=98914) }}} <<HTML(</BLOCKQUOTE>)>> == Nonparametric permutation tests == ==== Principle ==== A '''permutation test''' (or randomization test) is a type of test in which the distribution of the test statistic under the null hypothesis is obtained by calculating all possible values of the test statistic under rearrangements of the labels on the observed data points. ([[https://en.wikipedia.org/wiki/Resampling_(statistics)#Permutation_tests|Wikipedia]]) If the null hypothesis is true, the two sets of tested values A and B follow the same distribution. Therefore the values are '''exchangeable '''between the two sets: we can move one value from set A to set B, and one value from B to A, and we expect to obtain the same value for the test statistic T. . {{attachment:stat_exchange.gif||height="37",width="302"}} By taking all the possible permutations between sets A and B and computing the statistic for each of them, we can build a histogram that approximates the '''permutation distribution'''. . {{attachment:stat_perm_distrib.gif||height="184",width="400"}} Then we compare the observed statistic with the permutation distribution. From the histogram, we calculate the proportion of permutations that resulted in a larger test statistic than the observed one. This proportion is called the '''p-value'''. If the p-value is smaller than the critical value (typically 0.05), we conclude that the data in the two experimental conditions are significantly different. . {{attachment:stat_perm_pvalue.gif||height="183",width="400"}} The number of possible permutations between the two sets of data is usually too large to compute an exhaustive permutation test in a reasonable amount of time. The permutation distribution of the statistic of interest is approximated using a '''Monte-Carlo approach'''. A relatively small number of random selection of possible permutations can give us a reasonably good idea of the distribution. Permutation tests can be used for '''any test statistic''', regardless of whether or not its distribution is known. The hypothesis is about the data itself, not about a specific parameter. In the examples below, we use the t-statistic, but we could use any other function. ==== Practical limitations ==== '''Computation time''': If you increase the number of random permutations you use for estimating the distribution, the computation time will increase linearly. You need to find a good balance between the total computation time and the accuracy of the result. '''Memory (RAM)''': The implementations of the permutation tests available in Brainstorm require all the data to be loaded in memory before starting the evaluation of the permutation statistics. Running this function on large datasets or on source data could quickly crash your computer. For example, loading the data for the non-parametric equivalent to the parametric t-test we ran previously would require: <<BR>> 276(sensors) * 461(trials) * 361(time) * 8(bytes) / 1024^2(Gb) = '''0.3 Gb of memory'''. This is acceptable on most recent computers. But to perform the same at the source level, you need: <<BR>>45000*461*361*8/1024^3 = '''58 Gb of memory''' just to load the data. This is impossible on most computers, we have to give up at least one dimension and run the test only for one region of interest or one time sample (or average over a short time window). == FieldTrip implementation == ==== FieldTrip functions in Brainstorm ==== We have the possibility to call some of the FieldTrip toolbox functions from the Brainstorm environment. For this, you need first to [[http://www.fieldtriptoolbox.org/download|install the FieldTrip toolbox]] on your computer and [[http://www.fieldtriptoolbox.org/faq/should_i_add_fieldtrip_with_all_subdirectories_to_my_matlab_path|add it to your Matlab path]]. ==== Cluster-based correction ==== One interesting method that has been promoted by the FieldTrip developers is the cluster-based approach for non-parametric tests. In the type of data we manipulate in MEG/EEG analysis, the neighbouring channels, time points or frequency bins are expected to show similar behavior. We can group these neighbours into '''clusters '''to "accumulate the evidence". A cluster can have a multi-dimensional extent in space/time/frequency. In the context of a non-parametric test, the test statistic computed at each permutation is the extent of the '''largest cluster'''. To reject or accept the null hypothesis, we compare the largest observed cluster with the randomization distribution of the largest clusters. This approach '''solves the multiple comparisons problem''', because the test statistic that is used (the maximum cluster size) is computed using all the values at the same time, along all the dimensions (time, sensors, frequency). There is only one test that is performed, so there is no multiple comparisons problem. The result is simpler to report but also '''a lot less informative''' than FDR-corrected non-parametric tests. We have only one null hypothesis, "the two sets of data follow the same probability distribution", and the outcome of the test is to accept or reject this hypothesis. Therefore we '''cannot report the spatial or temporal extent''' of the most significant clusters. Make sure you read [[http://www.fieldtriptoolbox.org/faq/how_not_to_interpret_results_from_a_cluster-based_permutation_test|this recommendation]] before reporting cluster-based results in your publications. ==== Reference documentation ==== For a complete description of non-parametric cluster-based statistics in FieldTrip, read the following: * Article: [[http://www.sciencedirect.com/science/article/pii/S0165027007001707|Maris & Oostendveld (2007)]] * Video: [[https://www.youtube.com/watch?v=x0hR-VsHZj8|Statistics using non-parametric randomization techniques]] (E Maris) * Video: [[https://www.youtube.com/watch?v=vOSfabsDUNg|Non-parametric cluster-based statistical testing of MEG/EEG data]] (R Oostenveld) * Tutorial: [[http://www.fieldtriptoolbox.org/tutorial/eventrelatedstatistics|Parametric and non-parametric statistics on event-related fields]] * Tutorial: [[http://www.fieldtriptoolbox.org/tutorial/cluster_permutation_timelock|Cluster-based permutation tests on event related fields]] * Tutorial: [[http://www.fieldtriptoolbox.org/tutorial/cluster_permutation_freq|Cluster-based permutation tests on time-frequency data]] * Tutorial: [[http://www.fieldtriptoolbox.org/faq/how_not_to_interpret_results_from_a_cluster-based_permutation_test|How NOT to interpret results from a cluster-based permutation test]] * Functions references: [[http://www.fieldtriptoolbox.org/reference/timelockstatistics|ft_timelockstatistics]], [[http://www.fieldtriptoolbox.org/reference/sourcestatistics|ft_sourcestatistics]], [[http://www.fieldtriptoolbox.org/reference/freqstatistics|ft_freqstatistics]] ==== Process options ==== There are three separate processes in Brainstorm, to call the three FieldTrip functions. * '''ft_timelockstatistics''': Compare imported trials (recordings). * '''ft_sourcestatistics''': Compare source maps or time-frequency files include the entire cortex. * '''ft_freqstatistics''': Compare time-frequency decompositions of sensor recordings or scouts signals. * See below the correspondence between the options in the interface and the FieldTrip functions. Test statistic options (process options in bold): * cfg.numrandomization = "'''Number of randomizations'''" * cfg.statistic = "'''Independent t-test'''" ('indepsamplesT') or "'''Paire t-test'''" ('depsamplesT) * cfg.tail = '''One-tailed''' (-1), '''Two-tailed''' (0), '''One-tailed''' (+1) * cfg.correctm = "'''Type of correction'''" ('no', 'cluster', 'bonferroni', 'fdr', 'max', 'holm', 'hochberg') * cfg.method = 'montecarlo'<<HTML(<div style="padding: 0px; float: right;">)>> {{attachment:ft_process_options.gif||height="318",width="296"}} <<HTML(</div>)>> * cfg.correcttail = 'prob' Cluster-based correction: * cfg.clusteralpha = "'''Cluster Alpha'''" * cfg.minnbchan = "'''Min number of neighours'''" * cfg.clustertail = cfg.tail (in not, FieldTrip crashes) * cfg.clusterstatistic = 'maxsum' Input options: All the data selection is done before, in the process code and functions out_fieldtrip_*.m. * cfg.channel = 'all'; * cfg.latency = 'all'; * cfg.frequency = 'all'; * cfg.avgovertime = 'no'; * cfg.avgchan = 'no'; * cfg.avgoverfreq = 'no'; == Example 2: Uncorrected non-parametric t-test == Let's run the non-parametric equivalent to the test we ran in the first example. * In the Process2 tab, select the following files, from '''both runs '''(approximation discussed previously): * Files A: All the '''deviant '''trials, with the [Process recordings] button selected. * Files B: All the '''standard '''trials, with the [Process recordings] button selected. * Run the process "'''Test > FieldTrip: ft_timelockstatistics'''", set the options as shown below <<BR>>(expect this to run for at least 15min - check the Matlab command window for progress report): <<BR>><<BR>> {{attachment:ft_nocorrection_options.gif||height="431",width="576"}} * Open the parametric and non-parametric results side by side, the results should be very similar. <<BR>><<BR>> {{attachment:ft_nocorrection_display.gif||height="241",width="407"}} * In this case, the distributions of the values for each sensor and each time point (non-rectified MEG recordings) are very close to '''normal distributions'''. This was illustrated at the top of this page, in the section "Histograms". Therefore the assumptions behind the parametric t-test are verified, the results of the parametric tests are correct and very similar to the nonparametric ones. * If you get different results with the parametric and nonparametric approaches: trust the nonparametric one. If you want to increase the precision of a nonparametric test, increase the number of random permutations. == Example 3: Cluster-based test == Run again the same test, but this time select the cluster correction. * Keep the same files selected in Process2. * Run the process "'''Test > FieldTrip: ft_timelockstatistics'''", Type of correction = '''cluster'''<<BR>>(expect this to run for at least 20min - check the Matlab command window for progress report): <<BR>><<BR>> {{attachment:ft_cluster_process.gif||height="149",width="264"}} * Double-click on the new file to display it, add a 2D topography to is (CTRL+T).<<BR>>Note that in the Stat tab, the options for multiple comparisons corrections are disabled, because the values saved in the file are already corrected, you can only change the significance threshold. * Alternatively, you get a list of significant clusters, which you can display separately if needed. The colored dots on the topography represent the clusters, blue for negative clusters and red for positive clusters. You can change these colors in the Stat tab. Note that the clusters have a spatio-temporal extent: at one time point they can be represented as two separate blobs in the 2D topography, but these blobs are connected at other time points.<<BR>><<BR>> {{attachment:ft_cluster_display1.gif||height="210",width="604"}} * Additional options are available for exploring the clusters, try them all. Values used to represent the clusters: '''p'''=p-value, '''c'''=cluster statistic (maxsum), '''s'''=cluster size (connected data points). <<BR>><<BR>> {{attachment:ft_cluster_display2.gif||height="142",width="671"}} * '''Don't spend too much time exploring the clusters''': In the previous cases, all the tests at each sensor and each time point were computed independently, we could report, individually, whether each of them was significant or not. On the other hand, the cluster-based approach just allows us to report that the two conditions are different, without specifying where or when, which makes the visual exploration of clusters relatively useless. Make sure you read [[http://www.fieldtriptoolbox.org/faq/how_not_to_interpret_results_from_a_cluster-based_permutation_test|this recommendation]] before reporting cluster-based results in your publications. == Example 4: Non-parametric t-test on sources == To reproduce the same results at the source level, we need to limit the data we are looking at, alternatively the amount of data that has to be loaded to run the non-parametric tests will not fit in memory. Here we average a short time window during which we observed major differences ('''150-170ms'''). * Keep the same files selected in Process2. Select the button '''[Process sources]''' on '''both sides'''. * Run the process "'''Test > FieldTrip: ft_sourcestatistics'''"<<BR>><<BR>> {{attachment:ft_sources_process.gif||height="488",width="448"}} * Options: * Time window: '''[150,170]ms''', short time window around the peak at 160ms. * Select "'''Average over time'''": This will test the average source values over the selected time window (150-170ms) instead of each time sample independently. * Select "'''Test absolute values'''": This option convert the unconstrained source maps (three dipoles at each cortex location) into a flat cortical map by taking the norm of the three dipole orientations before computing the test. * Type of correction: '''no''', we want to use the on-the-fly FDR correction (Scout tab). * Double-click on the new file for displaying it. <<BR>><<BR>> {{attachment:ft_sources_display.gif||height="164",width="667"}} ==== Issues with unconstrained sources ==== * The results are very disappointing, because nothing survives the FDR-correction at (p<0.05), while the effect was very strong at the sensor level. The problem resides in the fact that we tested '''(|A|=|B|)''' instead of (A=B), because we selected the option "'''Test absolute values'''". As explained the [[http://Tutorials/Difference|Difference tutorial]], this measure is '''unable to extract the correct effect size'''. * However, the sign of the difference is meaningful, so we can report that the blue values we observe at (p<0.05, uncorrected) indicate a '''significantly lower''' activity in condition A (deviant) than in condition B (standard), in average during this time segment (150-170ms). * There is currently '''no independent test''' available to test '''(A=B)''' for unconstrained sources. The alternative is to use a source model with constrained orientations instead. The screen capture below shows the result you would get with a '''constrained minimum norm''' solution (no absolute value). The effect is now clearly significant, but the sign is useless. <<BR>><<BR>> {{attachment:ft_sources_constr.gif||height="169",width="444"}} * For dependent/'''paired '''tests, we do not have this problem, because we can test the norm of the difference: H0:'''(Norm(A-B)=0)''', with a non-parametric one-sided test. ==== Scouts and statistics ==== * From the Scout tab, you can also plot the scouts time series and get a summary of what is happening in your regions of interest. This is not very interesting in this particular case, because we don't have any time dimension, but it can be an interesting tool to remember. * Positive peaks indicate the latencies when '''at least one vertex''' of the scout has a value that is significantly higher in the deviant condition. The values that are shown are the averaged t-values in the scout. Make sure you select the option "Values: Relative" to display the scouts.<<BR>><<BR>> {{attachment:ft_sources_scouts.gif||height="150",width="616"}} == Example 5: Non-parametric t-test on scouts == The previous example was showing how to get rid of one dimension buy restricting the analysis to one averaged time window. Alternatively, we can keep the time dimension and run the test only on the regions of interest. * Keep the same files selected in Process2. Select the button '''[Process sources]''' on '''both sides'''. * Run the process "'''Test > FieldTrip: ft_sourcestatistics'''".<<BR>>Time window: all, Use scouts, Test absolute values, Do not average over time.<<BR>><<BR>> {{attachment:ft_scouts_process.gif||height="647",width="348"}} * We cannot represent this over the cortex since we have restricted the measure to the scouts and discarded all the spatial information. But it shows the time points at where the scout signals (averaged across vertices) are significantly different in the two conditions. As explained in the previous example: the effect size is wrong but the sign of the t-value is correct. <<BR>><<BR>> {{attachment:ft_scouts_display.gif||height="155",width="683"}} <<TAG(Advanced)>> == Example 6: Non-parametric t-test on time-frequency maps [TODO] == Two run a test on time-frequency maps, first you need to have all the time-frequency files available in the database, for each individual trials. In the [[Tutorials/TimeFrequency|time-frequency tutorial]], we saved only the averaged time-frequency decompositions of all the trials. * In '''Process1''', select all the trials from both conditions and '''one run''' (just to make it faster). * Run process "'''Frequency > Time-frequency (Morlet wavelets)'''". Select the options as below. <<BR>><<BR>> {{attachment:tf_trials.gif||height="532",width="654"}} * In '''Process2''', select the following files, from '''both runs''': * Files A: All the '''deviant '''trials, with the '''[Process time-freq]''' button selected. * Files B: All the '''standard '''trials, with the '''[Process time-freq]''' button selected. * You need at least 12Gb of RAM to run this process. If you don't, select a lower number of trials in FilesB (for instance, the same number as files selected in FilesA). * Run the process "'''Test > FieldTrip: ft_sourcestatistics'''". <<BR>>Get ready for this to run for a long time... Press Ctrl+C in the Matlab command if it's too slow.<<BR>><<BR>> {{attachment:tf_stat_process.gif||height="467",width="541"}} * Display results: '''TODO''' Now '''delete '''the TF decomposition for the individual trials (because it probably uses a lot of disk space): * In Process1, select the files for which you compute the TF decomposition. * Select the '''[Process time-freq]''' button selected. * Run process "'''File > Delete files'''". Option "Delete data files".<<BR>><<BR>> {{attachment:tf_delete.gif||height="213",width="434"}} <<TAG(Advanced)>> == Workflow: Single subject == For one unique subject, test for significant differences between two experimental conditions: * Compare the '''single trials''' corresponding to each condition. * In most cases, you '''do not need to normalize''' the data. * Use '''independent tests'''. * For help with the implications of testing the '''relative or absolute values''', see: [[Tutorials/Difference|Difference]]. '''Sensor recordings''': * Not advised for MEG with multiple runs, correct for EEG. * '''A vs B''': * Never use an absolute value for testing recordings. * '''Parametric''' or '''non-parametric''' tests, independent, two-tailed, FDR-corrected. * Correct effect size, ambiguous sign. '''Constrained source maps''' (one value per vertex): * Use the non-normalized minimum norm maps for all the trials (current density maps, no Z-score). * '''A vs B''': * Null hypothesis H0: (A=B). * '''Parametric''' or '''non-parametric''' tests, independent, two-tailed, FDR-corrected. * Correct effect size, ambiguous sign. * '''|A| vs |B|''': * Null hypothesis H0: (|A|=|B|). * '''Non-parametric''' tests only, independent, two-tailed, FDR-corrected. * Incorrect effect size, meaningful sign. '''Unconstrained source maps''' (three values per vertex): * Use the non-normalized minimum norm maps for all the trials (current density maps, no Z-score). * We need to test the '''norm '''of the three orientations instead of testing the orientations separately. * '''Norm(A) vs. Norm(B)''': * Null hypothesis H0: (|A|=|B|). * '''Non-parametric''' tests only, independent, two-tailed, FDR-corrected. * Incorrect effect size, meaningful sign. '''Time-frequency maps''': * Test the non-normalized time-frequency maps for all the trials (no Z-score or ERS/ERD). * The values tested are power or magnitudes, all positive, so (A=B) and (|A|=|B|) are equivalent. * '''|A| vs |B|''': * Null hypothesis H0: (|A|=|B|) * '''Non-parametric''' tests only, independent, two-tailed, FDR-corrected. * Correct effect size, meaningful sign. <<TAG(Advanced)>> == Workflow: Group analysis == ==== Subject averages ==== You need first to process the data separately for each subject: 1. Compute the ''' subject-level averages''', using the '''same number of trials''' for each subject.<<BR>> Sources: Average the non-normalized minimum norm maps (current density maps, no Z-score). 1. Sources computed on individual brains: '''Project '''the individual source maps on a template (see the [[Tutorials/CoregisterSubjects|coregistration tutorial]]). Not needed if the sources were estimated directly on the template anatomy. 1. Sources and time-frequency: '''Normalize '''the data to bring the different subjects to the same range of values (Z-score normalization with respect to a baseline - never apply an absolute value here). 1. Constrained sources: '''Smooth '''spatially the sources, to make sure the brain responses are aligned. ==== Group statistic ==== Two group analysis scenarios are possible: * '''One condition''' recorded for multiple subjects, comparison between '''two groups of subjects''': * Files A: Averages for group of subjects #1. * Files B: Averages for group of subjects #2. * Use '''independent tests''': Exactly the same options as for the single subject (described above) * '''Two conditions''' recorded for multiple subjects, comparison across '''all subjects''': * Files A: All subjects, average for condition A. * Files B: All subjects, average for condition B. * Use '''paired tests''' (= dependent tests), special cases listed below. ==== Paired tests ==== * '''Sensor recordings''': * '''(A-B=0)''': Parametric or non-parametric tests, two-tailed, FDR-corrected. * '''Constrained source maps''' (one value per vertex): * '''(A-B=0)''': Parametric or non-parametric tests, two-tailed, FDR-corrected. * '''(|A|-|B|=0)''': Non-parametric tests, two-tailed, FDR-corrected. * '''Unconstrained source maps''' (three values per vertex): * '''(Norm(A-B)=0)''': Non-parametric tests, __'''one-tailed'''__ (non-negative statistic), FDR-corrected. * '''(Norm(A)-Norm(B)=0)''': Non-parametric tests, two-tailed, FDR-corrected. * '''Time-frequency maps''': * '''(|A|-|B|=0)''': Non-parametric tests, two-tailed, FDR-corrected. * For help with '''relative/absolute options''', read the previous tutorial: [[Tutorials/Difference|Difference]]. <<TAG(Advanced)>> == Convert statistic results to regular files == ==== Apply statistic threshold ==== You can convert the results computed for a statistic test to a regular file. This can be useful because lots of menus and processes are not accessible for the files with the "stat" tag display on top of their icon. * In Process1: Select the results for the test you ran on scouts time series (example #5). * Run process: "'''Extract > Apply statistic threshold'''": '''p<0.05''', '''uncorrected'''. <<BR>><<BR>> {{attachment:extract_threshold.gif||height="323",width="434"}} * It produces one new file, we the same name but without the "stat" tag. This file is now a regular matrix that you can use with any process you want. Try to display it: the Stat tab doesn't show up. ==== Simulate recordings from these scouts ==== * Compute a head model for the intra-subject folder: <<BR>>Right-click on the channel file > '''Compute head model''', keep all the default options. * In Process1, select this new thresholded file. * Run process: "'''Simulate > Simulate recordings from scout'''", select option '''Save full sources'''. <<BR>><<BR>> {{attachment:simulate_process.gif||height="284",width="499"}} * Open the two simulated files (sources and estimated signals): <<BR>><<BR>> {{attachment:simulate_display.gif||height="171",width="609"}} <<TAG(Advanced)>> |
| Line 93: | Line 434: |
| Brainstorm does not offer a very large variety of statistical tests. However, it is easy to export your source results and process them with a specialized program. Some examples are illustrated in the advanced tutorials: | An alternative to running the statistical tests in Brainstorm is to export all the data and compute the tests with an external program (R, Matlab, SPM, etc). Multiple menus exist to export files to external file formats (right-click on a file > File > Export to file). Two tutorials explain to export data specifically to SPM: |
| Line 98: | Line 441: |
| == Additional discussions on the forum == Multiple comparisons: http://neuroimage.usc.edu/forums/showthread.php?1297 <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/TimeFrequency&next=Tutorials/Connectivity")>> |
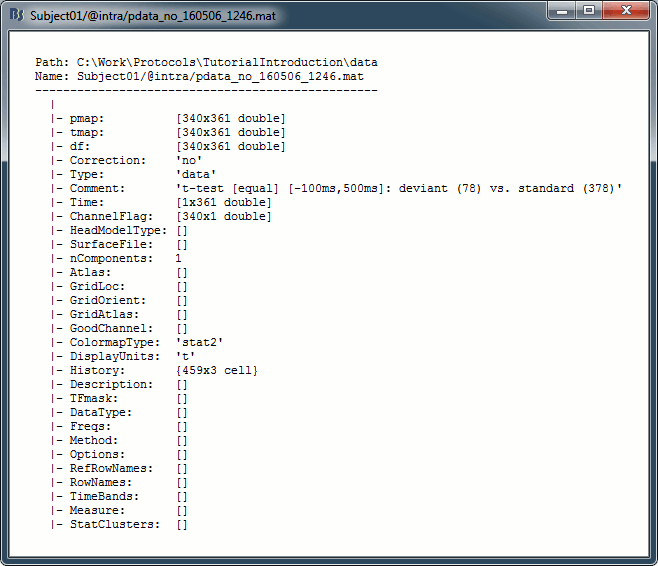
<<TAG(Advanced)>> == On the hard drive == Right click one of the first test we computed in this tutorial > File > '''View file contents'''. . {{attachment:stat_contents.gif||height="454",width="427"}} ==== Description of the fields ==== * '''pmap''': [Nsignals x Ntime x Nfreq]: p-values for all the data points. If empty, computed from tmap: <<BR>> pmap = process_extract_pthresh('GetPmap', tmap, df); * '''tmap''': [Nsignals x Ntime x Nfreq]: t-values for all the data points. * '''df''': Number of degrees of freedom for the test. * '''Correction''': Type of correction for multiple comparison that has already been applied to the p-values in this file ('no', 'cluster', 'fdr', ...) * '''Type''': Initial type of the data from which this file was computed ('data', 'results', 'timefreq', 'matrix') * '''Comment''': String displayed in the database explorer to represent the file. * All the other fields have been described previously and come from the files that have been tested. ==== Useful functions ==== * Brainstorm t-tests (Process2): '''process_ttest''', '''process_ttest_paired''' * Brainstorm t-tests (Process1): '''process_ttest_zero''', '''process_ttest_baseline''' * FieldTrip tests: '''process_ft_timelockstatistics''', '''process_ft_sourcestatistics''', '''process_ft_freqstatistics''' * Conversion Brainstorm to FieldTrip: '''out_fieldtrip_data''', '''out_fieldtrip_results''', '''out_fieldtrip_timefreq''', '''out_fieldtrip_matrix''' * '''bst_stat_thresh''': Computes the Bonferroni and FDR corrections in Brainstorm. * '''process_extract_pthresh''': Computes the pmap from the tmap, and saves thresholded files. <<TAG(Advanced)>> == References == * Bennett CM, Wolford GL, Miller MB, [[http://scan.oxfordjournals.org/content/4/4/417.full|The principled control of false positives in neuroimaging]] <<BR>> Soc Cogn Affect Neurosci (2009), 4(4):417-422. * Maris E, Oostendveld R, [[http://www.sciencedirect.com/science/article/pii/S0165027007001707|Nonparametric statistical testing of EEG- and MEG-data]] <<BR>>J Neurosci Methods (2007), 164(1):177-90. * Maris E, [[http://www.ncbi.nlm.nih.gov/pubmed/22176204|Statistical testing in electrophysiological studies]]<<BR>>Psychophysiology (2012), 49(4):549-65 * Bennett CM, Wolford GL, Miller MB, <<BR>>[[http://scan.oxfordjournals.org/content/4/4/417.full|The principled control of false positives in neuroimaging]]<<BR>>Soc Cogn Affect Neurosci (2009), 4(4):417-422. * Pantazis D, Nichols TE, Baillet S, Leahy RM. [[http://www.sciencedirect.com/science/article/pii/S1053811904005671|A comparison of random field theory and permutation methods for the statistical analysis of MEG data]], Neuroimage (2005), 25(2):383-94. * Kiebel SJ, Tallon-Baudry C, Friston K<<BR>>[[http://www.fil.ion.ucl.ac.uk/spm/doc/papers/sjk_eeg3.pdf|Parametric analysis of oscillatory activity as measured with EEG/MEG]], HBM 2005 * FieldTrip video: Non-parametric cluster-based statistical testing of MEG/EEG data: <<BR>> https://www.youtube.com/watch?v=vOSfabsDUNg <<TAG(Advanced)>> == Additional documentation == * Forum: Multiple comparisons: http://neuroimage.usc.edu/forums/showthread.php?1297 * Forum: Cluster neighborhoods: [[http://neuroimage.usc.edu/forums/showthread.php?2132-Fieldtrip-statistics|http://neuroimage.usc.edu/forums/showthread.php?2132]] * Forum: Differences FieldTrip-Brainstorm: http://neuroimage.usc.edu/forums/showthread.php?2164 == Delete all your experiments == Before moving to the next tutorial, '''delete '''all the statistic results you computed in this tutorial. It will make the database structure less confusing for the following tutorials. <<HTML(<!-- END-PAGE -->)>> <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/Difference&next=Tutorials/Connectivity")>> |
Tutorial 26: Statistics
[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]
Authors: Francois Tadel, Elizabeth Bock, Dimitrios Pantazis, Richard Leahy, Sylvain Baillet
In this auditory oddball experiment, we would like to test for the significant differences between the brain response to the deviant beeps and the standard beeps, time sample by time sample. Until now we have been computing measures of the brain activity in time or time-frequency domain. We were able to see clear effects or slight tendencies, but these observations were always dependent on an arbitrary amplitude threshold and the configuration of the colormap. With appropriate statistical tests, we can go beyond these empirical observations and assess what are the significant effects in a more formal way.
Contents
- Random variables
- Histograms
- Statistical inference
- Parametric Student's t-test
- Example 1: Parametric t-test on recordings
- Correction for multiple comparisons
- Nonparametric permutation tests
- FieldTrip implementation
- Example 2: Uncorrected non-parametric t-test
- Example 3: Cluster-based test
- Example 4: Non-parametric t-test on sources
- Example 5: Non-parametric t-test on scouts
- Example 6: Non-parametric t-test on time-frequency maps [TODO]
- Workflow: Single subject
- Workflow: Group analysis
- Convert statistic results to regular files
- Export to SPM
- On the hard drive
- References
- Additional documentation
- Delete all your experiments
Random variables
In most cases we are interested in comparing the brain signals recorded for two populations or two experimental conditions A and B.
A and B are two random variables for which we have a limited number of repeated measures: multiple trials in the case of a single subject study, or multiple subject averages in the case of a group analysis. To start with, we will consider that each time sample and each signal (source or sensor) is independent: a random variable represents the possible measures for one sensor/source at one specific time point.
A random variable can be described with its probability distribution: a function which indicates what are the chances to obtain one specific measure if we run the experiment. By repeating the same experiment many times, we can approximate this function with a discrete histogram of observed measures.
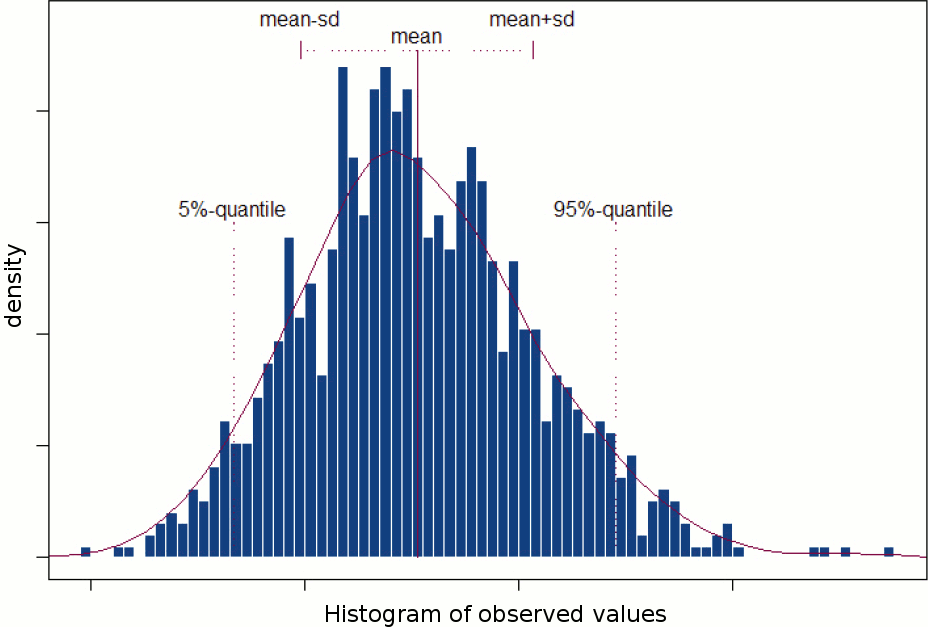
Histograms
You can plot histograms like this one in Brainstorm, it may help you understand what you can expect from the statistics functions described in the rest of this tutorial. For instance, seeing a histogram computed with only 4 values would discourage you forever from running a group analysis with 4 subjects...
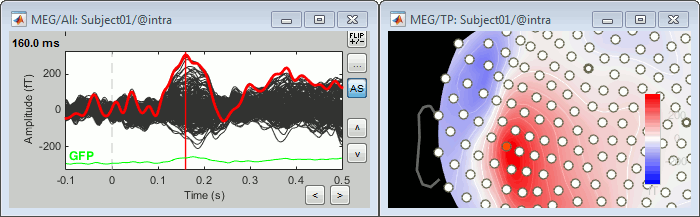
Recordings
Let's evaluate the recordings we obtained for sensor MLP57, the channel that was showing the highest value at 160ms in the difference of averages computed in the previous tutorial.
We are going to extract only one value for each trial we have imported in the database, and save these values in two separate files, one for each condition (standard and deviant).
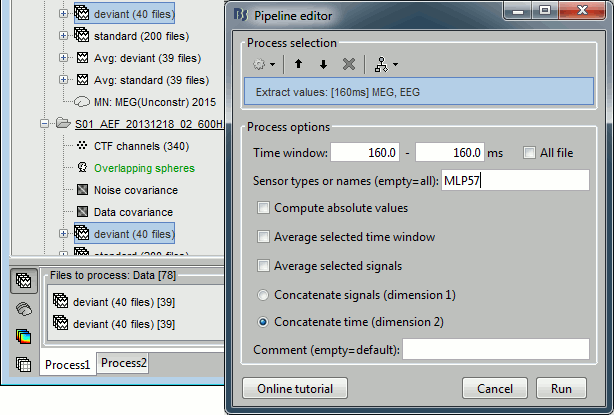
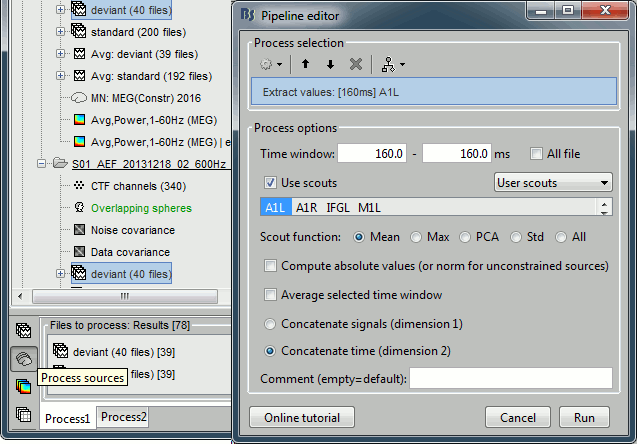
In order to observe more meaningful effects, we will process the trials together from the two acquisition runs. As explained in the previous tutorials (link), this is usually not recommended in MEG analysis, but it can be an acceptable approximation if the subject didn't move between runs.In Process1, select all the deviant trials from both runs.
Run process Extract > Extract values:
Options: Time=[160,160]ms, Sensor="MLP57", Concatenate time (dimension 2)
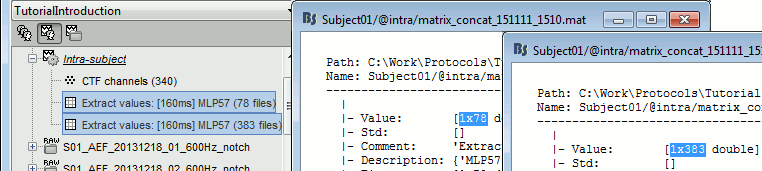
Repeat the same operation for all the standard trials.
You obtain two new files in the folder Intra-subject. If you look inside the files, you can observe that the size of the Value matrix matches the number of trials (78 for deviant, 383 for standard). The matrix is [1 x Ntrials] because we asked to concatenate the extracted values in the 2nd dimension.
To display the distribution of the values in these two files:
select them simultaneously, right-click > File > View histograms.
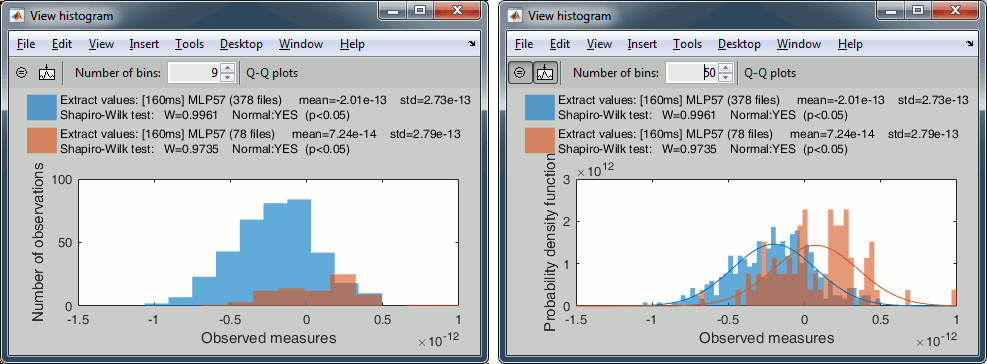
With the buttons in the toolbar, you can edit the way these distributions are represented: number of bins in the histogram, total number of occurrences (shows taller bars for standard because it has more values) or density of probability (normalized by the total number of values).
In addition, you can plot the normal distribution corresponding to the mean μ and standard deviation σ computed from the set of values (using Matlab functions mean and std).When comparing two sample sets A and B, we try to evaluate if the distributions of the measures are equal or not. In most of the questions we explore in EEG/MEG analysis, the distributions are overlapping a lot. The very sparse sampling of the data (a few tens or hundreds of repeated measures) doesn't help with the task. Some representations will be more convincing than others to estimate the differences between the two conditions.
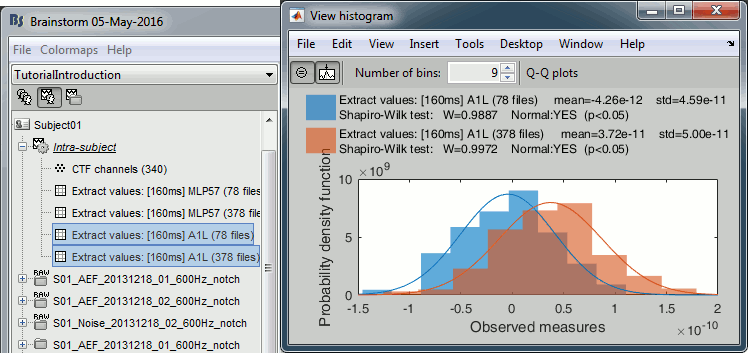
Sources (relative)
We can repeat the same operation at the source level and extract all the values for scout A1.
In Process1, select all the deviant trials from both runs. Select button [Process sources].
Run process Extract > Extract scouts time series:
Options: Time=[160,160]ms, Scout="A1", Flip, Concatenate
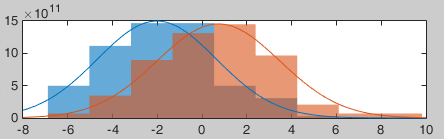
Repeat the same operation for all the standard trials.
Select the two files > Right-click > File > View histogram.
- The distributions still look Gaussian, but the variances are now slightly different. You have to pay attention to this information when choosing which parametric t-test to run (see below).
Sources (absolute)
In Process1, select the extracted scouts value. Run process "Pre-process > Absolute values".
Display the histograms of the two rectified files.
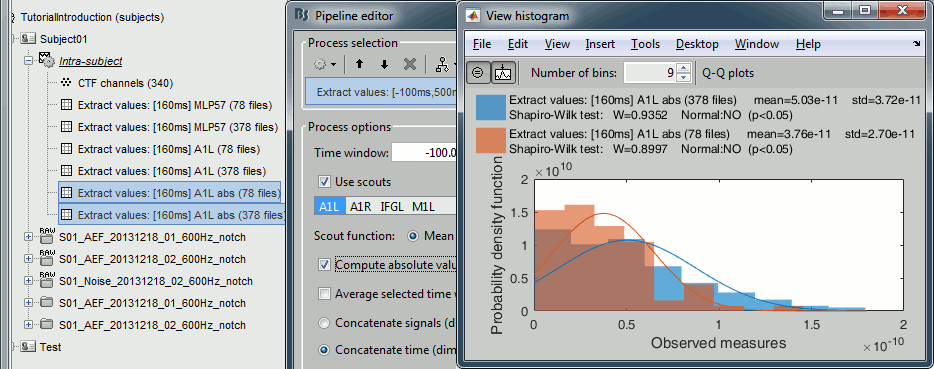
The rectified source values are definitely not following a normal distribution, the shape of the histogram has nothing to do with the corresponding Gaussian curves. As a consequence, if you are using rectified source maps, you will not be able to run independent parametric t-tests.
Additionally, you may have issues with the detection of some effects (see tutorial Difference).
Sources (norm)
When processing unconstrained sources, you are often interested in comparing the norm of the current vector between conditions, rather than the three orientations separately.
To get these values, you can run the process "Sources > Unconstrained to flat maps" on all the trials of both conditions, then run again the scout values extraction for A1/160ms. This is the distribution you would get if you use the option "Average of absolute values: mean(abs(x))" in the t-test of averaging processes.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
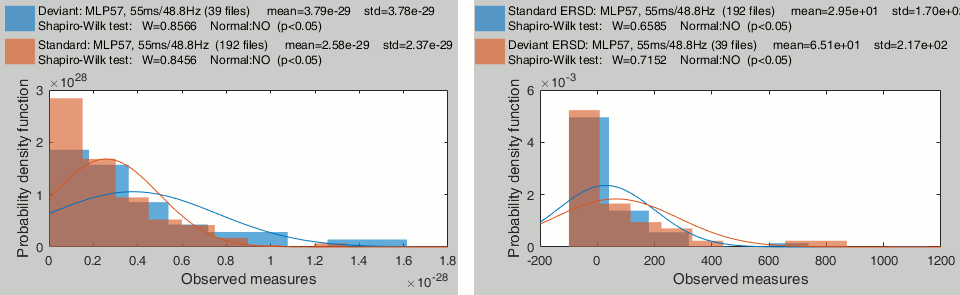
Time-frequency
Time-frequency power at 55ms / 48Hz, respectively for:
1) Sensor MLP57, 2) Scout A1, 3) Scout A1 (Z-score normalized)
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
- None of these sample sets are normally distributed. Independent parametric t-tests don't look like good candidates for testing time-frequency power across trials.
Group studies: different distributions
The observations above hold only for the specific dataset we are looking at: single subject analysis, testing across trials only one frequency, one time sample, one signal.
In the context of a group analysis, we test subject averages between conditions or populations. So we are comparing the distributions of the trial averages, which will tend to be normal when we increase the number of trials (Central-llimit theorem). We will have in many cases less problems to ensure the normal distributions of the sample sets at the group level.
Additionnally, some tricks can help bringing the samples closer to a normal distribution, like averaging in time/space/frequencies, or testing the square root of the data, in the case of time-frequency power. Some solutions are explored in (Kiebel, Tallon-Baudry & Friston, HBM 2005).
Statistical inference
Hypothesis testing
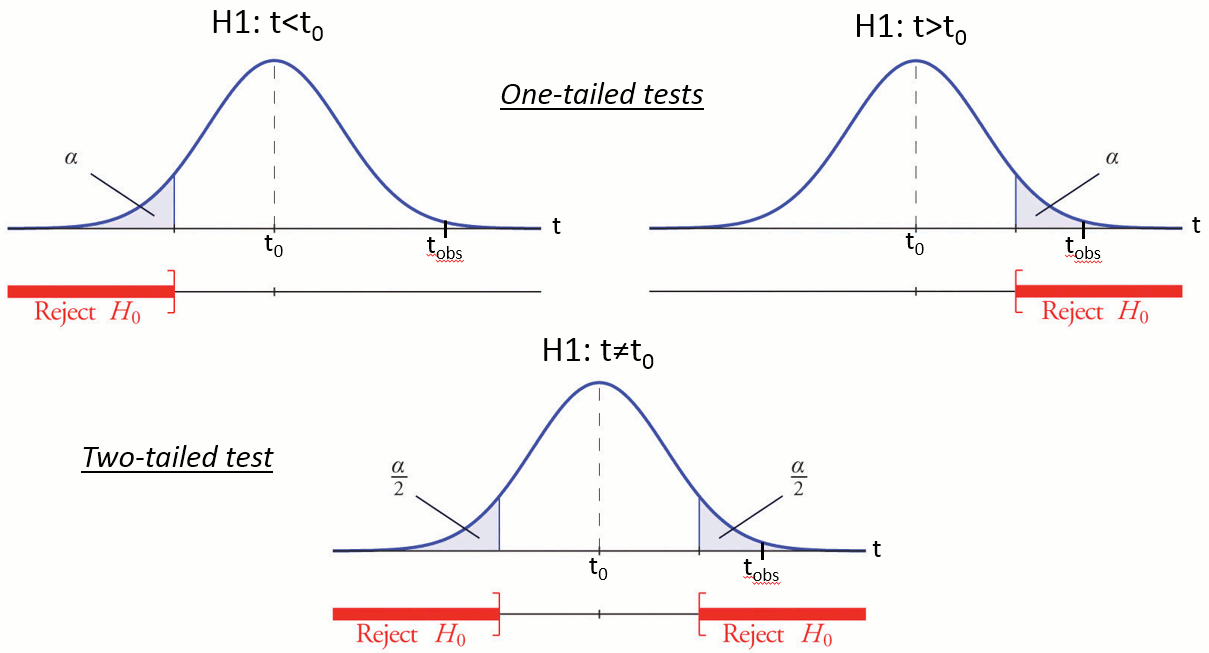
To show that there is a difference between A and B, we can use a statistical hypothesis test. We start by assuming that the two sets are identical then reject this hypothesis. For all the tests we will use here, the logic is similar:
Define a null hypothesis (H0:"A=B") and an alternative hypotheses (eg. H1:"A<B").
- Make some assumptions on the samples we have (eg. A and B are independent, A and B follow normal distributions, A and B have equal variances).
Decide which test is appropriate, and state the relevant test statistic T (eg. Student t-test).
Compute from the measures (Aobs, Bobs) the observed value of the test statistic (tobs).
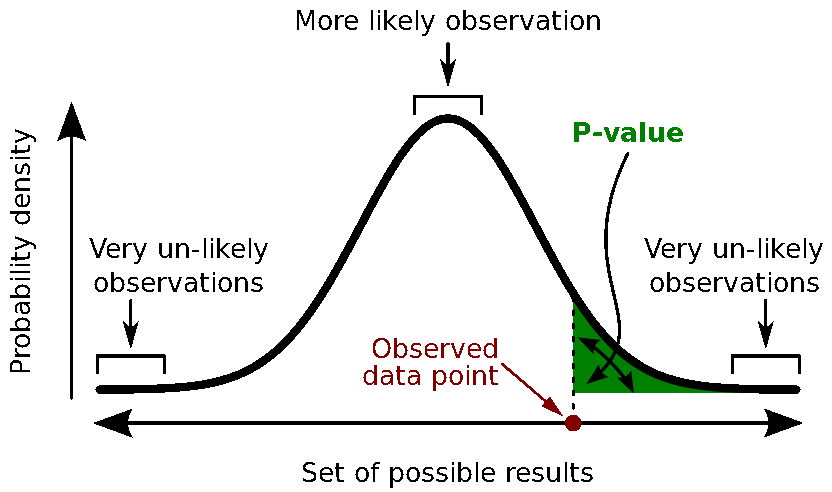
Calculate the p-value. This is the probability, under the null hypothesis, of sampling a test statistic at least as extreme as that which was observed. A value of (p<0.05) for the null hypothesis has to be interpreted as follows: "If the null hypothesis is true, the chance that we find a test statistic as extreme or more extreme than the one observed is less than 5%".
Reject the null hypothesis if and only if the p-value is less than the significance level threshold (α).
Evaluation of a test
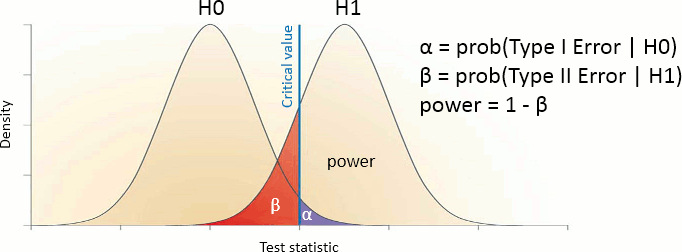
The quality of test can be evaluated based on two criteria:
Sensitivity: True positive rate = power = ability to correctly reject the null hypothesis and control for the false negative rate (type II error rate). A very sensitive test detects a lot of significant effects, but with a lot of false positive.
Specificity: True negative rate = ability to correctly accept the null hypothesis and control for the false positive rate (type I error rate). A very specific test detects only the effects that are clearly non-ambiguous, but can be too conservative and miss a lot of the effects of interest.
Different categories of tests
Two families of tests can be helpful in our case: parametric and non-parametric tests.
Parametric tests need some strong assumptions on the probability distributions of A and B then use some well-known properties of these distributions to compare them, based on a few simple parameters (typically the mean and variance). The estimation of these parameters is highly optimized and require very little memory. The examples which will be described here are the Student's t-tests.
Non-parametric tests do not require any assumption on the distribution of the data. They are therefore more reliable and more generic. On the other hand they are a lot more complicated to process: they require a lot more memory because all the tested data has to be loaded at once, and a lot more computation time because the same test is repeated many times.
Parametric Student's t-test
Assumptions
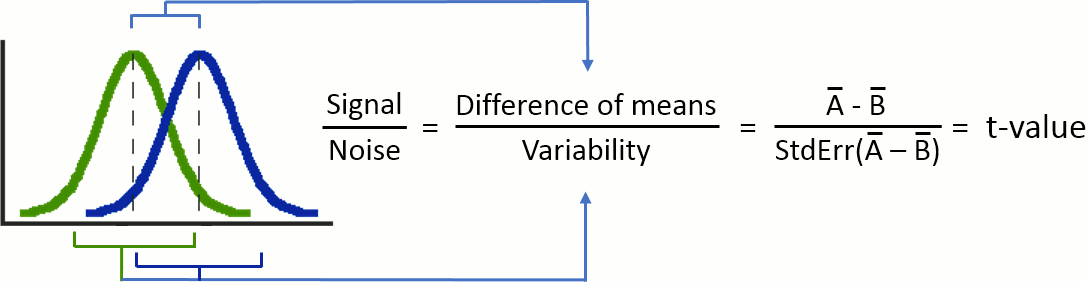
The Student's t-test is a widely-used parametric test to evaluate the difference between the means of two random variables (two-sample test), or between the mean of one variable and one known value (one-sample test). If the assumptions are correct, the t-statistic follows a Student's t-distribution.
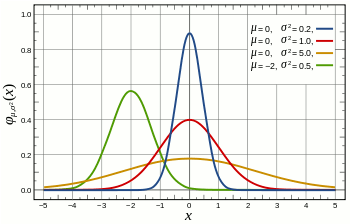
The main assumption for using a t-test is that the random variables involved follow a normal distribution (mean: μ, standard deviation: σ). The figure below shows a few example of normal distributions.
t-statistic
Depending on the type of data we are testing, we can have different variants for this test:
One-sample t-test (testing against a known mean μ0):

where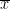 is the sample mean, σ is the sample standard deviation and n is the sample size.
is the sample mean, σ is the sample standard deviation and n is the sample size. Dependent t-test for paired samples (eg.when testing two conditions across subject). Equivalent to testing the difference of the pairs of samples against zero with a one-sample t-test:

where D=A-B,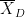 is the average of D and σD its standard deviation.
is the average of D and σD its standard deviation. Independent two-sample test, equal variance (equal or unequal sample sizes):
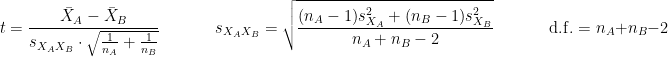
where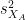 and
and 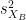 are the unbiased estimators of the variances of the two samples.
are the unbiased estimators of the variances of the two samples. Independent two-sample test, unequal variance (Welch's t-test):
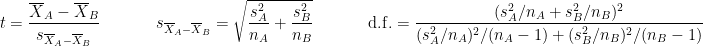
where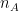 and
and 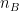 are the sample sizes of A and B.
are the sample sizes of A and B.
p-value
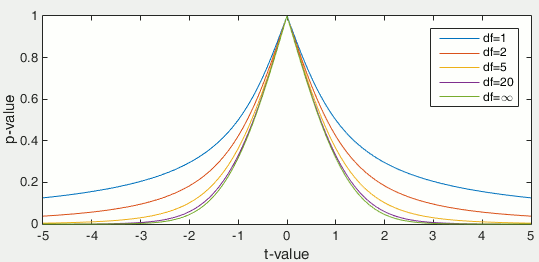
Once the t-value is computed (tobs in the previous section), we can convert it to a p-value based on the known distributions of the t-statistic. This conversion depends on two factors: the number of degrees of freedom and the tails of the distribution we want to consider. For a two-tailed t-test, the two following commands in Matlab are equivalent and can convert the t-values in p-values.
To obtain the p-values for a one-tailed t-test, you can simply divide the p-values by 2.
p = betainc(df./(df + t.^2), df/2, 0.5); % Without the Statistics toolbox p = 2*(1-tcdf(abs(t),df)); % With the Statistics toolbox
The distribution of this function for different numbers of degrees of freedom:
Example 1: Parametric t-test on recordings
Parametric t-tests require the values tested to follow a normal distribution. The recordings evaluated in the histograms sections above (MLP57/160ms) show distributions that are matching this assumption relatively well: the shape of the histogram follows the trace of the corresponding normal function, and with very similar variances. It looks reasonable to use a parametric t-test in this case.
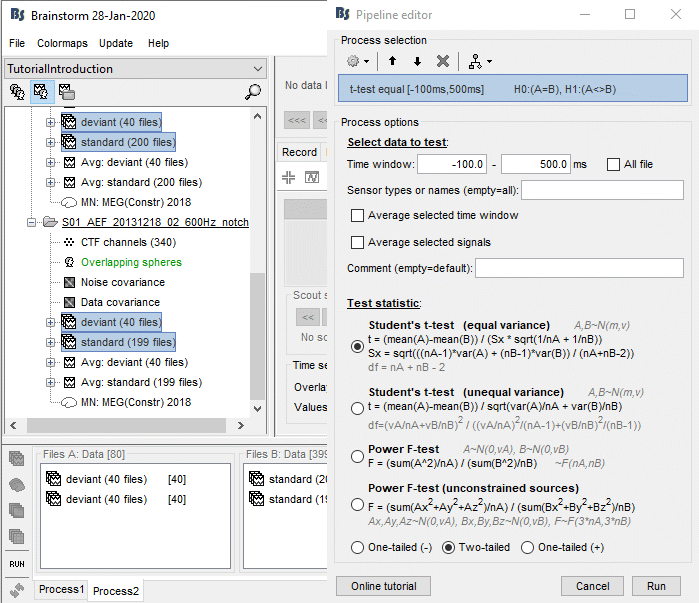
In the Process2 tab, select the following files, from both runs (approximation discussed previously):
Files A: All the deviant trials, with the [Process recordings] button selected.
Files B: All the standard trials, with the [Process recordings] button selected.
The t-tests work well with unbalanced number of samples: Unlike the difference of averages, it is better to use all the possible samples you have, even if you have 80 trials in one condition and 400 in the other.
Run the process "Test > Parametric t-test", Equal variance, Arithmetic average.
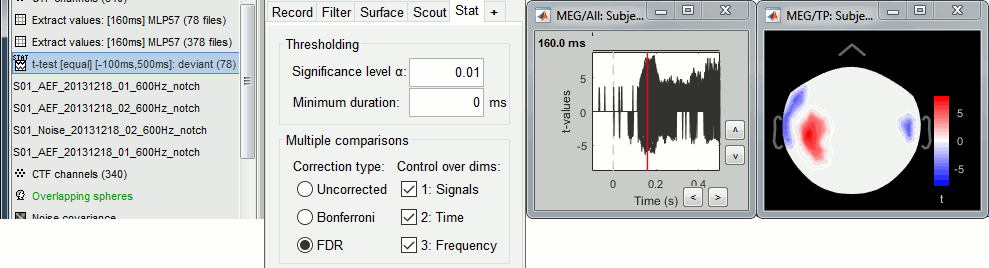
Double-click on the new file for displaying it and add a 2D topography (CTRL+T). The values displayed in the 2D view are the significant t-values. All the sensors that have p-values higher than the significance level threshold (α) are set to zero.
With the new Stat tab you can control the p-value threshold and the correction you want to apply for multiple comparisons (see next section).
Correction for multiple comparisons
Multiple comparison problem
The approach described in this first example performs many tests simultaneously. We test, independently, each MEG sensor and each time sample across the trials, so we run a total of 274*361 = 98914 t-tests.
If we select a critical value of 0.05 (p<0.05), it means that we want to see what is significantly different between the conditions while accepting the risk of observing a false positive in 5% of the cases. If we run the test around 100,000 times, we can expect to observe around 5,000 false positives. We need to better control for false positives (type I errors) when dealing with multiple tests.
Bonferroni correction
The probability to observe at least one false positive, or familywise error rate (FWER) is almost 1:
FWER = 1 - prob(no significant results) = 1 - (1 - 0.05)^100000 ~ 1
A classical way to control the familywise error rate is to replace the p-value threshold with a corrected value, to enforce the expected FWER. The Bonferroni correction sets the significance cut-off at  /Ntest. If we set (p ≤
/Ntest. If we set (p ≤  /Ntest), then we have (FWER ≤
/Ntest), then we have (FWER ≤  ). Following the previous example:
). Following the previous example:
FWER = 1 - prob(no significant results) = 1 - (1 - 0.05/100000)^100000 ~ 0.0488 < 0.05
This works well in a context where all the tests are strictly independent. However, in the case of MEG/EEG recordings, the tests have an important level of dependence: two adjacent sensors or time samples often have similar values. In the case of highly correlated tests, the Bonferroni correction tends too be conservative, leading to a high rate of false negatives.
FDR correction
The false discovery rate (FDR) is another way of representing the rate of type I errors in null hypothesis testing when conducting multiple comparisons. It is designed to control the expected proportion of false positives, while the Bonferroni correction controls the probability to have at least one false positive. FDR-controlling procedures have greater power, at the cost of increased rates of Type I errors (Wikipedia)
In Brainstorm, we implement the Benjamini–Hochberg step-up procedure for FDR correction:
Sort the p-values p(k) obtained across all the multiple tests (k=1..Ntest).
Find the largest k such as p(k) < k / Ntest *
 .
. Reject the null hypotheses corresponding to the first k smallest p-values.
In the interface
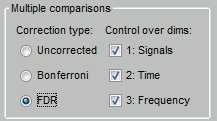
You can select interactively the type of correction to apply for multiple comparison while reviewing your statistical results. The checkboxes "Control over dims" allow you to select which are the dimensions that you consider as multiple comparisons (1=sensor, 2=time, 3=not applicable here). If you select all the dimensions, all the values available in the file are considered as the same repeated test, and only one corrected p-threshold is computed for all the time samples and all the sensors.
If you select only the first dimension, only the values recorded at the same time sample are considered as repeated tests, the different time points are corrected independently, with one different corrected p-threshold for each time point.
When changing these options, a message is displayed in the Matlab command window, showing the number of repeated tests that are considered, and the corrected p-value threshold (or the average if there are multiple corrected p-thresholds, when not all the dimensions are selected):
BST> Average corrected p-threshold: 5.0549e-07 (Bonferroni, Ntests=98914) BST> Average corrected p-threshold: 0.00440939 (FDR, Ntests=98914)
Nonparametric permutation tests
Principle
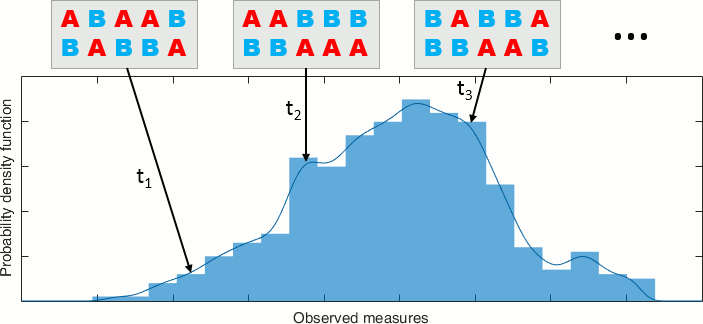
A permutation test (or randomization test) is a type of test in which the distribution of the test statistic under the null hypothesis is obtained by calculating all possible values of the test statistic under rearrangements of the labels on the observed data points. (Wikipedia)
If the null hypothesis is true, the two sets of tested values A and B follow the same distribution. Therefore the values are exchangeable between the two sets: we can move one value from set A to set B, and one value from B to A, and we expect to obtain the same value for the test statistic T.
By taking all the possible permutations between sets A and B and computing the statistic for each of them, we can build a histogram that approximates the permutation distribution.
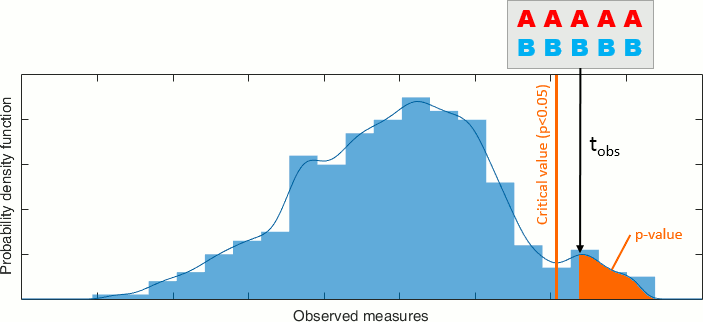
Then we compare the observed statistic with the permutation distribution. From the histogram, we calculate the proportion of permutations that resulted in a larger test statistic than the observed one. This proportion is called the p-value. If the p-value is smaller than the critical value (typically 0.05), we conclude that the data in the two experimental conditions are significantly different.
The number of possible permutations between the two sets of data is usually too large to compute an exhaustive permutation test in a reasonable amount of time. The permutation distribution of the statistic of interest is approximated using a Monte-Carlo approach. A relatively small number of random selection of possible permutations can give us a reasonably good idea of the distribution.
Permutation tests can be used for any test statistic, regardless of whether or not its distribution is known. The hypothesis is about the data itself, not about a specific parameter. In the examples below, we use the t-statistic, but we could use any other function.
Practical limitations
Computation time: If you increase the number of random permutations you use for estimating the distribution, the computation time will increase linearly. You need to find a good balance between the total computation time and the accuracy of the result.
Memory (RAM): The implementations of the permutation tests available in Brainstorm require all the data to be loaded in memory before starting the evaluation of the permutation statistics. Running this function on large datasets or on source data could quickly crash your computer. For example, loading the data for the non-parametric equivalent to the parametric t-test we ran previously would require:
276(sensors) * 461(trials) * 361(time) * 8(bytes) / 1024^2(Gb) = 0.3 Gb of memory.
This is acceptable on most recent computers. But to perform the same at the source level, you need:
45000*461*361*8/1024^3 = 58 Gb of memory just to load the data. This is impossible on most computers, we have to give up at least one dimension and run the test only for one region of interest or one time sample (or average over a short time window).
FieldTrip implementation
FieldTrip functions in Brainstorm
We have the possibility to call some of the FieldTrip toolbox functions from the Brainstorm environment. For this, you need first to install the FieldTrip toolbox on your computer and add it to your Matlab path.
Cluster-based correction
One interesting method that has been promoted by the FieldTrip developers is the cluster-based approach for non-parametric tests. In the type of data we manipulate in MEG/EEG analysis, the neighbouring channels, time points or frequency bins are expected to show similar behavior. We can group these neighbours into clusters to "accumulate the evidence". A cluster can have a multi-dimensional extent in space/time/frequency.
In the context of a non-parametric test, the test statistic computed at each permutation is the extent of the largest cluster. To reject or accept the null hypothesis, we compare the largest observed cluster with the randomization distribution of the largest clusters.
This approach solves the multiple comparisons problem, because the test statistic that is used (the maximum cluster size) is computed using all the values at the same time, along all the dimensions (time, sensors, frequency). There is only one test that is performed, so there is no multiple comparisons problem.
The result is simpler to report but also a lot less informative than FDR-corrected non-parametric tests. We have only one null hypothesis, "the two sets of data follow the same probability distribution", and the outcome of the test is to accept or reject this hypothesis. Therefore we cannot report the spatial or temporal extent of the most significant clusters. Make sure you read this recommendation before reporting cluster-based results in your publications.
Reference documentation
For a complete description of non-parametric cluster-based statistics in FieldTrip, read the following:
Article: Maris & Oostendveld (2007)
Video: Statistics using non-parametric randomization techniques (E Maris)
Video: Non-parametric cluster-based statistical testing of MEG/EEG data (R Oostenveld)
Tutorial: Parametric and non-parametric statistics on event-related fields
Tutorial: Cluster-based permutation tests on event related fields
Tutorial: Cluster-based permutation tests on time-frequency data
Tutorial: How NOT to interpret results from a cluster-based permutation test
Functions references: ft_timelockstatistics, ft_sourcestatistics, ft_freqstatistics
Process options
There are three separate processes in Brainstorm, to call the three FieldTrip functions.
ft_timelockstatistics: Compare imported trials (recordings).
ft_sourcestatistics: Compare source maps or time-frequency files include the entire cortex.
ft_freqstatistics: Compare time-frequency decompositions of sensor recordings or scouts signals.
See below the correspondence between the options in the interface and the FieldTrip functions.
Test statistic options (process options in bold):
cfg.numrandomization = "Number of randomizations"
cfg.statistic = "Independent t-test" ('indepsamplesT') or "Paire t-test" ('depsamplesT)
cfg.tail = One-tailed (-1), Two-tailed (0), One-tailed (+1)
cfg.correctm = "Type of correction" ('no', 'cluster', 'bonferroni', 'fdr', 'max', 'holm', 'hochberg')
cfg.method = 'montecarlo'
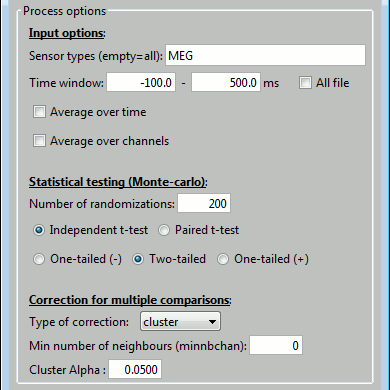
- cfg.correcttail = 'prob'
Cluster-based correction:
cfg.clusteralpha = "Cluster Alpha"
cfg.minnbchan = "Min number of neighours"
cfg.clustertail = cfg.tail (in not, FieldTrip crashes)
- cfg.clusterstatistic = 'maxsum'
Input options: All the data selection is done before, in the process code and functions out_fieldtrip_*.m.
- cfg.channel = 'all';
- cfg.latency = 'all';
- cfg.frequency = 'all';
- cfg.avgovertime = 'no';
- cfg.avgchan = 'no';
- cfg.avgoverfreq = 'no';
Example 2: Uncorrected non-parametric t-test
Let's run the non-parametric equivalent to the test we ran in the first example.
In the Process2 tab, select the following files, from both runs (approximation discussed previously):
Files A: All the deviant trials, with the [Process recordings] button selected.
Files B: All the standard trials, with the [Process recordings] button selected.
Run the process "Test > FieldTrip: ft_timelockstatistics", set the options as shown below
(expect this to run for at least 15min - check the Matlab command window for progress report):
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
Open the parametric and non-parametric results side by side, the results should be very similar.
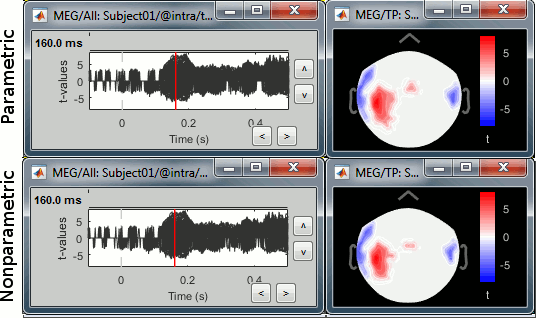
In this case, the distributions of the values for each sensor and each time point (non-rectified MEG recordings) are very close to normal distributions. This was illustrated at the top of this page, in the section "Histograms". Therefore the assumptions behind the parametric t-test are verified, the results of the parametric tests are correct and very similar to the nonparametric ones.
- If you get different results with the parametric and nonparametric approaches: trust the nonparametric one. If you want to increase the precision of a nonparametric test, increase the number of random permutations.
Example 3: Cluster-based test
Run again the same test, but this time select the cluster correction.
- Keep the same files selected in Process2.
Run the process "Test > FieldTrip: ft_timelockstatistics", Type of correction = cluster
(expect this to run for at least 20min - check the Matlab command window for progress report):
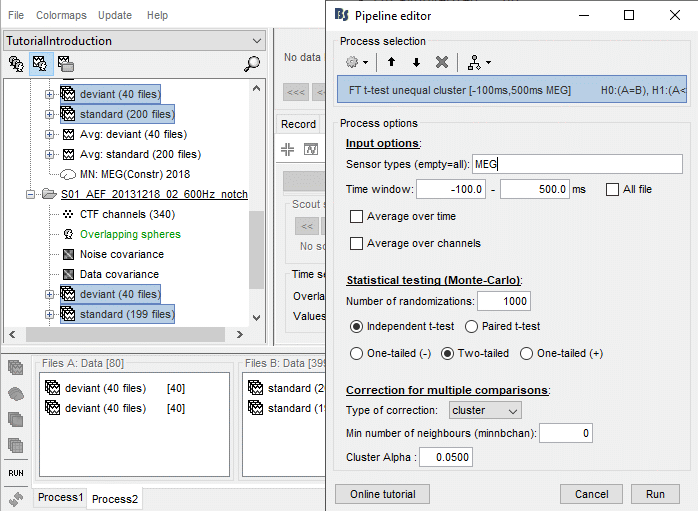
Double-click on the new file to display it, add a 2D topography to is (CTRL+T).
Note that in the Stat tab, the options for multiple comparisons corrections are disabled, because the values saved in the file are already corrected, you can only change the significance threshold.Alternatively, you get a list of significant clusters, which you can display separately if needed. The colored dots on the topography represent the clusters, blue for negative clusters and red for positive clusters. You can change these colors in the Stat tab. Note that the clusters have a spatio-temporal extent: at one time point they can be represented as two separate blobs in the 2D topography, but these blobs are connected at other time points.
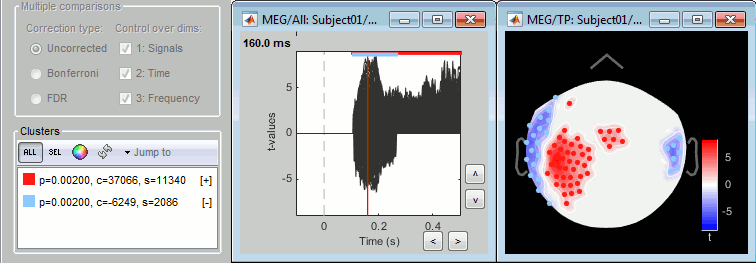
Additional options are available for exploring the clusters, try them all. Values used to represent the clusters: p=p-value, c=cluster statistic (maxsum), s=cluster size (connected data points).
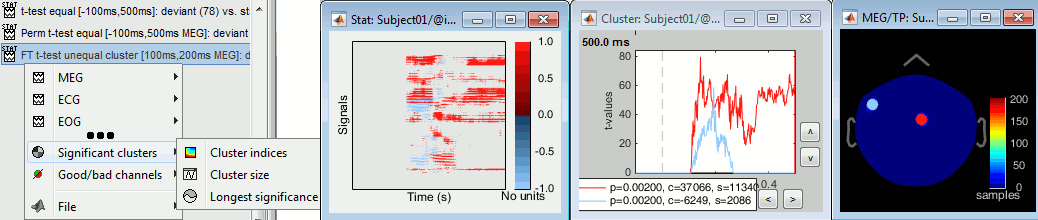
Don't spend too much time exploring the clusters: In the previous cases, all the tests at each sensor and each time point were computed independently, we could report, individually, whether each of them was significant or not. On the other hand, the cluster-based approach just allows us to report that the two conditions are different, without specifying where or when, which makes the visual exploration of clusters relatively useless. Make sure you read this recommendation before reporting cluster-based results in your publications.
Example 4: Non-parametric t-test on sources
To reproduce the same results at the source level, we need to limit the data we are looking at, alternatively the amount of data that has to be loaded to run the non-parametric tests will not fit in memory. Here we average a short time window during which we observed major differences (150-170ms).
Keep the same files selected in Process2. Select the button [Process sources] on both sides.
Run the process "Test > FieldTrip: ft_sourcestatistics"
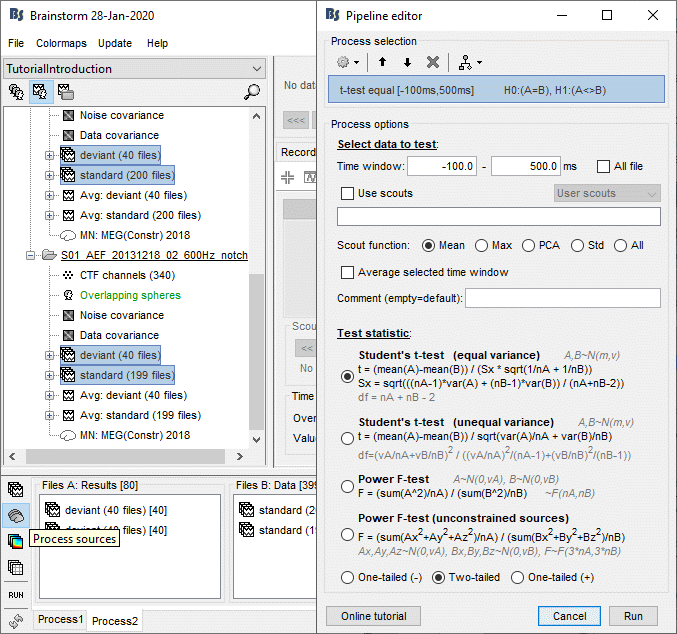
- Options:
Time window: [150,170]ms, short time window around the peak at 160ms.
Select "Average over time": This will test the average source values over the selected time window (150-170ms) instead of each time sample independently.
Select "Test absolute values": This option convert the unconstrained source maps (three dipoles at each cortex location) into a flat cortical map by taking the norm of the three dipole orientations before computing the test.
Type of correction: no, we want to use the on-the-fly FDR correction (Scout tab).
Double-click on the new file for displaying it.
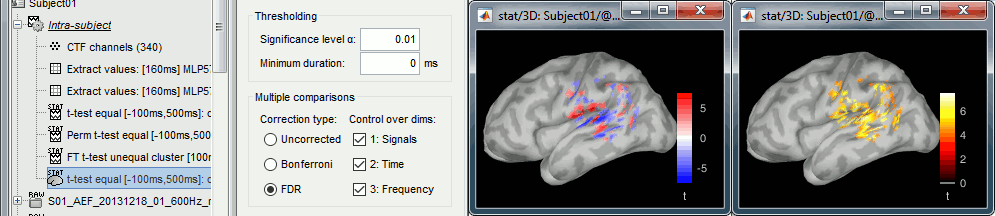
Issues with unconstrained sources
The results are very disappointing, because nothing survives the FDR-correction at (p<0.05), while the effect was very strong at the sensor level. The problem resides in the fact that we tested (|A|=|B|) instead of (A=B), because we selected the option "Test absolute values". As explained the Difference tutorial, this measure is unable to extract the correct effect size.
However, the sign of the difference is meaningful, so we can report that the blue values we observe at (p<0.05, uncorrected) indicate a significantly lower activity in condition A (deviant) than in condition B (standard), in average during this time segment (150-170ms).
There is currently no independent test available to test (A=B) for unconstrained sources. The alternative is to use a source model with constrained orientations instead. The screen capture below shows the result you would get with a constrained minimum norm solution (no absolute value). The effect is now clearly significant, but the sign is useless.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
For dependent/paired tests, we do not have this problem, because we can test the norm of the difference: H0:(Norm(A-B)=0), with a non-parametric one-sided test.
Scouts and statistics
- From the Scout tab, you can also plot the scouts time series and get a summary of what is happening in your regions of interest. This is not very interesting in this particular case, because we don't have any time dimension, but it can be an interesting tool to remember.
Positive peaks indicate the latencies when at least one vertex of the scout has a value that is significantly higher in the deviant condition. The values that are shown are the averaged t-values in the scout. Make sure you select the option "Values: Relative" to display the scouts.
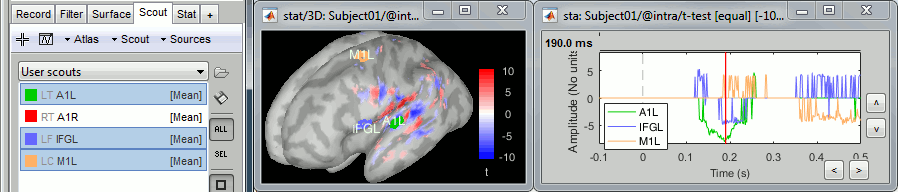
Example 5: Non-parametric t-test on scouts
The previous example was showing how to get rid of one dimension buy restricting the analysis to one averaged time window. Alternatively, we can keep the time dimension and run the test only on the regions of interest.
Keep the same files selected in Process2. Select the button [Process sources] on both sides.
Run the process "Test > FieldTrip: ft_sourcestatistics".
Time window: all, Use scouts, Test absolute values, Do not average over time.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
We cannot represent this over the cortex since we have restricted the measure to the scouts and discarded all the spatial information. But it shows the time points at where the scout signals (averaged across vertices) are significantly different in the two conditions. As explained in the previous example: the effect size is wrong but the sign of the t-value is correct.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
Example 6: Non-parametric t-test on time-frequency maps [TODO]
Two run a test on time-frequency maps, first you need to have all the time-frequency files available in the database, for each individual trials. In the time-frequency tutorial, we saved only the averaged time-frequency decompositions of all the trials.
In Process1, select all the trials from both conditions and one run (just to make it faster).
Run process "Frequency > Time-frequency (Morlet wavelets)". Select the options as below.
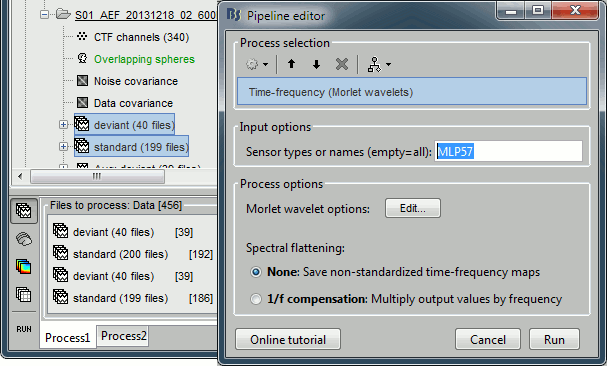
In Process2, select the following files, from both runs:
Files A: All the deviant trials, with the [Process time-freq] button selected.
Files B: All the standard trials, with the [Process time-freq] button selected.
- You need at least 12Gb of RAM to run this process. If you don't, select a lower number of trials in FilesB (for instance, the same number as files selected in FilesA).
Run the process "Test > FieldTrip: ft_sourcestatistics".
Get ready for this to run for a long time... Press Ctrl+C in the Matlab command if it's too slow.
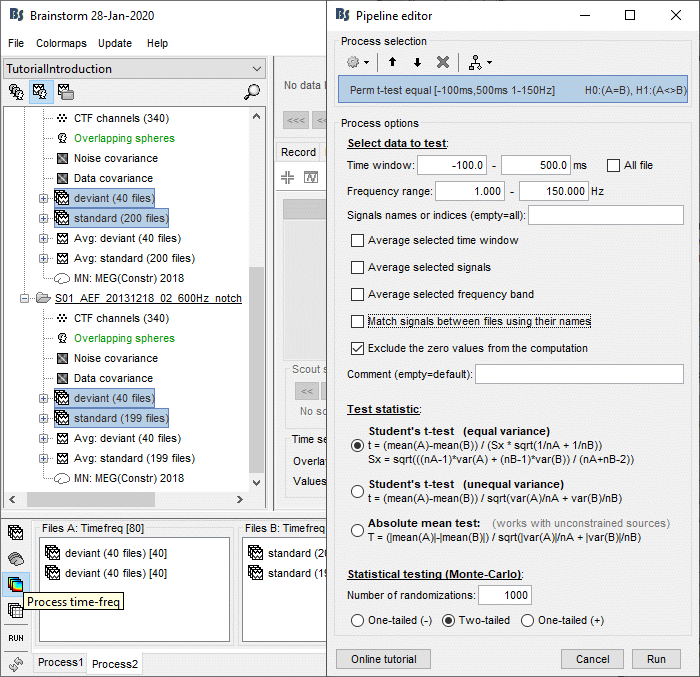
Display results: TODO
Now delete the TF decomposition for the individual trials (because it probably uses a lot of disk space):
- In Process1, select the files for which you compute the TF decomposition.
Select the [Process time-freq] button selected.
Run process "File > Delete files". Option "Delete data files".
Workflow: Single subject
For one unique subject, test for significant differences between two experimental conditions:
Compare the single trials corresponding to each condition.
In most cases, you do not need to normalize the data.
Use independent tests.
For help with the implications of testing the relative or absolute values, see: Difference.
Sensor recordings:
- Not advised for MEG with multiple runs, correct for EEG.
A vs B:
- Never use an absolute value for testing recordings.
Parametric or non-parametric tests, independent, two-tailed, FDR-corrected.
- Correct effect size, ambiguous sign.
Constrained source maps (one value per vertex):
- Use the non-normalized minimum norm maps for all the trials (current density maps, no Z-score).
A vs B:
- Null hypothesis H0: (A=B).
Parametric or non-parametric tests, independent, two-tailed, FDR-corrected.
- Correct effect size, ambiguous sign.
|A| vs |B|:
- Null hypothesis H0: (|A|=|B|).
Non-parametric tests only, independent, two-tailed, FDR-corrected.
- Incorrect effect size, meaningful sign.
Unconstrained source maps (three values per vertex):
- Use the non-normalized minimum norm maps for all the trials (current density maps, no Z-score).
We need to test the norm of the three orientations instead of testing the orientations separately.
Norm(A) vs. Norm(B):
- Null hypothesis H0: (|A|=|B|).
Non-parametric tests only, independent, two-tailed, FDR-corrected.
- Incorrect effect size, meaningful sign.
Time-frequency maps:
- Test the non-normalized time-frequency maps for all the trials (no Z-score or ERS/ERD).
- The values tested are power or magnitudes, all positive, so (A=B) and (|A|=|B|) are equivalent.
|A| vs |B|:
- Null hypothesis H0: (|A|=|B|)
Non-parametric tests only, independent, two-tailed, FDR-corrected.
- Correct effect size, meaningful sign.
Workflow: Group analysis
Subject averages
You need first to process the data separately for each subject:
Compute the subject-level averages, using the same number of trials for each subject.
Sources: Average the non-normalized minimum norm maps (current density maps, no Z-score).Sources computed on individual brains: Project the individual source maps on a template (see the coregistration tutorial). Not needed if the sources were estimated directly on the template anatomy.
Sources and time-frequency: Normalize the data to bring the different subjects to the same range of values (Z-score normalization with respect to a baseline - never apply an absolute value here).
Constrained sources: Smooth spatially the sources, to make sure the brain responses are aligned.
Group statistic
Two group analysis scenarios are possible:
One condition recorded for multiple subjects, comparison between two groups of subjects:
- Files A: Averages for group of subjects #1.
- Files B: Averages for group of subjects #2.
Use independent tests: Exactly the same options as for the single subject (described above)
Two conditions recorded for multiple subjects, comparison across all subjects:
- Files A: All subjects, average for condition A.
- Files B: All subjects, average for condition B.
Use paired tests (= dependent tests), special cases listed below.
Paired tests
Sensor recordings:
(A-B=0): Parametric or non-parametric tests, two-tailed, FDR-corrected.
Constrained source maps (one value per vertex):
(A-B=0): Parametric or non-parametric tests, two-tailed, FDR-corrected.
(|A|-|B|=0): Non-parametric tests, two-tailed, FDR-corrected.
Unconstrained source maps (three values per vertex):
(Norm(A-B)=0): Non-parametric tests, one-tailed (non-negative statistic), FDR-corrected.
(Norm(A)-Norm(B)=0): Non-parametric tests, two-tailed, FDR-corrected.
Time-frequency maps:
(|A|-|B|=0): Non-parametric tests, two-tailed, FDR-corrected.
For help with relative/absolute options, read the previous tutorial: Difference.
Convert statistic results to regular files
Apply statistic threshold
You can convert the results computed for a statistic test to a regular file. This can be useful because lots of menus and processes are not accessible for the files with the "stat" tag display on top of their icon.
- In Process1: Select the results for the test you ran on scouts time series (example #5).
Run process: "Extract > Apply statistic threshold": p<0.05, uncorrected.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
- It produces one new file, we the same name but without the "stat" tag. This file is now a regular matrix that you can use with any process you want. Try to display it: the Stat tab doesn't show up.
Simulate recordings from these scouts
Compute a head model for the intra-subject folder:
Right-click on the channel file > Compute head model, keep all the default options.- In Process1, select this new thresholded file.
Run process: "Simulate > Simulate recordings from scout", select option Save full sources.
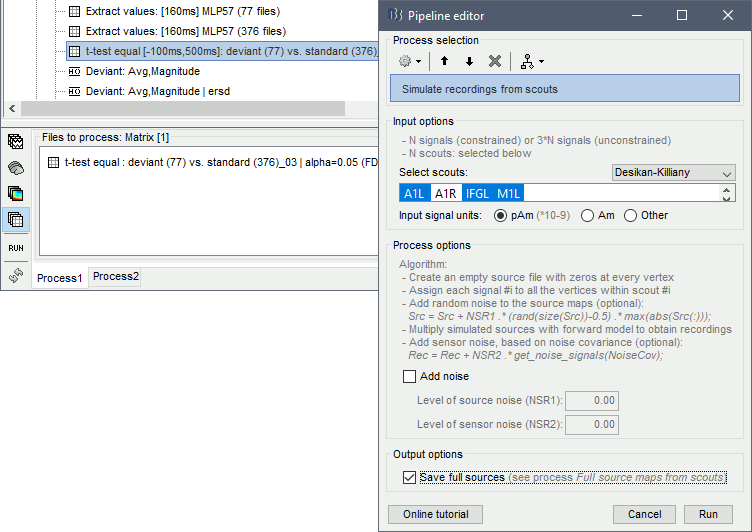
Open the two simulated files (sources and estimated signals):
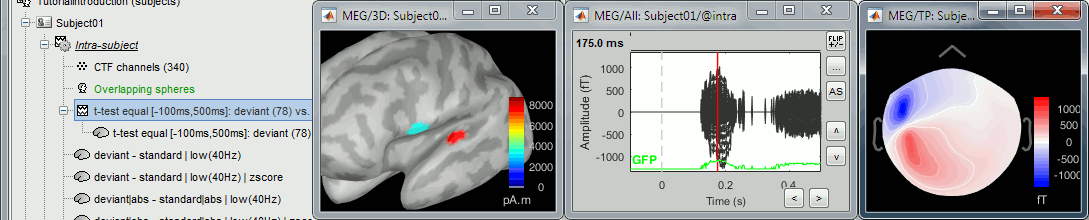
Export to SPM
An alternative to running the statistical tests in Brainstorm is to export all the data and compute the tests with an external program (R, Matlab, SPM, etc). Multiple menus exist to export files to external file formats (right-click on a file > File > Export to file).
Two tutorials explain to export data specifically to SPM:
Export source maps to SPM8 (volume)
Export source maps to SPM12 (surface)
On the hard drive
Right click one of the first test we computed in this tutorial > File > View file contents.
Description of the fields
pmap: [Nsignals x Ntime x Nfreq]: p-values for all the data points. If empty, computed from tmap:
pmap = process_extract_pthresh('GetPmap', tmap, df);tmap: [Nsignals x Ntime x Nfreq]: t-values for all the data points.
df: Number of degrees of freedom for the test.
Correction: Type of correction for multiple comparison that has already been applied to the p-values in this file ('no', 'cluster', 'fdr', ...)
Type: Initial type of the data from which this file was computed ('data', 'results', 'timefreq', 'matrix')
Comment: String displayed in the database explorer to represent the file.
- All the other fields have been described previously and come from the files that have been tested.
Useful functions
Brainstorm t-tests (Process2): process_ttest, process_ttest_paired
Brainstorm t-tests (Process1): process_ttest_zero, process_ttest_baseline
FieldTrip tests: process_ft_timelockstatistics, process_ft_sourcestatistics, process_ft_freqstatistics
Conversion Brainstorm to FieldTrip: out_fieldtrip_data, out_fieldtrip_results, out_fieldtrip_timefreq, out_fieldtrip_matrix
bst_stat_thresh: Computes the Bonferroni and FDR corrections in Brainstorm.
process_extract_pthresh: Computes the pmap from the tmap, and saves thresholded files.
References
Bennett CM, Wolford GL, Miller MB, The principled control of false positives in neuroimaging
Soc Cogn Affect Neurosci (2009), 4(4):417-422.Maris E, Oostendveld R, Nonparametric statistical testing of EEG- and MEG-data
J Neurosci Methods (2007), 164(1):177-90.Maris E, Statistical testing in electrophysiological studies
Psychophysiology (2012), 49(4):549-65Bennett CM, Wolford GL, Miller MB,
The principled control of false positives in neuroimaging
Soc Cogn Affect Neurosci (2009), 4(4):417-422.Pantazis D, Nichols TE, Baillet S, Leahy RM. A comparison of random field theory and permutation methods for the statistical analysis of MEG data, Neuroimage (2005), 25(2):383-94.
Kiebel SJ, Tallon-Baudry C, Friston K
Parametric analysis of oscillatory activity as measured with EEG/MEG, HBM 2005FieldTrip video: Non-parametric cluster-based statistical testing of MEG/EEG data:
https://www.youtube.com/watch?v=vOSfabsDUNg
Additional documentation
Forum: Multiple comparisons: http://neuroimage.usc.edu/forums/showthread.php?1297
Forum: Cluster neighborhoods: http://neuroimage.usc.edu/forums/showthread.php?2132
Forum: Differences FieldTrip-Brainstorm: http://neuroimage.usc.edu/forums/showthread.php?2164
Delete all your experiments
Before moving to the next tutorial, delete all the statistic results you computed in this tutorial. It will make the database structure less confusing for the following tutorials.