|
Size: 18240
Comment:
|
Size: 20258
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 10: | Line 10: |
| == Random variables == In most cases we are interesting in comparing the brain signals recorded for two populations or two experimental conditions A and B. '''A''' and '''B''' are two '''random variables''' for which we have a limited number of repeated measures: multiple trials in the case of a single subject study, or multiple subject averages in the case of a group analysis. To start with, we will consider that each time sample and each signal (source or sensor) is independent: a random variable represents the possible measures for one sensor/source at one specific time point. A random variable can be described with its '''probability distribution''': a function which indicates what are the chances to obtain one specific measure if we run the experiment. By repeating the same experiment many times, we can approximate this function with a discrete histogram of observed measures. {{attachment:stat_distribution.gif||height="205",width="351"}} {{attachment:stat_histogram.gif||height="222",width="330"}} When comparing two sample sets A and B, we try to evaluate if the distributions of the measures are equal or not. In most of the questions we explore in EEG/MEG analysis, the distributions are overlapping but not completely. The very sparse sampling of the data (a few tens or hundreds repeated measures) doesn't help with the task. . {{attachment:stat_distrib_example.gif||height="159",width="336"}} |
|
| Line 11: | Line 24: |
| When comparing the brain recordings for two populations or two experimental conditions A and B, we are most of the time interested in rejecting the null hypothesis '''H0: "the two sample sets are identical"'''. '''A''' and '''B''' are two '''random variables''' for which we have a limited number of repeated measures: multiple trials in the case of a single subject study, or multiple subject averages in the case of a group analysis. To start with, we will consider that each time sample and each signal (source or sensor) is independent: a random variable represents the possible values for one signal at one specific time point. A random variable can be described with its '''probability distribution''': a function which indicates what are the chances to obtain one specific measure if we run the experiment. By repeating the same experiment many times, we can approximate this function with a discrete histogram of observed measures. {{attachment:stat_distribution.gif||height="205",width="351"}} {{attachment:stat_histogram.gif||height="222",width="330"}} When comparing two sample sets A and B, we try to evaluate if the distributions of the measures are equal or not. In most of the questions we explore in EEG/MEG analysis, the distributions are overlapping but not completely. The very sparse sampling of the data (a few tens or hundreds repeated measures) doesn't help with the task. {{attachment:stat_distrib_example.gif}} either from a model (parametric tests) or by estimating it from the measures (non-parametric tests). These distributions Some key concepts explained on Wikipedia (the illustrations above are borrowed from these pages): * Hypothesis testing: https://en.wikipedia.org/wiki/Statistical_hypothesis_testing * p-value: https://en.wikipedia.org/wiki/P-value * Normal distribution: https://en.wikipedia.org/wiki/Normal_distribution * Student's t-test: https://en.wikipedia.org/wiki/Student's_t-test |
To show that there is a difference between A and B, we can use a statistical hypothesis test. We start by assuming that the two sets are identical then reject this hypothesis. For all the tests we will use here, the logic is similar: * Define a '''null hypothesis''' (H<<HTML(<sub>)>>0<<HTML(</sub>)>>:"A=B") and alternative hypotheses (eg. H<<HTML(<sub>)>>1<<HTML(</sub>)>>:"A<B"). * Make some assumptions on the samples we have (eg. A and B are independent, A and B follow normal distributions, A and B have equal variances). * Decide which test is appropriate, and state the relevant '''test statistic''' T (eg. Student t-test). * Compute from the measures (A<<HTML(<sub>)>>obs<<HTML(</sub>)>>, B<<HTML(<sub>)>>obs<<HTML(</sub>)>>) the observed value of the test statistic (t<<HTML(<sub>)>>obs<<HTML(</sub>)>>). * Calculate the '''p-value'''. This is the probability, under the null hypothesis, of sampling a test statistic at least as extreme as that which was observed. A value of (p<0.05) for the null hypothesis has to be interpreted as follows: "If the null hypothesis is true, the chance that we find a test statistic as extreme or more extreme than the one observed is less than 5%". * Reject the null hypothesis if and only if the p-value is less than the significance level threshold (<<HTML(α)>>).<<BR>><<BR>> {{attachment:stat_tails.gif||height="322",width="598"}} Two families of tests can be helpful in our case: parametric and non-parametric tests. * '''Parametric tests''' need some strong assumptions on the probability distributions of A and B then use some well-known properties of these distributions to compare them, based on a few simple parameters (typically the mean, variance and higher order moments). The examples which will be described here are the Student's t-tests. * '''Non-parametric tests''' only rely on the measured data, but are lot more computationally intensive. == Student's t-test (parametric) == {{attachment:stat_distrib_normal.gif}} |
| Line 216: | Line 225: |
| Some key concepts explained on Wikipedia (some illustrations are borrowed from these pages): * Hypothesis testing: https://en.wikipedia.org/wiki/Statistical_hypothesis_testing * p-value: https://en.wikipedia.org/wiki/P-value * Normal distribution: https://en.wikipedia.org/wiki/Normal_distribution * Student's t-test: https://en.wikipedia.org/wiki/Student's_t-test * Permutation test: [[https://en.wikipedia.org/wiki/Resampling_(statistics)|https://en.wikipedia.org/wiki/Resampling_%28statistics%29]] Journal articles: |
|
| Line 223: | Line 242: |
| == Additional discussions on the forum == | == Additional documentation == |
Tutorial 26: Statistics
[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]
Authors: Francois Tadel, Elizabeth Bock, Dimitrios Pantazis, Richard Leahy, Sylvain Baillet
In this auditory oddball experiment, we would like to test for the significant differences between the brain response to the deviant beeps and the standard beeps, time sample by time sample. Until now we have been computing measures of the brain activity in time or time-frequency domain. We were able to see clear effects or slight tendencies, but these observations were always dependent on an arbitrary amplitude threshold and the configuration of the colormap. With appropriate statistical tests, we can go beyond these empirical observations and assess what are the significant effects in a more formal way.
Contents
- Random variables
- Statistical inference
- Student's t-test (parametric)
- Recommendations
- Parametric Student's t-test [TODO]
- FieldTrip: Non-parametric cluster-based statistic [TODO]
- FieldTrip: Process options [TODO]
- FieldTrip: Example 1 [TODO]
- FieldTrip: Example 2 [TODO]
- Time-frequency files
- Workflow: Single subject
- Workflow: Group analysis
- Convert statistic results to regular files [TODO]
- Export to SPM
- On the hard drive [TODO]
- References
- Additional documentation
- Delete all your experiments
Random variables
In most cases we are interesting in comparing the brain signals recorded for two populations or two experimental conditions A and B.
A and B are two random variables for which we have a limited number of repeated measures: multiple trials in the case of a single subject study, or multiple subject averages in the case of a group analysis. To start with, we will consider that each time sample and each signal (source or sensor) is independent: a random variable represents the possible measures for one sensor/source at one specific time point.
A random variable can be described with its probability distribution: a function which indicates what are the chances to obtain one specific measure if we run the experiment. By repeating the same experiment many times, we can approximate this function with a discrete histogram of observed measures.
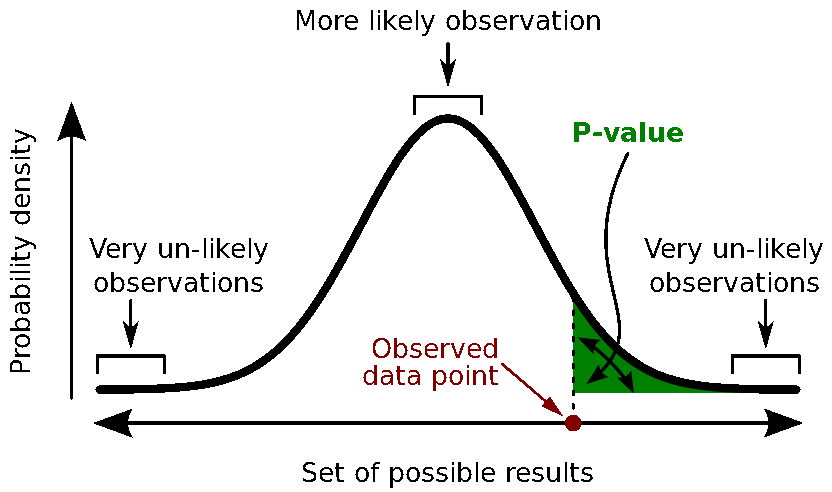
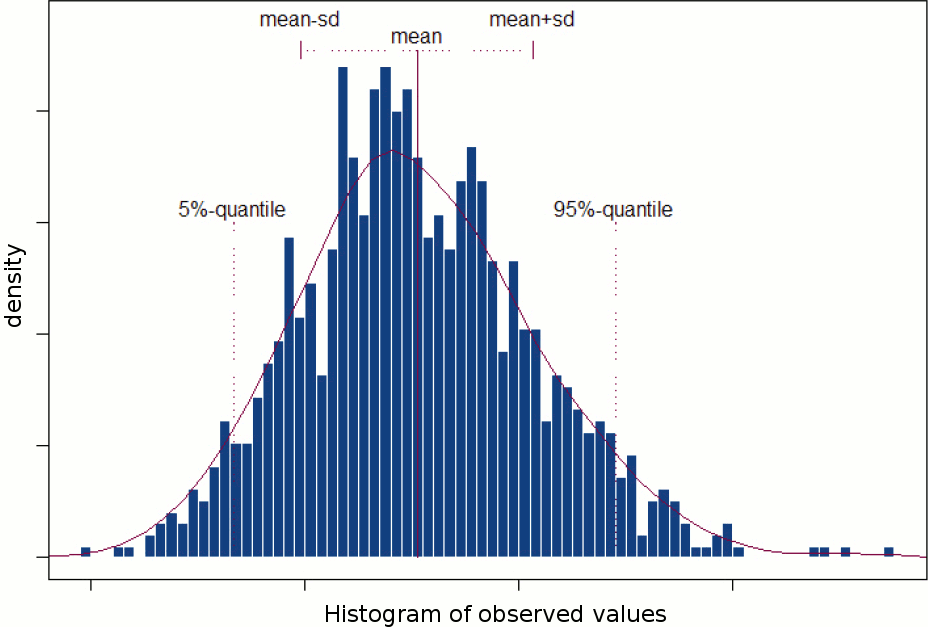
When comparing two sample sets A and B, we try to evaluate if the distributions of the measures are equal or not. In most of the questions we explore in EEG/MEG analysis, the distributions are overlapping but not completely. The very sparse sampling of the data (a few tens or hundreds repeated measures) doesn't help with the task.
Statistical inference
To show that there is a difference between A and B, we can use a statistical hypothesis test. We start by assuming that the two sets are identical then reject this hypothesis. For all the tests we will use here, the logic is similar:
Define a null hypothesis (H0:"A=B") and alternative hypotheses (eg. H1:"A<B").
- Make some assumptions on the samples we have (eg. A and B are independent, A and B follow normal distributions, A and B have equal variances).
Decide which test is appropriate, and state the relevant test statistic T (eg. Student t-test).
Compute from the measures (Aobs, Bobs) the observed value of the test statistic (tobs).
Calculate the p-value. This is the probability, under the null hypothesis, of sampling a test statistic at least as extreme as that which was observed. A value of (p<0.05) for the null hypothesis has to be interpreted as follows: "If the null hypothesis is true, the chance that we find a test statistic as extreme or more extreme than the one observed is less than 5%".
Reject the null hypothesis if and only if the p-value is less than the significance level threshold (α).
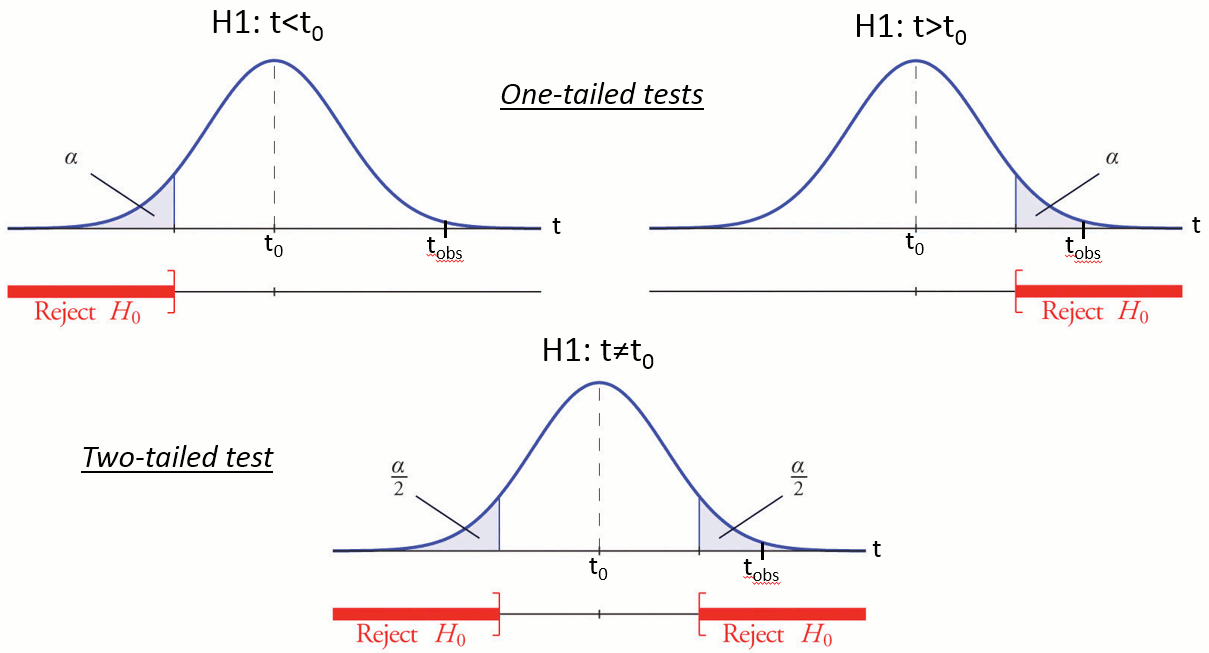
Two families of tests can be helpful in our case: parametric and non-parametric tests.
Parametric tests need some strong assumptions on the probability distributions of A and B then use some well-known properties of these distributions to compare them, based on a few simple parameters (typically the mean, variance and higher order moments). The examples which will be described here are the Student's t-tests.
Non-parametric tests only rely on the measured data, but are lot more computationally intensive.
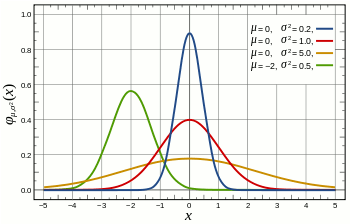
Student's t-test (parametric)
Recommendations
two-tailed test on either (A-B) or (|A|-|B|)
The statistic, after thresholding should be displayed as a bipolar signal (red – positive, blue – negative) since this does affect interpretation
Constrained (A-B), null hypothesis H0: A=B, We compute a z-score through normalization using a pre-stim period and apply FDR-controlled thresholding to identify significant differences with a two tailed test.
Constraine (|A|-|B|), null hypothesis H0: |A|=|B|, We compute a z-score through normalization using a pre-stim period and apply FDR-controlled thresholding to identify significant differences with a two tailed test.
Unconstrained RMS(X-Y), H0: RMS(X-Y)=0, Since the statistic is non-negative a one-tailed test is used.
Unconstrained (RMS(X) –RMS(Y)), H0: RMS(X)-RMS(Y)=0, we use a two-tailed test and use a bipolar display to differentiate increased from decreased amplitude.
Parametric Student's t-test [TODO]
Using a t-test instead of the difference of the two averages, we can reproduce similar results but with a significance level attached to each value. Parametric method require the values tested to follow a Gaussian distribution. Some sets of data could be considered as Gaussian (example: screen capture of the histogram of the values recorded by one sensor at one time point), some are not (example: histogram ABS(values) at one point).
WARNING: This parametric t-test is valid only for constrained sources. In the case of unconstrained sources, the norm of the three orientations is used, which breaks the hypothesis of the tested values following a Gaussian distribution. This test is now illustrated on unconstrained sources, but this will change when we figure out the correct parametric test to apply on unconstrained sources.
- In the Process2 tab, select the following files:
Files A: All the deviant trials, with the [Process sources] button selected.
Files B: All the standard trials, with the [Process sources] button selected.
Run the process "Test > Student's t-test", Equal variance, Absolute value of average.
This option will convert the unconstrained source maps (three dipoles at each cortex location) into a flat cortical map by taking the norm of the three dipole orientations before computing the difference.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
Double-click on the new file for displaying it. With the new tab "Stat" you can control the p-value threshold and the correction you want to apply for multiple comparisons.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
Set the options in the Stat tab: p-value threshold: 0.05, Multiple comparisons: Uncorrected.
What we see in this figure are the t-values corresponding to p-values under the threshold. We can make similar observations than with the difference of means, but without the arbitrary amplitude threshold (this slider is now disabled in the Surface tab). If at a given time point a vertex is red in this view, the mean of the deviant condition is significantly higher than the standard conditions (p<0.05).
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
This approach considers each time sample and each surface vertex separately. This means that we have done Nvertices*Ntime = 15002*361 = 5415722 t-tests. The threshold at p<0.05 controls correctly for false positives at one point but not for the entire cortex. We need to correct the p-values for multiple comparisons. The logic of two types of corrections available in the Stat tab (FDR and Bonferroni) is explained in Bennett et al (2009).
Select the correction for multiple comparison "False discovery rate (FDR)". You will see that a lot less elementrs survive this new threshold. In the Matlab command window, you can see the average corrected p-value, that replace for each vertex the original p-threshold (0.05):
BST> Average corrected p-threshold: 0.000315138 (FDR, Ntests=5415722)From the Scout tab, you can also plot the scouts time series and get in this way a summary of what is happening in your regions of interest. Positive peaks indicate the latencies when at least one vertex of the scout has a value that is significantly higher in the deviant condition. The values that are shown are the averaged t-values in the scout.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
FieldTrip: Non-parametric cluster-based statistic [TODO]
We have the possibility to call some of the FieldTrip functions from the Brainstorm environment. For this, you need first to install the FieldTrip toolbox on your computer and add it to your Matlab path.
For a complete description of non-parametric cluster-based statistics in FieldTrip, read the following article: Maris & Oostendveld (2007). Additional information can be found on the FieldTrip website:
Tutorial: Parametric and non-parametric statistics on event-related fields
Tutorial: Cluster-based permutation tests on event related fields
Tutorial: Cluster-based permutation tests on time-frequency data
Tutorial: How NOT to interpret results from a cluster-based permutation test
Video: Statistics using non-parametric randomization techniques
Video: Non-parametric cluster-based statistical testing of MEG/EEG data
Functions: ft_timelockstatistics, ft_sourcestatistics, ft_freqstatistics
Permuation-based non-parametric statistics are more flexible and do not require to do any assumption on the distribution of the data, but on the other hand they are a lot more complicated to process. Calling FieldTrip's function ft_sourcestatistics requires a lot more memory because all the data has to be loaded at once, and a lot more computation time because the same test is repeated many times.
Running this function in the same way as the parametric t-test previously (full cortex, all the trials and all the time points) would require 45000*461*361*8/1024^3 = 58 Gb of memory just to load the data. This is impossible on most computers, we have to give up at least one dimension and run the test only for one time sample or one region of interest.
FieldTrip: Process options [TODO]
Screen captures for the two processes:
Description of the process options:
The options available here match the options passed to the function ft_sourcestatistics.
Cluster correction: Define what a cluster is for the different data types (recordings, surface source maps, volume source models, scouts)
Default options:
- clusterstatistic = 'maxsum'
- method = 'montecarlo'
- correcttail = 'prob'
FieldTrip: Example 1 [TODO]
We will run this FieldTrip function first on the scouts time series and then on a short time window.
- Keep the same selection in Process2: all the deviant trials in FilesA, all the standard trials in FilesB.
Run process: Test > FieldTrip: ft_sourcestatistics, select the options as illustrated below.
![[ATTACH] [ATTACH]](/moin_static1911/brainstorm1/img/attach.png)
Double-click on the new file to display it:
- Display on the cortex: see section "Convert statistic results to regular files" below
FieldTrip: Example 2 [TODO]
short time window
Time-frequency files
Both ft_sourcestatistics and ft_freqstatistics are available.
Use ft_sourcestatistics if the input files contain full source maps, and ft_freqstatistics for all the other cases (scouts or sensors).
Workflow: Single subject
You want to test for one unique subject what is significantly different between two experimental conditions. You are going to compare the single trials corresponding to each condition directly.
This is the case for this tutorial dataset, we want to know what is different between the brain responses to the deviant beep and the standard beep.
Sensor recordings: Not advised for MEG with multiple runs, correct for EEG.
Parametric t-test: Correct
- Select the option "Arithmetic average: mean(x)".
- No restriction on the number of trials.
Non-parametric t-test: Correct
- Do not select the option "Test absolute values".
- No restriction on the number of trials.
Difference of means:
- Select the option "Arithmetic average: mean(x)".
- Use the same number of trials for both conditions.
Constrained source maps (one value per vertex):
- Use the non-normalized minimum norm maps for all the trials (no Z-score).
Parametric t-test: Incorrect
- Select the option "Absolue value of average: abs(mean(x))".
- No restriction on the number of trials.
Non-parametric t-test: Correct
- Select the option "Test absolute values".
- No restriction on the number of trials.
Difference of means:
- Select the option "Absolue value of average: abs(mean(x))".
- Use the same number of trials for both conditions.
Unconstrainted source maps (three values per vertex):
Parametric t-test: Incorrect
- ?
Non-parametric t-test: Correct
- ?
Difference of means:
- ?
Time-frequency maps:
- Test the non-normalized time-frequency maps for all the trials (no Z-score or ERS/ERD).
Parametric t-test: ?
- No restriction on the number of trials.
Non-parametric t-test: Correct
- No restriction on the number of trials.
Difference of means:
- Use the same number of trials for both conditions.
Workflow: Group analysis
You have the same two conditions recorded for multiple subjects.
Sensor recordings: Strongly discouraged for MEG, correct for EEG.
- For each subject: Compute the average of the trials for each condition individually.
- Do not apply an absolute value.
- Use the same number of trials for all the subjects.
- Test the subject averages.
- Do no apply an absolute value.
Source maps (template anatomy):
- For each subject: Average the non-normalized minimumn norm maps for the trials of each condition.
- Use the same number of trials for all the subjects.
If you can't use the same number of trials, you have to correct the Z-score values [TODO].
- Normalize the averages using a Z-score wrt with a baseline.
- Select the option: "Use absolue values of source activations"
- Select the option: "Dynamic" (does not make any difference but could be faster).
- Test the normalized averages across subjects.
- Do not apply an absolute value.
Source maps (individual anatomy):
- For each subject: Average the non-normalized minimumn norm maps for the trials of each condition.
- Use the same number of trials for all the subjects.
If you can't use the same number of trials, you have to correct the Z-score values [TODO].
- Normalize the averages using a Z-score wrt with a baseline.
- Select the option: "Use absolue values of source activations"
- Select the option: "Dynamic" (does not make any difference but could be faster).
- Project the normalized maps on the template anatomy.
- Option: Smooth spatially the source maps.
- Test the normalized averages across subjects.
- Do not apply an absolute value.
Time-frequency maps:
- For each subject: Compute the average time-frequency decompositions of all the trials for each condition (using the advanced options of the "Morlet wavelets" and "Hilbert transform" processes).
- Use the same number of trials for all the subjects.
- Normalize the averages wrt with a baseline (Z-score or ERS/ERD).
- Test the normalized averages across subjects.
- Do no apply an absolute value.
Convert statistic results to regular files [TODO]
Process: Extract > Apply statistc threshold
Process: Simulate > Simulate recordings from scout [TODO]
Export to SPM
An alternative to running the statical tests in Brainstorm is to export all the data and compute the tests with an external program (R, Matlab, SPM, etc). Multiple menus exist to export files to external file formats (right-click on a file > File > Export to file).
Two tutorials explain to export data specifically to SPM:
Export source maps to SPM8 (volume)
Export source maps to SPM12 (surface)
On the hard drive [TODO]
Right click one of the first TF file we computed > File > View file contents.
References
Some key concepts explained on Wikipedia (some illustrations are borrowed from these pages):
Hypothesis testing: https://en.wikipedia.org/wiki/Statistical_hypothesis_testing
Normal distribution: https://en.wikipedia.org/wiki/Normal_distribution
Student's t-test: https://en.wikipedia.org/wiki/Student's_t-test
Permutation test: https://en.wikipedia.org/wiki/Resampling_%28statistics%29
Journal articles:
Bennett CM, Wolford GL, Miller MB, The principled control of false positives in neuroimaging
Soc Cogn Affect Neurosci (2009), 4(4):417-422.Maris E, Oostendveld R, Nonparametric statistical testing of EEG- and MEG-data
J Neurosci Methods (2007), 164(1):177-90.Maris E, Statistical testing in electrophysiological studies
Psychophysiology (2012), 49(4):549-65Pantazis D, Nichols TE, Baillet S, Leahy RM. A comparison of random field theory and permutation methods for the statistical analysis of MEG data, Neuroimage (2005), 25(2):383-94.
FieldTrip video: Non-parametric cluster-based statistical testing of MEG/EEG data:
https://www.youtube.com/watch?v=vOSfabsDUNg
Additional documentation
Forum: Multiple comparisons: http://neuroimage.usc.edu/forums/showthread.php?1297
Forum: Cluster neighborhoods: http://neuroimage.usc.edu/forums/showthread.php?2132
Forum: Differences FieldTrip-Brainstorm: http://neuroimage.usc.edu/forums/showthread.php?2164
Delete all your experiments
Before moving to the next tutorial, delete all the statistic results you computed in this tutorial. It will make it the database structure less confusing for the following tutorials.
