|
Size: 169201
Comment:
|
Size: 12160
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| ## page was renamed from brainsuiteBDP ## page was renamed from brainsuite |
'''[TUTORIAL UNDER CONSTRUCTION: NOT READY FOR PUBLIC USE]''' ---- |
| Line 6: | Line 8: |
| '''[TUTORIAL UNDER WRITING: NOT READY FOR PUBLIC USE]''' | In this tutorial, we describe the estimation of realistic conductivity tensors of living brain tissues using the [[http://brainsuite.org/|BrainSuite software]]. These results are used in FEM forward modeling, as described in the tutorials: [[https://neuroimage.usc.edu/brainstorm/Tutorials/Duneuro#DUNEuro_options:_Advanced|FEM with DUNEuro]] and [[https://neuroimage.usc.edu/brainstorm/Tutorials/FemMedianNerve#FEM_tensors|FEM median nerve example]]. |
| Line 8: | Line 10: |
| Describe brainsuite here : here we will describe the process of the brain tissues anisotrpy estimation and the different functions that brainstorm offers. | The realistic tensors are estimated from the Diffusion-Weighted Images (DWI): Brainstorm calls the BrainSuite software to compute the diffusion tensors on each brain MRI voxel (DTI), then Effective Medium Approach (EMA) is applied to estimate the conductivity tensors for each element of a tetrahedral FEM mesh. |
| Line 10: | Line 12: |
| This tutorial explains how to use Brainsuite to estimate the anisotropy of the brain tissues. refer to this page [[https://neuroimage.usc.edu/brainstorm/Tutorials/SegBrainSuite?highlight=(anand)|https://neuroimage.usc.edu/brainstorm/Tutorials/SegBrainSuite?highlight=%28anand%29]] The realistic tensors are estimated from the Diffusion Weighted Images (DWI). For this purpose, Brainstorm calls internally the BrainSuite Diffusion Pipline to compute the diffusion tensors on each brain voxel. Afterwards, the Effective Medium Appeach is applied to convert the diffusion tensors to the conductivity tensors. The following section shows to the users how to do it from the graphical intefrace. Only the NIfTI are supported. All the diffusion data, inclusing the DWI file and direction and the value of the gradient files , respectively the the *.nii, the *.bval and the *.bvec are required. Ideally these files should have the same name and saved in the same folder. |
BrainSuite is also used for other purposes in Brainstorm, particularly the T1 MRI segmentation, as documented in this tutorial: [[Tutorials/SegBrainSuite|MRI segmentation: BrainSuite]]. |
| Line 22: | Line 16: |
| == Download and installation == ==== Requirements ==== * You have already followed all the introduction tutorials. * You have a working copy of Brainstorm installed on your computer. * For the DWI data, only the NIfTI files (.nii) are supported. |
|
| Line 23: | Line 22: |
| ==== Install Brainsuite ==== 1. Download the latest version of BrainSuite from http://forums.brainsuite.org/download/. |
|
| Line 24: | Line 25: |
| == Requirement == * You have already followed all the introduction tutorials * You have a working copy of Brainstorm installed on your computer |
1. Install it on your computer by following the instructions in [[http://brainsuite.bmap.ucla.edu/quickstart/installation/|BrainSuite's quick start installation guide]]. |
| Line 28: | Line 27: |
| == Brainsuite Installation == 1. Download the latest version of BrainSuite from http://www.brainsuite.org/download. 1. Install it on your computer by following the instructions in [[http://brainsuite.bmap.ucla.edu/quickstart/installation/|BrainSuite's quick start installation guide]]. 1. Note that you will be using BrainSuite Diffusion Pipeline(BDP), so you need to install a compatible [[http://www.mathworks.com/products/compiler/mcr|MATLAB Compiler Runtime]](last version). 1. Start BrainSuite to check if the installation (It's not required to open BrainSuite to run this tutorial). 1. The BrainSuite installation folder should be informed in the Brainstorm preferences |
1. You will be using BrainSuite Diffusion Pipeline (BDP), so you need to install a compatible [[https://www.mathworks.com/products/compiler/matlab-runtime.html|MATLAB Runtime]] (2019b for BrainSuite 21a). |
| Line 35: | Line 29: |
| {{https://user-images.githubusercontent.com/6920058/81406567-1c785400-913a-11ea-9048-28c7459af7da.png|image|font-size="10pt"}} | 1. In Brainstorm, menu File > Edit preferences > Enter the BrainSuite installation folder:<<BR>><<BR>> {{attachment:brainsuiteInstall.gif}} |
| Line 37: | Line 31: |
| ==== Download the dataset ==== * Download the files: [[http://brainsuite.org/WebTutorialData/BrainSuiteTutorialSVReg_Sept16.zip|MRI T1w]] and [[http://brainsuite.org/WebTutorialData/DWI_Feb15.zip|MRI DWI]] (from the [[http://brainsuite.org/tutorials/dtiexercise/|BrainSuite diffusion tutorial]]). |
|
| Line 38: | Line 34: |
| * Unzip it outside of any of the Brainstorm folders (program folder or database folder). * Start Brainstorm (Matlab scripts or stand-alone version) * Select the menu File > Create new protocol. Name it "'''TutorialTensors'''" and select: * No, use individual anatomy * No, use one channel file per condition |
|
| Line 40: | Line 41: |
| In this tutorial we use the Brainsuite dataset example available on the Brainsuite tutorial webpag | In this tutorial, we use the Brainsuite dataset example available on the BrainSuite [[http://brainsuite.org/tutorials/|tutorial webpage]]. |
| Line 42: | Line 43: |
| http://brainsuite.org/tutorials/. The T1w of the subject can be download from this link [[http://brainsuite.org/WebTutorialData/BrainSuiteTutorialSVReg_Sept16.zip|BrainSuiteTutorialSVReg_Sept16.zip]]. The DWI from this link [[http://brainsuite.org/WebTutorialData/DWI_Feb15.zip|DWI_Feb15.zip]] | The first file contains the T1 MRI data, with the name '2523412.nii.gz', as in this figure, |
| Line 44: | Line 45: |
| The first link contains the T1 MRI, with the name '2523412.nii.gz' | {{attachment:vierMriFolder.JPG||width="650",height="150"}} |
| Line 46: | Line 47: |
| {{data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABl0AAAE+CAYAAAAH09bAAAAgAElEQVR4Aey9DbRtV1WgeQExwS607aYwgF22cVANxLKEN8RwASVARlReglLEIe1fwJGrCC+kVdSOFStUEW9sTHiJFs0jSB5IMNUJ8vPgwesCnqEUArlP60EeJVyCYoJ5IybITxdJ+Fs95jlnrjX3PmutvfbZ+5x7zr7fHePc/bd+5vzW3OusNedZe6+5Hv8++Xnn7vkKHxhgA9gANoANxG1g2b8nRD7+IAABCEAAAhCAAAQgAAEIQAACEIAABCAwK4G1WTPG8i27Mw0naNwJChe4YAPYwKJsYNm/Jwi6xL7dOQcBCEAAAhCAAAQgAAEIQAACEIAABCBQSoCgCytzWJ2EDWAD2MDCbICgS+nXM+kgAAEIQAACEIAABCAAAQhAAAIQgAAEVpEAQRecrQtzti7ql/TUw6oNbGB5bYCgyyoOFZAZAhCAAAQgAAEIQAACEIAABCAAAQhAoJQAQReCLgRdsAFsABtYmA0QdCn9eiYdBCAAAQhAAAIQgAAEIAABCEAAAhCAwCoSIOiCs3VhzlZWHyzv6gPahrZZlA0QdFnFoQIyQwACEIAABCAAAQhAAAIQgAAEIAABCJQSIOhC0IWgCzaADWADC7MBgi6lX8+kgwAEIAABCEAAAhCAAAQgAAEIQAACEFhFAgRdcLYuzNm6qF/SUw+rNrCB5bUBgi6rOFRAZghAAAIQgAAEIAABCEAAAhCAAAQgAIFSAgRdCLoQdMEGsAFsYGE2QNCl9OuZdBCAAAQgAAEIQAACEIAABCAAAQhAAAKrSICgC87WhTlbWX2wvKsPaBvaZlE2QNBlFYcKyAwBCEAAAhCAAAQgAAEIQAACEIAABCBQSoCgC0EXgi7YADaADSzMBgi6lH49kw4CEIAABCAAAQhAAAIQgAAEIAABCEBgFQkQdMHZujBn66J+SU89rNrABpbXBgi6rOJQAZkhAAEIQAACEIAABCAAAQhAAAIQgAAESgkQdCHoQtAFG8AGsIGF2QBBl9KvZ9JBAAIQgAAEIAABCEAAAhCAAAQgAAEIrCIBgi44WxfmbGX1wfKuPqBtaJtF2QBBl1UcKiAzBCAAAQhAAAIQgAAEIAABCEAAAhCAQCkBgi4EXQi6YAPYADawMBsg6FL69Uw6CEAAAhCAAAQgAAEIQAACEIAABCAAgVUkQNAFZ+vCnK2L+iU99bBqAxtYXhsg6LKKQwVkhgAEIAABCEAAAhCAAAQgAAEIQAACECglQNCFoAtBF2wAG8AGFmYDBF1Kv55JBwEIQAACEIAABCAAAQhAAAIQgAAEILCKBAi64GxdmLOV1QfLu/qAtqFtFmUDBF1WcaiAzBCAAAQgAAEIQAACEIAABCAAAQhAAAKlBAi6EHQh6IINYAPYwMJsgKBL6dcz6SAAAQhAAAIQgAAEIAABCEAAAhCAAARWkQBBF5ytC3O2LuqX9NTDqg1sYHltgKDLKg4VkBkCEIAABCAAAQhAAAIQgAAEIAABCECglABBF4IuBF2wAWwAG1iYDRB0Kf16Jh0EIAABCEAAAhCAAAQgAAEIQAACEIDAKhIg6IKzdWHOVlYfLO/qA9qGtlmUDRB0WcWhAjJDAAIQgAAEIAABCEAAAhCAAAQgAAEIlBIg6ELQhaALNoANYAMLswGCLqVfz6SDAAQgAAEIQAACEIAABCAAAQhAAAIQWEUCBF1wti7M2bqoX9JTD6s2sIHltQGCLqs4VEBmCEAAAhCAAAQgAAEIQAACEIAABCAAgVICBF0IuhB02QU28IKfv8Ctra25p//oWe6Oz3+FNt8Fbb6sgSeCLqVfz6SDAATqBC64YPxddtZZZ7mvfOUr9cscQwACEIAABCAAAQhAAAIQgAAEloIAQRfjfP3ll7xs5JiW7bI6LLvKtRt07MpoJ/PPq30Iuizvyo+dtLedqLuPoMv7/8st7vZ/uHcu/bTIt+p/L3vZ+LtMtkP92w06rnLbzat9CLqsslUgOwQgAAEIQAACEIAABCAAgd1DYCFBlz/9s3eNghnyS/vY53FPOMNd/qpX7+gv8D915z3utNMeNZJPtnI8T4fkDW97t3vGs852D//2b68wefJT1t0brr9xLiwWrWOdX5MdxGxDz0neenlDO55n+7QNushqmJSNSpuI3aqtptohlV/zxVbctLGRPm1iFllTeq/a+Y9+/FPuST/0ZPcffv/KVvfYx2+/00mQUPpvvU9lK/3a29/7gWRZXYMuh9/35+6yyy5zf3DlVXMJvOSCLu96V/677IwzznCvfvWrd/QX+Pfcc4971KPG32WyleN5/r373e92Z599tvv22nfZ+vq6u/HGG+fCYtE61vk12YG9H+r7knfof/Nsn7ZBF1kNk7JRaRuxW7XVVLuk8mu+2IqbNjayG2wixZbzEIAABCAAAQhAAAIQgAAEhkpgKYIu6pQQR+7NHz2edNbN25k5r1UGVm7RTxycqnNqK05ym6+v/UXomJK1jUO9zqVPB3tKvmU4P6/2KQ26SCBEAqD1YGC9PfQ45qjvYuNtbKQPm+gi6zLYS1cZJMCrbR1ry1T5V/7ha30+tQW7zZXVJeiiARcJuswr8NIl6KIMxJF7/PjxHRs3zGuVgVVI9Hvyk5u/y8RJPo+/ReiYkruNQ11tQre7xcE+r/YpDbpIIEQCoPVgoLZDfXvllVdONXcXG29jI7vFJqYAcwICEIAABCAAAQhAAAIQgMCACSw06CLOPflF+a23bfvPdW+5afTLaJ0AD/mdE+LgVQenbH/hRRe6dxw5WmEh54TFvIIuKSeqntdf/Oecppp2lq1te92XOoVHzD40zSx1NeWZt65N9S/yeknQRQIucv/pvag2+p/eftjbqLSHHEtgRlY01O2kq41r0CVnC33ZRFdZF9l+TXW1tWVJXw/+1tsyVaekUxuR/ko4alpZ/SK2IUEZPVffzhp0ed/NHxoFWjTgotu+V7yUBF3EkSu/ft/e3vafm266abTiQ9kM+Z0T4oxWZ7ZsL7zwQnf06NEKCzknLOYVdGkal+nqhJgzvSlvyXXb9rovdQqPmH1ompKy26aZt65t5Zln+pKgiwRc5P7Te1Ft9PDhw95GpT3kWAIzslKrbiddbVyDLjlbmKdNzLMNKBsCEIAABCAAAQhAAAIQgAAEmgms3Xvvvc2pClOknGnWkWoddNYZZx15ffyC3Za9DPvWoS2PL5NH+qTkkmviuExdn9d5K2OpA7YPWdT5LY72lH30UY8tY6d0tTIscr8p6CKPNrNOeFlxI4zayGiZzmrjJX1FG5lSafuQNVX2os9bXZru2/oKFbnn5CPOyaa8ope2T2n6GIvU90QsrT0n73CRAIsGW+y2z8BLadBFnLKxP3HeqrN3iL9gtw5teXzZpz71qRiG0Tm5Jk7tRf9ZGevO9HnKoo56cbSn7KPv+ndK1771KC2vKegijzazK7BkxY0wavNnmc5q4zbosihbaKMjaSEAAQhAAAIQgAAEIAABCEBgvgTWrrrqKtdX4CXlTFNHXc6pro73Ls4866Bbtv1V0K+N87ZPvsomZx991idl7ZSufetRWl5T0EWvy/0nj5wqLdem03bscg+X9BW2zln3+5B11rr7zldqyzadtJEE1rY/d69f3dQUdLH5xV5m1SP1PVFS3iICL12DLup4F8aLdPjPd6gQSl8F/azTfJFtoGwIugR76XuvKeii1+X+k3cKzfKn7djlHiboMgt58kAAAhCAAAQgAAEIQAACEBgOgTX5tXBfgZeUM63EkWpfIt7k/Ctxzi1bGuvkFR7LJp/IY52qi2wDZUPQxc3NLjSoEnt8n96f4mDq0u7ajlLOrDausszbFvqQdVnu4dL7VtL9+LnPHQVb5DFgbe95bRtZxST99az6p74nSsubd+Cla9DFvkR8kQ7/RQ1LrEN6WVfyEHRZlDUsvh4NqsQe36eBji7BEtGoDxtXWRYZgFt8a1AjBCAAAQhAAAIQgAAEIAABCKQIjIIufQVeUs40ddblHKlNTlB1GusvrO0LoOuOZHEu6jsOZPKtn8c94YzRY7vkeszBp3XUy5O04oyWcvSalCG/FBedbPmpVQJWP9UhJkPqnNQndUtdOce4TRerJ6aj6qZ6xLYpJ3qMs7zrQ86ndKmfVzY5+9A8Vr9ZOHTRVeSUd1jYNhdWJfoqd22TlP1qOrUz1Vu3on+M+ay2bXl2daZrOwoT1VPlLt2W9BWlZeXS9SGrLT/WJk12obZouYtdSFvqPSi2JjYXexyh5te0sW3qvlXZbfvn7idJr7Y5a9tqnanvCb1esp1n4KVr0KXJYatOY9nKn/waXxyz0n51R7IED/R9HbZ9zzjjjNFju+R67E/rqJcnaSUQZOuSMuQRTCqDXJPyU6sErH6qQ0yG1LnSgIhNF6snpqPqZlnV91OBohhnedeHnC/9UzYljnarXy44Z9NZDl10FTnlnTu2zYVTib7KXWVJ2a+mi9mg8BS9YsxntW3LSR4JJsHPWf+0HYWJ6tm2LIIubYmRHgIQgAAEIAABCEAAAhCAwLAI+KBLH4GXlDOtyZEqjj916KWczXpdtlqeOlNsHnFOihNTr8W2Nr118Gkdsevq4JRr4rDN1ZFyXmr5IlMqjZXH7pc6R206qc+WIfsqg9VRdYux0nN1562tR9PUt7aOuhz2WB3gyxp0EV3F8V3Xr34s70SJOcctd+Gfs99Y+yiredi2shdd2tqkymW3Kv+s5SmbEluw9c6y31VWqbPLfaD3nfQlH/v0HT6oWrcrPa4HdDW/Xo9t6/dtnZOVP9f+diViU5n1OurHqe+Jerqm43kFXroEXcTx2+Rs1uuyVcestp11UMv7UMR5rNdiW5veDk20jth1ddbLNXEu5+pIBQO0fJEplcbKY/etczyX16aT+up/KoPVUXWLsdJz9aCLrUfT1Le2jroc9lid9csadBFdJdhS169+LO9ESb2rR7nLNme/mi7Gbh62rexFl5xd2fbK7av8s5anbEpsIScH1yAAAQhAAAIQgAAEIAABCEBgNQlUgi4SeHn9618/syYpZ1rOkSpOX32Bt/3Fd93hpg7Sc35i7yjgccllr4y+6FudyFKm/PpcnIpSlmy1DJlExxyMej0WLFAHp5SrH6lL5ZS6dAVEymFsHZcig5STctJrubotdY7adKKP5tdtTkebN8ZHy7DpRFdxBss5uS7by1/1as8iJoOWo1ttsxQ3TaflS/uk2lDTWhljMtjrpbpKnbK6SR/NJHXJvtU3ZcPKvcl+NV3MBpVTn7aduzeVZZttFxuXevqWJyd7V1mtDc1yH2ifIjYjdlEvQ2Qv6VesHDlbjrEozau2p/eo2H1spZ/cC1JmrC49l/qe0Otttsdu23byvRX7vPZ1r8/Kkapn1qCLOH31Bd65X9qrM3fv3r2jgMcrX/nK6Iu+1YksZcqKAHGYy59stQzpk2IOZr0ec3hrYELK1Y/UpX9Sl66ASDmM7SPURAYpJ+Wk13J1a4McMdlj6USf+l9Ox1nqEF1l1Ybl/OpXv9qziMlQl0nbLMXNpp9FxpgMs5QjbSarm+68804vkuxbfVM2rNyb7FfTxWxQOfVp230HObrYuEDtWx7fUOxAAAIQgAAEIAABCEAAAhCAwEoQqARdur7bJeVMU0eqTPRTH3Hg5Zx16oyW/JI25TCTIIY4KmPXrYMx5tTWOmLX1EEq9ceuS33qmJQ0UlZMBpFPnOaWgxxL3lh6PWdlzzlWbbqYDDkdbd5cHcpCnMWpoJG2uTppVY/YVrmVpC2V0aaLcbDXS3SV9hKdYvLLOdUh1fbKXa7n7FfTxWxsHratbVnCPqV7/fysNi7lqN3Y+yO2H2vTuhwlx11kVXaz3geaX/TL8bfBoZhdlNpyjEdpXm0X0fUdR476oGqsbaQ/E5lj9cm51PdEKn3q/E6udInprefEma2O+9goQJ3Rkl7Spv4kiJF6tJV1tMec2lpH7JoGXaT+2HWRR53ikkbKiv2JfOI0V71lK8c2gBPLZ2Xf6aCLspAAQypo1MZ5rtyWMeiiuko7iU6pP9Uh1fZqW3I9Z7+aLmZj87Bt1a+EfUr3+vlZbVzKUbsRTrlP6v6qy8IxBCAAAQhAAAIQgAAEIAABCKwWAR906RpwEbVTzjR12OUmnnJNnHUpJ746o3POyZRzzp5XR6c4D+uOQa0j5tjUfCJnyvluHZixMqwc9p0eyiWnvy1bZLFl2X2bLuaYzulo86bqsA7gFAeRp6QslVsDFiVtW1quTRfjYK+X6JpKozrIVtJIW+Zsq0nHXPvYumL7JfXX7TKXJ1ZHm3NtbVzKLu0rYm3aRrZ62ray9nEfKHuxGdmvy2SPNW3Mfkps2ZZl90vz1ttF5LAr3HTli/ZldTuzdaa+J2yapv15BVykXpEv9VfqSM2t/FBndFfnsDqZYysStI6Yw1vzSVulnO82MBIrw/Kx7/TQ9s/pb8sWWVJ/Nl3MMZ3T0eZN1WFXMqQ4iGwlZakOGrAoadvScm26GAd7vUTXVBrVQbaSRtoyZ1tNOubax9YV2y+pv26XuTyxOtqca2vjUnZpXxFr0zaykRYCEIAABCAAAQhAAAIQgAAElpPAKOjSR8BF1Es509RhJ446WYVy623b/iO/mv6dV1xe+eV0zJnfxRltHXjqvMw5xmMOw1y+WPmxMmw62ReHZ93Zq87MWFopUxwhOQetdaLGHNM5jjZvqg5tyxi/usxaV0wOm3ZZgy6qa8zRbeXXfdVD2qhuw8qiyS5K02mddpuz0VS5uTy27Fn329i41GGZ1/sK229IubPKlMrXRlaVs8t90IZ9zrZK7tucziX9iuortp27H1Sn2D2gMqS+J/R603aeARepuyToIg5nWYWyvb3tP0ePHnWXX365fxyVMIg587s4o+0wIudkztWRyxcrv+7ctml0Xxz/dce0MJJz9b+SIIHkselijumcjjav6Bv7U6d4LLBQT691xeSwaZc16KK6NgVKVBfVI2bDyqLJLkrTaZ12m7PRVLm5PLbsWffb2LjUYZnX+wrbb0i5/EEAAhCAAAQgAAEIQAACEIDA8Ais9RVwETQpZ5o67HLOOus4jDky1Wks2yannFyX8iSgc9UfHXC/+Esb7hnPOts97gln+Mc85OqIOcbVmRi7ZuUpTWfziKz2vSDi6JBy6mlKnKOWY4yVcozpYfPW61dZVD+RsfQTk0PLk606lHP2oelLZJS0Nl2sfnu9SdeYrag8dptb/aDcY7LYMjRdrH00ncjel21re5aw1/pn2YrMTTYu5Zb0FbPU3yZPiazKrfQekHT1ttcySuzL2lbdXktsOaV/aV5tF9GjXr8t28pZ11fTpb4n9HpuO++Ai9RdGnQRx3Tszzr8Yw59dRrLtuRPypOAzoEDB9zGxoY7++yz3RlnhO+yXB0xx7g6p2PXrDyl6WwekdW+F0TsRcqxf5ZP/VoqXYyVcozpUVKH6tfmHo7JYWXWYEVJcKNERinbpovVb6+neKquMVux8ut+bhWQco/Jovllq+li7aPpRPa+bFt1LGGv9c+yFZmbbFzKtUGXVF8xS/3kgQAEIAABCEAAAhCAAAQgAIHVILB277339iZpypmmDrsmx64638UJInms802d0SlHnqYVJ+IvvOjCxoBAzNGpdcQc3uogjV3TumVbms7m0X15tJrIJfrXWZU6R226GKucjjZvyrGq+rVxVMXkUJ1lq+1e19mm0f0SGSWtTRer315v0rWpzVU263Cul6ncY7JoftlqulidInPftq33Zuyes3L1tZ+zcalD5Smxhb5kSpWTk7WP+0DLiPVFdZlytlViy/Xy9Lg0b5t2ydmw1Jv6nlCZUttFBFxUvtSXYqkjVZ3vcl9JHvunzugmp7U4dy+8sPm7LOZI1zpiDm91TseuWTlL09k8ui/vwhC5RP+6E7wkSCDl2HQxVjkdbV7RI/an+rX5LovJYcvWdq/rbNPofomMktami9Vvrzfp2tTmKpsNutTLVO4xWTS/bDVdrE6RuW/b1nszds9Zufraz9m41KHylNhCXzJRDgQgAAEIQAACEIAABCAAAQgsD4G1PkVJOdNKHXY5x6I68nJOa5tfJt7ioL7uLTeNnPryzgFxqOUcnVpHzOGt+WLXrJOwNJ3NY/eVlcgvZem1UueoTRdjldPR5rV1qwyy7aqfLUv3lz3oUuIUF12s/Uk7qn6yVe6xNomlq9uZLbtP27blNslm5eyyn7JxKVOvLUPQxcpTvx/7uA+0jBL7su1Ut62S+zbVXqV529yjaut1G1YZUt8Tej21fd/NH3KXXXbZ1OcPrrzKSUAmla/teZEv9VfqSO3qtLb5xfbEQX3TTTeNXlJ/5513jsTToMEyBl1EQGUl8lvHfUmQQPLbdDEHf5NTX5z99bptuyq/WFDApmuzv+xBl5itxPSz9iftaP+Ue6xNYunqfG3Zfdq2LbdJNitnl/2UjUuZeo2gSxfC5IUABCAAAQhAAAIQgAAEILC6BAYVdLFOTPmVeszZZtOII9OmyTkLNV/KkajllKbT9PWtda5KWXrdOkdzzvGmdDkdbV5bt8ogW3WKlziKbb7cfhuHrpWxCwdbTpOupQGAnB7KPSezMNJ0dTtTuxLufdu21ikOsLpDP9dus15L2biUp/ZVynxWGUrzpWRVObvcB7ZN631RXT6tL8alxJbr5elxaV7LoclG1J5Stj5r0EVkPvy+P68EXfoOuEgdyxB00YCAOMnlF/WxP5tGHM72Tx3jdYe3pNF8sWu2jNJ0No/dt05wKUv/moIppelyOto6bN1atmzVKV4aiLB5U/uzBl1yQQKrSyydvd6ka2kAIKeHco/JYrlourqdqV3Nw7a1TvkuqweLrGx97adsXMpX+ypl3pdMlAMBCEAAAhCAAAQgAAEIQAACy0FgqYIu6liMOX+bHHniLGuTJuYs1fx1h7eUrQ7S2DW5rp/SdJq+vlXHvTCQsvS6dY7mZLD5Y07PnI62Dlu3yiBbW34qjU1fsq9lxhzK9fxWxi4cbDkpPayjOZXGyidppN1ythVrE1tGqn30fC6/psnVH2Om/FX2VFDHytll39ZX56p9QIktdJGhNG9K1tT50nIlndpLrL+rl6NtG2u/Eluul6fHbfKqDDkbLLlnugRdRG4NvMwj4CLl9xF0UYertG3d+auO4ZzTuk2aWNBA89cd3jLsUKd37JodlpSms3nsvjruhYENBtggQU4Gmz/GKqejrcPWXSKfTdN2X2UucbRbGbtwsOWkdM0FB2I6atvnbCvWJrasVPvo+Vx+TZOrP8ZM+YvN5YI6Vs4u+7a+OnvtA0psoYsM5IUABCAAAQhAAAIQgAAEIACB5SSwNEEX66zLOY1zDj91CsYck+JMs47SXB2x/OogjV1TB6ZsU+ne/t4PjF4kLk5Om76+rzrEnM5aduyalGMdqOJ0iLHS8mN62PyxvCqrlpGSQ9OJ815enq7Hqa22S1N5mr8PDm11FZ65X/irDpJO5FNZdavMclwlraart0/qvJZv629r21KGMhX5pR3ecP2NUzpoXbqVNFf+4Wt9uj5sfFFBlz5k1TZpstvUfWCZ19tbGctWmaRsq9SWbZm6b/PG7FbT1eVI3QuqU8wGtayuQRcp5/3/5ZZeHymmssm2a9DFOrhzTuMSp3PMsSxDCevszdURy68O9dg1O0xJpfvABz4wepG4OPtzf+o4jzmdtezYNSnTBhLE7mOstPyYHjZ/LK/KrWWk5NB0stpIXp7e9Kft0lSeltMHh7a6Cs96IFDlka3qIOlEvvqfMstxlTyart4+qfNaj62/rW1LGcpU5Jd2uPHGG7Xo5FbSvPa1r/XX+7Bxgi4eJzsQgAAEIAABCEAAAhCAAAR2JYGFB11ueNu73a23bfuPOIt/5xWXjxy9MkmWT8z5pw5O2VoHmd1Xh5+U8csvedkoCCHXxbEoDmJxjj75KeuNqxFiDlAtO3YtJkM9nXWcPuNZZ/t3zSiLq/7ogHvSDz15JJvIH9PTOtZFF2GpdYtjV/LL+cc94YxRObEylGNdPi1Hr9vypV5xUmuauhwSWNF35kga2Rf+UkZMBi1Ht1qepJd9PZ/aanrhZOWU9KUcJG2JrhIMtO0ietV1Ff1FDpGniWsTD5WpXo7a3zxsWznbOqQesSPRTXirnb7jyNHK/Sp5NH8fNq5laLtqvbGt3Ndad9ut1iN69nU/tr0P6rzFzuw9LfpdctkrfZ9Qtwmrs9qNcpNr0m72vrXpdb9N0EXyaD3CTWTTNtB7Xs7Lx9qF1qXbPoIuWtY8tqVBl3e/+91ue3vbf8RZfPnll48cvcphVqe1dRy/7GUvGwUhZIQiDnZxEIszeX19/F3W1jGtZded4fURUCqdOpNFx7PPPtu/a0ZZHDhwwD35yeG7LOact4510UVY6p8EOCS/nD/jjPF3WayMJue9XrflS73iUNe/uhwSWNF35kga2Rf+UkZMBi1Ht1qepJf9pj9NLyytnJKvlIOkLdFVgoG2XUSvuq6iv8gh8qTsQ+tq4qHp6uWoXUkdfdu28rZ1SD1iR6Kb8FY7PXr0aOV+lTz614eNaxnarlpvbCv3NX8QgAAEIAABCEAAAhCAAAQgMCwCCw26yOQ39xGHof3lvHWoqbNPtva83bcOxFg94jBXR2fsl9haR8y5qfli16wMqXTWyRuTzZ6zASNbtuxr+Ta97gu/IzffMnL8y7kYq5yOUr4NaGi5shX5rSypdDaP7Iu8Nl9sX8sS+WU/lqZ+risHKU/rrctc17UeeKmn1+Ncuyn3WJtY3TRd3c7madu2fnH62yCT6hbbSntZp34fNt6mjCaWVq/6fpt6cu2asqE6r9h9oDYsfZEEs4RnPZ8eS5uIHdb10OOUHHVb1vS6tXYVk1HT6damV9nq26ZyhhB0qetcPxZHq/3lvB02qDM657S2qxfqZcuxOKvVsbyTQUBUM3wAACAASURBVJeYbPacdapbBrKv8tv0ui/8brnllpHjX87FWCnHulNf67EBDS1XtuIMt3+pdDaP7FunvM1v97UskV/2S/66cpA6tN66zHVd64GXeno9zrWbco+1idVX09XbZ562beuXQJ4NMqlusa20lw3GacAklrZ+LsWqTRlNLK1e7EMAAhCAAAQgAAEIQAACEIDAahBYiqCL/KJeHJt2BYE6+XSrzugmR6s4Be3KA5kgS/n6uCTr6Kw7MbWOusNbZNB8sWsqY1M6WYUhq3pktU3dwSrn6r+Ut+XafXGMy6/z7eT/F1504WiVh3WKxljldNQ6xIFrHe+yL+f0um6Vta6sUXl0hUSuPbUM2arDuE3QRfJ14aD1l+pq67NtJ/vCPsZH65Ctco+1SSxdzM6Ut62/D9u29eu+sBW9Ym37/J/52cqKDM0j26423iYY0sTSyhXb7yqrlqntEmOVu6e1T9EAsMgjzPU+kq3c59IWWldu28aWtRzbXzQFSzSPbEUm20fofSA62HSx/SEHXeQX9eKEtSsI6kMBdUY3OVrFOW1XHog9SPn6uCR11i866CL6yCoMWdUjq23EYW1tVs7VV4zUGeixOMZltYzNf+GFF47Kt875GCvlWHfqa9mylWCEdbzLfiwYoqx1ZY3Koyskcu1Zr094tAm6SP4uHLT+Ul1tfbbtZF/Yx/hoHbJV7rE2iaWLtY/ytvX3Ydu2ft0XtqJXrG1/9md/trLKSvPItquNE3SxNNmHAAQgAAEIQAACEIAABCCw+wgsJOgSc7xxzjU6J2EEI2xguDZQD7rslrZe5aDL7hsioDEEIAABCEAAAhCAAAQgAAEIQAACEIBAWwIEXb4yXKfubnHioic2vIo2QNBlOe02906Xtl+wpIcABCAAAQhAAAIQgAAEIAABCEAAAhDYfQQIuhB0YcUNNrCyNiCPCJRHcMnj+Uo/qfdGLTpwQ9CFoMvuG3KgMQQgAAEIQAACEIAABCAAAQhAAAIQGD4Bgi443FfW4b5oJzn1LZ+TXIIu8k4UfQdDybbNu0vm2eYEXZbPnqS9Weky/IEPGkIAAhCAAAQgAAEIQAACEIAABCAAgXkSIOhC0IWgCzaADeyADRB0Iegyzy93yoYABCAAAQhAAAIQgAAEIAABCEAAAhDYGQIEXXbA2TrPX89T9nI6cmkX2qVuAwRdltMmWOmyM4MRaoUABCAAAQhAAAIQgAAEIAABCEAAAkMhQNCFoAurHLABbGAHbICgC0GXoQwk0AMCEIAABCAAAQhAAAIQgAAEIAABCEAgECDosgPO1vov3jleTucr7UK7YAP924CsJFlmrqx0CQME9iAAAQhAAAIQgAAEIAABCEAAAhCAAATaEyDoQtBlqR2gy+ycRbbldp7TPsvZPgRd2n9RkwMCEIAABCAAAQhAAAIQgAAEIAABCEBgdQgQdCHoQtAFG8AGsIGF2QBBl9UZICApBCAAAQhAAAIQgAAEIAABCEAAAhCAQHsCBF1wti7M2crKg+VceUC70C6LtAGCLu2/qMkBAQhAAAIQgAAEIAABCEAAAhCAAAQgsDoECLoQdCHogg1gA9jAwmyAoMvqDBCQFAIQgAAEIAABCEAAAhCAAAQgAAEIQKA9AYIuOFsX5mxd5K/pqYvVG9jActoAQZf2X9TkgAAEIAABCEAAAhCAAAQgAAEIQAACEFgdAgRdCLoQdMEGsAFsYGE2QNBldQYISAoBCEAAAhCAAAQgAAEIQAACEIAABCDQngBBF5ytC3O2svJgOVce0C60yyJtgKBL+y9qckAAAhCAAAQgAAEIQAACEIAABCAAAQisDgGCLgRdCLpgA9gANrAwGyDosjoDBCSFAAQgAAEIQAACEIAABCAAAQhAAAIQaE+AoAvO1oU5Wxf5a3rqYvUGNrCcNkDQpf0XNTkgAAEIQAACEIAABCAAAQhAAAIQgAAEVocAQReCLgRdsAFsABtYmA0QdFmdAQKSQgACEIAABCAAAQhAAAIQgAAEIAABCLQnQNAFZ+vCnK2sPFjOlQe0C+2ySBsg6NL+i5ocEIAABCAAAQhAAAIQgAAEIAABCEAAAqtDgKALQReCLtgANoANLMwGCLqszgABSSEAAQhAAAIQgAAEIAABCEAAAhCAAATaEyDogrN1Yc7WRf6anrpYvYENLKcNEHRp/0VNDghAAAIQgAAEIAABCEAAAhCAAAQgAIHVIUDQhaALQRdsABvABhZmAwRdVmeAgKQQgAAEIAABCEAAAhCAAAQgAAEIQAAC7QkQdMHZujBnKysPlnPlAe1CuyzSBgi6tP+iJgcEIAABCEAAAhCAAAQgAAEIQAACEIDA6hAg6ELQhaALNoANYAMLswGCLqszQEBSCEAAAhCAAAQgAAEIQAACEIAABCAAgfYECLrgbF2Ys3WRv6anLlZvYAPLaQMEXdp/UZMDAhCAAAQgAAEIQAACEIAABCAAAQhAYHUIEHQh6ELQBRvABrCBhdkAQZfVGSAgKQQgAAEIQAACEIAABCAAAQhAAAIQgEB7Ar0HXcShxgcG2AA2gA1gA6tqA+2/SskBAQhAAAIQgAAEIAABCEAAAhCAAAQgAIExgbVPfvKTjg8MsAFsABvABrABbAAbwAawAWwAG8AGsAFsABvABrABbAAbwAawAWwAG+hmA72udCGSBQEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR2KwGCLru15dEbAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBXgkQdOkVJ4VBAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCwWwkQdNmtLY/eEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEI9EqAoEuvOCkMAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACB3UqAoMtubXn0hgAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAoFcCBF16xUlhEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEI7FYCa1/4whdcyccCuu+++5x+7Hn2IQABCEAAAhCAAAQgsEwEPve5zy2TOMgCAQhAAAITAvTPmAIEILAqBOivVqWlkHMnCHB/xKkTdIlz4SwEIAABCEAAAhCAwAAIMAkYQCOiAgQgMEgC9M+DbFaUgsAgCdBfDbJZUaonAtwfcZAEXeJcOAsBCEAAAhCAAAQgMAACTAIG0IioAAEIDJIA/fMgmxWlIDBIAvRXg2xWlOqJAPdHHCRBlzgXzkIAAhCAAAQgAAEIDIAAk4ABNCIqQAACgyRA/zzIZkUpCAySAP3VIJsVpXoiwP0RB0nQJc6FsxCAAAQgAAEIQAACAyDAJGAAjYgKEIDAIAnQPw+yWVEKAoMkQH81yGZFqZ4IcH/EQRJ0iXPhLAQgAIGVI3DnnXe6n/u5n3Oy5Q8CEIAABMYEmARgCRCAAASWkwD983K2C1JBAALTBOivpplwBgJKgPtDSVS3BF2qPDiCAAQgsJIEJNBy1llnjYIusiXwspLNiNAQgMAcCDAJmANUioQABCDQAwH65x4gUgQEILAQAvRXC8FMJStKgPsj3nAEXeJcOAsBCEBgZQhowOWaa64ZySxbAi8r03wICgEIzJkAk4A5A6Z4CEAAAjMSoH+eERzZIACBhROgv1o4cipcIQLcH/HGIugS58JZCEAAAitBoB5wUaEJvCgJthCAwG4nwCRgt1sA+kMAAstKgP55WVsGuSAAgToB+qs6EY4hEAhwfwQWdo+gi6XBPgQgAIEVIpAKuKgKBF6UBFsIQGA3E2ASsJtbH90hAIFlJkD/vMytg2wQgIAlQH9labAPgSoB7o8qDz0i6KIk2EIAAhBYIQJNARdVhcCLkmALAQjsVgJMAnZry6M3BCCw7ATon5e9hZAPAhBQAvRXSoItBKYJcH9MM5EzBF3iXDgLAQhAYGkJlAZcVAECL0qCLQQgsBsJMAnYja2OzhCAwCoQoH9ehVZCRghAQAjQX2EHEEgT4P6IsyHoEufCWQhAAAJLS+C8885zEkhp8yfpJR9/EIAABHYbASYBu63F0RcCEFgVAvTPq9JSyAkBCNBfYQMQSBPg/oizIegS58JZCEAAAhCAAAQgAIEBEGASMIBGRAUIQGCQBOifB9msKAWBQRKgvxpks6JUTwS4P+IgCbrEuXAWAhCAAAQgAAEIQGAABJgEDKARUQECEBgkAfrnQTYrSkFgkATorwbZrCjVEwHujzhIgi5xLpyFAAQgAAEIQAACEBgAASYBA2hEVIAABAZJgP55kM2KUhAYJAH6q0E2K0r1RID7Iw6SoEucC2chAAEIQAACEIAABAZAgEnAABoRFSAAgUESoH8eZLOiFAQGSYD+apDNilI9EeD+iINc+aDLnj173E5+4lg5CwEIQAACEIAABCCwDASYBCxDKyADBCAAgWkC9M/TTDgDAQgsJwH6q+VsF6RaDgLcH/F2IOjSMWgTx8pZCEAAAhCAAAQgAIFlIMAkYBlaARkgAAEITBOgf55mwhkIQGA5CdBfLWe7INVyEOD+iLfDYIIucfXmd1ZX18yvBkqGAAQgAAEIQAACEOhKgElAV4LkhwAEIDAfAvTP8+FKqRCAQP8E6K/6Z0qJwyHA/RFvS4IucS6NZwm6NCIiAQQgAAEIQAACENhxAkwCdrwJEAACEIBAlAD9cxQLJyEAgSUkQH+1hI2CSEtDgPsj3hQEXeJcGs8SdGlERAIIQAACEIAABCCw4wSYBOx4EyAABCAAgSgB+ucoFk5CAAJLSID+agkbBZGWhgD3R7wpCLrEuTSeJejSiIgEEIAABCAAAQhAYMcJMAnY8SZAAAhAAAJRAvTPUSychAAElpAA/dUSNgoiLQ0B7o94UxB0iXNpPEvQpRERCSAAAQhAAAIQgMCOE2ASsONNsKIC3O1uvPQSt/eCS9xFh+6eWYc7jh11V07KkbL2Hjgxc1n9Z+xHx/7losTdQoD+ebe0NHpCYPUJ0F+tfhuiwfwIcH/E2RJ0iXNpPEvQpRERCSAAAQhAAAIQgMCOE2ASsONNsKIC5AMStxy4ehyQyQRR7jg0TjMKtkjAxQRdSvLPH1xex/nXTw27nQD98263APSHwOoQWJb+ajnGD6vTbki6GALLcn8sRtvyWgi6lLOqpNyxoMuxG8YTttHE7Wp3410VsTIHJ9yVk8nelccyybgEAQhAAAIQgAAEBkSgt0lAZQw2caCrI32yvejSq92VB466G4/NvjJiQOhXXJVcQCKMq/decIO7JabpXUfdRWoXh064OyppCvJX0s/rIKfjvOqkXAgEAp3754J+uRL0NH02c+LQDuxBAALNBDr3V5Eqxqthr/bjBe2vRuPJY3fXxg5SwLKMHyLKcGpXE5jH/TEEoARdZmzF5Qi6XOL2Xno00hHHlAqdMwPMGB/OQQACEIAABCAwRAK9TQJaO/eudldOOduHSHioOuUDEk2/NPWrXBJj9ab8i6Ga13ExMlDLbibQuX9u3S+HgDlz4t1seegOgfYEOvdXtsq7ao8eNQFhDbzY1bE263KMH6xE7EPAuV7vjwEBJegyY2MuTdDlgktc2YCRoMuMTU02CEAAAhCAAARWmEBvkwDv3Lt6tJLljrvudvZzy7ET7sZDN7iL7Ps7ZBKdcLr3gdT/QrLDO0f6kGOYZXQJSIS8y/UOl3pLBTm7vLemXirHECgl0Ef/bPthv39MV5rF+2tJxx8EIACBNgT66K9G9ZmVsHsvuNpddOCou0VWtUzGlbccO+punDzCdLnHEG3okXboBHq7PwYGiqDLjA2680GXG9yVB/SXOonHGlR0I+hSwcEBBCAAAQhAAAK7gkBvkwAbdGl6vOtdJ6ovT59L4AWH+XwNuAvfkHe5HSZBToIu87UmSo8T6K1/rhfvnZptHsddL4RjCEAAAoFAP/1V+N4dPZ40N56UseShE0EA9iCwxAT6uT+WWMEZRSPoMiO4ZQi63OIHk5e45gkdQZcZm5psEIAABCAAAQisMIHeJgFtgi4jXnZifYnr36kdyu+/7BVu8N5E78I35G0eo/cm8AwFBTmxoRnwkaUzgd7657okfp5M0KWOhmMIQGA2Ar30V75vmse4cDa9yAWBPgj0cn/0IciSlUHQZcYGWYqgi3POPy+68TFjBF1mbGqyQQACEIAABCCwwgR6mwS0DroItDD+6v8xYzjM52uWXfiGvARd5ttKlL7aBHrrn+sYvGOToEsdDccQgMBsBHrpr3zfVPqagNlkJRcEFk2gl/tj0UIvoD6CLjNCXpagi3NmUpd9dEWY9KffAXO302eDV17edWn+RbA+8KP133Vi9AzKi8zLwC46cMLdUWF9t7tFnntu0uyVeo6VPV83JudFl94wesZ6pRoOIAABCEAAAhDY1QR6mwTMFHSxP5BJOf/ajb/8uMuOoWr7qbHePMZPXp5FjgMjY00Zu7YdC6Z43DJ63EcYY8dWgdyij/lVveUu8zaijwCub4MNRPNH7tSUjDd2HDOX6BgRh1MQ6JVAb/1zXSrv2Az3nE3i778LSh7THfoCG0T1fZ8p445j9fd6Td7XkHuEkBGs6/1uimIXAhDomUAv/ZXvm0qeVhNXwPdfdvzhnPPna2PCim/PXFvkWDGuCWeHRKCX+2NIQCa6EHSZsVGXJ+jinDMdd2xSOFaxIegiz4s0HXC0Y6516orODzjlupFlugwd1Naec16rVwI06T8z6K3l8/Ul5EyXyRUIQAACEIAABIZKoLdJgHeox514SX5mbDQ1Tpth/OXHXalxUHT18/zGT16eRY0D9eWyGf33XnqDGwcVUq2SH4vKmFJ+CHTjpeOgyVS7WeeGHXd6G6kHW/Q42I53jtj8FXFD/X6MW9c5mVcK6q5jRRwOIDAHAr31z3XZfL8b7rlKEn+94NfmPm21LN/3jYIuzfdr/seFzfn7Xy1ZIcIBBCDQQKCv/sp//8uPRQ6V/ejYiubz18YA/nx9rBA7jvrc6IcsZ/bbEejr/mhX6/KnJugyYxstVdCl8pix6mAwqBeCKtGItg4mJ6tFwqqUuysR89iXgh9wXnr1eOXKpUfNRFfyX+38ZPHA0ckEVlbP3B1Wv1ReOJvSwX4JjFfFVOS0K2eiXyKBBnsQgAAEIAABCOwOAr1NArxDPTVOSfEMYzD7K+lR6g7jL7vaOTY+C9LMd/y0M+PAS9xoFbX99fhd9VXU+mOfQGK8V+NxqLoae/xLcw2StAy6+KpMHYkxqXeO1JwmURmPmTGzq+kZLd/Uf8H0ivVSHb067EBgTgR665/r8mnfekGqvzb3SPQeDAWm7lXf911wg7tytPKtPj91o6dIhCc7FMgi92vr+z3Iyh4EIDA/Av31V2ZcKAGRxh+KVHVK9UnVVNNHPp9ZnRdSmT6RfihgYa+YQH/3R3GVK5GQoMuMzbRsQZfmZ4aHjj0edDmReTSX6YAjg9Iw4EwvkQwd/HjyGpfhaHjcWGQCGerJ/HpxZofIjIZANghAAAIQgAAElppAb5OAmccYZhxVH9/IY7KSj4ky+SLjr9Kgy7zHT6H8RY0DG36Z7p2tcXmCvCkHqJizYZ/4Jaof2za0zVSgbXK35PIHGWcb84b83XRc6hsb4QZBoLf+uU7D9wOZe6CoTw9z6HpwO9xnMr/N1NPwbq9Qzmz3e111jiEAgfkQ6LW/qvzoePJDj1HwpXnlS278kNI89DPxvipcpx9KMeR8nkCv90e+qpW6StBlxuZavqBL9TnS9UGhDcpEAx4NHCqdcC1tuBbvwEfJ/cBXIvlHwwqXWlnpL5Aw4M3LHybJ0wxqlXEIAQhAAAIQgMDgCfQ2CShy0MVwhrFJygEfyyXnwhgrtmojlJse88x//BRkXMw4MK1roBhkqnMLPBrLMWPXWNr0mFXkCG2TavN0/iDjbGPekD8md6BU+ojiSg4OINArgd7657pU/v7N9EsmGJK8V3y/X+9LbP/c/Iig0CfV5Qn362z3e11xjiEAgXkRmEd/NXoPVP3xXw0rX9Ljh4Tmvj9M9VX0QwlynG5BYB73R4vqlzYpQZcZm2Ypgy72+dJTSwZLO9I4kDBQzA04p6+F0kL9yUGtlb8emMkMeEMd4z3/JVT/NWk9IccQgAAEIAABCAyeQG+TAD8WqTvNmhCGMVDKAZ8qITf+so795NjKy5wbo41rn3X8lJdRNQsMkrIWjQML2RsHQ8WR6XmUlJOX2fOqj1lHKncIungZZ2wzn7+7jtp6bCEwLwK99c91AX0fkL8PutzHZX3fRDAvT22lnr9fZ7zf63pzDAEIzI3A3Pord7ebDr6MHzUYUybfb9VzhLFMcgxKP1SHxvEMBOZ3f8wgzBJlIegyY2Msa9DFrmipdqqhs61MPqf0lw7/hLvl0FF35YEb3JXynpbJS0TH72WZHhD6AWd00qkVlNWfKsufr/8KIHdM0EXhs4UABCAAAQjsOIEvfvGLnWSYNX9vkwA/Kc078aaUNM62dMCh/firJOiyiPGTr2Mh48DpcegU79GJ+LjTyzr146RYKSFwEmu3vNMj5K2Ox0M9qfxBxsnjRnJjXb1mxrwhfwmrIGdMxyAte0MnMGv/qlxmzd9b/6yC6Nb3uw39tU9XC4ZIOf5avIx291rok+y9FsqY7X5XddlCYDcRmLW/UUaz5p9bf6WC1d/ZNtPjTX1hox0/1siMe+iHqsxW/WhW+1a9Z80///tDJVytLUGXGdtreYMu1ceMhQBLGOiFc1b5u92N9oX3Oomb2k5P4HwnvZDJNgNS22rsQwACEIAABCCQJ9DbJGDWoIvPF3HqyWOoZhx/7cqgS3asae0gjHujDs6icvIBCe/IiJYV8u5Y0CUql2Uk+0FOy6meimMIzItAb/1zXcCGgElIHu6B+r3aNMf11zPOzFBPQ580NefOzHlNkDWUzx4EIDBvAnPrr+qCy/tefJ8wHfTNjz9CYaGPmi4jpKo+KnH8Q+tM/6Ny0Q9ZhOw75xZ2f6wYbYIuMzbYUgddzARqrx8Eho57OugSrkkne9GBo+5GWe1y193ujrvGgEKHvcNBl6IJ5IyNSjYIQAACEIAABAZHoLdJgA+e5CevdYB+cuzHZJqi2/irxGHux29zHD+V1RF0nR6HKg8z8a/J6+uYYhjyVvfi9bUrJzhjYwEJ3641WcdyhLx1R67KmcrvZYyWq7nTW5+/iFWQM6ZjuhauQKAfAr31z3VxioMu9geLdp4b70NsNe3utXh5vowZ73crD/sQgMB8Ccytv4qJ7cec0+9hSY0fKsX4PnA6fyWdfX8g/VAdDcctCCz0/mgh104nJegyYwssd9DFLofWTjY+0BP1/WBPJmeTIEsdSyVN7aK/lu2k0/Xb4pJl+S8dOxi2OdmHAAQgAAEIQAAC0wR6mwT4sUiLoIvPo+OxIJ8f88w4/ioJujhf//zGT16PhYwDC9l7Z0MtvedROx+axeyFsWssIJF3eoRgRtugS+c261FHA4NdCMyFQG/9c126VB9QTzc6Dve6Dwr7+yjdd/q+ryTA6cur9T3+fLqeqMichAAEFk5gbv1VVJPQL9XHIPnxhxQW8qbGIJUq6YcqODiYjcBi74/ZZNyJXARdZqS+9EGXSjBFBneh4/WDyYnuvtPOLBH0aSKDSj/gnOdk2w+cp50WMzYh2SAAAQhAAAIQ2AUEepsE+ElpzWmWYmjGLmHlcUjsx1Yzjr+Kgi5GhvqkPUjSbW8h40DjQCjRw8tUH7e24eHbOz729O0XHf92CLq0kTHWdG3yN+gYK55zEOiTQG/9c10ofx+U9de+z5j0x3p/5/obn+eC2KMjqwJpeXvr/YWXM97PVEvhCAIQ2EkCc+uvYkpl+oZkfzIpx1+vj4Fi9ci5TF2pLJyHQJ3AQu+PeuVLfEzQZcbGWYWgi52M7730anfR5PmLyaBLfRCobEwnHHMa+AFnKv+onHTQR6uRba6s8OXRMHiWANOhE7ZY9iEAAQhAAAIQ2KUEepsEeAd1wzhk6kWo8fR+XJMaPzWMvyrjvKLATVwObxYzjp9yYzdftgma1MehIU3pOLDBwWm4TTtMTTDkggwP82Ol0aN3D91txRzt59vP1JNom1x+fy0no0gRbTNTdy5/gY5TSnMCAj0T6K1/rsvl+4HMfW7zVNIfncyb83l93ydz7FQ/LnX47454YKXb/W6VYB8CEJgngV76q2NHR76qOxoEzfUL/lqk3wn9Ur7/qlfvy8yNGyRTdNxRL43j3Uigl/tjgOAIuszYqKsRdKlGrfWlWPXJbuiY5X0uJ1z4Arjb3XHshtGg86JLr3bj/NNLn33+SKcf8HYPutgI/N4Lrh5/WdnHod11t7vlwCS4lJjgBnnYgwAEIAABCEBgNxDobRLgHWdXuxuPyXvv7OeEu+XYUXfjAR0v6UtI05NeP34avU+v/fhL2q4yST42CQzcJe/mMy3rnYkiU//jJ6/HvMeBEri5VLlOxqz1ceCh8bh1NGZNyePbccJD2tLjCmPfvZfe4OubDt4Y9tF6TOAjMSb1bRfL37XNetLRY2EHAnMi0Fv/XJfP30PpPriaJdyzft6buHc1n+/79MXSl94w+m7Q6xIYv+WQ+U6I3euS2Ms6nz46yMMeBCDQhUAv/ZX5fr5o1Gfou5THY8pbDh31Y4/RWCbSDyXHD6YviY1bsrqbvPMYK2br5uIgCPRyfwyCRFUJgi5VHsVHKxN0qUzIxxPVetCl8ktJHTSa7SgQ4weMOxh0kdapfBmEibcGlHTb+kumuOVJCAEIQAACEIDAKhHobRJgJso63shtqz9kiRELTr5YOU3jr1GJiXHR1Fgvka5e7yzjJ+94TDkUR4L28OMbLccEXury63ETe/1Rkaaf2l4q493QPjEuSafHSM6QN/U89Xz+7mPePnQcqcI/CMyRQG/9c11G3+eVqo5AEAAAIABJREFUBl2qK1KkT5jqR2t1+L5PHuHj60vMT0d9Sq0Ae9iUfzI3j/VFthj2IQCB+RHopb9qMZZMjWXi44cwzpoa0xjfXrgW6Rvph+ZnPLug5F7ujwFyIugyY6OuUtCl8iKt5ABSfoljfh0oHfOlV7srJ7+arAwqa8z8tYVMtqXyiaz1SbfIe+iEu8P+6rEmK4cQgAAEIAABCOwuAr1NApomyvIo18kvncPKiSbWs4+/fMl31X4VKTJEx0LzGT8tfhzo3B3yeA7z6NyxE+Fqd9GBo+6Wu6YfBeZZ2Z27ToxWJunjd0dl6FhylC4ETmKOzrjTQysIeWcOukxkGI3PZx3zdtRRtWELgXkR6K1/rgvonYcRx2I9rT82TsvsvHacwfd9+t6Eyf0WnJqX+O8EX0V2Zz59dLZKLkIAAsUEeuuvpK8Q39vUOEb6jGafVmz8EfqjROB3KvCS6hvph4oNgoQVAr3dH5VSV/+AoMuMbbhjQZcZ5SUbBCAAAQhAAAIQ2I0EmATsxlZHZwhAYBUILFf/HIIusUBrnWdwck4/CaKelmMIQGD1CSxXf7X6PNFgWAS4P+LtOZigiwZBFr2NY+UsBCAAAQhAAAIQgMAyEGASsAytgAwQgAAEpgksU/8cgiipX4BX5Q/pCbpUyXAEgWESWKb+apiE0WqVCXB/xFuPoMuePa5LoCaOlbMQgAAEIAABCEAAAstAgEnAMrQCMkAAAhCYJrA8/XPzIwHr0hN0qRPhGALDJrA8/dWwOaPdahLg/oi328oHXeJqcRYCEIAABCAAAQhAAALOMQnACiAAAQgsJ4Gl6Z/9O7vKVrkITYIuy2lTSAWBeRFYmv5qXgpSLgQ6EOD+iMMj6BLnwlkIQAACEIAABCAAgQEQYBIwgEZEBQhAYJAEdr5/vtvdcewGd5G+ZPrAiWLOBF2KUZEQAoMgsPP91SAwosRACXB/xBuWoEucC2chAAEIQAACEIAABAZAgEnAABoRFSAAgUES2LH+2a9sucTt1YDLpUfdHS0oE3RpAYukEBgAgR3rrwbADhWGT4D7I97GBF3iXDgLAQhAAAIQgAAEIDAAAkwCBtCIqAABCAySwI71z5Wgy9XuykMnWgVcpDEIugzSJFEKAkkCO9ZfJSXiAgSWhwD3R7wtCLrEuXAWAhCAAAQgAAEIQGAABJgEDKARUQECEBgkAfrnQTYrSkFgkATorwbZrCjVEwHujzhIgi5xLpyFAAQgAAEIQAACEBgAASYBA2hEVIAABAZJgP55kM2KUhAYJAH6q0E2K0r1RID7Iw6SoEucC2chAAEIQAACEIAABAZAgEnAABoRFSAAgUESoH8eZLOiFAQGSYD+apDNilI9EeD+iIMk6BLnwlkIQAACEIAABCAAgQEQYBIwgEZEBQhAYJAE6J8H2awoBYFBEqC/GmSzolRPBLg/4iAJusS5cBYCEIAABCAAAQhAYAAEmAQMoBFRAQIQGCQB+udBNitKQWCQBOivBtmsKNUTAe6POEiCLnEunIUABCAAAQhAAAIQGAABJgEDaERUgAAEBkmA/nmQzYpSEBgkAfqrQTYrSvVEgPsjDpKgS5wLZyEAAQhAAAIQgAAEBkCAScAAGhEVIACBQRKgfx5ks6IUBAZJgP5qkM2KUj0R4P6IgyToEufCWQhAAAIQgAAEIACBARBgEjCARkQFCEBgkATonwfZrCgFgUESoL8aZLOiVE8EuD/iIAm6xLlwFgIQgAAEIAABCEBgAASYBAygEVEBAhAYJAH650E2K0pBYJAE6K8G2awo1RMB7o84SIIucS6chQAEIAABCEAAAhAYAAEmAQNoRFSAAAQGSYD+eZDNilIQGCQB+qtBNitK9USA+yMOkqBLnAtnIQABCEAAAhCAAAQGQIBJwAAaERUgAIFBEqB/HmSzohQEBkmA/mqQzYpSPRHg/oiDJOgS58JZCEAAAhCAAAQgAIEBEGASMIBGRAUIQGCQBOifB9msKAWBQRKgvxpks6JUTwS4P+IgCbrEuXAWAhCAAAQgAAEIQGAABJgEDKARUQECEBgkAfrnQTYrSkFgkATorwbZrCjVEwHujzhIgi5xLpyFAAQgAAEIQAACEBgAASYBA2hEVIAABAZJgP55kM2KUhAYJAH6q0E2K0r1RID7Iw6SoEucC2chAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQCsCBF1a4SIxBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIgTIOgS58JZCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEINCKAEGXVrhIDAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAATiBAi6xLlwFgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQi0IkDQpRUuEkMAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBOAGCLnEunIUABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACrQgQdGmFi8QQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAIE6AoEucC2chAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQCsCBF1a4SIxBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIgTIOgS58JZCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEINCKAEGXVrhIDAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAATiBAi6xLlwFgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQi0IkDQpRUuEkMAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBOAGCLnEunIUABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACrQgMOuhy4LhzfGCADWAD2AA2gA1gA9gANoANYAPYADaADWAD2AA2gA1gA9gANoANlNtAqygDiSsEBh90qWjLAQQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAkkCEpzib3YCBF1mZ0dOCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMCgCBB06dacBF268SM3BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQGAwBAi6dGtKgi7d+JEbAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIDAYAgRdujUlQZdu/MgNAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEBgMAYIu3ZqSoEs3fjuS+7N33eVO/6lfdGvPPtc9TD4/dq572LnPc//juee775x8/vm557tHm8937/03Tj6P3nuee8ze57m/+pu/2RHZqRQCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAASWlwBBl25tQ9ClG7+F5/7wxz7mHn/h5e60F93sHnTZlttzYMvteceW27P1BfeLW3e7ja1vuo0t5353y7kDk891t97v/tOxL7q3fez/c2+89Q53/UfvdS961X90r3/72xcuPxVCAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDA8hIg6NKtbQi6dOO30NyywkUCLmuXfMCt/V9bo0816PJxt7H1jUrQ5Y23fsW95aNfcDf91y+7//fT97sj2/e5m//+a27rHufedOiQ23vxxY2fhSpJZRCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEILBjBAi6dENP0KUbv4Xmvu32293ak5/u1n70HLd21vhzylnnuFOefY475Zy97uHn/Jj79nPOG32+85zz3CPOOc898py9o893/di57lE/ca77j//5I6OAiwRdHvjqV93td97pP++87U531eFPuovfe6d7yoG/dN//qveOPue89KUL1ZPKIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYGcIEHTpxp2gSzd+C839zW9+033l/vs7fZ77a7/m3nnb50aBl098oSr+X93r3Js/+mX3iq2T7pk3HHOnHthyTzyw5Z5w/vnVhBxBAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDAIAkQdOnWrARduvGba+5/+sd/dJc+7xnu/Eevdf4895+vuT1ra+7md77TycqVN9/y39z9X6+KH4IuX3PPvOGT4/fFEHSpQuIIAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMCACRB06da4BF268Ztbbgm4vO5Xf9x95hVrzh3o/nnNj625vQ8fB11E6H/7mte4y//07RX5Q9DlS+6ZN3x8HHT596x0qUDiAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDAgAkQdOnWuARduvGbW25Z4dJXwOXlT1xzl/3LNffix4Sgiwj+pne9y5178cX+8yMvudg98YKXuv/thRe7R/z0he47nvdC9x3PeqE7urU1Nz0pGAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABJaHAEGXbm1B0KUbv7nlPvMha+68R/Tz+f0z1tyBPdNBlwe++lV3+513umf+yq+4P9/ach/5rze7d7z3Z9wvXLLHXfu2t42uyXX+IAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYHcQIOjSrZ0JunTjN7fcz3/8mrv/vu6fc793zb3mifGgiwq/9+KL3ZOe8hT3qEc9yj384d/mvuVbHuy+9ZRT3Kmnnuruu+8+TcYWAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEBk6AoEu3Bibo0o3f3HKff8aac27NPXDvmrvvH9p9vnTHmrv35Dj/eaengy4nTpxwD33oQ93a2lrl8+AHP9g95CEPcY997GPd/fffPzcdKRgCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAASWiwBBl27tQdClG7+55dagyz3Xr7m/fvGa29oo//zWv1pz1/xWc9Dl3nvvdT/90z/tHvnIR7pHPOIR7rnnPtNdcMH3u6c8+1+4n/ulX3Kf//zn56YfBUMAAhCAAAQgAAEIQAACEIAABCAAgTYEjh/c5/bt2+f2bR5xJ9tkJC0EIAABCLQiQNClFa6pxARdppAsxwkNurj3rrkv/cGa+8Jfr7kvHC/77FkrC7qIpp/97Gfds37+592f3nSTO3HbzW5r6xfc297zbHf7Z7eWAwRS7AoChzfWR6ut1jcOT+mbuzaVmBMQgAAEIAABCEAAAhCAAATmSOD4wc2R03/z4PE51tKt6FWQMadhTn6CLjlyXIMABCDQHwGCLt1YEnTpxm9uuW3QxR1Yc+7r45Urr33tmjv99OnP+98/vi6PJGsTdBEF3vO+97mfecEL3L/+19/vvvd7/yf3mMd8m/ue7/lud/rpp/f+eLHtw/vdxvrYwe4fa7a+7jYOb7vtBprb+2v5ao9FG5e37vZnCupSv9vedof3b7j19erj2NbXN9z+w5lKW+i1nhM+Vs72YbexvuZK83XSP1Z/L+cOuw3flhuuGnbJXeulcgqBAAQgAAEIFBM4eWTsaBv9wlZ+ZRv9bLojLX9668stdOD59Pv2uc22lTnnfP5IfSePH3EHN2t6bm66g8dPFv6i+KQ7efyg29y0fDbd5sEj7nhLLqOGOXncHdycTU9tWK/vjLy0nOi2q3xd80eFCic76T5X2Y67g/7+OeiKXdcnj7hNn2+fi5hwUD67Z+tvf89mi+biwggE+y5tw9DuRX2nsbeQPpSxb18L2y2kEnSyfWjZfrgf5itjoSryZVO5X+PfmRPdKqtW8vITdCluARJCYIEETrrjR2Ljv+Pu5Czjv4rkHco+Gcu7z21uHnRHigemPY9tVbfjBydziabvkkyf6MtIfE/IGP7I8cIxvAoWtgRdAotZ9gi6zEJtAXlSQZcrrqg6/DVwcehQ+6DLJz7xCXfqqae6U045xcl7XB70oAdV3u0iZX/lK1/pSdttt78WrFDZ/Xa97nCvVn14I667zz9y3KeCLh3rP7wxxaZa75qTVRrtQy82qFAePBEy24c33PokWNEcdOmof7Upej/KrWbJXetdEAqEAAQgAAEIZAh4R49x+k47kUqdf1pRmEgFh5lei21Deqk7OAJjaWPnQv5qfSfdkUqgJDJ522yaFDaVIcGbmEzxc6PgzYR1ez21zKDvbLy0nOltV/m65p+WqH5mdt3nLlvNSVBsF3UnbnHGKpuqY7vtPVsti6MdJGDsoaiPsHZXcfLHdQh2UrWR3CqMeEnlZ0OdkT44991T02eeMhZrY9pn+ruypl8L+f13cS1PsVwkhAAE+iXQeK+3G/9VhOtStu3zE/2nrFjMx4T6HdtWdPPy5cbXtv7qd9GoLF9GrU+d0jeStyJM/ICgS5xL6VmCLqWkFpzOBl3+/j+suds/tuZuP1H2KV3pcscdd7gnPvGJ7iEPe5j71lNOcd/9mO9y3/d93+ke+a/+V/e4H/5h97nPfa43rUPApLaqZbR6xKxgWd+fDFz4MiS4sb2d/MSE9nnXZqx/EnQZBVZMZGV7+3AlmNQc/KhKV1+9U5J/vFqlGoBqytdZ/6rYHEEAAhCAAAR2JQHv6JEJ2smTyU8rODpZKnQe1R1yRY5GK1CiPq/bvtqqltEvBM3Kl6Sc1UmhrIzRP1k9E1YnNE/6xqttqpPH1npOKu/MS5Uw267ydc1vRMnuzqL7omQL9jZp59LgyZTzpdmepiFVg1H79s1SxnSpnNkJAqbfSfZNQa6q3TW3u09fUHaopete+rul/r2jgZWltWFzv45WS2a+N9v8En5n2qVru5IfAkMlYL9Tx2NI1VTGFG3Gf5ovbDuWPRnzjgIrYVjqTp48XvmhUXqMab5jJuNjla27bs45HZMnV01W648ubvdlbI5W7tjvieP11eszfJcRdNEWn21L0GU2bnPPpUGX9/3emnvm/zB+ZJgEU0o/1/zWeOXLeaevudc8cc0d2LPmXvyYNXfzO99Zkf3YsWPu+3/yJ90lr3iF+9BfvG30TpcDb/kR99f/7ZZKuq4HI6d/JqBigw+R13qMqtfAQVOAISZr5/oP7888tsyuIsmv1qnKVl3lIitncrpty6PN/GO4JOiy7o9z+aTOzvpXBecIAhCAAAQgsCsJqKMnPTlriyVMpsrKtJPPsbO6LJ/Kla5vpFtmMmYd+FH/uJ30mYmt1lx5zEy0AHkSzUEzORf9Nv1xOz211q68tJzxtqt8XfNXpWk6aqf7Tsl28GDpozUm+non7mZ4hF3CnpKE1FY31b6ane/Jsriw4wS0X25+1Nf0PZE3HZM+n3BnGPh7YZYVjwsS2cjYJ0Lf5pnvrAVpSDUQ2PUEwvgw9V06e1/auezjRzKP/A1j4uT3h44XUj/OMH3cvlk6OV9+fKWL7+v2ZR6n6stI8TePFc6Vk7Bkgi4JMIWnCboUglp0Mg263PaRNffBQ+0/n/lEWdBF9HrTn/2Z+7Xf+A33vOed6575zO91T3/6I9055/yo27t3r3vggQd6Uf3w/vQKlnEFIQARDyCEwEb8el7M7vXnyw9Bo9TjzabzhyDSfv9Ok7RuQf9RcGb0KLNwLp1vQrcz/2n5OQMBCEAAAhDYXQTC5Gy2AECElp+sxSdb9Rw6+do8csS/D6OVLJn6jh850vB4hTBpnq4zsMlNOsPkOaavKUMemzZ63EM4N11nnc70cWdelSKDLKPHlLWWr2v+ijCNB+10X6xsFTvwNlnoOPbpN93BycvMk86SKKWg6+ZBDfKlHRXRIji5XAS8wynjlBKJve0cdAcPFqyw8ukbyt0RGsGO9y1z4GFODLV/W2rdd8QuqBQCiydQcj+WpIlJXpKvJE2sbDkXxiOxcYDpZzMBlVBGbGybqnly3n9/TecN5TaMj3wZMR0m9Zi+uO14mqBLQxs2XCbo0gBopy5r0MW58K6WWfZzK10+9alPudNPP909+tGPdg972MOi73Xp750uTSRDAGEtutQlXG8KMDTVFL8eyo/XH8/lz/p3vhSudNH0o9U/TQEnqUXkWx+/N8Y/3izI3J1JKGsm/T0IdiAAAQhAAAJDJRAmX20nLCkifqKYmcz5vDqpGjnYcgEQn2Nqp1V9U7mD/lOBFTOZy6qSTSflb46DLX6lTKizNfMeeFURdJWva/6qNNmj1rovUDYX2nRsR+a4xHnsbUicCzPcB8pGHuVRKStLlItLTSDYwVTfZOT2DqzNI+74EX1k4rSjS7P49MnHvmjKxW+DbBkn2+LFmq7R32P9Bq78d1lJnzEtFWcgAIHeCJjv8MwAMPRZ6T53WqR5lj2pzY4J6gKU9l+l6erly3Gqfn++IeBSKSP3fRC+J9uOpwm6xBqu/BxBl3JWC02pQZdP/99r7q9e0u7z7p9dc6/5t80rXT796U+PAi72hfAPetCD3Lc85jHunz360e5v/uZvFqhzcPrHAwghMBGNyXSWtKn+fAV+pUvmEWqhhLou4Tiue8hZ3esmc19lTeu+7Q5vhEefjexrffwunWqd4UhX/axF+OWuhRJye9tu/B4c8+4geZTb+oY7PApgpTn6uiuPdau+T8feP/OxzZxuXIMABCAAgcURCBOWzLyyhThaXm6SpMVpWnVchePyyZPmKalP67XbMPmdqtNPDpsm0ypDwSRyVHWmTiva1H6oZ9xW4XhK9qm8bU7MKp/WUZ5f390gK4Dyf0HXbrqXy5aXp3Y15pzw9lNgmz7/OK13vhY5xms61cqqScrhChHwdpB0wtfavtHmQvrYaopcfd656GU56eT+De812Of2bVbfe9AKtbfbfD9aJKO5b04ePxge2Td6AbMEwY8483quVmKOEhtZG7uuWuk5+XPXbDHjd1RpgG3ySM7Ng6P3Hth07EMAArMTKLkfS9LEJCjJV5ImVracm+6vTUr/PdH32LahDtNv5n5I4EvxcmbGUKbMtn0xQRdPeqYdgi4zYZt/Jg26uPeuuU/9xpo78e/W3InLyj7y3pfSd7rcdNNN7pFPfar7iZ/8SXfo7QdG73S59Oofdu/7yF/MX8lKDSHwEHdcN12vFDbDQZfyQ96SoIl35HtF2+UPyqWDBSFN6V6QwYtVmLUSdNkO5dhghO6n+HgmvQddDruN9XSQROTaOJzm6OUqCbq0BVfIl2QQgAAEILAsBOrO7G5yZSd6taL9hNLPlIIspUGENvXVqp8chjq9GJMr5WUbR2a9kGilIX2pnlJMH7yi4kydnE2+UExhfjNZbnphdn+6F8oWlCna8/IZZ69zwbYaHQyexcS54I81IJkRw6et5804KjLFcWl5CPg+qPG5+9rWwebifUv+urdjH1gJLLwscs2sxpLHEtY/8bpDWdN74b6MBYNs+iIZR/ehKTMio8h8cNbIi7/nCu5PK7ztxyOMc7qNi2nWqYlfTRwOIQCBFAHv9E/c56YfaN3nzbNsM/aIyVXpy1O6j86b/qZobGsK8/ppYCd89xT3Ub4M/X4z5U/ka+4z63nCMUGXwGKWPYIus1BbQB4bdHEH1pz7+njlyoc/vOauuGL6s70dHkPWJugiqvzegQPuNQcOuFe+8nfcxRf/kNu373Husste5q644gr3ta99bQHaOucd92upd6KknfmyYmH/eMnCzLI21x8penvbHTYvt18vcbrrY8XW7GPIgm6poESk9skjx8YBhXb5pkubSf9JMT7v+sY4wDFaQeKfgTZaZbLugxbx9vXBjV6DLoHr2tq629h/2AWp3GT1SzUg05ajl7vSntN8OQMBCEAAAkMgYCZCNcfUZutfzoayGudnfjKlEzJhGfLHJorTtEP6xvqmM4/O+MlnxKnpJ3MFhfu0EUfadNVhIlumZ+pRDUH/4nKmhYmcmUG+Sinl+YtWuvRiKypguWyao3mbbgdvF5VgTKRE77wJzgWft8GmfDq100hZkRo5tQoEfFsmVn9E7g1vDzG78emDnVkMuby+r9w86A5uyqoWeZSdf2aik9UXYdVLvHxbl933ZTfdJw1BC1vO+P0245U3QUrXSU4vs2kXve38tYadHOPcNWcfYbivrtdJd/yIvstpn2sM8jbIyGUIQGBMIPQp1VV8lf6ubScwgdt72Ser/UBqBbHvZwrk9mlj3yc5I/HfNTLGD+Ou0fdGLp+95suY/j4ZBf7le2g0b7HzCFtAfp+gS55P01WCLk2Eduh6KugiARddNWC3hw61D7p89rOfdXv37nVPfepT3SMe8Qj30Ic+dPReF1vuQt7psr3fqVM+6fQ2aax8lX3/uKiWjWbKTtYvRZp0tt7wmKqmekMQoBqfCeez9U8Vn16hMZU0d8Lo1a7+caE+6CKBlUjQZJTK1BF7Z4wPXkTy567l1dLHicUDPRPp3X6zEqaN/kHvXPk5CbkGAQhAAAIrRcA4j+q/VvbHI+dagVZ+gtQ0AQpO6uqcL5wvCiIU15eQ3egeq89PNqtCRgvzaYsmpmECGqt3uoLApSpKOF9WznTJ8TNt5auX0jW/LS/o2I/ufco2kdPb4bRjIDzXPPFLWVXV26IpI3ZO0+s2liZ2TtOzXTECwV5jjnTf75ibIzjypvvh3DUB48uL9GMhrwRcjjgbyPBQve21cPybPEYNX2R9p1jGSCA9lBX6laQuIfH0npHZf0/WfrQwPm/u50kpOflz1wJ/CXZNizQ6k+uLElk4DQEI5AmctAHN2n0ugY3U7ZgvdXy1U9mJfkh+MJXsI2w/X9Dh5vqkrH6+LzroxgFwCZBMfyeVlaHBleltF/4EXbL0Gy8SdGlEtDMJUkGXf/qnNXf77dOf//7f2wddtre33WmnnVYJ4oze6XLaae7bTjvNffCDH3Tf/OY35wvAOuMjDndbucg7/ozPjvYP73cb6+pcl4CUXUFicyf2W9SfCrqMAjC11R3TtYUAyXTQYQeDLm30n1ZqdCYEH+RRXYlEzugfaedcYCV3LVUhNZq4AAAgAElEQVSbcy2YGgbFQZdZ8qSF5QoEIAABCKwIgZMnT7rxZyzwaP/4EXdw0z4zvmmyFJyD+QBASDftRAyOsHwZImcopzltpCHsZDXqQAzlT8s5XV67iWkou1n2kHZajja8pmVOnwl1NssXK6Vrfi0zlNOf7qHM2XRT2cI23/ahjaZ1CGU4b4/WSRtkTeX1jlhrw9GyTF3srhQB38ZTDqtgWxXfmW//eqCv2Z5ythzkqJdrcZo6rE3aJJV9k76iRCVR5aBUxqb7O+hj77lKVekDw3gxQZdEW09JGHg26T+VlRMQgMA0AXmUol9RMe30l5UbR3IRjukSw5muZef6odpKRFOpO6L6FPS5uf42lBnZ80EXw6zoO8GUFSujFvQa9b8NQSZTYmWXoEsFR+sDgi6tkS0mgw26PP9Ra2791DW3/rCyT+njxSSg8prXvMb9sx/4AXf64x/v/uS6K9xf/uX/7l78iie5t77//XMPuGwf3vArXJIrJApxW8d/qeO8c/0SBBoFfcLqo1Td+cBBiwBBhUcIZKTqrSSvHXTWf1JeYJ8PePl0iwi6+Me4laxCacs/pJ8OoNUgcwgBCEAAAruGQHBMJR5voyT85C/vwMpP4IJjqdFhVFifime3oxcr68QtOQkMzquUw9uWmdfLppT9UHaTnvlyW/Cqi5A9LpcvXkzX/ONS56N7P7J5vb0dpu+PcA9l7g1fTi2NdzrUzo8ECO1f8Z2kyvJCs7NSBLwN1IId/nw9IJ6wcW8XtXIMjNw9F+y4Xp8poOkFztWk4WXPUwGlWkJz2IeMo+IKeJhqq7uVvPqjhfi2mjG/miipW7Kt66Wb8iudwnQ6zkAAAg0EzH0uK+IqsZWTJ92Rg+GHSa1vt3mULT+gGv1gKgQ6pseY4fuh/7Gt4Wn7rJquxSuDfBmbo8BW+IGY6HncHamtQGrbBgRdTHvNsEvQZQZoi8iiQZcrfnXNyX7bz5uvGq98Oe/0NfeaJ665f/f4U9z1V13lRf/EZz7jzjj//Mrn9Oed70479/nu4T9+rnvYs891D3r62W7taXvdp++4w+frZ2fbHd4Iq1PkXSj2XRuz1RECEM0BnP7r9wGF0YvZqxqEa6mgRHDitwueBJ3b5uuTv9cvEkyxJHLpckGp3DVbvt33dRWtfGrH0ctTVLaVin0IQAACEBg2ATNBSwYoyhw9zU674ESenihWKXvnVKtZ1kmn7xCRX8c1PZagTR1t0pYGXfrkVaXXdBTavKkd4iV1ze8KnLHltlKVsbtstrzQRrGgyCSlcTgkefo09XLS8vq66/dlsiwrOfurQyBu68n2TwU+rAMr4fXy/VjdplJlRiDm5Kok9/Kkg0CV9JODIhmLgjhxrrE6p875e6yd7FJOTv7UNc9UfyxQsm313TilIScgsMsJhP4hF5wI92b9uzuHb55lj+sNck33Ub6fKegj2qStaOz790mQ3h+3ePSkz5NjG8ZIbR9fRtCl0mKtDwi6tEa2mAwadHEuPDZsln0JuvzKo9cqAZfXvvWt7revuWZKkffffr+7dOs+d967ttyeK/6zO+VX/9h918Yh94Tzz59KO/uJw+OXrY9erL7u9h/uHm5RWcoc7fOqPzjuK6sf/IqL3KO3Fhl06V9/z30Zgy4NMo1tJ7RdU/DK67pWsoJGLZMtBCAAAQjsFgJh8pb6hbNOIDMTIz95mp4ABo5aTnrVwDitpsvUFwqd7NlHRIx/NTeVpHbCTzYjDshqUjPpK5jEFgVdeuVVlbb5KOiTDBJkC+mYf666d5StoncoK/+IofCr0+T7I7wTd9qm4/ef3gOReyVTVkV8DlaGwHRfFGwveo/6eyjY03QZ0+rn0ng7bOgPy9IF+805NKclzActfN0EXVxbrjHWnIPAbiUQ+pLQh8ZZhL4s2hdHMs2z7FBd+I6o9wW5fj7kl710GdV0kSP/HRTmDb5e+dHTkUTk3xbly2hoAz/myc0vbMHjfYIu00zanCHo0obWAtM+/eFr7uJzu3+e+m1r7v1vfauX/N9fe627/j3vcV//xjf8Odn5uy87d8OtX3S/+6FPuqe+ccvtefnN7l9uvME9aeNAf0EX8x6M5tUoFfHKDnyAI7GiZM71+xUQ3tEfnPmj976MAk3hUWT5cyVO/VB+U7BgBHBO+vtAhNc73ly5dNPsQhm5ayFVdc/XVbQapZCj4VfEuyoSRxCAAAQgsBsI+IlPmDxZtf0EMumMMxO3kl/oVtJMT7aa67PSjX6i7Ta1zKSMtTz2l92NDry2k+7AIz7xDNeLnfmqX/bl0dM6xs+E+uPyxXOFs13yh7zz0T2UP5tuQcvwHhYTVPHtkD4Xjct5p8G0vTsXsa/cPZkty8jP7uoQ8O09sY/GNg42M7a3Mrv3TrFIP1na75ak8/U09q3TTeTz5mQsKrfOaLqu5BnPv52TT8rLyZ+6VsI0KSsXIACB1gT8vdjYl4S+Nfmjilrt8yzbVuXrqfWVvj9p1C30ka3HS/47y84bDKt9BX2nLyM2Lqpo6g5Oxl5t5CToYhm23yfo0p7ZQnLcefvtrq+PvLtF/mSFy+/9P+9xf/WPX3Mf/ydX+Ry7x7k/vfWL7tW3brnnvGPL7fmjLbfnpQfdqb0FXcxqjl4eJzbdDHlH+/zrnw4OBGd+PsASC8T0HXSZn/6e+xIFXVxTAK5iPobN/tTKq5CmspKpUg4HEIAABCCw2wnkJ2hhEhV1Jo/ghTTdHemhrHR9tsXMpPHgcVfw27qQuXTC5x1wTRNDLTroEJ8ghuvdeWmdbbah/rh8TWV1yR/yzkf3UP5sugXdvUNDHBfyLPXs54h3CtR/dToqscGG/D04cp406NBQVtCAvZUh4Nt04qjyfZN1aFW18fYpHaXPn++jfJ6ak05KrtpgtS571JjOy17gdLMFT/aLZGx0Jo6iH27cx+SZREQwPNvrkJM/ec0zS7d3VE5OQgACMxHw92JjXxK+j1cl6OJ8f9LQ9xV+b0QB+zrqfVYYk+/bt+my43hfRoOcsR+mRIWqniToUuXR9oigS1tiO5he3sNy6plnzvz5yd95lbv+I593rz/2jVGA5a3Hv+ze/RnnfvuYcy8+5tyvbP21++WtrfHjxQ5suT37bnUP3ri2l5UuPiCxcXhOBE2AI+L8X2j9Vsftbbfd+AkO/fX9h336ZlBB56aVF/PUfymDLm1WpfgAzZpLcfT8ilbONLccKSAAAQhAYIgEGiaUflJUn1jVWGQd0uqwDpOxzSPHvRO7UlJpfZNMfuKcndlVajAHVp50uKbRyWhKHO8GpknHf1+8puouOVEgX7aYjvnnqntH2bzewTaiQRSfLux4W4w5cZqcG/76PnfwyJHJyq2EI8KnTVwPIrG3MgSC3Yq9eVvK9Gu+XxJ7K+w3fblzC7q0v2/qTVQkY8GvqHPl1OucOvb32IKCLqa+5HfGlJCcgAAEZiUQ+s+m79H2fdo8yw76Vr8zwnnZCzLn+hMvZ+T7oFpe5Cj3nWP6Mwm8JJ805svIpBmpc3ASQG/XHxN0ibRbi1MEXVrA2umk8kL7J+x7hfvBP/oLt0eCIlePt895x9+5ja2vu2u2nDuw5dy1W99w1916v3vLR7/gPnzXN9zWPc596B++4V5/69+6X9/6mHvV1gPuskOfGQVT5H0tD3/a09zaM3/crT373PHnaWe5f/Gc5/jr3fXWoELJ6o3ZavOO/8iL7J3rWP/2/sZ3z4T6Z9FR5Us7/eNUSoMuWv4sssVrtme97pFgV2k6H9SIlJG7Zsuv7gc2axIoSS1g2VY249VGsaCL14/3uFQRcwQBCEAAAhUCftKVcGKp4yo3casUmD1ongi2q0/La5iwZWQK+ifKMJPHjP+zVkOYDHfjpvoVPh+7JkX6sKt8XfOnJQtXZtW9J9m8M6DFJD+Xx9tRws7sY4n0EWYpgysoK3Bkb1UI+L5oc9M/LjFlAiOdjB1sbk4ed5fNkH/0Vaj/SHbFYC6d9t9tX3hs28iXEXEE+rrlHolc9+WYe3GmPtizbXH/TyrPyV90LeeklDpOHncHjxz3qrIDAQjMQMDc47m+xN+ziTFytOauZZ884o4cT/8QSOoMfWF8TNF0PayObN/HjXT2fWziB1n+unw3NaWJ6zBmG8aCyXKijeAcQZcEmMLTBF0KQS1Lsj8/dsz98G9e4X7wdz/o9vzytW7P5e8dPQ5sY+sLPujy5o9+eSro8p5P3ueuuPVvnaR7+lU3uZdf84depb0XX+yedd2H3I+945j7xXe81u35zV9077z5Zn+9845fSSDO75KVH9uu7iPf3r/h1jf2j/MbgbbFab6+7vzju+wqE03XtX5dNbG+MQq+BNlEl2r9Mae9ipHeBsd/u/whsJDN11V/59zhjTHj9QhfH5SIBEyszrl0ucBK/lparvCIMQmorLuNw9autt324Q23Lu/ZWd9wG+uJoIu2/VrbgJjVnH0IQAACEBgCgZNHDrrNg0fGj0cyCp0Ux83mpv/1WPTX/H7imJsQmUIbd8PkKeoIa1ufn9SVPP5pstpmSsYg0+gXeWaie/K4rjhocPBNldmT47/w14pT1Tee6Cpfef7jB8c2ttngDJ4WObRL1FamM0zOlMuWLMIGQHKO3akCgsxTTpwS2/ZpxEmRued8ukyaKdk4sfQEfLvq+4Ka2jfYuj6qr+k28w7EiF17J13kmmWXTOf7Y1mtpasby7a2/CIZNTC5ebDmnDzpjh8x32sNuth6K/umLZqYVvI19B053awTdPRYntFqUFP6yZNO+tPR+8vaCmWKYRcCEBgT8PfjKIg77kvCY0RljKx98T43PUYO/W9sjNKpbO1/Jv1bCL9If1odu8fqnmgXHnkq44lexrbGcnx/nwioVAJDiTG0L2MsX2A/1vOIzF+0r9/X/sdHBF1Me82wS9BlBmg7neUjt93mHvv8fe47nvk89x1nP9898gUvdN/zwpe673/hxe4HXnixe+IFL3U/+MKL3JMueKl72osvdk9/ycWj/ce/8JdH6a5793vc17/xDa+GBF0+9Im/cx/4wo1ua+sZbt/le+YUdIm9uyR+rh5E8A77zMvoJSAQAiJePYkYhKBMJr8P3NQd7MbxbtPU9+syGwkadhcVdImzrushxxVdKvpPr5bxbbPooEuDXALdB1ZS7b6+4cRq9keDLqFdYoymz02zaWh4LkMAAhCAwAoR8A4yM3FRB51uxSEeJnVBOZ+3NwdPcErHJoqt6/MTNjMxzugp+sbqrTq7ImW1dtzlJ+OBcNNenldT7vT1rvIV5lfHwahNmhzIdWln1b1Qtnp19tjIHbUXm7a27224HjTxZeY4BNmngja2nqKybAb2V4NAsPlR31zQ71Qce3Wbiyjt00fK9rYbuWaLiqeryd7QD+t3z3hbvSeKZJRfTvv7INJnS/2baWeg1Se6b8pu+/WXkz93bSSHqbfKqKpj234pqiMnIbDrCYwDmbl7Ta7JD5emxsj+Xq32XwFpH2VX7/u6nI39gJcxUU5DXx90iez58Xe+n/V9nvTJ9c7Ul5GQz3+PbI4C+REpsqcIumTxNF4k6NKIaDkT/P3Jk+72O++c6fPVr33NK/Xat77VfdtTn+r+l+c8xz3mvLPcY87Z477jR/a4084+20kdvfx1DXqIENuH3f6Ndbc+cY57h/f6+mQFTEbSOde/MXoPS6b+xkvBuV8JdjTmSwULahl70H8lV7ooBrUdG3hZX3ejdhuliXP0wSSbL7tP0EWRs4UABCAwSAInj7sj8utY+4u9kUNqc7ICJqV1cKLV50mpHM3nQ5nTk8Vwrbi+4glbmNBN16tSm18R60RvU14CenJ6sq1ZktvgPE/Xl8xsLgQm3coxRY52u8pXnn8VV7p4p3KBE7tO1gbwKm3mnR8pB82kpIlNZ++B0rKmhOPEshOwDqqK/aQEt31ggQPNlx9J6+0+cs1WH0vnz2nf2WpbvSeKZNTH1Uy+36wzcnNq9YuVvnDf32PtH72Tkz93LUgmq3UORr+z5bFifbk6Qn3sQWCXE9BxcqXf0jFywreofW9DfymPAxyNwduULc2h+SJj93b9QJ9jW2Mnqr/2xeZSdTeMF8cBLPNoRF9GGKPbvnyfPGpTfhSWaIJqPdNHBF2mmbQ5Q9ClDa0VTPv45z/fnXrmmVHJP/GZz7jfvuYad9/997utk/e7N33obvcHH/6w+6UPf9g9480fdt9+9nPcfQ884PM+7+UvH5Vlz/mL7EBgZQnMGvRaWYURHAIQgAAEFklAJ0NNE8q+ZFp0fX3JTTkQgAAEILAQAiG4k/919UKEoRIIQGDXEtC+qCg4vmsp7aziBF268Sfo0o3fUueWx4b94dE73a9sOfd9z32uu+322yufM84/38v/8X9y7k9v/aL7/a373Hnv2nJ7/vBDbs+v3+oe/ENnjvL8H1de6Q598IPunce/5L71zKf4fOxAYOUJmMeURV5Zs/LqoQAEIAABCOwkgfDLtMVMKBdd306ypW4IQAACEJiFgDo6275QeZa6yAMBCEAgTkDHrNVVevG0nN0pAgRdupEn6NKN31LnlqCLPILsJX/l3MN/9Jnu3P/zVZVPLOiyMQm6nP7yG9wPXvOX7sFPPnOU5/EveBFBl6VubYSblcDhDX3XjbzfhT8IQAACEIBAjwT8o1UW9GviRdfXIyqKggAEIACBxRAg6LIYztQCAQjkCEwe/bqoleA5UbiWJEDQJYmm6AJBlyJMq5nIBl1OferT3JMueGnlEwu6vHISdHncy292T/z1j45Wuki+xzznpwi6rKYZIHWGwLZ530279+lkCuUSBCAAAQhAAAIQgAAEIACBJSVA0GVJGwaxILCbCEweh7uYleC7CWy/uhJ06caToEs3fkudW4Iur3vfJ92Lt5x77E/91GjVi6x80c8Hbr3V/f4b3+j+7svOHbtn/HixqydBl+e9fMv9z894gfvE3/7tKP1vXn21+6PDH3Q3/TWPF1vqRkc4T2B7/7pbX99w+w8fdtvb2/68c9tue/uw27+x7tbWJqtc1vc7m8IkZhcCEIAABCAAAQhAAAIQgMBgCBB0GUxToggEIACBuRIg6NINL0GXbvyWOvcDX/2qe+zz/o17yJnr7v4HHpiS9Zvf/KbbvO46d8pT1kcfeVfLQ89cdw/54TPdQ37ozFHARTN97etfd8/9tV8bvc/l81/6kp5mC4GlJSBBFx9U0eBKbEvAZWnbEMEgAAEIQAACEIAABCAAgX4JEHTplyelQQACEBgqAYIu3VqWoEs3fuSGAASWlsC22z68322sr7v1erBFzm3sd4crK2CWVhEEgwAEIAABCEAAAhCAAAQg0AsBgi69YKQQCEAAAoMnQNClWxMTdOnGj9wQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgcEQIOjSrSkJunTjR24IQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwGAIEHTp1pQEXbrxIzcEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYDAECLp0a0qCLt34kRsCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgMBgCBF26NSVBl278yA0BCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQGAwBgi7dmpKgSzd+5IYABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIDIYAQZduTUnQpRs/ckMAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEBkOAoEu3phx80EUMhA8MsAFsABvABrABbAAbwAawAWwAG8AGsAFsABvABrABbAAbwAawgTIb6BZ22N25Bx102d1Ni/YQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgskgBBl0XSpi4IQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQGS4Cgy2CbFsUgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhBYJAGCLoukTV0QgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgMlgBBl8E2LYpBAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCwSAIEXRZJm7ogAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhAYLAGCLivWtG95y1vc9ddf79785jePPn/yJ3/i3vQm+bzJvfGNb3QH5XPwoLvuuoPuDddd597whje4P5bPH/+xe/3r/9hd+/rXu2uvvda97tpr3YHXvc4dOPA69+brr3f/eM89K0YCcSEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACy0WAoMtytUejNBJw+f/bu7Mdx41zgeP9XHog3fUrnBNvo/Gs8m7H9lh2zm1uG9BjKEAuAgVwgCDH8pIFCY6nt3EdFMX6qlisjYuGkvwfoEcSRX5V9SuKatbXRb569Sr6c//qlZKf+1fqXv/oZdXze+fxXv3yyy9KJ3G+/ctf1O9+9z/qxx9/zJbPCggggAACCCCAAAIIIIAAAggggAACCCCAAAIIIBAWIOkSdjnapXqGi0663N3dVT+3d3eq+rm9U7e3d+rm9rb+uVM3N7f7n9tbdV09v6ker2/04426v7+vki7//ve/1bfffqu+/uZ3JF6OtuepGAIIIIAAAggggAACCCCAAAIIIIAAAggggMCxC5B0OfYe8uq3T7r8MjDpopMwNunyn//8R/3zn/9Uf/7zn6vLkzHjxUPnJQIIIIAAAggggAACCCCAAAIIIIAAAggggAACBQIkXQqQjmkVfQ8XM9Pl97//vRry88c//rGa6fKvf/1L/eMf/6hmufzpT39SL75aqR+41NgxdTt1QQABBBBAAAEEEEAAAQQQQAABBBBAAAEEEDgBAZIuJ9BJbhW/+cYmXfxLi8UuL6YvLVb9XIcvL/b3v/9d/fTTT+qHH35Q3333ndLJmBcvXqgffuAeL649zxFAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQSAmQdEnpHOF733zzTTXTJZRwuZX7uej7uth7uuSSLjrZ8v3331cJl7/97W/qr3/9q/rDH/6gvnzx4ggFqBICCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAscpQNLlOPslWquvv/56n3S5vRt0aTF9WTJzebEnT56o0M/yvfei9eANBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQaAqQdGl6HP2rlZN00ZcTMz83kVkuerme6XJzYy4tpl/fqGt9qbHrG/W9vqTY7vv6Z6e++26n/ve7nfrxx5/U8yVJl6PfIaggAggggAACCCCAAAIIIIAAAggggAACCCCAwNEIkHQ5mq4oq8hqtZKZLvuEi76UmPtjLytmEi7u/VxeVvd1sUkX/dr+XKuXL6/Vzy+v1d3dvXq+XJZVirUQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEBAkXQ5sZ3gq69W6v7VqyrRoi8Rdogfk3R59nz6pMvVfKYuLi7UbH51Yj1FdRFAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQR+bQIkXU6sx1989ZUkXewMlzt1c+vMcNGXE5PLit3uLyV2U19WzLm0mJ3home72FkuJuny9Nnz8XSu5lXy5OJippbb0rBXan5xUW83V6RdSt1YDwEEEEAAAQQOJbDbrNVqsVCXl5f2Z7FQq81O7XoWulvX8VabdoTdTm1WC7VYeOWtNwcpb3j7dmq3WTXre7lQi9VabfoA7TZqtbhUi3V+Y3F0+6b1fKEKQrX7IbakQ/10iOG+sYqMEXvkvjNV3a3VotUPzf15v38k+tiLEfqomOLSjxu1krqMvC+kC+bdQwhsVvY4LP3q7FuJZf33oUM0pEfMgrYv9HfTaq3WvQ6+PerEJggggMCvQaDj735REjmOr1TgDMDZzP3dxVtXYkS++/T3wIBzBqcSPO0hQNKlB9qUm7x48aJOutSJlkiyZX8fFzfh0ky6NBMusaTLs/Ga2ivpohQzXcbrAiIhgAACCCCAwBCBnVq7iY/QYN7COxEqKs6eSPmDgFXyIlSOLFv1SGTEyhujfbkYOjlVhFKt5La/JOmyWUVOOMVLvz/eQHu3+uVsLtVlr/1HU40ROxejW981etlLmDQSlo2+uVSLVSSZ6MfosiM5lWkm5sbbF5wiePo6BXKDTd7+5e57PXeh19m6dFmd287AWxqUdxFAAIG8QLff/TLx5DieOn9wfz8L/N4iMXK/Awe2zVSPt4cLkHQZbvhaI3ypky73r9TNze1BLi2mL1dmZro8eTp90uW14v7KC9teLdV8NlOz8qlIncQOHb9TZVgZAQQQQACBjgJ2QN+b1aJnopiZKnqAb7HuNgPFnCz525nlVcxmcsU94bu8TJ2oBRpp4nrlDW9f86RQz/wx//TsDjvTIX/St58N0jx57JR00QP3u130x9Sr72Of+g33jdd2eOzx+i5YS0mYLKq/uG/2zUZt1itn/7hUl6HRcIlh9ov8ftSui0047gff+8RoR2XJtALN/an+3MsxJ7TP7deZstZmxlvJcS1aT3Ms14lkPdPSO+ZtNhu11p8t/48FvGN/ND5vnITAKPvSSbSUSiIwrUCf3/2yNZbjeOx3+ebvZ8GZ2hKj/V2w8Wfnc/zPdsnYK5B0GVv0wPG+/PJLSbroxIu5xJie2WJ+9PLr6xt5rWe1XEcvK9ae5WKSLo+fPh2vNT1nuoxXASKlBbZqOdtfyu0wSZdDx0+3jncRQAABBBAYKlANbCdOVty/oA+NGYfLtydTzcE3Z3C44C//m9uGS9ovjZWn1OD2uSd9Nt9iK+MOmkeAdv7gu74sWf2X6iVtNMmHknVtxcqfDanfYN9ENQfHHqHvEtVTSvo+leSw+6ZOiLR2ESeGDCK3VkrWQu/k+0tRLcx+lapPJhZvH7eAs78EB6kmrb3d1zJYGDYAACAASURBVAcdq8z+XDJ7r74Ujsz0SXyXTUpD4R0FRtqXOpbK6gj8mgSG/O6XdZLjeDjpYn6vDf5eZIJLjPjvNP3OUUwBPA4RIOkyRG+Cbb/44ku5p4tJspjHKgljkit1EqZPwkWSLk9IukzQxRMVeeikyKHjT8RGsQgggAACvxqBzTo3g8UmSooH0mRg0DvZKjiB0vByElU6gBYrTyk1rH124Cc4S6HeS6S+wdk5ToxLc5kpuyxv2mXdPrutja9PfveXwbLLcvUb5puu77DYtg39+y5dv7KkS7VDS5KtVRfZd/U9Ksw9lbzPTbIatp2LlZlZEx+gSIbizeMXcPYXki6mu+xnoDqGHR+MqSiPxQK2T3PfQcUhWREBBBwB+xnr87ufEyj8VH7fb/8+Y39nztzXUGIkfqeR78RMrHAtWTpAgKTLALwpNv38iy+qmS460aIvBXaIH5N0efT4yXhNZKbLeJYHiXTopMih4x8EhaAIIIAAAgh0EHBOzAr/Al/+gs1bX060cskUOYlKnGg5LYiV56ySeJpon9QjMEPBjZhcT8df7JMZMlPGlpkfUOqyrlup0udD65crx9a/lXDIbZp9PxE72SdO4NL1nE3kqWyb20+devr7fiNGjwSnDEroS/WZy93l6iMt4MmpCRx1H9v9PH9cS8DLPt1lP7afnc6XwkxUhbemEhhpX5qq+pSLwNEL6M/YkN9NMw2U47iXdJHlBUkSWTf1XWCP/YO+dzLN4e22AEmXtslRL/n888/V/f39/vJh+rJhzmXEzIwXmd1iZr1c60uIhX6u1cuX19U9XHSixf25u7tT7z5+PJ5Fz6TL1Xx/yauL2VJtU7XZXqnlfKZm9SWyLi7qS2XN5mp5Fd/S3GfErK8fZ7ltljNVrS912qorXXZd5v69mZonyt03ZauulnM1m9XxpM4zNV9eJdvbp94hvq1pi1t37/n8Sim1Xdr2VQtC0ZRS0s8XSq9WHD8SjsUIIIAAAgicjkDXwQ9zAtQ+SZLkiD/w3MIwMTLJjmo7s267vFbY4IJE++SEzztpbMUxdSg4iay2TZSZiO3lsFprjregS/1ypaZjberZHXqGTfd/idgH6zunlsUD4LaerQFhL4Z8RoKzppyyq6c2bjXY4MXy1+b1GQh07GNzXwz9l8zmZ7FYVfdKaWlI7Mj9h8wG8tnaH58lme6UYcoyj50+3hK/2zHd1iO93W63UeuVuRRfgYtpt/9o4nj3lmn7ep9TP468tuuFEtTSPvP9acp33PczFSWgnmbXvrfUYn//Nnet2PNO+08dpFVPXQffO1IH2dZpk9mHzGOnfSnWMJYjgEBAwB6DBicw5Dju/P5c+h1jaiYxEsd0JybHBgP3eh5Jurwe59FK+W2VdHkl92sJJlp0smVAwkUnX2510uXRKSRd9gkPN2nSeh5MEtiZF631TdJBkirN7pNEgn5/e6XmZv3AY/T+KG4SI7DdxcVc6VxH+1//erdjdUuKSLsv9gmVdjzHojZ3t4k5B7unHZwlCCCAAAIIHLmATSiUnNDIoIkZGHJaJwPKgfec1fRFwdSqHnTJnfilymvGjL2yZfntK49tT1RDg2Xtku36ufa5Fn792nHHWtKlfrky47728lx64DNxUh0tIh77cH3nVEZO9nN1t56t/cOPIa8LEo6ybl2+/9qpKk/PRKC4j519LjaAHTgOy+cmdP+hitB+5sy+7G5jBsb9x07HrpKBtlB3ik0s+b2rki1+3VqvF3rWWKgAs2yfRGht5zo3Gmz7In28t+sZW1OifhRn3W9OW9v1MIOcG7XyEkLuuulEt1MXt13u88D+066ns7+429bPfQ9pY2BdU/cGrQvEcwQQGChgP/f+Z7NzYDmOO8cj87mOHDtaZUiM2O9Y+lhcJ85LY7YKYUFfAZIufeUm2u6z3/52P9Pl5uYglxbTlyv7+eeXVdLl4aNH47VSZkDM1DI+8aRVXm6mi7yvZ6jMl6oxuWS7VduruZot/fSFm7jYz0ixVapnn5hESCAjIImE2VzN9cya2VxdbZ0IV86skItQe53kRLWt22xd56Wa6+Xu4ur5sHq3wjUW2NjRRJGy64RmHolLMGFkt43Hb1SIFwgggAACCJyUgB0EiZ30uM2xAyyhgZHiWHKiFRs8M2WmyzNrpR5TdZKTuVBjvKCybtGJX5cTW9tGM+hkHtt/Ue1VqvfLLvVLF5Ly1VsOmemSii39MXrfOe2Vgc/MZ0PWC+zP8p6NIXXP7EuynmljIJZTW56eg0BRH9vPr05mrjY7ZXMI3swHs++IjbNtYP+znzkzkCYbVrMq1vUg/6ABOzn+28+EW0r8uXOsTLXL3LvKoii181wSM83kc1fFWTcTNLud2m1WarF2Z+5Z07SLXS+ddKln6Szcsr1E0Gqt9n2xUKu10/87NxET83Xq0Xn/cZNDq33Sp0piWWw9e2ZhBl+jyXZbh7RZfG/gHQQQ6Cow4udOjuP6u8LGvdTHg9JqSYz2sUrPWLRJ5Q4xS8tmvawASZcs0XGt8NlnNulSzWbxZrVUlxsLXkrMXF4sfkmx6vJiP79U/1cnXRbvHnfSxQ7y65kXNumR6zG7nU6WRNZOJIns9jrhErnsmTuTxU/cJGJHalMttuX2q3cqtnISKsmkiNOuxnrOcr+5+3JJuqT9eRcBBBBA4KQFZIAvMFgcapicIEVOgJx4rcssSTzn5EwPaqVuipwrT2JGnjj1CZUjg2utAbx2PFk3MFDZXtu2MVRuY32njibZ0nrM/mV2I2LBiw71S0Vz6p5tZypO6L1MbOmP0fvOqYzUoT0gYNeylpehgdxQjNAyG3D/LLROaJm/Ha9PW6CgjxuJETvW3Wy3HDsD+66U4R1/neXhj5Xd1wd93lN1a7bCe2XL95MW1iQzg8xpox9DF9aME8P1quUMOKZd4vX3yw7VTa8jx706qRHsp+I2Jmb8JPrINYp+z2fqoC+LNkoCz+8KXiOAQEJgxM+dHCNWamVmo4R+B0rURkkMexlI//ff9iUVUwF5b0wBki5jar6GWJ9+9ln7ni7m3i7JZItOumQSLi+vq4SLJF0evjtei3omGmQmSyu54cwWCY/yR+put0tvFk8S2ORH7DJbumi7fSsx08tieL0jIPViW99GMiWwkW2/mY1jt72Iotp1cvEDRbIIAQQQQACB4xVwB0VGTCQ0B2T29xbY6b8ONn8h7F0OJT5INfDkMNs+Gz82wOV2ngx2jWhl4otPPca3t1qr1WIh92kIDuibAJ0fbdvj/pmgWd/M9qm3s7Ft/cfvO6diUo/AwLWq/+Ld2Z+DlsEY+frL58jd34KxnPry9PQFsn1sZ3sEB9xFwO5jof1S9i8ZJLPrxz9Tdp1QTCk690QG2kKfq9TGtvxmHa1JSb3abTdl2jjN+Ob92KOtV7p8u14ovq1XwkX2j0sVTXi4yRn3+FFV37ax7/5j65lKcDltbdVBV8S+nzaLmbMcAQS6C4z4uZPjuJMwCX7WE7UMxZBZcm7cRII4EZ63hgmQdBnm99q3/uTTTyXpoi8Fdogfk3R58PDheO3rlWjQ92W/8G5aX1epZzx7o3eTMIg3Ucr2EgntpEM4hqznJ4ycWSE6IROdbeOGlfb2r7cbrv28S1LErquTLPoSbvv7taTqZrch6dLWZwkCCCCAwGkKVJdHMSc2pSdJMtiTGBCqOLzLoJhynEd9OZzsX7kWl9fug7L22TqEBsD8qIdMuvhlua/dAa7xBqds2/vELPN1W1H+vCy2rf/4fefUVfZB5+Tf2Y/dv8iMOkoM73Mjgw3e8qr4yMBoLJZTZZ6euECuj2W/icw2dJovx6zg6HrzM6Q/d/v9ORXXbhPd353yo0+lrNC+H92qcS+wxue+azwx9pIGXeNIVUtd7HqN+tdx7LE+1Qf22JDqA+l7//td2pgqY18hieHtP2X1dGYN+XWowluLVDuEmCcIIDCCwIifO/dY4hxTU8ngVgMkxkKt9WUyzR9oVX+ktVHr9cq5VKF3vG4FY8HYAiRdxhY9cLxPPvlU3d3fq5fZWS31zJZ6dsvLl9equnxY7LG+rJhOuEjSZXG8SRdJaATvHxLvBLtdncwx925JPcaSLn4yxStWygqsJ+/V5c68+8J4oZS/fuym9I3lXr39mM3XHZMibuKobkO6uI7xm5XjFQIIIIAAAkcm0EyIdJm2HxuAiTVQX9e9OVPjUul7lOxvYGwHjrzxHAnXtbz9ht3a16WMLuuO+1e89iS508msSIae2JjdBry6+YZKji/rFrtLf3RZt1E/dyAhlmxZufddaGy9fyEx/AHmeB/IoKY/WBmNFSiXRacpkOlj2Tci+6ObCJTnsYOslGWTirFV6505nywvUXcH2kqv4KXjOvV1j1vWJJ9I2Fcv/P3TPY5pbPyzbNbYP9r1kkkX/3PfCBKue2MV9zJpXizbRtvnsp/E9ilvp5AYXuzSOvgWbl/6MXiNAAJjCthj0ODPnRzH6+OuvL5UoeNbsBWyjf/7kbu2rfO4M77dMngeEiDpElI54mUff/JJQdLlWi4llk226CSMl3AxSZd3HizGk5DZEKEby8eLkdkmXuJCkhDe8nik/TuyXSrJ4r/nZRMkRqbs3Hrbq6Waz/zkzyx4fxqJ5dct9dqrd9qme1JE+kbXIWPhXm6NmS7pnuBdBBBAAIFjF3BvSrn/q7LyGpuBntSJUXk0O3gWi9envO7tk8H4zOCRm0QpO5m0J4mDT2zdATS5FFAH6+CqferX3TdYdHBh99iH6zungjLIG/grTGe15FM3hjfALIOXjX41+753vw1dSCJWsg68eToCmT62+0z/QXMXQz5HesC9w3Fw0HGtaKDNrWX9XLZr/sWzmGTrb2KGP2Pd45h4pcdTu17oe6SsfFt3LxdiKlM9xmLJ8liCJbTcK0hiZLzT61mLQftSo9W8QACBtMCInzs5Httkt/t9UvS5lhixc4G6NfK92Dz2p9vKu0MFSLoMFXzN23/0sU26HOLSYjqmSbq8fQpJl74zXbJJgnjHSgIkE6N0PbW9Usv5TM3cBIoXuzhWvNqZdzomXVozXXLJtI7xM7XlbQQQQAABBCYRcE5Y8gNr7RqmB0/a62eXyImWPVlzt+lcXs/2STmNQW+3Jua5HegqOpEc+3r1GS9Ty/LHjifePX2L6tMz9uH6zqm11C0zIOBs0nqajBHYr1J9nYzVKpkFpyiQ6WPZ7zMD3kVNl7JMAie3n3c8bsQqIft4rrxmADug1/zeEJPscdzEs587N5/QPY6JV+pi15s86TJg/xGnTIz0etai7DvVWPOIAAL9BUb83Mlx3D0e2/h6Bp17fA3WWWLkvgvsMZvjRVDyIAtJuhyE9XBBP/r443qmS3M2i57RUjSrxVxeLDC7xVxaTJIu7zwYryEjz3Sx92bJDfZ7TZB6pO4/4m3jvSxNgJSuZ8Nv1dV8Vt8f5UI1JqqMUG9bTuhZl6SIXVff00VmvHiJomYpdhtmujRleIUAAgggcCoCzsnKaqO8P7YvaIQ9icqeQBVE06vI4FkwYNfyBrSv9IRPBidzJ4YGwLZhjBNEGbwqHlQ09Yg9dqnfAN9Y8bJ8QOyD9Z1UbpyZJZl9R/q2GsDM9EsmllNznp6qQK6PZb93B7r6NNbuazoBIMfk5EC63WbQcU3aUHo8rb406nvOBGaAdY0XM+4aR9itSyiZIqs5yfjQes1jgd2q+cweM4Nfn/XK0VjSxv77TzR2s6IqvZ41G7QveWXyEgEEUgIjfu6ixxJ7jLq8XKQTLxIj911gY3K8SPXvuO+RdBnX8+DRPvzoI3V3d5++P4tJrMQeMwkXk3R565iTLs5Mi06D+H23c3q2NJlSup4TWrmX4dIJDfk3Qr0lVvBJeVJE2mVmGRXVrTx+sHosRAABBBBAYGIBGUxLjdCk6ignRf0HaRrhYwNeZqWO5Q1rX9mJXHrwyFTcfRzxxNYdqEsOiLrl556X12+Yb7oew2Ifqu+cOuf2VWfV6NNcDHn/Uq3W6/qmsZEBCFk38n60ErxxMgK5Ppb3A8mHDo2UY5pJ5BbFLT9uJKsix/jC/dipW/ia/mXHAlOnVtvtG3LT5m4De9YlOZPUbUfg+1jqlTzO27YGQpiWxBMeTh26tVFCx2PbVapn6fZYs7718IrjJQIIZAVG/NzJcTxwbuAcZ3TiZR37ay+JkVhHt0nWK5g9kzVghVIBki6lUkey3ocf2qTLoS8v9ubb74zXapmp0W1mSmoWhbx30TNmbrvtlZovncRHrSFJh+TMDqVK12si2+REI+milJ1R0rPezXL8V/FyG2s6CZZmTsjM0In1RWH8RmG8QAABBBBA4FgEzABN5oQmUV0zMD7KwMjO1Cd+o81u5Zl4/dsnA0OxE0Pn5DE1yNUkHO/E1tZvzJPN0voN9226uK+Gx7Y2kf7v1XdOHWX7SHxn1ejTghhmn5cbWsd2tIJY0XrwxmkIFPSx3V8y+6U+3q437XZLGc1jSvbz5CaAY/tou7T2EhlAy9Rf7dRmvZJESGrwzpo029Qq3Gl76DvNxsnVrRm5k52+b0rAT2IcMunizjSNfeeZpkX2n7J66omCi/3spGB77HdQyMJUgUcEEBhTwH7uQse/TiXJcTyQdNGB5H19+crcOqnjrfldMRGnU8VZuVSApEup1JGs98GHH3af6VIws8W9tJiZ6fLmW2+P12o36XK1Vdtt4scpVRIrwQTHlZrLfVBmaja/Ututs/F2q66WczXzEydO4uDiYlYlVlrbmXusuJmFOnRpMiW2nl4+my/VlTZwqqsrby8vFkheDKy3ia2dQv/EWid1ruqabZfK8jmJk1Z/pN7bl5aPH6oVyxBAAAEEEDgCATnpWanNbqd2JT9utWWAKnVC5G6gB1pW1UCfLkv+7bzBs+AgTI8bhQ9tX1VB94Ruf8N0U+/dxsw8KLnJtNlKP5af2GqvxWq97x8nxE4PeC3qQavIIJ2zesenhfUbwXez2rdh4Q8yjhBbqUP0nUPZY/93tt4/LYkh6+hBhcRnTdZLrNOqAAtOSqCkj2Wd/f6iEyvu4Va/0J+7RfC4YT/77VkZqff2io2kxKY+xu/WKpTbibrLZ39/vG1+L23UZrNW6/q4IYnI1OeiKkgfL7XH/kcfb1ombgIn9h3kHVOicfwGe32yNja6btWxfN9XC1NH/3hYff2lkhRG0x7zAiHMSumEh1fXbvtPLpkiVUjXwU/+GK+u+5ItjmcIIJAVsMf4gydd3GOaPi6HjrmZ74K1e8y+HDa7M0vDCi0Bki4tkuNe8P4HpUmXl+rnHskWk3y5vbtTbxwk6XIh9yy5kIRJc5l7uTAZqG8N8tf9tL1S81lz+1bcUJKhkcCIb+/WxewZsWSKed88xtaT5ZH26/qHyq3i9q13Y7tAQkcHb6xjTQyfrXd++2D9M/GNG48IIIAAAggcnYCc0NjBKDMoFXt0T8TkL1VTozteo2WbevDLL0cnGJx0TGNr2ba0vIHtk8Ibg1ABq9DJomwcelJ+Yittjnhpv2rgL1RM72WF9Rvq23D1EgVDY5u2N8oYo+9M4GrEIH25L2fV6FOpn9f+xga2P4IDE2bdolhmZR5PUqC0j2W9wD7vHEvc47n2sMebyP7oxPW3rTyd991je+khu4rR8bNffvxrJl7c+rnPs/EkSZKwDTTY2oa2097O5zy1ffL7ZoSky35HcGYQheq7XxbaB6SdyXo6+1psvTH2pWqH4j8EECgTsMeg0Ge7LEa9lhzHI7NYZDXn+OIf9ySGs47z/WWP2wu1il6jrFOtWbmDAEmXDljHsOr7H3wgM10OfXmx37z51nhNlpkudjC/lRypkxDugH026VLVcKu2V0s1n5lLXNVlzAKzWBotqmfC+EmbzHaSfIglguoyouttr9RSz8AJlNuardOor3nRr965mS5V9K12dPpoNldLPenF6T+3f0yNzKP0V+wSaLH4JgCPCCCAAAIIHKNA8QmNPeGxJ2JlgzutZu821V8pV39lLSdPC5nN0VpfFvQob1D7pOD6ifPX4abeC30T0F00SeRHsK87nNgaL/MX0E7Z+xkwNup4zwrrN4JvfqaL3ffsCXZ4md03fYkx+86JLYOCkQFqZ9Xo09IYtbU/JtGIWxqrsREvTkqgUx/XMwgDx47W7AWN4Hye458lvZr5/EX2+926MavkcrGKX7M/hO/UI/iZXyzUQsfsdezVE0t0/eqZPuZ4elnyHeRWdidxGnXU3wn+zCJnM1O2u409jtvjbuiSWmXJjLLvybJYHfefup1lsQuSLjre0H3JsecpAgjkBOwxKPUdkItSvS/H8XTSxZ35rY+LOukt/ySG+c7xHvVx3J+1KBvz5NACJF0OLTxy/Pfe10mXu0GzWMxsltSjnukyatJlZAfCIYAAAggggAACJyFgToZif6U6diNed3lj1594CCCAAAIIIIAAAggggMCJC5B0ObEOXL7/vtIJkVTCZIz3dBn//cabJ6ZDdRFAAAEEEEAAgWMSGPGv4Yqa9brLK6oUKyGAAAIIIIAAAggggAACvyoBki4n1t3L996rki46KXLon//6zRsnpkN1EUAAAQQQQACBIxKQS9zkLhswUp1fd3kjVZswCCCAAAIIIIAAAggggMA5CZB0ObHefL58Tz1fLtWz50v19Nlz9fTZM/Xk6TP1+OlT9fjJU/Xo8RP17uPH6t1Hj9XDR4/U4t1HavHwXfXg4UP1YPFQvfNgod7WP+88UG+980C9+fY76s233lZvvPV2dTkxfUkxPcNFJ1xIupzYzkF1EUAAAQQQQAABBBBAAAEEEEAAAQQQQAABBCYVIOkyKT+FI4AAAggggAACCCCAAAIIIIAAAggggAACCCCAwLkIkHQ5l56kHQgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDCpAEmXSfkpHAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBM5FgKTLufQk7UAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFJBUi6TMpP4QgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIHAuAiRdzqUnaQcCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAghMKkDSZVJ+CkcAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFzESDpci49STsQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEBgUgGSLpPyUzgCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgiciwBJl3PpSdqBAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACkwqQdJmUn8IRQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEDgXARIupxLT9IOBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQmFSApMuk/BSOAAIIIIAAAggggAACCCCAAAIIIIAAAggggAAC5yJA0uVcepJ2IIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwKQCJF0m5adwBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQOBcBki7n0pO0AwEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBCYVIOkyKT+FI4AAAggggAACCCCAAAIIIIAAAggggAACCCCAwLkIkHQ5l56kHQgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDCpAEmXSfkpHAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBM5FgKTLufQk7UAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFJBUi6TMpP4QgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIHAuAiRdzqUnaQcCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAghMKkDSZVJ+CkcAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFzESDpci49STsQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEBgUgGSLpPyUzgCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgiciwBJl3PpSdqBAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACkwqQdJmUn8IRQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEDgXARIupxLT9IOBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQmFSApMuk/BSOAAIIIIAAAggggAACCCCAAAIIIIAAAggggAAC5yJA0uVcepJ2IIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwKQCJF0m5adwBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQOBcBki7n0pO0AwEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBCYVIOkyKT+FI4AAAggggAACCCCAAAIIIIAAAggggAACCCCAwLkIkHQ5l56kHQgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDCpAEmXSfkpHAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBM5FgKTLufQk7UAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFJBUi6TMpP4QgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIHAuAiRdzqUnaQcCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAghMKkDSZVJ+CkcAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFzESDpci49STsQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEBgUgGSLpPyUzgCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgiciwBJl3PpSdqBAAIIIIAAAggggAACCCCAAAIIIIAAAggggAACkwqQdJmUn8IRQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEDgXARIupxLT9IOBBBAAAEEEEAAAQQQQAABBBBAIgDVugAAAehJREFUAAEEEEAAAQQQmFSApMuk/BSOAAIIIIAAAggggAACCCCAAAIIIIAAAggggAAC5yJA0uVcepJ2IIAAAggggAACCCCAAAIIIIAAAggggAACCCCAwKQCJF0m5adwBBBAAAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQOBcBki7n0pO0AwEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBCYVIOkyKT+FI4AAAggggAACCCCAAAIIIIAAAggggAACCCCAwLkIkHQ5l56kHQgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIDCpAEmXSfkpHAEEEEAAAQQQQAABBBBAAAEEEEAAAQQQQAABBM5FgKTLufQk7UAAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFJBUi6TMpP4QgggAACCCCAAAIIIIAAAggggAACCCCAAAIIIHAuAiRdzqUnaQcCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAghMKkDSZVJ+CkcAAQQQQAABBBBAAAEEEEAAAQQQQAABBBBAAIFzESDpci49STsQQAABBBBAAAEEEEAAAQQQQAABBBBAAAEEEEBgUgGSLpPyUzgCCCCAAAIIIIAAAggggAACCCCAAAIIIIAAAgici8D/A75PHsBYm1ckAAAAAElFTkSuQmCC||font-size="10pt"}} | The second folder contains the diffusion data and should have at least three files, |
| Line 48: | Line 49: |
| The second file is the DWI and should contain at least three files | {{attachment:vierDWIFolder.JPG||width="650",height="180"}} |
| Line 50: | Line 51: |
| {{data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAABjkAAAGcCAYAAACLC8IvAAAgAElEQVR4Aey9ebMcx3XoiU/g//0ZNBMzEY5xxCBmIp7jjf+YCIbt57HDi/Qs2pJgj2RSnjdvws+yKenZoq8WkwK106YkWJthkZJIgrgkSAoASREEF5C6JEACuMRCYrsAQRI7QIDAmcjqPplZ2ZlZVd1Vfavv/XVER225nPPLzNOZ53RVrRE+EIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQGAGCayZQZkRGQIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgIQQ46AQQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAjNJgCDHTDYbQkMAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIECQgz4AAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDATBIgyDGTzYbQEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIEOSgD0AAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIDCTBAhyzGSzITQEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIEOegDEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIzCQBghwz2WwIDQEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAEEO+gAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIzSYAgx0w2G0JDAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCBAkIM+AAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwEwSIMgxk82G0BCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCBDkoA9AAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAwkwQIcsxksyE0BCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACBDnoAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCMwkAYIcM9lsCA0BCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgABBDvoABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACM0mAIMdMNhtCQwACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgQJCDPgABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMBMEiDIMZPNhtAQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQgQ5KAPQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgMJMECHLMZLMhNAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAgQ56AMQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQjMJAGCHDPZbAgNAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAAQQ76AAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAjNJgCDHTDYbQkOgGwI333yzrFmzRn7jN35DLl261E0llAoBCEBgSgTuuOOOwqb96q/+qpw+fXpKtS5/NdPW2/xemN8N8/th6uYDAQhAAAIQgAAEIAABCEAAAhCYJoFokGPnzp3y9ttvT1OOmarrk5/8ZLGQN9uV+lkNOs5y23XVPgQ5ZrlXIHtIgN+ykMjqO562s78vhKet9ywGObAPfemtyAEBCEAAAhCAAAQgAAEIQGByAiNBju3bt8tnP/tZufPOO6ce6HjooYeK4IH5J2Ds+4EPfEC+/OUvL+s/zM0/Qc0/Qo180/hn6ObNm+U3f/M35Vd+5VdKTNauXSv33ntvJyymrWPYjav6Qaxv6DmTd6V/umyfpkEO49hK9VHTJqbfal9NtUsqv+aL3VHSpI+02SfGkTWl96yd379/v/z6r/96439pHz16VExQzthvHadma+za1q1bO8PQ598yo7/p33/1V39VjJ8UBHVUm3G0sLCQSmbP+7ahzr/pTZn62+Kn1/FVt14rQGLHr8fvA7H9tu8iU4Zd/V43GRcqS0xvPdcWc62rK73Dpp61IAf2ofpuG3/cdmkfwr7EMQQgAAEIQAACEIAABCAAgXEIlIIcuugzQY7lCHSoY0UX+6ltW06AcYCZPF39i96XxywujUMxxUDPG6d0F59p6JiSu24/UAb+tk2Hdkq+Ppzvqn3qBjmMQ8sEHNVB6rdBbN93kCi/Sfp4kz7SRp+YRFbVd5a3JqCqbR1ry5Ru3/rWt2y+uv0iVVaT87PyW6ZMDNtYAD/lZEyx8MdFnWCBOsLD31QtJzyfqrfqvK+H6pza1pG7qj7/uurYhbO/6bhQ+5rS3Zxvi3mXevt8dX+WghzYh3qPpNQ+FPbJtu2D9iG2EIAABCAAAQhAAAIQgAAEJiFggxw7duwoAhsa4NDtNO/o8BdO5h/Ti4uL9nvfffcV//xV50DbjpBJILad13cImcXlxz72Mdm2bVuJhTlnWHQV5KjSSf/RbhbBXXz8ttd9U6fhYb5h/9A0XcjSta5dyDxumeqEy40v35mlTjnTH+fn520fNe1hjo3j1vxjP+wnk/bxnK3QvqDbcVlovkll1XL6sG3al036MNgatmVKL3WQmT5i+ofhqB9zd4fpGyYI0van779lOjZuv/32kbtbwnHnj7XwWoybjl8dlz7zXPqwbH98VZURKzc8548hExjQsRnbmr7R5kf7YZtBjnHHhbaP2cZ013Nt6N+F3jm5/L5a10bkyuvqGvZhcKd0GLiI8db+2rV9iNXNOQhAAAIQgAAEIAABCEAAAk0J2CCHeQeHCWhocMPfTivQUcexogt348Qx6Vfax3cUGKeMeRRG6mOuGUfhtD++jNN0ZqijrM7ivC0my6VrW/I3LSfl1NByzONwfKe3uaPEMGry8ZmO28fr2IomMqXStiFrquxpn/d1qRq34R0YGlw0drcqr9FL26du+jZZzMpvmeqsjzsyrMw3dCjqmKxy0vuPqtKycr+RfnpTh//R9mvL1qrtNnLlZPJlaGtf5wxV/OrUN+m40LasM4bqyJNL06beuXr0WhP7onmWY4t9cI+DzY3FadqH5egH1AkBCEAAAhCAAAQgAAEIrDwCNshhVFvuxV8dx4rvLJmGo2DaTT4L+i2XM0PZtOV4q9O2y6VrHdm6SKNOuNDRqnXpdeOsNP/IHuej7WjKGHcM17EV48gW5mlD1rDM5Tqu25f9dKaNTCDL/DaYPlGnzfz8ofN8WrrPwm+Zz8JnFjLWvm7O55yS2leNM/+mm26qvNNP08fK1TrbsrW5unwOXey35ewP22iScTGu3WvCpy2969bp85mGfnXliqXDPvTLPsTaiHMQgAAEIAABCEAAAhCAAASaEigFOUzm5Vz81XGs+P8u6/tCumljmPTL6QyqK+9yOTOUTVuOtzr6LpeudWTrIo0GMWJBDh2foRO2qRzajjHnat2yVJau+0IbstbVqet0dfuySffbv/3bRXBDHx1UN6/RQdumjX/OT8Kk779loW7+b5s//vzzuaCROrVN3s997nNFkCPXBpo+lkbbsK3xtZzjKKdn2Aa540nHRZMxlJOj7rW29K5b37T1qytXKh32YY3Exr7yyvWftu2D1skWAhCAAAQgAAEIQAACEIDAJARGghymsOVa/NVZOFU5S9RJq84g/8WgvuPI6GkW5fqMeuNw1e8HPvCB6EtgFbTWEZZnruvCUK+ZOsw/Po2zyC8/9S94Xz/VQeuts63raPDTxeqJ6ai6qR6xrWnD2CfG2byrwZyv+1E2dRxvvn5G7tTHT+dzmERXI6d5B4Hf5oZVHX2Vu8qS6r+aTvtZqJ/RK8Z83L7tc8o5RkI5YsfajoaJ6hlLlztXx1bk8te91oasfl2xNqnqF9oXfe6mX5i21DFo+prpc7HH22l+TRvbpsatyu63f248mfTaN8dtW62zjW2ff8ti+mlbhTZOmebGu7lm2taUUTU+/PaMlVmVPyZ77pw/jqr6Wq6c5Rg/OXl8jlXjwg9WTcIgJ49/TfvSuHbDL0v3U/yN3ali0YU8Kte4W+zDr5TelaQc/bachn3QetlCAAIQgAAEIAABCEAAAhCYhEA0yGEKXI7FX5VjxSy8qpw9et1stTx16vmLNbMoN4t/vRbb+ul9yFpH7Lou5M0149jJ1ZFyimj56rDy667a9xenqfJNGX46U1/4URl8HVW3GCs9Fzpv/Ho0Tbj16wjl8I/VURY6AP00uu/XOw6HcXU1juZQv/DYvNMi5ow2sit3s831X00XY9dF31b2RpccT+VftVX5xy1P2dTpC1WyVF2fVFZTvt8fw/6gx7G2NHm1LxpbcuTIEfvYKM0XbsMAquYP0/nH4bgNmfjy59p/2o7cUM7YcR9/y2JymnOpcaZtmOrvmk+v++0Qa6+q622PL5XP9LmqvhZj4/c/v9/6+22MH8MvHD8xefScL1eMs6YzW5/5OAz8sursa5+pYzeq9Day++9i8rnrvuFm2sAcx1g0kceU0aQd6vBIpcE+jP4JxO+rsbZs2z6k2obzEIAABCAAAQhAAAIQgAAEmhBIBjlMIYuLi9EXkZuXkt9zzz1N6qmVNrdwMk4SXWSbRbtZhMU+6pA0zyQ36cxjO4wjIvyo08WUaf6dqGnMVstILdb1esypogt5U65+TV36MXUZh4IpWx1Sek23/gLTpDPlpJzimke3dZ0ufjqjT/jJ6ejnjS2AtSw/nTpRzDnzMVvz0nRlEZNBy9GttlmKm6bT8nMOF03ryxiTwb9eV1fTZubuHX3Uj6nL7Pv6pvqwcq/qv5ou1geVU5t9Ozc2lWWT7SR93NTTtjw52SeV1e9D44wDtSmmz5h+EZZhZK9jV3w5cn05xqJuXu17OkZNv4/dyWbGgilzWp8+/ZbldPb7mm+PlGvqN0nHg29XcjZC02s7hTJVXQ/TVx378puym3z8vhf2fXPNt6s+M62jrfGj5flbX7aqMeW3rWlH/1t1N5dfZ939tvT2dTT8w7FrbI/5rfH1ibFoS566+jdJh30o2+Kq8V91vQl70kIAAhCAAAQgAAEIQAACEGiLQDLIsZz/bvMXy+G+cZiZRXfqo44dk8+kTX1M0MAszmMff1EfcyJrHbFrupA39ceum/p8h0/MKWPSGPlCx4E5NnlzH1/2mKNB8/rpYjLkdPTz5upQFsbxlgrSNFksK7eUY051M9u6MvrpYhz863V0Ne2ec+KpDiZdrD7lXtV/NV2sj3XRt7Ut67D32yG3P24fN2VqvzGcct8Y45xMqWuTyKrsxh0Hmt/omePvO1Fj/aJuX44xqJtX28Xoum3bNhvEjLWRsWdG5q4/y/lblmuvmN4+Z7/vps5rGWoP/Dzab/zAh6bPXTNptB2byq/lh1vf7sX6gp6L1efLOs7viOafdPyEOpljv11MPblPHQZmTKR0zJUdu9aW3lpOrG20Xp+D4RxjoeV00Q4qxzhb7MPon4a0rWK2wzBu2z6M027kgQAEIAABCEAAAhCAAAQgEBKIBjmWY9FnBNOFkzo8UtucI0CdPbkFeQghdpxb5GkdMUei5jOyG31iH98hECvDz2Me2WB08Vnk9PfLNrKkPn463zGm6XM6+nlTdfgO1xQHU1edslQmdRLVadu65frpYhz863V0TaVRHczWpDHtGXMgKPcqHTVdVf/x69X9OvWH5ebyaLnjbpv2cVNPXVsRa9Nx5TT5msraxjhQ9qbPmP3cR9PG+k+dvpwqu27esF2MHIaZyW8+emeH2rOwn6XqH/f8cv+Wxdohp4vPOey72rah3Uj1MbWXhrVvg3N1qGzajk3l1/zh1pdF2z62DetL6RaW7+sUjhHlZuoLr4XlaNpQjjCdHufq1TT+1twxYL56l5/ZN3+2MHdyKI+wff38TfZVl0n09vlXsfPbOJa2DXma6F8nLfZhMLdcbvtQp61IAwEIQAACEIAABCAAAQhAoIrASJBjuRZ9RlDfsWIW/uoQMFvzr+Dbb7+95PD3F2aq6CTOXy3DbHVBHnM45OrI5YuVX8fJZxwpoXPVOGHMufBT1+nipwudaabMnI5+3pgzw+TXtozxC2XWumJy+GnViVLHAVVHRlO2ny5Wv3+9Stc6cpk6VQ/jfAr7sLKo6hd10/n8dD/XR1Pl5vJouZNsDee6fdzUo/3LMA9thW83TLltf5rIqnJOMg6asM/1rTp9OcWqbl7V1/Tt3HhQnWJjICVD0/N9+S0zbVL34zuVQ3vkszX7+tHzYR9LtVmuj4Rl5tpQ09bZ+nWace6P0XDfLy+lm59G99V2hdy0r4V8NJ+/9eX0Gftp/P0UYz9N3X2Vs05Qok6ZWt4keiv/Ov3A77um7vDThjxhmZMcYx8uRd+hUmcMNOkXk7QReSEAAQhAAAIQgAAEIAABCDQhUApyLOeizwhdZ+HkOxVii/eUoyMFxZRnAih33323rFu3rvhH5Qc+8IHsvyq1jpgjWhfysWu+DHXT+XmMrP7zx2POEJ9PzNGg5fnpQqeQSZPT0c+bqkP1MzLW/cbkUHnNVhffdRwudWQ0ZfrpYvX716t0jfVHX37d951BoSNNucdk0fxmq+ly/czI3lbf1vasw96Xs+m+kbmqj5sy69iKpnU3TV9HVuVWdwyYdGHbaxl1+pfft8L+WqcvpxjUzavtYvQI6/fL9uUM9fXTjbs/C79lMd3UxsX4+cx8tto/YrYgdk3bKDeW66SJyZ865+tlyq77Ufn7MH5iMtcdF7G84Tm/rFhbhumrjpXdJHajSRm+/CZf+GlSVqqvh2WOe4x9GJDTNvH7W52xXyfNuG1DPghAAAIQgAAEIAABCEAAAuMSsEGO5V70GQXqLpxyDhN1/lY5zsyC/GMf+1ilAz7mINA6/IWhNkBs0ajX/G3ddH4e3TfP7DZyGcdP6KiqcjRoGX66GKucjn5eo0fso/pN4pwKy9V2D3UO05njOjKG6WIc6pSjusb6Q0y2nANHucdk8cvSdLE6jcxt920dm6Y9zX7Xn1wfN3WrPHX6wnLKqn1jknGgZcRsUahbrm/V6ctheXpcN2+Tdsn1Ya13nO0s/ZaF+im/1DgLmVW1i5bnj5OwjFAGcxzLF0tX95za7pReqXK07/dh/MRkrOIfy5M7p/rWGeu5csy1JmWl7IaWEfudCeuvYqFl1dEtJU9Y5zjH2AdHLTbOl8M+OInYgwAEIAABCEAAAhCAAAQgMD4BG+TYsWOHfPaznx353nnnnWIWhdP4xBZcsXpzC2BdoJlt6uPnN84T4xC+7777ijsF9FnZuQW51hFb+Gu+2DVfnrrp/Dz+vrIy8puy9FPlaIili7HK6Vinjkn1Uzn9rTrKfIedf93fryOjSe+ni3Hwr/uc/bpU1zrOG5PP73+mHf2Pco/JEksX9jO/7Db7tl9ulWy+nJPsp/q4KVOv1ekLk8hQN6/KE45H7RthO9Ut16TTMur0L7+dwr5Vpy+n5Kqbt8kY1b4+CZuYvLP0WxbKr0xSba39TPt9Fe+wP9Rtx7CeUM6mxyqnGR9hv8yVpX1/kj6iZaSY+vWHvPxrsf26PGN5Y+eUex1ZY/n9c23o3aSMKhZNymraDr7eVfvYB0co5FzVhppT+6naIT3PFgIQgAAEIAABCEAAAhCAwHISsEEOI8T27dtLQY5pBjhM/XUXTv7CzCyc/Y86iXKOWH+xbf4xHvv4aUx9/kfriDleNF/sml9G3XR+Hn8/xcBfpOYYVKXL6ejnNXrEPtqWbThrtHx1lNVZWPsyTsLBL6dK1zpyGV1yeij3nMymDE0X9jPtV4Z7231b62zqqNT2a7pN9XFTjvavusyb1t00fUpWlXOSceC3aWiLQjm1vhiXOn05LE+P6+b1ORhZch/tT1V9PVdG6tqs/Jb58mvbhYEyP43aDh2DmifXv3zOmj/WP/x6tNyqdH6e3L7Wq3Ln0vrXVI6cfn762H5b4ydWdt1xEcsbO9dE1lh+/1yTspRz2N6p8349uu+PfVN3+GlDnrDMcY+xD45cH+yDk4Y9CEAAAhCAAAQgAAEIQAAC4xMoBTlMMbr4m3aAw9Rdd0Gt6WIOE3/BlsLSJE3MuaL5QwezqU8X8rFrvjx10/l5/H3faeQ7FHynS04GP7/RJ/zkdPTr8Ov2y/DLT6Xx09fZ1zJDR0wsry/jJBz8clJ6VDl3QvlMOabv5vpWrE38clLto+dz+TVNrv4YM+WvsqeCKL6ck+z79YXs1QbU6QuTyFA3b0rW1Pm65Zp02l9i9i4sR9s21n51+nJYnh43yasy5Ppg0zGjcjTZzsJvmerj95PYuNR0fjsYvnVYa/8x5X7ve99L2h6tw2zbHl++fqbsuh8/X2gD6pah+k86fmL1+e0xrnxarl9WbPxqurrbNvRuwl/7jOEcY9GGPHV1r5MO+zCgpO2ynPahTnuRBgIQgAAEIAABCEAAAhCAQBWBkSCHybBz586pPaLKF1AXyTnHpe8cizmD6jh9NE3KkeAv7HN1xPLrgjF2zdc1lW7r1q3Fi5eNwyP3UR1irLTs2DVTpu9MMQ4JU1b40fJjevj5Y3m1LC0jJYemM85y87Lpqo+2S1V5Wk4bHJrqWuVIUx1SjiBlluNq9NN0YfukzisTv/6mfduUoUyN/KYd7r33Xi06uTVpvvWtb9nrbfTxOrbCVjjBThuyaptU9dvUOPCZh+3tq6ZMUn2rbl/2y9R9P6+RJ/fx5TD7sY/qFOuDsfTjnuvzb5nRyXA1ts/0DR1TZozmPsruAx/4gM2X4mzK0TFv6jB5TD1V9kXbsKrP5uT0r6kMpu6crH4e3e/L+FF5/G2TceHni+1ru47DqKq8ce2Gr1+uLxjbZcaykd18YzbC129ceWJ6TnIO+9AP+zBJG5IXAhCAAAQgAAEIQAACEICAEogGOfTitLe+Y2Xz5s2yuLhov8ZJcvvtt1unTmohrQ6RnBPHX2x/8pOfLBxNRlezoDcOWbOYX7t2bbFYjznhtI7YQl3Ljl3zeabSKQOj32/+5m/ad4Uoi7vvvlt+/dd/3ToTYnr6DiWji2GpH+OMMPnN+ZzDK6ejKUuv++Wbeo1TWD+hHMaZp+88MWnMvuFvyojpoeXoVssz6c1+1UfTG5a+nCZfXQ4mbR1dTfDNbxejV6ir78xM9Q+tq4qHpgvL0X5ldG67bytvvw5Tj+lHRjfDW/vptm3bSuPV5NFPG31cy9B21XpjWzOux/1oPW2Ox6bjIORt+pk/po1+n/vc56xNCPuEr7v2G+Vmrpl288etn173fWen35Z6PdxqPYabkU3bQMe8OW++dcoKy56FY+03ytnvl4a3eQeUeReUcjBbk9Zcq/qYNCat5q3K57ed5jHy5T6+/HVkypVlrvkyV9UdluXnNbou5/gJZfPZVvVlE+g1bW700fGgbMxvvbZNle0PZUgdt2U3tC9oHzVzJJXfbHXOZOyS/gbGWLQlT0rfWTqvTE1/js11V5t9mKW2Q1YIQAACEIAABCAAAQhAoL8Eehnk0MV+amsWhv4/w3286lzLOQp8x0SsDuMc1gX5cgY5YrL553wnts/A7Kv8fnrdN/zMPxiNM9Sci7FSjimHqe940nLNNnRgpdL5ecx+zCkS6qRlGfnNfp3PpBxMHVpvKHOoaxjoCNPrca7dlHusTXx9NV3YPl32bb9+45hRh5bqldqa9vKd6OrgSaX3z6dYNSmjiqWvV7jfpJ6UrKbMVB/ydTX7sXGgfdjYIhM8MjzDfHps2sT0w9QnJUfYl8P8fr+KyZhLr7KF2zrlhOXOynGTfmO45PpOqLN/N6PJG9qAML05Vnth0texnyp/nbSx+sJzfr+r6mthXnPs5w/7kX8c61Ntjp9QtibjQuXw5Q33m/SDUJbwWOtrw25oICOUV4+N3Tly5IidU0y7HULd+36s40v5VW2b9ItZtA99by/kgwAEIAABCEAAAhCAAARmg8BMBTnMP8bNYs//h3yIWZ05VY5N45zw/1lvFpmmfLOYNx/fQRA6DbWOmHNJ88Wu+bLm0pm7DMxdK+ZuktChac6F/2T1y/X3jSPa/4eo0dH8k9SU7ztnYqxyOmodxvHkO7rNvjkXfpS13jmiC3q9AyDXnn5Z6uhq6nibhIPWX1dXk17r89vO7Ou/eLXM2Fa5x9rET6/pYv1Mefv1t9G3/fp13+hq9Iq17Qc/+MHSHQeax2wn7eNNnERVLH25YvuTyqplarvEWOXGtNoKDbgaeQxzHUdma8a5aYs6nyZ9Wcvz7YWRp+7HyOTbCB0HRoeV/Knqn6YPaJsZtk0/Ov5N29dpD1+emM0I69f0pr1iNj1MX3WsttvIa8oe59OX8ePL3mRc6LiNjX/9XfbLnnS/bbuh8oe/K8Z2GQ5VLNqWZ1I+y5lfx5dvw/391WYflrMtqBsCEIAABCAAAQhAAAIQWDkEehXkWDlY0QQCEIBAOwRC52A7pVIKBCAAgekRwI5NjzU1QQACEIAABCAAAQhAAAIQWI0ECHKsxlZHZwhAYGYI4BycmaZCUAhAIEEAO5YAw2kIQAACEIAABCAAAQhAAAIQaIUAQY5WMFIIBCDQZwLmkXPm8UDmcW91v6n3/kxbT5yD0yZOfTECszyGYvrMwrmVxBw7Ngs9DhkhAAEIQAACEIAABCAAAQjMLgGCHLPbdkgOAQjUJGCcheadFv5zz6v2jVOuDx+cg31oBWSY5TE0q623kphjx2a1FyI3BCAAAQhAAAIQgAAEIACB2SBAkGM22gkpIQCBVUoA5+AqbXjUhsAKIoAdW0GNiSoQgAAEIAABCEAAAhCAAAR6SIAgRw8bBZEgAAEIKAGcg0qCLQQgMKsEsGOz2nLIDQEIQAACEIAABCAAAQhAYDYIEOSYjXZCSghAYJUSwDm4ShsetSGwgghgx1ZQY6IKBCAAAQhAAAIQgAAEIACBHhIgyMT/mUoAACAASURBVNHDRkEkCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEqgkQ5KhmRAoIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR6SIAgRw8bBZEgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCoJkCQo5oRKSAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEOghAYIcPWwURIIABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQKCaAEGOakakgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAoIcECHL0sFEQCQIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgWoCBDmqGZECAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHhIgyNHDRkEkCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEqgkQ5KhmRAoIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR6SIAgRw8bBZEgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCoJkCQo5oRKSAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEOghAYIcPWwURIIABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQKCaAEGOakakgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAoIcECHL0sFEQCQIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgWoCBDmqGZECAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIACBHhIgyNHDRkEkCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEqgkQ5KhmRAoIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAR6SIAgRw8bBZEgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCoJkCQo5oRKSAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEOghgTX79u0TvjCgD9AH6AP0AfoAfYA+QB+gD9AH6AP0AfoAfYA+QB+gD9AH6AP0AfoAfWDW+gB3cvQw8oRIEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIVBMgyFHNiBQQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQj0kABBjh42CiJBAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCBQTYAgRzUjUkAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEINBDAgQ5etgoiAQBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgEA1AYIc1YxIAQEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQA8JEOToYaMgEgQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAtUE1pw5c0ba/PpVXr58WfTrn2cfAhCAAAQgAAEIQAACfSJw7NixPomDLBCAAAQgMCSAfaYrQAACs0IAezUrLYWcy0Gg6/FBkGM5WpU6IQABCEAAAhCAAAR6RaDrSXevlEUYCEAAAjNEAPs8Q42FqBBY5QSwV6u8A6B+lkDX44MgRxY/FyEAAQhAAAIQgAAEVgOBrifdq4EhOkIAAhDoggD2uQuqlAkBCHRBAHvVBVXKXCkEuh4fBDlWSk9BDwhAAAIQgAAEIACBsQl0PekeWzAyQgACEFjlBLDPq7wDoD4EZogA9mqGGgtRp06g6/FBkGPqTUqFEIAABCAAAQhAAAJ9I9D1pLtv+iIPBCAAgVkhgH2elZZCTghAAHtFH4BAmkDX44MgR5o9VyAAAQisSAJHjx6VD33oQ2K2fCAAAQhAYECg60k3nCEAAQhAYDwC2OfxuJELAhCYPgHs1fSZU+PsEOh6fBDkmJ2+gKQQgAAEJiZgAhu/8Ru/UQQ5zJZAx8RIKQACEFghBLqedK8QTKgBAQhAYOoEsM9TR06FEIDAmASwV2OCI9uqIND1+CDIsSq6EUpCAAIQkCKgYQIbX/nKVwocZkugg54BAQhAYECg60k3nCEAAQhAYDwC2OfxuJELAhCYPgHs1fSZU+PsEOh6fBDkmJ2+gKQQgAAExiagd3BogEMLItChJNhCAAKrnUDXk+7Vzhf9IQABCIxLAPs8LjnyQQAC0yaAvZo2ceqbJQJdjw+CHLPUG5AVAhCAwBgEUgEOLYpAh5JgCwEIrGYCXU+6VzNbdIcABCAwCQHs8yT0yAsBCEyTAPZqmrSpa9YIdD0+CHLMWo9AXghAAAINCFQFOLQoAh1Kgi0EILBaCXQ96V6tXNEbAhCAwKQEsM+TEiQ/BCAwLQLYq2mRpp5ZJND1+CDIMYu9ApkhAAEI1CBQN8ChRRHoUBJsIQCB1Uig60n3amSKzhCAAATaIIB9boMiZUAAAtMggL2aBmXqmFUCXY8Pghyz2jOQGwIQgEAFgd/6rd+yLxmvSGovm0CHyccHAhCAwGoj0PWke7XxRF8IQAACbRHAPrdFknIgAIGuCWCvuiZM+bNMoOvxQZBjlnsHskMAAhCAAAQgAAEItEKg60l3K0JSCAQgAIFVSAD7vAobHZUhMKMEsFcz2nCIPRUCXY+PNTfffLOcOXOmta9P5fLly6Jf/zz7EIAABCAAAQhAAAIQ6BOBrifdfdIVWSAAAQjMEgHs8yy1FrJCYHUTwF6t7vZH+zyBrsdHEeRoM9Dhq6MBDrPlAwEIQAACEIAABCAAgb4S6HrS3Ve9kQsCEIBA3wlgn/veQsgHAQgoAeyVkmALgVECXY8PG+RoK9Dhq0CQw6fBPgQgAAEIQAACEIBAXwl0Penuq97IBQEIQKDvBLDPfW8h5IMABJQA9kpJsIXAKIGux0cpyNFGoMNXoU9Bjl/7tV+T5fz6XNiHAAQgAAEIQAACEOgXga4n3f3SFmkgAAEIzA4B7PPstBWSQmC1E8BerfYegP45Al2Pj5Egx6SBDl8ZghwusOJzYR8CEIAABCAAAQhAoF8Eup5090tbpIEABCAwOwSwz7PTVkgKgdVOAHu12nsA+ucIdD0+okGOSQIdvjJ9DHL48k1jX+8emUZd1AEBCEAAAhCAAAQgMB6Brifd40lFLghAAAIQwD7TByAAgVkhgL2alZZCzuUg0PX4SAY5xg10+JAIcoh9RJbPhX0IQAACEIAABCAAgX4R6HrS3S9tkQYCEIDA7BDAPs9OWyEpBFY7AezVau8B6J8j0PX4IMiRo9/CNe7kaAEiRUAAAhCAAAQgAIGOCXQ96e5YfIqHAAQgsGIJYJ9XbNOiGARWHAHs1YprUhRqkUDX42PNmTNnxNy1Efuaa02/vu7cycGdHH5/YB8CEIAABCAAAQj0lUDXk+6+6o1cEIAABPpOAPvc9xZCPghAQAlgr5QEWwiMEuh6fBRBjlSgo2mAw6T3PwQ5CHL4/YF9CEAAAhCAAAQg0FcCXU+6+6o3ck1K4JTce9un5KabPyW3bjo1dmFHdm2TO4blmLJuunvP2GW1n7EdHduXixJXCwHs82ppafSEwOwTwF7NfhuiQXcEuh4fNsgRC3QQ5Ji8YXlc1eQMKQECEIAABCAAAQh0TaDrSXfX8lP+chHIBwB23n3XIACSCVoc2TRIUwQ3TIDDC3LUyd+95nkdu6+fGlY7Aezzau8B6A+B2SHQF3vVj/nD7LQbkk6HQNfjoxTkCAMdBDkmb+RlC3Ls2jhYIBULpbvk3hN1ddkjdwwXV3fsqpuHdBCAAAQgAAEIQGC2CbQ26S7NwYYOa3VcD7e33naX3HH3Nrl31/j//J9t2itJ+lwAwM2rb7p5o+yMqX1im9yq/WLTHjlSSlMjfyl9Vwc5Hbuqk3Ih4AhMbJ9r2OVSkNGz2ayJXTuwBwEIVBOY2F5Fqhjc7XmXnS+ovSrmk7tOBXMHU0Bf5g8RZTi1qgl0MT58oCNBDj/QQZDDRzXefj+CHJ+Sm27bFjF8MZ2cMWRCF+PDOQhAAAIQgAAEViKB1ibdjZ1pd8kdI87tlUh4peqUDwBU/ZPS3sWRmKtX5Z8O1byO05GBWlYzgYntc2O77ALUrIlXc89Ddwg0JzCxvfKrPBE8ytILwGqgw7/708/aj/mDLxH7EBBpdXxEgEaDHBroIMgRIdbwVG+CHDd/SupN0AhyNGxikkMAAhCAAAQgsAIItDbpts60u4o7NY6cOCX+d+euPXLvpo1yq//+BbNoTTi520Br/wE4wTsj2pBjZZYxSQDA5e3XOzjClnJyTvLekbBUjiFQl0Ab9tm3w3Z/l95JFbfXJh0fCEAAAk0ItGGvivq8Oz1vuvkuufXubbLT3LUxnFfu3LVN7h0+ErPfc4gm9Ei70gm0Nj4SoJJBjnECHCaP/+HF48v44nG7wN4od9yt/0RJ3CbvN5p3W1u9oEgpMwcQgAAEIAABCEBgJgm0Num2c7Aajws9saf8sulOAh04qLvtkJPwdXn77aBwchLk6LY3UXqcQGv2OSzeOhFr2OswL8cQgAAEIgTasVfud7d43GXu8fNmLrlpT0QSTkGgfwTaGR9pvQhypNm0cmX57+TYKDvt5O1TUr2A4k6OVhqeQiAAAQhAAAIQmCkCrU26mwQ5CkL+QvZT0r4T2ZXfftkz1cQdCTsJX5e3eo7ekfi1inVy0odqASNRywRas8+hXHadTJAjRMMxBCAwHoFW7JW1TV3MC8fTi1wQaINAK+MjIwhBjgycNi71IsghIvZ5v5WPrSLI0Ua7UwYEIAABCEAAArNFoLVJd+Mgh+Hk5l/tP7YKB3W3PXESvi4vQY5uW4nSZ5tAa/Y5xGAdiQQ5QjQcQwAC4xFoxV5Z21T3sfPjyUouCEybQCvjIyM0QY4MnDYu9SXIIeItorKPQnCL7PTjqk6JPtu59LKj2/IvzrSBFq3/xJ7iGYK3ei9PuvXuPcEL0k/JTvPcai/NTaaeXfWejxqT89bbNhbPyG6jfSkDAhCAAAQgAIGVQaC1SfdYQQ7/DykpZ1uz+Zedd/lzqGA/NdfrYv5k5ZnmPDAy1zRz16ZzwRSPncXjI9wcO3aXw059bKzqbYaL7SP6SNlw6/pANH9kyKVkvHfCOXMdHSPicAoCrRJozT6HUllHohtzfhI7/m6u89hnZwv8oKW1fV4ZR3aF72UaPm8/90gaT7BJx7tXFLsQgEDLBFqxV9Y21XkaS1wBa7/8+YeI2PPBnLDk2/OuTXOuGNeEsyuJQCvjIwOEIEcGThuX+hPkEBHPUMYWYQN9K4Ic5nl/nsGLGsLAiCpHO8Ez1z1ZRsvQSWTwnOqgXhMQSX+8SWaQz9aXkDNdJlcgAAEIQAACEFipBFqbdFsHdtxpluTnzY1G5mljzL/svCs1D4re3dvd/MnKM615oL6MM6P/TbeZx7omW2Rwh034gvigPPPHm3uHaUbazXcm+PNO20fC4IYeu75jnRF+/pLIrn47xw1kzN8dlJ9vmzKrdCyJwwEEOiDQmn0OZbN21425UhJ7vca/qW3aclnW9hVBjurxmv8zX3X+/HgvaccBBCDQAYG27JX9/Td/zthU70++vjo2fzB/sOfDuULsOOpzww75nNlvRqCt8ZGqlSBHikxL53sV5Cg9tqo8+XLquiBGNGKrk7fh3RBHbMZTpYhwzAjbCd5tdw3uzLhtm7ewNPnvErs4u3vbcMFo7g455e7uKL2gM6WDb3QHd32U5PTvDIkabasUOxCAAAQgAAEIrBICrU26rQM7NU9JAXVzMP9fwEXqCeZf/t28sfmZk6bb+dPyzAM/JcVdwn4g40R4l7D+ucaRGOwFPDaV7zYe/JNagxKDbYyvdSYEToaROhJz0tr5bx5nztuOjiE5jiHQNoHW7HMomNrWm1P22hsj0THsCkyNVWv7bt4odxR3doVjVYqnJLgnF9SQZazx7mRlDwIQ6I5Ae/bKmxeaAETlHzPKOqVsUjnV6JHN59195lJ5NhE75LCwV5tAe+MjXiVBjjiX1s72LchR/cxnZ0jjQY49mUc9eQYvMgl0E7z0LXfOoA4Wi3EZtrnHV0UWhK6ezL/zxnZAtNY1KAgCEIAABCAAgR4RaG3SPfYcw5tHhfMb89il5GOHvHyR+VfdIEfX8ydX/rTmgRX/vLbOzbg8Tt6Uw9F0Xo994p+Wdm5b0TYjga3h2MjldzKON+d1+SfTsUfDGFFWKIHW7HPIx9qBzBioZdPdGjoMdrpxZta3mXoq3s3kyhlvvIeqcwwBCHRDoFV7VfqT7/CPFUWwo/rOjtz8IaW5szNxW+WuY4dSDDmfJ9Dq+IhURZAjAqXNU/0LcpSfAxxOwvwgSDTAUAGnZPSCtO5a3GAWye1E00Sqt7k7OIKy0gbbTTDz8rtF6SiDoDIOIQABCEAAAhBY8QRam3TXcojFcLq5ScrhHctlzrk5VuyuBFdues7T/fzJyTideWBaV0fRyRRyczwqy/HmrrG06TmrkcO1TarN0/mdjOPNeV3+mNyOUt1H3pZycACBVgm0Zp9Dqez4zdglL/iQHCvW7oe2xLfP1Y+ccTYplMeN1/HGe6g4xxCAQFcEurBXxXt8wsdJVdzZkZ4/JDS39jBlq7BDCXKcbkCgi/HhV0+Qw6fRwX4vgxz+84FHbkGra7jisNzELDfBG73mSnP1JyeRvvxhICQzwXR1DPas0Q//LRkm5BgCEIAABCAAgRVPoLVJt52LhE6qKoRuDpRyeKdKyM2/fEd6cm5lZc7N0Qa1jzt/ysuomjkGSVlrzQNrsvcW9CXHoeVRp5y8zJZXOGctVJ4gyGFlHLPNbP7JddTWYwuBrgi0Zp9DAa0NyI+DScZxPds3FMzKE9yJZsfrmOM91JtjCECgMwKd2Ss5JaPBjsHj72LK5O1WmMPNZZJzUOxQCI3jMQh0Nz4GwhDkGKNRmmTpa5DDv2OjbMSccSst9kaUNgZ2j+zctE3uuHuj3GHes1F6MePoBMxO8KKLPK2gXv2psuz5MMqdOybIofDZQgACEIAABJadwNmzZyeSYdz8rU267SIw7zQbUdJzbqUd/M3nX3WCHNOYP9k6pjIPHJ2HjvAuTsTnnVbWkT8DxUpxgYpYu+WdDC5veT7u6knldzIOH1+Rm+vqNW/O6/LXYeXkjOnopGVvpRMY174ql3Hzt2afVRDdWrtbYa9tuiD4YMqx1+JlNBtrzib5Y82VMd54V3XZQmA1ERjX3iijcfN3Zq9UMAnfLRa/8yI1f7DFeDs2bWbegx3ygK2A3XH7t6o+bv6uxwdBDm2hjrb9DXKUH1vlAhpuYuXO+XBOyb3+C8J10TSyHV0wWaM4lcUtE0C/1diHAAQgAAEIQCBPoLVJ97hBDpsv4kQzjzUac/61KoMc2bmm3w/cvDfqUKxVTj4AYB0H0bJc3mULckTl8hmZfSenzylMxTEEuiLQmn0OBawIULjkbgyEY7VqjWuvZ5yHrp4KmzSy5s6seb2gpiufPQhAoGsCndmrUHDzvg5rE0aDrPn5hyvM2ajRMlyq8qP3brL1ZmyQSYMd8hGyLyJdjw+CHB13s14HObwFy0120uUM5WiQw10zRu3Wu7fJveZujhOn5MiJAUhnIJc5yFFrwdZx41M8BCAAAQhAAAIzQ6C1SbcNVuQXiyEYuxi1czJNMdn8q46D2s7fOpw/1avD6To6D1Ue3kI7kNfWMcLQ5S3vxetrVo5zfsYCALZdA1kHcri8KUdAKr+VMVpuWcvYkc1fi5WTM6ZjrHzOQaBNAq3Z51Co2kEO/w+C/jo3bkP8apqNtXh5towxx7svD/sQgEC3BDqzVzGx7Zxz9G6O1PyhVIy1gaP5S+n8979hh0I0HDcg0PX4IMjRoDHGSdrvIId/e60atfjEyuhuJ1dmMTQMaoRMSmmCi/Za1iim6/eLS5Zljbw/+fRzsg8BCEAAAhCAAARGCbQ26bZzkQZBDptH52NOPjvnGXP+VSfIIbb+7uZPVo+pzANrsreL+yC95RGcd83i7bm5aywAkHcyuOBB0yDHxG3Woo4eDHYh0AmB1uxzKF3KBoTpimM31m0Q1o6jtO20tq9OQNGWF9geez5dT1RkTkIAAlMn0Jm9imri7FI4B8nPP0xhLm9qDlKqEjtUwsHBeAS6Hh8EOcZrl9q5eh/kKAUvzGTKGTo7eRtqa41k5pYzmyYyibMTvC4Xt3aiOuokqN1oJIQABCAAAQhAYNURaG3SbReBgZMqRdSbu7g7a11iO7cac/5VK8jhyRAukp0kk+1NZR7oLdjr6GFlCuetTXjY9o7PPW37Ree/EwQ5msgYa7om+St0jBXPOQi0SaA1+xwKZcdBPXttbcbQHuv4ztkbm+fm2KMIywJpeTeF9sLKGbcz5VI4ggAElpNAZ/YqplTGNiTtybAcez2cA8XqMecydaWycB4CIYGuxwdBjpB4y8ezEOTwF783mReID5+vlwxyhJMuZeYZvdgi3U7wUvmLctJBFq3GbHNlOWNdMVk1AZ1Ne/xi2YcABCAAAQhAYJUSaG3SbR3CFfOQkRdHxtPbeU1q/lQx/yrN82oFSuJy2G4x5vwpN3ezZXtBinAe6tLUnQdWOBQ9bqMOSi/4cHOGh/fnoOJRrptO+WIW+/n28+pJtE0uv72Wk9FIEW0zr+5c/ho6jijNCQi0TKA1+xzKZe1AZpz7eUrptw3Xzfm81vaZNXbKjps67G9HPJAx2Xj3lWAfAhDokkAr9mrXtsJXdaRC0JxdsNcidsfZpbz9Cqu3ZebmDSZTdN4RlsbxaiTQyvjIgCPIkYHTxqXZCHKUo7L6EqFwcekMoXkfxx5xBveUHNm1sZjk3XrbXTLIP3orrc0fMbKO9eRBDj/CfNPNdw1+HPzHa504JTvvHgZzEgtKJw97EIAABCAAAQisBgKtTbqto+ouuXeXeW+Z/90jO3dti7xEPL3ItPOn4n1ozedfpu1Ki9JdQ0f8CfNuNa9lrfPOvESy/fmT1aPreaAJlNzmXoRZzFnDeeCmwby1mLOm5LHtOORh2tLicnPfm27baOsbDZZ47KP1eIGGxJzUtl0s/6Rt1pKOFgs7EOiIQGv2OZTPjqG0DS5ncWPWrnsTY1fzWdunL+q9bWPx26DXTSB65yZdQ2cCIVbWbmy0k4c9CEBgEgKt2Cvv9/nWwmbou3AHc8qdm7bZuUcxl4nYoeT8wbMlsXlLVncvbxdzxWzdXFwRBFoZHxkSBDkycNq4NDNBjtICeLAwDIMcpX8C6iTN2xaLSDtBW8Ygh2m4kvF1C10N4Oi2sVFvo1NQBgQgAAEIQAACvSPQ2qTbW5jqfCO3Lf9xJIbFOdVi5VTNv4oSE/OikbleIl1Y7zjzJ+voiznrrdot/NmlKKsc6Ajl1+Mq9vonHk0/sr3NzHdd+8S4JJ0MhZwub+p52Pn8k89529DRNh87EOiIQGv2OZTP2ry6QY7yHRfGJozY0aAOa/vMI2FsfYn1aWFTggL8w6r8w7V5zBb5xbAPAQh0R6AVe9VgLpmay8TnD26eNTKn8Xx77lrENmKHuus8q6DkVsZHhhNBjgycNi7NUpCj9OKh5ITN/NPE+/ebMYS33SV3DP8VWJrEBQDttaksbk3lQ1m9f/MVxtrIu2mPHPH/1RfIyiEEIAABCEAAAquLQGuT7qqFqXk06PCfvO7OgCrW48+/bMkngn/9GRmic6Fu5k/TnweKHDGPe/AexTpYtN8lt969TXaeGH20lGXl75zYU9x5o49zLc0li3QuUBFzLMadDFqByzt2kGMoQzE/H3fOO6GOqg1bCHRFoDX7HAponXURR16Y1h57TsLsunaQwdo+fe79cLw5J+Kn7G+CrSK7042NzlbJRQhAoDaB1uyVsRXG9zYyjzE2o9qnFZt/OHuUCLSOBDpSthE7VLtDkLBEoLXxUSrVHRDkcCw62Vu2IEcn2lAoBCAAAQhAAAIQWJkEup50r0xqaAUBCECgewL9ss8uyBELbIY0nFNx9EkHYVqOIQCB2SfQL3s1+zzRYGUR6Hp8rLoghwYdpr1dWd0SbSAAAQhAAAIQgMDKItD1pHtl0UIbCEAAAtMj0Cf77IIWqX84l7m49AQ5ymQ4gsDKJNAne7UyCaPVLBPoenwQ5Pi1X5NpBDxmuRMiOwQgAAEIQAACEFjpBLqedK90fugHAQhAoCsC/bHP1Y+YCxkQ5AiJcAyBlU2gP/ZqZXNGu9kk0PX4WDVBjtlsfqSGAAQgAAEIQAACEJgGga4n3dPQgTogAAEIrEQCvbHP9p1L9e7iMG1BkGMl9kh0gkCaQG/sVVpErkBg2Qh0PT4Icixb01IxBCAAAQhAAAIQgEBfCHQ96e6LnsgBAQhAYNYILL99PiVHdm2UW/WlvHfvqY2QIEdtVCSEwIogsPz2akVgRIkVSqDr8UGQY4V2HNSCAAQgAAEIQAACEKhPoOtJd31JSAkBCEAAAj6BZbPP9s6NT8lNGuC4bZsc8YWr2CfIUQGIyxBYYQSWzV6tMI6oszIJdD0+CHKszH6DVhCAAAQgAAEIQAACDQh0PeluIApJIQABCEDAI7Bs9rkU5LhL7ti0p1GAw6hAkMNrSHYhsAoILJu9WgVsUXH2CXQ9PghyzH4fQQMIQAACEIAABCAAgQkJdD3pnlA8skMAAhBYtQSwz6u26VEcAjNHAHs1c02GwFMk0PX4IMgxxcakKghAAAIQgAAEIACBfhLoetLdT62RCgIQgED/CWCf+99GSAgBCAwIYK/oCRBIE+h6fBDkSLPnCgQgAAEIQAACEIDAKiHQ9aR7lWBETQhAAAKtE8A+t46UAiEAgY4IYK86AkuxK4JA1+ODIMeK6CYoAQEIQAACEIAABCAwCYGuJ92TyEZeCEAAAquZAPZ5Nbc+ukNgtghgr2arvZB2ugS6Hh8EOabbntQGAQhAAAIQgAAEINBDAl1PunuoqHBlkAAAIABJREFUMiJBAAIQmAkC2OeZaCaEhAAERAR7RTeAQJpA1+ODIEeaPVcgAAEIQAACEIAABFYJga4n3asEI2pCAAIQaJ0A9rl1pBQIAQh0RAB71RFYil0RBLoeHwQ5VkQ3QQkIQAACEIAABCAAgUkIdD3pnkQ28kIAAhBYzQSwz6u59dEdArNFAHs1W+2FtNMl0PX4IMgx3fakNghAAAIQgAAEIACBHhLoetLdQ5URCQIQgMBMEMA+z0QzISQEIMDjqugDEMgS6Pr3nCBHFj8XIQABCEAAAhCAAARWA4GuJ92rgSE6QgACEOiCAPa5C6qUCQEIdEEAe9UFVcpcKQS6Hh8EOVZKT0EPCEAAAhCAAAQgAIGxCXQ96R5bMDJCAAIQWOUEsM+rvAOgPgRmiAD2aoYaC1GnTqDr8UGQY+pNSoUQgAAEIAABCEAAAn0j0PWku2/6Ig8EIACBWSGAfZ6VlkJOCEAAe0UfgECaQNfjgyBHmj1XIAABCEAAAhCAAARWCYGuJ92rBCNqQgACEGidAPa5daQUCAEIdEQAe9URWIpdEQS6Hh8EOVZEN0EJCEAAAhCAAAQgAIFJCHQ96Z5ENvJCAAIQWM0EsM+rufXRHQKzRQB7NVvthbTTJdD1+CDIMd32pDYIQAACEIAABCAAgR4S6HrS3UOVEQkCEIDATBDAPs9EMyEkBCAgItgrugEE0gS6Hh8EOdLsuQIBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgECPCRDk6HHjIBoEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAJpAgQ50my4AgEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQI8JEOToceMgGgQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAmkCBDnSbLgCAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIBAjwkQ5Ohx4yAaBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACaQIEOdJsuAIBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgECPCRDk6HHjIBoEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAJpAgQ50my4AgEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQI8JEOToceMgGgQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAmkCBDnSbLgCAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIBAjwkQ5Ohx4yAaBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACaQIEOdJsuAIBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgECPCRDk6HHjIBoEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAJpAgQ50my4AgEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQI8JEOToceMgGgQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAmkCBDnSbLgCAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIBAjwkQ5Ohx4yAaBCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACaQIEOdJsuAIBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgECPCRDk6HHjIBoEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAJpAgQ50my4AgEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQI8JEOToceOMI9r5y1fk6Omzy/I9d+nKOCKTBwIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAwFgGCHGNh62em999/Xx557lX56JcfkL/8+sOJ7/zwvNm67y1fnxf9mvNm/y+/vnnk+4mvbZaPf+0h+b+/+pD8xVc2yZ9/ZZN85M775UNfvE/u3f5LuX79ej/hIBUEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQisOAIEOVZQk7733nty/xMvyZ/d8aCsu/MR+cgdj8hHi+/D8tE7H5aP3uG+H7ljfnDuTrOdl4/Z72b56Jc3y8fu3Cwf1e8dD8lH79gkH7ljk/zpPz0oH/7SA/KhL9wvfzz3U/nDf/yJ/P7n7pPf+9yP5UePPy9Xr15dQURRBQIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABPpMgCBHn1unoWwmyHHfthfk5i89KH/y+c3yx/+4ST5ovnMPygfnzL7ZPigf+sdN8sdzD9jjD37+AfnQ3APyoeH2g5+/Xz70+fvlg5//mXxw7mfyx+b7jz+TP7r9p/KHt98nv/8P98nv/v298juf+Xf5rU9vlN/57Eb5vc/dK997+BmCHA3bjOQQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAwPgGCHOOz613OQZDjefmzf3pQ/vSL80Wg40++8JCY74e/sHm4NfsPyZ988SH58Bc3yZ98cZN8+Eub5OYvbCqOP/zFB+VPvmju1hh+i+MH5D9/YRj4mPup/NHcz+QPbv+J/F9/f6/8p//+Y/ndv/+x/P7t98l3Nj1JkKN3vQKBIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQisXAIEOVZQ25ogx0O/+KWsW/8TueUbD8rHv/qAfPxrD8gnvua2n/jq4Nhuh9f/stjeL3/5tfuL9J8otmb/fvnEV8vfj3/1ftGvuf7Jr5s7RzbKDx/+BUGOFdSfUAUCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAQN8JEOToews1kM+8eHzp1Gn57D2PyE937JXvbt0jG7btkX/dtke+t22PfH/74PuD7Xvkh08Mvj96Yo/82xO75d+e3CP/9qTZDr4bvf3iuknzxG75UfD99yf3yJMvvia//9/ulv379/Pi8QbtRVIIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCYjABBjsn49Sr3jRs35OLl9+RLP35Onj58QR567axs3jv4PrzvrDyy76xs2XdWHtt/Vh4330XzPTP8+vtn5Of2/Bl5fH/5+9j+M6Lfba+fkcWl8/Lhz/1Yjh8/3iseCAMBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIrmwBBjhXWvpffuyZfvPcFefboFXlk8aJsef2iPGq+By7KYwcuys8PXpTthy/J0sIWObawVZ44dFG2F98Lsv3QBXni0GBr9rcfHO6b7cELsi34bj14QZ48dFEOnb4if/qPP5GlpaUVRhN1IAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAoM8ECHL0uXXGkO3Se9dk7t+flWePXZFHXr9ggxwmwPH4MMix69Db8t4Dn5QLm/9Onj30TinIUQQ3/ECHBjuCAIcJeAyCHBfk4NuXCXKM0VZkgQAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAgckIEOSYjF/vcl+6ck1u/7dn5LkiyDG8k2N4F4cJcpi7Nt7adb9c+/GfytWf/LkceGWHPHHYnI/cyeEFOGJ3cphAx1OHL8qhd67IR+Z+yp0cvesNCAQBCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAYGUTIMixwtr30pWr8vff/0UR5DCPqioeV+U9quqXr78hlx78r3LtRx+Uaz/6Izm97Rvy7MHTNshhgh1bD5yXTbvPys8W3pWfvvSu/PTFd+S+XW/LvS+clh8/f1r+/bm35N+fOyWbd78rT79xUd48c1U+9sUHCHKssL60fOosyvq1a2TNmjWydv3i8olRs+bF9WsLWdesWSfzNfP0Jdn8ugHnNWvXS/9J94UackAAAhCAAAQgAAEIQAAC4xBY2HCL3HLLLXLL3BbhYdfjECQPBCAAAQikCBDkSJGZ0fMmyPGZDU/aIId5H4c+qmrboYtyfOeP5erPPiHXfvAHcu17vydXfvJxeeXV3aV3ccy/dk4+f/9x+et/PSz/77cPyF/98z75+NdflXV3vSx/dueL8idffE7+8+eflfWbDsozRy7KsXPX5C/ueIggx4z2mf6JvTxBjvl1g2DF2nXNQhUEOfrXg5AIAhCAAAQgAAEIQAACEFgeAgsb5opAxtyGhREBCHKMIOEEBCAAAQi0RIAgR0sg+1KMCXL83Xe2y/PHrpTu4jCPqtr1+lE5t/kz8u4z35MrD39arm34Hbn23d+W48/cK08fOmPv5jDv2nj4tXPy0O6zsumVM8X3wZfflQdeflfMdtMr78jmV96R7Yvn5Pmjl+XEuWvyifXzrQY5FufXy7q1+g95/bf5Wlk3v1j5j3PndB7mWxPbrpXcTQKT1C+LizK/fp2sHd6NYO5IKO5KWLtO1s+P/395X6/Gdzgszsu6tfXvjJhI/4kHw3IEOeZlne0nze7IcO3SLN/EmFoogDs5WoBIERCAAAQaEFjaMnD8mH+xzm1p/h9Wmz90HC0tycKWDTI3N/yHrPmXrKljboNsWWhej6qUrE9Elha2yIY5p8/gn7lzsmFhqea/c5dkaSGUeU7mNmyRsUReWpANczW5dsRLuUW3TeRrhW9UivjJBrLZPjHsY0W7j+zPyRjdW2Rpi8yNlOX16TntH5k+HZQRDpU4gNjZBdlgZRlTn1ixnFteAgsbBncR2Lb1+pc5NzcnG7YsRG2Y6/tj9AevX6Ztv9/nNshoeCCBzuo0hlyJIovTnszxce6xK92VkdeDIEcOOtcgAIEVRaDB/Cqrt7XzVb8NGftry/Bst/9bmPn9y8rWs4sEOXrWIJOKY4Icn7pnaxHkMHdxPKqPqjpwURZfelKu/uwW2b1/UY7teUqufecmuXrP/ymXf/pJeX7xmA1yPLZ4Xn6082359vZT8i/bTso/bz0h3/r5cfnmY8fkm1uOyDe2vCnf3PKGPPjiaXnx+GVZOv++/D9ff1SOHz8xqfgi4hzcGhwY2a7NO5Ot49Y6rZsEOSasf37d8NFFsTqHwY5185WBmlGQvhO+frDClLM4v07WaqAlF9kpKp1Q/1HBxzjjZGgczBmjNs3CnRxKgi0EIAABCHRDwF941HTGlwRx+UuO26pFiwl2bIg77UrFjxwk6pMl2RIEU0YcYHNVi7CqMkywZESg5IkiWDJcqKUdiMPsnfFKijcI5tSVrxW+aVnCK43YiYh1UPoL45H9MZ2tDZyqyT4dltGkI3lwnEPbOAPG1Mcrj92eEKgx/gf2LNLmXt+qtDOBuq4/RcrVtIFstbuuzZcpW+tosvX0HbHx4ZgvBTmMneBOjiaoSQsBCKw8Ak3nV1kC1s7n5tf+3Drye2DLSAQ5rF2P5M0K16+LBDn61R4TS3PxylX5m3/5uQ1y6KOqnjrwrpza9nU5s+0rsvPAaXnm8Hm58uOPydW7/w+5+q3/KIdffFyePHy+CHSYuzjmfnZc/r8Nh+W/fPuAfPLu/fKJr++RP//Ky/KRO1+Um7/0vHz4C8/KNx8+LC8vvScnz78vf/vt7fLGkeMTy+8CFMFdG8XdEd6dHZl3CNgyTDBhcTH5jQlr864Zs/5hkMM88mjRu2ljcXHevmeiuKujMthQls7dLTAMlNTIP7gboxxsqQoaTKx/Wewxj5YnyDGmsOLaJh98G7f8LvPZ9s6Mpy7rp2wIQAACq4mAc3INFhdNnWSii5PAmaTnC6ev9wf3paWFUjCirfqckzu4a6O4O8K7syOU0zZ2eRFm7vzQj7k7xP2Tv3qRNbibpLxYq9RzyLF1XqqEtx1Hvsn5egJkdseRzRRn5TOBs6Wl5DdTdfqSdarOFXcglctfGNytZBfht8gtMS+wLUP7RXU/GhXIBfiSDu/RTJyZBQJqR03gytx15vXhhfDutBEb5tmukWs55evls2NL+3isf8eq8XVy5jSWstk5bywVd+h5rHxug/36RVs9GzGsXz4pIQABCCwngXHnV1mZrZ1PBTm835nUHzNsGeP8/mWl69VFghy9ao7JhTl/6Yr8zT2jQY5f7l2U9+77uBzf+RN5de+e4ntm+9fk6jf+g1z92v8ulzd+RJ47dLp4N4d58bh5VNUDC2fkgYV3i++mhXfkoYV3ZPPCOzL/8tvyyMtvyzMHz8trb12Vkxevyz/+6BlZPHRkYgUKp2vG4eocymsk9eoEddxWOfRjwk5c//z6zGOwnPO+2Uuqy3dxVAVJFs2jskp3say1x1VMJtY/BrXxOcepSt7GRXeQwfVJghwd4KVICEAAAiuEQOg0bXonh1u8jDjxF7ZkHg3k8t1yS2phFEPs8oX1FQ6qjHPKD+ZEfXT+IivmkPMca1EntnmUk3k0lzoCi+2cPQ7lHdGuE17lWiaRb2K+ZVFGjiaRzRSmDspKziM11zhh2z4XmHB90wQgRvqYV4Z9fNtIogpZtI+ax2MN+9dYj9+qqIbLy0BA2zblBCrsiwvWhl3H2bdcHw30sn0y0l9tUvcbsWGDPlKrps2uoZOtpslOLbmbFDhIqzaEF483Z0cOCECgvwQmnV9lNbN2Pv67YO1qbF6kBdsy0r9f7jcu93ulBfZzS5Cjn+0ytlTvnLskn/7utsGdHMNHVW09dElO7fhB8f6Ny/92s1zc+FG5+G8fkcv/+gdy9Wv/m1z9yv9afI8994A8efiiPPLaOflC8eLxN+S/fueA/Jd/2S+3fPM1+fhXX5F161+Sj9zxgvzZl56Tbz/6hux/+6qcunhd1v90l7z6+ptjy60Z59evr3iUk3P4xx3gkznIJ69fNYlvnUM8/04QP7cL2qy3742I625yOf2LYEjxaCx3Lp1vUGPX+vt6pffry5suY3pXXJsS5JgedWqCAAQgMFsEdPExt2WLfc5/IyexdTbFFzc5Gm7Bkl7UjOTP1LewZUv0efWuDOesG9XRc1CH3kNXgDiZY/p6ZdhHcblzo3V6BdfYdXU34FUq18linPCDxyq5c1XyTca3JEjkwMkxjmziPUqrSo9I5dWnbL+rYG/TRe7msNfmZMPwkTljB/g2aDCtQp5qzUjRFwI1nDz+u2FG+7mzb6kgbKiqsykxezZIXUpj+3DNYHgdnUKh6hx7cmTMdZ2SSmn095AgRwkLBxCAwEwTmHR+VaG8tfOjvyPu96PiN8OWkZnTeHZ/9PevQsaeXCbI0ZOGaEuMt89elM9s2C4vHLsi5lFVPz9wUXYcPivv/fijcuypH8iuvYfkhb0H5MW9B2XhtX3y1qa/l6vr/xe5euevyZXv/q48+8YFefLQRfn5/vPy+N5zsnXfOdm+/7w8sf+8PPX6eXn69XOy48B52XngnCwcuySvv3OtCHJ8+5HdsrDvjbbUyJTjHOBrordyuOtVDv1MJZlLrvx4/Zms5pJ9Z0dNh7imL+5uqQrwmAqMfGul/LgsJ/PkTFxZY+lfgWdw2dUxuby1KpwoEUGOifCRGQIQgMDKJ6CLiuLuB+cga7J4sE6hcTxNWn+DOzkmqs9zhI84Ab3FU1aVbDqzkDQvoDaPS9Lu4xaXTbhq7tJ2DF6l/IX+HcqX41sWJHI0KbsWOUekc87lzAK8yOfkGHGU2r5jyhhjvPntXyorJjDnZo6Abd9cH8v3G2sfa9lUV9aIPbTwvP5cGEbvOHPXnM1eSyebuv6O7f/t/qPX8qujW31pSQkBCEBgGQkYu93h3M/a+SDIYc9XBDgMGZt2/N+/ZQRcu2qCHLVRzUbCI6fOyu0//IW8cHwQ5Nh66KKcfOEBufSDD8ruvXtl+6GLsu3QhWL7xOGLcmDnJnnvG/9Rrv7T/yxX/+l/kjcXtsuzRy7Kc0cvya5jl+Wl41fk5aUrsufkFdn71tXizo3X374qB965JgfevSYH3x0EOTY+uV+ef/XQFCBVOcBdICAaA5lYwqr68xVYh3jmkVyuhFAXd9zM+T+ZzE4es9dOWYP3hXjvWFmzRtaaF8oX7zGJ12HZrckFiOowiqfRO2bW1GobRyUmV/Gy97X++1BM4Gn9UD+X1+zZerN6ldmPBpgWJcZ0zdq1sm59+kX3tu6GOpc14AgCEIAABNIEnINr4NR3x/Wd8ZontyhJS2D/4VXboTRZfdl/+9sFVrBIGxFfZaixaCvyOqdgfa4jlQ5K2jJ8VE1tXvFyymfbky/Lt1jDpl/4W5ZJj5rI5tolG6TSopturVO1qq87mfNBDvd4rXp3c7hyi35UW56mipJ+2QhYG5TpY7bdE859W0biuq9cnbSx+my+jJxaT5O0mqfONiZXnXzeY+1GxmfFNb/4wXPt3aPDirvP5jYU71Lx07EPAQhAoJ8EgjnFJEJaO+/Nnz0bnQ6ie5XaMjK/K16ZnczzPHG62iXI0RXZZSr34PF35IsbdxRBjm0HzsrLr+2X977/R3L++x+SFw6clO0HLwy+hy7KE4cuyu69r8mFDX8oV7/0P8rVL/4Pcv6HfyavvPGWvHT8siycuCK7T16R1956T/adviqD4MbVIrBx6N1rcvjM+8XXPK7q4V1vylO/PDAFrZ2DOh7EqLo+qYiTlO/y1glSWAe0VbRZfqdpPGjgrjfZczJYsZpkl3lZV3L++4GAwf66+YS8i+vtu0WSdeudL+adJCnHvS2n/MgwyzuVL6FnOcjhZDePCxv9Dl5oXyrKkzmpl8lg5Q7eR7Po2mS0vqEMCZ3G1bkkPwcQgAAEIJAkYP+xalcKzklc1xnfPEjhizPt+kzdrk6r9lCk+rq4hWGthZt3d0Ndrj4lt+9kn6wcV+Jgz+kzeblOxpCvuxPCvHQ7s4gtiddEtkzdpTLHPLCL6yrZncwj/SMswx7XcEjbtMP6w+Mx1SJbjwhUOnmW7HtnYg76gSZuHIz0v0BV+xuQCZraNKU7Q+rXUe/fuYFgdQ5t/68xdoLyrE4RvXPXBsV447v07iVj14bfSLmBCBxCAAIQWGYCzpZNPPezv10a5PB+I+raQ1tGao5V5/dvmZHWqJ4gRw1Is5Rk96GTsv4nz8qLJ67Iay8/L+cf+Zxc3vhRuXTvJ2TpmY2ya+/B4uXi5o6OHQfekmPP3CcXN/6FXPnOf5Ir3/4dufKvfyinn/6+7Dvylrx66orsO/2evP724K6NQWDjmrxx9n15036vF4+rembfSXn0+eJv+J3icg7lsoPaVZp2+Jo7BdYPbhVwyRvuVdcfKXBxUea9l4GbR0lVfqzj279rwelWJ0ji6nCO92b5XAm6N5b+mtm7C2TNmtE7DAZ3IpQDA2V5nR6jdzIMKrFO+yLAEO8jVofA8W/zBuet+IkdW96adbJunZF/EMjwR4PRzb0MPpSrWi9Tta0nlE+DH8P+7epd9O4SWSNllgGvsMyErpyGAAQgAIEGBOxiQhckJq9blNRb8Lj0Iw7tnChLS7LgvZzbPNqp3mfM+rzCbSAj4mS3zq0a8ti0tRZvEy4kx+blKZ7dnVA+r+wcX5NsYfgeivpt3kQ21z+ss3HodJxr4x/W1qmaWoAPQdh0kTt97DVXRt2+ZNNp/4yU5TUFu7NIwNpl1z9UjSXzeLM5daT7dltTuK3tK6XAhLs+2HPjJW3v02nq1VEM+qHzf1SnUKJGx7b/TzPI4eyRCdRuWFjy3gFV/l2rCjA10pXEEIAABFon4OxZ+jegZqX2t8v8Nrlyb5nL/1aVSrdljP5WNPn9K5XZwwOCHD1slElEevbVI/KNTbvkxeNXZOfeN+WXe16VheK7RxZ275ZnXl+S7YcuFC8Yf+bQu/Lanldk32uvyOt7X5YDe1+Rw/tekcMH9sni0jlZHD6WSoMbJrBx5Ox1OXrufTl6zmyvy5Fz1+XEheuy79g5+ekv9k0ienVedeaaRxutd67cUkYvTfpf7fpYpFLO6gOv7GT9phQvnS+DexxTVVUumFGOh7jz2fpHindO9Gb5goI8vcYpxzrp14ROfr8eJ6thF9Zjy4g65ZXPWlk7vFukzG9QjwYzwrL1fPIOEF9Mb9/KlAmsDGu2L44P63Bl+EEtrxIvQBTKLYvzmeCdxzPCbFydfcnYhwAEIACBGAHnuFJ/6SCVO19rwWMXJBWLGM8Z5TufjeN5wb63IiZncK5ufUE2e+jJEdPPOu3KUGx2f8em7SLI4ck5ES9f4Oy+W5DGuGSz+hc9uScqxy/TWyxXlunV73Mr7Tftc74stvzRBbhL5lhGH0EVKyN2zhU42IuliZ0L83E8WwSsjdNgxui2eN9PlVa2b2QCALauTH/OpbHXMnUYOW26TD1V+sSuezqWxrjeTWG3o/Xm7HfumgviZn67utI3xoBzEIAABMYm4OYrlfOrqjqs3dsgGzbo71bF2iAs05ah+Ue3tX7/wnJ7dkyQo2cNMqk42186JN955OXiTo7HzYvHD16UrQcvyraDF2X7wcEjqp48fFGefvOS7Hzzkjxv3r0xfDTVKyevyKun3pP9p9+TA28P3rdx+Mw1efPsNTlydhDYOHb+uhwffs3+0fPXpTh35or8YOveScVP5/cc7KGDOMy0uLgog+/gSrE/v17WrfXfAZFyJoelDY8b1J8KchQBj+K9E4kATVGV55Qe8dCrE3/U+Z+QWoWX9UOn/4iDPJ/RXW2iv8vl7TWQ3atrRF57LRIo0Wvr5t1dDxmG4aVxHf4uQFHdLi5tIL/KviZ4FJUStNeDfHo9s3V1jvb5cXXOVMclCEAAAhDwnMaj/zRtEuRosDjKOaMKp3OdSEeD+mKt7MsQDUy48ke5jBaYc4SNpnZl11pI+rJaR91wsVeb16gU6TMN5YsV5Msc5RvLVOdcM9mWlpZk8B2UXewvbJENc/6z8xsuvFVMq+Oo09S8i2RpYYPM2X/aR+7iMOVEy3A6pvqeda76bKNlqbBsZ5JADSdP4dCvDNZ5fcrvMxZK1fVBwrydc78XqX5blGJ1io0bK1DzHdv/Rx1h5aDHaL05vdLXnL75OLhjW8veN9ecHBCAAARaINCirbJ23rPH0d+ejNixMsI5sDn46VOSAAAgAElEQVSu/P3L1NGDSwQ5etAIbYpw/1Ovycbte0eCHCbQYR5R9eQbF+XpNy7Js0cGAY4XTYBjafDujb1vmQDH4KXi5u6NN2xw4/1BIOP84K4Nc+fGiQs3ijs4TIDjyLkbcvbKdbnnkT1y40ab2gzKKl7irO83iPwbvUmNzuFb7ZDWcieu3wRdiiCLexTTiPN+WFne6dwgUKDCF1sXOEnVW0oeHEysvynPPn6rjpM+p2f6mrZtEbywQYHAsW/lCM77LwBv2Me03jWVLw4v3+VTDrK4Noo9isvWUc4UtFT80OaNyJfvb/HyOAsBCEAAAnkCaQeOyeecOJXOGetgGnUg5SUwjl7jEDaOZ7cY6rK+wvmsC6Xkosst9rIOu6FyeY4hAVd2pZ5hVnM8Dq9YOclzk8lXj2+y8ooLk8nmF24DBbckAhB+4ti+7fOu35adqe58sp1tGcG4sYv74HwhhxuXJedqqqyY7JybDQJ+PzCPQrJBO2MzF2SL95g/0/dK/SHQ0PX3SJ+yfSdThpcm1Z+zdag8vk514tmar2rryVc8NspnFeyHReXsd/Ka1aM6SGrLyDVQKBTHEIAABKZKoL35lbtjz9zltkXmKufcEUWtjZ2TLRP+/kVK780pghy9aYp2BPnhYwty/84DxeOqHj9wQeaf2Sebn3hZHn7yFXnkqVdky1O75dFf7JHHduyRn+/YI1t3virbn31Ntj+7V558bq88+fw+eeqFffKLF/bJ07v2F98du/aLfp82157fJ88uHJCj71wpgh9Hzl+XM1duyA+27pcLl6+2o0hRinmngLv7wrzLIncPRL2KPWdypTO7/fqdw3n0H/vu2qgDfqBb2sGf193p3CzI0Z7+1br5GuTltY75ksNf82gQRVnp8aB8K0cp75Bu8T6NzAvLfRG9fVtmJIjgJRvuqlyRIFsyAOPyRMT2qjDBtHmZX79e1q1bV9y5pI/tGjw2bbRfWZaVY8Grhl0IQAACEEgScA6plJPGOVNTTi0tvC0njpMp42wrnngydCA3chqZlxS6f/BX3ebeRKcmac2//LcMAzpVXJVvaluXVyp//Py48jXjG6+76uy4ssXKdWWlX9ocyzc85y/cdQEfbOc2bMk/gs2WETqenWxhH7FtHgbokmVldOBSvwn4Tp5kQMD1legj0VRD2z9Gg3q2T2Xe2eHShH1VK/DvTBqtw6aqpZNNXX/H06/Rz4L/exKOqcw1x8MFM1NBTnu+qWD1tSclBCAAgQkJuN+ScN7RuGBr54frC3t8i9T541BRn82T+c3x5tPZ37/GCkwvA0GO6bGeSk3fuP85eezlY/L8sSvy89fPy6O/PCqPvviGPP7Sm7L1l0dk+8tH5MlXjsovdh+VHXuOyrOvHZPn9x6XF/adkBf3n5CXFpdk4fUlefnAkrxy4KTsPnhS9pjvoZPy6qGTcuL8NTl58UbxNXdzHDt/o3gvx1sXb8hDzx6W429faEnPeVk3fMSSeZHzpC8M94Wq55Tuqn51xq+R0j/2rYN7NPjhZHfO7qbBiuaPq2pXf8u8ljPdMYrqaVl5Tnu9c8MrXx34rgxXbixYoOmrHofm2mOwZ3WbNMghrn1L8sX0LQmxKOu9YKD/HpjyvsdrmH9cnUvVcwABCEAAAgMCdvGQCybUDXJoutxCpC54t8hKL4TGqc9/Se/gX2FVEtnARcTxVc5bR2Y/h0s/8ULSX+C15kAbR77mfH0i9ffHkS1dunNUpgJ96bylR02F/zLMZCtdso7Z0bETl037fsSJnCmrVCcHs0PA2unR/lFSwrZ9zp6b12EMHfIlm+bGVNrmemmCQJ514IfnS3V40tbVyctSa7cmg1hZcS6DlKlrbnwS5Igx5RwEIDBrBJydn3huau28m1tZW1r37llbRju/f31tDYIcfW2ZMeWa+/4TsmP/W7Lz6GXZdvCCbHvtLdn+6kl5au8peXrfW7Jz8S157vXTsuvgafnlobfl5Tfekd1vvCOvHnlHXjv6ruw7ekYWj52R14+flQMnBt+DJ87KwaXB99SF9+XUpWGQ4+INOXr+hrxxbvCejh2vnpA9h98eU3IvmzqszSOqPKe1l2Ky3Sqnccf1jzqWnfO97JR2j7dKny/fqRAH48p3Dv94yuJsB/o3CwRUyTsaDNDyS/ppO2sfsnqNOvuN3qPtkmHkXdK6az2uKhXIGJZnZfCiHHqupJut37EwfWTtuvWy3tzNYR6RNrztKSeflt3JOLMysgMBCEBgdRDQOwmSDqrQYWWPRxcb1tmTcmo1RGoXQonyGtfnOb+a/GPf1pP5d/NAtYzjOap7iwvJzD+No1XXOtlQvjH51hJlJFFD2UbyByfsItotxIMU6UOr9+iYSGcKrmTLiPSrnLzZsoJ6OZwNAra9q/pYpK/ENIyVZ89lAiS2bzVw6Kcen2Xrq9IppkDmnCdj03hv7jcndc3+PiR+pzKScgkCEIBADwm0OL+ydt6fW7nyzdqj0k7bMqp+K2r+/vWQuBGJIEdPG2Zcsf76W4/KwtFzsuPNy7L11ZMy/+Qrsnn7gjz8xMvyyJMvy5anXpFHf7FbHnt6t/z86d2y9Zk9st08smrnq/LEs6/Jk8/ulaeeG3zNY6neunhdTl++UfpqkOP4hcFdHAfPvC8H3r0mrx59R57afWxc0Yf5nNO2ncdTjYqTc/qK54Tuqv5Rx7Jz6qeDGamAR9tBjo74a8DB3JVT+cwxT4ZEYmU4cPwrv7BsLWcY1FAZvACC3zu0zKYO/3x/8muo8W4SldHeFaI6hLoNyi3VneBaSjMizrBfaSAouM4hBCAAAQjUJ9BekMMtWioXLDXFSzmVBtmb1uctfjYsSPKJLzHZ6i6wrHOtaiGmlTgdJv633LIHOSbgqzgabdtlZx2VlYGsiJCN2715GVa+wpFaoXsb8kRE5NQyEqhrg2q/P8kbr1sG1jBvbwe62zRmnATvtyi9J6S4tkU2aFA89qNQW6eG3G3/r+E8C4q2+kUCFslrVg/fiRcUzCEEIACBmSFQMcdookfSPrrfoFtumcsHOmwZVXNrV2Ybc+omaraRliBHGxR7VMaff+kB2X/6ijz95mXZ8ebgBeMvHL0kLx2/LK+cuCyvnroi+956T14/fVUOvnNVDp+5KkfOXJOjZ6/J8XPvy9L563LywnU5ZYIbF6/LO5dvDL8ib5tgx6UbxZ0cS8VdHNfl8Nn3ZfGd92XPW9fkjbcuypYXDsnV96+PTcQ6mhOO6LELthnVIR6/S2Sq9fs6Fv+8N/++z33V4W3e5zBv01rVkjtO5/jdAC5jZ/rbuygi76Jw1Q/2rKM/k1bTGOe8lj3iqHd6G9SqW4qBXh8/yJF71JiqVhVUcG1cdA9fz5CTf/eJ35eCdFYvGzhxCey1EXYuDXsQgAAEIFCTQKWjyrzk1l84LNiX3pZqsIuQthw9bpEVfXRKw/qsgyrmbCspEjvw9U+HR8qO6Fg54Tmn4+QLMldWlFdYda1jV2aVfJPxrSVMkKi+bEHGyKErq8kdPrYg61StWoDbHKM7VWXY67fIhi368s5EfTZt4vpo7ZzpOwFr7yra1KardvDbMVs49OvYOJemro2xdcSCh1bWCp2ato3t/9UMwqKtvE2CHF59VXYyrI9jCEAAAv0j4OZEE9s0a+cjawPPdppAxzDePorDlpFJY3LZdM1t/2il0z9DkGP6zDur8e1zl+Svvjpf3FVh7uTY9tIbxcvGzQvH9e6Nx58evnD8Ge/uDXPnxvN7ixeKD144vk927DLf/bLjxf3yzIvuxePm+onz14sXjpsAx+vvXJNX37omv1y6KodOX5aHnz8kp89eGlNHdfDG/7U+ZqGlbO5f7TGH9IT1L5pHBSX+Tj+UwtU/jo4qX8b5X9JWD5yzP+XgH6TU8seRTetKbZ0MxTtWUpgWVYZBMCAprwY2zJ0h69dJ8aimyF0flrd5jFPxjpe0buM6/G0dVY9X04CFeaxURFYlZ8tbN28DM6kYRqXMlpPhOfqYrsr8KhRbCEAAAhBoiYBzbqUWPOocSl0vCbK0RbYspIMFJq0NGCQWPo3qs/9urlgglYQsH1TJ497L0GRxVXMh2QKvsjZ1j2rK1wLfuhK5dHVlczlSe65tm7SdV5pdqI/fv1z/SZehfd4+Wi4VsGtDHk89dntAwDpv0v1D7Dg0j5KKOJRCNfwyt2yQQb/KlG/TNxgnuTz2WqbOUOY6x7b/N5BzWK4dY02CHP5ddInfKyu2+cPAlgV7yA4EIACB/hFob37lAg+J3yT7O5D53bJpcr8Vbp1S6/evf9B5XFUP22RskfYcPiVf2rhDDr57TZ47elmefu1k8ZLxp3cflWf2HPNeMn68eMn4L/efkJdfNy8YX5LdB07KqwcHLxd/7fBJ2Vt8T8new4PvG29dkLcu3RBzB8ex89fljVKA4z157tgVeWXpimx+/oC8fuxduXHjRnM9rBN43fCdArm7GobXgloW168r3ktQvJPAu7ZonOdr1xbO8OKRUDGv8aT1q0N57boi2OH8+EbWcv05J7cndrDrAgDN8rsAQzbfpPoXdxYMGJtHfY18bPnG4b5W1s0vSonR/DpZWwQK1tmXzqfldToNHvGVCF7YNlk7LHu9V2dZwpzDf374Yu+YXjYoYWQfyl8Odi3K/Hqv71XdNaEyr1kra4vAzGhwQiX36y4/Xm1RFoc819p+P1pOTmetgy0EIAABCLRJwC0eokEM61TKLUA8eTT93IYi2OHCHcO7Rubmhg63yEuVTTGav8qhpFXaBVKdR6wYGZYij7NyDIp/nHlBmqUF/Wf9LdLsToCaC0nVd1xeyqHxtqZ8LfBd2DBo87mU435E9pqyFd1lg8xt2DJ4vI5XTnGHktfX6v473StisKvtU7c/jhRQs0/beowzIDPWbLpMmpgMnOsvATvG5gY2s3QH3oJs2bJB5vTRUHVf5ireGNJxkBl/uQBAGpxnN8PAQVanoR1WPdMVjF6x/X96QQ73mzQYmyaQseR+2MQcGBtXtFGG8agynIEABCAwbQLeb0Py9oqaMlk7nwhylP7UlJhD2zLa/P2rKf8Uk3EnxxRhd13V47sOyA+3vSqHz1yTl45fkV2HzsiuA6flpYOnZeHQ2/LKG2/LnjffkdfefFf2HXlX9h81Lxg/IwdOnJFDS2fk8NLZ4vvGyXOi38Mnz4n5Hn33spy8YF40PnhE1eAOjquysDQIcPzizcuy88hleWL3MXnqlSNy9doYj6wqOcGHDmN1HCe2oRPcd/oOnN+j5ZSdwV6rTFq/dU6P1unLEsrsSVCxO60gR17+pC4l/eNBB3W8+2WU9tcaR7wLYORYldo6GThwZZl6cuUlHf4Vejk5THBu/SCYkuivawr9KprZ079gEwsY2SLK+pVYFi8in5eSfDbfYCepc5COQwhAAAIQaIuAc1TFghz2n/B1nTeeE8r+K91z0Om5WF1Go8b12QWScUDV+0brrpI7dOJV4q+5kKyqd6hTVOZKGXIJaso3Kd+SfnUd8zVl8/tLpu1NcMX3SeaojFyz8teVfaSEmoE7p3M2mNaGPBERObWMBGqPsTnZ0MApZW3pcGwkTbjtU4nAcwaNqyMYH7V1alinJ2tSn4S8uUBO7lpRnFdv7nemfTudUIbTEIAABMYi4OYaE9sra+fTQQ4jorWv5rcoNNy2jKr5e7Pfv7HQdJiJIEeHcKdd9L889II8ve+kHDt3XY6de19ODN+t8dal68X7NN69fEPOvndDzr13Q85fvSEXrt6Qi9dELl0Tuex/3xe5/P7gvLl+8aoUed69ckPevjR4X4d5ZNWRs+/LwXffl31vX5Pdb12V3Sevyt7j5+VHW1+VsxeuNFd/0iCDqXFxXtav03/Ae876tWuHd3hkxOq4/nXFezQy9Vde6nmQo+pODtVP28gPBKxdKwWfIo1z3OeCEuIFFHLprCO/4qXnNl0kYFLvTo7hnRJD/fyAw9rh3T2KoGrrAhPxYFE5v7lTZHgXjDI1PIePTnNlcSdHmRtHEIAABJaDQC7I4a6F65KspEsLssX8s3UuWLTMmUVK8C/YUkFj1Fd7geRkSS/svH/kqtPcyLwQu/ujJHjkoMFCcmxekWprn6opXwt8u7yTQzLsBnd41AYST2idm4ETN546frZuGUPW2bFWt6y4JJztI4GqMTY3J0WgrmmkzvYVY/vSTqhkoKIOK6+Okl2t0knta+07U4bCePVlx0lEdutoiwSsc9dcUUuyYO6qafy75kpgDwIQgMDyEqg596sjpLXz6d+XQTGuThMkLt3Va8twc/RSIHnc37868k8xDUGOKcLuuqpfvn5C/uprm+XmuZ9O5funn/+ZfOQL98vHvvSArPunTfIXX94sf3vPVtm8c1Euv3eta3UpHwIQgAAEIAABCKwcArr4iDiFOlFy2vV1ogSFQgACEIAABCAAAQhAAAIQEN7JsdI6wTcfeE7u/Pcn5Mv3bpd/2rhVvvCjx2Xuh4/J7d9/VP7hXx+R/77hYfnMd+fl09+Zl9u+bYISD418/+6eh4prJs1nvvuw/P2GR+Rz33tU5n7wWFHelzb+XO788Xa5674n5Gs/e0q++cAO+damZ+Se+efkyYXD8v71MR5VtdIaAn0gAAEIQAACEIBAbQLun1elf+jWzt804bTrayof6SEAAQhAAAIQgAAEIAABCNQnwJ0c9VnNRMqDx9+Rv/6mCUo8Lv+w4TH57He2yGe/87B8+tvz8ul7Nsvf/ctm+bt/fkj+9lub5G++9aD8zTcflP9mvt8Yfr85OGeumTQm7d/982b59L9slk/fMy+f+c58Ud4/fHeL3P69x2TuBz+Xz/9wm/zN3Y/KY8++Ku+evzwTnBASAhCAAAQgAAEI9IaAfSxI1W3oLUn8/7P3LlByHeW9bwdCDLmHk5t7OYTg3JMTZ3FuSMjD0coJNJCTOGQ5OdgGHJxAIBhjaMD23OiQkISEmJdN+81gjI2wLbVsyQjjlyyrpbatp23Jkka2W2+pNRrJerXez9G8pPnuqr27vqq9d1XtR/fM9LT+vdZevR9VX331q9q1d33frqrxTq9FakMMCIAACIAACIAACIAACIAACJgIwMlhojLJz81+9jW69ZGlVJy1hG5+eJG/zVxEN3nb83TTTN8BIpwg3xLbjNBWes5zkIjr3yn54UWcm2cu8jbPsTFrCd06exndMecF6v7pcrr/8SV06NChSU4O6oMACIAACIAACIAACIAACIAACIAACIAACIAACIAACEwmAnByTKbSSqjr6TNDtGvfQdqwZTut27RtDLcardtco/Wba9S3azcNDGAUR8IiQjAQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAIEWEICTowUQ21XE6OgojefWrhygFwiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAQGcSgJOjM8sVuQIBEAABEAABEAABEAABEAABEAABEAABEAABEAABEACBjicAJ0fHFzEyCAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAKdSQBOjs4sV+QKBEAABEAABEAABEAABEAABEAABEAABEAABEAABEAABDqeAJwcHV/EyCAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIdCYBODk6s1yRKxAAARAAARAAARAAARAAARAAARAAARAAARAAARAAARDoeAJwcnR8ESODIAACIAACIAACIAACIAACIAACIAACIAACIAACIAACINCZBODk6MxyRa5AAARAAARAAARAAARAAARAAARAAARAAARAAARAAARAoOMJwMnR8UWMDIIACIAACIAACIAACIAACIAACIAACIAACIAACIAACIBAZxKAk6MzyxW5AgEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAIGOJwAnR8cXMTIIAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAp1JAE6OzixX5AoEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEOp4AnBwdX8TIIAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAh0JgE4OTqzXJErEAABEAABEAABEAABEAABEAABEAABEAABEAABEAABEOh4AnBydFgRnxoYpD2HT0zIdvLMYIfRRHZAAARAAARAAARAAARAAARAAARAAARAAARAAARAAATamQCcHO1cOil1O3v2LC1cvYk+/725dMMPF1i2cuO8+Fdb1w/LJDdxXuzf8MP5ke36e+bTdfc8Q1/+wTP0pbvn0RfvnkfX3vUUffq2x+hnS1+jc+fOpdQawUEABEAABEAABEAABEAABEAABEAABEAABEAABEAABEAgGwE4ObJxa8tYQ0ND9NSyV+lzdz5NhbsW0rV3LqTPe9sC+vxdC+jzd6rt2jvL/rm7xH+ZvsDbfPr89+bTF+6aT5+X253P0OfvnEfX3jmPrrnjabr69rn06Vufor8rPkGf+O7jdNVNj9HHb3qUHnl+DQ0PD7clGygFAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiDQeQTg5OigMhVOjseW9NBnb3+aPnPLfPq7786jT4mt+DR9qij2xf/T9OnvzqO/K87l40/dMpc+XZxLn278f+qWp+jTtzxFn7rlSfpU8Un6O7F990n65M1P0Cdufoyu+s5jdOW3f0Yf/cZP6Yob59BHvzmHPn7Tz+ihBSvh5Oig+oSsgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgEC7E4CTo91LKIV+vpNjDX3ujqfpmtvKnqPjM7c+Q2K7+tb5jX+x/wx95rZn6Orb5tFnbptHV98+jz576zzv+OrbnqbP3CZGazQ273gu/f2tDcdH8Qn6ZPFJ+tubH6e//vbP6GPfepSu/PajdNXNj9H0ecvh5EhRXggKAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiDQHAE4OZrj11axhZPjmRdfo0L349R179N03Q/m0nX3zKXr71H/1//AP+b/xvUbvP+n6IZ7nvLCX+/9i/2n6PofBLfrfvAUyU1c/4cfipEjc2j2ghfh5GirGgFlQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQKCzCcDJ0UHlKxYerx88TN98YCE9sWILzVi8kUpLNtLMJRvpoSUb6eGl/jZr6UaavczfHlm2kX6ybAP9ZPlG+sly8e9vc7R977oIs2wDPRLafrp8Iy1/ZTNd9a/TaNu2bVh4vIPqE7ICAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAu1OAE6Odi+hFPqNjo5S/8AQ3f7oanpp52l6ZvMJmr/F3xZsPUELt56gytYT9Ny2E/S82GpiO97Y9P3jtIjPH6fntwW357YdJ7kt2X6cavVTdPVNj9K+fftSaIugIAACIAACIAACIAACIAACIAACIAACIAACIAACIAACINAcATg5muPXdrEHhkbotp/10Ko9g7Sw1k+V7f30rNh6++m53n5atKOflu48Q/VqhfZWF9Oyvn5a6m2naWnfaVrW5/+L/aU7Gvvif8dpWhLaFu84Tcv7+qnv8CBd893HqV6vtx0PKAQCIAACIAACIAACIAACIAACIAACIAACIAACIAACINC5BODk6LCyPTM0QsWfrqJVewdp4fbT7OQQDo7nG06OtX1HaGjuP9Dp+V+nVX1HA04Oz7mhOzqksyPk4BAOD9/JcZp2HBmAk6PD6hGyAwIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAKTgQCcHJOhlFLoeGZwhG7+yUpa7Tk5GiM5GqM4hJNDjNo4tPYpGnn0Ghp+/IvUu34FLdspzhtGcmgODtNIDuHoeGFnP/UdHaRri09gJEeKckJQEAABEAABEAABEAABEAABEAABEAABEAABEAABEACB5gnAydE8w7aScGZwmL798Iuek0NMVeVNV6VNVfXa9l105ul/opFHPkUjj3ySDi+5l1btOMxODuHsWNx7iuZtOEFPVo/RE68eoydeOUqPrT1CP+s5TI+uOUw/XX2Ifrr6IM3fcIxe2tVPrx8fpi/cNhdOjraqCZNZmRp153OUy+Uo311r+4zUuvOerrlcgcptry0UBAEQAAEQAAEQAAEQAAEQAIGJJ1AtdVFXVxd1FSuEia8nvjygAQiAAAhMdgJwckz2EgzpL5wc3ygtZyeHWI9DTlW1pK+f9r38KA0/eT2NzPpbGnno4zT4+HW0ftOGwFoc5c0n6Zan9tG/zNxJ//hgL0398Va67oebqPD9dfS5u16hz9y2mv7+llXUPW8HrdzdT3tPjtCX7nwGTo5QWeAwK4GJcXKUC76zIl9I56qAkyNrOSMeCIAACIAACIAACIAACIBAJxOoloqeI6NYqkayCSdHBAlOgAAIgAAINEEATo4m4LVjVOHk+Pr0pbRm72BgFIeYqmrt9j10cv436NjKh2hwwY00Uvoojcz4CO1b+TN6qe84j+YQa20s2HySntlwguatP+5tT687RnPXHSPxP2/9UZq//igtrZ2kNXsGaP/JEbq+u9xSJ0et3E2FvPxC3v+qP5fPU6Fco7hv+5XRuREvZ/rPk2uQQDPpU61G5e4C5RujEcSIBG9UQr5A3eU47e21Ss9X6hEOtTIV8slHRjSVf3sWEl6ZCCdHmQpcT9KNyFDlki5eQhgIBgIgAAIg0EEE6hXf2CO+XC1W0n+3yvHDxqJ6naqVEhWLja9ixZexIo1iiSrV9OlI5Nb0iKherVCpqPLjf41bpFK1nvCL3DrVq2Gdi1QsVSiTyvUqlYoJuY4RL8nN+J9Gv5bwNWphPplCN64TjTrmlXtkv0gZqjdRvULFiCytThdl/XDU6ZCM8K1iBmA6W6US65IxPyaxODexBKolfyZiEjoAACAASURBVOQAl61Wv8S5YpFKlaqxDVN1P0N90OploO2P00fTM1ldFu2q3zab76UiFUUe0zaymv7me17jGBiVod9HJQq7OeDkmNjbAamDAAiMPQH17Ej4jmpSiZ8V0XY0GNzR5rIMrb3WnjGu518wjfY+gpOjvcsntXbCyfFvDyz2nBxiFMezcqqq3n6qvbqchp/sog3barR34ws0Mv0yGn7gr2jgiX+gNbW97OR4rnaKHnn5CD249CDdv+QA/XjxfvrRon1033N76b7Kbrq38jrdV9lFT79ymF7ZN0D1U2fpf//wWdq3b39qfaMRlIFbOgci/3m3MblcMDk1wudsTo4m0y8XGlMXhdNTx2KkQHpXh26ET+6sEHxr5QLlpaPF5dnxCqPJ/EcLNMMZpUNqZ06G1GQUjOSQJPAPAiAAAiAwNgT0jkeWjo6KHzB2xXVahLOjZDbaufNpSY/qVAk5UyJGr2JcJyxOhjDCubXTr3rOkkZHLWBA1APJ/THjJROI/qfSryV8ozrYzqTTjYiNknrHOLKfwQgsFExhSLXW6bCMNBVJg6QbJbq6MuZHk4fdNiGQ4P732zNDmWt1K7adCWVX1aeQ3MT6dMW0iQ1Hd+ReNBuz0uqf5t4MTz2FkRyhyoBDEACB84iAepcWz5bUba8kxc8K1/u1/m4detYIOSzD/FxQ7/KGuFKPSfAPJ8ckKKQ0KvYPDtPX7l/ETg45VdULvcfo4JIf0vEld9PLvYdp5c5TNPjoF2h42odo+Ed/TjtfeZ6W7zzlOTrEKI7ik/voq6Wd9JUHe+kfpm2j63+4kb549zq69q5X6LO3r6Grb11F9y3YSevqQ3Tg1Fn69weX0q7d+9KoagyrHBShURve6AhtZEe+2+ooYBnCmVCrWTeTAhw3lzH9hpPDc2RonoxarczrTHijOmKdDUHt1GgB31mSxPjvj8ZQzpUk6Tad/6DaGY8mxsmRUVlSZeN2vmWVj3ggAAIgAAKdQUAZufzOReqOjuycBL6SVZ0Wz+irfeBer1cDzohWpaeM3KFRG97oCG1kR1hPLsZgJ0z/olh8gay+Po7vZPlfLAc7a7H5bHBsOS/On9rJol/zfFX6rr0sugl5rJ9wnNXr1s2VtvUaG5GL3gikoPyqP1pJN+KaHBgsQ9aL+HoU1SdolICTI0po0p6R7ahwXIlRZ1odroZHp0XaMK3tilxzEXHEc+ij6yb27T9Nvnd/NEY8VYP3aLXq30NiBF5sOxlOTLuvvNF6Grewnk5VQ3K5PUnFMyQEhyAAAiDQpgSafveX+eJnhc3JoT8HLO89LCPL808q0v7/cHK0fxml0vDUmUH62gNRJ8drW2o09Nh1tO/lx2nTlo3ednzpPTR875/S8D0fpIE519LqvsPe2hxi4XExVdXc6nGaWz3mbfOqR+mZ6lGaXz1K5XVHaOG6I7RyxynafGiYDvSfo+8+spJqfbtT6WoK7BnZHQ4MZVDOkW3pBGmoT+IICOvQdPrlbsc0WMp4n26R6uAojjhnRU1MlcVTLwknR56P45g0nf8w0EzHilOcvpnEtziSqpNwcrQYLcSBAAiAQAcRCBtN037NpTovEeNUteKYGkjF6+qydYxMmFW8cHqeUcphkNI7dCYbtPqSzNIJ04xpXUYB4oP/kuYMEcbsIh+H9Y3kbkx4BVNpRr+m+QZViRw1o5sQJo2SsZwjKSc4wWVvqRueCFU3xVeHkSqiyeDp2yKBYnSRhgBhDG4YjTNNvxWTDC5PAAFZto7ROa42TF1z1dFQvrhOGuprAn1C0kKH/jR98gtc6winUKzUh648pBamIsj2JDz6Q4XAHgiAAAhMVgLNvvtr+eZnhfldnttS03uRFMMy7M8v9YwzPK+knDb/h5OjzQsorXpHT56hG2cs8UdyNKaqWtx3hg6umOWtvzHwk89S/5zPU/9PrqWBmX9Lw/d8gIbvfp+37V09l5bv7KeFm0/Srd7C47von6b30lfu30Zd922m636wngrdr9K1d/bQ525fTQ8+u4u2HRmmg/3nqPuJtbRp++tp1Y2EL3fbR2j4gZXB32wAb85A3nz6kSwFTiiDuG26rEBw70A5bbp53Qhz3kVwlX/PGeJNjaXO2eP56Y51/qO5M51Jrq8p9nifU2UKJ8d4s0d6IAACIDBZCMjOR7FS4Xn+UxmJ2cBk7ty4OKgOi71TE4nvSK9aqRjnq1cyVKcumkfNQO0wPCudTfnVZPBUXOpcNE2lWZI9lXYKXgHBShdvagJvqjB1Lk6/5vgGFDEcKD2y6EbaVFpx+TAkHn+K610Mew7XRRFHGF8rUqmx4HFmB19JOtNi9InPGUK0C4EERh59aqZoPVftW6TuWfKo2hRDe5ZEH4tccVo+W3yHn2u0h0NIkkt8X7XW8MX6OxznSdRDGBAAARBoNwKyfcv87q9niJ8V0eeIesbEfEDFMhzvNFpbH33+6Qq17z6cHO1bNpk0O3Kin75RWko9ewdJTFW1qLefVuw8QUOPfp72vjCL1m7po54tvfTKlh1U3byVDs37Ng13/xEN3zWFBmdcSat2nablff20aNspen7LSVq89SQt3XaKlm07RS9sP0UvbT9JK3pP0cu9J6m69wxtPzriOTkeXLiBqlt3ZdI5XSRlAM8Zh3Ko63EG/XTpytBKvjl9Gc7yz2t2JDSIy/De6JY4B49IU+iXp+B0WUrn5pkoWZnyb8ESPK3SaF7foOSxOIKTYyyoQiYIgAAIdBAB2anwjDjKQJam8yA7SkmNagF6Mv0UIzmaSk8zhEf01TpPDh9HYG2GaDhhqBfTsYipWGROlfE+DVcZO/CfgVcgvpf/MdTPxTeoiOGoWXYt5GzQThmXHR1wL57SI/IFONcxISPD/aaXf0CWSWGcm3QEuHxddcxdb7h9TNSmKlmR9lDAS6SPhTLHjTFsWaKnOs33ApwcqbghMAiAwPlJQLbPTbz7B8BJeeHnDp9P8BzgsNmffwGd2vQATo42LZisau0+eIJunv0i9ezznRyL+/rpQM9cOjPrU7RhyxZa2tdPS/pOe//LdvZT78vzaOjeP6fhO/6Ahu/4fXq9upRW7e6n1XvO0Nq9A/TqvkFaVx+kjQcGacuhYW/kxvYjw9R7dIR6j43QjmO+k2PO8m20ZlNfVrVTxIszgCtHgNEHkiIlc9C49M2x5Fk2iDum5JJhicJ5UcfpjP/N6az0EXutkeWvF6KtsZLLUV4sKO+tY2JOg9nlXA6iJIzMYeSImVyislFUTHp5i73n9fVQhOOpu5E/FVfscbrOfAXZ2xxMNq7dPthgwqYjsXZMIU/5gO5+2SSWYZKLcyAAAiBw3hJQBi7fWK+OkxvjZRxXp8QOmL/wSvylbHPpOb/25w5W9Eu0YA6kDgk6bV5EZfROzjWYojxKz0vGdP23Tj8nX89m6q+LIpxAyX5pdFPlklh8MiX8UGxIjavrSme3k0P/0j2uzgkVlFyvHiXWJ00mEXZCCXAb5KhjXO4Wgz7LsFzXMxgXlq879NHl8b6qq+lGKrGAdDtxTBzS2ClkeAa5ruki/TWEtDWfxCi+YslbV0UPh30QAAEQmHgC4XcldZz5HZWfFdq7jNYuG53oYRAsw/G80WSOyXteWKcxOIaTYwygTqTIHfuO0m1zVnhOjiW9J2jd5m009PAn6dTDn6ae3gO0dMdpf+vrp2V9/bRhy2Y6XfoEDd/+uzR823vo1OzP0fpdh+jVfQNU3T9IGw4M0uZDQ7T18DD5zo1hz7HRd2yEdh4/621iuqoFa1+nF17rHYesKwO12YkRd71ZFZuRr+ImcVKw8Zszmi6+yqnZaaCup9lTOrBaaaILx03IgC6m1dK3Qtmib62b1xaxpi1HvgiZNmcFywlOGca8bfEs+Qw6OZTuep7Uvr+gfUCUprM1XyIC621ajyYuXQcPT5kalQtBp5PSuVE+TuUCOcIBCIAACIBAgwAbcLinkL6j05zRfbzTExlXaXK2GzyS50Uz4IWFGGuXCp+5A+nJVbo3JyesZKv0E3KVjhE0Wuc0+WLZaXRzpB3OcpZj1t/RAffkKp0jHfuwDD5OYJDmsI30w8dZ8oQ47UUg1shTV1NAGYzyfmbUfRCpf6Hc8jPAJitWn5BAech1M6kjWEbM+K+lF2l3YkS6GLiu+WK1e91bH0eswRTabGxj9MJlEAABEBgLAtyucWOpnhmZ3y35WSGdHEpm5GMPW6ZYhu0dK8nzzya8fc7DydE+ZdESTTb0HaDux1fRK/sHafO6NXRq4U00MOfzdOZn11N95Rxau2WHt7i4GNGxovcQ7V35GPXP+RINTv8YDT74URqc+Qk6/NLDtHX3Idp0cJC2Hh6i7Uf8URu+Y2OEdp04S6/zds6brmrl1gP07BrvM/yW5MMmRBmUgwZqFV4Z4cNGWjFSoNmv0ePTV5rwXq1GZW0xcDGVVOyPDd/6qAWVtyROEpWGMoCni6ckyL1M+ZeRtVEgYjH0QneZ9Brjj0IIOjyC+qp82EYysKPCc5yY6wjnIeTM4Lih86y+ZYfl5QpUKAj9fUdGOG9qMfiwXvH5EklzOhH9tPiRtIN1Lwm3yIiTWo28kSndCeqthRFOgwAIgMB5SYA7E7JDIiioTkmyjo4Kz32lJDDrdapqi3Mn/6o/Y3qaTuzIMCzsG+34aRFDuxw2kQFLGcKScQ0llplXSI71sEn9NLkuviJYtbEORfIyT6Obqh9hQ2NLvqpmQ6qtA94AweEMBl6+pmQkrUscTt5sBllaUWB3MhLgdlnVD5mNupjerCgN6Hq7LUOof64r4alDVJBk7b1Dn4Co8EHWeGE5SY/5XkjgLAzJZFaGttx1TR9ZJZy2pWpdWw8q+IyLczaFVMIhCIAACIwNAW6b9WeIenfK9I4qNA3IVe9tXUU9nZgssYzmnn8xqUz4ZTg5JrwIWqvAqk276d55a+mVfYP08pbX6bWNm6jqbRupumEDrdxep6V9p70Fxlf2HaPNG9fT1s3rafuWddS7ZT3t3LqedvZupVr9JNUa01JJ54ZwbOw+cY72nDxLe06K/3O0++Q52n/6HG3de5KeeHFrazMTlqZ9yR40fmsBtTBhJwcf87RIWrwku5psa/pCjhaO0wxMxxSXmHJmBP0h6rwz/Yh4ZQRPFy8kSMtXFjlspM+Fjfx6OkpXwS6cDsuIGPqFDMlHTbcU5OenI50ZYdnyvHUEiK6mts86ORwrjZR54fhwGkqG7tTSEtEcRGG9A3F1z4oenZ1mUfYqvhghYhOgC8M+CIAACIBAPAHVoZH2Uj+OOp+oo8MdkphOjGaA0o3PwvBc5XUr4rUOdqIShA8H0fQw5Y8NWkEoYSneMYc1GMaiEVSHz5RuJLymZ1O8IoJtJ1LqZxVToWLjK+ZE+bTJCZxPoZuFm87Q63CnqXO6Liw/2gFXwZS+xml6TDJM55RAf88UxnQuHA/Hk4sAt6nSmRH999b7icsV1w2H0Z/TctRnDhPVI3BfhdrMOGdnnPqpr2v5DegVHlXhcm4b2nJXO6/y6HiOMT8H49SZRQQQAAEQyEJAveMHm2x1PvO7G7d1JSqV5PMipm8QzgLLkPGj/4mef2G5bXYMJ0ebFUiz6ix9tY+mL1znjeR4Xiw8vqOfFu/opyU7+mnpDn+KquU7++ml18/Qy6+foTVi7Y3G1FTrDwzSpoNDtO3wEPUe8dfb2Hl8hF4/MUK7T/iOjb2nztG+xib295w6R96544M0a/GWZtW3x9cM7GEDcThSTXx57m3+FW+/3E2FvD4dj82YHJbWOE6Rvs3J4Tk8PAeLy5CsGfkjFnppxI8a/y1aS+WpuzFFVNhA7o6nXU2Tfy2a2k2hu5ZWRF++FjXWM/dCWY16cDAMX2qFkyOirwLg7SmHQkh/zpdpKirdcRaKx44dSzxOX9WroI6qXGyjPFgEdkAABEAABBIS0IywwV5Osi97ORUlJ7ZT5DJAeY6OJFbnFOmxjtqOroPBmBX4KjfCRZPT2HUZv6KhU+qu6xo20iXmFdXCfialfiZBus5GvqZISc6l061er5O/+bK9/WqFSkV9vvyUHW+pJufRZLCsU71aoiJ/aW8YxSHkGGWoPNq++GaDqs7WKEsqi/9JSSCBkccz4sc6iLU6pdcZhhJ3vREwqT6hNpPrq3MkCSvT/A7fC1GjWNDpEb13XW25/ZoyCoayHsqL4hz7nAzFxCEIgAAItI6Aaoui7xmqPcvcTpmeFcZnjyNHJhnhd2BxHPv8c6TRBpfg5GiDQmilCk+9sJnmLN0ScXIIR4eYomr5rn56adcZWrXbd3C8IhwcdX/tjS2HhIPDX1RcjN7Yxc6Ns74j45Q/akOM3Nh/etQbwSEcHLtPjtKJwXP0wMKNNDraytz4srypcuS6DcYv+JOnqYzMyR0FTafvTfcjnCxqKqagoVnp7za0K4O0Lb6SpO/ZDNx6GPt+0/kXoh0jCaIpu/JpvybL1nNesNMg5MxiPULn9QXAU9YxmW4uduFw3VkRdkqoMjI5GziNqGemsZ5JND9hrly3dBnMI+w8CcfGMQiAAAiAQFICdqONkJCio8NGpajRKFYXYYj2DM/KIBXbsWoiPc/4LDtK1k6XqwMYzZGbYzi8kh2bz3BUcZyFl0mO9Vxz+iXja0085kJzuunCleHV4oDQA5v2uQ6qehs0oKrz1nJmGaH7hjv3ofOeHuq+DBhUbbJMuuPc5CCg1wMx/RE77USbWaWKNs2fqHuB+hDKoarvhjrFdcctQ42eK3qLaAf00XWzpp3RoRiSF3sYyE+Im65nPepQd7Xl1mtcTvH5YxmuworNIAKAAAiAQHYC3A4Z34HVO4b13SUuab1N1NrjxOtxCPksw/C8Sfn8i1N3Iq/DyTGR9Mcg7dnPVempl3u96aqe7z1N5ZVbaf6ydbRg+Xpa+MJ6qrywgZ59cSM9t2IjLVqxkRa/vImWrtpMS1dtoeWrt9DyNVvphZ6t9GLPVnpp7TZvW7F2G8ntJXFtzVZaVe2lPUcHPefH7lPn6PjgKM1avI1ODwy3MFfBxZDFWhauMRDJEtaMybHG7Nanz8bqXNjIra25YDWW2w387ryrPKd1juiLUTfDX+U73hhPjqmZRD6NxnqOI431kpU89gmxHrqhvwGP5cbWiyBtlmktNz281MvgZGOHQ5iRihNWW6WtHGj6FGnGfU2Iih9OU9cZ+yAAAiAAAkkJKKOXzTCTvKPDHaYmDTdKJ7exLVt6YpFC9QV/3DD3NGmkCauPEsncgWwUclJeSeuEHy6rIyEd33Q6ydBZdZPx9X8lK1XHW4rQO+7SaRb6L5Yq7inYWEbY8Kx0C9cRLvOwccIqSyqM/0lHQDfyRO3xjeyoumKcEk1mmutH1KnHdSpupEUifWSC6l/JD9dzFaale1pe0z6SuC0P31+eza3huAxdU/lTjk2bw5PPp1WspYAgDARA4HwloNqr5t/9rQz5WdFIg4+7KDpyxCKF47ieGwmff5Yk2uE0nBztUAot1OHep1bTc+v20pq9g7Ro+yl69rU99Owru+j5V1+nxa/tpqXrdtPy9XvoxQ17aMXGPbRq815as2Uf9WzdT69s20+v1upU3V6ndb11Wt97gDbsOEAbxdZ3gDb1HaD9p0boQP+ot4nRHHtPjXrrchzqH6VnVu2kfUdOtyg3ZW3kQ77pBcN1pZIZdscqfeVwCHyxzwbuqPND6a6M3WmdFemnq2pt/pl5IgeCYmTMJ7PSDPNy5IYmXzotlAwlV7PzM14ZPm46NI7Q2OG8NevksE09ZcpvJO0mnRwat3D+cAwCIAACIJCQAHceXM6EpE4OGc7VEUmoF2kdFqsRKEt6+iK9/ldhcRq5jF3BuEl01mOo8GEDth4q2b6SlbjjGCtYyUyuX3q+sWoYA2TRzSjIOxnf2bfHDUw1Ff7K3hEtcImNsdF7x6ybrPtRQ3VAH6tBPJA6DtqdALfT0foRUJ3rkas9Fx/Gmoz06p6KbUOS6hNQTv8i161fOFrm44Q8TPLNjPyQtmvqXoWTw8QU50AABNqEALfhrrbY8Z6RNBucjnKkcPvZZXh/McllGa15/pmSaIdzcHK0Qym0UIfiw8toxbZD9PKeAVqy4zQt2XyIlm46QC9sOUgvbT1EL9cO0erth2ntjsP0Wt8RWrfrKG3YdZQ27T5Km/cco617jlNt73Havu8E9e73tx37T9COur8dPH2WDp5pODn6R2nPqVHaddJfp2PFpv20ceeR5nMjDdZiiqqxML46jMae8mOcftSYrozvxi/v5VRdxv/gSAUzfCVfGfzNIccq/+kcAXH6KmePdFZI+YH8yXKWdYjLVXOOaBii5aJddOzKtBNNV2VzZDTksw4yY9rIlUDeGuE5bZlHh56mSxw/kYPGJAHnQAAEQAAEJIGKtlYAf1ka+grdfD7a2WADT+jrVplW2n/uCFnkpU5PM3il+WKf04n7ujnNtF4eDGVUTO5EsFOM42WPabuSUr+MfG2pu8+n1M0tTJsOQXXE46Lwdc539J7gMHE7ThkGQwN3+g36OmXFKYLrbUmAyzuujhnqiilDJnl8zmX0agjjsHH6hBNX+sU6UsJRsxzzvZAgTyH5rvbUdo2fFZZnVigJHIIACIDABBBQ70/m93uXkzZlm8/PCv1dJZi+9TsmSYZlxKWtni+teKeWyY/XP5wc40V6nNL5lx89S9U9J2nF6wO0eNMBKi9fT/OXVmnBsnW0cPk6qrywnp59cQM999IGWvTSBlq8ciMtFVNWvbyJlq3aTMtXbaEXVvubmJbqUP85OjwwGtikk2PfaX8Ux47jZ6n32Aht2nOUXtiwt8mcKgN2M9MjuZRwG3bHPn02ZLNhWhn1J97JMUb5lw6HXBKnjKZDt3mCMsnQN/xLfmHZUk7DqSF10BwIej2RMtM61tz1SU8hwdokUkd2Osg8hPPWkBsJH0ov7pDjW+THxcd1EAABEAABJtA6J4fqtMR2WDh1947NkOTHSpue1vkpVSnVB+5JO1hsUIvriMl8qzy0okPm5iXTTPOfRr8m+KZRicOm0Y0jWXfYOBnryDKISF3u6WWwfp7xNCbvrdDHoCJOTSCBpG1QYkerdr9W/NYwVfuRWJ8oM04nZu2QaMwMZ/heGB8nh5o7XjfoZdAbUUAABEBgzAiod4iJcXKIjKlnUFdX0bmOlGpX496tlcxWvFOPGX6LYDg5LGAm6+kv3j6Xth0epJdeH6AVr/sLjPfsOUOv7hug9fsHaNPBQdp6aIi2Hx6mHUeHaefxYdp9fIT2nBihfSfPUv3UOTpw+hwdFM6N/nN0dGC0sREdEc6OM6PeSI66N4rjHO08cZZqR8/SxkMjtOtQP1V6+mj47LnM+NjQbDFEZxbMEaVB3DxKZFzT1/MoFieP3aTBW6znUObwnDXrjsqzaTSAHm3M8s+jKAxrUegKiH02vDvCyjDCUSRls9NIClT5Fqhl3mwM5PXsTg7XVGO+TvFpqDL2qoeeT5kt/V/mPedgpYcP7zcbPywPxyAAAiBwPhMILb5qXkBW7zhUedHbADY2erXKuKN1wkxek5TpsWHNJCuQEdOBnn+7eyRoiDbJCZ9TeWy+Q6Zkte4LaSUzTr/m+Ia5JDlOrlu8NCUrzQgflsuG1LgOOMeI7sTJ4OtdVKpUqOiNtrKkx2Et16Op40y7E+D2LqZMOVy8UZ/vWc9xlqyNY0ycTow+HEHb4fopvhYuudeq0aJl2tXSStv0B/kEU7de09KLazODEnEEAiAAAuNIoFXv/nEq87PC0DfQ2kvh6Gj426MSWYYjjIjF4eKff9FEJv4MnBwTXwYt0+DIyTM09Qdlb1SFGMmx5NVd3mLjYsFxOXrj+ZcaC46v1EZviJEba7Z4C4r7C45vpRVrxbaNVryyjVa+ohYeF9f3nzrnLTguHBzbj47QpkMj9Fp9mPoOD9CCNX10+MSZjHmSBt6x+6pcfXVvMkg3mX6tO3btEJV+ljxK/dIatJWx32bg9wtMys+iW1yRKx1yrtEcNamDv8aEVV82zuepu7tAYgSMKSzzLnSTvy6JPW/xDghzHjmNuOnVpMPCoquUzvIKZXbM6P4wGU7+s94uriKwYNtdltH4P3F8joEdEAABEACB7ATiDWDS6JPIsFOvUKVqdxYIPdlhYOn4pEqPvxiL6SA5AMXpo9ZBSNO5UsZ1J7cW8HJkzXEpoX4t4OtQwnIpqW6W6NppVbZpyi4gwO100IJad7mzb6+jss7zl5c2q20CWVY9cKE9CbDxxl4/gl/GGgxK4ZzpMisl8uuVS74mQI/rbsq1SGpXv+f8r3jjhdSrJSpZrWBKdmCP74X09zbfb4appxJdszy7WL96lUqVKh9iBwRAAATai0D8u3+svvyssDyT+HrD6W0SyGFczyelq+c8N8lp83NwcrR5AaVRb+POg3T7nBW049gIrd4zQC9tPuAtMv7Shj20cuNebZHxfd4i469t20/rtosFxuu0ofcAbdrhLy6+eecB2uJtB2nLTn/bdeg0HTozSmIEx95T52hXwMExRKv3DtL6+iDNX9NL2/ceo9HR0TSq+2HZCFygcuyohsbIh1Aqte4C5QvdfnztWk0YePN5zxjuTQllsho3m740vOcLnrNDTbQkdA2mbzLIa+padpUDIF185WBwxms2/94gDJ+xmGos8mP5woGRp0K5RgFG5QLlPUdBgRedt+ur8uRP8WVxXnCZ5Buyu7U0gxqysT8yIkSMArHni50Scs2URvkr6TUqd2t1zyBfhRXOiG5f11ye8nnByryGCMfh8A2u3igfvkpUq3n6e2xN5aKtEyLKxZsmThWMH1/cVwYHiZYKdkEABEAABBIRUJ0HozGeDUmuDoiWkAxfLHnODmXeqlNdGH6KxYbBzbIooYwfZ0SSSXIHSXw1LNJIsMm4/K8YeF+caU6aelV+Wd9F6UYCJDTU5pikKwAAIABJREFUy/xm5cV5SLuTUL8W8K2W/DIv2gz3EdUT6uY5zEpULFX8stfkhOta5hEwsnyS1kdNB95NIoPDCGOA417jcI4wnDB2JgUBvseKfpsZaMOqVKmUGo42fy51Yzsdyah2D8k2N+n959Qn1L5G0vVPBB0dou0sekb/QBtdDeYtWb60BPleGD8nh+7w9hw4FTH6UdepTqK980ZjJeWtRccuCIAACIwPAfXem7rtlQrys8Li5Ah81GR5h2YZrXz+SQXb5x9OjvYpi6Y1eX5tL81esol2Hh+hV/cN0tq+47S29zC9uuMwVfuO0PpdR2jj60dp8+vHaOvuY7Rtj1hg/Dj17j9OffXjtLN+wtt2HThJctt54CSJbc+xATpwWiw07k9R5Y/gGKZq3XdwvPj6AL28e4CWbdhLL6zfTcMjGaasChjB/S/549aoCBvBIwZnaXjW/q1rfTSbfsDYbNc/rHPygh8vJ4dd93B5BPISyL/Z6VCTjgytPAIy88KgrxwYAfkhUIGytjoOlCyRjkue1ckRky+lh3DOSQeFhaGXv1BGIodBnXNGx0QoUly6Dd7W/HtOOIvOsqyS6BFSC4cgAAIgAAJhAu6ODhurkhpsNMMTf5VuWOzc1qlKnR53kHwDoCtNec2Ydpzehi9+wySDx5qR0fWFcly6DXZGnYMJpjxKqF+zfAP5S2qYT6hbuANtqGeizIVzRbdDpgLF+ifV3SA9kQyVZ6czLZEsgw441b4EEt9jwlGQvCZzW9q4L5I24fq0ILLNtP47hAoHcamYtF0WBq6URcT3wjg6OYSKWrpWLqLdSVFWKXOO4CAAAiDQJAH3u38i4fzssjs5hBweHSeeReFnBsuIe1ake/4l0n8cA8HJMY6wxzqp+5/poZe2HqC9J8/R3pNnaX9jbY1DZ85562kcGxilE0OjdHJolE4Nj9Lp4VHqHyE6M0I0oG9niQbO+ufF9f5h8uIcGxylI2f89TrElFW7T5ylHcfO0tYjI7Th0DBtODBMW/adokcWb6ITpwfTZ7dZJ4NIsVam7oL8Al4z2ubFF+pihIdDrTFOX0wVVHOl71DNv9TmTo64kRwyf7KMpPFc/Ofz3lRKPh5l5Lca5YUszbDvCsfOi5jpnDicwWGSbCRHY8RFI3+68yYfGd0hYZj/lePE7CyyxKKyGHHhjf4I1v1kda9GtXJ3cMSTXjZN1V2zxjgLAiAAAucfAVdHR10L90ucnOpVqoivWcMGrsbXvIEvXwOCMqSXuIOkOlB245P2Fa40mAudq/UMRnJltLan18h8Zl4BeCkPEurXAr5jOZKDHOz8ER4psYSDs0FzrJ0cas5p573WCn3CecTxxBKIu8eKRd9Rl9y/4eeH64po+9xGqACAOH1k22gyWAUENdSoVqzPg2LJH/FniBZ/Ssuf854xSGKjm8F57bqmRNWpKkbYpH7GKQnYAwEQAIGJI6Det2PfUW1K8rMi7vmi3jflhycskmWod/SA8zjr848TaI8dODnaoxxaosVr2/fT1Hvm02eLT4zLds0tT9K1tz5FX7h9LhXumEdf+t58+vcHFtP8l2s0MDTSkjxBCAiAAAiAAAiAAAicFwRk58NgCBqT/I93emOSCQgFARAAARAAARAAARAAARAAASI4OTqsFtw3dzXd9dNl9L2fLaU75iymWx95noqzn6ObH36WvjNzIX2rtIC+MaNMN04v0388KJwSz0S2rz/wjHdNhPnGjAX07dJCuumhZ6k46zlP3u1zFtFdjy6l7z+2jO558gW6b+4K+tG8lfRAeTUtr+6ks+cyTFXVYeWA7IAACIAACIAACIBAcgLqy6vMX3klT0zMAUKVxlex45NeKuUQGARAAARAAARAAARAAARAAARSEYCTIxWu9g+8Y99R+pf7hFPiefpO6Tn65vQKfXP6ArrxwTLd+MB8+vr98+nrP36G/v1H8+hrP3qavnbf0/SvYru3sd3nnxPXRBgR9us/nk833j+fbnygTN+YXvbkfWdGhW5+6DkqzlpEt8xeQl+b9iw9t2oTHTs10P6QoCEIgAAIgAAIgAAItBMBngokbhh6i5Qe7/RapDbEgAAIgAAIgAAIgAAIgAAIgICJAJwcJiqT/NzsZ1+jWx9ZSsVZS+jmhxf528xFdJO3PU83zfQdIMIJ8i2xzQhtpec8B4m4/p2SH17EuXnmIm/zHBuzltCts5fRHXNeoO6fLqf7H19Chw4dmuTkoD4IgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgMBkIgAnx2QqrYS6nj4zRLv2HaQNW7bTuk3bxnCr0brNNVq/uUZ9u3bTwABGcSQsIgQDARAAARAAARAAARAAARAAARAAARAAARAAARAAARBoAQE4OVoAsV1FjI6O0nhu7coBeoEACIAACIAACIAACIAACIAACIAACIAACIAACIAACHQmATg5OrNckSsQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQ6HgCcHJ0fBEjgyAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiDQmQTg5OjMckWuQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQKDjCcDJ0fFFjAyCAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAQGcSgJOjM8sVuQIBEAABEAABEAABEAABEAABEAABEAABEAABEAABEACBjicAJ0fHFzEyCAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAKdSQBOjs4sV+QKBEAABEAABEAABEAABEAABEAABEAABEAABEAABEAABDqeAJwcRDStig0MUAdQB1AHUAdQB1AHUAdQB1AHUAdQB1AHUAdQB1AHUAdQB1AHUAdQB1AH0tSBdvCgwMnRcHK0Q2FABxAAARAAARAAARAAARAAARAAARAAARAAARAAARAAARCYDASEM6QdfnBywMnRDvUQOoAACIAACIAACIAACIAACIAACIAACIAACIAACIAACEwiAnBytFFhtUthtBESqAICIAACIAACIAACIAACIAACIAACIAACIAACIAACIAACVgLtYlfHSA6M5LBWUlwAARAAARAAARAAARAAARAAARAAARAAARAAARAAARAAARMBODlMVCboXLsUxgRlH8mCAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAQCoC7WJXx0iODh7JsWv/frroY1dT7kOX01vE9peX01suv5L+z8uvol9ubP/l8qvondr2a5f9NYntnZddQRdediW9smVLqoqNwCAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAp1PAE6ONirjdimMViJZuW4dvfsLN9M7PreMfu6bPTRlWg9NmdtDU3qO09U9B6nQM0qFHqIbe4imNbYZawbpp2tP0JPrTtPMNbtp9uoj9Lnbf0gPPPVUK1WDLBAAARAAARAAARAAARAAARAAARAAARAAARAAARAAgUlOoF3s6hjJ0YEjOcQIDuHgyP3bYsrd1uNtQSfHeir0nAs4OWauOUOPrD5Oj712ip7dPkiV2gAte32Eeg4TPTRvHl02dWrsNsnvSagPAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiCQkACcHAlBjUewdimMVuV1Q28v5f7HByn3Py+l3J/52wV/dild8KFL6YJLL6O3XvqX9J8vvcLbfvnSK+htl15Bb7/0Mm/7lb+8nH71f11OP3xulefgEE6OoeFh6t2zh7enN+yhu8pbaerCPfS+aS/Re25f6G2X3nBDq7IAOSAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAm1MoF3s6hjJ0YEjOUZHR+nM4GBT20e+8hV6esNez9Gx6XjwTnrlCNGs1afoWz11umTOWnrztB66eFoP/fZVVwUD4ggEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQKAjCcDJ0UbF2i6FkRXJsUOH6D+u/FO66p25preP/JccTcnlaNnTT5MYmTHr5c00eDaomXJyjNAlc7b6633AyRGEhCMQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQ6GAC7WJXx0iOST6SQzg4fnzdX9GOb+WIpjW/3fuXObrsrb6TQ9x/X7/3Xrr5J8GFx5WT4yRdMme97+T4NkZydHB7hayBAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAQIAAnBwBHBN70C6FkYWCGMHRKgfHVy/O0Tf/e46+fKFycgidHnrmGbp86lTe/uT6qXTxZ2+g//eaqfS2v/kC/dKV19Av/fk1tKSnJ0sWEAcEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQGCSEWgXuzpGckzykRzvfWOOrnhba7ZbfydH06ZEnRxy4fFLvvQlWtrTQ6teW0ZzF36CPvNvU+j+J5/kBckn2T0IdUEABEAABEAABEAABEAABEAABEAABEAABEAABEAABDISgJMjI7ixiNYuhZElbx9/d44GB5rfLv+NHN17sdnJIfW6bOpU+sP3vY9+9Vd/ld761l+kn//5N9AvXHABvfnNb6aBgQEZDP8gAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIdTqBd7OoYyTHJR3Jc9Ts5IsrR0JEcDexLt53cnaMjdT/+FRfZnRwbN26kN73pTZTL5QLbG97wBnrjG99I73rXu2hwcLDDb1lkDwRAAARAAARAAARAAARAAARAAARAAARAAARAAARAQBKAk0OSaIP/dimMLCikk+Pw7By9+uUc9RSSb//yuzm6+1/inRxHjhyhv/mbv6G3v/3t9La3vY0+cvkl9NnPvofe96H/Sp++9lo6evRoFtURBwQsBGrUnfcdavnumiUMToMACIAACIAACIAACIAACIAACICAmUC11EVdXV3UVaxQ3RwEZ0EABEAABFpAoF3s6hjJ0SEjOWhhjk7ekaPjr+boeDXZNiWXzMkh6vuuXbvoz//+7+knjz1GGzcso56ez9CTCz5Evbuw2HgL2gOICBCYGCdHuZD3RirlC+WANuNx4ErbdW08dEMaIAACIAACIAACIAACIAAC6QlUS0XPyF4sVdNHHqcYk0FHFwqX/nByuMjhGgiAAAi0jgCcHK1j2bSkdimMLBmRIzmEk4Om5YjO+iMzfvSjHF10UXRbtMi/Lqa4SuPkELoteP55+sQnP0m///vvod/4jf+LLrzwF+nXf/3X6KKLLmr5dFW1cjcV8r7RmafJyuepUK5R3Lf9te5QvNA0W768PLkGCTSTPtVqVO4uUL4xGkHqn88XqLscp729Fuj5Sj3CoVamQj5HSeM1lX97FhJemQgnR5kKXE8KNL5uDlfarmsJcSIYCIAACIBA2xCoV3yDl/iytFhJ/10pxw8bzOp1qlZKVCw2vloVX66KNIolqlTTpyOBWdMjonq1QqWiyo//tWyRStV6wi9m61SvhnUuUrFUoUwq16tUKibkOka8JDfjfxr9WsLXqIX5ZArduE406phX7pH9ImWo3kT1ChUjsrQ6XZT1w1GnQzLCt4oZgOlslUqsS8b8mMTi3IQQUPU2aVmq8k/UVmv1ToVXMrq6StRqN4fKk3aPcJ11n1P3xdjqmLiwNX7mNkXLT2BUhlt/ODkSlwACgkAiAsnaHUc7O+bvX82+W5rep8W7R5XqjlcPBa/Z+EpSYK9a8kelxT5LHG0iy9DaU/2ZUSxSqVJN+A4f0M47aBe7OkZydNBIDt3JccstwfUzpKF93rz0To5NmzZ5i4tfcMEFJNbh+Lmf+7nA2hxC9pkzZ6K1PNMZZeCWOkf+824jdLlgzntQjs3J0WT65UKETTDdHImRAuldHbqxO7mzQhRBrVygfMOAH+/kaDL/mco8HEnpEK9vOG7244kcMeFK23Ute24REwRAAARAYPwJ6B2PhMb4gJIqvjJQEVFcp0U4O0TnLCAryYElPapTJeRMiRilinEGvTgZwlmSREc/jOcsaXTUlIHREn/MeFnS8xwWJTbex+rXEr52XcJXUrHzqpulc6x3lLscBo6wAvpxCkOntU6HZaSpSJouQUNOxvxo8rA7wQS0ehF/D4ba1YBR3ZwPVV+CdcU1ysAsKflZlWaSe1ILE8rPWOqYODda+USeJ4G2JTr1lEt/ODkSlwACgkAiAnxPhe/LwHGwHWTBY/7+1eS7ZWw7FPNu2mx8BmXYYXau92s9/4YyYBna8yBQbvK8Ia5BpfApODnCRCbwuF0KIwsCfSTH69/JUe+6HPVuTLYlHcmxe/duuvjii+mNb3kL/cIFF9CvXfgr9Ju/+cv09t/9b/Rbf/zHtHfv3iyqG+MoB0Vo1IY3OkIboZHvtjoKWIZwJtRq1s2kAMfNZUy/4eTwHBmaJ6NWK/M6E8LpkdZ4r4/iSBrfH40RdPjEpdt0/k1QU5+bGCdHajURAQRAAARAAARSEAgbpBIZ2nT5snMSMlBJJ0f4K7N6vRpwRrQqPdXBDY3a8L7O00Z2hPXkvAQ7YWLkh/yJ0SHqS/74TpY/mkR2yvz/2Hw2OLacl8yE9p9Fv+b5ago4drPoJsSxft5XjXWq182bI2n7JTYQFL0RSEHZVX+0kt4hNzkwWIasF/H1KKqQcvD5BtcsMqJScWYiCWjtjrVtUvpxPffqW3z5c/gEslUqze6Z773gfeOHkY6ArqwOyGZVjYuv3bfeaEBLu+LnLU6Yuj4x5aLSxx4IdBoBvqeyvAOM6fuX1sZ3+e+nkn2yd0v9uT8R8aW2ln/ZB7CO5Ajm3zialmVE37Gq4dHZGZ5l7WJXx0iODhnJ8fx3c3TJ/+FPQSWcF0m3JAuPi9ts7dq19J6PfpT+7VvfohUvPumtyTHtkT+hVze/bLkLs532jOwOB4Zu7LctnSAN9XEGfZOGTadf7nZMg6WM97mcezRKULfgKI44J0dNTJXFUy8JJ0eej+OYNJ3/oOIZjxSnOH0zJoBoIAACIAACIDDOBPTOU0JjfEBD1XmJGPGrFcfUQCpeuulSVLxwel4H19H50Z05Jhu0dMpYjW2asavLKEDMaqRGRkgjtHSOhPUNYBQHY8IrmEoz+jXNN6hK5KgZ3Tx8jYV8YzlHUk5wgsveZVRWdVOUfaSKaDJ4+rZIoBhdpCFATI+V0MgdIxGX24AAG+esRiKpZLS9dlchLbw7oExgfP/5nsgygnCcVNV0bCVCLnPHM2uccohkQKAjCMh7KtM7wFi+f8nnts2Rq7UxpndL9e5qe/9wt/PNxo+tHJw/80gOWS7G9yIpnGXY8ijer9XHSmnbYjg5JOg2+G+XwsiCQo7k2LAqR8vnpd92bPKnr7riohzde3GOpk3J0ZcvzNGyp5+OqPPQE0/QV/7pn+jKKy+nSy75DfrgB99Ol176P+myyy6joaGhSPgsJ8rd9hEavjxl8DcbwJszkDefvjvXykljmy4rGl85bbp53Qhz3kVclX/PGeJNjaXO2eM16DbNP6p/+jPJ9U0vGzFAAARAAARAYPwJyM5HsVLhef5TdRC5c2bu3LhypDos9k5NJL4jvWqlEjP1leoIRvOoGagdvSelsym/mgyeikudi6YZyZ3zhEo7Ba+ARKWL6Gz60yqpc3H6Ncc3oIjhQOmRRTfSptKKy4ch8fhTXO9i2HO4LooYK/hakUqNRZ8zO/hK0pkWo098zhCiHQiwgcfgHNP14zpUolLDqRepZ8bwMXL1OOO2r93z7WzoZ+atZSifvV3tnPdxqwtICASaJaDak7F4B8j+/qX0crXVSn703TJJW+EK47omqScJI8NG/vn5FdVd5SvGkc0yHO80Wluctozbxa6OkRwdMpJDLCTezOZycmzbts1bXPyd73wnveUtbzGuy9G6NTkit3PohDKA54xDOdT1OIN+SHDCQyXfnH6MGF6zI+FIDhneG90S5+ARaQv98v66HzxdltK5eSZKVqb8x+DxL6s0mtc3UYIIBAIgAAIgAAJjR0B2Kjwji8sBYFeBO0YOx4A1tkw/9utlJaGp9DRDeKSzqXWenFlxhhOd2fAikKqDm7ZTpnLd2MvAKyhjjPVz8Q0qYjhqVrcWcjZopxYed3TAvXhKj4jxkuuOkJHhftPLPyDLpDDOTS4Cqj5E2iYtI2wwKlaoyl+1Rg1LMgqHT9HGyrhj/a90i7unxlqTGPl8r8HJEUMKl0FgAgmoZ2/T71qmXOjPX9N127mk7Yc1nMpXomdDpK1vNr4tY9p5Gxs+H+PgEKI4rOt5oJ6TacsYTg6tvCZ6t10KIwsHOZJj+305euX6dNv8T+Xo3q/Hj+TYvn07CQeHGBkgN7H4+M9feCH9p3e+k7Zs2ZJF9Yxx4gzgyhFg9IFkTFVFi0tfhTTt8UgOx5RcKl44L+o4nfG/OZ2VPmKvNbL89UK0NVbEOiViQXnPMWNOg9k5p/pKwsgcRo6YySUqG0WF9eJ4NRKLhQemDMv7a7yoWME9V9qua0EptqMaZeEtpHHa2r0v2wDT/9jcc7Z84TwIgAAITAYCqrPgG/XVcfLOg4zj6pTYWbCRK/GXrM2l5/zanztYdoOhnxOpQ4JOmxdBdTCTczUzS8/LLCd4tnX6Ofl6fVh/qgExgiTZL41uqlwSi0+mhB+KDRBxdV3p7HZyaGuIRIwSJsWUXK8eJdbHJAvn2pEAO3Ct7WGoDnCbZauTKnykLupr2BjSi7Y1dRJrZ8ip98Roq65icG74VEy5/rrbURcT1lG7f+rVEvFUcI3p3IqlCmnLK6VS0wus6Zq2bXHp77qmK+mvUaSmafFGuhVL3tpAejjsg8D5TWBs3wG4vTG0l07u3E5nf7dM0la4wriuSd2ThJFhI/+mPGrtpss5w7JYhu15RmK+Kn4GpW2L28WujpEcnTKSY2GOtv1TjjZ+I0cbv5lsS7rwuLgpHnvsMXr7+99P/+ujH6V5T03z1uT4j+//MT2/6kW+Z8ZnRxmozQbVuOvNatmMfBU3iZOCDcyc0XTxVU7NTgN1Pc2e0oHVShOdylTIK2eZ2VBu0bfWzY4Da9py5IswyrPTIaQgywlOGca8bfFCYuRhwMlRU3xMebOVuytt1zWpg/2/Cd5pnRzWQrFrhysgAAIg0OkEuEPDPQXVQUxqjM/c6fPgjnd6IlGVJme7UdDJ86IZDsNCjJVGhU/K1ShG0705OWHprdJPyLXz1Tun1jVPwqppI0Pi8+xIOyI3wwnuXDs64J5YxTPSsQ/L4OMEX4hz2Eb64eMMWUKU9iLAbVDsvO2yDqo6b74/3Nf5GWAw2rEu4po26shzbnjOA3/9Js/gblxF1sVWu0cMaesxE+noOTk0mSH9pM5i0fBMP77XEtynoQRc+ruu+WLi82RyXoVUwCEInCcEVHuX6NUsFRUl29zW2oUF2lJ7MGHBp0qx0a6GM8AOAEsbpLVRRv2aje/U2/OYk9/OSkeO4pW4jWId5fMtnKhwtDf4xDw3wjHFMZwcJioTdK5dCiNL9uVIDlqYI5qWIzrrj8xYuTJHt9wS3Wo1Na1VGieH0O2706bRvdOm0U03/TtNnfpH1NX1W/TNb/4D3XLLLTQyMpJF/dRx2KCcCxqolSC7kVmMFOj2hwqo4Cn34tM3CKzVqKwtBp5PYgxmY70+rZXKm81Ybki9ZaMvhOxM+WellPNCLIZe6C4Tz6glZJe7Iw6QYD61+BaG7BDwRh6Y6wjnIeTM4Lih86y+ZUfJK/j6eyNSVM5EvtSoDrNOrrRd1ywqNU6r+pKNt1u6uMq6OUfXxMtBCBAAARDoSALcmZAdEpFL1SkxdpIiIFT4cH8sElQ/Ua9TVVucO/lX/RnT09LmzqbBiMidpwSZ4bCJOlqq45qMq6aw2M3MKyTHetikfppcF18RTHwJ7hlFEzD2xabRTdUPadSU/8VWfPXMRgRbB7wBgsMZvlDna0pG0rrE4SQ7gyytKLA7GQlwmRrqjsiPod3memFqizi8qm86FldcvpeLJSoJw1uxRNW6chKI0QVqVIdZvp6Wvs+ytREY+nV9P5GOXXJ9En9kidKSqBk9WQ+tXOTtx9didlz6u64FDJ5d4XwFn6ERZ2qMTrgMAp1JYAzeAVrw/sX3eYLGg8Ma2nPVbgZH0AXaOEcazcZ31hl+1og+hXpv854bzojaRZYRfZ54jnbpAErw3NCk8m672NUxkqONPE5cO1Ls2JwcwsFh+pJ83rz0To5du3Z5i4u///3vp7e97W30pje9yVuXQ5c/Lmty8Bf4OQoavzVgWhhdv8A+T4ukxUuyq8m2pi/kaOH0dNV0THGJKeN00JavzjvTj4hXzoF08UKCtHxlkcPOAKuDyoNH3dpIj3A6LMPoiJB88pRvyAjy8/MjDfNh2fK8dQRICIc8ZJ0SjR7JkWktE1farmtSB9O/0svsWPHjqLoh6mqYiUmuPJdMvgyNfxAAARA43wiojmCwP6TOJzLGc4dEd5QYWGoGIml09gzdntHMEN52Kml6tviaHqb8cecyCMUojcMaOqLRCKrDZ0o3El7TsyleEcG2Eyn1s4pRRs9E+bTJCZxPoZuFm87QN9QGEkh+wPKjHXAlROlrXFDcJMN0Tgn090xhTOfC8XA8yQho9cfQDnG7o11ThqtoO+y6JsCwPEM7puIKB0eFdMcBQ+U62EWJDe1aHC0bLDK8k1hHg+NayVLPNmteVODonqZzoD2JjBiJtg0u/V3XFH/hXIqq5J3hZ2I0XUsMnAaBziWQ5D6Ne++0yBAfSljvwxiifJ8naPA4rKXNrWsfCIXbIvHBkK2pkCo2G1/KifxzWyQdzmLERfSZFImnn2AZapRgljzqIvV9ODl0GhO83y6FkQWDzclx7FiOenujW39/eidHrVajd7zjHQGnibcmxzveQb/4jnfQ8uXLaXR0NIv6yeNoBvY4I7TQ19988d6wG+WcAAAgAElEQVS+N0pAXwNCHyGRQI0U6ducHJ7DI/SVfzRlzegcsdBLI346Y3RL1tFIk/9opsQ3/1RorOsQa0jX0oqE5WsGw728ViirEScOhuFLzTsTchSWqVBo5Wpw0LjSdl1T8sN7LeIdFiuPJeuUjhEZHf8gAAIg0NkEXEY0ZQiKN1IrObFhLZ1Gr/MS+jrYzj5FeiYhug7GzqOSn8RYF9cRDaqgZMeyEhF1XcNGtMS8ghq4j1LqZxKm62zka4qU5Fw63er1OvmbL9vbr1aoVNTns0/Z8ZZqch5NBsU6hdcCMJa1UYbKo63uscFTZ2uUJZXF/2QlwGUdMRCp9jlgK+N6EJ7GJL5eudoxpUdYrk5WS0Ovm3qQwL4WPpCJQKDAQVIdjfebJknlx3T/agFNuxrjsNEteByV7dLffs1S1hHdFM+4/Eei4gQIdCCBpt8BXPd6pvcvdY/anu96MdjbBPFuWPVH1YXfC+Vx3IjVZuPriob3TQ6KRM8ETZBJhsyb/p/R4dQudnWM5OigkRwf/9Uc5d+co/xbkm1Jp6sSDox7772X/tPv/R5d9O5308MzbqGXXvo7+vK3/pAeX7RozB0ctXJBTfdjMBBrt23srvr6PLmjoOn0hdMlNBVTxHjf0Nxt0E5huA6QUAZ2W7qB4KGDpvMv5PH0WwbnRCg9t0PEzkCWredoYCN8yJnFeoTO61MvpaxjMt1czJRNHM4g31XurmsRdPIE57NZ3lKg/q/KwDQqRQ+JfRAAARA4Hwk4O1BppqvijmDUqBPLVRiiPcOz+lor1kDTRHqe8Vl2kKydrhZ2RCMAlOzYfEbi+tNVpeZlkmM915x+yfhaE4+50JxuunBl5LRMBaQHNu1zHVT1NmjgVOet5cwyQvcNd+5D5z09LAZPmyyT7jg3eQhwXQg5F/h82ElnuUe4foTkaCRczwN1v4TT0wR4PtmGA9HatqrwSWWqGElHm7h19OQl4KGnG9gPxJWOVPN/IF7MaBkrf2tZh6VrfBI6jaIScAYEzg8Cqv1J8Q6Q5X01gFO1z005ObQ2SIxGC4wqqdep0pgKVLyTGJuCZuMH8mQ40NusUFpxo0tYGssoUqUaal+rVaqERrEY88nCojtwckSZTNiZdimMLADkSI5brsuR2E+7zbrLH9lxxUU5uvfiHH3j3RfQ7LvuYlU27dhBv3PVVYHtoiuvondc/nF6619dTm/50OX0cx/8C8p94DLavns3x2vNTo3KBTX6QqxloVY6yJqCMvjHjQgRIyBanT4bunPRr/7VtagB3s+tMi6nc1aoPKeN16r8x+dNL0+3vmz0DwybkHGkUV+ykse+fNYjELdBt9CY4s3ghNC1C++zzJh4rnCcJ4MM17WwLvKY04pxvPjhJbtkjj/WJ5FsqRH+QQAEQOD8IKA6eDaDkDKmWo20DVRsnEnbywihVjpZOmZNpScWKVRf8McN5U+TpzRh9bnV47iG8EQOk/KKRHSeUJ3wdPql4+tUwXoxq24mgUrWWE1ZUyyFjA9hNbjzH3ZmKN3CZcBlHjYiW2WFE8Xx5CJgboet9cDmaNANRhYrE7dj4bplk2kA6dIrEJz1cbf1gTgxTgJOOzLqJSxFHJu5mkJGzvG9lk53L1XHQrk2/ipfynFqc6jy+SafxZE84wQIdBwB9ZzN8g6g35dpbje+zxNEModVbZfLUaL0C79fNBs/QUXg9r3Rv+DjFFMZcpyw/nr6WhkmavdV3Haxq2MkR6eM5CA1DRVl2BdOji+9MxdwcPzo8cfpX+++W9Xaxt6i3kH6j54BuuKZHppyy3N0wXUP0q8U5tFvX3VVJGz2E2VtEep80wuG63okMwCPVfrKoBz4Cp6/vI86P5Tu0nCfzBit4qk0kzs5Wpt/Zm4w4is95V6MvsxKcwbJkRuafGmMV3lWcg0+DrWItiZDauT6T5o3Vzipq8nx5rpm08uVVjSO4qJYRUOJMyzXua6KOS7OggAIgEDHE+DOg8tIozpCYUNrkI8M5+qIBGPYj7QOi7UDmCU9fVi//1WYXQf/CncuDQa/YNwkOusxVHg3Vz2ObV/JcnV2bbHN55XM5Pql52tOO+5sFt3sMpURwObos8dV04gZvjJ0RAtcYmNp9N4x6ybrvuHLU4esQJo4mHQEom1RzH3A7buqV1EZUQyuMFwfY9rDZOFUPU7bbiXSMZGxS+mQvJ1rMON7zfX8jPIVZ1z6264xUzkCMcm/9flp1gtnQeB8JKDurQzvAPqC2inuN9t9HuWv2nm9nVQ6q/Y9GlecMbdxzcY3pxU6y88gxZXz3WV4fwlF9w5ZRkw+M7bHcHKYoE/QuXYpjCzZ/+BbczT18ua39/9ijhY9/jir8O3776fZCxbQ2XPn+JzY2XmKaM6aE3Tjiq30/pk9NOWry+i/F6bTHxamtc7JIQ3WroWcA1qlPDAZyXURY5x+1GitjMz6QuXJ9oMjFfRsqH0lP86I7cUZg/wr47jmmFAKhvbi9FXOHumskPID+ZPlLJ0WnC+zDtFyCallOZRpmxwUehRXOFfarmu6fH2f00o02iKOd0My80vrZNM1wz4IgAAIdC6BSjHFF6EBg0q0s8EdphjjV1Ka3BGyyEudntYBSvO1HqcTazAzdyTt+VUd19TGNYPQOF6GKDGnUuqXkW+MEpbLKXWzSOHT3IlWHXG+FrfD+Y7eE3FR+bpThqFeufR1yuIUsTMZCXC5N+pabFmruuPb3pLdN662hNtDS7sssSYJx+nEtq1SqvrnuAY9OO1EcsOMVBqxe8x/nJ0chjzH6ooAIAACdgLctmZ4B4hxWtoSTd5OqTZKf1fkNjC2nVPtvv7u22x8W74C541cNX1s02jpQlhG3DuWmZMuyrTfLnZ1jOSY5CM59vT2Uqs2uXi4GMHx3UcX0CuHRmj9MQpsaw8T/WTNCfremh768NwemnJPD025oURvbpmTQxmwWzM9VfT2cxuAxz79qNFaGZmTOTYa0yp5C3m32skxRvmXDodEIwA0HbrNE5RJhr5TQ/ILs5ByGk4NqYP0jISqhpQZ56wIRVOjG6QzJRygccz1zhDOlbbrmiUpbQ0Us0MnGE9ycjkvVJjACKSgIByBAAiAwHlNoHVODtVpSfEhm5M9d8CMBp206Wmdn1KVLLO0mPVJ2sFig1dcR0wmo/Kgd1zl1bT/bl5ppYnwafRrgm8W1VLpFp9AcmODQVbqck8vg/Xz7oWYcmmFPgYVcaoNCHDZNozq3DbZDXPcLoiGmeO72yiOY2h7g3XRziQ2HOue3kEgUk2kY6zxzxNE/tRObibGnDLP9Hlw6W+9xszs5W3UEydBAAScBLi9StJmGCRZ71lDWD7F93NM28PtTDAcpxmrs3pnaA8nhyCg3hm7uorm9UIkqKScNJlp3qnh5JCg2+C/XQqjVSjEOhpvfu97M28f/ffbafaqo/TA2nOeQ+Px6imav4PoX9cSfXkt0Zd6XqUv9vT401VN66EpXWvoDYX7WzKSgw26FkN084ykQTxHJmP2uKav51EsTh67KUNzvrvM4eOZqDwHRjoYIo5Z/tOMApDOiJzD6C7DCIeBlB1xHqh8C9QybzYG8rqpXhhQ8SmX84ID6VM9RfRUupnSzqSXZOJiKJWTLB1hWYdEI0OkYPyDAAiAwHlGQCyeGLupzkixUuXwAVLcCWmV8UXrlJm8JinT486gSVYgI6YDPf929wh3kg2GQZPUdE4EswR1NoaXCphiT8mM6zA2xzeFShw0uW4cxbqjZOkGAGvw8AWLASIczHkcJ4Ovd1GpUqGiN6oqaPBg+RzWcp0DYmfyEdDqaqmqDP2Odo3bJWEIS9hu8v1saMtYnuGaztMdTrWp+vQrevy4/UQ6JvhK2CUnTgflNBonJwff2wmneYnNAAKAAAjo72KZ3gG0jy7StWeqHXS9Y9naUj7fFfesV+no+jUbP1HNcT1ztPZMODoqttdrluEII5ThcOna43axq2MkxyQfyWG6IcQC4L/d9S36g3tepCnCCfF9///Dc3dSoecs3d1DNK2H6P6eczRjzSA9svo4rdx/jnoOE63Yd44eWNNH/9izjm7vGaJvztvhOS/Eehtv/cAHKHfJX1HuQ5f72wf+jP7rhz/M1026pDsnjfjhL/LTSXGFZoO0YeFvoibTr3XHrh2i0s+SR6mfw/hvzLwy9tsM/H40KT+LbsaEtZNKh5xrNEdN6uCPVrHqy0b8PHV3F0iMgDGFZd6FburOC5n2vLEh3+CE0DIS2eU0YuK5wrnSdl2LKMMndN4FKpsHxBAl4M16O9hxstgBARAAARCIIaA6SLaOmDQU2a4HEqhXqFK19Wb8kHGdr1Tp8dddMR2kgJLBgzh9shm7lMHSya0FvIK5SXqUUL8W8E2qkQqXVDcVw7anyjZdx5jlcUc9e/1S9ccuQ9b52AWFW6EPZw477UaA62ux2HB2xdRbrT4U5fSEDqeIyC/XNYMjQ6VfcY6Ic4Vj+bFfINvpswyXjsIZaLjOUjWjmLMN5gihHWYbUwahaOLQpX+iay6joEigXqVSpWpIGadAAAR0AtxWmZyiY/z+pdK2PPtdbYx2zdXOcXsSzl+z8XWItn1uYy0fQPF1MXVuXBgLIy9t1U+xyrHoCCeHBcxEnG6Xwmhl3peuXUt//M+30B/cuJymfPF+mnLzQm96qULPcXZyzFp9KuLkWLB1gG5Z00ci3Afveoy+evcPWK3Lpk6lP5+xgv5y7lq6eu6PaMo/X01PL1vG15ve4S/KhVE2yciGGoVtt7XuAuUL3X58TaGaMObm854x3JsSSh9FIcM1m740vOcLnrND6SbyEkzfZJCXatj/lQMgXXxl8HbGazb/JEYk+IzFVGORH8v3nQ2Fsl5+NaqVC5T31mEp8KLzdn1VnvwpvizOCy6TfEN2d6TOSD1dzgRXvtgJMAFODpde1Arekp/FiSTZ4R8EQAAEQCApAdV5MBqCuKPk6oBoacnwxZLn7FDuDjGqRCxcXWxMH2L5WlXGjzPyyCS5E1WiauyolcbIFhmX/xUD74szzUlTr8ov62MMaixL7iQ01Mv8ZuUlk0v9n1C/FvCtlvwyL8YYX1UWEuombH2VEhVLFb/slYBIXdO/cNSCxe/K8klaH00Sk8jgMMIY4LjXOJwjjEkHnJscBLh85XpKceWs7hXpIIu7zdgoZnAQsFHOcE0HaA3H7YUYlZRkJKEKo8tPpKNcR6rRdqr4dapW1HPGZSBUcQx7WlnEMQ3HdunvuqYcon47IBwZdfUQJXEg2lNvtFdapcJK4hgEOoBAU+8A8h7P/P6l2l/j+zN/JNJ4rqd8t+S2wnPoNt6p+T1XvE/L50QXmd5xmo0fWz24vbc4MLx3tJi2mGUU/T4D58/vM1TEO55s65MuZq4p3i52dYzk6MCRHLKerdqwgd718S76pUuupF/6i4/T2z95Df36NTfQe66ZSr93zVS6+LM30B9c8//RH372BvrAl6fSB6+f6u2/+5oveuFmzA8uPC6cHCs27aTFx39GPT1/Sl03TxkjJ4e+5oR7P2wEZ4Ozt16FOa51rY+AUdgcN7xmRiB9zSAcDqcfB+LIwkr0P15OjmR5F3kK5CWQf7PTgR0ZtvLJizUklAMjID/EKFDWVgeDkhXRNyTP6uSIyRfrYdXBT8gVzpq25zhqlEdYfoxeItXmeKv6ptdf+765zEOYcQgCIAAC5zkBZeA3ddLYmJXUoCI7jVqnRBrf9H9TWqIgUqfHHSSts5cl7Ti9Y4x+0UoU1/ltxIhLt5EXG69ouknPJNSvWb6B/MUZbKXuCXXT64ujzIVzRbcTylQS/bP+SXU3SE0kQ+XZaZRNJMugA05NEgKqPfbaywTtTsCQ5XKQNQhweINsbn8N13SA5nAh3R33pP4s8PeD91ciHcWXwXw/WNr/ot34pufHuK/JTvr4k3Jc+ruuefG1dKOcVD5b/0yQ2uMfBCYPAW6LHO2N9R2g2XuN4wfbrwA9DqPu3cB97WxrfadmILwhn+JDD/M7TrPxAzmJHvD7obud5TZP6B5uTFmGhQ/nt+g5zqNKuM/AyeHmM65X26UwxiLTr9fr1LtnT6ZteGSEVRKLkf/i+99P/8+HP0wXXvFndOGlU+iX/mQKveMv/oJEGi35NetkEErUytRdyFPem5pIM9bn840RHg5Nxzj9greOhiP92EvK6Owy/kfFKEO/M14L8u8cWSAVk2WkOzryefL4eGES6qsZ+V35YgdCzHRLHC7sTIgZoeJyXsgsi39XOHfaFidHjF6cdkberK9eTs59ODmYOXZAAARAwEpAGaaiRhN1LdwvsYoTF+pVqoivTfWvzERHpSg6KaEvUwOCMqSXuIOkOlDRfEoltK9kZcdK6FytWzqQMp7pXxmt7ek14mXmZUo36bmE+rWA71iO5HDVNX+ER1IelnBsoHAYMSxR+XRSGQ3WznstqSxOHDuTjYBuEIptO0Tm9HvUaTDzSbB8Q1g2GBqu6RxN4ficbDtT/Qfvr0Q6yulPGu2nbggsRkZ36Non3Od7bfymq1KaidEopQzPUCUBeyBwXhBwvD8legdwxHe/r2ptb0x7KdYF4RFYsl1M824pdZRxvf8ij2KNLedm49sS4GeP28kRWBdFjMbQX3JYhnpH19ty0W/wnFQZzbvtYlfHSI4OHslhuz9M59/98Y97C5WbromFzP/17rtpYHCQeuqD9NCKg3THypV07cqV9KezVtJ//osP08DQEEe98qtf9WTp5/gidkAABNqMQFbnWZtlA+qAAAiAwGQnIDsfsR24FmV0vNNrkdoQAwIgAAIgMD4ElDMlzrA2PvogFRAAgfOTgGyLEjmjz09EE55rODkmvAiUAu1SGEqj8d27bOpU+sGSPfSlHqLf/MhHaENvb2D7nauuYoXWHyP6yZoTdGvPAF3xTA9N+cEKmvKPa+gNf/ReL87/vvNOmrd8OT1dPUm/8N73cTzsgAAItCkBbUSMaSmVNtUaaoEACIBAhxFI+KV/y3I93um1THEIAgEQAAEQGCcC0rCYdgHacVIPyYAACJwXBOQ7a3AU2nmR9UmUyXaxq2MkB0ZykHByiCmtrn+F6K3/8xK6/Gu3BzaTk6PQcHJc9NU59Ad3v0Rv+B/v9eK8+5Ofg5NjEjVEUBUEeKqsnFgPBT8QAAEQAIEJIcBTdYzT17Ljnd6EQEWiIAACIAACzRCAk6MZeogLAiDQGgKN6VXHa6Rza5Q+76TAydFGRd4uhTFRSHQnx5vf/wFv8XGxGLncTE6OmxpOjt/66jK6+B9XeyM5RPgLP/wxODkmqiCRLgikJCAWJpcLibvWNUkpFsFBAARAAARAAARAAARAAAQmOQE4OSZ5AUJ9EOgEAo3pVTFVVXsXZrvY1TGSAyM5vJEcP35+K325h+hdH/tYZJHyxWvW0K0zZ9LOU0RrD/vTVX2/4eS48qs99H//6SdpU1+fF++fv/99uqe8nB57FdNVtXcTBO06nYBYODyfL1B3uUy1Wk3Lbo1qjcXIpYMjZ1hsXYuAXRAAARAAARAAARAAARAAgfOMAJwc51mBI7sgAAIgkJEAnBwZwY1FtHYpjLHIWxKZQ8PD9K4r/5re+N48DWoLiMu4o6OjVJwxgy54X97bxFobb3pvnt74x++lN/7Rez0Hhww7cvYsfeQrX/HW4zh68qQ8jX8QAIFxJiCcHOzEyOXs+3BwjHPJIDkQAAEQAAEQAAEQAAEQaH8CcHK0fxlBQxAAARBoBwLtYlfHSA6M5GiH+wE6gAAItJxAjWrlbirk85QPOznEuUI3lQMjPFquAASCAAiAAAiAAAiAAAiAAAhMUgJwckzSgoPaIAACIDDOBODkGGfgruTapTBcOuIaCIAACIAACIAACIAACIAACIAACIAACIAACIAACIAACLQLgXaxq2MkB0ZytMs9AT1AAARAAARAAARAAARAAARAAARAAARAAARAAARAAAQmCQE4OdqooNqlMNoICVQBARAAARAAARAAARAAARAAARAAARAAARAAARAAARAAASuBdrGrYyQHRnJYKykugAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgICJAJwcJioTdK5dCmOCso9kQQAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQCAVgXaxq2MkB0ZypKq4CAwCIAACIAACIAACIAACIAACIAACIAACIAACIAACIAACcHK0UR1ol8JoIyRQBQRAAARAAARAAARAAARAAARAAARAAARAAARAAARAAASsBNrFro6RHI2RHKJAsIEB6gDqAOoA6gDqAOoA6gDqAOoA6gDqAOoA6gDqAOoA6gDqAOoA6gDqAOpAsjpg9YCM4wU4OcYRNpICARAAARAAARAAARAAARAAARAAARAAARAAARAAARAAARBoHQE4OVrHEpJAAARAAARAAARAAARAAARAAARAAARAAARAAARAAARAAATGkQCcHOMIG0mBAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAiAAAi0jgCcHK1jCUkgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAALjSABOjnGEjaRAAARAAARAAARAAARAAARAAARAAARAAARAAARAAARAAARaRwBOjtaxhCQQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAIFxJAAnxzjCHs+kHnnkEZo9ezbNmjXL2x5++GF66CGxPUQzZ86kkthKJZoxo0TTZ8yg6dOn04Nie/BBeuCBB+n+Bx6g+++/n358//007cc/pmnTfkyzZs+mQ4cPj2c2kBYIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIgAAIWAnAyWFFM7kvCAfHuXPnrNvZc+eIt7Pn6KzYxDlv/6z2f5ZGR0dJOE36du6khx+eRYcOHZrccKA9CIAACIAACIAACIAACIAACIAACIAACIAACIAACIBARxCAk6MjijGaCTGCQzg5RkZGvG14ZIS8bXiEhodHaGh4uLGN0NDQsL8ND9Ogtz/k/Q8Oif8hOnv2rOfkOHnyJPX19dHMhx6GoyOKHGdAAARAAARAAARAAARAAARAAARAAARAAARAAARAAATGmQCcHOMMfLyS850co006OYTTQzk5Tp06RceOHaPt27d7011hRMd4lSbSAQEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQAAEQMBGAk8NEpQPOiTU45EiOxx9/nJrZNm7c6I3kOH78OB09etQbxbF161aaPqNEBzF1VQfUFmQBBEAABEAABEAABEAABEAABEAABEAABEAABEAABCYnATg5Jme5xWotFhmXTo7wVFW26arEVFXeNmierurIkSN0+PBhOnjwIO3fv5+E80MsWH7wINboiC0QBAABEAABEAABEAABEAABEAABEAABEAABEAABEAABEGg5ATg5Wo60PQQ+9NBDnpPD5OAY5vU4xLocak2OOCeHcG4cOHDAc3Ds3buXdu/eTevWraMHp09vj0xDCxAAARAAARAAARAAARAAARAAARAAARAAARAAARAAgfOKAJwcHVrcM2fO9J0cwyNNTVUlprmS01XdcccdZNq6v//9DqWIbIEACIAACIAACIAACIAACIAACIAACIAACIAACIAACLQzATg52rl0mtCtpDk5xPRUchuyjOIQ58VIjqEhOVWVv+j4oJi6anCIDogpquoHGlud9u+v0779dTp06DB9rxtOjiaKClFBAARAAARAAARAAARAAARAAARAAARAAARAAARAAAQyEoCTIyO4do9WKpV4JIfv4BBTU+mbmqZKOjj09TgGvHU5fAeHcHKIY7UN0sDAIJ0ZGKSRkbP0ve7udscB/UAABEAABEAABEAABEAABEAABEAABEAABEAABEAABDqQAJwcHVioIkszZpTo7LlznmNDTDk1Fpt0ctz1vYl3cpQLecrlcpQvlDu0RJEtEAABEAABEAABEAABEAABEAABEAABEAABEAABEACBMAE4OcJEOuR4+owZ7ORQIzhGAguND4npqXiaqmFvWip/8XExZVX8KA7p5Ljzru+1jlq54Dkrcrk8ddeSii1TIZdrxCsQ3BxJuSEcCIAACIAACIDAWBGoVytUKhapq6tLbcUilap1qmdMtF5pyCtVoxLqdaqWilQshtKrVMckvebzV6d6tRTUt6tIxVKFqlkA1atUKnZRsRIfmTnqZRPZL1ICUdFysJ1JoZ8Q0TxfmyKtkN3ispOq1itUjJRDsD779cNRxiEZpltFJuf+r1KJdWlxXXAnjKtjQaBaUu0wl6tWtxznstehschIBpkJ8l4Uz6ZShSqZGt8MOiEKCIAACJwPBFK++1mRcDteIkMPQIumv7uEwrIMy7NPPAea6DNoSkzoLpwcE4p/7BKfPn16w8nRcGwMa9NTac4Nfx0O3cHRWIuj4eRQU1TJ6arUVFXKyXFX6zKSyclBhJEcrSsCSAIBEAABEAABEGiGQJ0quqPBZDwrhjoeiZJTHZew0c1zFpjS4XOlDI4DW3qtyF+cDOEMSgTFC6TnP4mTo1qydPCYl7jeOsN2Ov3i2HRRV6b6I1C1QnacjHRlFyjlkIMi4CAMlE0XFUsW511YRpqKpCkTdIS1ri5oSWB3PAnEGXdC9Uuvexmr0Hjmzp1W6rx3hqHLDQVXQQAEQGBsCaR794vRhdtxV/9Bfz8zvLewjLh3YEPcGPXa6TKcHO1UGi3U5UHh5Dh7jsRojbGYqkrIlE6OO+6ceCdHC9FBVAyBWrmbCvk85ZMPtYmRGLw81vKDqeEIBEAABEAABFpLQBnQQ6M2xEgLORJDGNSKlXQjLGTnJBxPnvdkBp0Zegerq8vVMTIwkHJD6TWfv2AnTIxskT8xekF9yR/fyfJHOwQ7a6mcHMJQXq9bN6lX1v8s+jXP121QuE4AACAASURBVK5t87JbV3ZGLdlBUfS+KA+WTZWqlZJWP7qoy2R9ZhmyXsTXo6guysHnG7uzyIhKxZmJJRCsT437ntscU53zw0yk1nJEV5J2zaqnbMuF41aMJAy1edVqlSri3go750Ntv1U+LkwKAi2pS5Mip1ASBCaWQJZ3v1iNuR23vcsH38+MI5FZRvRZUA2PPp/E7T+cHLG1aXIGePDBB9nJIaelklNT+VNSDXsOELGouDx2LzYuRnIER3FIJ8ftd97ZOkgZR3K0TgFIchOoUXfenxpsbJwcYy3fnTtcBQEQAAEQAIFmCXiGZEfnQP9C3GSjNaevOi9BY5dmjE3wZXswrjkl/6wtPaKm86d3spR/QymjG6ktgOphY7eY5qrxJXaSPEpjf5KwSrHke83o1zRfh5pNy25B2TnUI+KydzkVVN0UDohIFdFksNE2Esiphajk/tRGRVmvXPrEyMLl9iag1RejUWhCtVd1vam2StbnJKPTGlOr8EgWx7NsQtEg8ZQEWlSXUqaK4CBwPhFo5t0vlhO342Ynh3yvNb4XSeEsw/5Ok62PIhNoj384OdqjHFquxQMPPMhrckgnhvz3nB5yzY0hMT3VMGVxcLCT4w44OVpegG0rcKydEGMtv23BQjEQAAEQAIEOIVCtxI3QUI6JxIYrNsSFOjcJOiz/f3vnluQ2jqzhWpcWpDdv4Zxpt2350u5W32/zoA30a0VoGfWsDdQGZtwz9gmcAElkJkHcKFEu0fE5wiFegETiAwgV8hdAj1UmLa0Bq1x5zrnL6qeBluSv8Ic+IP4mV58YG8/CtkV6rc50TtpzOqXa95PNflslvVbz7zK+ZX8vs611OL/tyv61iRxdhxZRa+KL9F3/joHwTpzouSm6ofXcHcLKkXxAoGiKm7dPwPQXRI7QXPoMdGPY7YEJjvLZTEDbtPYd1GyShBCAgCGgz9g5f/sZQ+lD+Xt/+veM/s1ceS+d2Cj8TSPfiRVbaS9v4ioix000w/JO/PnPf3YrObyAce3tqt6++2a5CrCSYzmWV7F0bRHi2vavAgWjEIAABCAAgRkEzESo8Rfm8gutKL1MbGrihUxaChMbU4NceSZJ4bBQP/Ej8Qt8a7GYztv3Lyj3W02FTFpmPYAzJ22wP+fzUv9qZan/kwB/LWv1fsF2sU2M4dZ0JoscSt5aPzV+xn1/ZOMMQVGCAH7rt7B9Ws0fqQEHayNw022s/bw+rhXAS5+e04/12Zm9tWLBFW49FYGF+tJTuU+5ELh5Av4Zu+Rv00oFZRyPRA653iBKSNrSd4GO/Rd971Sqc83biBzXpPuEtv/880/36dMn121H5bekMttShRUdsnojrOr4O7xcPP6cblPlV3H0Kzk+ujfv3i1X0zNFjvttv4XS3WbvTiVvTvduv924zbDl0t3dsPXSZuv29/mc4T0RIb3/3NTy7DeuSy8+nboXpG+GMvt7G7ctlNtX5eTu91u32Qz2xOeN2+7vi/U9x+8UvlOoi/U9Ot7eO+dOeyf16y6krDn/pviezd2d88ma7WfMcRkCEIAABCCwHgJzgw1hwjGdlIgYEQd6JzCCjYq40OULaaflTcwmLxTqJxOsaJI2sRN8aJi0dXkLZRZsR5rRJOVyF+b4Vyu1bOthWL3gRaD5/wq2r9Z2xsvmgLP6OQnARjbkGUmuCjJld4dqt5vcR7bi1Jx/AQRmtnF4r4H/pW74v9sdunddTGiI7cz7Y0IGebb68VnEa1NGKCt8znq8xf68MV39KOd7fHxwx0PY2q2BS6h3/BnsRO8GmfKNntPYjpxrupQgLPUL35+hfMO9X4knBv0ysum7gXb9+7dsqtzxrP4zGJn46X2IeWd8kLymTqEPhc9ZfSlXMa5DAAIJAjoGXSwYyDhu/n5u/Y4JnomNwphubK51bEDkCA3+hX3+0Ykc/yfv20gKG17cuEDg8CLHfz9+dG/erkHk6AUGK1JMjpNBeV1ZMEkfgvwiYow7kQTu/f3TvduG9InP7PstrGiQyHd3t3VeW5j+O9/vqa15IoTUexAwpvYMi4G5zZPjnGyeqXGuQAACEIAABG6cgAbwWyYQEqQIgRhTOwngJu6ZZH6TKXcYghy1iVapvLHN3JmWFdev3bZODFPBqWnJmr5WP8si9m9qd6krc/yrlZnnq9s9+UBjYRKbLSJv+3ptZ5yRyXXNd+U56R+xDTlvEPgk7VB+fG5c5fALIdDcxqbP5QLGiXFYnpvU+2M6hPrMhb5s84RAdPw5a+xqCWylmlPY5MTmx07ciH2bnO/8qqhUAeFaH7Sf5LOcRxXWtiiP95ousA0l+k/h7NvN1HXqRwgqPrhDJMDYtGVh2fhi62WPE/1n6qfpLzbvcBzzkDom0gbfR2gtII4hAIELCehzHz+bsw3LOG7Go/BcZ8aOSRliI/c3lh+LB6G61eakkKe/gMjx9G1wFQ9+/+OPfiXHf/5zve2q/v2hEzlev327XB3kF/4bt88vrJiUV1vJIff9Cozt3o0WT5xO7nS/dZt9LBdYoaBfcaEuDasrgvCQiMBL4H6zdVu/cmSzdfcnY+HerHq4S9XXiAFdXltt7/Pebf11e7k7vszvibnRBbWdFWacpkmtrBEuSYFG8+btjxziBAIQgAAEILAqAhp0yE0ybHU0oJEKRDTbkolNLlgVyiyXF1KVPks+yeQpVZnIqKRtmmjNmUhqHUOQJ3xOfzEcOXX26Rz/yoWU+Pqcl6zkKNmW9li87Ux9JdBYeTYkXaI/yz21Ib5X+pKkC3VM2DLecvglEGhqY31+vXh4eHh0GrOPftkf+o6wMXkT/U+fuRC4kozdqoHjEFS/KEAm478+E7aU/LEZK0v1Cu8eUijO7yX4cAzvtPFBs1T9+pLluevsHMeCyOOje3w4uN3RrkxTpmUumq4scgyrUHa27Eh4ORxd3xY7dzia9h+9qD3H1/gxu/9YMebQiyydaKSw/eqQXQh2ZsVt9aHMLN8buAMBCMwlsOBzJ+O4H0vV7jM/HrS6JTamY5Vfkaci7gybrWV/xnSIHJ8R9ucs6vffVeToVmtEqzbCNlZ+y6r0//wWVd1WVf/+4P41iBy7N7ctcmhQ3W+NpCJDrT00nxcnMqkLoozm9wJHZhstu1IjFkoKtjPedJe13PP8Ltl2RsAoihCmXqN05npc3b5cRI4yf+5CAAIQgMCqCUhALRGcTVVMJiSZCYexN9m2R+yZyZAPIpVeIlsrT2xmDow/qXIkmDUJmE3tSdpEYHCaWuuYKneU3vgYxI3JZ/WXxyOLDScz/CtZM75X61myk7pXsS3tsXjbGWfEh+kEXFMpy2TgNGUjdU0N9kepNKlrcT7O102goY1HQoTGlsf1lrEz0XeljGj8NdfTj5X29Yue95Jv41pEZ1p+LBIok8oKKVPH2IYvbGwnBzdyywT4ylzy/sdlp3zzaWTcG0SEZDs117GwoqXQRpZR9nu+4oPfZmsRwSxuCs4hAIECgQWfOxkjDu4QVlsUxOOkU2JDtxWM//6dbtGXtHTTFxE5brp5znfut99/n76TI7ybIytsBMGjInB8+LsTOETkeP3mfEfjnGcG9mWlxkRMMKsh0lH12IPhXPOVs+WD8io29O+dSBek+SdCyFksLvc77We4qv6OxItw23xq/cNqE817l4WqaWr2TVEcQgACEIAABG6fgA1CLBi4HwdA+r3hH/2vX8MvYKPtNfJBoQsnY9X6qf1cQMk2ogSXFmQV7AufIabWszq6w24n++wnA+jBwOxPrXuef8VolW8lf+l21bb6v3zbGcfEj0Sg2A2/6Db9OckyaaPuvzxHtr8lbRl/OVw/gWob62qGZIBbCGgfS/VL6V8SlNL0+WdK06RsStG1AwlspZ6rUmYtf+yjMmnxa1r3UKbaGdsP93Of6le5fE2Xsq9+FbhI/3jmsgKDFUPs+NG5r3U8t/+onyVBydR14oN3RO+XmeWYcx0CEJhPYMHnTsZxI1Akn/WClykbsgrM2i0IsgXzt3ILkeNWWmJhP3797TcROf7666+rbFkVRI5Xr18v5/1ZgX3/HuvMi8fPtKcvxg4B+nwVpewocD8N8qdtSLpYoDGrHrwAkl1NYs1Kfc/325qbHs8RITStFzX8lmD9+zZKvmkeRI4pfa5AAAIQgMA6CXTbbYSJROukRIIrhQBMhyPaViOUYz799irVX3E2lzdtg7b6qQ+pgFNs9ZoiR1yWPbcBpeWCQVr3c2y28bW1aD9us63+L992xlfpg2aybfqx/cVhlqPYiJ4bmdxH17viM4HInC3jMocrJ1BrY+k3mdV0pvoyZiWj2eNnyD93fX8u2dU82f5uys8eSlmpvp/NNXqX0+i5n2tPGEdB+rl2xNVWLppu5P9gR8f6Uhvo2FBqA2n7+Ptd6lgqo3dIbET9p81Psyom9qEzryxK9RDEHEAAAgsQWPC5s2OJGVNL4uukAmJj545+28Xwg6juR1EP7jjaYjAaryfGbvcCIsftts1Fnv3662/u46dPma2owoqN8Pm3+/B3v3rjw4e/XbcdVe5z2KbKCxwicuxuV+QQASH5/oc8Ys03iCfh3Rulz5zIEYsXUbFSViKd3BvK3UTv9YhMuTh97iXeo+uR37HN8flMEcIKNUMdysXNtD92jjMIQAACEIDAjREYCxBzloHnAh65Cvp9uccrEZ45/46J/oWvGqiJ4idibm55fcZ59ZtTxpy0y/5KVSelsyaPQjJ1oDbnBZjm8U2VnL82z/ac9piTduSfnbjnxI2D3Td/lLs/ERtxQDffBhJEjIODWVuJcrm0TgKVNpa+kemPVniT49wgK2WpiJdLOnTmujjdQt0Gtlp3hPJ2jb923FIm9cB97176+2e+nVDZ/LMcUvSfmq4ocsTP/chI2vdRErvtVmRL66htLv0k16eiTiE2ItutPsQsbFvGNjiHAASWJKBj0MXPnYzjw7gr589canxL1kLyxH8f2dTq87Irmm0Z1z1G5Lgu3yez/suvvzaIHDPEDS96RAJHEDlevtotV0/5tX/qRdz5YmQ1RSQUSNA/up631N+RfCVRI74XRe/FRqXsWrr+BeOx2NK/CD2uh9iKfSudR37HNsfn80UIaRvvQ4VF8zs/xk5xBgEIQAACELhBAvYlfv2vptqdDIGV0kSk3ZoGq3L2zilvfv0k+F0J1ljRom3yppOyiyeSNmAlW8vMYJ1Meo5/8/kmi05enG/7em1nHJSgauJXhiZZ8dDaiAK6EiwctWvo+9H7EnwhBVtFH7i5HgKVNtY+c36Q2sKQ58gHuGeMgxeNa02BLevlcCz5xr/oFSZV/4PN9DM2306w1zqearrU90hb+ep7pD0EZ7rPnC25nhM0UtejgsRGhXc5nbK4qC+Nas0JBCBQJrDgcyfjsYrL9vuk6bkWG7m5wFAb+V4cj/3lut7OXUSO22mLRT35+RcVOa69XdWLNYgc567kqAbl880mgkPFRms6d7p3++3GbaxgEdlutpV3u3JnpsgxWclRE69m2q94y20IQAACEIDAkxAwE4R6IGvqYTlYMU1fvSITG50c2TyzyzuzflLOKMhsPQnHGlhqmrgtvd94hVfwsv1z5kT3TL5N/pxp+3ptZ7wW3yoTcJNlcli0kehXpbYu2pqUzIU1Eqi0sfT7SoC5qepSVhBMav185riRc0L6eK28sQENoI2/N4RJdRwP9vS5s/H7+XaCvVYumu7JRY4L+o9wqtgop1MWbd+pgTWfEIDA+QQWfO5kHLfjsdr3K8Ts+Jr0WWzUvgt0zF7jeIHIkWz99V/8+ZdfhpUc49Uafjuq6pZUdquqxOqNsFVVWMnx4uWr5YAtvJJD361RC65HVRA/Su+PiPJEp62CQ2s6NX9y99vN8H6L6KXmC/it5aSO5ogQmta/k0NWdETCzLgUzcM7OcZkOIMABCAAgbUQMJODw4OLfkzeUAmdtFQnLA3WfBIJViUNzi3vgvq1TrAkGFibiAUAWoclJmQSLGoO4gU/cp9z/LuAb654uX6B7au1nTi3zMqJSt+Rtu0ChpV2qdgynnO4VgK1NpZ+bwNL51RW+5oPuMuYXAxca56LxjWpQ+t42n1pDO8MSaxwmmsvx3iuHcGuXFLihSQz4ncq3Xgs0FzjIx0zk1+fQ+KsLanj+f0na3vsqCunU2YX9aWoTE4hAIESgQWfu+xYomPUs2e7stAhNmrfBWpzjeMFIkepT6743k8//+w+fvxUfr+GFTNSxxWBI4gcX9+yyGFWEswKmp+bz/SZVvGiNZ0x7ey2Tl5AkH8L+C22kgftIoTUK6yiafKt3X7SPS5CAAIQgAAEnpiABK9KEZGSjzIJOT8oMjKfCzCFRDPLu6x+bROncrAmOG4/F5xI2sBYMQBpy68dt/t3Gd+yH5fZvlbbGZ9rfdUkzR7WbMj9Z+5wPLpdt11MZsIvaTP3s05wYzUEam0s9xPB/hmVlDEtCKdNdtvHjaIrMsY39mPjW3pP9raxIPg0qbveGJ6/uWyVS3GlpK1H4vtY/CqO81rXhIlQk7zAYHw4N1jY5icvHpfG4AACN0NAx6pzn3+piozjibmBGWe80HHM/bpKbBTS+AIlXcPqEHHwdg4QOW6nLRb15KefVOS49nZVz1+8XM53WYkwb+VFaZWA3Ls702Yt3+nebfdGaBhoSJC/uHLB6cvCK+nGkFUMGIkczumKiTP9HpcTn+XLHaU0gsZYgwkrUHJt0Wh/VBgnEIAABCAAgVshEAIilQlEwd0QiL54QuTLeAz+5F9MOK+8YO/8+knAJjcRM5O1UlBpjHC5iaT6t+TkrtW/y/mOudizy20rm0z7n9V2xkfJn7FvkmYPG2yEPi8vAM51tAZbWT+4sQ4CDW2s/aXSL/14e3yY1lvKGI8p1efJCq65PjotbXpFAlYV/92jezgeRHgoBcuUybhOk8JN3VPfaWqn5tvY8ix2XshM8BMb1xQ57ErK3HdeqFqm/7T52S5ypFgEF/iEAASWJND6t19DmTKOJ0QOn13u++0Qa2lK4234W7Fgp8Hdp0yCyPGU9K9Y9o8//TR/JUfDyg27VVVYyfH86xfL1cSKHPcndzoV/ptSRchICgX3bivvsdi4zfbenU4m8+nk7vdbt4mFChOov7vbdELGJF94R4aN5A+mLxU5fP7Ndu/uPQPjrndet6tKiAUX+h1se06pf8Laiyj3g2envVN8RqiYtEfpXl9a3X7KK65BAAIQgAAEboCATDIO7uHx0T22/LduS0CoNAGxGXxg49AF1nxZ8u8xClblgjhzy7u0fp2DdgI1fiH740P4ZX3LS3mltl7Nccddv899KpA2SumDeIdj3z7mxqMPMO12skXLsoGgRv8W4Ptw6Ouwi4N6C9h27hptZxshtH97/ze5+8OWPi1pfJ8plCXpCmkmDnBhVQRa2ljS9P3FCxl2uPUn/rnrVgXFz50Zm6arDnRcmN7rKY5EgIdhjH88upSWkuUuz34/3o6/lx7cw8PRHYdxQ4S/0nPRFeTHy37M9Xn8eDNhYgWT3HdQNKZk7cQVjtrkGNh437qxvG+rXfBx0i41USDQ1DEvYSIkyq/k6PwJ49o5/afVz3q6RfqS1JgDCECgTkDH+NrfplVbMo5nBAw/9B3N37CpMVdspL8LjnbM9uN6dklI1dsnTYDI8aT4r1f4Dz+2ihwf3L/PEDeC2PHfjx/dV1cROe7knRN3IlCMr9ntpyQwPgmqD4z9aovNOP/EbiqoPxIM8vmtL6FVlxA5Jj5GLFLlduWf6/coX0JA8cZHaZRJwCf1zq0kMfmT/pv7tv7BfuDLJwQgAAEIQODmCMgEQoM/GjRKX7OTCJmglKIpUaUlT7ftzrQMH9A38scot+RtLe/C+knhowDV1OdcwE/yTw7aJ5JS5wwvCdhNyrjkQqN/l/IdcY0C85faDtUflbFE2wXD3Qy9vH2USZo9FP+i+o8yaHsU+1qTrZFhTtZGoLWNJV2iz5uxxI7nHoWON5n+aOzGeTuU5r79LmkdsjsbM5/9Tmhoasex0GH9s8dVeyJKFNgmKqxsU/k8b/Ocl/KngoFS/wVEDm8r046Wkz9O9QGpZ9FP09dy6TI+JNBI7TmAAAQuIaBjUOrZnmVZxvG8yOHtqZiZWMEmNlJjpr22c4eVChyeASLHrJ61nsQ//PijrOS49nZV/3j+9XJgZCWHBs9toNse2wB5VeToPDy50/3ebTdhy6ShjE1ilcaoRsNKj1gkqeSTYH9OeBnKyKY73bu9X2GSKHeyGmXkbzg5z+/aSo7O+slzNG202bq9X9Rh2s+2T/AofEp7FYSQpP1ggE8IQAACEIDALRJonkDoZEInPm3BlEm1Hx+6X+H27xYIdneyWmGSXi6cUd5F9ZOChwPz6+cQJNz5lyY+ZkWZ2IKez5hIBl7hF76m7H6Fh1pd7qjRvwX41ldyhD5S/9S+GZNYsu2MbQnCZQLCJmn2sNXGwLoY4Gu1lXWGGzdPYFYbDyvkEmPHZHWHr7h5nvPPkg1KZfr943G0auLZ7pDfcz0F3PgRB9W7893O7bzNs8Zev3DC+zesZAnj6bOW7yDr7KPYGfnovxPilTMmWyjb5tFxXMfd1Mq8NvGg7XuyzdbM/jPUs812g8jh7V3alwx7DiEAgRoBHYNK3wE1K919GcfLIodd2ezHRS8yyz+xkfn7z4/j8ao8ybyeA0SO9bTVLE+//8GLHB8vWqURVmuUPv1KjkVFjlm1JDEEIAABCEAAAhD4QgiEyUfuV5hLV/Nzl7e0/9iDAAQgAAEIQAACEIAABCAwEEDk+EK7wv6HH5wXIEoCxRL3fBn/+9XzL5Qi1YIABCAAAQhAAAKfg8CCv/Zqcvdzl9fkFIkgAAEIQAACEIAABCAAAQicRQCR4yxst59p//33ncjhRYhr//+ff3x1+0DwEAIQgAAEIAABCNwqAdkypbYMfaEKfO7yFnIbMxCAAAQgAAEIQAACEIAABFIEEDlSVL6Aa9/tv3ff7ffu2+/27v2337n3337rvnn/rXv3/r1798179/bdN+7Nu3fuzdt37vXbt2735q3bvX7jXr1+7V7tXruXr3buhf//8pX7+uUr9/zFS/f86xfdS8b99lT+v1/B4QUORI4voMNQBQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACKySAyLHCRsNlCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEnEPkoBdAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCwSgKIHKtsNpyGAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAkYM+AAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwCoJIHKsstlwGgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAUQO+gAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAKrJIDIscpmw2kIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQQOegDEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIrJIAIscqmw2nIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQQOSgD0AAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEILBKAogcq2w2nIYABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQACRgz4AAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDAKgkgcqyy2XAaAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABRA76AAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAqskgMixymbDaQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABBA56AMQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQiskgAixyqbDachAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhBA5KAPQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgsEoCiByrbDachgAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAJGDPgABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgMAqCSByrLLZcBoCEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAFEDvoABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACqySAyLHKZsNpCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEEDnoAxCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCKySACLHKpsNpyEAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEEDkoA9AAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCCwSgKIHKtsNpyGAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAkYM+AAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAwCoJIHKsstlwGgIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAUQO+gAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAKrJIDIscpmw2kIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQQOegDEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIrJIAIscqmw2nIQABCEAAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQQOSgD0AAAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEILBKAogcq2w2nIYABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQACRgz4AAQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIDAKgkgcqyy2XAacKDeMgAAANtJREFUAhCAAAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABRA76AAQgAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAqskgMixymbDaQhAAAIQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABBA56AMQgAAEIAABCEAAAhCAAAQgAAEIQAACEIAABCAAAQiskgAixyqbDachAAEIQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhBA5KAPQAACEIAABCAAAQhAAAIQgAAEIAABCEAAAhCAAAQgsEoC/w+nwZbLeiqJ9gAAAABJRU5ErkJggg==||font-size="10pt"}} | Where the *.bval is a text file that contains the value of the gradient, and the *.bvec is also a text file that contains the orientation of the gradient. |
| Line 52: | Line 53: |
| Where the *.bval is a text file that contains the value of the gradient, and the *.bvec is also a text file that contaons the orientation of the gradient. The nii.gz file is the NifTi file of the DWI where the images are stored. | The nii.gz file is the NifTi file where the DWI where the images are stored. |
| Line 54: | Line 55: |
| '''Bvals and Bvecs are '''the bvalue and the gradient vectors. The files .bval and .bvec should be created from for the DWI acquisition. If you don't have those files (and you can't create them yourself (no easy task)) you should talk to the person who programmed your DWI sequence and get the files that are specific to your use case. | |
| Line 55: | Line 57: |
| For simplicity place your bval and bvec files in your same data directory where your raw DWI NIFTI file is with the same prefix as your raw DWI NIFTI. | |
| Line 57: | Line 60: |
| First you need to create a new subject in your protocole, let call it the 'BrainSuiteSubject'. Then import the T1 MRI of the subject and set the fidicials points as explained in the previous tutorial. | === Load the T1 MRI data to brainstorm === First, you need to create a new subject in your protocol, let call it the 'BrainSuiteSubject'. Then import the T1 MRI of the subject and set the fiducials points as explained in the [[https://neuroimage.usc.edu/brainstorm/Tutorials/ImportAnatomy|previous tutorial]]. |
| Line 59: | Line 63: |
| {{data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAekAAAB5CAYAAAAd39lgAAAbvElEQVR4Ae2d6dPUxLfH57+xeM8L593vlQWoF0uu4i1uCW5D+cblqmVpuYAoWqiPIgWu4PKAPriAheWDAiIqoLiglpaWD7jvO+6759bpmdPp9HQ66elkMst3qk4lk6S7T3+S9Den00kahw8fpiNHjtCyZcuo6t/k5CSxLV++nBYvXqxs4cKFxLZgwQKaP3++snnz5hHb3Llzac6cOX2zquuP/EFgsAhMU6vRoIayJrUmpmlmsByENyAw9gQasSIdIu4Q6bE/3gAABEAABEAggEC0SAeUhU1BAARAAARAAAQCCESLdEgkHeAXNgUBEAABEACBsScQLdJjTxAAQAAEQAAEQKAiAtEijUi6oj2DbEEABEAABMaeQLRIjz1BAAABEAABEACBighEizQi6Yr2DLIFARAAARAYewLRIj32BAEABEAABEAABCoiEC3SiKQr2jPIFgRAAARAYOwJRIv02BMEABAAARAAARCoiEC0SCOSrmjPIFsQAAEQAIGxJxAt0mNPEABAAARAAARAoCIC0SKNSLqiPYNsQQAEQAAExp5AtEiPPUEAAAEQAAEQAIGKCESLNCLpivYMsgUBEAABEBh7AtEiPfYEAQAEQAAEQAAEKiIQLdKIpCvaM8gWBEAABEBg7AlEi/TYEwQAEAABEAABEKiIQLRII5KuaM8gWxAAARAAgbEnEC3SY08QAEAABEAABECgIgLRIo1IuqI9g2xBAARAAATGnkC0SIcQfPbZZ8m2PXv2ENvTTz9Nu3fvVrZz505i27FjBz355JPKpqenie3xxx+nxx57TNnWrVuJbcuWLfTwww8r27x5M7FNTU3RAw88oGzTpk3EtnHjRpqcnMy0kLpgWxAAARAAARComkC0SIdE0rZA83+IdNW7GPmDAAiAAAgMK4FokQ6puIj066+/Th9++KGyDz74gNjef/99be+++y6JHT58mNgOHTqkbGZmht555x1lb7/9NrG99dZb2t58801ie+ONN7RxeWyvvfYavfrqq8p4nu3BBx+ka665RllIXbAtCIAACIAACFRNIFqke4mkWaCr+v37779k299//01if/31F7HJ/23bttHSpUuVVeUT8gUBEAABEACBXghkijRHnLfffjutXr26FLvtttv0/ejhEukZmmg2qNHIsWaTWhPTNNPLXigjzcwENTs+tqbLyNDOY4amJ1rUbDYtFk1qtiZoeqaimufWa4amuXzb3dL+11RvmqZWZ382J0LZxqQtDZyVUdX7ySoOf0FgRAhkivStt96qo02JOmOncv+Zu7flJ93dDz30EF100UXKrr76amK7/PLL9bL9+/cTG2//559/KpM8eGpHz//884/2/48//iDbXnzxRWJbs2YNLVq0SJmZXzJfUKS1iDcpuE1NCut9LlfMIrKebukLAO/FSnOi/IsUT71mtF+tSkQ6yT/vAq2Ceo+QSCccq9lPvR/ZSAkCg08gU6Q5gpau4bKmQy/SmSHqDM1MT1BLR9wj1BhNt5LIuemImGc6kaZcpFQh1Bnn0cyERPUV8K693oMYDWfsiJzFle6nnLKxGgSGnYBXpCViLWvKj1mx8SAx+cnjUTfeeKOOmicmJoht1apVtHLlSmX33HMPsT3//PP07bffKpPo2YyaeV7+y8XFb7/9RrYdOHCA2G666SY66aSTlIlP6akRSWeKdCeFEfWFd1GmSx2Mf4Nd9+oa/0GoN0R6MM4BeAEC9RLwirTdRRz7/6mnniK29957T3dPn3322cR27rnn0oUXXqiM71+zcZf7unXrlF166aXE9sgjj6gub+72NgVZLiREmPm/+PvLL7+QbS+88AKx3XDDDTR//nxl7l0R0GBTyLbu0gZqqb7oKNaFP93qdAv3KZquTKQHot4Q6YE6F+AMCNREwCvSv//+O5Vpoy/SRJlCpRt+7prlQTTSVdugRrOVvo8tXciZg7QcR4vOv0GpgN9ePjNNLSvf9sAvX57FRJp0F7HV/Wz74CgqSWuV5Uqry+m+V5yqe6ecGVedmfl0xoAsXabli8tvXqb9KbHe9j3pmWmaMI+ZBg/YyxqomC/wwUyMuqt7zPrWDu+DjEGTmkux/WQUgVkQAIEOAa9I213Esf/l7WH8nLNEuccddxyxzZs3j+bMmaPs448/JjZ+3nnv3r3KLrnkEmLj55r5WWk28eeTTz5Rz0Hzs9DPPfecsmeeeUa/weyJJ54gNn5jmbytTPLl7nQp131UhEXHWqRttdANf4taEnHKfdyG0bjrwVDdDZs5aMvOnnT+HpFu+QaAOQTJyLORKQhuaqmlRj5dfsuGukG3/HCl1dt2M7LzT10Mad5GOlfUb5RZW71NkQ7db2ZaxyjGnpio/WScC0VYBuwnOQwwBQEQSBPwivSvv/5KZdrIi7TRuNtiYYooi21TP641Q9M6oksioIYapGXuLB6cZoqsIey8WVbZxnIl8s2W8bgUD/oyIvoup42eAW6Ue33MzPDBUUS7krpBLyDSHSx53d3JepO3gkUz/DiZCI3DKX2xVVe9DaFtX5w1qaWPE0ofC10XGslxZI+NKItJcvy2fZELSLu89qEpx5h1zHb2IyYgAALZBLwi/fPPP1OZJhEtR9Jy7/iUU04hNo5mjz76aGUvv/wysXHkKwPGzjvvPGLje9JffvmlMumK54FkH330kTLzbWTyJjJ54xg/+/3KK68ok4ib3zZWRiSdGt3d1WimRZQF2NXRmjSg2Y1Zsk1BMTMEsmFG7MYxkQiSq1zuHjciTxE21d3KXcZZXa5GAYYPDj1sb1i2SKfKdNE2u6ktlsqjmuttibSTm1HHtDhmiLSxvSn4xp4yuu4tJkbadFnt1Mlx2X0M+dalysYfEACBLgJekf7pp5+oTJOPZLCQyjPXZ555JrEdc8wxdNRRRynjj2iw8ctULrvsMmXyVrBHH31U3yeXLnOO9n/88Udl33//PbF99913ehT4V199RWxffPEFffbZZ8q4O5wtSKS1QLlEq7OMI9UuzGmRdjVyriTOZaFiltO4qjJ0nhm+d+6h68jTyaEd6Tnl0PDBKTbshPYhWxzstL7GX6/LuCAStvoCxc5cbdAeO1BLvU2R9tRB+5/axi3SMUx02owLvcyeHHXoI5KW4w1TEAgl4BXpH374gUw79owHKMTMtDw/FiLNg2iMbkm9Q4oIld7YnOH77/wFsAlqWQOHUrcbs/LPWm4WkSWQ5jadefZlgu+ROqPr9iC4rouUGB88abOFI7l3mndBpPNIiVx3xfteb0OkfXXQ/qfE0yXScUz0xYDzYqabl7nE7aO5BeZBAASyCHhFWqJSmYYING8r6WTK78lm449iSHe3fEBjw4YNtHjxYmXy2NUtt9yinpfmZ6aXLFmi7K677lLpOQ/piv/000/1BzbMz1PKZymly/zuu++m9evXK5NntvnNZmV0d5MakS0RA98DtWJKj9jYO6fddZ7kJff70tOCEWeRcgNEuttXe9QxC7XVnR/jgydtduOfiFSamacHJCVydi27/89MV1xvQ6S9uujcd0n9k+MwWRbOJBF4HkgX+sveT6E5YXsQGD8CXpHmLuMybaRFunPsJA1SQRG1jjkdsaS6lPlxm/YjQzx4rN3IFszfI3K66Kw89QZFZrhrOBHBVFse44MnbcLa7qaPEaQidTW3qajeAyrSieibDPzz2fvJnw5rQQAEiLwi/c0331CZxveT2fgzkjJqnN/ZzcYvL5FPRl5xxRXEdtVVV9G1116r7LTTTiM2Xn7nnXcqk/vQfK+ZX5DCtm/fPmX8iJV8GlOi5t27d6uXqfDz2jzPtmLFinIiaTmaDFFJNWjG8pSASbrUvbtG9kcrsgQ1K/+s5Ua57vvBidCl6mGm65rPSNOzD+l7+Ta37MY/w48uf10LekmbkSam3hWKdPH9KXwQSQsJTEGg3wS8Iv31119TmbZlyxZi4+84y/1qef6Zu7ZFsFstfpa4RRdccAFdeeWVyk4//XRiY6GWbvEjR44QG/vIXd5s8ow1j/aWb1aLgPM3qqV7XV6sMjgiXawhTISp6ki6mD/pAzZJkxKCGLHypE1Y2JF04kd492wvaZM0pdXbEOlUnmng5GbgumhIfAxnYjyKZ18paX+y83f7qBNiBgRAwEPAK9LyqFNZ07EQaR3pWvelPWLT3j+uhtXec0ZD2KhapPnRa7kvbpVluyX/s+qYtVzSqcHd0lVuleVJm/hni7QhKoH3mtmlJF/LF8Pf1GyWj1nLjcTJLQK7rOR48ImqTp8SzyStKfB62ygm3azb1XGXyesSnllpDSCYBQEQSBHwijR3I5dp/LYwtpdeeklH6Oeccw6x8Ycutm7dquzmm28mtvPPP59OPPFEZTzPduqpp9Kxxx6rTB6t4ueh5ZGqqakpYrv//vtJBo7de++9xMYDyHiAGtuuXbuUcZd6KQPHOliThtBqdHMbbEOAUw2usb+MCwB+FWNqbFpW/lnLjWzd3d28QdLw8qtLXYPWk2zMe7N2Y2zk46ybsb5ovfIaf6Pe2SKXxdzwp656m+xtJgLdOB7SWBP/TZE2H5MKZmLwTOXZ8cUnxL51UhVMQQAE3AS8Iv35559TmTbSIs2ju81HpNKtZvYbwYz9kgh89xuyUnl3BpWlijAa0ULLjXKzRdp8fpkj3c47mlMD1+3PdFqvJe2Uk1W31EtgVL0KXnxwvlqkrDSuMlv8mc2k0u13V2dE76m8a6p3SqQ7PhgVSL19zh5Nb6S1BTW1HwKZJGnTjxmavtjlKeI5+ynZK5gDARCwCXhFWl78UdZ08+bNxMZvE5P7yWvWrCE2jqSvv/56ZRdffDGxnXHGGXTCCScoO+uss4iNv5Yl97Elyuf7zPJWMRksxt+uNgeMmYPG+H70zp07lQVF0qkR19LAO6ZdjaZ/AFSyU5IIyPmYjPooxIR+nWWqQaxKpNn11OtIHfXVXNKNd1IvlQm19HZ2Hi2azmrIs+rFmRvrhFeKif0hE2f57HPKU/2n1nobQtuaSPa51FNPnS/PSY6jNA8FLX0xGcTE6HlwpXMd94X2k0aOGRAAAYuAV6RlMFZZU3mG+eDBg/oZZ3lVKHdvy1vFuEub7eSTT6bjjz9embw+lAeScVc2m1w88GAx/nQl26FDhwrZjh07iG358uXFu7tdDZNe1qRmoS8ruSPNZL+0I/LUW65S78w2GkpTXQzBMhebQpZanhSYG5G2N5WIuakvEkQomin/zIyt+c6XnJK6GV9y6kWkHRcQ3aLEFxkTXV/+4veQq69IGdG15W3nb031NkWaLyIcX8Fq6fe/2577RLq9bQwTdfFivsyG978R5dve8H/7gse1n1zpsAwExp1Apkjzt5z561Jl2nCK9LgfIqj/8BHIF+nhqxM8BoHxJJAp0vwxCn539urVq0sxfg5606ZNyvjjFhL58mNRbPwGMX40i+3AgQPK9u/frz89KR/EMKdm17Y892xO5TEriZp5Kl/ikgh+2bJlOZH0eB4YqPUwE0hEOrP3ZJirB99BYIwIZIp0FQwg0lVQRZ4gkCbAn+Fs34pwD6hLb41/IAACg0wgWqQ5Ei3627hxI7Hdd999+hOUd9xxB7GtXbtWPXbF96ZXrVql7LrrrqOVK1dmmryhjN+/zS8lyTK+72wb+83GX+DyP4JVtHbYDgTqJJBEzzJWoOsd6nW6h7JBAAR6IhAt0iGlynPLLJjy1rCFCxcS24IFC2j+/PnK5s2bR2xz587VAipCWuU0pC7YFgQGisDMRGr0fLNlfeRkoJyFMyAAAkUJRIt0SCQNkS66W7AdCIAACIAACHg+sAE4IAACIAACIAAC9RLoayRdb1VROgiAAAiAAAgMF4FokR6u6sJbEAABEAABEBgeAtEiHXJPeniwwFMQAAEQAAEQqJ9AtEjXXwV4AAIgAAIgAAKjSSBapBFJj+aBgVqBAAiAAAjUTyBapOuvAjwAARAAARAAgdEkEC3SiKRH88BArUAABEAABOonEC3S9VcBHoAACIAACIDAaBKIFmlE0qN5YKBWIAACIAAC9ROIFum6qnDGVU8TDAzKPAbqOpZRLgiAAAhkEYgW6TIj6ZC8uHF+4tVPYWBQyjHAxxN+IAACIDBoBKJFuq4KQaRxgVLmRRpEuq4zGeWCAAj4CESLdEj063OE14XkBZGGSEOk884orAcBEBh2AtEiXRcAiDREGiJd19mHckEABPpFIFqkQ6LfvEqF5AWRhkhDpPPOKKwHARAYdgLRIl0XAIg0RBoiXdfZh3JBAAT6RSBapEOi37xKheQFkYZIQ6TzziisBwEQGHYC0SJdFwCINEQaIl3X2YdyQQAE+kUgWqRDot+8SoXkBZGGSEOk884orAcBEBh2AtEiXRcAiDREGiJd19mHckEABPpFIFqkQ6LfvEqF5AWRhkhDpPPOKKwHARAYdgLRIl0XgBiR/t+l/0e2SYO/6s6Hu9bxMlmP6WheHPDxhB8IgAAIDBqBaJEOiX7zKh+SV4xINxoNsk3El8XbXsfLZD2mEOm84xjrQQAEQKAsAtEiXZYjofkMs0hv37eXVmxbRLM2NKixLrFZGxbRin2feC8I1m+bnUpjptfzU5POPGLK5YuT9bssn9fOpllTk7Q+x2fXhc32fcto1toGNdbOpqUB6bcf3EtLmdvaRbTioJ9VSH0RSYeegdgeBECgHwSiRTok+s2rUEheoSJtRshcjm0SPf/nP//pWsfLZL1LcEKWbWehY3EyxNmen7Vtr1NkuZwVU/60Ki+HSMeUq4Uxy+dehZbzC0yrL1JyRDq0vhDpvLMT60EABOogEC3SdTjNZQ6jSOvokcVJRc2JGG/fN9mOEDtCOHdXd5S4/eAkze0l+pSotcdy9YXB2tk0d1fa57nSG5AjmuaFjBbaQJFOp8uOpHvhDJGu60xGuSAAAj4C0SIdEv36HOF1IXkVFWkZIPZf//0/xBGxK1LmciVSdq1fsmSJTiv59TKYTItMhqClItYNy2i91Z2rxcexzhRBez6mXF3mugZ5LxzWNcjXAyA+mfmpqL9AJM1cVkxZ3fwZDLmcXuoLkc47O7EeBECgDgLRIl2H01xmUZH2ia/Z5R26XehgspQAO7qjtYjtWtTuCneIF3fhZnVnS3p7GltunuBxeTrS9tSLtzN9mTuVXU+zDut3LSMdrfOFwIaOWGeItFlGw+OPZtnhDJGu60xGuSAAAj4C0SIdEv36HOF1IXkNm0ibwuOb15GmQ6RFMF0RrS/PIut85ealLyrS4j+Lpy2SrjJ0936nW5y72pN02d3drrzsZXZ9IdJ5ZyfWgwAI1EEgWqTrcJrLjBFp8XnPnj1dg8TM6Nq1nUTcoZG0LRJZ/xMR6h71rMRw7SJayvevp2anBqC1R4Yn94uz8s9a7is3Kw0v12KX0R0uafV2nQi4SHki0moEeafrP0kXKdLSK4FIWg5zTEEABAaQQLRIh0S/efUPyWtURVpHpVZ3rgiWPRLc/l/kvrAIpznNKtfcxp7nrmg9Ut1zn9zsgpZegERsuy9GzHLsx7uSdHEibdcXkXTe2Yn1IAACdRCIFuk6nOYyR1GkdbTJ3bvW/dTUOh5lvW1SDyxTzwMbA6tChTqVt1WuKZg8bwquXCDMMnyxt+f/Zje3rE/E1i/Ssr1Mk3S9i7SrvhDpus5klAsCIOAjEC3SIdGvzxFeF5LXqIl0SvysKJoFSouTp1vZjg5F2HzTvHLttO2IfrYawKWjaB7QNdU9Gl35LY9/WXXS9XHce7fLNP8n6XoT6az6QqTzzk6sBwEQqINAtEjX4TSXOUoinRIOjwibYuWaN7vEi0TTZZTr6/I285dubvE7Edv+RdKmP9wLYPoEka7rTEa5IAACPgLRIh0S/foc4XWSV5HpqIi0LRxFxFWEzp6m8grsto4qVwZhWcLn6uYWn/st0ik2jme6IdJ5ZyfWgwAI1EEgWqTrcJrLHAWRzhMOEbSQqe7y9oh02eWm8uuUq+/7Wt3cUpd+inTKP4dAs08Q6brOZJQLAiDgIxAt0hL1+gopum7Lli1FNx16kVZd0/JKTRWB9v74lAgfT/NEul/l6iiaB8EVNc+FhdQxEfdi96SL1hciXfjUw4YgAAJ9JBAt0n30NVXUMEfS/J5u9Q5u/ZKO7vd0iyiFTM2I0dV93Y9yZVT6IIh0SH0h0qnTC39AAAQGhEC0SJcZSYcwGVaRNgd3hXwBSkfIvueRZSS1dW+Yhb7ScuXDHxldya4LjSQirmbgWGh9IdIhZx+2BQEQ6BeBaJHul6N2OTEizRcWtsmbxFwf2DC3le16eeOYGemGCLQSWRmclfHIUipvS8hT6zLSu4Q0Va5D+CWNvoAIyLtKke6lvhBp+wzDfxAAgUEgEC3SwxhJm6Ir8yK+VYq02QVsPv4jYueb2sKT+clIh5iWXa58nYtfosKvJ5V7zq4u9qw6VSnSvdQXIj0IzRF8AAEQsAlEi7SdYb/+F42k5dOSdX+qMtX9WnAglS166h6rMdhMxFFPre89s0CWUi53Z/vKDejmFtGuSqR7rS9Eul9nLsoBARAIIRAt0oMeSYsosFhLtCzRszmVda5ImpfJeskvdKofSSoo0Cy8tkhzmRxRr9i2iGaZorl2tnrj14p93QPQyix3/a7i5ebxqUykjfvy+uIlhzlzhkiHNBvYFgRAoF8EokW6X47a5RSNpEUs6hZp8QPTT2kQGUCk7TMM/0EABAaBQLRID0skbQqDRMXmVNabYi7reZmsx3QwRTZ2v0CkB6E5gg8gAAI2gWiRtjPs1//QSNpsxEV8zamsh0iPpgjL/s2aQqT7deaiHBAAgRAC0SI9jJE0C7Ft0nivuvPhrnW8TNZjOpoiDpEOaTawLQiAQL8IRIt0vxy1y4mJpCG0oym0MfsVIm2fYfgPAiAwCASiRXoYI+mYxhxpR1PgIdKD0BzBBxAAAZtAtEjbGfbrPyLp0RTLui6CINL9OnNRDgiAQAiBaJFGJA2xrEtYyywXIh3SbGBbEACBfhGIFul+OWqXg0gaFwcQafuswH8QAIFRIxAt0oikIZZlimVdeSGSHrWmDfUBgdEgEC3SdWFAJI2LgzIFHSJd15mMckEABHwEokUakTTEskyxrCsviLSvmcA6EACBughEi3RdjiOSxsVBmYIOka7rTEa5IAACPgLRIo1IGmJZpljWlRdE2tdMYB0IgEBdBKJFui7HEUnj4qBMQYdI13Umo1wQAAEfgWiRrjOS5oYVBgZlHQO+EwXrQAAEQKAOAtEiXYfTKBMEQAAEQAAExoFAtEjXFUmPw85BHUEABEAABMabQLRIjzc+1B4EQAAEQAAEqiMQLdKIpKvbOcgZBEAABEBgvAlEi/R440PtQQAEQAAEQKA6AtEijUi6up2DnEEABEAABMabQLRIjzc+1B4EQAAEQAAEqiMQLdKIpKvbOcgZBEAABEBgvAlEi/R440PtQQAEQAAEQKA6Av8PFZ1QCPgOoaAAAAAASUVORK5CYII=||font-size="10pt"}} | The T1 MRI is required since the BDP uses the T1 space for its computation. Furthermore, this is required since it will be used to align the tensors to the FEM mesh later. |
| Line 61: | Line 65: |
| === Diffusion tensor generation from DWI === Right click on the subject and then select the item "Convert DWI to DTI". |
{{attachment:mri.JPG||width="250",height="100"}} |
| Line 64: | Line 67: |
| Then follow the popup windows by selecting the DWI, bval and bval. If these files are in the same folder, Brainstorm will detect them automatiquely, otherwise user will be asked to browse the files one by one (as it's the case in this tutorial). | === Diffusion tensor generation (DTI) from DWI === In this step, Brainstorm calls the Brainsuite internally, and the diffusion tensors are computed. |
| Line 66: | Line 70: |
| In this step, Brainstorm calls the Brainsuite internally, and the the diffusion tensors are computed. At the end of this process, a new node will appeare in the Brainstom database with the name 'DTI-EIT'. This name refers to, DTI: diffusion tensors images, and EIG for eigen value, since the eigenvalues and eigenvectors are computed at voxel and stored in Brainstorm database. | Right-click on the subject and then select the item "Convert DWI to DTI". |
| Line 68: | Line 72: |
| {{data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWwAAACUCAYAAAC3KRN5AAAfDElEQVR4Ae2d58/cRLTG3/+GzxFf2Pspuh8QEFAQXRcJwgssQpEoCogiILQAoiwElNAJhBJqQCAWQkvoJRBAIBALofcSei9zdWb3jI/H41nPzuzau++z0pG99pQzj8c/nx2PvXPvvfee+uGHH9SZZ56pxv05/OzN6uFXP4NBA/SBBd4HiAX4hCswFwvsENAD2LhY4YKNPkB9AMAOhzXliAZ2SLUANk5WABt9AMAOoWY+bTSwEWHjBASE0QdC+wAi7DyIq36LBnbViigdImyc2KEnNtLPZp8BsEPImaWNBjYi7Nk8oQBKHNdx9gEAO4NwyFo0sEMqQ4QNCIwTAih7evoXgB1CzixtNLARYU/PSQKg4Vg1pQ8A2BmEQ9aigR1S2VNPPaVs27JliyLbvHmzeuKJJ7Q9+uijiuyRRx5RmzZt0tbtdhXZgw8+qB544AFt9957ryLbuHGjuvvuu7Xdcccdiuz2229XGzZs0HbrrbcqsltuuUXdfPPNpdaUzgw/ANZZ7wMAdgg5s7TRwA6JsG1Y03cAG3CadTihfcU+DmBnEA5ZiwZ2SGUM7Ndff1199NFH2j788ENF9sEHHxjbvn27YqMHe8jeffddbb1eT73zzjva3n77bUX21ltvGXvzzTcV2RtvvGGM6iN77bXX1KuvvqqN1snuvPNOtWrVKm04sYonFjSBJuPoAwB2CDmztNHAHiXCJliP6/Pff/8p2/755x/F9vfffysy/n7//fero446Sts4OibKBPDQB4p9AMAejYClwKZI9Oqrr1arV69OYldddZUZv54mYD+07UV18tJFauedd/baoqX7qflVG9X6bZ/W8p6Mh7qr1ZJFfT/n16X3gXTorFqhlizdL6fDokX7qSXLV6tO98WxtHtYu7RfVP+YdK+t3ds2qvnB8VyyKkzbhyLyjuviYh8nADsxsK+88koThXI0Grvk8WoaAuEPD4ncdddd6sQTT9R27rnnKrLTTz/dbHvuuecUGaX/66+/tHEZtLSj6n///df4/+effyrbXnrpJUV2xRVXqIMPPlibq7NSR6sCbAY6AezkbnpgunyT24aBTaYNXV+/boW5GHA7XctFS1cnv2D52sV+LVq0YizA5vJdbZXbxtLuCOg2DdisozxOALakV/X10gibImsePki1nHZgL1q+0RlFEtTXr1ut5geRuOyYoXBsWvqH1q0wETWByY6kH+oOIu9BNDgOeJVpsn5VP9ofh951t7tp0C07BlW2u44TgF0d0jKlF9gcyaZa0tQ9MrrByB+ecnfJJZeYaLrT6SiyCy+8UJ133nnabrzxRkX2/PPPq++++04bR9UymqZ1/s4Xmt9//13Z9uKLLyqySy+9VO2///7aXJ1PRthlwOZ8MhoM/RnLZTRp2fS2u0CQQr8mtBvAZkJgKRXwAtseRoj9/vjjjyuy999/3wxhHH300Yrs2GOPVSeccII2Gu8mo2GZtWvXajv11FMV2T333KOHRWhoRMKZLyoMafrO/v7666/KthdeeEGRXXzxxWrp0qXaXCd70Mkrhk+Gwd1VV9O28QWo6jBPZ3l/DH1SUfbYgD24H1BnuwFsiSmsswJeYP/xxx8qpc06sAm4ZdDK4EfjrS+qzvLs5t2ipSty495mmKH0Bl9xjJzLp7FVedPR3v5Qd6Oat8rt3zQsL7MquHgYwR6isH1wXZiyvPl7AK68nFaOI/O6bDvXs97VZtJ8nftmHtdZa7utMWw6bifLPqNv9rpvcleBfagmrCUt9Zi0uBFPOrluuPuO0/8e/QQzCMsABbzAtocRYr/zU4s0j5qj3z333FOR7bHHHmq33XbT9sknnygymk/9zDPPaDvllFMUGc2bprnYZOzPp59+qudZ01zrp59+WtuTTz5pnpx8+OGHFRk9KclPSXK5NOTC9cpOyeshETblMcC2xrszCKxQ84NIlCEjAUednGd78H7X0gYTl09p5b7c9uXlZbvgJPPSL4ZRZ8DIcqRvrDEt+eS2/XDl5bRVdJEXRld6168BWWdt7ZbADj1uMq9jhskomuhjJH5BVtHSd5wA7ABKi6ReYP/2228qpc06sOWJboNJ7qPOvmQwBZAuCJ1BpCcjo/4NvizqpXR8t53yS8jrk6lkWp9dL0XzfONQ1z24cafLtC4yVC5fgPT+EacuSh9sXagO7f/g5mYVYHOeYUMivF/qresiLWmKIt8obWK7BXT7x3s/NS9+EeT6gjU7R/Yj+15KKk24/5Ke5Av52Ne5+KuF65R9FjcdBYUDVr3A/uWXX1RK40iXImweaz7ooIMUGUW5u+yyi7aXX35ZkVFEzDcbjzvuOEVGY9hfffWVNh6uoZuQH3/8sTb5FCQ/AclPOtLc8ldeeUUbR+L0lGOKCDs3S8Q6gTQkBFBdUZ3u+BVmPWSdf/jQQaHekulvDGV5QlFenZ/AIX7+8olJYF2ynIYVhkfedQA7X2cRIrptJReJRrTbArbrQifbKMFcBmyZXsKfj7VPE5lX1sV5s35ZnGLp2gdgB1BaJPUC++eff1YpjV/gRFDlOd1HHHGEItt1113VTjvtpI1e8ERGD+6cdtpp2vhpxPvuu8+Mq/OwCv0K+Omnn7R9//33imzHjh1mNsnXX3+tyL788kv1+eefa6MhE7IQYDOsfEsdwToe4hjW4bnjD1vyz8yqkWiVerMyiyebPokHY+4ckbraT/4QBFzDJtIHF3h0HSXw9OV1gYD1M/scF09OQ0tzsXJE2foXyPL9TCQ+0XYLYJdd4HP+i3aWATtGE5O35KIfepwAbEHhgFUvsH/88UclbcnhG1SIyby0viCAPQCXhAKt+zq0nVZ+10Mh3Y2qQ/O8rZtO8gGdsvLLtufqKIGlTMPrdLPqZBpTdUTdBDTXBSvGB1/eMoiQZvywkysa5LbQ0pQhgCf38/rE2y2A7WuD8V+A1AXsWE18FzbWqGzp8hHADqC0SOoFNkervAyBNaXlfLyk93aQ0QubeEiEX+50ww03qEMPPVQbT+W7/PLL9XxsmpO9bNkybdddd53OT2XwcM1nn31mXv4kX6nKr1LlYZV169ap66+/XhvPCacnKlMMifRndmQzP+yTzAceu6P3h1eyssoiuzqAXfQ1P3uhD+38E49V2p5F+dWGesgPFwhouwSWSzvXNtdwkN1W+X39ujG3WwC77FeJbqvjYivbz/1QbnO137WNNZGwH2W6qus4AdiCwgGrXmDTsEJKm2Vg88mcdc7q4OG8tORIRp5A2Xhx/8Yj7RtlSKTsxC+DpfRr2Dqd1NJ3WdcsApv1GFu7GwpsvgBw+6sss3MiG3IDsAMoLZJ6gf3tt9+qlEbjz2T06lOefULvECGjB2X4NadnnHGGIjv77LPV+eefr+2www5TZLT92muv1cbj1jQ2TQ/jkD377LPaaNoev86Vo2n6gwSeC85/lnDOOeckibC540o4yc4tt0uYcT5acscmIJe9UKkMrmXll22X9brKlBGZbIfMZ6+X5RnVByrfl5f14kiQ/Snzg/f7lqPkLcvj8519cGlP+2SZZf1Fpxshwq56PI2PYogJEbagZw2rXmB/8803KqXRP8OQ0XuoeXyb51fT8AfDu91uK7IVK1aolStXapufn1dkBG0eOvnhhx8UGflIwyJkPIebZo3wO7cZ5vSObR6CYXA3BdhVf3ZmkKoWwY8Kjar+8Endh4x77HhUH3SZYnaNDa5Miyxys/0IBUxj2i0ibB9gXRpI2HPeUdoljy3/eirT01e+y0dE2KPR3gtsnj6XarkggD2IeHSULB5aGAYt10kmT5gCiKy3ApaVX7Zdll0W5WUnWv7iIPPK9bK6yrbLvAYIFdtFeTP/8sCmfVl5xX2yXtd6Vm6N7RbALoNkrp1ilktZX0qjiVvPsjrJx0zPLC+APQZg01BDSqOnFMm2bt1qIvdjjjlGkdFLmPg/Gi+77DJFdvzxx6t99tlHG62THXLIIWrJkiXaeLoezbfmaXr0X45kt912m/nvxptuukmR0c1HurlJ9thjj2mjYZcUNx35xM9OivzJPgxavgiFy2awTmoMW56E/Qdusgd52Cdekv9Z27MTk/bnyhFgyfJm736uOjZPeV0gMGWKyLwMeGWa5/zVDxrV0G4JbOsiZtooggP560P6zxE25ZF9MFgToacsk33xHQvXPgB7DMD+4osvVEqbZWDrWSJy2p0FJnmyyJOLOzwtGXj96Dx7IKUPw+KsEVlOWfll22W9fCGwYUlpeB9fJPQ7I8T7vsk3+dAQpZN+cT1lbbPz2j74/Gff7DzOOvWfLGTg7b9LY/CyKgcQueza2i2AbXxI8KRj7jgEasJ5SW/54I186tIFc9ZSHicAewzA5odMUi35H83pKUYef6Y/ECCjCPuiiy7SdtJJJymyww8/XO29997ajjzySEVGb/XjcW+O/mlcmp9m5BuN/E/sdMORbzDyuDUt+Z/ZQyJsOnGqmOtBBx94GDAyMnLVQ1Huyeuyf5aRJ0dZ+WXbuU5auk4ouV+ekC6/eJt9Issy9EunBo+Cc3pe6puGjptn2jcR2dkXAtk2LiunyeCBH97nWvZ9zkAufa613QLY86uyY263wTnvXeSVemg9IzSRv0hsP+i7q9/bx5Dz/c//3TEasRZ4Lu8YNt/IS7XkOdLbtm0zc6j5cXUaAuGnGWnYg+yAAw5Qe+21lzZ+hJ1uQtJwBxlfSOhGI/9zDf9Z77DlI488osjOOuusykMi3NlcSzrxl1R4AxzltcEjIcHRtHyqUP79mDxp5M9aCS9Zftn2XJ0lsMylMZF08ck/+tsw19vaZH5a5zfOcdu0ZoOXSpVdNIb5b0PVBhTV65rXTpouobrFrwXbX+1zXe0W0KXjydpx39MXmpK/pJMXfpcesZpozcWDU7p/iujfpaN9nADs0a48pcCmd1HTW/BS2jQC29X5sK34p6rQpDmaVAF23ccLQyKJgT2OP+Hlf5ehFy9xRExT7cjoyUWa7kfG/wZD/+HIL2lyLeXwBw97yCUPgXA0TUt+YyBH9vSv776bjnV3bNTfHBBOy7GQwJa/tprkP4CdGNijFefPBWADPk2Cxqz6Qq+OpaETGjaRry9oUnsBbD8ry/aWDomUZbC3U4Ra9XPLLbcosvXr15vXpl5zzTWKbM2aNXoqH41l0385kl1wwQXmPx35vx3lkp+MpPeB0AMwZUbj1LaR32T0pkBE2LiQNAlmo/gio2ozzj3khVaj1JMqD4BdlZr5dNHAzhfn/8YvYyJ48tOKBx54oCLbd999zX8r0r/PkO2+++4GpgzVcS5TdUaUgwvApPsA3ZydF7Nw6NUGrlfdTtqvsvoAbD8ry/ZGAzskwgawAbKyExjbF1bfALDLkOzfHg1sf/H5vXSQcGIurBMTxxvH29UHAOw8G6t+iwZ2SIQNYOPkdZ282Lbw+gWAXRXR+XTRwM4X5/8GYC+8ExMwxjF39QEA28/Ksr3RwEaEjRPSdUJiG/qFrw8A2GVI9m+PBra/+PxeRNg4iX0nMfYtnP4BYOfZWPVbNLARYS+ckwxAxbFO1QcA7KqIzqeLBna+OP83RNg44VOd8ChnuvsSgO1nZdneaGAjwp7uEwfgw/Grow8A2GVI9m+PBra/+PxeRNiAQx1wQJ3N63cAdp6NVb9FAzs0wqYDBYMG6APoA1UhhXSZAtHAzorCGhSAAlAACoxTgWhgh0TYwxqSsqxhdWE/FIACUGDaFIgG9rQ1GP5CASgABaZVgWhgp4yKU5Y1rQcEfkMBKAAFyhSIBnZZwdgOBaAAFIACaRWIBnbKqDhlWWllQmlQAApAgfoViAZ2/U2AB1AACkCBhaFANLBTRsUpy1oYhw+thAJQYCEpEA3shSQW2goFoAAUqFOBaGCnjIpTllWnqKgbCkABKDAOBaKBPQ6nUCYUgAJQAAoUFYgGdsqoOGVZxaZiCxSAAlBguhWIBvY0Nn/lypXKNm7H5s2bC/toGz5QAApAgboViAZ2yqg4ZVk+Yefm5pRtnJ5Abu+jbfhAASgABepWIBrYdTdglPptINN3/kwE2Dt6qru1rVob5tTc2sxaG9qqu4M9cS97W1u5PDK/Wd/UdWeOqJcK7G23fF7TUq1NXdUb4rPTmR0d1Vozp+bWtFQnKH9PdUi3NW1V0sqsusj2ZgVhDQo0Q4FoYKeMilOWZcsrQUz12MYQX7x4cWEfbeP9drnB3wl6BCoBanu9tbVXWmx3kz+vLssF7Kh6B5As83lU6FJ5gXnNBWsYsKPaWyo/dkCBWhWIBnat3gdU3ghgc1RJoNLRtADzjm4/chxAsb3d1biuao8SlUbWay4Sa1qqvT3vc5t/JQwDqGiOgW4gsPP5PBF2ZHuFq1iFAo1SIBrYKaPilGWxygRqsmXLlimKlF0RNNXLEbRrv8zL5Y1yI9IApxRuIpLd0FECjf3mMIhc+7jBjmVUvVzn2jnlvYisnVO+XwbGLVGe/jVQKcLuqe4mayioVEOlotprHMUKFGieAtHAbl6T8h75QCyHRULTEbjDPgLGriELLmx7uz9c4gIZ7/Pl53LMMq7e4fBTykTgQ/3KfGlv8rTT+E7j5h1loni6KGwYgLsU2Fkdcz5/WEuXzqJ+rEKBJikQDeyUUXHKsljkUBC7ImwX2MOBzR4NWXIE6gAJw9Md6Q4pd9huT73DslYFNvuvQVoJmIMhoMHQiR6OMfk8QyLDHKb9Ee2tUjzSQIFxKBAN7HE4lbJMF7C5/C1bthRuMEo4u9JxeWMDtgFScfaEBuOaturQePemVu7mZX+GSWEQhZswfOmp15uZwVc6ZDLIzek4Mq5UXx/YeiYKO2HyRQLblFPUmavCEgo0TYFoYKeMilOWxUIzYGXkzPuaCGwTrTLY2Fklos3BjUl7dgl9rzSObMrMVsrrzdLYazRcYWa8eMfVs2EK8+ugIjALUwZNvjhgj9Jeu/34DgUmrUA0sCftcGh9UwVsjkIJyPb4q9xHszW2drObkjTfWNyUC4a2LNuutyB4Bl++YLSkL4X04iagLNuANzDCNfkigB3UXkeDsAkK1KRANLBTRsUpy2I9pwfYAoSF6FopxaDyDD2MFjUOqZeFNEuK9Fv65p+Jrimy3+SY1UJ5GI52m7g9jrF6U5VrxeQbFdih7XU5gW1QoB4FooFdj9vVa50OYAuIeIA8vNXZsEm1KDu+Xv+wSFa+GQrhRhjwTjLCzvyhXwcFn9g3LKFAQxWIBnbKqJjLqrqsomnzgZ2HSDXQlrVclCWHH5zJRdqIsW9dNMPXgmBuVojtA+eZWISdsL12W/AdCkxIgWhgT8jPkatpNrDTQ8QMi3iBnbpeUR7XWzYUwkdyosAW/sVenNh/LKFADQpEA5uj4RS+pyyL/WkusLu5B0Jyj3yz8yMshwN7MvWa6Nozo4VvWpolw97XbgP6qmPY42mvz0XsgwLjUiAa2ONyLFW5jQT2jmysmV5+lG4sNYsknUMrE6iXZ7c0Athja2+q3olyoECYAtHAThkVpyyLZWgesPOwrvpqURM5++Y78zCENZbc12KM9Yo54s4LBR8MuTSR8rhuOo7WXuki1qFA0xSIBnbTGmT74wI2XRhsC0032pOOWQQc+lpRM62v9CadKLsAdbGvNL+t3OA7g9V5EeinMReTkLK53JA8VJ3J5xsSiWhviQzYDAWaoEA0sFNGxSnLYnFDQSyfiLShTt+5vFGALYcJwodB8hDKjXnTT39+zakDrKnrNQ/A7+jpR+R5DLpydE0Hx4A3fYQd117uOVhCgeYpEA3s5jUp7xGBlUy+ItUHYhewZV4uL/z1quInesUbcQUAWmBmUJql/b5qLUWCemnIQ1wQTH2iHQVf84eh+G1swE7R3qK72AIFmqBANLBTRsUpy7LFJdBydBwKbII457XLrfxdjC+7gOfa5oag4+/F9F91ddx/L5awXvdfhJXUO0yYcQE7WXuHNQD7ocDkFYgG9uRdHq3G2oE9mtvIBQWgABQwCkQDO2VUnLIs00LHCkfLcsnJJNh5P23DBwpAAShQtwLRwK67AaPUzyCWSy4HwGYlsIQCUKBpCkQDO2VUnLIsn9AEZds4Pd1MtPeF32Dk0rCEAlAACqRTIBrY6VxBSVAACkABKOBTIBrYKaPilGX5Go19UAAKQIFpVCAa2NPYaPgMBaAAFJhGBaKBnTIqTlnWNB4M+AwFoAAU8CkQDWxf4dgHBaAAFIAC6RSIBnbKqDhlWekkQklQAApAgWYoEA3sZjQDXkABKAAFZl+BaGCnjIpTljX7hw4thAJQYKEpEA3shSYY2gsFoAAUqEuBaGCnjIpTllWXoKgXCkABKDAuBaKBPS7HUC4UgAJQAArkFYgGdsqoOGVZ+WbiGxSAAlBg+hWIBvb0S4AWQAEoAAWmQ4FoYKeMilOWNR3yw0soAAWgQHUFooFdvSqkhAJQAApAgRgFooGdMipOWVaMKMgLBaAAFGiiAtHAbmKj4BMUgAJQYBYViAZ2yqg4ZVmzeLDQJigABRa2AtHAXtjyofVQAApAgckpEA3slFFxyrImJyFqggJQAApMRoFoYE/GTdQCBaAAFIAC0cBOGRWnLAuHFgpAASgwawpEA3vWBEF7oAAUgAJNVSAa2Cmj4pRlNVVw+AUFoAAUGFWBaGCPWnGd+VauXKlsY382b95c2Efb8IECUAAK1K1ANLBTRsUpy/IJOzc3p2zj9ARyex9twwcKQAEoULcC0cCuuwGj1G8Dmb7zZ9zA7raLF4uiPy3VarVVp9tTPXbMWlYrx11XqyNK7bYHF6iWkput6jxfe6rTctdTbJdM56gv2Jee6nY6qt1qqZZ1ESb92p1uqX6eBmEXFGisAtHAThkVpyzLVlyCmOqxjeGyePHiwj7axvvtckO/B4OWwC34yvUFlyOANgvA7nXaBUjzMcovW6rtEpCFxBIKTJEC0cCelrY2Dtjtbrl0vZ7qdSWQHNFoWe7QKDU0faFeEWH72lTI59hQyRdRH12EnL9EBvqJyD93kXJUjU1QYBoUiAZ2yqg4ZVksPoGabNmyZYoiZVcETfVyVObaL/NyeaPeiDSRcSW4dVXbRMZt5UE8N1epStDLkgenF1n7qwKgldpUKCDbUMF3o9/cnGp3HT89stKUUj2VpQ+46OXKwBco0BwFooHdnKa4PfGBWA6LhKYjcI/yMQCpCrdex/z0rxQlVoBezu/Q9LnM9GWCwA7VQvsqLnpVNS+0ERugQDMUiAZ2yqg4ZVksbyiIXRG2C+wTA7aioHlws67VGX4TLRTAoelZWLOcHLCDdDD+KdXrtPq/oKroJ/JhFQo0TYFoYDetQbY/LmBzmi1bthRuMEo4u9JxeZMEdtCwRSiAQ9OzKGY5KWBnkXKlXxrGP1opn22TS4YvUKDhCkQDO2VUnLIs1p0BKyNn3jc1wBZDAUN/1YcCODQ9i2eWEwJ2tJ/GYaxAgalVIBrYTW/5TABbBUSXoWALTV844JMBthnWmKt487XgJzZAgelXIBrYKaPilGXxoQGwWYmSZUpgmxkt8gEZ97rzl4LHFwNsjEOXHEhsXggKRAO76SIB2EOOkAeSQ3IOdosIu3ZgD/fFeaGo1lCkggK1KxAN7JRRMZdVdVlFPQB7iEopgR1LQ48vJsL2DokA2EOONnZPuQLRwG56+2cC2HXcdBR1sobZUj6EIiA5RmAHzZSxO6VoS6yLdtH4DgUmqUA0sDkanqTTIXUxZKZ6logn8ixoEZKWMpelF5BjDbNlDcAWN16DoSvaEpy3IDA2QIH6FIgGdn2uV6uZITPNwA56YKQMwGVyhaYvlDOhCDv0ASLpJ4At1cD6FCsQDWxE2GFH38C3aqgXCptQAIemLzR3csBWQough2dEvqqyF5qJDVCgAQpEA7sBbfC64Iqw6SJjW2i6yTzpmM2/nqs6nS0UwKHpC2pPENgyyp6bU5Wg3euqtnhrH4BdOIDYMEUKRAN7GiNsG9b0vUnA7vXoxfx4var7PKI38A3eDaJfr9rSb+3r5V7cR69X7f+xAR9XWrba+EMDt6bYOi0KRAO76Q2lSJhMviI1FNgyL5cX/XrVqnOWW2019C2i8iCERsyh6WVdel1E2FXbNEhXiJADfMm/L9z9cI6B9eCd2QXXsQEKTJkC0cBueoTNx4NAyydwKLDphiXn5fJGXZoxbB/c6C+v2h39F2HB9QRAT5cdmr7gUD3AZjd0JN12/UUY/dNMJ+xix4ViCQUaqkA0sBvaroJbTQF2wTFsgAJQAApUVCAa2NMSYUs9OFqWS94vwc77aRs+UAAKQIG6FYgGdt0NGKV+BrFccjkANiuBJRSAAk1TIBrY0xhhE5Rt4wNDNxPtfaPeYOQysYQCUAAKpFAgGtgpnEAZUAAKQAEoMFyBaGBPY4Q9XBakgAJQAAo0T4FoYDevSfAICkABKDCbCkQDGxH2bHYMtAoKQIHmKRAN7OY1CR5BASgABWZTgWhgI8KezY6BVkEBKNA8BaKB3bwmwSMoAAWgwGwqEA1sRNiz2THQKigABZqnQDSwm9ckeAQFoAAUmE0FooGNCHs2OwZaBQWgQPMUiAZ285oEj6AAFIACs6lANLARYc9mx0CroAAUaJ4C/w9XVJXtbq6wHAAAAABJRU5ErkJggg==||font-size="10pt"}} | {{attachment:dwi2dti.jpg||width="550",height="300"}} |
| Line 70: | Line 74: |
| Then follow the popup windows by selecting the DWI, you may need to extract the zip file before. | |
| Line 71: | Line 76: |
| {{attachment:importDWI.JPG||width="650",height="280"}} | |
| Line 72: | Line 78: |
| You have already generated the FEM mesh as explained here (link to the FEM mesh tutorial) | If the bval, and bval files are in the same folder, Brainstorm will detect them automatically, otherwise, the user will be asked to browse the files one by one (as it's the case in this tutorial). |
| Line 74: | Line 80: |
| Brainstorm calls internally the BrainSuite process, and compute the diffusion tensors. | |
| Line 75: | Line 82: |
| At the end of this process, a new node will appear in the Brainstorm database with the name 'DTI-EIT'. This name refers to, DTI: diffusion tensors images, and EIG for eigenvalue, since the eigenvalues and eigenvectors are computed at voxel and stored in Brainstorm database. | |
| Line 76: | Line 84: |
| The FEM head model to use for tensors should be selected and highlighted with the green color (double click on the FEM mesh node to select it) | {{attachment:mriAndDTI-EIG.JPG||width="230",height="100"}} |
| Line 78: | Line 86: |
| When this is done, then right-click on the subject > Convert DWI to DTI, | If you check the structure of the file DTI-EIG, by right click -> File and then 'Display file contents', the following figure is displayed. |
| Line 80: | Line 88: |
| Brainstorm will load the avialbale tissue in the FEM head model and the following windows appears. | {{attachment:EIG-hardDisc.JPG||width="450",height="200"}} |
| Line 82: | Line 90: |
| Select the WM anisotropy and kee all the oher tissues as isotropic. | The size of the matrix is 128x256x256x12, where the first 3 values are the same as the size of the T1 MRI and 12 corresponds to the 3 eigenvectors components (9) and eigenvalues (3) |
| Line 84: | Line 92: |
| The process of conversion from DWI to Conductivity tensors use the EMA, furthermore, brainstorm propose the option to use the adaptative EMA with the volume constraint option [ref]. In this example we select the EMA with the VC. | === Conductivity tensor generation from DTI === The Effective Medium Approach is applied to convert the diffusion tensors to the conductivity tensors. |
| Line 86: | Line 95: |
| The process will take around 10 min, and then the FEM tensors are computed and stored in the FEM strucutre. [explain how it is organised and how to use it outside brainstorm ] | www.pnas.org/content/98/20/11697 |
| Line 88: | Line 97: |
| === Display the tensors === | ==== FEM mesh head model ==== This step requires the FEM mesh of the head model. You can generate the FEM head model from the MRI data as explained on [[https://neuroimage.usc.edu/brainstorm/Tutorials/FemMesh|this page]]. |
| Line 90: | Line 100: |
| == Artificial/simulated conductivity tensors == In the case where the DWI is not available, or the users desire to evaluates the effect of the conductivity change on the model, the artificial conductivity can be use. |
For the following, we used the SimNibs FEM mesh generation. The following figure shows the FEM mesh obtained with the SimNibs method using the T1 MRI. |
| Line 93: | Line 102: |
| Two approaches are integrated within Brainstorm. Either the | {{attachment:Mri&femMeshView.JPG|Mri&femMeshView.JPG|width="260",height="300"}} {{attachment:femMeshView.JPG||width="280",height="300"}} Note that this mesh is obtained only from the T1, the use of the T2 is highly recommended if it's available, as recommended in the [[https://neuroimage.usc.edu/brainstorm/Tutorials/FemMesh|FEM mesh tutorial]]. ==== Computation of FEM mesh tensors ==== Once the FEM mesh and the DTI tensors are available in the Brainstorm database, the next step for the FEM tensors can be performed by the following: - Right-click on the FEM mesh - Compute FEM tensors {{attachment:menuGenerateFemTensors.png||width="250",height="280"}} Brainstorm checks the available tissues in the FEM head model and displays the following panel {{attachment:FEMConductivitiesIsoPanel.JPG||width="250",height="220"}} This panel lists the tissues available in the FEM head model and assigns a default value of the conductivity for each compartment. Users can change these values to their own if needed. DTI values can be used to generate conductivity tensors for the white matter (and in some cases for the grey matter). Please, note that the DWI can be used only for the brain tissues and not for the outers compartments (skull and skin) In this tutorial (and in most cases) we select the white matter. Select the WM anisotropy and keep all the other tissues as isotropic, then these additional options appear asking for the method to use. {{attachment:FEMConductivitiesAnisoPanel.JPG||width="250",height="300"}} The available methods are: - Effective Medium approach (EMA) - Effective Medium approach with volume constraints (EMA + VC) - Simulated or the artificial anisotropy Only the two first methods require the DTI. More information about these methods can be found on these references [ref1][ref2] and in our main paper [link] In this tutorial, we use the method "EMA + VC", where the final tensors are constrained to fits the volume of the equivalent isotropic tensor volume. ==== Visulation of FEM mesh tensors ==== Once the FEM tensors are successfully computed, they are stored in the FEM head node. By right-clicking on the FEM head, new menu items are added that gives the possibilities to display the FEM tensors either as ellipsoids or as vectors in the direction of the main eigenvector. {{attachment:menuDisplayTensors.jpg||width="250",height="300"}} The tensors can be displayed either on the FEM mesh or overlaid on the MRI. The following figures show an example of the obtained tensors displayed on the white matter. {{attachment:meshViewTensorsLines.JPG||width="350",height="300"}} {{attachment:meshViewTensorsTensorsTops.JPG||width="350",height="300"}} On the left, the tensors as a line on the direction of the main eigenvector. On the right, the tensors displayed as ellipsoids. The orientation of the tensor is color-coded as follows: red for right-left, green for anterior-posterior, and blue for superior-inferior. Note that the quality of the tensors depends on the DWI data and the number of acquisition direction. Users can also display the tensors on specific tissues, for example on the white matter (left figure) or overlay on the MRI (right figure). {{attachment:meshViewTensorsLinesWM2.JPG||width="350",height="300"}} {{attachment:tensorsOnMri.JPG||width="300",height="300"}} ==== Recommendation ==== In the case where the user wants to use generate isotropic tensors, then the DTI is not required. For that case, keep all the options to 'isotropic', the recommended display is the 'Ellipsoids', and the final shape will be a sphere (isotropic direction). In the case where more than one FEM head model is in the database, the highlighted one in the green color will be used. <<TAG(Advanced)>> == Simulated conductivity tensor == In the case where the DWI is not available, or in the case where the users desire to evaluate the effect of the conductivity change on the head model, the artificial conductivity can be used. Users can reach this option by following this tutorial and select the third method in this panel. {{attachment:artificialTensors.JPG||width="280",height="450"}} Two approaches are integrated within Brainstorm. Either Wang's constraint or the volume's constraint (Wolters). The common feature between these methods is the ratio between the transversal and longitudinal conductivity ratio. A common example is the skull anisotropy simulation, where the longitudinal conductivity can be higher than the transversal conductivity, the ratio can vary from 2 to 10 [ref]. In this tutorial, we keep all the tissue as isotropic, except the skull, we use a ratio of 0.1 and select the volume constraint. The following figures show the results of this example. "eigenvalues parallel (longitudinal) and perpendicular (transverse) to the fiber directions" for 1:10 anisotropy (transverse:longitudinal) {{attachment:skullAniso.JPG||width="300",height="250"}} {{attachment:skullAniso2.JPG||width="300",height="250"}} == Troubleshooting == To be completed soon and linked to BrainSuite website |
| Line 96: | Line 176: |
| ===TODO=== Check the error in the simnibs mesh in X direction and overlay on mri check the error with the brain2mesh Correct the ratio from integer to float check the meaning of transversal/longitidunal in the code add an interactive way yo change the size of the tensor.. important correct the name of the simulated method, correct the EMC and remove the VC and change the coefficcient |
[TUTORIAL UNDER CONSTRUCTION: NOT READY FOR PUBLIC USE]
FEM tensors estimation with BrainSuite
Authors: Takfarinas Medani, Francois Tadel, Anand Joshi and Richard Leahy
In this tutorial, we describe the estimation of realistic conductivity tensors of living brain tissues using the BrainSuite software. These results are used in FEM forward modeling, as described in the tutorials: FEM with DUNEuro and FEM median nerve example.
The realistic tensors are estimated from the Diffusion-Weighted Images (DWI): Brainstorm calls the BrainSuite software to compute the diffusion tensors on each brain MRI voxel (DTI), then Effective Medium Approach (EMA) is applied to estimate the conductivity tensors for each element of a tetrahedral FEM mesh.
BrainSuite is also used for other purposes in Brainstorm, particularly the T1 MRI segmentation, as documented in this tutorial: MRI segmentation: BrainSuite.
Contents
Download and installation
Requirements
- You have already followed all the introduction tutorials.
- You have a working copy of Brainstorm installed on your computer.
- For the DWI data, only the NIfTI files (.nii) are supported.
Install Brainsuite
Download the latest version of BrainSuite from http://forums.brainsuite.org/download/.
Install it on your computer by following the instructions in BrainSuite's quick start installation guide.
You will be using BrainSuite Diffusion Pipeline (BDP), so you need to install a compatible MATLAB Runtime (2019b for BrainSuite 21a).
In Brainstorm, menu File > Edit preferences > Enter the BrainSuite installation folder:
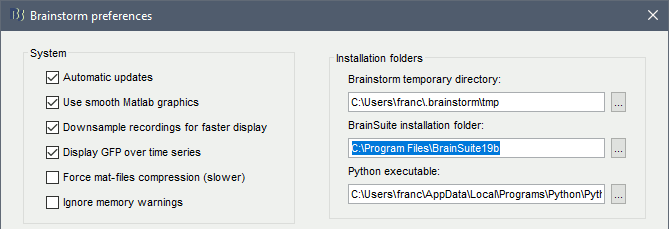
Download the dataset
Download the files: MRI T1w and MRI DWI (from the BrainSuite diffusion tutorial).
- Unzip it outside of any of the Brainstorm folders (program folder or database folder).
- Start Brainstorm (Matlab scripts or stand-alone version)
Select the menu File > Create new protocol. Name it "TutorialTensors" and select:
- No, use individual anatomy
- No, use one channel file per condition
Dataset
In this tutorial, we use the Brainsuite dataset example available on the BrainSuite tutorial webpage.
The first file contains the T1 MRI data, with the name '2523412.nii.gz', as in this figure,
The second folder contains the diffusion data and should have at least three files,
Where the *.bval is a text file that contains the value of the gradient, and the *.bvec is also a text file that contains the orientation of the gradient.
The nii.gz file is the NifTi file where the DWI where the images are stored.
Bvals and Bvecs are the bvalue and the gradient vectors. The files .bval and .bvec should be created from for the DWI acquisition. If you don't have those files (and you can't create them yourself (no easy task)) you should talk to the person who programmed your DWI sequence and get the files that are specific to your use case.
For simplicity place your bval and bvec files in your same data directory where your raw DWI NIFTI file is with the same prefix as your raw DWI NIFTI.
Realistic condctivity tensors
Load the T1 MRI data to brainstorm
First, you need to create a new subject in your protocol, let call it the 'BrainSuiteSubject'. Then import the T1 MRI of the subject and set the fiducials points as explained in the previous tutorial.
The T1 MRI is required since the BDP uses the T1 space for its computation. Furthermore, this is required since it will be used to align the tensors to the FEM mesh later.
Diffusion tensor generation (DTI) from DWI
In this step, Brainstorm calls the Brainsuite internally, and the diffusion tensors are computed.
Right-click on the subject and then select the item "Convert DWI to DTI".
Then follow the popup windows by selecting the DWI, you may need to extract the zip file before.
If the bval, and bval files are in the same folder, Brainstorm will detect them automatically, otherwise, the user will be asked to browse the files one by one (as it's the case in this tutorial).
Brainstorm calls internally the BrainSuite process, and compute the diffusion tensors.
At the end of this process, a new node will appear in the Brainstorm database with the name 'DTI-EIT'. This name refers to, DTI: diffusion tensors images, and EIG for eigenvalue, since the eigenvalues and eigenvectors are computed at voxel and stored in Brainstorm database.
If you check the structure of the file DTI-EIG, by right click -> File and then 'Display file contents', the following figure is displayed.
The size of the matrix is 128x256x256x12, where the first 3 values are the same as the size of the T1 MRI and 12 corresponds to the 3 eigenvectors components (9) and eigenvalues (3)
Conductivity tensor generation from DTI
The Effective Medium Approach is applied to convert the diffusion tensors to the conductivity tensors.
www.pnas.org/content/98/20/11697
FEM mesh head model
This step requires the FEM mesh of the head model. You can generate the FEM head model from the MRI data as explained on this page.
For the following, we used the SimNibs FEM mesh generation. The following figure shows the FEM mesh obtained with the SimNibs method using the T1 MRI.
Note that this mesh is obtained only from the T1, the use of the T2 is highly recommended if it's available, as recommended in the FEM mesh tutorial.
Computation of FEM mesh tensors
Once the FEM mesh and the DTI tensors are available in the Brainstorm database, the next step for the FEM tensors can be performed by the following:
- Right-click on the FEM mesh - Compute FEM tensors
Brainstorm checks the available tissues in the FEM head model and displays the following panel
This panel lists the tissues available in the FEM head model and assigns a default value of the conductivity for each compartment. Users can change these values to their own if needed.
DTI values can be used to generate conductivity tensors for the white matter (and in some cases for the grey matter). Please, note that the DWI can be used only for the brain tissues and not for the outers compartments (skull and skin)
In this tutorial (and in most cases) we select the white matter. Select the WM anisotropy and keep all the other tissues as isotropic, then these additional options appear asking for the method to use.
The available methods are:
- Effective Medium approach (EMA)
- Effective Medium approach with volume constraints (EMA + VC)
- Simulated or the artificial anisotropy
Only the two first methods require the DTI. More information about these methods can be found on these references [ref1][ref2] and in our main paper [link]
In this tutorial, we use the method "EMA + VC", where the final tensors are constrained to fits the volume of the equivalent isotropic tensor volume.
Visulation of FEM mesh tensors
Once the FEM tensors are successfully computed, they are stored in the FEM head node. By right-clicking on the FEM head, new menu items are added that gives the possibilities to display the FEM tensors either as ellipsoids or as vectors in the direction of the main eigenvector.
The tensors can be displayed either on the FEM mesh or overlaid on the MRI. The following figures show an example of the obtained tensors displayed on the white matter.
On the left, the tensors as a line on the direction of the main eigenvector. On the right, the tensors displayed as ellipsoids. The orientation of the tensor is color-coded as follows: red for right-left, green for anterior-posterior, and blue for superior-inferior.
Note that the quality of the tensors depends on the DWI data and the number of acquisition direction.
Users can also display the tensors on specific tissues, for example on the white matter (left figure) or overlay on the MRI (right figure).
Recommendation
In the case where the user wants to use generate isotropic tensors, then the DTI is not required. For that case, keep all the options to 'isotropic', the recommended display is the 'Ellipsoids', and the final shape will be a sphere (isotropic direction). In the case where more than one FEM head model is in the database, the highlighted one in the green color will be used.
Simulated conductivity tensor
In the case where the DWI is not available, or in the case where the users desire to evaluate the effect of the conductivity change on the head model, the artificial conductivity can be used.
Users can reach this option by following this tutorial and select the third method in this panel. ![]()
Two approaches are integrated within Brainstorm. Either Wang's constraint or the volume's constraint (Wolters). The common feature between these methods is the ratio between the transversal and longitudinal conductivity ratio.
A common example is the skull anisotropy simulation, where the longitudinal conductivity can be higher than the transversal conductivity, the ratio can vary from 2 to 10 [ref]. In this tutorial, we keep all the tissue as isotropic, except the skull, we use a ratio of 0.1 and select the volume constraint. The following figures show the results of this example.
"eigenvalues parallel (longitudinal) and perpendicular (transverse) to the fiber directions" for 1:10 anisotropy (transverse:longitudinal)
Troubleshooting
To be completed soon and linked to BrainSuite website
References
===TODO===
Check the error in the simnibs mesh in X direction and overlay on mri check the error with the brain2mesh Correct the ratio from integer to float check the meaning of transversal/longitidunal in the code add an interactive way yo change the size of the tensor.. important correct the name of the simulated method, correct the EMC and remove the VC and change the coefficcient
