|
Size: 10012
Comment:
|
Size: 16459
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| = Tutorial 13: Head model = | = Tutorial 20: Head model = |
| Line 4: | Line 4: |
| This tutorial is still based on Sabine Meunier's somatotopy experiment, called ''TutorialCTF ''in your Brainstorm database. The recordings have already been imported and analyzed at the sensors level, they are ready for source estimation. | The following tutorials describe how the brain activity can be estimated from the MEG/EEG recordings we have processed until now. This process consists in solving two separate problems: the modeling of the electromagnetic properties of the head ('''head model''' or '''forward model''') and the inversion of this model. This tutorial will explain how to compute a head model for the subject of our auditory oddball experiment. Its scope is limited to linear distributed source models (there is no dipole fitting available in the software). |
| Line 8: | Line 8: |
| <<TAG(Advanced)>> == Why estimating sources? == Reconstructing the activity of the brain from MEG or EEG recordings can be a difficult and long process. We tried to make it as automatic as possible, but you have to understand its advantages and issues before deciding if it can bring anything to your study. The primary objective is to '''localize''' the regions of the brain that generated our signals of interest. From the sensor topographies in MEG and EEG, we can have a general idea of where the signal generators are located, but we cannot be more precise than identifying the hemisphere and the lobe. Using source estimation methods, we can expect to get a spatial resolution in the range of the centimeter, or even a few millimeters in the good cases. While localizing the signals, we can also expect some form of '''deconvolution''' of our signals. In EEG, the scalp topographies are very smooth and it is common to have different effects that are superimposed in the signals recorded by most of the electrodes. Moving to the source space may help separating the sources and obtain cleaner and unmixed signals. Specifically for '''MEG''', working in source space solves many of the problems associated with this modality. The subject's head is not fixed in an MEG system, so it has a great chance of moving during the experiment. Also, the position of the sensors do not adapt to the shape and size of the head. Therefore between two acquisition runs, or between subjects with different morphologies, there is a high chance that '''the same MEG sensor records different parts of the brain'''. This problem does not exist in EEG, where the electrodes are in standard positions and follow the subject in all the movements. Another point that makes '''MEG signals difficult to review''' is the variability in the sensors. Every manufacturer uses different types of sensors, that are sensitive to different orientations and distances, and that produce signals with different shapes. Again, this is not a problem in EEG: the only variability you can get between two EEG systems is the level of noise and the ease of use of the cap, the signals will look very similar. Projecting all the data on the individual brains addresses these last two issues. However, if your interest is only in the latency of an event, in detecting the lateralization of a known effect or in training blindly a classifier, you might not be interested in those complicated models that multiply by 50 the size of your files. Go for fancy methods only when you think they can bring some added value to your analysis, not because everybody around uses them. <<TAG(Advanced)>> == The origins of the MEG/EEG signals == To understand how we are reconstructing the sources, it is interesting to have an idea of the physiological origins of MEG and EEG signals. The models we use are based on some physiological assumptions that are not always valid, understanding them may help you selecting the appropriate method. It is assumed that most of the currents we record are related with the postsynaptic activity of the pyramidal neurons in the cerebral cortex. These cells are '''aligned spatially''' and '''perpendicular to the cortex surface'''. Millions of post-synaptic potentials in the apical dendrites of neighbouring pyramidal neurons sum up in time and space to form what we can approximate at a macroscopic level with a few electric dipoles (green arrows below). The primary and volume currents generated by these dipoles create a potential distribution and a magnetic field at the surface of the head. We can record them with bipolar montages of electrodes placed on the skin (EEG) or very sensitive superconducting detectors (SQUIDs/MEG). . {{attachment:origins.gif||height="342",width="538"}} . <<HTML(<div align="right"><FONT size="-1" color="#CCCCCC"><I>Matti Hamalainen, 2007</I></FONT></div>)>> <<TAG(Advanced)>> == Source space == The source estimation process consists in estimating the position and activity of a set of electric dipoles, to approximate the activity of the brain that produced the MEG/EEG data we recorded. Two families of solutions were explored in the past decades: the '''dipole fitting methods''' (we estimate the position and amplitude of a very limited number of dipoles over short time windows) and the '''distributed methods''' (we define a priori a dense grid of dipoles and then estimate their activity from the recordings). The single dipole fitting approaches are very efficient in specific cases were we know in advance the number or regions involved and their latencies of activity. But they are difficult to generalize and automate, and not adapted for group analysis. With Brainstorm, we decided to work only with source distributed models, which require less manual tuning for getting acceptable results. Our first step of modeling is then to define the '''position and orientation of the dipoles''' for which we want to estimate the activity. This set of dipoles is our referred to as our '''source space'''. By default, we limit our analysis to the '''cortex envelope''', based on this observation that most of the MEG/EEG signals is related with the synchronous activity of assemblies or cortical pyramidal cells. The simple solution we recommend is to use directly the vertices of the cortical surface we imported in the first tutorials (the nodes we can see in the grey mesh in the left image below). In order to represent all the possible dipole orientations, we define '''three dipoles for each vertex''' of the cortex surface, corresponding to three orthogonal directions (X,Y,Z). When importing the anatomy of the subject, we downsampled the cortex surface to '''15,000 vertices'''. This will correspond to a source space of '''45,000 dipoles'''. We will compute a forward model that connects the activity of these 45,000 dipoles with the 275 MEG sensors we have in this dataset. This default number of 15,000 vertices is empirical. Over the years, our experience seemed to show that it represents a good balance between the representation of the brain circumvolutions, the surface sampling and the amount of data that is generated. Using less vertices makes it difficult to preserve the shape of the brain, using more vertices produces more data without adding to the spatial resolution of the method and may lead to memory issues. Additionally, we can impose '''constraints of orientation''' on the dipoles, to match the physiological observation that the pyramidal cells are mostly organized perpendicularly to the cortex surface. This has the advantage of limiting the number of dipoles to 15,000 (one per vertex) and making the results much easier to display and process. However, this constraint is most of the time too strong and distorts the reconstruction. This orientation constraint is an option of the inverse model and will be discussed in the following introduction tutorials. The spatial constraint of imposing all the dipoles to be on the cortical surface might also be too restrictive in some cases, because our model is then not able to represent correctly the activity in deeper brain structures or in the cerebellum. Therefore we also offer an option to use the entire brain volume as our space space (the green dots below represent dipoles locations in volume model). This produces results that can be better or worse depending on the data, but in all the cases much more difficult to review. Volume and mixed head volumes are discussed in the advanced tutorials about source modeling. . {{attachment:source_space.gif||height="200",width="243"}} {{attachment:source_volume.gif||height="200",width="255"}} <<TAG(Advanced)>> |
|
| Line 9: | Line 57: |
| The first step consists in computing a model that explains how an electric current flowing in the brain can influence what is recorded out of the head, by the EEG or MEG sensors. | The first step of the source reconstruction consists in computing a model that explains how the electric currents or the magnetic fields flow from the electric generators in the brain (source space) through the different tissues of the head (mostly brain, CSF, skull and skin), to finally reach the sensors. |
| Line 11: | Line 59: |
| * This problem is called forward problem. * Its result is called ''head model ''in Brainstorm interface, but can also be referred as ''forward model'' or ''leadfield matrix''. * In the Brainstorm software, we consider by default that the electric or magnetic activity which is recorded by the sensors is produced mainly by a set of electric dipoles located at the surface of the cortex.<<BR>> * The grid of sources (dipoles) that is used is defined by the cortex surface we have imported in one of the previous tutorials; each vertex of this surface is considered as a dipole. * The default surface distributed with Brainstorm have around 15,000 vertices. So we will have 15,000 dipole amplitudes to estimate. Using less vertices would just lower the resolution of the results; using more produces too much data and might lead to memory issues. * What we expect to get at the end of this process is a matrix whose size is [Number of sensors x Number of sources] * For computing this matrix, three methods are available for MEG recordings in Brainstorm: * '''Single sphere''': the head is considered a homogeneous sphere * '''Overlapping spheres''': Refining the previous model by fitting one local sphere for each sensor * '''OpenMEEG BEM''': Symmetric Boundary Element Method from the open-source software OpenMEEG. Described in an advanced tutorial: [[Tutorials/TutBem|BEM head model]]. |
* The question of building a model that connects the values we observe outside of the head (MEG/EEG) to the electric activity of the cortical dipoles in the brain is called '''forward problem'''. * The model we obtain after solving this problem is called '''head model''' in Brainstorm, but can also be referred to as '''forward model''', '''leadfield matrix''' or '''gain matrix'''. * In this tutorial we will use the default source space: the low-resolution cortex surface with 15,000 vertices, as the support of 45,000 dipoles. We will use indifferently the terms '''dipole''' and '''source'''. * What we expect to get at the end of this process is a matrix '''[Nsensors x Nsources]'''. <<BR>><<BR>> {{attachment:forward_inverse.gif}} |
| Line 22: | Line 64: |
| {{attachment:forwardInverse.gif}} | Available methods for MEG forward modeling: |
| Line 24: | Line 66: |
| == Single sphere model == Select the ''TutorialCTF ''protocol, close all the figures, and follow these steps: |
* '''Single sphere''': The head is considered to be a homogeneous sphere. * '''Overlapping spheres''': Refining the previous model by fitting one local sphere for each sensor. * '''OpenMEEG BEM''': Symmetric Boundary Element Method from the open-source software OpenMEEG. Described in an advanced tutorial: [[Tutorials/TutBem|BEM head model]]. |
| Line 27: | Line 70: |
| 1. Right-click on the ''Right'' condition and select ''Compute head model''. The ''Head modeler'' window will appear.<<BR>><<BR>> {{attachment:popupHeadModel.gif}} --- {{attachment:headModeler.gif}} 1. Set the options for your head model: * Source space: '''Cortex surface'''. <<BR>>The MRI volume option will be introduced in an advanced tutorial: [[Tutorials/TutVolSource|Volume source estimation]]. * Forward modeling method: '''Single sphere'''. * You can also edit the '''Comment '''field of the file that will be created (the string that will be representing the head model in the database explorer). * Click on ''Run''. |
Models recommended for each modality: |
| Line 34: | Line 72: |
| 1. Two other windows appear, to help you define the sphere. Estimating the best fitting sphere for a head is not always as easy as it looks like, because a human head is usually not spherical. <<BR>><<BR>> {{attachment:helpBfs.gif|editBfs.gif}} <<BR>><<BR>> {{attachment:editBfsFigure.gif}} * Read and follow the instructions in the help window. * Click on the ''Scalp ''button, move and resize the sphere manually, just to see how it works. * Click again on ''Scalp'': here we will use directly the estimation of the sphere based on the vertices of the ''Scalp ''surface (a simple least-squares fitting using all the vertices of the surface). * For EEG 3-shell spheres models, you just estimate and manipulate the largest sphere (scalp), and then use the ''Edit properties...'' button in the toolbar to define the relative radii of the 2 other spheres, and their respective conductivities. This will be described in another tutorial. * Click on ''Ok'', and wait for a few seconds. |
* '''MEG''': Overlapping spheres.<<BR>>The magnetic fields are not too much affected by the heterogeneity of the tissues of the head. The is no real need for modeling the head with too much details. * '''EEG''': OpenMEEG BEM.<<BR>>The electric currents are strongly affected by jumps between very conductive tissues (brain, CSF, skin) and an isolant medium (the skull). A realistic head model is strongly advised for modeling the properties of the skull correctly. When computing a BEM model is not an option, for instance if OpenMEEG crashes for unknown reasons, the Berg's three-layer sphere can be an acceptable option. * '''sEEG/ECoG''': The OpenMEEG BEM option is the only one available. |
| Line 41: | Line 76: |
| 1. A new file appeared just below the channel file, it represents the head model.<<BR>><<BR>> {{attachment:headModelPopup.gif}} * There is not much you can do with this file, as it is only a matrix that converts the cortical sources into MEG/EEG recordings, and we do not have any sources information yet. * You may just check the sphere(s) that were used to compute the head model. |
== Computation == The forward models are related with the anatomy of the subject and the description of the sensors, therefore the menus associated to its computation are attached to the channel file. |
| Line 45: | Line 79: |
| == Overlapping spheres model == Let's compute a more advanced forward model. The overlapping spheres method is based on the estimation of a different sphere for each sensor. Instead of using only one sphere for the whole head, it estimates a sphere that fits locally the shape of the head in the surroundings of each sensor. |
* In the imported '''Run#01''', right-click on the channel file or the folder > '''Compute head model'''. <<BR>>Keep the default options selected: Source space='''Cortex''', Forward model='''Overlapping spheres'''.<<BR>><<BR>> {{attachment:compute_popup.gif||height="161",width="254"}} {{attachment:compute_options.gif||height="247",width="211"}} * You obtain one new file in the database. It is always saved in the same folder as the channel file.<<BR>>There is nothing much you can do with it except for using it for estimating sources. This will be the purpose of the following tutorials. * Right-click on the new head model > ''Check spheres''. This window shows the spheres that were estimated. You can check them by following the indications written in green at the bottom of the window: use left/right arrows. At each step, the current sensor marker is displayed in red, and the sphere you see is its local estimation of the head shape. <<BR>><<BR>> {{attachment:headmodel_popup.gif||height="124",width="258"}} {{attachment:headmodel_spheres.gif||height="181",width="272"}} * This algorithm is supposed to use the inner skull surface from the subject, but we usually do not have this information. In this case, a pseudo-innerskull is reconstructed using a dilated version of the cortex envelope. |
| Line 48: | Line 84: |
| 1. Right-click on ''Right'' condition and select ''Compute head model'' again. 1. Select the ''Overlapping spheres'' method and click on ''Run''. 1. This algorithm is supposed to use the inner skull surface from the subject, but we usually do not have this information. In this case, a pseudo-innerskull is reconstructed using a dilated version of the cortex envelope. 1. Right-click on the new head model > ''Check spheres''. This window shows the spheres that were estimated. You can check them by following the indications written in green at the bottom of the window: use left/right arrows. At each step, the current sensor marker is displayed in red, and the sphere you see is its local estimation of the head shape. 1. Close this window when you reviewed them all.<<BR>><<BR>> {{attachment:osTree.gif}} {{attachment:checkSpheres.gif}} 1. Compute a head model for the Left condition (Overlapping spheres). |
Repeat the same operation for the other file. We have two different acquisition runs with two different relative position of the head and the sensors, therefore we need to compute to different head models. |
| Line 55: | Line 86: |
| == Selection of a head model == We now have two head models in for our ''Subject01 / Right'' condition. |
* In the imported '''Run#02''', right-click on the channel file > '''Compute head model'''. {{attachment:run02_popup.gif||height="220",width="265"}} {{attachment:run02_files.gif||height="220",width="193"}} |
| Line 58: | Line 88: |
| * You can have several head models computed for the same dataset, but it is not recommended as it might be difficult afterwards to know which one was used to compute the sources. * If you want to keep them anyway, you have to indicate which one is the default one. You do that by double-clicking on one of them (or right-click > set as default head model), and it is supposed to turn green. The head model displayed in green is the one that will be used for the following computation steps. * For MEG, when it works properly, the overlapping spheres model usually gives better results than the single sphere one. In this particular case, it produces more focal results, so we are going to use it for the next steps. * For EEG, always prefer the "OpenMEEG BEM" model. * Now to make things clearer: delete the'' Single sphere'' head model, and keep the ''Overlapping spheres''. |
<<TAG(Advanced)>> |
| Line 64: | Line 90: |
| == Batching head model computation == You can run in two clicks the computation of the overlapping spheres model for all the conditions or subjects you want in the database. |
== Database explorer == Additional considerations about the management of the head model files. |
| Line 67: | Line 93: |
| * The ''Compute head model'' menu is available in popup menus in the tree at all the levels (protocol, subject, condition). It is then applied recursively to all the subjects and conditions contained in the node(s) you selected. * Example: If you want to compute it on all the subjects and all the conditions, select the ''Compute head model'' menu from the protocol node ''TutorialCtf''. For all the conditions of ''Subject01'', run it from the ''Subject01 ''popup menu. Etc. * If you only want to compute it on some subjects of the protocol, select them at once holding the ''Ctrl ''key, right-click on one, and select the ''Compute head model ''menu''.'' * To process all the subjects for one condition, switch to the ''Functional data (sorted by conditions)'' view of the database. |
* If you have '''multiple head models''' computed in the same folder, you would see one displayed in green and the others in black. The one in green is selected as the default head model, it will be used for all the following computation steps. To change the default selection, double-click on another head model file (or right-click > Set as default head model). |
| Line 72: | Line 95: |
| == Additional discussions on the forum == * Sensor modeling: http://neuroimage.usc.edu/forums/showthread.php?1295 * Gain matrix: http://neuroimage.usc.edu/forums/showthread.php?918 * EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718 * EEG and default anatomy: http://neuroimage.usc.edu/forums/showthread.php?1774 * Mixed head models indices: http://neuroimage.usc.edu/forums/showthread.php?1878 |
* You can use the database explore for '''batching the computation''' of the head model. The menu "Compute head model" is available in popup menus in the database explorer at all the levels (protocol, subject, condition). It is applied recursively to all the subjects and conditions contained in the node(s) you selected. |
| Line 79: | Line 97: |
| = From continuous tutorials: = == Source analysis == Let's reproduce the same observations at the source level. The concepts related with the source estimation are not discussed here; for more information, refer to the introduction tutorials #6 to #8. |
<<TAG(Advanced)>> |
| Line 83: | Line 99: |
| First, '''delete''' all the files related with the source estimation calculated in the previous tutorials, available in the ''(Common files)'' folder: the head model, the noise covariance and inverse model. We can now provide a better estimate of the noise (affects the inverse model), and we defined new SSP operators (affects the head model). | == On the hard drive == Right-click on any head model > File > View file contents: |
| Line 85: | Line 102: |
| === Head model === Right-click on any node that contains the channel file (including the channel file itself), and select: "'''Compute head model'''". Leave all the default options: cortex source space, and overlapping spheres. The lead field matrix is saved in file "Overlapping spheres" in ''(Common files)''. |
. {{attachment:headmodel_contents.gif||height="440",width="486"}} |
| Line 88: | Line 104: |
| {{http://neuroimage.usc.edu/brainstorm/Tutorials/TutRawAvg?action=AttachFile&do=get&target=forward.gif|forward.gif|class="attachment"}} | ==== Structure of the files ==== * '''MEGMethod''': Forward model used for MEG sensors ('os_meg', 'meg_sphere', 'openmeeg' or empty). * '''EEGMethod''': Forward model used for EEG sensors ('eeg_3sphereberg', 'openmeeg' or empty). * '''ECOGMethod''': Forward model used for ECoG sensors ('openmeeg' or empty). * '''SEEGMethod''': Forward model used for sEEG sensors ('openmeeg' or empty). * '''Gain''': Leadfield matrix, [Nsensors x Nsources], equivalent to [Nsensors x 3*Nvertices] * '''Comment''': String displayed in the database explorer to represent this file. * '''HeadModelType''': Type of source space used for this head model ('surface', 'volume', 'mixed'). * '''GridLoc''': [Nvertices x 3], (x,y,z) positions of the grid of source points. In the case of a surface head model, it corresponds to a copy of the .Vertices matrix from the cortex surface file. * '''GridOrient''': [Nvertices x 3], direction of the normal to the surface for each vertex point (copy of the .VertNormals matrix of the cortex surface). Empty in the case of a volume head model. * '''GridAtlas''': In the case of mixed head models, contains a copy of the "Source model options" atlas structure that was used for the creating the model. * '''SurfaceFile''': Relative path to the cortex surface file related with this head model. * '''Param''': Description of the sphere that was estimated for each sensor (Center/Radius).<<BR>> |
| Line 90: | Line 118: |
| = From auditory = === Head model === * Select the two imported folders at once, right-click > Compute head model . {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=headmodel1.gif|headmodel1.gif|height="221",width="413",class="attachment"}} * Use the '''overlapping spheres''' model and keep all of the options at their default values. . {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=headmodel2.gif|headmodel2.gif|height="234",width="209",class="attachment"}} {{http://neuroimage.usc.edu/brainstorm/Tutorials/Auditory?action=AttachFile&do=get&target=headmodel3.gif|headmodel3.gif|height="208",width="244",class="attachment"}} * For more information: [[http://neuroimage.usc.edu/brainstorm/Tutorials/TutHeadModel|Head model tutorial]]. |
'''Gain matrix''' |
| Line 98: | Line 120: |
| == What's in the headmodel file == <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/ExploreRecordings&next=Tutorials/NoiseCovariance")>> |
* The Gain matrix stores the leadfield for 3 orientations (x,y,z) at each grid point (p1, p2, ...). <<BR>>The successive columns of the Gain matrix are: ['''p1'''_x, '''p1'''_y, '''p1'''_z, p2_x, p2_y, p2_z ...] * To convert this unconstrained leadfield matrix to a '''constrained model''', where the orientation of each dipole is fixed and normal to the cortex surface: * Export the head model file to the HeadModel structure: Right-click > File > '''Export to Matlab'''. * > Gain_constrained = '''bst_gain_orient'''(HeadModel.Gain, HeadModel.GridOrient); * The dimension of the output matrix is three times smaller: [Nsensors x Nvertices] == Additional documentation == * Tutorial: [[Tutorials/TutBem|BEM with OpenMEEG]] * Tutorial: [[Tutorials/TutVolSource|Volume source estimation]] * Forum: Sensor modeling: http://neuroimage.usc.edu/forums/showthread.php?1295 * Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718 * Forum: EEG and default anatomy: http://neuroimage.usc.edu/forums/showthread.php?1774 * Forum: Mixed head models indices: http://neuroimage.usc.edu/forums/showthread.php?1878 <<HTML(<!-- END-PAGE -->)>> <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/ChannelClusters&next=Tutorials/NoiseCovariance")>> |
Tutorial 20: Head model
Authors: Francois Tadel, John C Mosher, Richard Leahy, Sylvain Baillet
The following tutorials describe how the brain activity can be estimated from the MEG/EEG recordings we have processed until now. This process consists in solving two separate problems: the modeling of the electromagnetic properties of the head (head model or forward model) and the inversion of this model. This tutorial will explain how to compute a head model for the subject of our auditory oddball experiment. Its scope is limited to linear distributed source models (there is no dipole fitting available in the software).
Contents
Why estimating sources?
Reconstructing the activity of the brain from MEG or EEG recordings can be a difficult and long process. We tried to make it as automatic as possible, but you have to understand its advantages and issues before deciding if it can bring anything to your study.
The primary objective is to localize the regions of the brain that generated our signals of interest. From the sensor topographies in MEG and EEG, we can have a general idea of where the signal generators are located, but we cannot be more precise than identifying the hemisphere and the lobe. Using source estimation methods, we can expect to get a spatial resolution in the range of the centimeter, or even a few millimeters in the good cases.
While localizing the signals, we can also expect some form of deconvolution of our signals. In EEG, the scalp topographies are very smooth and it is common to have different effects that are superimposed in the signals recorded by most of the electrodes. Moving to the source space may help separating the sources and obtain cleaner and unmixed signals.
Specifically for MEG, working in source space solves many of the problems associated with this modality. The subject's head is not fixed in an MEG system, so it has a great chance of moving during the experiment. Also, the position of the sensors do not adapt to the shape and size of the head. Therefore between two acquisition runs, or between subjects with different morphologies, there is a high chance that the same MEG sensor records different parts of the brain. This problem does not exist in EEG, where the electrodes are in standard positions and follow the subject in all the movements.
Another point that makes MEG signals difficult to review is the variability in the sensors. Every manufacturer uses different types of sensors, that are sensitive to different orientations and distances, and that produce signals with different shapes. Again, this is not a problem in EEG: the only variability you can get between two EEG systems is the level of noise and the ease of use of the cap, the signals will look very similar. Projecting all the data on the individual brains addresses these last two issues.
However, if your interest is only in the latency of an event, in detecting the lateralization of a known effect or in training blindly a classifier, you might not be interested in those complicated models that multiply by 50 the size of your files. Go for fancy methods only when you think they can bring some added value to your analysis, not because everybody around uses them.
The origins of the MEG/EEG signals
To understand how we are reconstructing the sources, it is interesting to have an idea of the physiological origins of MEG and EEG signals. The models we use are based on some physiological assumptions that are not always valid, understanding them may help you selecting the appropriate method.
It is assumed that most of the currents we record are related with the postsynaptic activity of the pyramidal neurons in the cerebral cortex. These cells are aligned spatially and perpendicular to the cortex surface. Millions of post-synaptic potentials in the apical dendrites of neighbouring pyramidal neurons sum up in time and space to form what we can approximate at a macroscopic level with a few electric dipoles (green arrows below).
The primary and volume currents generated by these dipoles create a potential distribution and a magnetic field at the surface of the head. We can record them with bipolar montages of electrodes placed on the skin (EEG) or very sensitive superconducting detectors (SQUIDs/MEG).
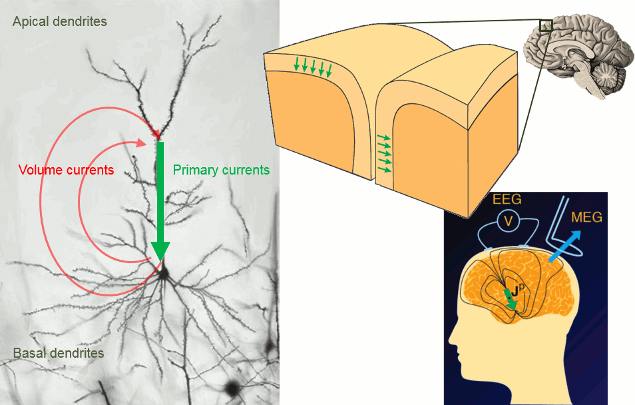
- Matti Hamalainen, 2007
Source space
The source estimation process consists in estimating the position and activity of a set of electric dipoles, to approximate the activity of the brain that produced the MEG/EEG data we recorded. Two families of solutions were explored in the past decades: the dipole fitting methods (we estimate the position and amplitude of a very limited number of dipoles over short time windows) and the distributed methods (we define a priori a dense grid of dipoles and then estimate their activity from the recordings).
The single dipole fitting approaches are very efficient in specific cases were we know in advance the number or regions involved and their latencies of activity. But they are difficult to generalize and automate, and not adapted for group analysis. With Brainstorm, we decided to work only with source distributed models, which require less manual tuning for getting acceptable results.
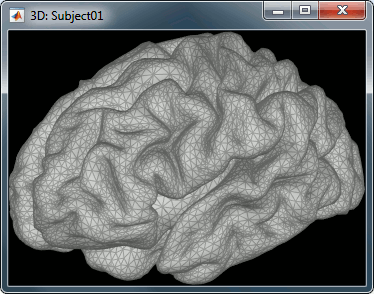
Our first step of modeling is then to define the position and orientation of the dipoles for which we want to estimate the activity. This set of dipoles is our referred to as our source space. By default, we limit our analysis to the cortex envelope, based on this observation that most of the MEG/EEG signals is related with the synchronous activity of assemblies or cortical pyramidal cells. The simple solution we recommend is to use directly the vertices of the cortical surface we imported in the first tutorials (the nodes we can see in the grey mesh in the left image below).
In order to represent all the possible dipole orientations, we define three dipoles for each vertex of the cortex surface, corresponding to three orthogonal directions (X,Y,Z). When importing the anatomy of the subject, we downsampled the cortex surface to 15,000 vertices. This will correspond to a source space of 45,000 dipoles. We will compute a forward model that connects the activity of these 45,000 dipoles with the 275 MEG sensors we have in this dataset.
This default number of 15,000 vertices is empirical. Over the years, our experience seemed to show that it represents a good balance between the representation of the brain circumvolutions, the surface sampling and the amount of data that is generated. Using less vertices makes it difficult to preserve the shape of the brain, using more vertices produces more data without adding to the spatial resolution of the method and may lead to memory issues.
Additionally, we can impose constraints of orientation on the dipoles, to match the physiological observation that the pyramidal cells are mostly organized perpendicularly to the cortex surface. This has the advantage of limiting the number of dipoles to 15,000 (one per vertex) and making the results much easier to display and process. However, this constraint is most of the time too strong and distorts the reconstruction. This orientation constraint is an option of the inverse model and will be discussed in the following introduction tutorials.
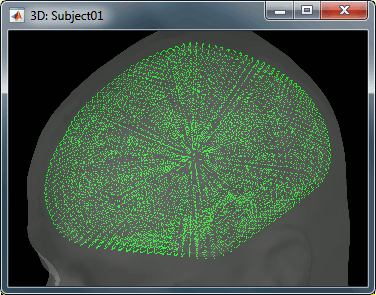
The spatial constraint of imposing all the dipoles to be on the cortical surface might also be too restrictive in some cases, because our model is then not able to represent correctly the activity in deeper brain structures or in the cerebellum. Therefore we also offer an option to use the entire brain volume as our space space (the green dots below represent dipoles locations in volume model). This produces results that can be better or worse depending on the data, but in all the cases much more difficult to review. Volume and mixed head volumes are discussed in the advanced tutorials about source modeling.
Forward problem
The first step of the source reconstruction consists in computing a model that explains how the electric currents or the magnetic fields flow from the electric generators in the brain (source space) through the different tissues of the head (mostly brain, CSF, skull and skin), to finally reach the sensors.
The question of building a model that connects the values we observe outside of the head (MEG/EEG) to the electric activity of the cortical dipoles in the brain is called forward problem.
The model we obtain after solving this problem is called head model in Brainstorm, but can also be referred to as forward model, leadfield matrix or gain matrix.
In this tutorial we will use the default source space: the low-resolution cortex surface with 15,000 vertices, as the support of 45,000 dipoles. We will use indifferently the terms dipole and source.
What we expect to get at the end of this process is a matrix [Nsensors x Nsources].
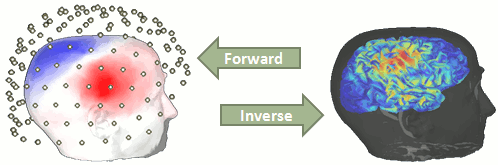
Available methods for MEG forward modeling:
Single sphere: The head is considered to be a homogeneous sphere.
Overlapping spheres: Refining the previous model by fitting one local sphere for each sensor.
OpenMEEG BEM: Symmetric Boundary Element Method from the open-source software OpenMEEG. Described in an advanced tutorial: BEM head model.
Models recommended for each modality:
MEG: Overlapping spheres.
The magnetic fields are not too much affected by the heterogeneity of the tissues of the head. The is no real need for modeling the head with too much details.EEG: OpenMEEG BEM.
The electric currents are strongly affected by jumps between very conductive tissues (brain, CSF, skin) and an isolant medium (the skull). A realistic head model is strongly advised for modeling the properties of the skull correctly. When computing a BEM model is not an option, for instance if OpenMEEG crashes for unknown reasons, the Berg's three-layer sphere can be an acceptable option.sEEG/ECoG: The OpenMEEG BEM option is the only one available.
Computation
The forward models are related with the anatomy of the subject and the description of the sensors, therefore the menus associated to its computation are attached to the channel file.
In the imported Run#01, right-click on the channel file or the folder > Compute head model.
Keep the default options selected: Source space=Cortex, Forward model=Overlapping spheres.
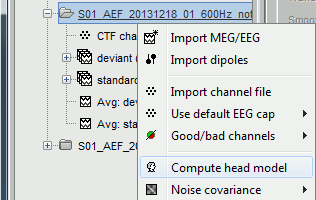
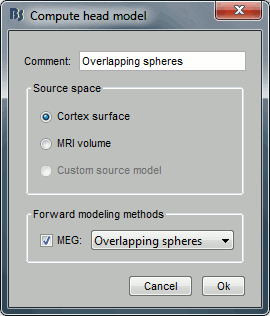
You obtain one new file in the database. It is always saved in the same folder as the channel file.
There is nothing much you can do with it except for using it for estimating sources. This will be the purpose of the following tutorials.Right-click on the new head model > Check spheres. This window shows the spheres that were estimated. You can check them by following the indications written in green at the bottom of the window: use left/right arrows. At each step, the current sensor marker is displayed in red, and the sphere you see is its local estimation of the head shape.
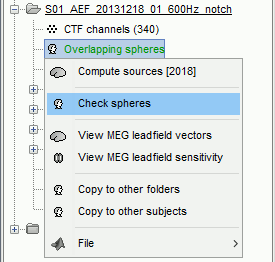
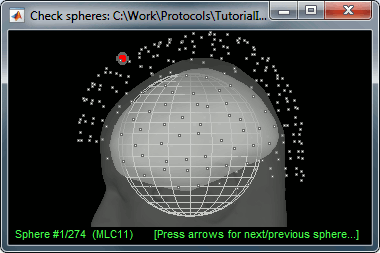
- This algorithm is supposed to use the inner skull surface from the subject, but we usually do not have this information. In this case, a pseudo-innerskull is reconstructed using a dilated version of the cortex envelope.
Repeat the same operation for the other file. We have two different acquisition runs with two different relative position of the head and the sensors, therefore we need to compute to different head models.
In the imported Run#02, right-click on the channel file > Compute head model.
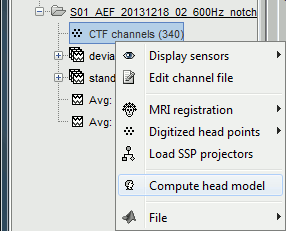
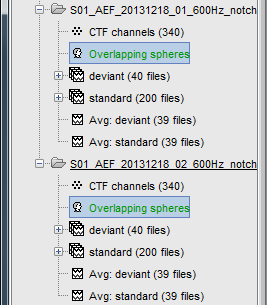
Database explorer
Additional considerations about the management of the head model files.
If you have multiple head models computed in the same folder, you would see one displayed in green and the others in black. The one in green is selected as the default head model, it will be used for all the following computation steps. To change the default selection, double-click on another head model file (or right-click > Set as default head model).
You can use the database explore for batching the computation of the head model. The menu "Compute head model" is available in popup menus in the database explorer at all the levels (protocol, subject, condition). It is applied recursively to all the subjects and conditions contained in the node(s) you selected.
On the hard drive
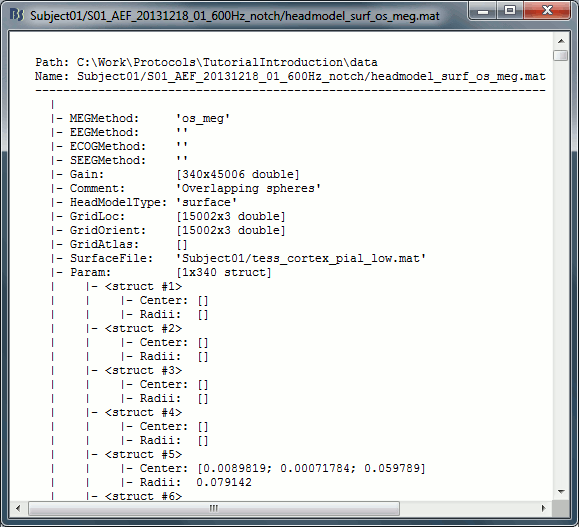
Right-click on any head model > File > View file contents:
Structure of the files
MEGMethod: Forward model used for MEG sensors ('os_meg', 'meg_sphere', 'openmeeg' or empty).
EEGMethod: Forward model used for EEG sensors ('eeg_3sphereberg', 'openmeeg' or empty).
ECOGMethod: Forward model used for ECoG sensors ('openmeeg' or empty).
SEEGMethod: Forward model used for sEEG sensors ('openmeeg' or empty).
Gain: Leadfield matrix, [Nsensors x Nsources], equivalent to [Nsensors x 3*Nvertices]
Comment: String displayed in the database explorer to represent this file.
HeadModelType: Type of source space used for this head model ('surface', 'volume', 'mixed').
GridLoc: [Nvertices x 3], (x,y,z) positions of the grid of source points. In the case of a surface head model, it corresponds to a copy of the .Vertices matrix from the cortex surface file.
GridOrient: [Nvertices x 3], direction of the normal to the surface for each vertex point (copy of the .VertNormals matrix of the cortex surface). Empty in the case of a volume head model.
GridAtlas: In the case of mixed head models, contains a copy of the "Source model options" atlas structure that was used for the creating the model.
SurfaceFile: Relative path to the cortex surface file related with this head model.
Param: Description of the sphere that was estimated for each sensor (Center/Radius).
Gain matrix
The Gain matrix stores the leadfield for 3 orientations (x,y,z) at each grid point (p1, p2, ...).
The successive columns of the Gain matrix are: [p1_x, p1_y, p1_z, p2_x, p2_y, p2_z ...]To convert this unconstrained leadfield matrix to a constrained model, where the orientation of each dipole is fixed and normal to the cortex surface:
Export the head model file to the HeadModel structure: Right-click > File > Export to Matlab.
> Gain_constrained = bst_gain_orient(HeadModel.Gain, HeadModel.GridOrient);
- The dimension of the output matrix is three times smaller: [Nsensors x Nvertices]
Additional documentation
Tutorial: BEM with OpenMEEG
Tutorial: Volume source estimation
Forum: Sensor modeling: http://neuroimage.usc.edu/forums/showthread.php?1295
Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718
Forum: EEG and default anatomy: http://neuroimage.usc.edu/forums/showthread.php?1774
Forum: Mixed head models indices: http://neuroimage.usc.edu/forums/showthread.php?1878