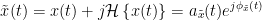Tutorial 28: Connectivity
[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE]
Authors: Hossein Shahabi, Raymundo Cassani, Takfarinas Medani
Cognitive and perceptual functions are the result of coordinated activity of functionally specialized regions in the brain. Brain connectivity investigates how these different regions (or nodes) interact as a network, with the goal of having a better understanding of how the brain processes information. Depending on which connectivity characteristic is studied, a distinction is made between structural (fiber pathways), functional (non-directed statistical dependency) and effective (causal interaction) connectivity between regions. Effective connectivity is often referred as directed functional connectivity. In this tutorial we will see how to compute different connectivity metrics for non-directed and directed functional analyses in Brainstorm, first with simulated data and later with real data.
Contents
- General considerations in connectivity analysis
- Simulated data (MVAR model)
- Correlation
- Coherence
- Granger causality
- Spectral Granger causality
- Envelope correlation (2020)
- Phase locking value
- Phase transfer entropy
- Method selection and comparison
- Sensor- and source-level connectivity analyses
- Correlation on real data
- Sections to add
- On the hard drive
- Additional documentation
General considerations in connectivity analysis
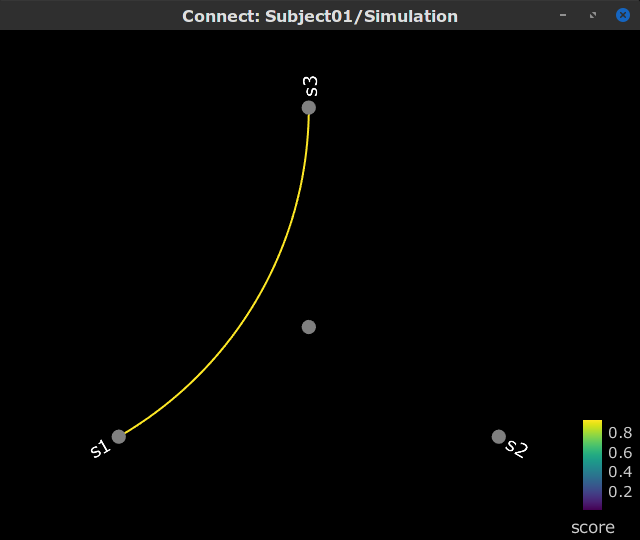
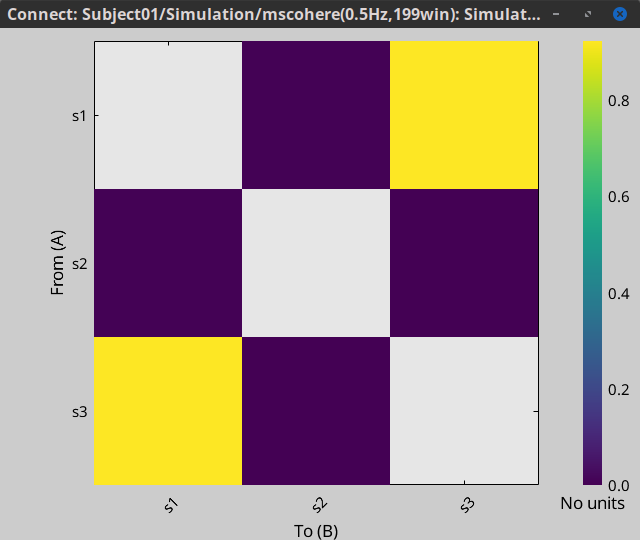
Connectivity analyses are commonly performed by computing a bivariate connectivity metric for all the possible pairs of time series or signals. The result of such approach can be presented as a connectivity graph (left image), where each signal is represented as a node, and the value of the connectivity metric is the value of the edge between the corresponding nodes. This graph representation becomes overwhelming when too many nodes are considered, as such, the connectivity graph can be represented with its connectivity matrix, aka adjacency matrix (right image).
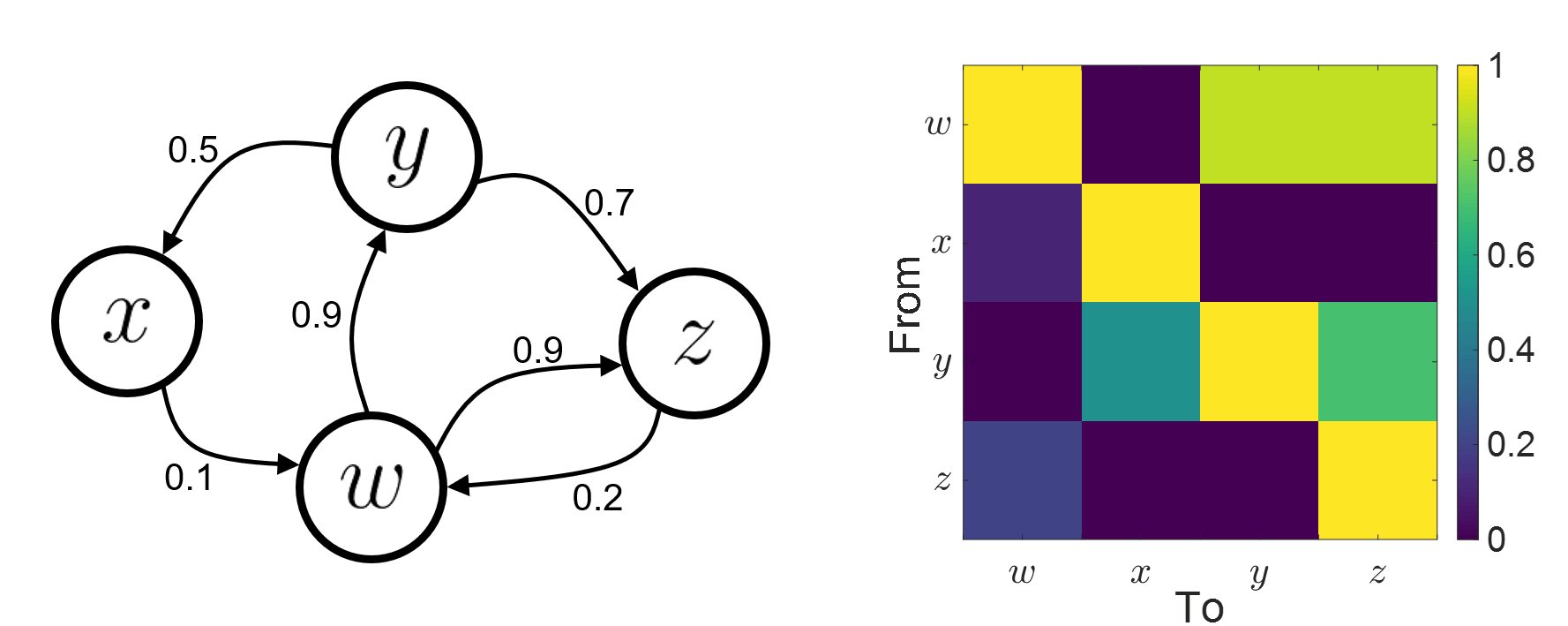
Sensors or sources: The signals used for the connectivity analysis can be derived from the sensor data (EEG/MEG signals) or from the reconstructed sources (voxels or scouts).
Directed and non-directed: The direction of the interaction between signals (as statistical causation) can be measured with directed metrics. However, this is not possible with non-directed metrics, as result, the connectivity metric "from Signal  to Signal
to Signal 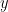 " is equal to the connectivity metric "from Signal
" is equal to the connectivity metric "from Signal 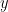 to Signal
to Signal  ".
".
Recording condition: Connectivity analyses can be performed on resting-state (spontaneous) and event-related (trials) recordings, the appropriate connectivity method depends on the recording condition.
Full network vs point-based connectivity: In full network, the connectivity metric is computed for all the possible node pairs in the network (N×N approach), and gives as result a detailed connectivity graph. Alternatively, point-based analysis is performed solely between one node (aka seed) and the rest of the nodes in the network (1×N approach), this approach is faster to compute and is more useful when you are interested in the connectivity of a specific sensor or source.
Temporal resolution: Connectivity analyses can be performed in two ways: static and dynamic. Time-varying networks can present the dynamics of brain networks. In contrast, the static graphs illustrate a general perspective of brain connectivity which is helpful in specific conditions. Users need to decide which type of network is more informative for their study.
Time-frequency transformation: Several connectivity metrics rely on the time-frequency representation of the signals, which is obtained with approaches such as the short-time Fourier transform, Hilbert transform, and Morlet wavelet.
Simulated data (MVAR model)
To compare different connectivity metrics, we use simulated data with known ground truth using a multivariate autoregressive (MVAR) model. This model consist in three signals in a way that:
- The first signal has components at 10 and 25 Hz with a dominant peak at 25 Hz (beta band).
- The second signal has the same components, but dominant peak is at 10 Hz (alpha band).
- The third signal has similar power for both components (10 and 25 Hz).
- Additionally, the third signal is influenced by the first signal by the filter, with a peak at 25 Hz.
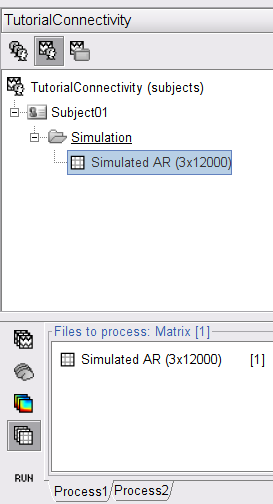
To simulate this data, first clear the process panel, and select the Simulate > Simulate AR signals (ARfit) with spectra process.
Process options
Subject name Target subject for the simulated signals. Select Subject01.
Condition name Target condition for the simulated signals. Set to Simulation.
Number of time samples Set to 12 000.
Signal Sampling frequency Fs for the simulated signals. Set to 120 Hz.
Interaction specifications: Spectral parameters for the interaction between signals in the MVAR model, given as: From, To / Peak frequencies [Hz] / Peak relative magnitudes [0-1]
Set to:1, 1 / 10, 25 / 0.3, 0.5 2, 2 / 10, 25 / 0.7, 0.3 3, 3 / 10, 25 / 0.2, 0.2 1, 3 / 25 / 0.1
By pressing the View spectral metrics button, spectral metrics related to the MVAR process are displayed before simulating the signals. These spectral metrics include: transfer function, cross-spectral power density, magnitude square coherence, directed transfer function (DTF) and partial directed coherence (PDC). The transfer function, 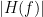 , contains information about the relationships between signals and their spectral characteristics; it is non-symmetric, so it allows for finding causal dependencies. Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values. The auto-transfer function (diagonal elements in the image) correspond to the power spectrum of the signals. The off-diagonal terms represent the interactions between different signals.
, contains information about the relationships between signals and their spectral characteristics; it is non-symmetric, so it allows for finding causal dependencies. Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values. The auto-transfer function (diagonal elements in the image) correspond to the power spectrum of the signals. The off-diagonal terms represent the interactions between different signals.
Moreover, the Get coefficients matrix button provides the coefficients related to the MVAR model. These coefficients can be used in the Simulate > Simulate AR signals (ARfit) process to simulated the same model.
Finally, click in the Run button to simulate the signals described by the MVAR model. In the next sections we will compute different connectivity metrics for these simulated signals. As such, place the simulated data in the Process1 tab, select recordings, click on [Run] ( ![]() ) to open the Pipeline editor, and select the connectivity metric.
) to open the Pipeline editor, and select the connectivity metric.
Correlation
Correlation is a non-directed connectivity metric that can be used to show similarity, dependence or association among two random variables or signals. While this metric has been widely used in electrophysiology, it should not be considered the best technique to evaluate connectivity. Due to its nature, correlation fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals.
Let's compute the correlation for the simulated signals. Select the Connectivity > Correlation NxN process.
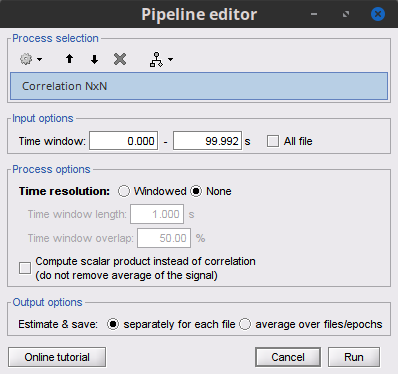
Process options
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Compute scalar product instead of correlation: If uncheck, the mean of the signals will be subtracted before computing the correlation. Uncheck it.
Output options: Select Save individual results.
Result visualization
When a N×N connectivity process ends, the results are stored as a N×N connectivity file, icon ![]() . Right-click on this file to see its display options:
. Right-click on this file to see its display options:
Display as graph: plots the connectivity graph using a chord diagram where the color of the edges shows the connectivity metric value. See the connectivity graph for a detailed explanation of the options of this visualization.
Display as image: plots the adjacent matrix for the connectivity file.
In addition, the visualization option Display fibers is available for source connectivity results when a fiber track surface is available, as shown here.
In Display as image, the value of the connectivity metric between a signal and itself plotted as zero so that it doesn't force scaling the colormap to 1 if the other values are much smaller.
Coherence
Coherency or complex coherence, 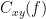 , is a complex-valued metric that measures of the linear relationship of two signals in the frequency domain. And, its magnitude square coherence (MSC),
, is a complex-valued metric that measures of the linear relationship of two signals in the frequency domain. And, its magnitude square coherence (MSC), 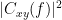 , often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals
, often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals 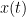 and
and 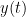 , with spectra
, with spectra 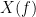 and
and 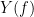 , the MSC is defined as:
, the MSC is defined as:
Two related measures, which alleviate the problem of volume conduction, are imaginary coherence (Nolte et al., 2004), 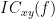 , and the lagged coherence (Pascual-Maqui, 2007),
, and the lagged coherence (Pascual-Maqui, 2007), 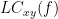 , which are defined as:
, which are defined as:
where 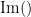 and
and 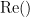 describe the imaginary and real parts of a complex number.
describe the imaginary and real parts of a complex number.
To calculate coherence values in Brainstorm, select the Connectivity > Coherence NxN process.
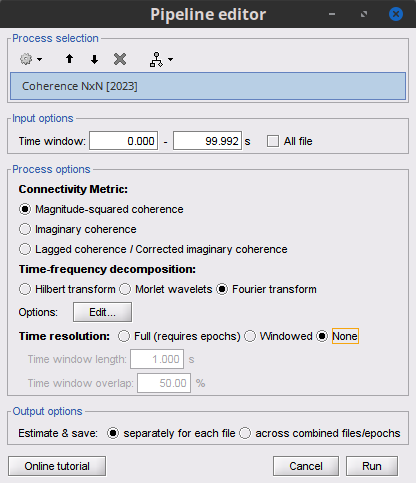
Process options
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Remove evoked response: If checked, removes the averaged evoked from each trial. Uncheck it.
Process options: Different types of coherence. Select Magnitude squared coherence.
Window length for PSD estimation Duration in seconds for the PSD estimation. Set to 1 s.
Overlap for PSD estimation: Percentage of overlap between consecutive windows for PSD estimation. Set to 50%.
Highest frequency of interest: Highest frequency for the analysis, it should be <= Fs/2. Set to 60 Hz.
Output options: Select Save individual results.
Result visualization
Coherence is a function of frequency, as such, for each frequency point there is a connectivity graph and a connectivity matrix. Right-click on the coherence result file to see its display options:
Display as graph: Plot the connectivity graph at a given frequency point.
Display as image: Plot the connectivity matrix at a given frequency point.
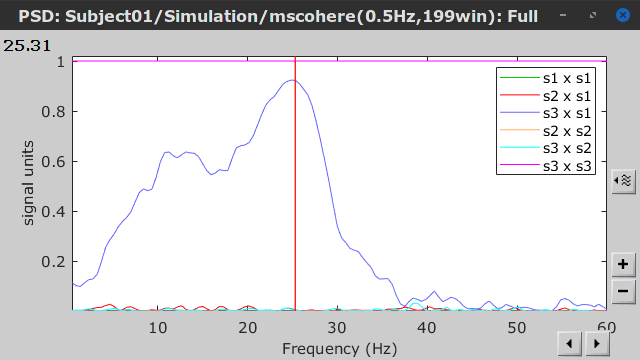
Power spectrum: Plot coherence as a function of frequency for all the possible node pairs.
Open the 3 representations. These representations are linked such as by clicking on the spectral representation of the coherence, we change the frequency that is displayed in the connectivity graph and matrix. This frequency can be also changed in the Time panel.
|
|
|
|
|
|
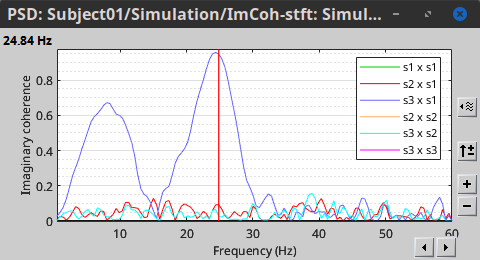
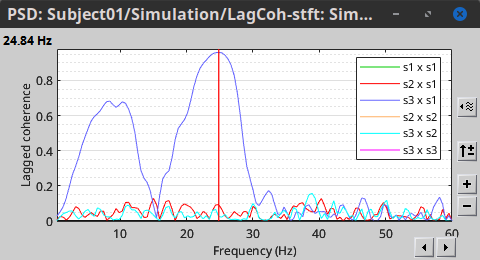
In the same way, we can compute the other types of coherence. The figure below presents the spectra for the imaginary coherence (left) and the lagged coherence (right). Both, imaginary and lagged coherence aim to address the volume conduction problem, although they present small differences.
|
|
|
Granger causality
Granger causality (GC) is a method of directed functional connectivity, which is base on the Wiener-Granger causality methodology. GC is a measure of linear dependence, which tests whether the prediction of signal 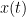 (using a linear autoregressive model) is improved by adding signal
(using a linear autoregressive model) is improved by adding signal 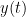 (also using a linear autoregressive model). If this is true, signal
(also using a linear autoregressive model). If this is true, signal 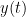 has a Granger causal effect on the first signal. In other words, independent information of the past of signal
has a Granger causal effect on the first signal. In other words, independent information of the past of signal 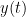 improves the prediction of signal
improves the prediction of signal 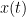 obtained with the past of signal
obtained with the past of signal 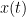 alone. GC is nonnegative, and zero when there is no Granger causality. As only the past of the signals is considered, the GC metric is directional. The term independent is emphasized because it creates some interesting properties for GC, such as, that it's invariant under rescaling of
alone. GC is nonnegative, and zero when there is no Granger causality. As only the past of the signals is considered, the GC metric is directional. The term independent is emphasized because it creates some interesting properties for GC, such as, that it's invariant under rescaling of 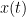 and
and 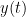 , as well as the addition of a multiple of
, as well as the addition of a multiple of 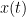 to <<latex($$y(t)$$).
to <<latex($$y(t)$$).
See Granger causality - mathematical background for a complete formulation of the method.
Despite the name, Granger causality indicates directionality but not true causality.
For example, if a variable 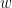 is causing both
is causing both  and
and 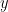 , but with a smaller delay for
, but with a smaller delay for 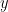 than for
than for  , then the GC measure between
, then the GC measure between  and
and 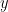 would show a non-zero GC for
would show a non-zero GC for 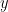 -->
-->  , even though
, even though 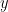 is not truly causing
is not truly causing  (Bressler and Seth, 2011).
(Bressler and Seth, 2011).
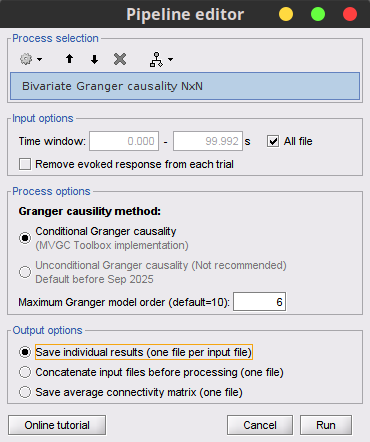
To compute the Granger causality values in Brainstorm, select the Connectivity > Bivariate Granger causality NxN process.
Process options
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Remove evoked response: If checked, removes the averaged evoked from each trial. It is recommended by some authors as it meets the zero-mean stationarity requirement (improves stationarity of the system). However, the problem with this approach is that it does not account for trial-to-trial variability. For a discussion see (Wang et al., 2008). Uncheck it.
Maximum Granger model order: The most common criteria used to define the order of the model are the Akaike’s information criterion, the Bayesian-Schwartz’s criterion, and the Hannan-Quinn criterion. Too low orders may lack the necessary details, while too big orders tend to create spurious values of connectivity. While our simulated signals were created with a model of 4, here we used as model order of 6 for a decent connectivity result.
Output options: Select Save individual results.
Result visualization
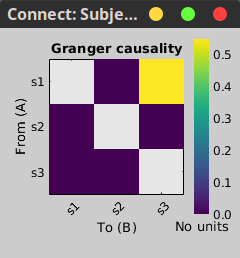
In the connectivity graph (left) the directionality is shown with an arrow head at the center for the arc connecting nodes. As GC metric is not symmetric, the connectivity matrix (right) is not symmetric. The upper right element of this matrix shows there is a signal flow from signal 1 to signal 3.
|
|
|
Spectral Granger causality
GC lacks of resolution in the frequency domain, as such, the spectral Granger causality was developed (Dhamala et al., 2008). The process to calculate this metric is found in Connectivity > Bivariate Granger causality NxN.
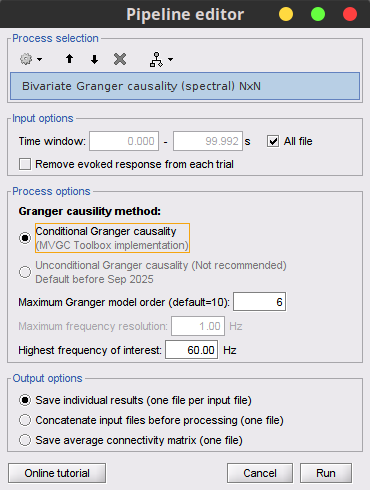
Process options
With respect to GC, spectral GC presents two extra parameters:
Maximum frequency resolution: Width of frequency bins in PSD estimation. Set to 1 Hz.
Highest frequency of interest: Highest frequency for the analysis, it should be <= Fs/2. Set to 60 Hz.
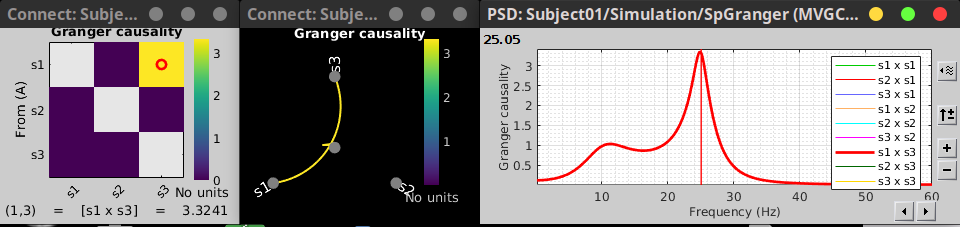
Result visualization
As with coherence, spectral GC can be plotted as a function of frequency. The plot below clearly shows a peak around 25 Hz for the interaction from signal 1 to signal 3, as expected.
Envelope correlation (2020)
In the time-frequency tutorial the Morlet wavelets and Hilbert transform were introduced as methods to decompose signals in the time-frequency (TF) domain. The result of this TF transformation can be seen as a set of narrowband complex signals, which are analytic signals.
The analytic signal, 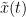 , is a complex signal uniquely associated to a real signal,
, is a complex signal uniquely associated to a real signal, 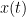 , that has been useful in signal processing due to its characteristics, more specifically, its module
, that has been useful in signal processing due to its characteristics, more specifically, its module 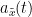 , and phase
, and phase 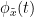 , correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the associated real signal
, correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the associated real signal 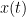 . The real part of
. The real part of 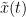 is its associated real signal
is its associated real signal 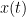 , and the imaginary part is the Hilbert transform of the same real signal
, and the imaginary part is the Hilbert transform of the same real signal 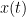 .
.
The instantaneous amplitude (or envelope) of these band analytic signals can be used to carry out pairwise connectivity analysis with metrics such as correlation and coherence (including lagged coherence).
In computing the envelope correlation, an optional step is to orthogonalize the envelopes by removing their real part of coherence before the correlation (Hipp et al., 2012). This orthogonalization process alleviates the effect of volume conduction in MEG/EEG signals. These connectivity metrics can be computed with the Connectivity > Envelope Correlation N×N [2020] process. B
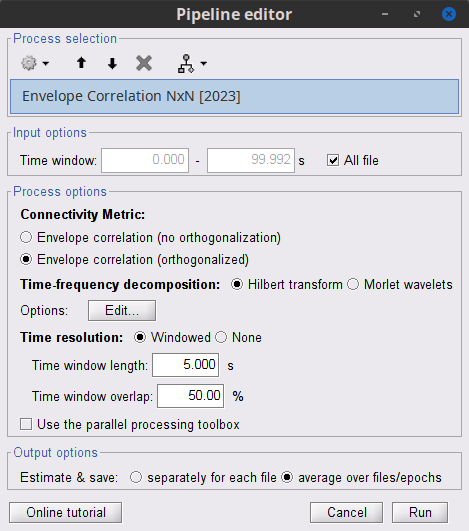
Process options
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Remove evoked response: If checked, removes the averaged evoked from each trial. Uncheck it.
Time-frequency transformation method: Either Hilbert transform or Morlet wavelets. Each of this methods requires additional parameters that are found in an external panel that opens by clicking on Edit. See the time-frequency tutorial.
|
|
|
Signal splitting: This process has the capability of splitting the input data into several blocks for performing time-frequency transformation, and then merging them to build a single file. This feature helps to save a huge amount of memory and, at the same time, avoid breaking a long-time recording to short-time signals, which makes inconsistency in dynamic network representation of spontaneous data. The maximum number of blocks which can be specified is 20. Set to 1.
Connectivity measure: This is the connectivity metric that will be used with the envelopes. Select Envelope correlation (orthogonalized).
Time resolution: If Dynamic is selected, connectivity is saved for each window of analysis. If Static is selected, the connectivity results from all the windows are averaged. Select Dynamic.
Estimation window length: Duration in milliseconds to compute the connectivity measure. Set to 5000 ms
Sliding window overlap: Percentage of overlap between consecutive windows to compute the connectivity measure. Set to 50%.
Use the parallel processing toolbox: Enables the use of the parallel processing toolbox in Matlab to accelerate the computational procedure. Uncheck it.
Output configuration: Generally, the above calculation results in a 4-D matrix, where dimensions represent channels (1st and 2nd dimensions), time points (3rd dimension), and frequency (4th dimension). In the case that we analyze event-related data, we have also several files (trials). However, due to the poor signal-to-noise ratio of a single trial, an individual realization of connectivity matrices for each of them is not in our interests. Consequently, we need to average connectivity matrices among all trials of a specific event. The second option of this part performs this averaging.
Result visualization
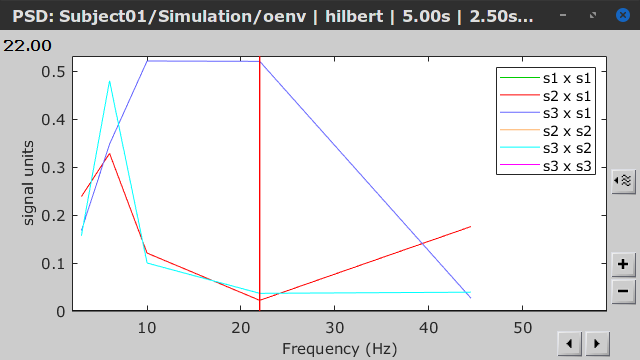
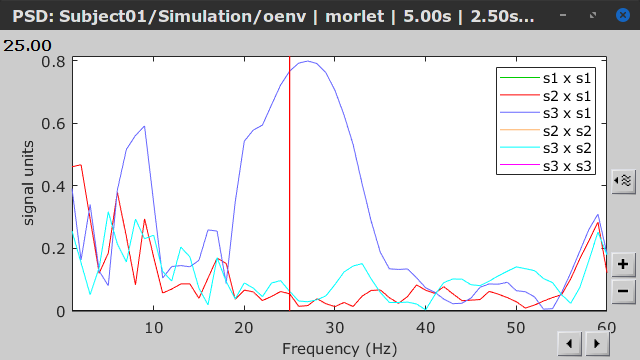
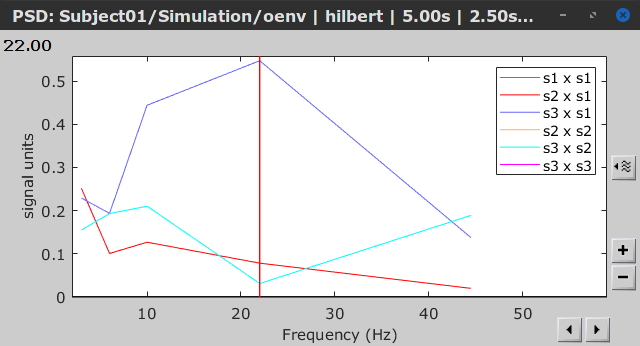
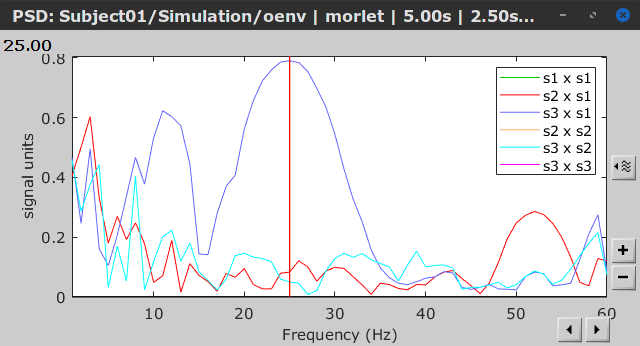
Similar to the results from coherence and spectral Granger causality, the envelope correlation can be plotted as a function of frequency, and as a function of time if the Time resolution option is set to Dynamic. Below, the results obtained with the Hilbert transform (left) and with Morlet wavelet (right) for the first 5-s window (top) and the 5-s last window (bottom).
|
First 5-s window |
|
|
Last 5-s window |
|
Phase locking value
An alternative class of connectivity metrics considers only the relative instantaneous phase between the two signals, i.e., phase-locking or synchronization (Tass et al., 1998). Phase locking is a fundamental concept in dynamical systems that has been used in control systems (the phase-locked loop) and in the analysis of nonlinear, chaotic and non-stationary systems. Since the brain is a nonlinear dynamical system, phase locking is an appropriate approach to quantifying connectivity. A more pragmatic argument for its use in studies of LFPs, EEG, and MEG is that it is robust to fluctuations in amplitude that may contain less information about interactions than does the relative phase (Lachaux et al., 1999; Mormann et al., 2000).
The most commonly used phase connectivity metric is the phase-locking value (PLV), which is defined as the length of the average vector of many unit vectors whose phase angle corresponds to the phase difference between two signals (Tass et al., 1998). If the distribution of the phase difference between the two signals is uniform, the length of such an average vector will be zero. Conversely, if the phases of the two signals are strongly coupled, the length of the average vector will approach unity. For event-related studies, we would expect the phase difference across trials to be uniform distributed unless the phase is locked to the stimulus. In that case, we may have nonuniform marginals which could in principle lead to indications of phase locking between two signals. Considering a pair of narrow-band analytic signals 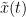 and
and 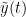 , obtained from the TF transformation using the Hilbert transform:
, obtained from the TF transformation using the Hilbert transform:
![\begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*} \begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_34340c3731fe7904b2885462bc74b6a893456cc5_p1.png)
with:
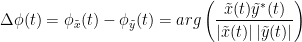
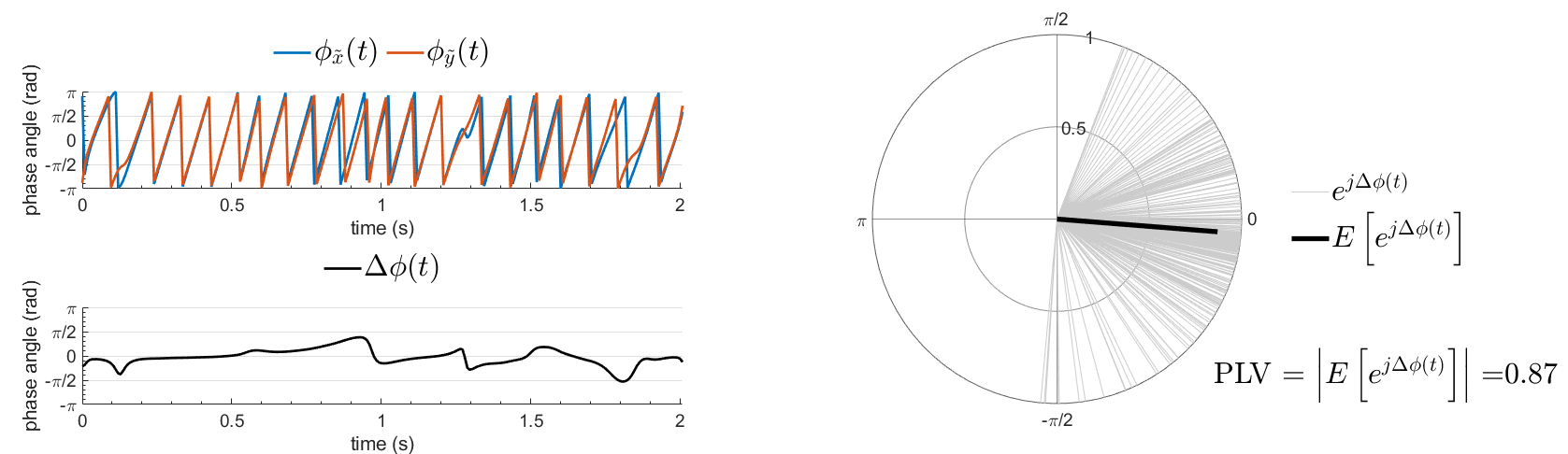
To calculate PLV in Brainstorm, select the Connectivity > Phase locking value NxN process.
Process options
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Frequency bands for the Hilbert transform: Frequency bands used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial.
Keep time information: Computes PLV across trials, thus the result is a PLV time series for each frequency band.
Measure: How the resulting vector is reported. Select Magnitude.
Output options: Select Save individual results.
Result visualization
PLV is frequency resolved, and it was computed for the delta, theta, alpha, beta and gamma bands. With the simulated data, we expect a higher PLV value in the beta band (15 to 29 Hz), between signal 1 and signal 3. This result is seen as a peak at 22 Hz (center of beta band) shown in PLV as a function of frequency.
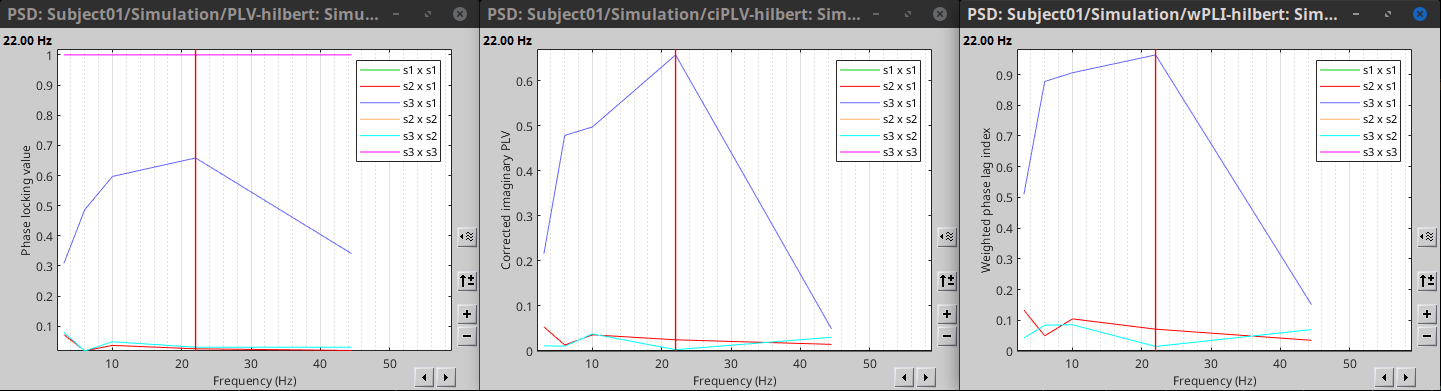
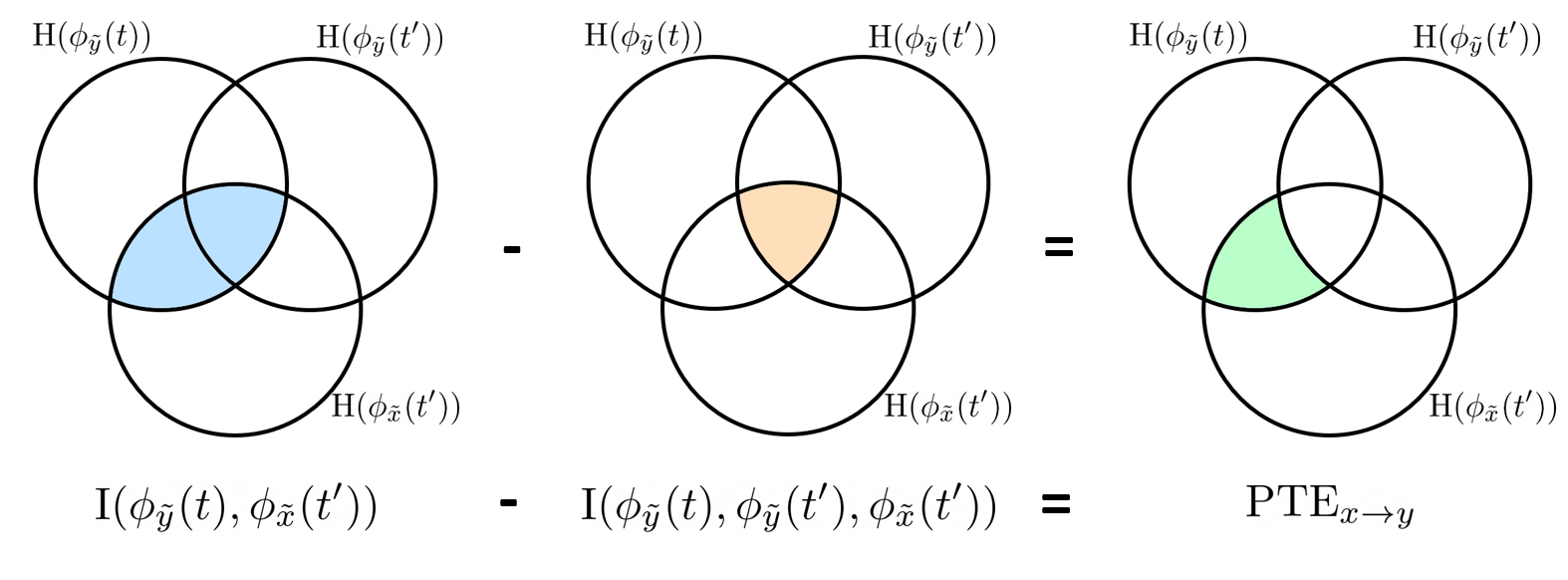
Phase transfer entropy
Phase transfer entropy (PTE) is a directed connectivity metric that quantifies the transfer entropy (TE) between two instantaneous phase time series (Lobier et al., 2014). Similar to GC, TE estimates whether including the past of both source and target time-series influences the ability to predict the future of the target time-series. In PTE, if a phase signal 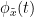 causes the signal
causes the signal 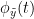 , the mutual information, between
, the mutual information, between 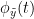 and the past of
and the past of 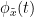 i.e.
i.e. 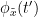 is larger than the mutual information of
is larger than the mutual information of 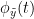 , the past of
, the past of 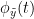 i.e.
i.e. 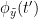 and
and 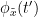 . This relationship can be seen on the Venn diagram below, where
. This relationship can be seen on the Venn diagram below, where 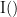 and
and 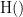 , indicate mutual information and the individual entropies respectively. Lastly, PTE cannot be negative, and its magnitude does not have a meaningful upper bound.
, indicate mutual information and the individual entropies respectively. Lastly, PTE cannot be negative, and its magnitude does not have a meaningful upper bound.
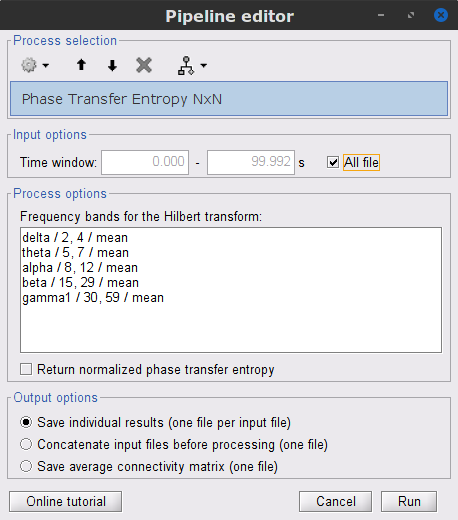
Process options
Time window: Segment of the signal used for the connectivity analysis. Select All file.
Frequency bands for the Hilbert transform: Frequency bands used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial.
Return normalized phase transfer entropy: Divides the each directional PTE value between two signals by the sum of both directional PTE values for those two signals. TODO: THIS NEEDS TO BE CLARIFIED, SEE: https://neuroimage.usc.edu/forums/t/confusing-values-of-normalized-pte/32069
Result visualization
PTE was computed for the delta, theta, alpha, beta and gamma bands. With the simulated data, we expect a higher PTE value in the beta band, From signal 1 To signal 3, as PTE is directed metric. This is confirmed with a peak at 22 Hz (center of beta band) shown in PTE frequency representation. 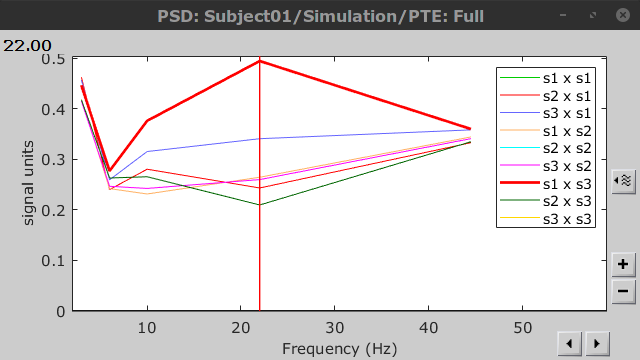 .
.
Method selection and comparison
The following table list the available connectivity metrics in Brainstorm and their description.
Metric |
Directionality |
Domain |
1×N |
N×N |
Time resolved |
Process |
Info |
Correlation |
Non-directed |
Time |
✅ |
✅ |
✅ |
bst_corrn.m |
|
Coherence |
Non-directed |
Frequency |
✅ |
✅ |
✅ |
bst_cohn.m |
|
Granger causality |
Directed |
Time |
✅ |
✅ |
❌ |
bst_granger.m |
|
Spectral Granger causality |
Directed |
Frequency |
✅ |
✅ |
❌ |
bst_granger_spectral.m |
|
Envelope Correlation (2020) |
Non-directed |
T-F |
✅ |
✅ |
✅ |
bst_henv.m |
|
Phase locking value |
Non-directed |
Phase |
✅ |
✅ |
❌ |
bst_connectivity.m |
|
Phase transfer entropy |
Directed |
Phase |
❌ |
✅ |
❌ |
PhaseTE_MF.m |
Sensor- and source-level connectivity analyses
As mentioned above, the different connectivity metrics can be computed with sensor or source data. However, sensor connectivity analyses present two important limitations:
They are not interpretable, as the relation between the estimated connectivity and the underlying neuroanatomy is not straightforward.
Sensor data is severely corrupted by effects of field spread and volume conduction. Due to these effects the activity of a single brain area could cause a spurious connectivity between MEG/EEG sensors.
Despite these limitations, sensor connectivity analyses are commonly used. One approach to reduce the negative impact of field spread on connectivity analyses is to perform them in the source level. In addition, source connectivity analyses are interpretable as neuroanatomy is considered. As consequence, findings in the source level can be easily used in group studies using a normalization / registration. Regardless of the data, sensors or sources, it is highly recommended to have a clear hypothesis to test before starting the connectivity analysis. Although sensor- and source-level connectivity analyses use different assumptions, the outcomes regarding the topology of the underlying networks should be consistent (Lai et al., 2018).
Depending on the source estimation method the number of sources can be in the order of tens of thousands, making the full network analyses (N×N) impractical. For example, we could compute the source connectivity matrix for each trail, then average overall trial. However, this process is time and memory consuming. For example, for each trial, a matrix of 15002×15002 elements is computed and saved in the hard disk (~0.9 Gb per trial). In the case of the unconstrained source, the size is 45006x45006 (~8.1 Gb per trial).
As such, the strategy is to reduce the dimensionality of the source space, this is done by grouping the sources in regions of interests (ROIs) or scouts in Brainstorm jargon. Therefore, the most critical step in performing a source-domain connectivity analysis is the definition of these ROIs, which is not a trivial procedure as it depends on the source estimation method, experimental task, and data available (Schhoffen and Gross, 2009). Common approaches found in the literature to select the ROIs for connectivity analysis are:
A priori: ROIs are selected based on a priori knowledge in a given experimental task.
Coherence with a no-neuronal signal: ROIs that present a strong coherence with an external no-neuronal signal are selected.
Power maps: ROIs showing the strongest activity in an experimental task or ROIs that present the strongest differences of activity between experimental conditions are selected.
Full brain: A set of ROIs covering the full brain, a cortical parcellation, is selected. In this selection approach, there are not any a priori assumptions or hypotheses. A fair choice for this set of ROIs is a parcellation based on anatomy, as in (Glasser et al., 2016). Although this approach to select ROIs can be used for exploratory analyses, it should not be taken as default for connectivity analyses.
Being an exploratory analysis, the full-brain connectivity analysis can help to get a better understanding of the acquired data, and to develop hypotheses to test. However its outcomes should not be considered conclusive, as they may be the result of circular analysis (Kriegeskorte et al., 2009).
The optimal selection of ROIs to perform source connectivity analysis is still an open question.
Correlation on real data
In this section we will use the results obtained in the [[|introduction tutorial]] to provide a simple example of correlation in the source level. A more complete tutorial on connectivity can be found at CORTICOMUSCULAR COHERENCE TUTORIAL.
Let's go back to our auditory oddball dataset. According to the literature, we expect to observe bilateral activity in the primary auditory cortices, in both experimental conditions (standard and deviant beeps), around 0 to 150 ms after the stimulus due to auditory evoked responses at 50 and 100 ms (M50, M100).
In the rest of this section, correlation is computed on the scouts time series of the average response for the standard and deviant conditions. On practice connectivity metrics are computed trial-wise and the results are aggregated. An example of this approach can be seen in CORTICOMUSCULAR COHERENCE TUTORIAL.
In the Scouts tutorial, we have created 4 scouts for these regions of interest: A1L and A1R for the left and right primary cortices respectively, IFGL for the left inferior frontal gyrus, and M1L for the left primary motor cortex.
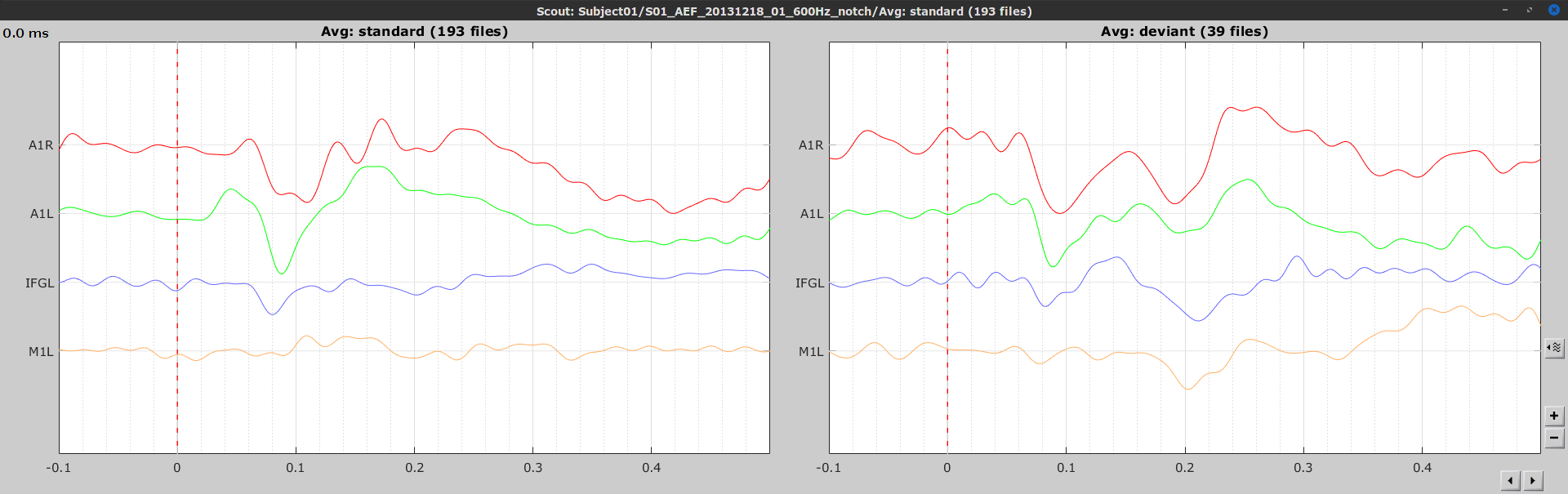
We will perform source-domain correlation among these scouts for the Run #1: S01_AEF_20131218_01_600Hz_notch data.
Let's compute correlation for standard and deviant conditions for the Run #1: S01_AEF_20131218_01_600Hz_notch data.
Drag and drop the source file associated to the average standard response (Avg. standard (193 files)) within the Process1 tab, select the option 'source process' (
 ), and click on the [Run] button.
), and click on the [Run] button. Add a the process, Connectivity > Correlation NxN. Set the time window from 0 to 150 ms. Check the Use scouts option, and select User scouts as atlas in the drop menu. Set the Scout function to Mean, for When to apply the scout function select Before. Finally click on [Run].
Display the connectivity matrix as Image (top) and adjust the Colormap to show absolutes values from 0 to 0.8. Then, display the connectivity matrix as Graph and set the same range. By adjusting the Intensity threshold for the graph to 0.7, only the strongest correlations are kept, mainly, between scouts in the left and right temporal lobes and near scouts (bottom).
Standard |
|
Deviant |
|
|
|
|
|
|
In this early response period, we appreciate that the correlation matrices for the standard ann deviant response are quite similar, and the strongest correlation happens between the scouts on the primary auditory cortices; just as expected.
Sections to add
Discuss option concatenate vs. average for the estimation of coherence on single trials: https://neuroimage.usc.edu/forums/t/difference-between-averaging-coherence-and-concatenate/22726/4
- Discuss pValues computed for the various methods
How to choose the best parameters. ex : plv better with 100 samples & narrow bands
On the hard drive
TODO: Document data storage.
Additional documentation
Articles
Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M.
Identifying true brain interaction from EEG data using the imaginary part of coherency.
Clinical Neurophysiology. 2004 Oct;115(10):2292–307.Pascual-Marqui RD.
Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions.
arXiv preprint arXiv:0706.1776. 2007 Jun 12.Bressler SL, Seth AK.
Wiener–Granger causality: a well established methodology.
Neuroimage. 2011 Sep 15;58(2):323-9.Dhamala M, Rangarajan G, Ding M.
Estimating Granger causality from Fourier and wavelet transforms of time series data.
Physical review letters. 2008 Jan 10;100(1):018701.Hipp JF, Hawellek DJ, Corbetta M, Siegel M, Engel AK.
Large-scale cortical correlation structure of spontaneous oscillatory activity.
Nature neuroscience. 2012 Jun;15(6):884-90.Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, et al.
Detection of n : m Phase Locking from Noisy Data: Application to Magnetoencephalography.
Phys Rev Lett. 1998 Oct 12;81(15):3291–4.Lobier M, Siebenhühner F, Palva S, Palva JM.
Phase transfer entropy: a novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions.
Neuroimage. 2014 Jan 15;85:853-72.Barzegaran E, Knyazeva MG.
Functional connectivity analysis in EEG source space: The choice of method
Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105.Lai M, Demuru M, Hillebrand A, Fraschini M.
A comparison between scalp- and source-reconstructed EEG networks.
Sci Rep. 2018 Dec;8(1):12269.Schoffelen J-M, Gross J.
Source connectivity analysis with MEG and EEG.
Hum Brain Mapp. 2009 Jun;30(6):1857–65.Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI.
Circular analysis in systems neuroscience: the dangers of double dipping.
Nat Neurosci. 2009 May;12(5):535–40.
Forum discussions
Connectivity matrix storage:http://neuroimage.usc.edu/forums/showthread.php?1796
Comparing coherence values: http://neuroimage.usc.edu/forums/showthread.php?1556
Reading NxN PLV matrix: http://neuroimage.usc.edu/forums/t/pte-how-is-the-connectivity-matrix-stored/4618/2
Export multiple PLV matrices: https://neuroimage.usc.edu/forums/t/export-multiple-plv-matrices/2014/4
Scout function and connectivity: http://neuroimage.usc.edu/forums/showthread.php?2843
Unconstrained sources and connectivity: http://neuroimage.usc.edu/forums/t/problem-with-surfaces-vs-volumes/3261
Unconstrained / PCA: https://neuroimage.usc.edu/forums/t/functional-connectivity-unconstrained-sources-and-pca/30486/4
Diagonal values: http://neuroimage.usc.edu/forums/t/choosing-scout-function-before-or-after/2454/2
Connectivity pipeline: https://neuroimage.usc.edu/forums/t/help-for-connectivity-pipeline/12558/4
Ongoing developments: https://neuroimage.usc.edu/forums/t/connectivity-tutorial-and-methods-development-on-bst/12223/3
Granger causality: https://neuroimage.usc.edu/forums/t/is-granger-causality-analysis-a-linear-operation/12506/12
Amplitude Envelope Correlation: * https://neuroimage.usc.edu/forums/t/problem-with-time-dynamic-envelope-correlation/21542/9
* https://github.com/brainstorm-tools/brainstorm3/issues/142

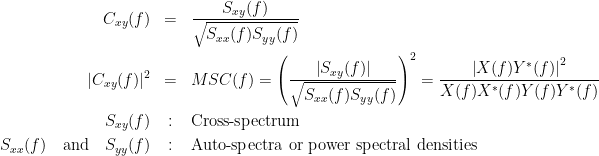
![\begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*} \begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_697a31e2ea80e1d7e07fbd14e43c910e44e14e3c_p1.png)