|
Size: 45990
Comment:
|
Size: 57887
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| ''Authors: Francois Tadel, Elizabeth Bock, Rey R Ramirez, John C Mosher, Richard Leahy, Sylvain Baillet'' | ''Authors: Francois Tadel, Elizabeth Bock, Rey R Ramirez, John C Mosher, Richard M Leahy, Sylvain Baillet'' |
| Line 6: | Line 6: |
| __'''WARNING'''__: The methods presented here use some new functions that are not fully tested (menu "Compute sources 2016"). For more stable results, it is advised that you keep on using the previous version of these functions (menu "'''Compute sources'''", described in the [[Tutorials/TutSourceEstimation|old tutorials]]). | __'''WARNING'''__: The new interface presented here do not include all the options yet. The mixed head models are not supported: to use them, use the old interface (menu "Compute sources" instead of "Compute sources 2016", described in the [[Tutorials/TutSourceEstimation|old tutorials]]). |
| Line 17: | Line 17: |
| Many solutions have been proposed in the literature, based on different assumptions on the way the brain works and depending on the amount of information we already have on the effects we are studying. Among the hundreds of methods available, two classes of inverse models have been widely used in MEG/EEG source imaging in the past years: '''minimum-norm solutions''' and '''beamformers'''. Both approaches have the advantage of being '''linear''': the activity of the sources is a linear recombination of the MEG/EEG recordings. It is possible to solve the inverse problem independently of the recordings, making the data manipulation a lot easier and faster. Both are available in Brainstorm, so you can use the one that is most adapted to your recordings or to your own personal expertise. Only the minimum norm estimates will be described in this tutorial, but the other solutions work exactly the same way. == Source estimation options [TODO] == Before we start estimating the sources for the recordings available in our database, let's start with an overview of the options available. The screen capture below represents the basic options for the minimum norm estimates. The options for the other methods will be described in advanced tutorials. {{attachment:minnorm_options.gif}} === Method [TODO] === * '''Minimum norm''': __Priors, justification, application case?__<<BR>> Require an estimation of the noise at the level of the sensors (noise covariance matrix). * '''LCMV beamformer''': __?__<<BR>>Require both a noise covariance matrix and a data covariance matrix (representation of the effect we are trying to localize in the brain, covariance of the latencies of interest). * '''Dipole modeling''': __?__<<BR>>Warning: This is not a imaging method! * __'''Recommended option'''__: Provided that we know at which latencies to look at, we can compute a correct data covariance matrix and may obtain a better spatial accuracy with a beamformer. However, in many cases we don't exactly know what we are looking at, therefore the risks of misinterpretation of badly designed beamforming results are high. Brainstorm tends to favor minimum norm solutions, which have the advantage of needing less manual tuning for getting acceptable results. === Measure [TODO] === The minimum norm estimates produce a measure of the current density flowing at the surface of the cortex. To visualize these results and compare them between subjects, we can normalize the MNE values to get a standardized level of activation with respect to the noise or baseline level (dSPM, sLORETA, etc). * '''Current density map''': Whitened and depth-weigthed linear L2-minimum norm estimates algorithm inspired from Matti Hamalainen's MNE software. For a full description of this method, please refer to the [[http://www.nmr.mgh.harvard.edu/meg/manuals/MNE-manual-2.7.pdf|MNE manual]], section 6, "The current estimates". <<BR>>Units: picoamper per meter (pA.m). * '''dSPM''': Noise-normalized estimate (dynamical Statistical Parametric Mapping [Dale, 2000]). Its computation is based on the MNE solution. <<BR>>Units: Unitless ratio [ '''???''' ] * '''sLORETA''': Noise-normalized estimate using the sLORETA approach (standardized LOw Resolution brain Electromagnetic TomogrAphy [Pasqual-Marqui, 2002]). sLORETA solutions have, in general, a smaller location bias than either the expected current (MNE) or the dSPM. The noise covariance is not used at all for the standardization process, it is purely based on the smoothness of the maps. <<BR>>Units: Square root of units of current (MNE/sqrt(MNE) => (pA.m)^1/2^). |
Many solutions have been proposed in the literature, based on different assumptions on the way the brain works and depending on the amount of information we already have on the effects we are studying. Among the hundreds of methods available, in Brainstorm, we initially present three general approaches to the inverse models widely used in MEG/EEG source imaging: '''minimum-norm solutions''', '''beamformers''', and '''dipole modeling'''. These approaches have the advantage of being implemented in an efficient '''linear''' form: the activity of the sources is a linear recombination of the MEG/EEG recordings, such that it is possible to solve the inverse problem as a '''linear kernel''' which is easily stored. Subsequent data manipulation and source visualization is then much simpler, as are comparisons among these techniques. Below we first describe the minimum norm imaging approach and its options, followed by the beamformer and dipole modeling, both of which are actually quite similar and only use a subset of the options found in the minimum norm. == Source estimation options == Before we start estimating the sources for the recordings available in our database, let's start with an overview of the options available. The screen capture below represents the options for the minimum norm estimates. The options for the other methods will be described in advanced tutorials. {{attachment:Mininum_Norm_2016.gif}} === Method === Selecting one of the three Methods automatically switches the input screen automatically to reveal the options available for each. Above are the options revealed for the mininum norm imaging. First we brieflly describe the Methods options: * '''Minimum norm''': Bayesian Estimation of the sources, assumes a noise and signal prior.<<BR>> User may synthesize the noise covariance as the "identity matrix", or estimate a noise covariance matrix from recordings. The source covariance prior is generated from the options discussed in detail below. The signal covariance prior (i.e. the source prior as "propagated" to the sensor array) is generated from the options selected. The data covariance (the sum of the signal and noise covariance) is therefore synthesized. * '''LCMV beamformer''': "Linearly constrained minimum variance," requires a data covariance. <<BR>> The data covariance matrix is assumed to also contain the signal(s) of interest. In practice, the data covariance is estimated directly from the recordings. A linear kernel is formed from this data covariance matrix, after which the beamformer scanning image can be stepped through the data, and the best peak can be fit with a dipolar model at every time instance, as described later. * '''Dipole modeling''': Single equivalent current dipole, requires a noise covariance. <<BR>>The noise covariance matrix is assumed to NOT contain the signal of interest. In practice, this noise covariance matrix is calculated directly from recordings. In MEG, these recordings are often "empty room." In EEG, no such "empty room" is possible, so "quiet periods" of ongoing brain data are selected, as can also be selected in MEG. A linear kernel is formed from this noise covariance matrix, after which a scanning image (analogous to the beamformer) can be viewed, and the best dipole location and orientation can be found for every time instance. * __'''Recommended option'''__: Still under much debate, even among our Brainstorm team. One advantage of Brainstorm is that all three approaches can be easily run and compared. If the results are concordant among all three techniques, then our underlying assumptions of source modeling, head modeling, and data statistics are confirmed. If the results are disparate, then a more indepth study is needed to understand the consequences of our assumptions and therefore which technique may be preferred. The next several sections discuss in detail the options as revealed by selecting the "mininum norm imaing" Method above. === Measure === As directly formed and computed, the minimum norm estimate produces a measure of the current found in each point of the source grid (either volume or surface). As discussed elsewhere in the forum (__link to Mosher's discuss on units of the minimum norm__), the units are strictly kept in A-m, i.e. we do not attempt to divide out the area (yielding A/m, i.e. a surface density) or volume (yielding A/m^2, i.e. a volume density) of each source point; nonetheless, it is common to refer these units as a "source density" or "current density" map when displayed directly. More commonly, however, users often prefer to "normalize" each source point in order to compensate for the rapid falloff in signal intensity for deeper dipoles. Because of their popularity, we provide directly in the Measure box two forms of standardization, the dSPM and sLORETA. Summarizing the Measures selection: * '''Current density map''': The Minimum Norm Estimate (MNE)<<BR>>"Whitened" (i.e. noise covariance matrix is accounted for) and "depth-weighted" (if user selected the option) linear L2-minimum norm estimates algorithm inspired from Matti Hamalainen's MNE software. For a full description of this method, please refer to the [[http://www.nmr.mgh.harvard.edu/meg/manuals/MNE-manual-2.7.pdf|MNE manual]], section 6, "The current estimates". Units: picoamper-meter (pA-m). * '''dSPM''': dynamical Statistical Parametric Mapping [Dale, 2000]<<BR>>The MNE is computed as above, but then we use exactly the same linear kernel with given noise covariance matrix to essentially "z-score" each point in the current density map. Units: unitless "z". * '''sLORETA''': standardized LOw Resolution brain Electromagnetic TomogrAphy [Pasqual-Marqui, 2002])<<BR>>As originally presented (2002), sLORETA also uses the same MNE solution from above, then we use exactly the same linear kernel with the MNE data covariance matrix (instead of noise covariance) to again weight each point in the current density map. Subsequent theoretical developments show an alternative form of a "resolution" kernel that may be calculated instead. We use the "resolution" form, but the interested researcher is invited to review the details of our coding. |
| Line 44: | Line 51: |
| === Source orientation === * '''Constrained: Normal to cortex''': Only one dipole at each vertex of the cortex surface, oriented normally to the surface. This is based on the anatomical observation that in the cortex, the neurons are mainly organized in macro-columns that are perpendicular to the cortex surface.<<BR>>Size of the inverse operator: [Nvertices x Nchannels]. * '''Unconstrained''': At each vertex of the cortex surface, we define a base of three dipoles with orthogonal directions, then we estimate the sources for the three orientations independently. <<BR>>Size of the inverse operator: [3*Nvertices x Nchannels]. * '''Loose''': A version of the "unconstrained" option with a weak orientation constraint that emphasizes the importance of the sources with orientations that are close to the normal to the cortex. The value associated with this option set how "loose" should be the orientation constrain (recommended values in MNE are between 0.1 and 0.6, --loose option). <<BR>>Size of the inverse operator: [3*Nvertices x Nchannel]. |
=== Source model: Dipole orientations === At each point in the source grid, the current dipole may point arbitrarily in three directions. In this section of the options, we prescribe if the inverse method will constrain the orientation, leave it unconstrained, or if we impose a "soft" constraint to the orientation. * '''Constrained: Normal to cortex''': Only for "surface" grids. At each grid point, we model only one dipole, oriented normally to the cortical surface. This is based on the anatomical observation that in the cortex, the neurons are mainly organized in macro-columns that are perpendicular to the cortex surface.<<BR>>Size of the inverse operator: [Nvertices x Nchannels]. * '''Loose''': Only for "surface" grids. As introduced by Lin (cite), at each point in the surface grid the dipole direction is constrained to be normal to the local cortical surface. Two additional elemental dipoles are also allowed, in the two directions "tangential" to the cortical surface. As contrasted with "unconstrained," these two tangential elemental dipoles are only modeled to have an amplitude that is a fraction of the normal dipole, recommended to be between 0.1 and 0.6. Thus the dipole is only "loosely" constrained to be normal to the local cortical surface. <<BR>>Size of the inverse operator: [3*Nvertices x Nchannel]. * '''Unconstrained''': Either "surface" or "volume" grids. At each grid point, we leave undefined the assumed orientation of the source, such that three "elemental" dipoles are needed to model the source. In Brainstorm, our elemental dipoles are in the x, y, and z ("Cartesian") directions, as compared to other software that may employ polar coordinates. Thus for "N" vertices, we are calculating the estimate for "3*N" elemental dipoles. <<BR>>Size of the inverse operator: [3*Nvertices x Nchannels]. |
| Line 50: | Line 61: |
| === Sensors === We automatically detect and display the sensors found in your head model. In the example above, two types of magnetometers are found, gradiometers and magnetometers. You can select one or all of the sensors found in your model, such as MEG and EEG. However, cross-modality calculations are quite dependent on the accuracy by which you have provided adequate covariance calculations. As of Fall of 2016, we have also elected to NOT account for cross-covariances between different sensor types, since regularization and stability of cross-modalities is quite involved. For multiple sensor types, the recommendation is that you try each individually and then combined, to test for discordance. |
|
| Line 51: | Line 67: |
| Using the above selections, we now discuss explicit directions on how to compute and visualize. |
|
| Line 59: | Line 77: |
| * Double-click on the '''recordings '''for the deviant average to have time reference. <<BR>>In the filter tab, add a '''low-pass filter at 40Hz'''.<<BR>><<BR>> {{attachment:display_cortex.gif||height="163",width="482"}} | * Double-click on the '''recordings '''for the deviant average to have a time reference. <<BR>>In the filter tab, add a '''low-pass filter at 40Hz'''.<<BR>><<BR>> {{attachment:display_cortex.gif||height="163",width="482"}} |
| Line 73: | Line 91: |
| Visually, you should not always interpret disconnected colored patches as independent sources. You cannot expect a very spatial resolution with this technique (~0.5-1cm). Most of the time, a cluster of disconnected source patches in the same neighborhood that show the same evolution in time can be interpreted as "there is some significant activity around here, but we don't know where exactly". To get more continuous maps for visualization or publication purposes, you can either smooth the values explicitely on the surface (process "'''Sources > Spatial smoothing'''") or use '''unconstrained source models'''. |
Visually, you should not always interpret disconnected colored patches as independent sources. You cannot expect a very spatial resolution with this technique (~5-10mm). Most of the time, a cluster of disconnected source patches in the same neighborhood that show the same evolution in time can be interpreted as "there is some significant activity around here, but we don't know where exactly". To get more continuous maps for visualization or publication purposes, you can either smooth the values explicitly on the surface (process "'''Sources > Spatial smoothing'''") or use '''unconstrained source models'''. |
| Line 88: | Line 106: |
| * '''Smooth level''': The sources values can be smoothed after being re-interpolated in the volume. Right-click on the figure to define the size of the smoothing kernel. | * '''Smooth level''': The sources values can be smoothed after being re-interpolated in the volume. Right-click on the figure to define the size of the smoothing kernel (in number of slices). |
| Line 120: | Line 138: |
| * We have to be careful with the visual comparisons of constrained and unconstrained source maps displayed on the cortex surface, because they are very different types of data. In unconstrained source maps, we have '''three dipoles with orthogonal orientations at each cortex location''', therefore we cannot represent all the information at once. To display them as an activity map, Brainstorm computes the '''norm of the vectorial sum of the three orientations at each vertex'''. <<BR>><<BR>> {{attachment:minnorm_unconstr_sketch.gif||height="158",width="476"}} * This explains that we only observe '''positive values''' (no blue values even when the colormap is set to display positive and negative values): the norm displayed at each vertex is always positive. The underlying values along each orientation (x,y,z) can be positive or negative and oscillate around zero in time, but we cannot get access to this information with these static cortical maps. |
* We have to be careful with the visual comparisons of constrained and unconstrained source maps displayed on the cortex surface, because they are very different types of data. In unconstrained source maps, we have '''three dipoles with orthogonal orientations at each cortex location''', therefore we cannot represent all the information at once. To display them as an activity map, Brainstorm computes the '''norm of the vectorial sum of the three orientations at each vertex'''. <<BR>>S = sqrt(Sx^2^ + Sy^2^ + Sz^2^) <<BR>><<BR>> {{attachment:minnorm_unconstr_sketch.gif||height="158",width="476"}} * This explains that we only observe '''positive values''' (no blue values when the colormap is set to display positive and negative values): the norm displayed at each vertex is always positive. The underlying values along each orientation (x,y,z) can be positive or negative and oscillate around zero in time, but we cannot get access to this information with these static cortical maps. |
| Line 124: | Line 142: |
| * '''Delete''' the unconstrained file, we will not explore more this option in the tutorials. You may refer to the advanced tutorial [[http://neuroimage.usc.edu/brainstorm/Tutorials/Epilepsy|EEG and epilepsy]] for an example of analysis using unconstrained sources. | * '''Delete''' the unconstrained file, we will not explore this option in the introduction tutorials. You can refer to the tutorial [[http://neuroimage.usc.edu/brainstorm/Tutorials/Epilepsy|EEG and epilepsy]] for an example of analysis using unconstrained sources. |
| Line 138: | Line 156: |
| * In Run#01, right-click on the average recordings for the '''deviant''' stim > '''Compute sources [2015]'''.<<BR>>Select successively the two normalization options: dSPM, sLORETA, ('''constrained''').<<BR>><<BR>> {{attachment:minnorm_normfiles.gif}} | * In Run#01, right-click on the average recordings for the '''deviant''' stim > '''Compute sources [2016]'''.<<BR>>Select successively the two normalization options: dSPM, sLORETA, ('''constrained''').<<BR>><<BR>> {{attachment:minnorm_normfiles.gif}} |
| Line 146: | Line 164: |
| * '''sLORETA''': Produces a smoother maps where all the potentially activated area of the brain (given to the low spatial resolution of the source localization with MEG/EEG) is shown as connected, regardless of the depth of the sources. However, the units are difficult to interpret. | * '''sLORETA''': Produces smoother maps where all the potentially activated area of the brain (given to the low spatial resolution of the source localization with MEG/EEG) is shown as connected, regardless of the depth of the sources. However, the units are difficult to interpret. |
| Line 152: | Line 170: |
| * Run process "'''Standardize > Z-score normalization'''", baseline = '''[-100,-1.7]ms.''' <<BR>>Do not select "Use absolute values": We want the sign of the current values.<<BR>>Do not select "Dynamic": This option offers a storage optimization that can save a lot of disk space for long time series, but which is not very relevant here (we use short epochs).<<BR>><<BR>> {{attachment:zscore_process.gif||height="330",width="544"}} | * Run process "'''Standardize > Baseline normalization'''", '''[-100,-1.7]ms''', '''Z-score transformation''' <<BR>>Do not select "Use absolute values": We want the sign of the current values.<<BR>><<BR>> {{attachment:zscore_process.gif||height="530",width="558"}} |
| Line 158: | Line 176: |
| * A value of 3 in this figure means: at this vertex, the value is 3 times higher than the standard deviation from zero during the baseline. If the values during the baseline follow a normal distribution '''N(<<HTML(μ)>,<<HTML(σ<SUP>2</SUP>)>>)''', then the values we computed follow a N(0,1)='''Z distribution'''. We can infer a level of significance from this well know distribution, for instance a value Z=1.96 corresponds to a p-value of 0.05. These questions will be discussed in more details in the statistics tutorial. * The '''colormap '''used to display these Z-score maps is different than the other maps. It uses the colormap "Stat 1" instead of the colormap "Sources", and the color set is by default "hot" instead of "jet". You can redefine this: right-click on the figure > Colormap: Stat 1 > Colormap > jet. <<BR>>Double-click on the colorbar to reset it to its default values. * The Z-normalized source maps are '''not impacted by the''' '''visualization filters'''. If you open simultaneously the time series and all the files you have now (MN, dSPM, sLORETA, Z-score) and modify the options in the Filter tab, all the figures are updated except for the Z-score. We can filter easily all the linear models (MN, dSPM, sLORETA), but we would lose the interesting properties of the Z-values if we were filtering them (the values would not follow a Z-distribution anymore). |
* A value of 3 in this figure means: at this vertex, the value is 3 times higher than the standard deviation from zero during the baseline. If the values during the baseline follow a normal distribution '''N(<<HTML(μ)>>,<<HTML(σ<SUP>2</SUP>)>>)''', then the values we computed follow a N(0,1)='''Z distribution'''. We can get a level of significance from this well known distribution, for instance a value Z=1.96 corresponds to a p-value of 0.05. These questions will be discussed in more details in the statistics tutorial. * The Z-normalized source maps are '''not impacted by the''' '''visualization filters'''. If you open simultaneously the time series and all the files you have now (MN, dSPM, sLORETA, Z-score) and modify the options in the Filter tab, all the figures are updated except for the Z-score one. We can filter easily all the linear models (MN, dSPM, sLORETA), but we would lose the interesting properties of the Z-values if we were filtering them (the values would not follow a Z-distribution anymore). |
| Line 177: | Line 193: |
| * Z-normalized current density maps are also easy to interpret. They represent explicitely a "deviation from experimental baseline" while dSPM indicates a "deviation from noise" (as represented by the noise covariance matrix). | * Z-normalized current density maps are also easy to interpret. They represent explicitly a "deviation from experimental baseline" while dSPM indicates a "deviation from noise" (as represented by the noise covariance matrix). |
| Line 180: | Line 196: |
| * Select all the normalized source maps (everything but the link) and '''delete''' them. <<BR>><<BR>> {{attachment:delete_norm.gif||height="172",width="474"}} | * Select all the source files you computed until now and '''delete''' them. <<BR>><<BR>> {{attachment:delete_norm.gif||height="172",width="474"}} |
| Line 185: | Line 201: |
| * Right-click on the '''head model''' or the '''folder '''for Run#01 > '''Compute sources [2016]'''.<<BR>>Select the options: '''Minimum norm''' imaging, '''Current density''' map, '''Unconstrained'''<<BR>><<BR>> {{attachment:minnorm_shared_popup.gif||height="273",width="500"}} * Because we did not request to compute and inverse model for a specific block of recordings, it computed a '''shared inverse model'''. If you right-click on this new file, you get a warning message: "Inversion kernel". It does not contain any source map, but only the inverse operator that will allow us to convert the recordings in source maps.<<BR>><<BR>> {{attachment:minnorm_shared_kernel.gif}} * The database explorer now shows one '''source link''' to this inverse model for each block of recordings available in this folder, single trials and averages. These links are not real files saved on the hard drive, but you can use them exactly like the first source file we calculated for the deviant average. If you load a link, Brainstorm loads the corresponding MEG recordings, loads the inverse kernel and multiplies the two on the fly before displaying it. This optimized approach saves a lot of computation time and lot of space on the hard drive.<<BR>><<BR>> {{attachment:minnorm_links.gif||height="176",width="513"}} |
* Right-click on the '''head model''' or the '''folder '''for Run#01 > '''Compute sources [2016]'''.<<BR>>Select: '''Minimum norm''' imaging, '''Current density''' map, '''Constrained''': Normal to cortex<<BR>><<BR>> {{attachment:minnorm_shared_popup.gif||height="273",width="500"}} * Because we did not request to compute and inverse model for a specific block of recordings, it computed a '''shared inverse model'''. If you right-click on this new file, you get a warning message: "Inversion kernel". It does not contain any source map, but only the inverse operator that will allow us to convert the recordings into source maps.<<BR>><<BR>> {{attachment:minnorm_shared_kernel.gif}} * The database explorer now shows one '''source link''' to this inverse model for each block of recordings available in this folder, single trials and averages. These links are not real files saved on the hard drive, but you can use them exactly like the previous source files we calculated for the deviant average. If you load a link, Brainstorm loads the corresponding MEG recordings, loads the inverse kernel and multiplies the two on the fly before displaying it. This optimized approach saves a lot of computation time and lot of space on the hard drive.<<BR>><<BR>> {{attachment:minnorm_links.gif||height="176",width="513"}} |
| Line 194: | Line 210: |
| * Thanks to the linearity of the minimum norm model, the two following approaches are equivalent: * 1) Averaging the sources of all the individual trials across runs, * 2) Averaging the sources for the sensor averages that we already computed for each run. For non-standardized current density maps: MN(Average(trials)) = Average(MN(trials)) * The second solution is a lot faster because it needs to read 4 files (one average file per run and per condition) instead of 456 files (total number of good trials in the two runs). |
* Thanks to the linearity of the minimum norm model: MN(Average(trials)) = Average(MN(trials))<<BR>>The two following approaches are equivalent: 1. Averaging the sources of all the individual trials across runs, 1. Averaging the sources for the sensor averages that we already computed for each run. * We will use the second option: using the sources for the sensor-level averages. <<BR>>It is a lot faster because it needs to read 4 files (one average file per run and per condition) instead of 456 files (total number of good trials in the two runs). |
| Line 201: | Line 217: |
| * The file comments say "2 files" because they result in the averaging of two averages each (one from each run), but the number of corresponding trials is correctly updated in the file structure. Right-click on each of them > File > View file contents, and check the '''nAvg''' field: <<BR>>78 trials for the deviant condition, 378 trials for the standard condition. * Double-click on the source averages to display them (standard=top, deviant=bottom). <<BR>>Open the sensor-level averages as a time reference. <<BR>>Use the pre-defined view "Left, Right" for looking at the two sides at once (shortcut: "7").<<BR>><<BR>> {{attachment:average_display_mn.gif||height="296",width="530"}} |
* The file comments say "2 files" because they were computed from two averages each (one from each run), but the number of corresponding trials is correctly updated in the file structure. <<BR>>Right-click on each of them > File > View file contents, and check the '''nAvg''' field: <<BR>>78 trials for the deviant condition, 378 trials for the standard condition. * Double-click on the source averages to display them (deviant=top, standard=bottom). <<BR>>Open the sensor-level averages as a time reference. <<BR>>Use the predefined view "Left, Right" for looking at the two sides at the same time (shortcut: "7").<<BR>><<BR>> {{attachment:average_display_mn.gif||height="296",width="530"}} |
| Line 207: | Line 223: |
| * The visualization filters will not be available anymore after we apply a Z-score normalization. If we want to display Z-score source maps that are smoothed in time, we will have to apply explicitely the filters on the file, with the Process1 tab. | * The visualization filters will not be available anymore after we apply a Z-score normalization. If we want to display Z-score source maps that are smoothed in time, we will have to apply explicitly the filters on the file, with the Process1 tab. ==== Low-pass filter ==== * Clear the Process1 list, then drag and drop the new averages in it. * Run process "'''Pre-process > Band-pass filter'''": [0,40] Hz<<BR>><<BR>> {{attachment:average_filter.gif||height="238",width="476"}} |
| Line 210: | Line 230: |
| * Clear the Process1 list, then drag and drop the new averages in it. * Select process "'''Standardize > Z-score normalization'''", baseline = '''[-100,-1.7]ms.''' <<BR>>Do not run the computation, we will add the low-pass filter immediately after.<<BR>><<BR>> {{attachment:average_zscore.gif||height="310",width="506"}} * Add process "'''Pre-process > Band-pass filter'''": [0,40] Hz<<BR>><<BR>> {{attachment:average_filter.gif||height="277",width="508"}} * Four new files are accessible in the database: two filtered and two filtered+normalized. <<BR>><<BR>> {{attachment:average_zscore_files.gif||height="158",width="341"}} * Double-click on the source averages to display them (standard=top, deviant=bottom).<<BR>><<BR>> {{attachment:average_display_zscore.gif||height="295",width="530"}} |
* In Process1, select the two filtered averages. * Run process "'''Standardize > Baseline normalization'''", baseline='''[-100,-1.7]ms, ''''''Z-score.'''<<BR>><<BR>> {{attachment:average_zscore.gif||height="292",width="539"}} * Four new files are accessible in the database: two filtered and two filtered+normalized. <<BR>><<BR>> {{attachment:average_zscore_files.gif||height="205",width="341"}} * Double-click on the source averages to display them (deviant=top, standard=bottom).<<BR>><<BR>> {{attachment:average_display_zscore.gif||height="295",width="530"}} * The Z-score source values at 90ms are higher for the standard condition (~25) than for the deviant condition (~15). We observe this because the two conditions have very different signal-to-noise ratios. The standard condition has about 5x more trials, therefore the standard deviation over the baseline is a lot lower, leading to higher Z-score. * '''Delete''' the non-normalized filtered files, we will not use them in the following tutorials. <<BR>><<BR>> {{attachment:average_zscore_files2.gif||height="147",width="294"}} |
| Line 229: | Line 250: |
| * The same SNR issues arise while averaging Z-scores: the average of the Z-scores is lower than the Z-score of the average. But this time we do not have an easy analytical expression to compensate the modifications in SNR, the average would not be reflecting the increase in SNR. * Always '''avoid averaging Z-score maps'''. Average the current density maps, then normalize. |
* The same SNR issues arise while averaging Z-scores: the average of the Z-scores is lower than the Z-score of the average. But this time we do not have an easy analytical expression to compensate for the modifications in SNR, the average would not be reflecting the increase in SNR. * When computing averages at the subject level: Always '''avoid averaging Z-score maps'''. <<BR>>Average the current density maps, then normalize. |
| Line 242: | Line 263: |
| A time stamp is added to the captured figure. The size of the text font is fixed, so if you want it to be readable in the contact sheet, you should make you figure very small before starting the capture. | A time stamp is added to the captured figure. The size of the text font is fixed, so if you want it to be readable in the contact sheet, you should make you figure very small before starting the capture. The screen captures below where produced with the colormap "hot". |
| Line 250: | Line 271: |
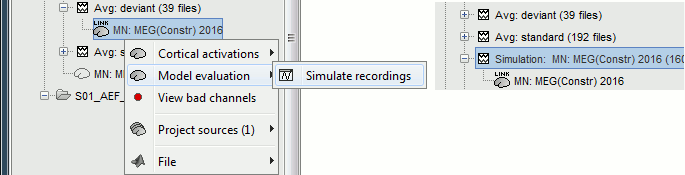
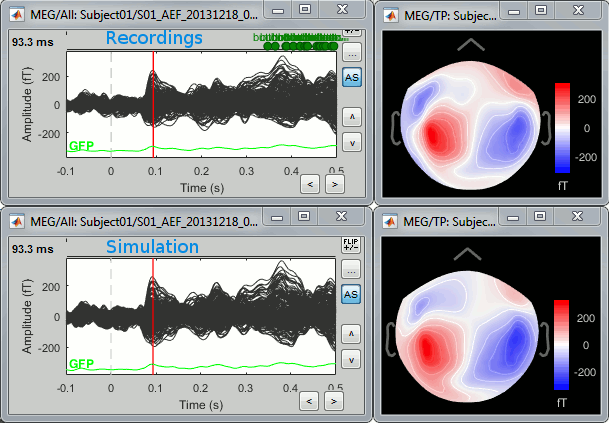
| One way to evaluate the accurracy of the source reconstruction if to use simulate recordings using the estimate source maps. This is done simply by multiplying the source time series with the forward model:<<BR>>MEG_simulated [Nmeg x Ntime] = Forward_model [Nmeg x Nsources] * MN_sources [Nsources x Ntime]<<BR>>Then you can compare the original MEG recordings with the simulated ones visually. More formally, you can compute an error measure from the residuals (recordings - simulated). | One way to evaluate the accuracy of the source reconstruction if to simulate recordings using the estimated source maps. This is done simply by multiplying the source time series with the forward model:<<BR>>MEG_simulated [Nmeg x Ntime] = Forward_model [Nmeg x Nsources] * MN_sources [Nsources x Ntime]<<BR>>Then you can compare visually the original MEG recordings with the simulated ones. More formally, you can compute an error measure from the residuals (recordings - simulated). |
| Line 254: | Line 275: |
| . {{attachment:model_popup.gif}} | . {{attachment:model_popup.gif||height="151",width="597"}} |
| Line 258: | Line 279: |
| . {{attachment:model_results.gif||height="251",width="332"}} | . {{attachment:model_results.gif||height="218",width="332"}} |
| Line 262: | Line 283: |
| == Advanced options [TODO] == | == Advanced minimum norm options == |
| Line 265: | Line 286: |
| . {{attachment:minnorm_details.gif||height="443",width="460"}} === Depth weighting [TODO] === The minimum-norm estimates have a bias towards superficial currents. This tendency can be alleviated by adjusting these parameters. To understand how to set these parameters, please refer to the MNE manual (options --depth, --weightexp and --weightlimit). === Noise covariance regularization [TODO] === Explain the influence of this parameter. * '''Regularize noise covariance''': Regularize the noise-covariance matrix by the given amount for each type of sensor individually (value is restricted to the range 0...1). For more information, please refer to the MNE manual, section 6.2.4 (options --magreg, --gradreg and --eegreg). * '''Diagonal noise covariance''': * '''No covariance regularization''': * '''Automatic shrinkage''': === Regularization parameter [TODO] === Explain the influence of this parameter. * '''Signal-to-noise ratio''': Fixed SNR... * '''RMS source amplitude''': === Output mode [TODO] === * '''Full results''': Saves in one big matrix the values of all the sources (15,000) for all the time samples (361). The size in memory of such a matrix is about 45Mb for 600ms of recordings. This is still reasonable, so you may use this option in this case. But if you need to process longer recordings, you may face "Out of memory" errors in Matlab, or fill your hard drive quickly. |
{{attachment:Mininum_Norm_Options_2016.gif||height="422",width="600"}} === Depth weighting === Briefly, the use of various depth weightings was far more debated in the 1990s, before the introduction of MNE normalization via dSPM, sLORETA, and other "z-scoring" methods, which mostly negate the effects of depth weighting. At each point in the source grid, the deeper points are "boosted" to increase their signal strength relative to the shallower dipoles; otherwise, the resulting MNE current density maps are too dominated by the shallower sources. If using dSPM or sLORETA, little difference in using depth weighting should be noted. To understand how to set these parameters, please refer to the [[http://www.nmr.mgh.harvard.edu/meg/manuals/MNE-manual-2.7.pdf|MNE manual]]. (options --depth, --weightexp and --weightlimit). === Noise covariance regularization === MNE and dipole modeling are best done with an accurate model of the noise covariance, which is generally computed from experimental data. As such, these estimates are themselves prone to errors that arise from relatively too few data points, weak sensors, and strange data dependencies that cause the eigenspectrum of the covariance matrix to be somewhat deficient. In Brainstorm, we provide several means to "stabilize" or "regularize" the noise covariance matrix, so that source estimation calculations are more robust to small errors. * '''Regularize noise covariance''': The L2 matrix norm is defined as the largest eigenvalue of its eigenspectrum. This option adds to the covariance matrix a diagonal matrix whos entries are a fraction of the matrix norm. The default is 0.1, such that covariance matrix is stabilized by adding to it an identity matrix that is scaled to 10% of the largest eigenvalue. * '''Median eigenvalue''': The eigenspectrum of MEG data can often span many decades, due to highly colored spatial noise, but this broad spectrum is generally confined to the first several modes only. Thus the L2 norm is many times greater than the majority of the eigenvalues, and it is difficult to prescribe a conventional regularization parameter. Instability in the inverse is dominated by defects found in the smallest eigenvalues. This approach stabilizes the eigenspectrum by replicating the median (middle) eigenvalue for the remainder of the small eigenvalues. * '''Diagonal noise covariance''': Deficiencies in the eigenspectrum often arise from numerical inter-dependencies found among the channels, particularly in covariance matrices computed from relatively short sequences of data. One common method of stabilization is to simply take the diagonal of the covariance matrix and zero-out the cross-dependencies. Each channel is therefore modeled as independent of the other channels. The eigenspectrum is now simply the (sorted) diagonal values. * '''No covariance regularization''': We simply use the noise covariance matrix as computed or provided by the user. * '''Automatic shrinkage''': Stabilization method of Ledoit and Wolf (2004), still under testing in the Brainstorm environment. Basically tries to estimate a good tradeoff between no regularization and diagonal regularization, using a "shrinkage" factor. See Brainstorm code "bst_inverse_linear_2016.m" for notes and details. * '''Recommended option''': This author (Mosher) votes for the '''median eigenvalue '''as being generally effective.The other options are useful for comparing with other software packages that generally employ similar regularization methods. === Regularization parameter === In MNE, as mentioned above in the comparisons among Methods, the data covariance matrix is essentially synthesized by adding the noise covariance matrix to a modeled signal covariance matrix. The signal covariance matrix is generated by passing the source prior through the forward (head) model. The source prior is in turn prescribed by the source model orientation and the depth weighting. A final regularization parameter, however, is how much weight the signal model should be given relative to the noise model, i.e. the "signal to noise ratio" (SNR). In Brainstorm, as of Fall 2016, we follow the definition of SNR as first defined in the original MNE software of Hamalainen. The signal covariance matrix is "whitened" by the noise covariance matrix, such that the whitened eigenspectrum has elements in terms of SNR (power). We find the mean of this spectrum, then take the square root to yield the average SNR (amplitude). The default in MNE and in Brainstorm is "3", i.e. the average SNR (power) is 9. * '''Signal-to-noise ratio''': Use SNR of 3 as the classic recommendation, as discussed above. * '''RMS source amplitude''': An alternative definition of SNR, but still under test and may be dropped. === Output mode === As mentioned above, these methods create a convenient linear imaging kernel that is "tall" in the number of elemental dipoles (one or three per grid point) and "wide" only in the number of sensors. At subsequent visualzation time, we efficiently multiply the kernel with the data matrix. For some custom purposes, however, a user may find it convenient to pre-multiply the data matrix and generate the full source estimation matrix. This would only be recommended in small data sets, since the full results can become quite large. |
| Line 288: | Line 313: |
* '''Full results''': Saves in one big matrix the values of all the sources (15,000) for all the time samples (361). The size in memory of such a matrix is about 45Mb for 600ms of recordings. This is still reasonable, so you may use this option in this case. But if you need to process longer recordings, you may face "Out of memory" errors in Matlab, or fill your hard drive quickly. |
|
| Line 290: | Line 318: |
| === LCMV beamformer [TODO] === Explain the method briefly. * '''Beamformer time-series''': * '''Neural activity index''': |
== LCMV beamformer == As mentioned in the introduction above, two other Methods can be selected for source estimation, a beamformer and dipole modeling. In this section, we review the options for the beamformer. By selecting "LCMV beamformer, the options automatically switch to the below figure (shown with details). {{attachment:LCMV_options_2016.gif||height="414",width="600"}} === Measure === The Measure has switched to a single option, the "Pseudo Neural Activity Index," (PNAI), after the Van Veen definition of the Neural Activity Index (NAI). We have altered the definition to rely strictly on the data covariance, without need for a noise covariance matrix, but the basic premise is the same as in dSPM, sLORETA, and other normalizations. Viewing the resulting "map," identically as is done with MNE, dSPM, and sLORETA above, reveals possibly multiple sources as peaks in the map, scored analogous to z-scoring. The PNAI can then be dropped into the Process Box and the optimal dipole and orientations extracted for every time instance. === Source Model: Dipole orientations === The definitions here are identical to the MNE above;''' however, we do not recommend you select "constrained" '''(although technically allowed). Choose only "unconstrained" and let the "dipole scanning" process optimize the orientation with respect to the data. === Sensors === Same considerations as in MNE. === Data covariance regularization === Same definitions as in MNE, only applied to the data covariance matrix, rather than the noise covariance marix. Recommendation is to use '''median eigenvalue'''. === Output mode === Recommend to use kernel only. == Dipole modeling == Although not widely recognized, dipole modeling and beamforming are more alike than they are different. Below is the options screen when dipole modeling is selected. {{attachment:ECD_options.gif||height="353",width="600"}} You will notice that "Measure" is now missing, but the resulting imaging kernel file is directly analogous to the PNAI result of LCMV beamforming. The user may identically display this scanning measure as well, where again the units are a form of z-scoring. Source model, Sensors, Noise covariance regularization, and output mode all follow from the explanations given above for the LCMV and for the MNE. Again, the recommendation is to ALWAYS use "unconstrained" source modeling and let the Process "dipole scanning" optimize the orientation of the dipole for every time instance. Similarly, use "median eigenvalue" for the optimization. The tutorial "MEG current phantom (Elekta)" demonstrates dipole modeling of 32 individual dipoles under realistic experimental noise conditions. |
| Line 301: | Line 356: |
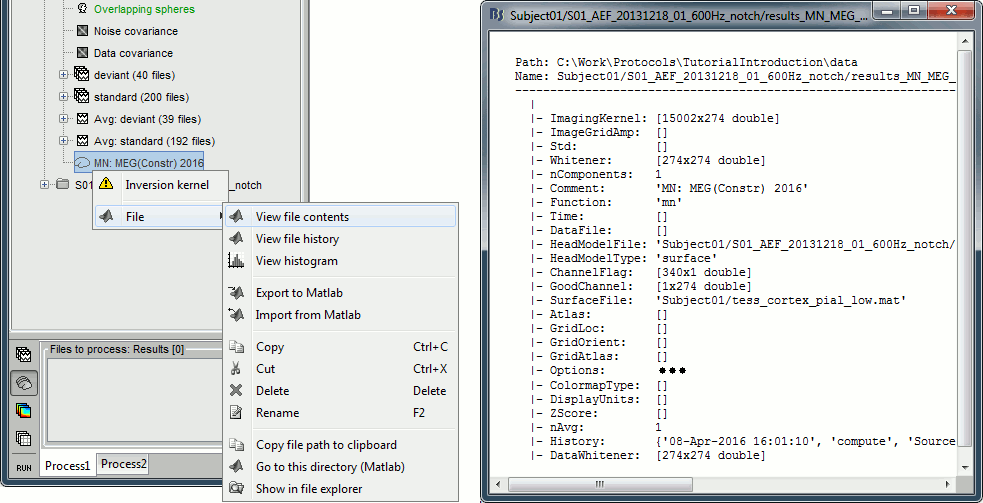
| == On the hard drive [TODO] == | == On the hard drive == |
| Line 305: | Line 360: |
| . {{attachment:kernel_contents.gif||height="376",width="626"}} | . {{attachment:kernel_contents.gif||height="342",width="669"}} |
| Line 330: | Line 385: |
| * '''Whitener''': Noise covariance whitener computed in bst_inverse_linear_2015.m * '''DataWhitener''': Data covariance whitener computed in bst_inverse_linear_2015.m |
* '''Whitener''': Noise covariance whitener computed in bst_inverse_linear_2016.m * '''DataWhitener''': Data covariance whitener computed in bst_inverse_linear_2016.m * '''SourceDecompVa''': [3 x Nsources] Concatenated right singular vectors from the SVD decomposition of the whitened leadfield for each source (only for unconstrained sources). * '''SourceDecompSa''': [3 x Nvertices] Vector diagonal of the singular values from the SVD decomposition of the whitened leadfield for each source (only for unconstrained sources). |
| Line 337: | Line 394: |
| ==== Flattened full source maps ==== | ==== Full source maps ==== |
| Line 344: | Line 401: |
| * This file contains the full time series (ImageGridAmp) instead of an inverse operator (ImagingKernel). * The Z-score process computed the norm of the three unconstrained orientations, so ImageGridAmp only describes 15,000 signals instead of 45,000 previously. |
* It contains the full time series (ImageGridAmp) instead of an inverse operator (ImagingKernel). |
| Line 357: | Line 413: |
| * '''in_bst_results'''(ResultsFile, LoadFull, FieldsList): Load a source file and optionnally reconstruct the full source time series on the fly (ImagingKernel * recordings). | * '''in_bst_results'''(ResultsFile, LoadFull, FieldsList): Load a source file and optionally reconstruct the full source time series on the fly (ImagingKernel * recordings). |
| Line 361: | Line 417: |
| == References [TODO] == | == Additional documentation [TODO] == ==== Articles [TODO] ==== |
| Line 364: | Line 421: |
== Additional documentation == |
* Baillet, Mosher, Leahy, Electromagnetic Brain Imaging, IEEE SP MAG, 2001. ==== Tutorials ==== |
| Line 372: | Line 430: |
| ==== Forum discussions ==== | |
| Line 374: | Line 433: |
| * Forum: Spatial smoothing of sources: http://neuroimage.usc.edu/forums/showthread.php?1409 * Forum: Units for dSPM and sLORETA: [[http://neuroimage.usc.edu/forums/showthread.php?1535-Dipole-strength-units-for-dSPM-and-sLORETA|http://neuroimage.usc.edu/forums/showthread.php?1535]] |
* Forum: Spatial smoothing: http://neuroimage.usc.edu/forums/showthread.php?1409 * Forum: Units for dSPM/sLORETA: [[http://neuroimage.usc.edu/forums/showthread.php?1535-Dipole-strength-units-for-dSPM-and-sLORETA|http://neuroimage.usc.edu/forums/showthread.php?1535]] |
| Line 377: | Line 436: |
| * Forum: Sign of the MNE values: http://neuroimage.usc.edu/forums/showthread.php?1649#post7014 * Forum: Combining magneto+gradiometers: http://neuroimage.usc.edu/forums/showthread.php?1900 |
* Forum: Sign of the MNE values: [[http://neuroimage.usc.edu/forums/showthread.php?1649#post7014|http://neuroimage.usc.edu/forums/showthread.php?1649]] * Forum: Combine mag+gradiometers: http://neuroimage.usc.edu/forums/showthread.php?1900 |
| Line 380: | Line 439: |
| * Forum: Dipole fitting: http://neuroimage.usc.edu/forums/showthread.php?2400 * Forum: Simulate recordings from sources: http://neuroimage.usc.edu/forums/showthread.php?2563 |
Tutorial 22: Source estimation [TODO]
Authors: Francois Tadel, Elizabeth Bock, Rey R Ramirez, John C Mosher, Richard M Leahy, Sylvain Baillet
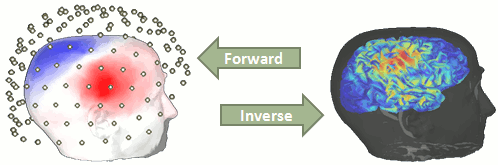
You have in your database a forward model that explains how the cortical sources determine the values on the sensors. This is useful for simulations, but what we need is to build the inverse information: how to estimate the sources when we have the recordings. This tutorials introduces the tools available in Brainstorm for solving this inverse problem.
WARNING: The new interface presented here do not include all the options yet. The mixed head models are not supported: to use them, use the old interface (menu "Compute sources" instead of "Compute sources 2016", described in the ?old tutorials).
Contents
- Ill-posed problem
- Source estimation options
- Computing sources for an average
- Display: Cortex surface
- Why does it look so noisy?
- Display: MRI Viewer
- Display: MRI 3D
- Sign of constrained maps
- Unconstrained orientations
- Source map normalization
- Delete your experiments
- Computing sources for single trials
- Averaging in source space
- Averaging normalized values
- Display: Contact sheets and movies
- Model evaluation
- Advanced minimum norm options
- LCMV beamformer
- Dipole modeling
- Equations [TODO]
- On the hard drive
- Additional documentation [TODO]
Ill-posed problem
Our goal is to estimate the activity of the thousands of dipoles described by our forward model. However we only have a few hundred variables in input (the number of sensors). This inverse problem is ill-posed, meaning there is an infinite number of combinations of source activity patterns that can generate exactly the same sensor topography. Inverting the forward model directly is impossible, unless we add some strong priors to our model.
Wikipedia says: "Inverse problems are some of the most important and well-studied mathematical problems in science and mathematics because they tell us about parameters that we cannot directly observe. They have wide application in optics, radar, acoustics, communication theory, signal processing, medical imaging, computer vision, geophysics, oceanography, astronomy, remote sensing, natural language processing, machine learning, nondestructive testing, and many other fields."
Many solutions have been proposed in the literature, based on different assumptions on the way the brain works and depending on the amount of information we already have on the effects we are studying. Among the hundreds of methods available, in Brainstorm, we initially present three general approaches to the inverse models widely used in MEG/EEG source imaging: minimum-norm solutions, beamformers, and dipole modeling.
These approaches have the advantage of being implemented in an efficient linear form: the activity of the sources is a linear recombination of the MEG/EEG recordings, such that it is possible to solve the inverse problem as a linear kernel which is easily stored. Subsequent data manipulation and source visualization is then much simpler, as are comparisons among these techniques.
Below we first describe the minimum norm imaging approach and its options, followed by the beamformer and dipole modeling, both of which are actually quite similar and only use a subset of the options found in the minimum norm.
Source estimation options
Before we start estimating the sources for the recordings available in our database, let's start with an overview of the options available. The screen capture below represents the options for the minimum norm estimates. The options for the other methods will be described in advanced tutorials.
Method
Selecting one of the three Methods automatically switches the input screen automatically to reveal the options available for each. Above are the options revealed for the mininum norm imaging. First we brieflly describe the Methods options:
Minimum norm: Bayesian Estimation of the sources, assumes a noise and signal prior.
User may synthesize the noise covariance as the "identity matrix", or estimate a noise covariance matrix from recordings. The source covariance prior is generated from the options discussed in detail below. The signal covariance prior (i.e. the source prior as "propagated" to the sensor array) is generated from the options selected. The data covariance (the sum of the signal and noise covariance) is therefore synthesized.LCMV beamformer: "Linearly constrained minimum variance," requires a data covariance.
The data covariance matrix is assumed to also contain the signal(s) of interest. In practice, the data covariance is estimated directly from the recordings. A linear kernel is formed from this data covariance matrix, after which the beamformer scanning image can be stepped through the data, and the best peak can be fit with a dipolar model at every time instance, as described later.Dipole modeling: Single equivalent current dipole, requires a noise covariance.
The noise covariance matrix is assumed to NOT contain the signal of interest. In practice, this noise covariance matrix is calculated directly from recordings. In MEG, these recordings are often "empty room." In EEG, no such "empty room" is possible, so "quiet periods" of ongoing brain data are selected, as can also be selected in MEG. A linear kernel is formed from this noise covariance matrix, after which a scanning image (analogous to the beamformer) can be viewed, and the best dipole location and orientation can be found for every time instance.Recommended option: Still under much debate, even among our Brainstorm team. One advantage of Brainstorm is that all three approaches can be easily run and compared. If the results are concordant among all three techniques, then our underlying assumptions of source modeling, head modeling, and data statistics are confirmed. If the results are disparate, then a more indepth study is needed to understand the consequences of our assumptions and therefore which technique may be preferred.
The next several sections discuss in detail the options as revealed by selecting the "mininum norm imaing" Method above.
Measure
As directly formed and computed, the minimum norm estimate produces a measure of the current found in each point of the source grid (either volume or surface). As discussed elsewhere in the forum (link to Mosher's discuss on units of the minimum norm), the units are strictly kept in A-m, i.e. we do not attempt to divide out the area (yielding A/m, i.e. a surface density) or volume (yielding A/m^2, i.e. a volume density) of each source point; nonetheless, it is common to refer these units as a "source density" or "current density" map when displayed directly.
More commonly, however, users often prefer to "normalize" each source point in order to compensate for the rapid falloff in signal intensity for deeper dipoles. Because of their popularity, we provide directly in the Measure box two forms of standardization, the dSPM and sLORETA. Summarizing the Measures selection:
Current density map: The Minimum Norm Estimate (MNE)
"Whitened" (i.e. noise covariance matrix is accounted for) and "depth-weighted" (if user selected the option) linear L2-minimum norm estimates algorithm inspired from Matti Hamalainen's MNE software. For a full description of this method, please refer to the MNE manual, section 6, "The current estimates". Units: picoamper-meter (pA-m).dSPM: dynamical Statistical Parametric Mapping [Dale, 2000]
The MNE is computed as above, but then we use exactly the same linear kernel with given noise covariance matrix to essentially "z-score" each point in the current density map. Units: unitless "z".sLORETA: standardized LOw Resolution brain Electromagnetic TomogrAphy [Pasqual-Marqui, 2002])
As originally presented (2002), sLORETA also uses the same MNE solution from above, then we use exactly the same linear kernel with the MNE data covariance matrix (instead of noise covariance) to again weight each point in the current density map. Subsequent theoretical developments show an alternative form of a "resolution" kernel that may be calculated instead. We use the "resolution" form, but the interested researcher is invited to review the details of our coding.Recommended option: Discussed in the section "Source map normalization" below.
Source model: Dipole orientations
At each point in the source grid, the current dipole may point arbitrarily in three directions. In this section of the options, we prescribe if the inverse method will constrain the orientation, leave it unconstrained, or if we impose a "soft" constraint to the orientation.
Constrained: Normal to cortex: Only for "surface" grids. At each grid point, we model only one dipole, oriented normally to the cortical surface. This is based on the anatomical observation that in the cortex, the neurons are mainly organized in macro-columns that are perpendicular to the cortex surface.
Size of the inverse operator: [Nvertices x Nchannels].Loose: Only for "surface" grids. As introduced by Lin (cite), at each point in the surface grid the dipole direction is constrained to be normal to the local cortical surface. Two additional elemental dipoles are also allowed, in the two directions "tangential" to the cortical surface. As contrasted with "unconstrained," these two tangential elemental dipoles are only modeled to have an amplitude that is a fraction of the normal dipole, recommended to be between 0.1 and 0.6. Thus the dipole is only "loosely" constrained to be normal to the local cortical surface.
Size of the inverse operator: [3*Nvertices x Nchannel].Unconstrained: Either "surface" or "volume" grids. At each grid point, we leave undefined the assumed orientation of the source, such that three "elemental" dipoles are needed to model the source. In Brainstorm, our elemental dipoles are in the x, y, and z ("Cartesian") directions, as compared to other software that may employ polar coordinates. Thus for "N" vertices, we are calculating the estimate for "3*N" elemental dipoles.
Size of the inverse operator: [3*Nvertices x Nchannels].Recommended option: The constrained options use one dipole per grid point instead of three, therefore the source files are smaller, faster to compute and display, and more intuitive to process because we don't have to think about recombining the three values into one. On the other hand, in the cases where its physiological assumptions are not verified, typically when using a MNI template instead of the anatomy of the subject, the normal orientation constraint may fail representing certain activity patterns. Unconstrained models can help in those cases.
Sensors
We automatically detect and display the sensors found in your head model. In the example above, two types of magnetometers are found, gradiometers and magnetometers. You can select one or all of the sensors found in your model, such as MEG and EEG.
However, cross-modality calculations are quite dependent on the accuracy by which you have provided adequate covariance calculations. As of Fall of 2016, we have also elected to NOT account for cross-covariances between different sensor types, since regularization and stability of cross-modalities is quite involved. For multiple sensor types, the recommendation is that you try each individually and then combined, to test for discordance.
Computing sources for an average
Using the above selections, we now discuss explicit directions on how to compute and visualize.
In Run#01, right-click on the average response for the deviant stim > Compute sources [2016].
Select the options: Minimum norm imaging, Current density map, Constrained: Normal to cortex.
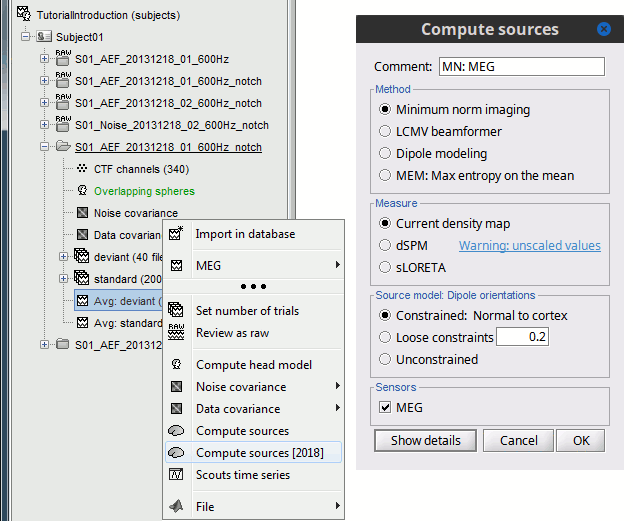
- The other menu "Compute sources" brings the interface that was used previously in Brainstorm. We are going to keep maintaining the two implementations in parallel for a while for compatibility and cross-validation purposes.
The result of the computation is displayed as a dependent file of the deviant average because it is related only to this file. In the file comment, "MN" stands for minimum norm and "Constr" stands for "Constrained: normal orientation".
Display: Cortex surface
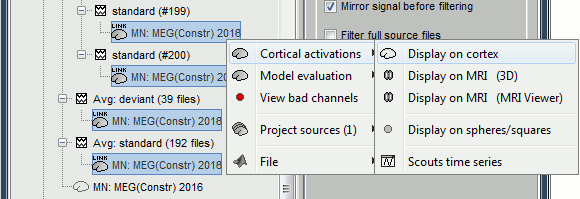
Right-click on the sources for the deviant average > Cortical activations > Display on cortex.
Double-click on the recordings for the deviant average to have a time reference.
In the filter tab, add a low-pass filter at 40Hz.
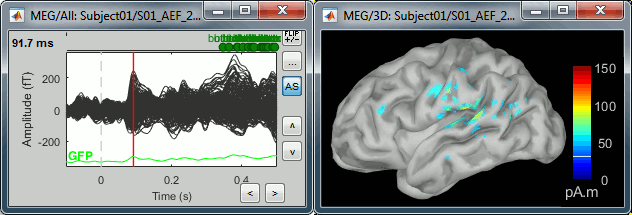
- Change the current time (click on the time series figure or use the keyboard arrows) and note it updates the source maps in the 3D figure. You can also use all the menus and shortcuts introduced in the anatomy tutorial (like setting the view with the keys from 0 to 6).
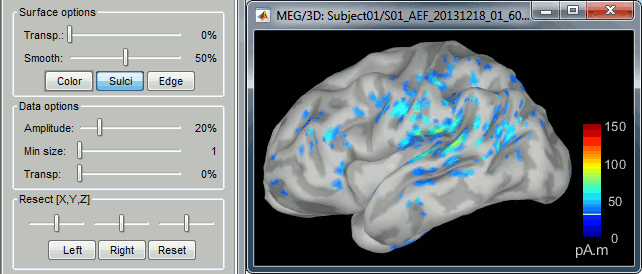
- You can edit the display properties in the Surface tab:
Amplitude: Only the sources that have a value superior to a given percentage of the colorbar maximum are displayed.
Min size: Hide all the small activated regions, ie. the connected color patches that contain a number of vertices smaller than this "min size" value.
Transparency: Change the transparency of the source activity on the cortex surface.
Take a few minutes to understand what the amplitude threshold represents.
The colorbar maximum depends on the way you configured your Sources colormap. If the option "Maximum: Global" is selected, the maximum should be around 130 pA.m. This value is a rough estimate of the maximum amplitude, and this default value is not always adapted to your figure. To edit the maximum value, use the colormap option "Maximum: Custom".
On the screen capture below, the threshold value is set to 20%. It means that only the sources that have a value over 0.20*130 = 26 pA.m are visible.
The threshold level is indicated in the colorbar with a horizontal white line.
At the first response peak (91ms), the sources with high amplitudes are located around the primary auditory cortex, bilaterally, which is what we are expecting for an auditory stimulation.
Why does it look so noisy?
The source maps look very noisy and discontinuous, they show a lot of disconnected patches. This is due to the orientation constraint we imposed on the dipoles orientations. Each value on the cortex has to be interpreted as a vector, oriented perpendicular to the surface. Because of the brain circumvolutions, all the sources have different orientations, two adjacent sources have very little chance to have the same orientation in this model, therefore the minimum norm method may attribute completely different values to them. This causes all these gaps we see here.
Visually, you should not always interpret disconnected colored patches as independent sources. You cannot expect a very spatial resolution with this technique (~5-10mm). Most of the time, a cluster of disconnected source patches in the same neighborhood that show the same evolution in time can be interpreted as "there is some significant activity around here, but we don't know where exactly".
To get more continuous maps for visualization or publication purposes, you can either smooth the values explicitly on the surface (process "Sources > Spatial smoothing") or use unconstrained source models.
For data exploration, this is a good enough representation of the brain activity, mostly because it is fast and efficient. You can get a better feeling of the underlying brain activity patterns by making short interactive movies: click on the figure, then hold the left or right arrows of your keyboard.
Activity patterns will also look sharper when we compute normalized measures (later in this tutorial). In most of the screen captures in this following sections, the contrast of the figures has been enhanced for illustration purposes. Don't worry if it looks a lot less colorful on your screen.
Display: MRI Viewer
Right-click on the source file > Cortical activations > Display on MRI (MRI Viewer).
The MRI viewer was introduced in tutorials #2 and #3.
Additionally you can change the current time and amplitude threshold from the Brainstorm window.This figure shows the sources computed on the cortical surface and re-interpolated in the MRI volume. If you set the amplitude threshold to 0%, you would see the thin layer of cortex in which the dipoles where estimated.
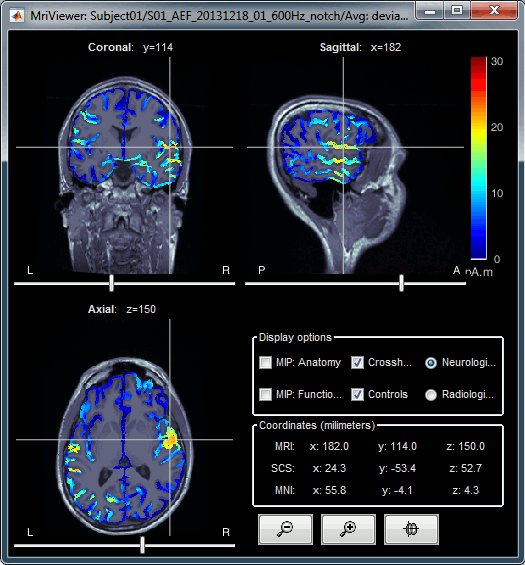
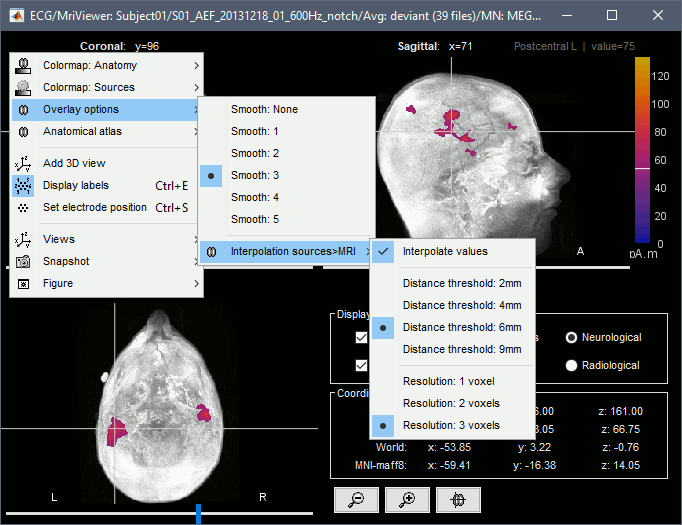
- You can configure this figure with the following options:
MIP Anatomy: Checkbox in the MRI Viewer figure. For each slice, display the maximum value over all the slices instead of the original value in the structural MRI ("glass brain" view).
MIP Functional: Same as for MIP Anatomy, but with the layer of functional values.
Smooth level: The sources values can be smoothed after being re-interpolated in the volume. Right-click on the figure to define the size of the smoothing kernel (in number of slices).
Amplitude threshold: In the Surface tab of the Brainstorm window.
Current time: At the top-right of the Brainstorm window (or use the time series figure).
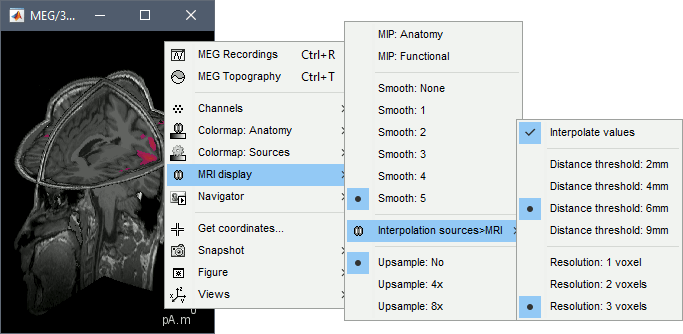
Display: MRI 3D
Right-click on the source file > Cortical activations > Display on MRI (3D).
This view was also introduced in the tutorials about MRI and surface visualization.
Right-click and move your mouse to move the slices (or use the Resect panel of the Surface tab).
Sign of constrained maps
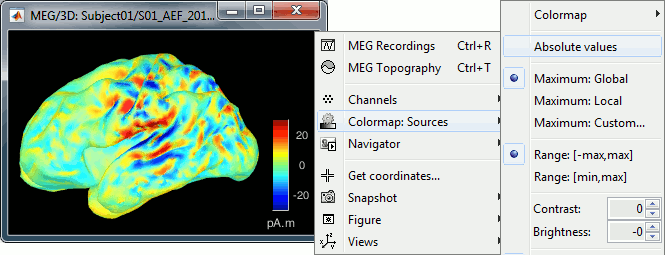
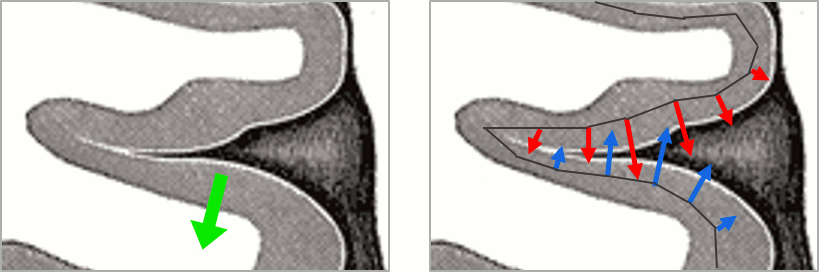
You should pay attention to the sign of the current amplitudes that are given by the minimum norm method: they can be positive or negative and they oscillate around zero. Display the sources on the surface, set the amplitude threshold to 0%, then configure the colormap to show relative values (uncheck the "Absolute values" option), you would see those typical stripes of positive and negative values around the sulci. Double-click on the colorbar after testing this to reset the colormap.
This pattern is due to the orientation constraint imposed on the dipoles. On both sides of a sulcus, we have defined dipoles that are very close to each other, but with opposite orientations. If we have a pattern of activity on one side of a suclus that can be assimilated to an electric dipole (green arrow), the minimum norm model will try to explain it with the dipoles that are available in the head model (red and blue arrows). Because of the dipoles orientations, it translates into positive values (red arrows) on one side of the sulcus and negative on the other side (blue arrows).
When displaying the cortical maps at one time point, we are usually not interested by the sign of the minimum norm values but rather by their amplitude. This is why we always display them by default with the colormap option "absolute values" selected.
However, we cannot simply discard the sign of these values because we need them for other types of analysis, typically time-frequency decompositions and connectivity analysis. For estimating frequency measures on the source maps, we need to keep the oscillations around zero.
Unconstrained orientations
In the cases where the orientation constraint imposed on the dipoles orientations looks too strong, it is possible to relax it partially (option "loose constraints") or completely (option "unconstrained"). This is typically something to consider when using a MNI template instead of the subject's anatomy, or when studying deeper or non-cortical brain regions for which the normal to the FreeSurfer cortex surface is unlikely to match any physiological reality.
In terms of data representation, the option "unconstrained" and "loose constraints" are very similar. Instead of using one dipole at each cortical location, a base of three orthogonal dipoles is used.
Here we will only illustrate the fully unconstrained case.
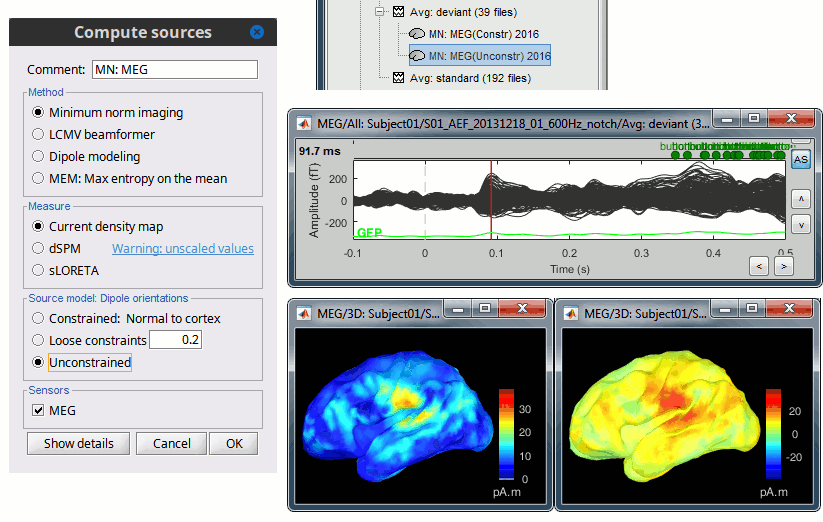
In Run#01, right-click on the average response for the deviant stim > Compute sources [2016].
Select the options: Minimum norm imaging, Current density map, Unconstrained.Double-click on the new source file for the deviant average, open the time series simultaneously. The two brain maps below represent the same file at 91ms, with different colormap options (absolute values on the left, relative values on the right). Explanations below.
We have to be careful with the visual comparisons of constrained and unconstrained source maps displayed on the cortex surface, because they are very different types of data. In unconstrained source maps, we have three dipoles with orthogonal orientations at each cortex location, therefore we cannot represent all the information at once. To display them as an activity map, Brainstorm computes the norm of the vectorial sum of the three orientations at each vertex.
S = sqrt(Sx2 + Sy2 + Sz2)
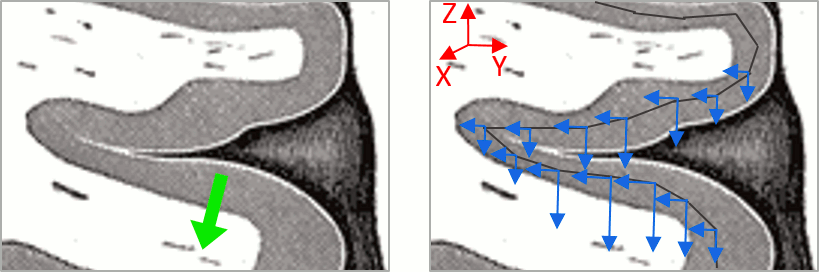
This explains that we only observe positive values (no blue values when the colormap is set to display positive and negative values): the norm displayed at each vertex is always positive. The underlying values along each orientation (x,y,z) can be positive or negative and oscillate around zero in time, but we cannot get access to this information with these static cortical maps.
The maps we observe here look a lot smoother than the constrained sources we computed earlier. This can be explained by the fact that there is no sharp discontinuity between two adjacent points of the grid, while the normal to the surface between two nearby points can be very different.
Delete the unconstrained file, we will not explore this option in the introduction tutorials. You can refer to the tutorial EEG and epilepsy for an example of analysis using unconstrained sources.
Source map normalization
The current density values returned by the minimum norm method have a few problems:
They depend a lot on the SNR of the signal, which may vary significantly between subjects.
Their amplitude is therefore difficult to interpret directly.- The values tend to be higher at the surface of the brain (close to the sensors).
- The maps are sometimes patchy and difficult to read.
Normalizing the current density maps with respect to a reference level (estimated from noise recordings, pre-stimulus baseline or resting state recordings) can help with all these issues at the same time. Some normalizations can be computed independently from the recordings, and added to the linear inverse operator (dSPM or sLORETA). Another way of proceeding is to divide the current density maps by the standard deviation estimated over a baseline (Z-score).
The normalization options do not change the temporal dynamics of your results, they are just different ways for looking at the same minimum norm maps. If you look at the time series associated with one given source, it would be exactly the same for all the normalizations, except for a scaling factor. Only the relative weights change between the sources, and these weights do not change over time.
dSPM, sLORETA
In Run#01, right-click on the average recordings for the deviant stim > Compute sources [2016].
Select successively the two normalization options: dSPM, sLORETA, (constrained).
Double-click on all of them to compare them (screen capture at 143ms):
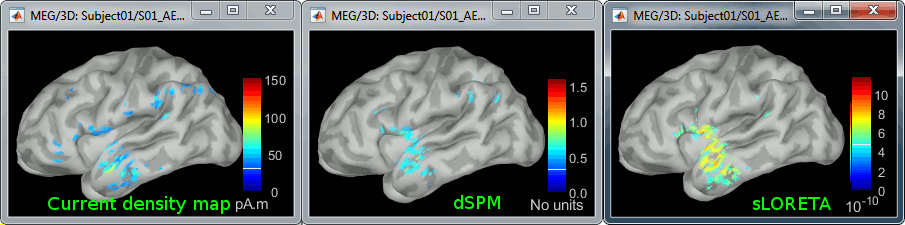
Current density maps: Tends to highlight the top of the gyri and the superficial sources.
dSPM: Tends to correct this behavior and may give higher values in deeper areas. The values obtained are unitless and similar to Z-scores, therefore they are easier to interpret.
sLORETA: Produces smoother maps where all the potentially activated area of the brain (given to the low spatial resolution of the source localization with MEG/EEG) is shown as connected, regardless of the depth of the sources. However, the units are difficult to interpret.
Z-score
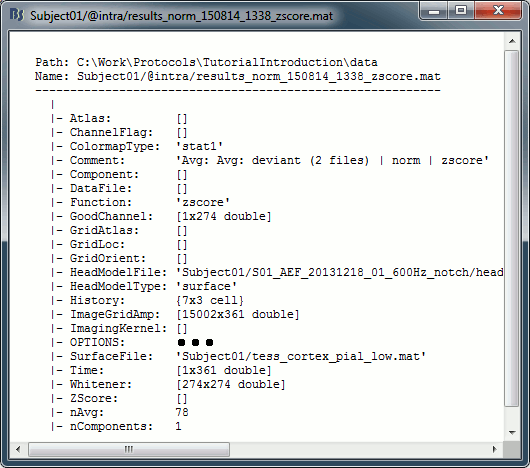
The Z-transformation converts the current density values to a score of deviation from a baseline. We define a baseline period in our file (in this case, the pre-stimulus baseline) and compute the average and standard deviation for this segment. Then for every time point we subtract the baseline average and divide by the baseline standard deviation. Z = (Data - μ) / σ
- This measure tells how much a value deviates from the baseline average, in number of times the standard deviation. This is done independently for each source, so the sources with a low variability during baseline will be more salient in the cortical maps post-stimulus.
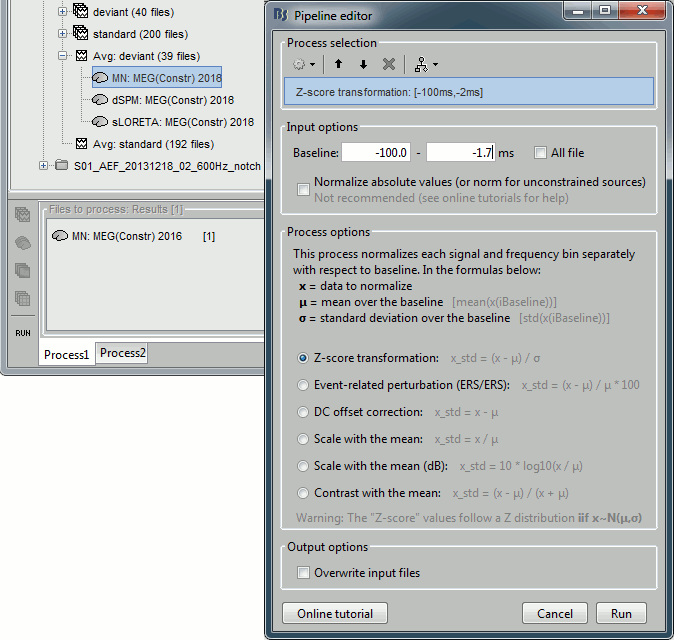
In Process1: Select the constrained current density maps (file MN: MEG(Constr)).
Run process "Standardize > Baseline normalization", [-100,-1.7]ms, Z-score transformation
Do not select "Use absolute values": We want the sign of the current values.
Double-click on the new normalized file to display it on the cortex (file with the "| zscore" tag).
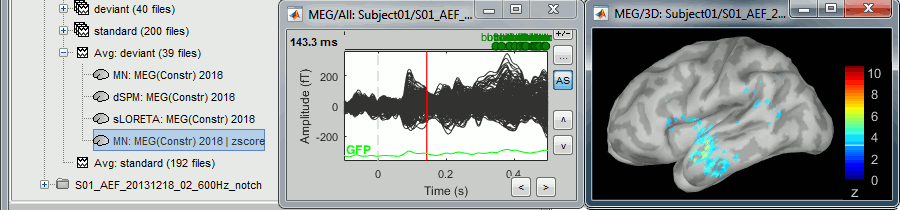
You can see that the cortical maps obtained in this way are very similar to the other normalization approaches, especially with the dSPM maps. The units are different but the global observations are the same.
A value of 3 in this figure means: at this vertex, the value is 3 times higher than the standard deviation from zero during the baseline. If the values during the baseline follow a normal distribution N(μ,σ2), then the values we computed follow a N(0,1)=Z distribution. We can get a level of significance from this well known distribution, for instance a value Z=1.96 corresponds to a p-value of 0.05. These questions will be discussed in more details in the statistics tutorial.
The Z-normalized source maps are not impacted by the visualization filters. If you open simultaneously the time series and all the files you have now (MN, dSPM, sLORETA, Z-score) and modify the options in the Filter tab, all the figures are updated except for the Z-score one. We can filter easily all the linear models (MN, dSPM, sLORETA), but we would lose the interesting properties of the Z-values if we were filtering them (the values would not follow a Z-distribution anymore).
If the baseline and the active state are not in the same file, you can use the Process2 tab: place the baseline in the left list (Files A) and the file to normalize in the right list (Files B).
Typical recommendations
Use non-normalized current density maps for:
- Computing shared kernels applied to single trials.
- Averaging files across MEG runs.
- Computing time-frequency decompositions or connectivity measures on the single trials.
Use normalized maps (dSPM, sLORETA, Z-score) for:
- Estimating the sources for an average response.
- Exploring visually the average response (ERP/ERF) at the source level.
- Normalizing the subject averages before a group analysis.
- Recommended normalization approach:
- It is difficult to declare that one normalization technique is better than another. They have different advantages and may be used in different cases. Ideally, they should all converge to similar observations. If you obtain results with one method that you cannot reproduce with the others, you should question your findings.
- dSPM and sLORETA are linear measures and can expressed as imaging kernels, therefore they are a lot easier to manipulate in Brainstorm. sLORETA maps can be smoother but its units are difficult to understand. dSPM units are much easier to understand and interpret.
- Z-normalized current density maps are also easy to interpret. They represent explicitly a "deviation from experimental baseline" while dSPM indicates a "deviation from noise" (as represented by the noise covariance matrix).
Delete your experiments
Select all the source files you computed until now and delete them.
Computing sources for single trials
Because the minimum norm model is linear, we can compute an inverse model independently from the recordings and apply it on the recordings when needed. We will now illustrate how to compute a shared inverse model for all the imported epochs.
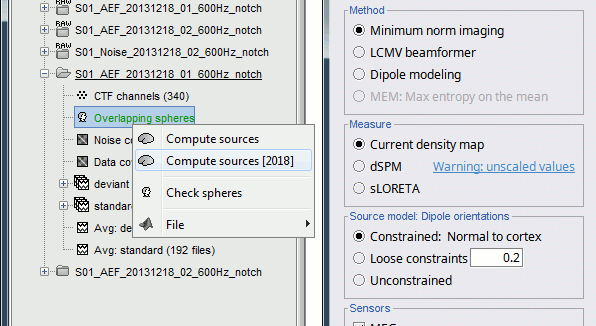
Right-click on the head model or the folder for Run#01 > Compute sources [2016].
Select: Minimum norm imaging, Current density map, Constrained: Normal to cortex
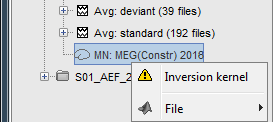
Because we did not request to compute and inverse model for a specific block of recordings, it computed a shared inverse model. If you right-click on this new file, you get a warning message: "Inversion kernel". It does not contain any source map, but only the inverse operator that will allow us to convert the recordings into source maps.
The database explorer now shows one source link to this inverse model for each block of recordings available in this folder, single trials and averages. These links are not real files saved on the hard drive, but you can use them exactly like the previous source files we calculated for the deviant average. If you load a link, Brainstorm loads the corresponding MEG recordings, loads the inverse kernel and multiplies the two on the fly before displaying it. This optimized approach saves a lot of computation time and lot of space on the hard drive.
Averaging in source space
Computing the average
First compute the same source model for the the second acquisition run.
In Run#02, right-click on the head model or the folder > Compute sources [2016].
Select: Minimum norm imaging, Current density map, Constrained: Normal to cortex
Now we have the source maps available for all the trials, we can average them in source space across runs. This allows us to average MEG recordings that were recorded with different head positions (in this case Run#01 and Run#02 have different channel files so they could potentially have different head positions preventing the direct averaging at the sensor level).
Thanks to the linearity of the minimum norm model: MN(Average(trials)) = Average(MN(trials))
The two following approaches are equivalent:- Averaging the sources of all the individual trials across runs,
- Averaging the sources for the sensor averages that we already computed for each run.
We will use the second option: using the sources for the sensor-level averages.
It is a lot faster because it needs to read 4 files (one average file per run and per condition) instead of 456 files (total number of good trials in the two runs).Drag and drop to the Process1 tab the average recordings for Run01 and Run02, then press the [Process sources] button on the left to select the source files instead of the MEG recordings.
Run process "Average > Average files":
Select "By trial group (subject average)" to average together files with similar names.
Select "Weighted average" to account for the different numbers of trials in both runs.
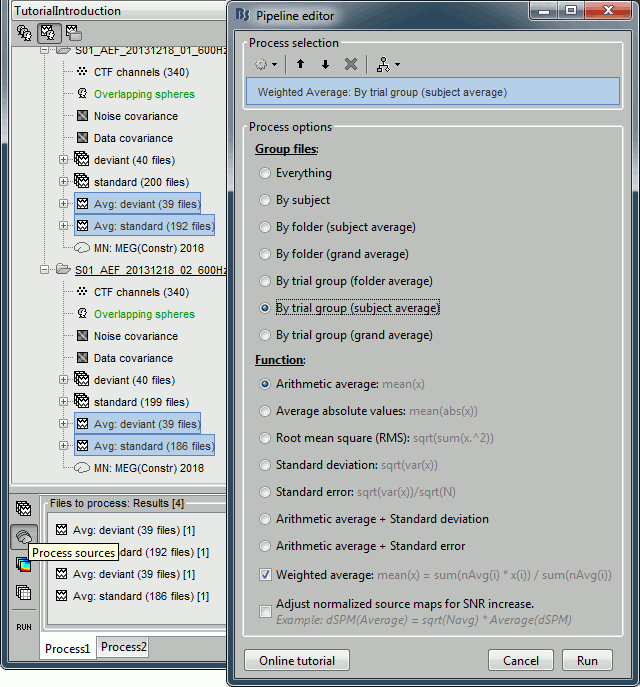
The two averages that are produced (one for each condition) are saved in the folder Intra-subject. This is where all the files computed using information from multiple folders within the same subject are saved. If you prefer to have them somewhere else, you can create new folders and move them there, just like you would do with a regular file explorer.
The file comments say "2 files" because they were computed from two averages each (one from each run), but the number of corresponding trials is correctly updated in the file structure.
Right-click on each of them > File > View file contents, and check the nAvg field:
78 trials for the deviant condition, 378 trials for the standard condition.Double-click on the source averages to display them (deviant=top, standard=bottom).
Open the sensor-level averages as a time reference.
Use the predefined view "Left, Right" for looking at the two sides at the same time (shortcut: "7").
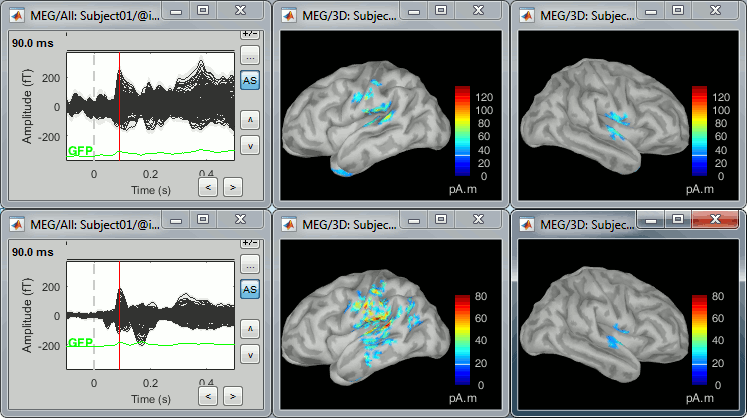
Visualization filters
Note that opening the source maps can be very long because of the filters for visualization. Check in the Filter tab, you may have a filter applied with the option "Filter full source files" selected. In the case of averaged source maps, the 15,000 source signals are filtered on the fly when you load a source file. This filtering of the full source files can take a significant amount of time, consider unchecking this option if the display is too slow on your computer.
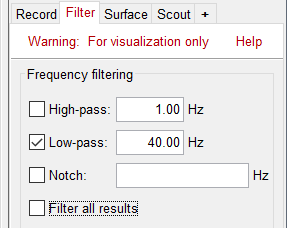
- It was not a problem until now because the source files were saved in the compact form (Kernel*recordings) and the visualization filters were applied on the recordings, then projected to the source space. This fast option is not available anymore with these averages across runs.
- The visualization filters will not be available anymore after we apply a Z-score normalization. If we want to display Z-score source maps that are smoothed in time, we will have to apply explicitly the filters on the file, with the Process1 tab.
Low-pass filter
- Clear the Process1 list, then drag and drop the new averages in it.
Run process "Pre-process > Band-pass filter": [0,40] Hz
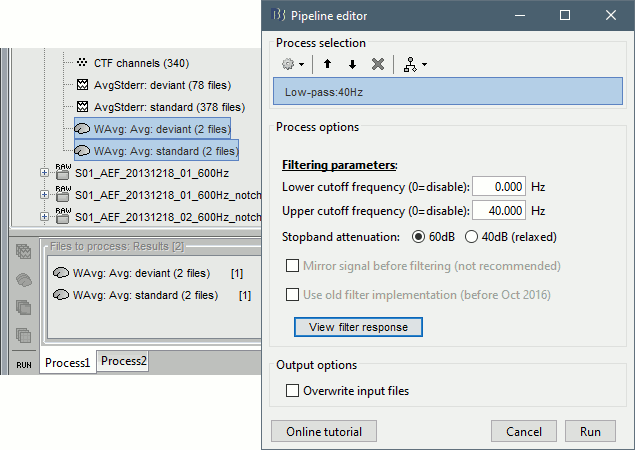
Z-score normalization
- In Process1, select the two filtered averages.
Run process "Standardize > Baseline normalization", baseline=[-100,-1.7]ms, Z-score.
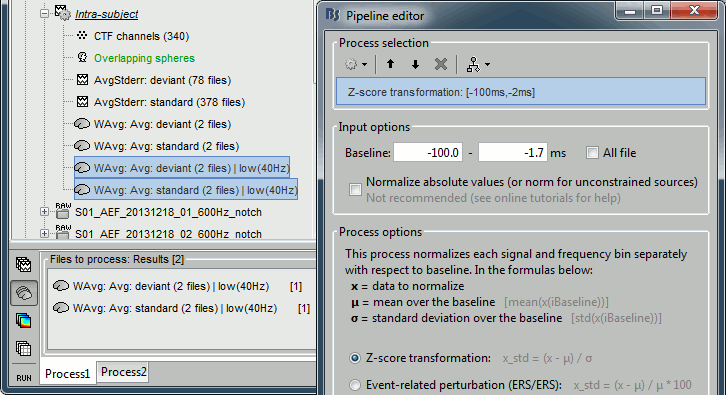
Four new files are accessible in the database: two filtered and two filtered+normalized.
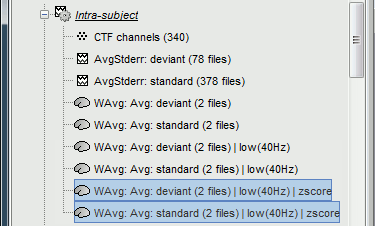
Double-click on the source averages to display them (deviant=top, standard=bottom).
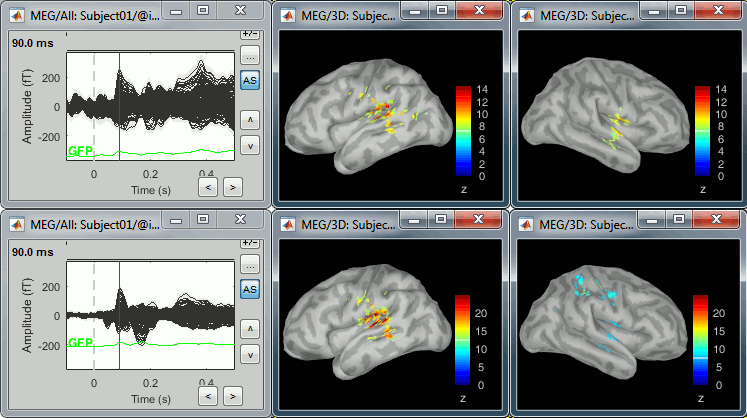
- The Z-score source values at 90ms are higher for the standard condition (~25) than for the deviant condition (~15). We observe this because the two conditions have very different signal-to-noise ratios. The standard condition has about 5x more trials, therefore the standard deviation over the baseline is a lot lower, leading to higher Z-score.
Delete the non-normalized filtered files, we will not use them in the following tutorials.
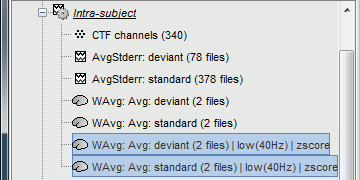
Averaging normalized values
Averaging normalized source maps within a single subject requires more attention than averaging current density maps. The amplitude of the normalized measures increase with the SNR of the signal, the higher the SNR the higher the normalized score. For instance, the average of the dSPM for the single trials is lower than the dSPM of the averaged trials.
dSPM
- From the expression of the dSPM, we know exactly what factor should be applied to compensate for this effect. When computing the average of dSPM or other normalized values, we have to also multiply the average with the square root of the number of files averaged together.
MinNorm(Average(trials)) = Average(MinNorm(trials))
dSPM(Average(trials)) = sqrt(Ntrials) * Average(dSPM(trials))This can be done automatically during the averaging for dSPM values, it corresponds to the option: "Adjust normalized source maps for SNR increase":
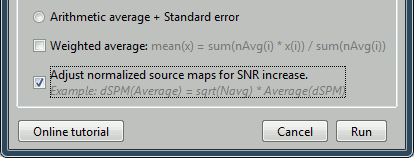
Z-score
- The same SNR issues arise while averaging Z-scores: the average of the Z-scores is lower than the Z-score of the average. But this time we do not have an easy analytical expression to compensate for the modifications in SNR, the average would not be reflecting the increase in SNR.
When computing averages at the subject level: Always avoid averaging Z-score maps.
Average the current density maps, then normalize.
sLORETA
- This normalization is not based on the SNR of signal, but rather on the smoothness of the maps. There is no problem related with the average of sLORETA-normalized source maps.
- sLORETA(Average(trials)) = Average(sLORETA(trials))
Display: Contact sheets and movies
A good way to represent what is happening in time is to generate contact sheets or videos. Right-click on any figure and go to the menu Snapshot to check out all the possible options. For a nicer result, take some time to adjust the size of the figure, the amplitude threshold and the colormap options (hiding the colorbar can be a good option for contact sheets).
A time stamp is added to the captured figure. The size of the text font is fixed, so if you want it to be readable in the contact sheet, you should make you figure very small before starting the capture. The screen captures below where produced with the colormap "hot".
Contact sheet: Right-click on any figure > Snapshot > Time contact sheet: Figure

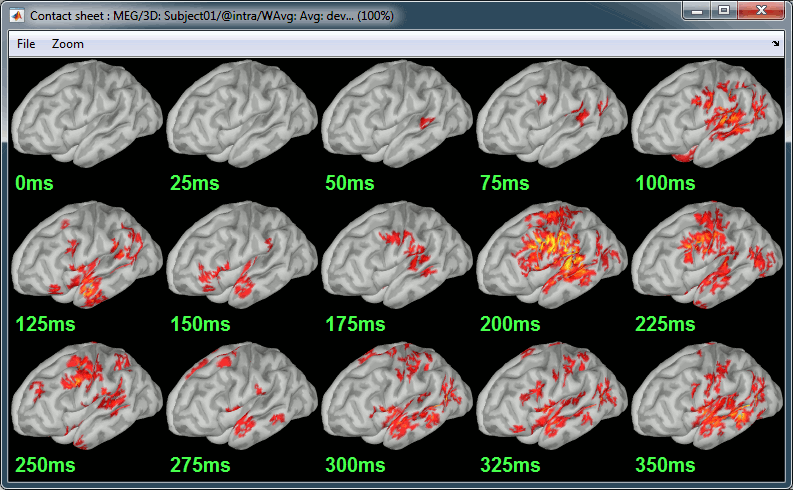
Movies: Right-click on any figure > Snapshot > Movie (time): All figures
Model evaluation
One way to evaluate the accuracy of the source reconstruction if to simulate recordings using the estimated source maps. This is done simply by multiplying the source time series with the forward model:
MEG_simulated [Nmeg x Ntime] = Forward_model [Nmeg x Nsources] * MN_sources [Nsources x Ntime]
Then you can compare visually the original MEG recordings with the simulated ones. More formally, you can compute an error measure from the residuals (recordings - simulated).
To simulate MEG recordings from a minimum norm source model, right-click on the source file, then select the menu "Model evaluation > Simulate recordings".
Open side-by-side the original and simulated MEG recordings for the same condition:
Advanced minimum norm options
Right-click on the deviant average for Run#01 > Compute sources [2016].
Click on the button [Show details] to bring up all the advanced minimum norm options.
Depth weighting
Briefly, the use of various depth weightings was far more debated in the 1990s, before the introduction of MNE normalization via dSPM, sLORETA, and other "z-scoring" methods, which mostly negate the effects of depth weighting. At each point in the source grid, the deeper points are "boosted" to increase their signal strength relative to the shallower dipoles; otherwise, the resulting MNE current density maps are too dominated by the shallower sources. If using dSPM or sLORETA, little difference in using depth weighting should be noted. To understand how to set these parameters, please refer to the MNE manual. (options --depth, --weightexp and --weightlimit).
Noise covariance regularization
MNE and dipole modeling are best done with an accurate model of the noise covariance, which is generally computed from experimental data. As such, these estimates are themselves prone to errors that arise from relatively too few data points, weak sensors, and strange data dependencies that cause the eigenspectrum of the covariance matrix to be somewhat deficient. In Brainstorm, we provide several means to "stabilize" or "regularize" the noise covariance matrix, so that source estimation calculations are more robust to small errors.
Regularize noise covariance: The L2 matrix norm is defined as the largest eigenvalue of its eigenspectrum. This option adds to the covariance matrix a diagonal matrix whos entries are a fraction of the matrix norm. The default is 0.1, such that covariance matrix is stabilized by adding to it an identity matrix that is scaled to 10% of the largest eigenvalue.
Median eigenvalue: The eigenspectrum of MEG data can often span many decades, due to highly colored spatial noise, but this broad spectrum is generally confined to the first several modes only. Thus the L2 norm is many times greater than the majority of the eigenvalues, and it is difficult to prescribe a conventional regularization parameter. Instability in the inverse is dominated by defects found in the smallest eigenvalues. This approach stabilizes the eigenspectrum by replicating the median (middle) eigenvalue for the remainder of the small eigenvalues.
Diagonal noise covariance: Deficiencies in the eigenspectrum often arise from numerical inter-dependencies found among the channels, particularly in covariance matrices computed from relatively short sequences of data. One common method of stabilization is to simply take the diagonal of the covariance matrix and zero-out the cross-dependencies. Each channel is therefore modeled as independent of the other channels. The eigenspectrum is now simply the (sorted) diagonal values.
No covariance regularization: We simply use the noise covariance matrix as computed or provided by the user.
Automatic shrinkage: Stabilization method of Ledoit and Wolf (2004), still under testing in the Brainstorm environment. Basically tries to estimate a good tradeoff between no regularization and diagonal regularization, using a "shrinkage" factor. See Brainstorm code "bst_inverse_linear_2016.m" for notes and details.
Recommended option: This author (Mosher) votes for the median eigenvalue as being generally effective.The other options are useful for comparing with other software packages that generally employ similar regularization methods.
Regularization parameter
In MNE, as mentioned above in the comparisons among Methods, the data covariance matrix is essentially synthesized by adding the noise covariance matrix to a modeled signal covariance matrix. The signal covariance matrix is generated by passing the source prior through the forward (head) model. The source prior is in turn prescribed by the source model orientation and the depth weighting. A final regularization parameter, however, is how much weight the signal model should be given relative to the noise model, i.e. the "signal to noise ratio" (SNR). In Brainstorm, as of Fall 2016, we follow the definition of SNR as first defined in the original MNE software of Hamalainen. The signal covariance matrix is "whitened" by the noise covariance matrix, such that the whitened eigenspectrum has elements in terms of SNR (power). We find the mean of this spectrum, then take the square root to yield the average SNR (amplitude). The default in MNE and in Brainstorm is "3", i.e. the average SNR (power) is 9.
Signal-to-noise ratio: Use SNR of 3 as the classic recommendation, as discussed above.
RMS source amplitude: An alternative definition of SNR, but still under test and may be dropped.
Output mode
As mentioned above, these methods create a convenient linear imaging kernel that is "tall" in the number of elemental dipoles (one or three per grid point) and "wide" only in the number of sensors. At subsequent visualzation time, we efficiently multiply the kernel with the data matrix.
For some custom purposes, however, a user may find it convenient to pre-multiply the data matrix and generate the full source estimation matrix. This would only be recommended in small data sets, since the full results can become quite large.
Kernel only: Saves only the linear inverse operator, a model that converts sensor values into source values. The size of this matrix is: number of sources (15000) x number of MEG sensors (274). The multiplication with the recordings is done on the fly by Brainstorm in a transparent way. For long recordings or numerous epochs, this form of compact storage helps saving a lot of disk space and computation time, and it speeds up significantly the display. Always select this option when possible.
Full results: Saves in one big matrix the values of all the sources (15,000) for all the time samples (361). The size in memory of such a matrix is about 45Mb for 600ms of recordings. This is still reasonable, so you may use this option in this case. But if you need to process longer recordings, you may face "Out of memory" errors in Matlab, or fill your hard drive quickly.
- Full results [15000x361] = Inverse kernel [15000x274] * Recordings [274x361]
LCMV beamformer
As mentioned in the introduction above, two other Methods can be selected for source estimation, a beamformer and dipole modeling. In this section, we review the options for the beamformer. By selecting "LCMV beamformer, the options automatically switch to the below figure (shown with details).
Measure
The Measure has switched to a single option, the "Pseudo Neural Activity Index," (PNAI), after the Van Veen definition of the Neural Activity Index (NAI). We have altered the definition to rely strictly on the data covariance, without need for a noise covariance matrix, but the basic premise is the same as in dSPM, sLORETA, and other normalizations. Viewing the resulting "map," identically as is done with MNE, dSPM, and sLORETA above, reveals possibly multiple sources as peaks in the map, scored analogous to z-scoring. The PNAI can then be dropped into the Process Box and the optimal dipole and orientations extracted for every time instance.
Source Model: Dipole orientations
The definitions here are identical to the MNE above; however, we do not recommend you select "constrained" (although technically allowed). Choose only "unconstrained" and let the "dipole scanning" process optimize the orientation with respect to the data.
Sensors
Same considerations as in MNE.
Data covariance regularization
Same definitions as in MNE, only applied to the data covariance matrix, rather than the noise covariance marix. Recommendation is to use median eigenvalue.
Output mode
Recommend to use kernel only.
Dipole modeling
Although not widely recognized, dipole modeling and beamforming are more alike than they are different. Below is the options screen when dipole modeling is selected.
You will notice that "Measure" is now missing, but the resulting imaging kernel file is directly analogous to the PNAI result of LCMV beamforming. The user may identically display this scanning measure as well, where again the units are a form of z-scoring.
Source model, Sensors, Noise covariance regularization, and output mode all follow from the explanations given above for the LCMV and for the MNE.
Again, the recommendation is to ALWAYS use "unconstrained" source modeling and let the Process "dipole scanning" optimize the orientation of the dipole for every time instance. Similarly, use "median eigenvalue" for the optimization.
The tutorial "MEG current phantom (Elekta)" demonstrates dipole modeling of 32 individual dipoles under realistic experimental noise conditions.
Equations [TODO]
...
On the hard drive
Constrained shared kernel
Right-click on a shared inverse file in the database explorer > File > View file contents.
Structure of the source files: results_*.mat
Mandatory fields:
ImagingKernel: [Nsources x Nchannels] Linear inverse operator that must be multiplied by the recordings in order to get the full source time series. If defined, ImageGridAmp must be empty.
ImageGridAmp: [Nsources x Ntime] Full source time series, in Amper.meter. If this field is defined, ImagingKernel must be empty.
Time: [1 x Ntime] Time values for each sample recorded in F, in seconds.
nComponents: Number of dipoles per grid point: 1=Constrained, 3=Unconstrained, 0=Mixed. In the case of mixed head models, the atlas GridAtlas documents region by region how the list of grid points matches the list of dipoles.
Function: Type of values currently saved in the file: 'mn', 'mnp', 'dspm', 'sloreta', 'lcmv', 'lcmvp', 'lcmvnai', 'lcmvpow', 'gls', 'glsp', 'glsfit', 'glschi', 'zscore', 'ersd'...
HeadModelType: Type of source space used for this head model ('surface', 'volume', 'mixed').
HeadModelFile: Relative path to the head model used to compute the sources.
SurfaceFile: Relative path to the cortex surface file related with this head model.
Atlas: Used only by the process "Sources > Downsample to atlas".
GridLoc: [Nvertices x 3], (x,y,z) positions of the grid of source points. In the case of a surface head model, it is empty and you read directly the positions from the surface file.
GridOrient: [Nvertices x 3], direction of the normal to the surface for each vertex point (copy of the 'VertNormals' matrix of the cortex surface). Empty in the case of a volume head model or unconstrained sources.
GridAtlas: Atlas "Source model" used with mixed source models.
GoodChannel: [1 x Nchannels] Array of channel indices used to estimate the sources.
DataFile: Relative path to the recordings file for which the sources where computed. If this field is set, the source file appears as a dependent of the DataFile.
Comment: String displayed in the database explorer to represent this file.
History: Operations performed on the file since it was create (menu "View file history").
Optional fields:
Options: Structure that contains all the options of the inverse calculation. This is saved in the file only for bookkeeping.
Whitener: Noise covariance whitener computed in bst_inverse_linear_2016.m
DataWhitener: Data covariance whitener computed in bst_inverse_linear_2016.m
SourceDecompVa: [3 x Nsources] Concatenated right singular vectors from the SVD decomposition of the whitened leadfield for each source (only for unconstrained sources).
SourceDecompSa: [3 x Nvertices] Vector diagonal of the singular values from the SVD decomposition of the whitened leadfield for each source (only for unconstrained sources).
Std: For averaged files, number of trials that were used to compute this file.
DisplayUnits: String, force the display of this file using a specific type of units.
ChannelFlag: [Nchannels x 1] Copy of the ChannelFlag field from the original data file.
nAvg: For averaged files, number of trials that were used to compute this file. For source files that are attached to a data file, we use the nAvg field from the data file.
Full source maps
In Intra-subject, right-click on one of the normalized averages > File > View file contents.
This file has the same structure as a shared inverse kernel, with the following differences:
It contains the full time series (ImageGridAmp) instead of an inverse operator (ImagingKernel).
The Z-score process updated the field Function ('mn' => 'zscore')
Source links
- The links are not real files on the hard drive, if you select the menu "View file contents" for any of them it would display the structure of the corresponding shared kernel.
They are saved in the database as strings with a specific structure: "link|kernel_file|data_file". This string associates a shared inverse operator with some recordings. The two files have to be available to load the this file. All the functions in Brainstorm are equipped to reconstruct the full source matrix dynamically.
Filename tags
_KERNEL_: Indicates that the file contains only an inverse kernel, it needs to be associated with recordings to be opened.
Useful functions
in_bst_results(ResultsFile, LoadFull, FieldsList): Load a source file and optionally reconstruct the full source time series on the fly (ImagingKernel * recordings).
in_bst(FileName, TimeBounds, LoadFull): Load any Brainstorm data file with the possibility to load only a specific part of the file.
bst_process('LoadInputFile', FileName, Target, TimeWindow, OPTIONS): The most high-level function for reading data files, can compute scout values on the fly.
Additional documentation [TODO]
Articles [TODO]
Dale AM, Liu AK, Fischl BR, Buckner RL, Belliveau JW, Lewine JD, Halgren E
Dynamic statistical parametric mapping: combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron 2000 Apr, 26(1):55-67Pascual-Marqui RD, Standardized low-resolution brain electromagnetic tomography (sLORETA): technical details, Methods Find Exp Clin Pharmacol 2002, 24 Suppl D:5-12
- Baillet, Mosher, Leahy, Electromagnetic Brain Imaging, IEEE SP MAG, 2001.
Tutorials
Tutorial: Volume source estimation
Tutorial: Deep cerebral structures
Tutorial: Computing and displaying dipoles
Tutorial: Dipole fitting with FieldTrip
Tutorial: Maximum Entropy on the Mean (MEM)
Forum discussions
Forum: Minimum norm units (pA.m): http://neuroimage.usc.edu/forums/showthread.php?1246
Forum: Imaging resolution kernels: http://neuroimage.usc.edu/forums/showthread.php?1298
Forum: Spatial smoothing: http://neuroimage.usc.edu/forums/showthread.php?1409
Forum: Units for dSPM/sLORETA: http://neuroimage.usc.edu/forums/showthread.php?1535
Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718
Forum: Sign of the MNE values: http://neuroimage.usc.edu/forums/showthread.php?1649
Forum: Combine mag+gradiometers: http://neuroimage.usc.edu/forums/showthread.php?1900
Forum: Residual ocular artifacts: http://neuroimage.usc.edu/forums/showthread.php?1272
Forum: Dipole fitting: http://neuroimage.usc.edu/forums/showthread.php?2400
Forum: Simulate recordings from sources: http://neuroimage.usc.edu/forums/showthread.php?2563