|
Size: 16106
Comment:
|
Size: 23440
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| = Tutorial 20: Head model = ''Authors: Francois Tadel, John C Mosher, Richard Leahy, Sylvain Baillet'' |
= Tutorial 20: Head modeling = ''Authors: Francois Tadel, Elizabeth Bock, John C Mosher, Richard Leahy, Sylvain Baillet'' |
| Line 4: | Line 4: |
| The following tutorials describe how the brain activity can be estimated from the MEG/EEG recordings we have processed until now. This process consists in solving two separate problems: the modeling of the electromagnetic properties of the head ('''head model''' or '''forward model''') and the inversion of this model. This tutorial will explain how to compute a head model for the subject of our auditory oddball experiment. Its scope is limited to linear distributed source models (there is no dipole fitting available in the software). | The following tutorials describe how cerebral currents can be estimated from the MEG/EEG recordings we have processed so far. To achieve this, we need to consider two distinct modeling problems: the modeling of the electromagnetic properties of the head and of the sensor array (a.k.a. '''head model''' or '''forward model'''), and the estimation of the brain sources which produced the data, according to the head model in question. That second step is known as '''source modeling''' or solving an '''inverse problem'''. It requires that forward modeling of head tissues and sensor characteristics is completed first. This tutorial explains how to compute a head model for the participant to the auditory oddball experiment.'' '' |
| Line 6: | Line 6: |
| <<TableOfContents(2,2)>> | <<TableOfContents(2,2)>> '' '' |
| Line 8: | Line 8: |
| <<TAG(Advanced)>> | <<TAG(Advanced)>> '' '' |
| Line 10: | Line 10: |
| == Why estimating sources? == Reconstructing the activity of the brain from MEG or EEG recordings can be a difficult and long process. We tried to make it as automatic as possible, but you have to understand its advantages and issues before deciding if it can bring anything to your study. |
== Why estimate sources? == Reconstructing the activity of the brain from MEG or EEG recordings involves several sophisticated steps. Although Brainstorm simplifies the procedures, it is important to decide whether source modeling is essential to answer the neuroscience question which brought you to collect data in the first place. '' '' |
| Line 13: | Line 13: |
| The primary objective is to '''localize''' the regions of the brain that generated our signals of interest. From the sensor topographies in MEG and EEG, we can have a general idea of where the signal generators are located, but we cannot be more precise than identifying the hemisphere and the lobe. Using source estimation methods, we can expect to get a spatial resolution in the range of the centimeter, or even a few milimeters in the good cases. | If one of your primary objectives is to '''identify and map''' the regions of the brain involved in a specific stimulus response or behavior, source estimation can help address this aspect. Empirical interpretations of sensor topographies can inform where brain generators might be located: which hemisphere, what broad aspect of the anatomy (e.g., right vs. left hemisphere, frontal vs. posterior regions). Source estimation improves anatomical resolution further from the interpretation of sensor patterns. The spatial resolution of MEG and EEG depends on source depth, the principal orientation of the neural current flow, and overall SNR: still, a sub-centimeter localization accuracy can be expected in ideal conditions, especially when contrasting source maps between conditions in the same participant. As for other imaging modalities, spatial resolution of group-level effects (i.e. after averaging across multiple participants) is limited by the accuracy of anatomical registration of individual brain structures, which are very variable between participants, and intersubject variations in functional specialization with respect to cortical anatomy. |
| Line 15: | Line 15: |
| While localizing the signals, we can also expect some form of '''deconvolution''' of our signals. In EEG, the scalp topographies are very smooth and it is common to have different effects that are superimposed in the signals recorded by most of the electrodes. Moving to the source space may help separating the sources and obtain cleaner and unmixed signals. | Source mapping is a form of '''spatial''' '''deconvolution''' of sensor data. In EEG in particular, scalp topographies are very smooth and it is common that contributions from distant brain regions overlap over large clusters of electrodes. Moving to the source space can help discriminating between contributing brain regions. '' '' |
| Line 17: | Line 17: |
| Specifically for '''MEG''', working in source space solves many of the problems associated with this modality. The subject's head is not fixed in an MEG system, so it has a great chance of moving during the experiment. Also, the position of the sensors do not adapt to the shape and size of the head. Therefore between two acqusition runs, or between subjects with different morphologies, there is a high chance that '''the same MEG sensor records different parts of the brain'''. This problem does not exist in EEG, where the electrodes are in standard positions and follow the subject in all the movements. | In '''MEG''', source maps can be a great asset to alleviate some issues that are specific to the modality. Indeed in MEG and contrarily to EEG, the head of the participant is not fixed with respect to sensor locations. Hence data sensor topographies depend on the position of the subject's head inside the MEG sensor array. Therefore, between two runs of acquisition, or between subjects with different head shapes and sizes and positions under the helmet, '''the same''' '''MEG sensors may pick up signals from different parts of the brain'''. This problem does not exist in EEG, where electrodes are attached to the head and arranged according to standard positions. '' '' |
| Line 19: | Line 19: |
| Another point that makes '''MEG signals difficult to review''' is the variability in the sensors. Every manufacturer uses different types of sensors, that are sensitive to different orientations and distances, and that produce signals with different shapes. Again, this is not a problem in EEG: the only variabiliy you can get between two EEG systems is the level of noise and the ease of use of the cap, the signals will look very similar. Projecting all the data on the individual brains addresses these last two issues. | Another important point to consider when interpreting MEG sensor maps and that can be solved by working in the MEG source space instead, is that MEG manufacturers use different types of sensor technology (e.g., magnetometers vs. gradiometers; axial vs. tangential gradiometers, etc. yielding different physical measures). This is not an issue with EEG, with essentially one sensor type (electrodes, dry or active, all measuring Volts). |
| Line 21: | Line 21: |
| However, if your interest is only in the latency of an event, in detecting the lateralization of a known effect or in training blindly a classifier, you might not be interested in those complicated models that multiply by 50 the size of your files. Go for fancy methods only when you think they can bring some added value to your analysis, not because everybody around uses them. | Nevertheless, if your neuroscience question can be solved by measuring signal latencies over broad regions, or other aspects which do not depend crucially on anatomical localization (such as global signal properties integrated over all or clusters of sensors), source modeling is not required. To sort out this question will influence the time and computational resources required for data analysis (source analysis multiplies the needs in terms of disk storage, RAM and CPU performance). |
| Line 23: | Line 23: |
| <<TAG(Advanced)>> | <<TAG(Advanced)>> '' '' |
| Line 25: | Line 25: |
| == The origins of the MEG/EEG signals == To understand how we are reconstructing the sources, it is interesting to have an idea of the physiological origins of MEG and EEG signals. The models we use are based on some physiological assumptions that are not always valid, understanding them may help you selecting the appropriate method. |
== The origins of MEG/EEG signals == To better understand how forward and inverse modeling work, we need to have a basic understanding of the physiological origins of MEG/EEG signals. Note that, as always with modeling, we need to deal with various degrees of approximation. '' '' |
| Line 28: | Line 28: |
| It is assumed that most of the currents we record are related with the postsynaptic activity of the pyramidal neurons in the cerebral cortex. Those cells are '''aligned spatially''' and '''perpendicular to the cortex surface'''. Millions of post-synaptic potentials in the apical dendrites of neighbouring pyramidal neurons sum up in time and space to form what we can approximate at a macroscopic level with a few electric dipoles (green arrows below). | Overall, it is assumed that most of - but not exclusively - the MEG/EEG signals are generated by postsynaptic activity of ensembles of cortical pyramidal neurons of the cerebral cortex. The reason is essentially in the morphology and mass effect of these cells, which present '''elongated shapes, '''and are''' grouped in large assemblies of cells ''''''oriented''' '''in a similar manner approximately normal to the cortex'''. Mass effects of close-to-simultaneous changes in post-synaptic potentials across the cell group add up in time and space. These effects can conveniently be modeled at a mesoscopic spatial scale with electric dipoles distributed along the cortical mantle (green arrows in figure below). Note that there is growing evidence that MEG and EEG are '''also sensitive to deeper, cortical and subcortical structures''', including brain nuclei and the cerebellum. Brainstorm features advanced models of these structures, as an option to your analysis. The emphasis in this tutorial is on cortical source models, for simplicity. |
| Line 30: | Line 30: |
| The primary and volume currents generated by these dipoles create a potential distribution and a magnetic field at the surface of the head. We can record them with bipolar montages of electrodes placed on the skin (EEG) or very sensitive superconducting detectors (SQUIDs/MEG). | The primary and volume currents generated by current dipoles create differences in electrical potentials and magnetic fields that can be detected outside the head. They can be measured with electrodes placed on the skin (EEG, with respect to a reference) or very sensitive magnetic detectors (MEG). '' '' |
| Line 32: | Line 32: |
| . {{attachment:origins.gif||height="342",width="538"}} . <<HTML(<div align="right"><FONT size="-1" color="#CCCCCC"><I>Matti Hamalainen, 2007</I></FONT></div>)>> |
. {{attachment:origins.gif||width="538",height="342"}} '' '' . <<HTML(<div align="right"><FONT size="-1" color="#CCCCCC"><I>Matti Hamalainen, 2007</I></FONT></div>)>> '' '' |
| Line 35: | Line 35: |
| <<TAG(Advanced)>> | <<TAG(Advanced)>> '' '' |
| Line 37: | Line 37: |
| == Source space == The source estimation process consists in estimating the position and activity of a set of electric dipoles, to approximate the activity of the brain that produced the MEG/EEG data we recorded. Two families of solutions were explored in the past decades: the '''dipole fitting methods''' (we estimate the position and amplitude of a very limited number of dipoles over short time windows) and the '''distributed methods''' (we define a priori a dense grid of dipoles and then estimate their activity from the recordings). |
== Source models == ==== Dipole fitting vs distributed models ==== MEG/EEG source estimation consists in modeling brain activity with current dipoles. A current dipole is a convenient model equivalent to the net post-synaptic electrophysiological activity of local assemblies of neurons. Two main approaches have been explored for source MEG/EEG estimation: '''dipole fitting methods''' - where the position and amplitude of one to a few equivalent current dipoles (ECD) are estimated over relatively short time windows - and '''distributed models''' - where the location (and typically, the orientation) of a large number dipoles is fixed; the dipoles sample a spatial grid covering the entire brain volume or the cortical surface - requiring estimation of the amplitude of a vast number of dipoles in a fixed grid at each time point. '' '' |
| Line 40: | Line 41: |
| The single dipole fitting approaches are very efficient in specific cases were we know in advance the number or regions involved and their latencies of activity. But they are difficult to generalize and automate, and not adapted for group analysis. With Brainstorm, we decided to work only with source distributed models, which require less manual tuning for getting acceptable results. | Equivalent dipole fitting approaches are quite straightforward and can be adequate when the number of brain regions expected to be active is small (ideally only one). Therefore, it is most adequate for responses at early post-stimulus latencies. They cannot generalize to capture complex dynamics over extended period of time (epochs) and the associated estimation techniques are quite sensitive to initial conditions (how many dipoles to fit? where does the search start? etc). Our strategy in Brainstorm is to promote distributed source models, which are less user dependent, can generalize to all experimental conditions, and yield time-resolved image volumes that can be processed in many different, powerful ways (group statistics, spatial segmentation, use of regions of interest, correspondence with fMRI, etc.) |
| Line 42: | Line 43: |
| Our first step of modeling is then to define the '''position and orientation of the dipoles''' for which we want to estimate the activity. This set of dipoles is our referred to as our '''source space'''. By default, we limit our analysis to the '''cortex envelope''', based on this observation that most of the MEG/EEG signals is related with the synchroneous activity of assemblies or cortical pyramidal cells. The simple solution we recommend is to use directly the vertices of the cortical surface we imported in the first tutorials (the nodes we can see in the grey mesh in the left image below). | ==== Source constraints ==== When opting for distributed source models, the '''positions and orientations of the elementary dipoles''' that will define the "voxel" grid of the source images produced need to be defined. This set of dipoles is called the '''source space'''. By default, Brainstorm constrains the source space to the '''cortex''', where signal-to-noise and sensitivity is maximum in MEG/EEG. Note however that more complete models that include subcortical structures and the cerebellum are available in Brainstorm. Therefore, one decision you need to make before proceeding with source imaging is whether more complete source spaces are required to answer your neuroscience question. |
| Line 44: | Line 46: |
| In order to represent all the possible dipole orientations, we define '''three dipoles for each vertex''' of the cortex surface, corresponding to three orthogonal directions (X,Y,Z). When importing the anatomy of the subject, we downsampled the cortex surface to '''15,000 vertices'''. This will correspond to a source space of '''45,000 dipoles'''. We will compute a forward model that connects the activity of these 45,000 dipoles with the 275 MEG sensors we have in this dataset. | For this tutorial, we use the simple approach where current dipoles are automatically assigned to each of the vertices of the cortical surface (see the nodes in the grey mesh in the leftmost image below). When importing the anatomy of the subject, we downsampled the cortex surface to '''15,000 vertices'''. |
| Line 46: | Line 48: |
| This default number of 15,000 vertices is empirical. Over the years, our experience seemed to show that it represents a good balance between the representation of the brain circumvolutions, the surface sampling and the amount of data that is generated. Using less vertices makes it difficult to preserve the shape of the brain, using more vertices produces more data without adding to the spatial resolution of the method and may lead to memory issues. | This default number of 15,000 vertices is empirical. In our experience, this balances the adequate geometrical sampling of cortical folds with the volume of data to be analyzed. To use a smaller number of vertices (sources) oversimplifies the shape of the brain; to use more vertices yields considerably larger data volumes, without necessarily adding to spatial resolution, and may lead to practical hurdles (CPU and memory issues.) |
| Line 48: | Line 50: |
| Additionally, we can impose '''constraints of orientation''' on the dipoles, to match the physiological observation that the pyramidal cells are mostly organized perpendicularly to the cortex surface. This has the advantage of limiting the number of dipoles to 15,000 (one per vertex) and making the results much easier to display and process. However, this constraint is most of the time too strong and distorts the reconstruction. This orientation constraint is an option of the inverse model and will be discussed in the following introduction tutorials. | ==== Orientation constraints ==== After defining the locations of the dipoles, we also need to define their '''orientations'''. Brainstorm features two main options: unconstrained dipole orientations or orientations constrained perpendicularly with respect to the cortical surface. |
| Line 50: | Line 53: |
| The spatial constraint of imposing all the dipoles to be on the cortical surface might also be too restrictive in some cases, because our model is then not able to represent correctly the activity in deeper brain structures or in the cerebellum. Therefore we also offer an option to use the entire brain volume as our space space (the green dots below represent dipoles locations in volume model). This produces results that can be better or worse depending on the data, but in all the cases much more difficult to review. Volume and mixed head volumes are discussed in the advanced tutorials about source modeling. | In the '''unconstrained '''case, '''three orthogonal dipoles '''are assigned to each vertex of the cortex surface. This triplet can account mathematically for local currents flowing in arbitrary directions. The total number of elementary sources used in that case amounts to '''45,000 dipoles''' (3 orientations x 15,000 vertices). |
| Line 52: | Line 55: |
| . {{attachment:source_space.gif||height="200",width="243"}} {{attachment:source_volume.gif||height="200",width="255"}} | In the '''constrained''' case, '''one dipole''' is assigned to each vertex with its orientation perpendicular to the cortical''' '''surface. The benefit to this option is that it restricts the number of dipoles used to '''15,000''' (one per vertex). Results are also easier to process and visualize. However, there are some instances where such constraint is exaggerated and may bias source estimation, for instance when the individual anatomy is not available for the participant. |
| Line 54: | Line 57: |
| <<TAG(Advanced)>> | In the Brainstorm workflow, this orientation constraint is offered as an option of the inverse model and will be discussed in the following tutorial sections. In the present tutorial, we compute the forward model corresponding to a grid of 15,000 cortical sources without orientation constraints (hence a total of 45,000 dipoles). Note that the orientation constraint can be applied subsequently in the workflow: We do not have to take such hard decision (constrained vs. unconstrained source orientation) at this stage. '' '' |
| Line 56: | Line 59: |
| == Forward problem == The first step of the source reconstruction consists in computing a model that explains how the electric currents or the magnetic fields flow from the electric generators in the brain (source space) through the different tissues of the head (mostly brain, CSF, skull and skin), to finally reach the sensors. |
==== Whole-brain model ==== The constraint of restricting source locations to the cortical surface can be seen as too restrictive in some cases, especially if subcortical areas and cerebellum are regions of interest to the study. Brainstorm features the possibility to use the '''entire brain volume''' as source space (see green dots below: they represent dipole locations sampling the entire brain volume). One minor drawback of such model is that the results produced are impractical to review. We encourage users interested in more sophisticated approaches to add non-cortical structures to their MEG/EEG model to consult the sections concerning Volume and Mixed Head Volumes in the advanced tutorials about source modeling. '' '' |
| Line 59: | Line 62: |
| * The question of building a model that connects the values we observe outside of the head (MEG/EEG) to the electric activity of the cortical dipoles in the brain is called '''forward problem'''. * The model we obtain after solving this problem is called '''head model''' in Brainstorm, but can also be referred to as '''forward model''', '''leadfield matrix''' or '''gain matrix'''. * In this tutorial we will use the default source space: the low-resolution cortex surface with 15,000 vertices, as the support of 45,000 dipoles. We will use indifferently the terms '''dipole''' and '''source'''. * What we expect to get at the end of this process is a matrix '''[Nsensors x Nsources]'''. |
. {{attachment:source_space.gif||width="243",height="200"}} {{attachment:source_volume.gif||width="255",height="200"}} '' '' |
| Line 64: | Line 64: |
| Available methods for MEG forward modeling: | <<TAG(Advanced)>> '' '' |
| Line 66: | Line 66: |
| * '''Single sphere''': The head is considered to be a homogeneous sphere. * '''Overlapping spheres''': Refining the previous model by fitting one local sphere for each sensor. * '''OpenMEEG BEM''': Symmetric Boundary Element Method from the open-source software OpenMEEG. Described in an advanced tutorial: [[Tutorials/TutBem|BEM head model]]. <<BR>><<BR>> {{attachment:forward_inverse.gif}} |
== Forward model == We now need to obtain a model that explains how neural electric currents (the source space) produce magnetic fields and differences in electrical potentials at external sensors (the sensor space), given the different head tissues (essentially white and grey matter, cerebrospinal fluid (CSF), skull bone and skin). '' '' |
| Line 70: | Line 69: |
| == Single sphere model == Select the ''TutorialCTF ''protocol, close all the figures, and follow these steps: |
* The process of modeling how data values can be obtained outside of the head with MEG/EEG from electrical current dipoles in the brain is called forward modeling or solving a '''forward problem'''. '' '' * In Brainstorm, we call the outcome of this modeling step a "'''head model'''", a.k.a. '''forward model''', '''leadfield matrix''' or '''gain matrix '''in the MEG/EEG literature. '' '' * In this tutorial we will use the default source space: a lower-resolution cortical surface representation, with 15,000 vertices, serving as location support to 45,000 dipoles (see above: models with unconstrained orientation). Note that we use the terms '''dipole''' and '''source '''interchangeably. '' '' * We will obtain a matrix '''[Nsensors x Nsources] '''that relates the activity of the 45,000 sources to the sensor data collected during the experiment. <<BR>><<BR>> {{attachment:forward_inverse.gif}} '' '' |
| Line 73: | Line 74: |
| 1. Right-click on the ''Right'' condition and select ''Compute head model''. The ''Head modeler'' window will appear.<<BR>><<BR>> {{attachment:popupHeadModel.gif}} --- {{attachment:headModeler.gif}} 1. Set the options for your head model: * Source space: '''Cortex surface'''. <<BR>>The MRI volume option will be introduced in an advanced tutorial: [[Tutorials/TutVolSource|Volume source estimation]]. * Forward modeling method: '''Single sphere'''. * You can also edit the '''Comment '''field of the file that will be created (the string that will be representing the head model in the database explorer). * Click on ''Run''. |
==== Available methods for MEG forward modeling ==== * '''Single sphere''': The head geometry is simplified as a single sphere, with homogeneous electromagnetic properties. '' '' * '''Overlapping spheres''': Refines the previous model by fitting one local sphere under each sensor. '' '' * '''OpenMEEG BEM''': Symmetric Boundary Element Method from the open-source software OpenMEEG. Described in an advanced tutorial: [[Tutorials/TutBem|BEM head model]]. '' '' * '''DUNEuro FEM''': Finite Element Method from the open-source software DUNEuro. Described in an advanced tutorial: [[https://neuroimage.usc.edu/brainstorm/Tutorials/Duneuro|FEM head model]] |
| Line 80: | Line 80: |
| 1. Two other windows appear, to help you define the sphere. Estimating the best fitting sphere for a head is not always as easy as it looks like, because a human head is usually not spherical. <<BR>><<BR>> <<BR>><<BR>> * Read and follow the instructions in the help window. * Click on the ''Scalp ''button, move and resize the sphere manually, just to see how it works. * Click again on ''Scalp'': here we will use directly the estimation of the sphere based on the vertices of the ''Scalp ''surface (a simple least-squares fitting using all the vertices of the surface). * For EEG 3-shell spheres models, you just estimate and manipulate the largest sphere (scalp), and then use the ''Edit properties...'' button in the toolbar to define the relative radii of the 2 other spheres, and their respective conductivities. This will be described in another tutorial. * Click on ''Ok'', and wait for a few seconds. |
==== Models recommended for each modality ==== * '''MEG''': Overlapping spheres.<<BR>>Magnetic fields are less sensitive to heterogeneity of tissue in the brain, skull and scalp than are the scalp potentials measured in EEG. We have found that this locally fittedspheres approach (one per sensor) achieves reasonable accuracy relative to more complex BEM-based methods: [Leahy 1998], [Huang 1999]. '' '' * '''EEG''': OpenMEEG BEM.<<BR>>Since EEG measures differential electric potentials on the scalp surface it depends on the effects of volume conduction (or secondary currents) to produce the signals we measure. As a result EEG is very sensitive to variations in conductivity not only in the tissue near the brain's current sources but also with the skull and scalp. Some tissues are very conductive (brain, CSF, skin), some are less (skull). A realistic head model is advised for integrating their properties correctly. When computing a BEM model is not an option, for instance if OpenMEEG crashes for unknown reasons, then Berg's three-layer sphere can be an acceptable option. '' '' |
| Line 87: | Line 84: |
| 1. A new file appeared just below the channel file, it represents the head model.<<BR>><<BR>> {{attachment:headModelPopup.gif}} * There is not much you can do with this file, as it is only a matrix that converts the cortical sources into MEG/EEG recordings, and we do not have any sources information yet. * You may just check the sphere(s) that were used to compute the head model. |
* '''sEEG/ECoG''': The OpenMEEG BEM option is the only model available for this data modality. '' '' |
| Line 91: | Line 86: |
| == Overlapping spheres model == Let's compute a more advanced forward model. The overlapping spheres method is based on the estimation of a different sphere for each sensor. Instead of using only one sphere for the whole head, it estimates a sphere that fits locally the shape of the head in the surroundings of each sensor. |
== Computation == The forward models depend on the anatomy of the subject and characteristics of EEG/MEG sensors: the related contextual menus are accessible by right-clicking over channel files in the Brainstorm data tree. '' '' |
| Line 94: | Line 89: |
| 1. Right-click on ''Right'' condition and select ''Compute head model'' again. 1. Select the ''Overlapping spheres'' method and click on ''Run''. 1. This algorithm is supposed to use the inner skull surface from the subject, but we usually do not have this information. In this case, a pseudo-innerskull is reconstructed using a dilated version of the cortex envelope. 1. Right-click on the new head model > ''Check spheres''. This window shows the spheres that were estimated. You can check them by following the indications written in green at the bottom of the window: use left/right arrows. At each step, the current sensor marker is displayed in red, and the sphere you see is its local estimation of the head shape. 1. Close this window when you reviewed them all.<<BR>><<BR>> {{attachment:osTree.gif}} {{attachment:checkSpheres.gif}} 1. Compute a head model for the Left condition (Overlapping spheres). |
* In the imported '''Run#01''', right-click on the channel file or the folder > '''Compute head model'''. <<BR>>Keep the default options selected: Source space='''Cortex''', Forward model='''Overlapping spheres'''.<<BR>><<BR>> {{attachment:compute_popup.gif||width="254",height="161"}} {{attachment:compute_options.gif||width="211",height="247"}} '' '' * A new file will then appear in the database. Headmodel files are saved in the same folder as the channel file's.<<BR>>This file is required for EEG/MEG source estimation: This next step will be described in details in the following tutorial sections. '' '' * Right-click on the head model file > ''Check spheres''. This window shows the spheres that were estimated to compute the head model. You can visualize and verify their location by following the indications written in green at the bottom of the window: use left/right arrows. At each step, the current sensor marker is displayed in red, and the sphere shown is the local estimation of the shape of the inner skull immediately below the sensor. <<BR>><<BR>> {{attachment:headmodel_popup.gif}} {{attachment:headmodel_spheres.gif||width="272",height="181"}} '' '' * Although in principle, the overlapping-sphere method requires the inner skull surface, this data is not always available for every participant. If not available, a pseudo-innerskull surface is estimated by Brainstorm using a dilated version of the cortex envelope. '' '' |
| Line 101: | Line 94: |
| == Selection of a head model == We now have two head models in for our ''Subject01 / Right'' condition. |
Repeat the same operation for the other file. We now have two different acquisition runs with two different relative positions of the head and of the sensors. We now need to compute two different head models (one per head/sensor location set). '' '' |
| Line 104: | Line 96: |
| * You can have several head models computed for the same dataset, but it is not recommended as it might be difficult afterwards to know which one was used to compute the sources. * If you want to keep them anyway, you have to indicate which one is the default one. You do that by double-clicking on one of them (or right-click > set as default head model), and it is supposed to turn green. The head model displayed in green is the one that will be used for the following computation steps. * For MEG, when it works properly, the overlapping spheres model usually gives better results than the single sphere one. In this particular case, it produces more focal results, so we are going to use it for the next steps. * For EEG, always prefer the "OpenMEEG BEM" model. * Now to make things clearer: delete the'' Single sphere'' head model, and keep the ''Overlapping spheres''. |
* In the imported '''Run#02''', right-click on the channel file > '''Compute head model'''. <<BR>><<BR>> {{attachment:run02_popup.gif||width="265",height="220"}} {{attachment:run02_files.gif||width="193",height="220"}} '' '' |
| Line 110: | Line 98: |
| == Batching head model computation == You can run in two clicks the computation of the overlapping spheres model for all the conditions or subjects you want in the database. |
<<TAG(Advanced)>> '' '' |
| Line 113: | Line 100: |
| * The ''Compute head model'' menu is available in popup menus in the tree at all the levels (protocol, subject, condition). It is then applied recursively to all the subjects and conditions contained in the node(s) you selected. * Example: If you want to compute it on all the subjects and all the conditions, select the ''Compute head model'' menu from the protocol node ''TutorialCtf''. For all the conditions of ''Subject01'', run it from the ''Subject01 ''popup menu. Etc. * If you only want to compute it on some subjects of the protocol, select them at once holding the ''Ctrl ''key, right-click on one, and select the ''Compute head model ''menu''.'' * To process all the subjects for one condition, switch to the ''Functional data (sorted by conditions)'' view of the database. |
== Database explorer == This section contains additional considerations about the management of the head model files. '' '' * If '''multiple head models '''were computed in the same folder (e.g., after experimenting different forward models), one will be displayed in green and the others in black. The model in green is selected as the default head model: it will be used for all the following computation steps (e.g., source estimation). To change the default to another available head model, double-click on another head model file (or right-click over that file > Set as default head model). '' '' * You can use the database explorer for '''batching the computation''' of head models (across runs, subjects, etc.). The "Compute head model" item is available in contextual menus at multiple instances and all levels of the database explorer. The same forward model type is obtained recursively, visiting all the folders contained in the selected node(s) of the database explorer. '' '' <<TAG(Advanced)>> '' '' |
| Line 119: | Line 110: |
| how to get the constrained leadfield | Right-click on any head model entry > File > View file contents: '' '' . {{attachment:headmodel_contents.gif||width="486",height="440"}} '' '' ==== Structure of the head model files: headmodel_*.mat ==== * '''MEGMethod''': Type of forward model used for MEG sensors ('os_meg', 'meg_sphere', 'openmeeg' or empty). '' '' * '''EEGMethod''':''' '''Type of forward model used for EEG sensors ('eeg_3sphereberg', 'openmeeg' or empty). * '''ECOGMethod: '''Type of forward model used for ECoG sensors ('openmeeg' or empty). * '''SEEGMethod: '''Type of forward model used for sEEG sensors ('openmeeg' or empty). * '''Gain''': Leadfield matrix, [Nsensors x Nsources] (in practice, equivalent to [Nsensors x 3*Nvertices]). * '''Comment''': String displayed in the database explorer to represent this file. '' '' * '''HeadModelType''': Type of source space used for this head model ('surface', 'volume', 'mixed'). '' '' * '''GridLoc''': [Nvertices x 3], (x,y,z) positions of the grid of source points. In the case of a surface head model, it corresponds to a copy of the 'Vertices' matrix from the cortex surface file. '' '' * '''GridOrient''': [Nvertices x 3], directions of the normal to the surface for each vertex point (copy of the 'VertNormals' matrix of the cortex surface). Empty in the case of a volume head model. '' '' * '''GridAtlas''': In the case of mixed head models, contains a copy of the "Source model options" atlas structure that was used for creating the model. '' '' * '''SurfaceFile''': Relative path to the cortex surface file related with this head model. '' '' * '''Param''': In case of a surface head model, it contains a description of the sphere that was estimated for each sensor (Center/Radius).<<BR>> '' '' * '''History''': Date and brief description of the method used for computing the head model. '''Gain matrix''' '' '' The Gain matrix is the most important piece of information in the structure. It stores the leadfields for 3 orthogonal orientations (x,y,z) at each grid point (p1, p2, etc). The information relative to each pair sensor <-> grid source point is stored as successive columns of the matrix are ordered as: ['''p1'''_x, '''p1'''_y, '''p1'''_z, p2_x, p2_y, p2_z ...]. For the tutorial introduction dataset, with 15002 sources, the gain matrix has 45006 columns. To convert this unconstrained leadfield matrix to that of an '''orientation-constrained model''', where the orientation of each dipole is fixed and normal to the cortex surface: '' '' * Export the head model file to the HeadModel structure: Right-click > File > '''Export to Matlab'''. '' '' * At the Matlab prompt:<<BR>> > Gain_constrained = '''bst_gain_orient'''(HeadModel.Gain, HeadModel.GridOrient); '' '' * The dimension of the output matrix is three times smaller (now only one source orientation at each location): [Nsensors x Nvertices] '' '' ==== Useful functions ==== * '''in_bst_headmodel'''(HeadModelFile, ApplyOrient, FieldsList): Read contents of the head model file. * '''bst_gain_orient'''(Gain, GridOrient): Apply orientation constraints. |
| Line 122: | Line 144: |
| * Tutorial: [[Tutorials/TutBem|BEM with OpenMEEG]] * Tutorial: [[Tutorials/TutVolSource|Volume source estimation]] * Forum: Sensor modeling: http://neuroimage.usc.edu/forums/showthread.php?1295 * Forum: Gain matrix: http://neuroimage.usc.edu/forums/showthread.php?918 * Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718 * Forum: EEG and default anatomy: http://neuroimage.usc.edu/forums/showthread.php?1774 * Forum: Mixed head models indices: http://neuroimage.usc.edu/forums/showthread.php?1878 |
==== Articles ==== * Mosher, Leahy RM, Lewis PS<<BR>>[[http://neuroimage.usc.edu/paperspdf/IEEEBME99.pdf|EEG and MEG: Forward solutions for inverse methods]]<<BR>>IEEE Trans Biomedical Eng, 46(3):245-259, Mar 1999 * Leahy RM, Mosher JC, Spencer ME, Huang MX, Lewine JD (1998)<<BR>>[[http://neuroimage.usc.edu/paperspdf/Phantom_Ver2.pdf|A study of dipole localization accuracy for MEG and EEG using a human skull phantom]]<<BR>>Electroencephalography and Clinical Neurophysiology, 107(2):159-73 * Huang MX, Mosher JC, Leahy RM (1999)<<BR>>[[http://neuroimage.usc.edu/paperspdf/PMB99.pdf|A sensor-weighted overlapping-sphere head model and exhaustive head model comparison for MEG]]<<BR>> Phys Med Biol, 44:423-440 '' '' * Gramfort A, Papadopoulo T, Olivi E, Clerc M<<BR>>[[http://www.biomedical-engineering-online.com/content/9/1/45|OpenMEEG: opensource software for quasistatic bioelectromagnetics]]<<BR>>BioMedical Engineering OnLine 45:9, 2010 |
| Line 130: | Line 150: |
| <<HTML(<!-- END-PAGE -->)>> | ==== Tutorials and forum discussions ==== * Tutorial: [[Tutorials/TutBem|BEM with OpenMEEG]] '' '' * Tutorial: [[Tutorials/TutVolSource|Volume source estimation]] '' '' * External documentation: [[http://www.canada-meg-consortium.org/EN/MegBaillet5|Electromagnetic neural source imaging]] |
| Line 132: | Line 155: |
| <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/ChannelClusters&next=Tutorials/NoiseCovariance")>> | * Forum: Sensor modeling: http://neuroimage.usc.edu/forums/showthread.php?1295 '' '' * Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718 '' '' * Forum: EEG and default anatomy: http://neuroimage.usc.edu/forums/showthread.php?1774 '' '' * Forum: Mixed head models indices: http://neuroimage.usc.edu/forums/showthread.php?1878 '' '' * Forum: Gain matrix units for EEG: http://neuroimage.usc.edu/forums/showthread.php?1837 |
| Line 134: | Line 161: |
| <<EmbedContent(http://neuroimage.usc.edu/bst/get_feedback.php?Tutorials/HeadModel)>> | <<HTML(<!-- END-PAGE -->)>> '' '' <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/ChannelClusters&next=Tutorials/NoiseCovariance")>> '' '' <<EmbedContent(http://neuroimage.usc.edu/bst/get_feedback.php?Tutorials/HeadModel)>> '' '' |
Tutorial 20: Head modeling
Authors: Francois Tadel, Elizabeth Bock, John C Mosher, Richard Leahy, Sylvain Baillet
The following tutorials describe how cerebral currents can be estimated from the MEG/EEG recordings we have processed so far. To achieve this, we need to consider two distinct modeling problems: the modeling of the electromagnetic properties of the head and of the sensor array (a.k.a. head model or forward model), and the estimation of the brain sources which produced the data, according to the head model in question. That second step is known as source modeling or solving an inverse problem. It requires that forward modeling of head tissues and sensor characteristics is completed first. This tutorial explains how to compute a head model for the participant to the auditory oddball experiment.
Contents
Why estimate sources?
Reconstructing the activity of the brain from MEG or EEG recordings involves several sophisticated steps. Although Brainstorm simplifies the procedures, it is important to decide whether source modeling is essential to answer the neuroscience question which brought you to collect data in the first place.
If one of your primary objectives is to identify and map the regions of the brain involved in a specific stimulus response or behavior, source estimation can help address this aspect. Empirical interpretations of sensor topographies can inform where brain generators might be located: which hemisphere, what broad aspect of the anatomy (e.g., right vs. left hemisphere, frontal vs. posterior regions). Source estimation improves anatomical resolution further from the interpretation of sensor patterns. The spatial resolution of MEG and EEG depends on source depth, the principal orientation of the neural current flow, and overall SNR: still, a sub-centimeter localization accuracy can be expected in ideal conditions, especially when contrasting source maps between conditions in the same participant. As for other imaging modalities, spatial resolution of group-level effects (i.e. after averaging across multiple participants) is limited by the accuracy of anatomical registration of individual brain structures, which are very variable between participants, and intersubject variations in functional specialization with respect to cortical anatomy.
Source mapping is a form of spatial deconvolution of sensor data. In EEG in particular, scalp topographies are very smooth and it is common that contributions from distant brain regions overlap over large clusters of electrodes. Moving to the source space can help discriminating between contributing brain regions.
In MEG, source maps can be a great asset to alleviate some issues that are specific to the modality. Indeed in MEG and contrarily to EEG, the head of the participant is not fixed with respect to sensor locations. Hence data sensor topographies depend on the position of the subject's head inside the MEG sensor array. Therefore, between two runs of acquisition, or between subjects with different head shapes and sizes and positions under the helmet, the same MEG sensors may pick up signals from different parts of the brain. This problem does not exist in EEG, where electrodes are attached to the head and arranged according to standard positions.
Another important point to consider when interpreting MEG sensor maps and that can be solved by working in the MEG source space instead, is that MEG manufacturers use different types of sensor technology (e.g., magnetometers vs. gradiometers; axial vs. tangential gradiometers, etc. yielding different physical measures). This is not an issue with EEG, with essentially one sensor type (electrodes, dry or active, all measuring Volts).
Nevertheless, if your neuroscience question can be solved by measuring signal latencies over broad regions, or other aspects which do not depend crucially on anatomical localization (such as global signal properties integrated over all or clusters of sensors), source modeling is not required. To sort out this question will influence the time and computational resources required for data analysis (source analysis multiplies the needs in terms of disk storage, RAM and CPU performance).
The origins of MEG/EEG signals
To better understand how forward and inverse modeling work, we need to have a basic understanding of the physiological origins of MEG/EEG signals. Note that, as always with modeling, we need to deal with various degrees of approximation.
Overall, it is assumed that most of - but not exclusively - the MEG/EEG signals are generated by postsynaptic activity of ensembles of cortical pyramidal neurons of the cerebral cortex. The reason is essentially in the morphology and mass effect of these cells, which present elongated shapes, and are grouped in large assemblies of cells oriented in a similar manner approximately normal to the cortex. Mass effects of close-to-simultaneous changes in post-synaptic potentials across the cell group add up in time and space. These effects can conveniently be modeled at a mesoscopic spatial scale with electric dipoles distributed along the cortical mantle (green arrows in figure below). Note that there is growing evidence that MEG and EEG are also sensitive to deeper, cortical and subcortical structures, including brain nuclei and the cerebellum. Brainstorm features advanced models of these structures, as an option to your analysis. The emphasis in this tutorial is on cortical source models, for simplicity.
The primary and volume currents generated by current dipoles create differences in electrical potentials and magnetic fields that can be detected outside the head. They can be measured with electrodes placed on the skin (EEG, with respect to a reference) or very sensitive magnetic detectors (MEG).
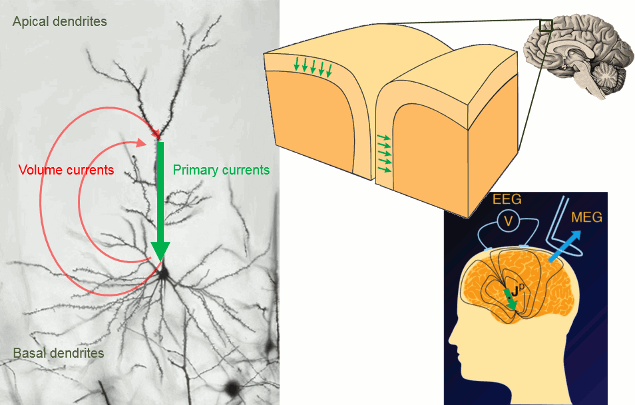
- Matti Hamalainen, 2007
Source models
Dipole fitting vs distributed models
MEG/EEG source estimation consists in modeling brain activity with current dipoles. A current dipole is a convenient model equivalent to the net post-synaptic electrophysiological activity of local assemblies of neurons. Two main approaches have been explored for source MEG/EEG estimation: dipole fitting methods - where the position and amplitude of one to a few equivalent current dipoles (ECD) are estimated over relatively short time windows - and distributed models - where the location (and typically, the orientation) of a large number dipoles is fixed; the dipoles sample a spatial grid covering the entire brain volume or the cortical surface - requiring estimation of the amplitude of a vast number of dipoles in a fixed grid at each time point.
Equivalent dipole fitting approaches are quite straightforward and can be adequate when the number of brain regions expected to be active is small (ideally only one). Therefore, it is most adequate for responses at early post-stimulus latencies. They cannot generalize to capture complex dynamics over extended period of time (epochs) and the associated estimation techniques are quite sensitive to initial conditions (how many dipoles to fit? where does the search start? etc). Our strategy in Brainstorm is to promote distributed source models, which are less user dependent, can generalize to all experimental conditions, and yield time-resolved image volumes that can be processed in many different, powerful ways (group statistics, spatial segmentation, use of regions of interest, correspondence with fMRI, etc.)
Source constraints
When opting for distributed source models, the positions and orientations of the elementary dipoles that will define the "voxel" grid of the source images produced need to be defined. This set of dipoles is called the source space. By default, Brainstorm constrains the source space to the cortex, where signal-to-noise and sensitivity is maximum in MEG/EEG. Note however that more complete models that include subcortical structures and the cerebellum are available in Brainstorm. Therefore, one decision you need to make before proceeding with source imaging is whether more complete source spaces are required to answer your neuroscience question.
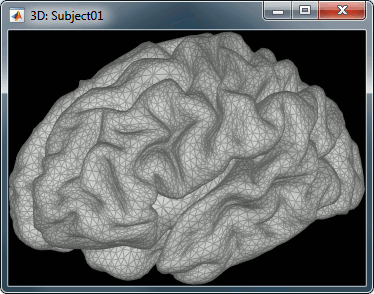
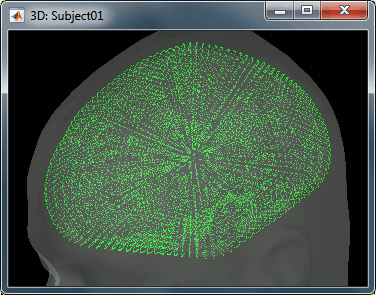
For this tutorial, we use the simple approach where current dipoles are automatically assigned to each of the vertices of the cortical surface (see the nodes in the grey mesh in the leftmost image below). When importing the anatomy of the subject, we downsampled the cortex surface to 15,000 vertices.
This default number of 15,000 vertices is empirical. In our experience, this balances the adequate geometrical sampling of cortical folds with the volume of data to be analyzed. To use a smaller number of vertices (sources) oversimplifies the shape of the brain; to use more vertices yields considerably larger data volumes, without necessarily adding to spatial resolution, and may lead to practical hurdles (CPU and memory issues.)
Orientation constraints
After defining the locations of the dipoles, we also need to define their orientations. Brainstorm features two main options: unconstrained dipole orientations or orientations constrained perpendicularly with respect to the cortical surface.
In the unconstrained case, three orthogonal dipoles are assigned to each vertex of the cortex surface. This triplet can account mathematically for local currents flowing in arbitrary directions. The total number of elementary sources used in that case amounts to 45,000 dipoles (3 orientations x 15,000 vertices).
In the constrained case, one dipole is assigned to each vertex with its orientation perpendicular to the cortical surface. The benefit to this option is that it restricts the number of dipoles used to 15,000 (one per vertex). Results are also easier to process and visualize. However, there are some instances where such constraint is exaggerated and may bias source estimation, for instance when the individual anatomy is not available for the participant.
In the Brainstorm workflow, this orientation constraint is offered as an option of the inverse model and will be discussed in the following tutorial sections. In the present tutorial, we compute the forward model corresponding to a grid of 15,000 cortical sources without orientation constraints (hence a total of 45,000 dipoles). Note that the orientation constraint can be applied subsequently in the workflow: We do not have to take such hard decision (constrained vs. unconstrained source orientation) at this stage.
Whole-brain model
The constraint of restricting source locations to the cortical surface can be seen as too restrictive in some cases, especially if subcortical areas and cerebellum are regions of interest to the study. Brainstorm features the possibility to use the entire brain volume as source space (see green dots below: they represent dipole locations sampling the entire brain volume). One minor drawback of such model is that the results produced are impractical to review. We encourage users interested in more sophisticated approaches to add non-cortical structures to their MEG/EEG model to consult the sections concerning Volume and Mixed Head Volumes in the advanced tutorials about source modeling.
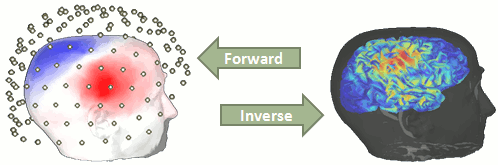
Forward model
We now need to obtain a model that explains how neural electric currents (the source space) produce magnetic fields and differences in electrical potentials at external sensors (the sensor space), given the different head tissues (essentially white and grey matter, cerebrospinal fluid (CSF), skull bone and skin).
The process of modeling how data values can be obtained outside of the head with MEG/EEG from electrical current dipoles in the brain is called forward modeling or solving a forward problem.
In Brainstorm, we call the outcome of this modeling step a "head model", a.k.a. forward model, leadfield matrix or gain matrix in the MEG/EEG literature.
In this tutorial we will use the default source space: a lower-resolution cortical surface representation, with 15,000 vertices, serving as location support to 45,000 dipoles (see above: models with unconstrained orientation). Note that we use the terms dipole and source interchangeably.
We will obtain a matrix [Nsensors x Nsources] that relates the activity of the 45,000 sources to the sensor data collected during the experiment.
Available methods for MEG forward modeling
Single sphere: The head geometry is simplified as a single sphere, with homogeneous electromagnetic properties.
Overlapping spheres: Refines the previous model by fitting one local sphere under each sensor.
OpenMEEG BEM: Symmetric Boundary Element Method from the open-source software OpenMEEG. Described in an advanced tutorial: BEM head model.
DUNEuro FEM: Finite Element Method from the open-source software DUNEuro. Described in an advanced tutorial: FEM head model
Models recommended for each modality
MEG: Overlapping spheres.
Magnetic fields are less sensitive to heterogeneity of tissue in the brain, skull and scalp than are the scalp potentials measured in EEG. We have found that this locally fittedspheres approach (one per sensor) achieves reasonable accuracy relative to more complex BEM-based methods: [Leahy 1998], [Huang 1999].EEG: OpenMEEG BEM.
Since EEG measures differential electric potentials on the scalp surface it depends on the effects of volume conduction (or secondary currents) to produce the signals we measure. As a result EEG is very sensitive to variations in conductivity not only in the tissue near the brain's current sources but also with the skull and scalp. Some tissues are very conductive (brain, CSF, skin), some are less (skull). A realistic head model is advised for integrating their properties correctly. When computing a BEM model is not an option, for instance if OpenMEEG crashes for unknown reasons, then Berg's three-layer sphere can be an acceptable option.sEEG/ECoG: The OpenMEEG BEM option is the only model available for this data modality.
Computation
The forward models depend on the anatomy of the subject and characteristics of EEG/MEG sensors: the related contextual menus are accessible by right-clicking over channel files in the Brainstorm data tree.
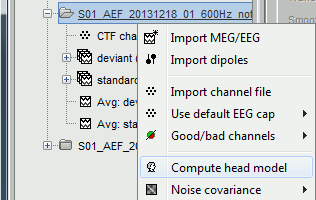
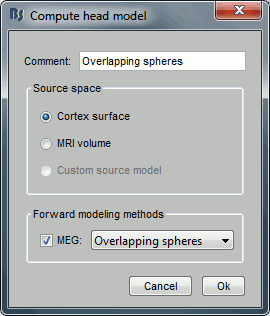
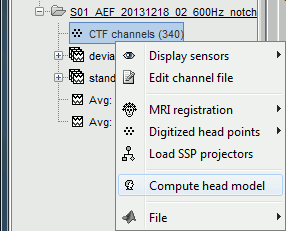
In the imported Run#01, right-click on the channel file or the folder > Compute head model.
Keep the default options selected: Source space=Cortex, Forward model=Overlapping spheres.
A new file will then appear in the database. Headmodel files are saved in the same folder as the channel file's.
This file is required for EEG/MEG source estimation: This next step will be described in details in the following tutorial sections.Right-click on the head model file > Check spheres. This window shows the spheres that were estimated to compute the head model. You can visualize and verify their location by following the indications written in green at the bottom of the window: use left/right arrows. At each step, the current sensor marker is displayed in red, and the sphere shown is the local estimation of the shape of the inner skull immediately below the sensor.
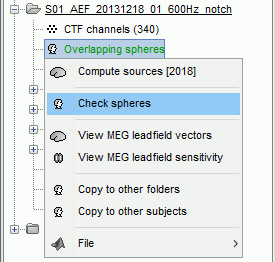
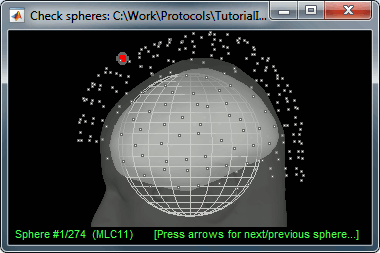
Although in principle, the overlapping-sphere method requires the inner skull surface, this data is not always available for every participant. If not available, a pseudo-innerskull surface is estimated by Brainstorm using a dilated version of the cortex envelope.
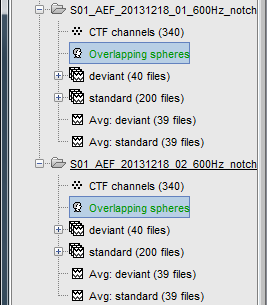
Repeat the same operation for the other file. We now have two different acquisition runs with two different relative positions of the head and of the sensors. We now need to compute two different head models (one per head/sensor location set).
In the imported Run#02, right-click on the channel file > Compute head model.
Database explorer
This section contains additional considerations about the management of the head model files.
If multiple head models were computed in the same folder (e.g., after experimenting different forward models), one will be displayed in green and the others in black. The model in green is selected as the default head model: it will be used for all the following computation steps (e.g., source estimation). To change the default to another available head model, double-click on another head model file (or right-click over that file > Set as default head model).
You can use the database explorer for batching the computation of head models (across runs, subjects, etc.). The "Compute head model" item is available in contextual menus at multiple instances and all levels of the database explorer. The same forward model type is obtained recursively, visiting all the folders contained in the selected node(s) of the database explorer.
On the hard drive
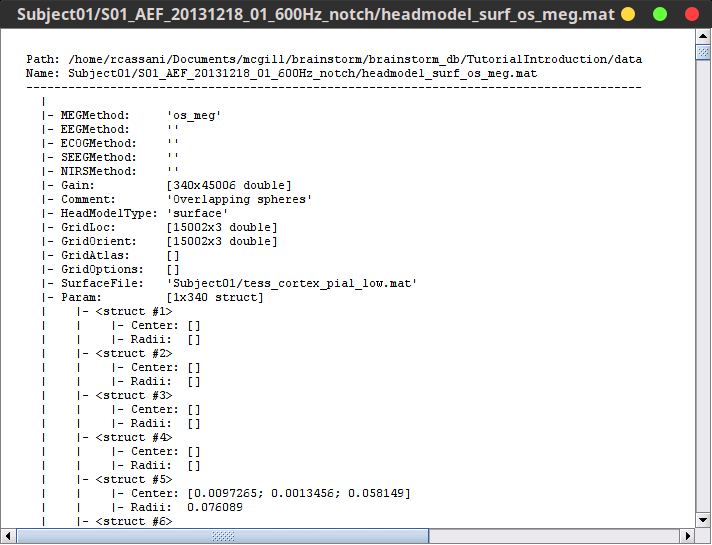
Right-click on any head model entry > File > View file contents:
Structure of the head model files: headmodel_*.mat
MEGMethod: Type of forward model used for MEG sensors ('os_meg', 'meg_sphere', 'openmeeg' or empty).
EEGMethod: Type of forward model used for EEG sensors ('eeg_3sphereberg', 'openmeeg' or empty).
ECOGMethod: Type of forward model used for ECoG sensors ('openmeeg' or empty).
SEEGMethod: Type of forward model used for sEEG sensors ('openmeeg' or empty).
Gain: Leadfield matrix, [Nsensors x Nsources] (in practice, equivalent to [Nsensors x 3*Nvertices]).
Comment: String displayed in the database explorer to represent this file.
HeadModelType: Type of source space used for this head model ('surface', 'volume', 'mixed').
GridLoc: [Nvertices x 3], (x,y,z) positions of the grid of source points. In the case of a surface head model, it corresponds to a copy of the 'Vertices' matrix from the cortex surface file.
GridOrient: [Nvertices x 3], directions of the normal to the surface for each vertex point (copy of the 'VertNormals' matrix of the cortex surface). Empty in the case of a volume head model.
GridAtlas: In the case of mixed head models, contains a copy of the "Source model options" atlas structure that was used for creating the model.
SurfaceFile: Relative path to the cortex surface file related with this head model.
Param: In case of a surface head model, it contains a description of the sphere that was estimated for each sensor (Center/Radius).
History: Date and brief description of the method used for computing the head model.
Gain matrix
The Gain matrix is the most important piece of information in the structure. It stores the leadfields for 3 orthogonal orientations (x,y,z) at each grid point (p1, p2, etc). The information relative to each pair sensor <-> grid source point is stored as successive columns of the matrix are ordered as: [p1_x, p1_y, p1_z, p2_x, p2_y, p2_z ...]. For the tutorial introduction dataset, with 15002 sources, the gain matrix has 45006 columns.
To convert this unconstrained leadfield matrix to that of an orientation-constrained model, where the orientation of each dipole is fixed and normal to the cortex surface:
Export the head model file to the HeadModel structure: Right-click > File > Export to Matlab.
At the Matlab prompt:
> Gain_constrained = bst_gain_orient(HeadModel.Gain, HeadModel.GridOrient);The dimension of the output matrix is three times smaller (now only one source orientation at each location): [Nsensors x Nvertices]
Useful functions
in_bst_headmodel(HeadModelFile, ApplyOrient, FieldsList): Read contents of the head model file.
bst_gain_orient(Gain, GridOrient): Apply orientation constraints.
Additional documentation
Articles
Mosher, Leahy RM, Lewis PS
EEG and MEG: Forward solutions for inverse methods
IEEE Trans Biomedical Eng, 46(3):245-259, Mar 1999Leahy RM, Mosher JC, Spencer ME, Huang MX, Lewine JD (1998)
A study of dipole localization accuracy for MEG and EEG using a human skull phantom
Electroencephalography and Clinical Neurophysiology, 107(2):159-73Huang MX, Mosher JC, Leahy RM (1999)
A sensor-weighted overlapping-sphere head model and exhaustive head model comparison for MEG
Phys Med Biol, 44:423-440Gramfort A, Papadopoulo T, Olivi E, Clerc M
OpenMEEG: opensource software for quasistatic bioelectromagnetics
BioMedical Engineering OnLine 45:9, 2010
Tutorials and forum discussions
Tutorial: BEM with OpenMEEG
Tutorial: Volume source estimation
External documentation: Electromagnetic neural source imaging
Forum: Sensor modeling: http://neuroimage.usc.edu/forums/showthread.php?1295
Forum: EEG reference: http://neuroimage.usc.edu/forums/showthread.php?1525#post6718
Forum: EEG and default anatomy: http://neuroimage.usc.edu/forums/showthread.php?1774
Forum: Mixed head models indices: http://neuroimage.usc.edu/forums/showthread.php?1878
Forum: Gain matrix units for EEG: http://neuroimage.usc.edu/forums/showthread.php?1837