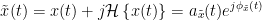|
Size: 40193
Comment:
|
← Revision 713 as of 2024-07-29 16:24:05 ⇥
Size: 55711
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 3: | Line 3: |
| = Tutorial 28: Connectivity = '''[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE] ''' ''Authors: Hossein Shahabi, Raymundo Cassani, Takfarinas Medani'' Cognitive and perceptual functions are the result of coordinated activity of functionally specialized regions in the brain. [[http://www.scholarpedia.org/article/Brain_connectivity|Brain connectivity]] investigates how these different regions (or nodes) interact as a network, with the goal of having a better understanding of how the brain processes information. Depending on which connectivity characteristic is studied, a distinction is made between '''structural''' (fiber pathways), '''functional''' (non-directed statistical dependency) and '''effective''' (causal interaction) connectivity between regions. Effective connectivity is often referred as directed functional connectivity. In this tutorial we will see how to compute different connectivity metrics for non-directed and directed functional analyses in Brainstorm, first with simulated data and later with real data. |
= Connectivity = ''Authors: Hossein Shahabi, Raymundo Cassani, Takfarinas Medani, François Tadel, Marc Lalancette, [[https://www.neurospeed-bailletlab.org/sylvain-baillet|Sylvain Baillet]]'' Brain functions (e.g., in cognition, behavior and perception) stem from the coordinated activity of multiple regions. [[http://www.scholarpedia.org/article/Brain_connectivity|Brain connectivity]] measures are designed to probe how brain regions (or nodes) interact as a network. A distinction is made between '''structural''' (fiber pathways), '''functional''' (non-directed statistical associations) and '''effective''' (causal interactions, or "directed functional connectivity") connectivity between regions. Here we explain how to compute various connectivity metrics for non-directed and directed functional connectivity analyses with Brainstorm, both with simulated (ground-truth) and empirical data. We encourage the interested reader to [[https://pubmed.ncbi.nlm.nih.gov/34906715/|learn more]] about the specific aspects of electrophysiology for studying human ''connectomics''. |
| Line 12: | Line 12: |
| == General considerations in connectivity analysis == Connectivity analyses are commonly performed by computing a bivariate connectivity metric for all the possible pairs of time series or signals. The result of such approach can be presented as a '''connectivity graph''' (left image), where each signal is represented as a node, and the value of the connectivity metric is the value of the edge between the corresponding nodes. This graph representation becomes overwhelming when too many nodes are considered, as such, the connectivity graph can be represented with its '''connectivity matrix''', aka adjacency matrix (right image). |
== Introduction == === Definitions === Connectivity analyses are commonly performed by computing a bivariate measure between pairs of regional time series of interest. The outcome (a.k.a a ''connectome'') can be represented as a '''connectivity graph''' (left panel below), with each brain region as a node (x, y, z,...), and the connectivity measures shown above each edge of the graph. The ''connectome ''can also be represented by a '''connectivity array''', a.k.a. an adjacency matrix (right panel below). |
| Line 17: | Line 18: |
| '''Sensors or sources:''' The signals used for the connectivity analysis can be derived from the '''sensor data''' (EEG/MEG signals) or from the reconstructed '''sources''' (voxels or scouts). '''Directed and non-directed:''' The direction of the interaction between signals (as statistical causation) can be measured with '''directed metrics'''. However, this is not possible with '''non-directed metrics''', as result, the connectivity metric "from Signal <<latex($$x$$)>> to Signal <<latex($$y$$)>> " is equal to the connectivity metric "from Signal <<latex($$y$$)>> to Signal <<latex($$x$$)>>". '''Recording condition:''' While connectivity analysis can be performed on resting-state (spontaneous) and event-related (trials) recordings, the appropriate connectivity method depends on the recording condition. '''Full network vs point-based connectivity:''' In full network, the connectivity metric is computed for all the possible node pairs in the network (N×N approach), and gives as result a detailed connectivity graph. Alternatively, the analysis can be performed solely between one node (aka seed) and the rest of the nodes in the network (1×N approach), this approach is faster to compute and is more useful when you are interested in the connectivity of a specific sensor or source. '''Temporal resolution:''' Connectivity analyses can be performed in two ways: static and dynamic. Time-varying networks can present the dynamics of brain networks. In contrast, the static graphs illustrate a general perspective of brain connectivity which is helpful in specific conditions. Users need to decide which type of network is more informative for their study. '''Time-frequency transformation:''' Several connectivity metrics rely on the [[Tutorials/TimeFrequency|time-frequency representation]] of the data, which is obtained with approaches such as the short time Fourier transform, Hilbert transform, and Morlet wavelet. /* {{attachment:GeneralFlowConn.png||width="700",height="230"}} */ /* {{attachment:SimSignals1.PNG||width="550",height="400"}} */ == Simulated data (MAR model) == To compare different connectivity metrics, we use simulated data with known ground truth. Consider three channels constructed using the following multivariate autoregressive (MAR) process of 4th order. {{{#!latex \begin{eqnarray*} x_1(n) & = & \sum_{k=1}^{4} A_{(1,1,k)}x_1(n-k) + e_1(n) \\ x_2(n) & = & \sum_{k=1}^{4} A_{(2,2,k)}x_2(n-k) + e_2(n) \\ x_3(n) & = & \sum_{k=1}^{4} A_{(3,3,k)}x_3(n-k) + \sum_{k=1}^{d} A_{(1,3,k)}x_1(n-k) + e_3(n)\\ \end{eqnarray*} }}} where <<latex($$A_{(i,i,:)}$$)>> with <<latex($$i = 1, 2 \textrm{ and } 3$$)>> are coefficients of 4th order all-pole filters. To compute these coefficients, we can consider a frequency response with desired pole and zero locations and use MATLAB zp2tf function for finding them. Here, these coefficients were calculated in a way that the first channel has a dominant peak in the beta band (25 Hz), the second channel shows the highest power in the alpha band (10 Hz), and the third channel a similar level of energy in both bands. Additionally, the signal in the third channel is influenced by the signal in the first channel by the filter <<latex($$A_{(1,3,:)}$$)>>. We simulate data using the ARfit process. To run that, first clear the process panel and then select simulate -> simulate AR signals (ARfit) and use the following coefficients '''box for code''' '''Screenshot''' For a MAR model, the transfer function (or frequency response) is defined as: {{{#!latex $$H_{i,j}(f) = \frac{1}{A_{i,j}(f)}$$\\ }}} {{attachment:TransferMatrix3_AR3.png||width="550"}} The diagonal elements show the auto-transfer function, which in our specific case is the spectrum of the signals. The off-diagonal terms represent the interactions between different signals. Here, we see the transfer function from channel 1 to channel 3. These transfer functions are our ground truth for connectivity values. In the next sections we will compute different connectivity metrics for these simulated signals. As such, place the simulated data in the '''''Process1''''' tab, select recordings, click on '''''[Run]''''' ( {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconRun.gif}} ) to open the [[Tutorials/PipelineEditor#Selecting_processes|Pipeline editor]], and select the connectivity metric. {{{#!wiki comment/dotted This seems beyond the goal of the tutorial: Besides the original transfer functions, we can compute the [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Directed_Transfer_Function|directed transfer function (DTF)]] and [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Partial_Directed_Coherence|partial directed coherence (PDC)]]. {{attachment:Directed transfer function_AR3.png|Directed transfer function_AR3.png|width="550",height="400"}} {{attachment:Partial Directed Coherence_AR3.png|Partial Directed Coherence_AR3.png|width="550",height="400"}} }}} |
'''Sensors or sources:''' The time series used for connectivity analyses can be from '''sensor data''' (EEG/MEG signals) or from '''source time series''' (brain voxels or scouts). '''Directed vs. non-directed:''' The direction of interactions between signals (as a measure of statistical causation) is estimated with '''directed metrics'''. '''Non-directed metrics '''produce symmetrical connectivity graphs/matrices: the connectivity measure "from Signal <<latex($$x$$)>> to Signal <<latex($$y$$)>> " is identical to the connectivity measure "from Signal <<latex($$y$$)>> to Signal <<latex($$x$$)>>". '''Experimental condition:''' Depending on the neuroscience question, connectivity analyses can be performed on resting-state or task (e.g., ongoing or trial-based) data. '''Full (NxN) vs. seeded (1xN) connectivity:''' In a '''full connectivity analysis''', the connectivity metric is computed for all the possible pairs of nodes between N time series (noted N×N here). Alternatively, '''seeded connectivity''' (noted 1×N) is measured between one time series of interest (a ''seed, ''e.g., one brain region or a behavioral marker) and N other regions/time series. '''Time-frequency transformations:''' Some connectivity metrics rely on a [[Tutorials/TimeFrequency|time-frequency representation]] of the signals. These latter are obtained with approaches such as the short-time Fourier transform, Hilbert transform, or Morlet wavelets. Just as in other areas of electrophysiology studies, connectivity analyses need to be'''guided by mechanistic hypotheses concerning the expected neurophysiological effects'''. === Sensor-level analyses === 1. '''Their anatomical interpretation is limited and ambiguous'''. 1. Sensor data is affected by '''field spread''' and '''volume conduction of brain activity '''across the scalp/sensor array. Hence, activity from one single brain area is picked up at multiple, possibly distant sensor locations. Connectivity measures may show strong interactions between sensor time series, which may be wrongly interpreted as inter-regional brain connections. === Source-level analyses === Connectivity measures between source time series are '''neuroanatomically interpretable''' and can be derived across participants. We recommended that the outcomes of sensor and source connectivity analyses are mutually compatible; see ([[https://doi.org/10.1038/s41598-018-30869-w|Lai et al., 2018]]). '''Full-brain connectomes''' Whole-brain connectivity analyses at the typical resolution of cortical surfaces in Brainstorm involve '''thousands''' of source locations, making the N×N derivations impractical. For instance, 15000 cortical vertices would yield a connectivity matrix of 15000x15000x8 bytes = 1.6 GB. If unconstrained cortical sources are used and coherence is computed across 50 frequency bins, the memory allocation increases to 45000x45000x50x8 = 754 GB per participant/condition/trial/etc. Reducing the N (via e.g., cortical parcellations, ROIs) may be required for practical reasons, depending on computing resources. '''Regions of interest''' Grouping individual brain sources into ROIs, defined on the [[http://Tutorials/Scouts|cortical surface]] or in the brain [[https://neuroimage.usc.edu/brainstorm/Tutorials/TutVolSource#Volume_scouts|volume]] helps contain the computational resources required for connectivity analyses (see above). ROIs can be defined based on neuroscience priors and the purpose of the study ([[https://doi.org/10.1002/hbm.20745|Schhoffen and Gross, 2009]]). You may consider: * '''Study priors '''from the literature in your field, specific working hypotheses in terms of neuro-anatomical brain structures expected to be involved. * '''Association with a non-neuronal signal''' (e.g., cortico-muscular coherence). * '''Signal strength''', by defining ROIs from brain regions with strongest activity in current data. * '''Whole-brain '''[[https://neuroimage.usc.edu/brainstorm/Tutorials/LabelFreeSurfer#Cortical_parcellations|cortical parcellation]] to reduce N. The tutorial [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence|Corticomuscular coherence]] explains the computation of connectivity measures '''constrained''' and '''unconstrained''' brain maps for these cases: 1. '''One signal x full-brain source maps''': [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence#Method|link]] 2. '''One signal x scouts''': [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence#Coherence:_EMG_x_Scouts|link]] 3. ROI-based connectomes, i.e., '''scouts x scouts''': [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence#Coherence_Scouts_x_Scouts|link]] {{{#!wiki note Studies have reported similarities and differences between electrophysiological connectomes (from MEG/EEG) and fMRI connectomes. See how the '''electrophysiological connectomes provide unique insights on how functional communication is implemented in the brain''' in [[https://doi.org/10.1016/j.neuroimage.2021.118788|Sadaghiani et al., 2022]]. }}} {{{#!wiki caution On whole-brain connectivity analyses and the issue of circular analysis, please see [[https://doi.org/10.1038/nn.2303|Kriegeskorte et al., 2009]]. }}} == Pre-requisites == Here we focus on the specifics on connectivity analyses with Brainstorm. Please make sure you are familiar with Brainstorm and go through all [[http://neuroimage.usc.edu/brainstorm/Tutorials#Get_started|introduction tutorials]] first, before following the present tutorial. We first use simulated, synthetic data to emphasize the theoretical aspects of each connectivity metric with respect to groundtruth outcomes. Real, empirical MEG data are featured later in the tutorial (same auditory oddball dataset as in the other tutorial sections). Let's start by creating a new protocol in the Brainstorm database: * Select the menu File > Create new protocol > type in "'''TutorialConnectivity'''" and select the options: * '''Yes''', use protocol's default anatomy, * '''No''', use one channel file per condition. * Right-click on the TutorialConnectivity folder > New subject > Subject01<<BR>><<BR>> {{attachment:protocol_connect.gif}} == Simulated data == To compare connectivity metrics, let's use synthetic time series simulated with known ground truth interactions. We will use a [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Multivariate_Autoregressive_Model|multivariate autoregressive (MVAR)]] model that consists of the following three signals: * '''Signal 1''': two oscillatory (rhythmic) components: One at 10 Hz (alpha band), and a stronger peak at 25 Hz (beta band). * '''Signal 2''': Same as Signal 1, with the strongest peak at 10 Hz. * '''Signal 3''': Same as above, with the two components (10 and 25 Hz) of same magnitude. The 25-Hz component of''' '''Signal 3 will be driven in part by the 25-Hz component of Signal 1 (denoted '''Signal 1>>Signal 3'''). Let's now generate the three time series: * In the '''Process1''' tab, leave the file list empty and click on the button '''[Run]''' * Select process: '''Simulate > Simulate AR signals'''.<<BR>><<BR>> {{attachment:sim_process.gif}} Process options: * '''Subject name''': Target subject for the simulated signals: Select '''Subject01'''. * '''Condition name''': Target folder where to store the simulated data in your database: Set to '''Simulation'''. * '''Number of time samples''' for each simulated time series: Set to '''12,000'''. * '''Sampling frequency''' (Fs): Set to '''120 Hz'''. * '''Interaction specifications:''' Spectral parameters for the signal components and their interactions in the MVAR model: '''From, To / Peak frequencies [Hz] / Peak relative magnitudes [0-1]'''<<BR>> Set to: {{{ 1, 1 / 10, 25 / 0.3, 0.5 2, 2 / 10, 25 / 0.7, 0.3 3, 3 / 10, 25 / 0.2, 0.2 1, 3 / 25 / 0.1 }}} * '''Display the groundtruth spectral metrics''' of the MVAR-generated time series: transfer function, cross-spectral power density, [[#Coherence|magnitude square coherence]], [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Directed_Transfer_Function|directed transfer function (DTF)]] and [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Partial_Directed_Coherence|partial directed coherence (PDC)]]. The '''transfer function '''(<<latex($$|H(f)|$$)>>) characterizes the relationships between signals in the frequency domain. It is a non-symmetric representation, which enables the identification of causal dependencies between signal components. The ''auto-transfer functions'' (shown in the graphs along the diagonal below) display the power spectra of each signal. The off-diagonal representations display the interactions between each pair of signals (see Signal 1 >> Signal 3 above). Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our '''ground truth for connectivity values'''.<<BR>><<BR>> {{attachment:sim_ar_spectra_metrics.png||width="100%"}} * '''Get coefficients matrix:''' Shows the coefficients related to the MVAR model. These coefficients can be used in the process '''Simulate > Simulate AR signals (ARfit)''' to simulate the same model.<<BR>><<BR>> {{attachment:sim_coef.gif}} Execution: * Click '''Run''' to generate the time series with the MVAR model. <<BR>><<BR>> {{attachment:sim_db.gif}} * In the next sections, we will compute different connectivity metrics from these synthetic time series. Drag and drop the simulated data in the '''Process1''' tab, click on '''[Run]''' ( {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconRun.gif}} ) to open the [[Tutorials/PipelineEditor#Selecting_processes|Pipeline editor]], and select the connectivity metric.<<BR>><<BR>> {{attachment:sim_select.gif}} * This tutorial illustrates the computation of full connectivity graphs ('''Process 1: NxN'''). It is also possible to obtain connectivity measures between one of the time series of a given data file and the other time series in the same file (use '''Process1: 1xN'''), or between time series from two different data files (use '''Process2: AxB'''), as shown further below. References used: * This process relies on the ARSIM function from the '''ARFit toolbox''': <<BR>>https://github.com/tapios/arfit * Neumaier A, Schneider T<<BR>>[[http://dx.doi.org/10.1145/382043.382304|Estimation of parameters and eigenmodes of multivariate autoregressive models]]<<BR>>ACM Transactions on Mathematical Software, 2001 * Schneider T, Neumaier A<<BR>>Algorithm 808: [[http://dx.doi.org/10.1145/382043.382316|ARfit – A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models]]<<BR>>ACM Transactions on Mathematical Software, 2001 <<BR>><<BR>> |
| Line 68: | Line 131: |
| [[https://en.wikipedia.org/wiki/Correlation_and_dependence|Correlation]] is a non-directed connectivity metric that can be used to show similarity, dependence or association among two random variables or signals. While this metric has been widely used in electrophysiology, it should not be considered the best technique to evaluate connectivity. The correlation metric by its nature fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals. Let's compute the correlation for the simulated signals. Select the '''''Connectivity » Correlation NxN''''' process. {{attachment:gui_corr1n.png||width="400"}} <<BR>> === Process options === * '''Time window:''' Segment of the signal used for the connectivity analysis. Check '''''All file'''''. * '''Sensor types or names:''' Leave it empty. * '''Include bad channels:''' Check it. * '''Process options:''' Uncheck it so the mean of the signals will be subtracted before computing the correlation. * '''Output configuration''': Select Save individual results. <<BR>> |
[[https://en.wikipedia.org/wiki/Correlation_and_dependence|Correlation]] is a relatively simple, non-directed connectivity metric of association between two time series. It is relatively limited without further preprocessing of the input time series: correlation is sensitive to volume conduction and is not frequency specific. === Process options === * Process '''Connectivity > Correlation NxN''':<<BR>><<BR>> {{attachment:gui_corr1n.png}} * '''Time window:''' Time segment of the signals for connectivity analysis. Select: '''All file'''. * '''Time resolution:''' Select '''None''' * '''Windowed:''' correlation is computed in windows of a given '''length''' with a certain '''overlap''' percentage * '''None:''' correlation is computed using the entire time series * '''Compute scalar product:''' If left unchecked, the mean of the time series is subtracted before computing the correlation. Leave it unchecked. * '''Output options''': Select Estimate and save '''separately for each file'''. |
| Line 82: | Line 143: |
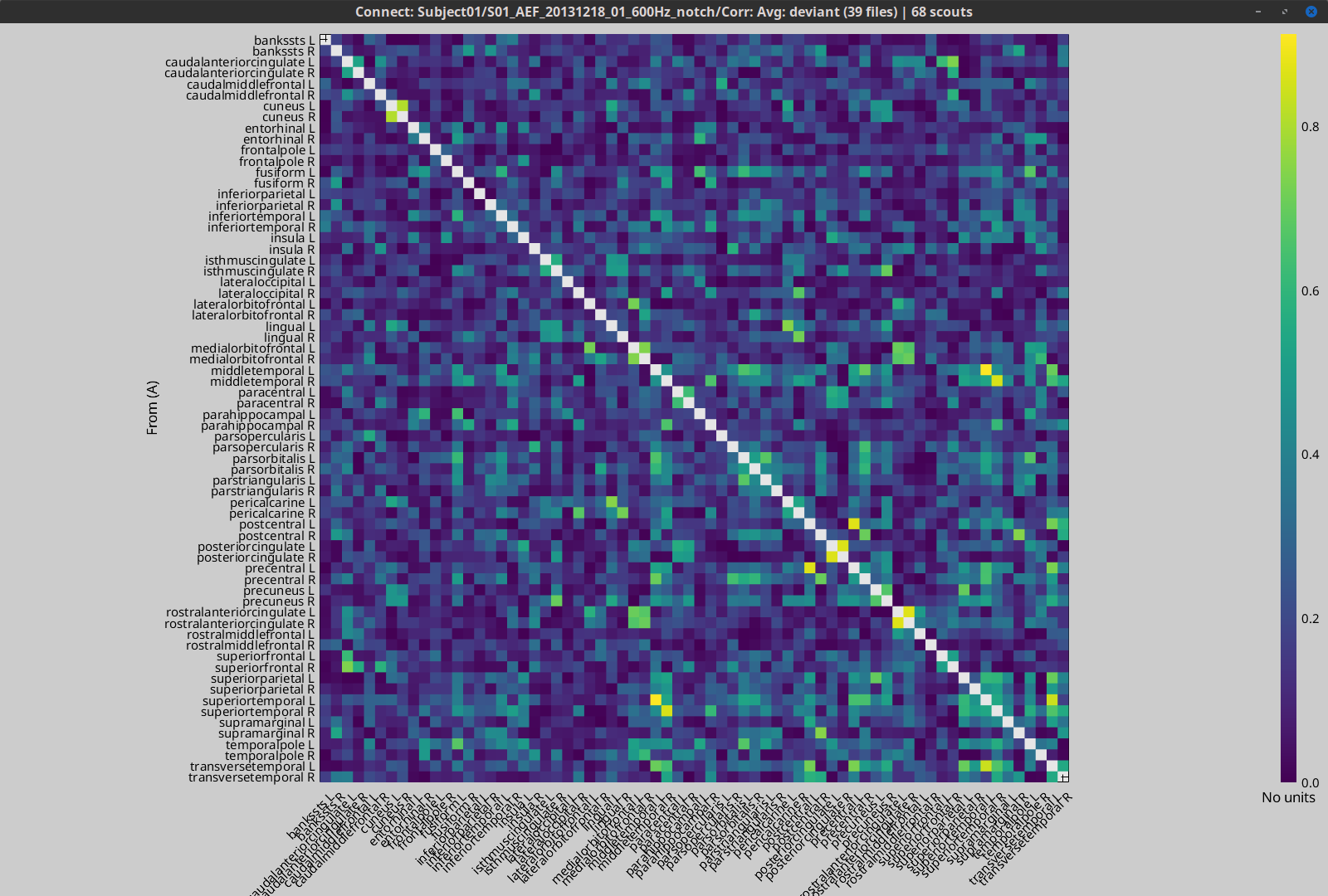
| After running a N×N connectivity process, the results are stored as a N×N connectivity file (with the icon {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconConnectN.gif}} ). Right-click on this file to see its display options: * '''Display as graph''': plots the connectivity graph using a [[https://en.wikipedia.org/wiki/Chord_diagram|chord diagram]] where the color of the edges shows the connectivity metric value. * '''Display as image''': plots the [[https://en.wikipedia.org/wiki/Adjacency_matrix|adjacent matrix]] for the connectivity file. <<BR>><<BR>> {{attachment:res_corr1n.png||width="700"}} <<BR>> {{{#!wiki note In '''Display as image''', the value of the connectivity metric between a signal and itself plotted as '''zero''' so that it doesn't force scaling the colormap to 1 if the other values are much smaller. }}} |
* The results are stored as a N×N connectivity file, with a new icon {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconConnectN.gif}} . Right-click for display options:<<BR>><<BR>> {{attachment:corr1n_file.gif}} * '''Display as graph''': Plots the connectivity graph using a [[https://en.wikipedia.org/wiki/Chord_diagram|chord diagram]] where the color of the edges shows the value of the connectivity metric. See the [[Tutorials/ConnectivityGraph|connectivity graph tutorial]] for a detailed explanation of the options of this visualization. * '''Display as image''': Plots the connectivity measures in an [[https://en.wikipedia.org/wiki/Adjacency_matrix|adjacency matrix]]. * '''Display fibers''': Displays source connectivity edges as virtual white fiber tracts, as shown [[#Tutorials.2FFiberConnectivity|here]]. <<BR>><<BR>> {{attachment:corr1n_graph_image.png}} Display options: * '''Show labels''': Click on the figure to display the names of the times series and the connectivity values in the figure legend. To display the labels corresponding to each column and row: right-click on the figure > Figure > '''Show labels'''. If the time series names are too long, use the option '''Use short labels'''. * '''Hide self-connectivity''': In a square NxN connectivity matrix, the diagonal values correpond to the values of the connectivity metric between a time series and itself. These self-connectivity values are typically much higher than the other values of the matrix. When checked, these values are hidden so that to display the off-diagonal values more clearly. * '''Colormap''': By default, the NxN colormap is configured to display the absolute values of the connectivity measures. Correlation values may be positive or negative. To display the '''negative values''', make sure to change the colormap configuration: right-click on the figure > Colormap > Uncheck '''Absolute values'''. <<BR>><<BR>> {{attachment:corr1n_image_relative.png}} <<BR>><<BR>> |
| Line 91: | Line 160: |
| Coherency or complex coherence, <<latex($$C_{xy}(f)$$)>>, is a complex-valued metric that measures of the linear relationship of two signals in the frequency domain. And, its magnitude square coherence (MSC), <<latex($$C^2_{xy}(f)$$)>>, often referred to as coherence, measures the covariance of two signals in the frequency domain. For a pair of signals <<latex($$x(t)$$)>> and <<latex($$y(t)$$)>>, with spectra <<latex($$X(f)$$)>> and <<latex($$Y(f)$$)>>, the MSC is defined as: | Coherency or complex coherence, <<latex($$C_{xy}(f)$$)>>, is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Magnitude square coherence (MSC), <<latex($$|C_{xy}(f)|^2$$)>>, or ''coherence'', measures the covariance of two signals in the frequency domain. For a pair of time series <<latex($$x(t)$$)>> and <<latex($$y(t)$$)>>, with spectra <<latex($$X(f)$$)>> and <<latex($$Y(f)$$)>>, the MSC is defined as: |
| Line 95: | Line 164: |
| C^2_{xy}(f) &=& \left(\frac{\left |S_{xy}(f) \right |}{\sqrt{ S_{xx}(f)S_{yy}(f) }}\right)^2 = \frac{\left |X(f)Y^*(f) \right |^{2}}{X(f)X^*(f)Y(f)Y^*(f)} \\ | C_{xy}(f) &=& \frac{S_{xy}(f)}{\sqrt{ S_{xx}(f)S_{yy}(f)}}\\ |C_{xy}(f)|^2 &=& MSC(f) = \left(\frac{\left |S_{xy}(f) \right |}{\sqrt{ S_{xx}(f)S_{yy}(f) }}\right)^2 = \frac{\left |X(f)Y^*(f) \right |^{2}}{X(f)X^*(f)Y(f)Y^*(f)} \\ |
| Line 101: | Line 171: |
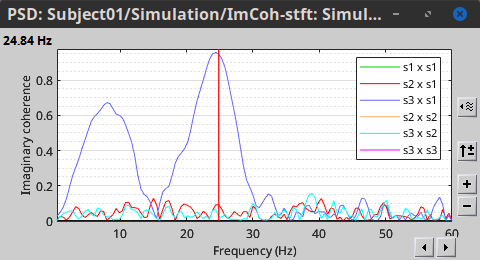
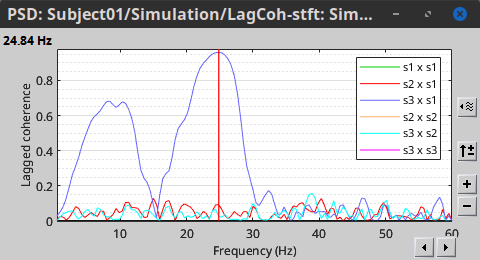
| Two related measures, which alleviate the problem of volume conduction, are [[www.|imaginary coherence]], <<latex($IC_{xy}(f)$)>>, and the [[www.|lagged coherence]], <<latex($LC_{xy}(f)$)>>, which are defined as: | Two related measures, which address the problem of volume conduction, are '''imaginary coherence''' ([[https://doi.org/10.1016/j.clinph.2004.04.029|Nolte et al., 2004]]), <<latex($IC_{xy}(f)$)>>, and '''lagged coherence''' ([[https://arxiv.org/pdf/0706.1776|Pascual-Maqui, 2007]]), <<latex($LC_{xy}(f)$)>>, which are defined as: |
| Line 105: | Line 175: |
| IC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \qquad \qquad \qquad \qquad LC_{xy}(f) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\ | IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\ LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\ |
| Line 109: | Line 180: |
| where <<latex($$\mathrm{Im()}$$)>> and <<latex($$\mathrm{Re()}$$)>> describe the imaginary and real parts of a complex number. To calculate coherence values in Brainstorm, select the '''''Connectivity » Coherence NxN''''' process. {{attachment:gui_cohere1n.png||width="400"}} <<BR>> === Process options === * '''Time window:''' Segment of the signal used for the connectivity analysis. Check '''''All file'''''. * '''Sensor types or names:''' Leave it empty. * '''Include bad channels:''' Check it. * '''Removing evoked response''': Check this box to remove the averaged evoked * '''Process options:''' Different types of coherence. Select Magnitude squared coherence. * '''Overlap for PSD estimation:''' Percentage of overlap between consecutive windows for PSD estimation. * '''Maximum frequency resolution''': Width of frequency bins in PSD estimation. * '''Highest frequency of interest''': Highest frequency for the analysis, it should be <= Fs/2. * '''Output configuration''': Select one file per input file. |
where <<latex($$\mathrm{Im()}$$)>> and <<latex($$\mathrm{Re()}$$)>> are the imaginary and real parts of a complex number, respectively. Note that the cross-spectrum (<<latex($$S_{xy}(f)$$)>>) and the power spectral densities (<<latex($$S_{xx}(f)$$)>> and <<latex($$S_{yy}(f)$$)>>), and as consequence also coherency (<<latex($$C_{xy}(f)$$)>>) can be obtained through different time-frequency decomposition methods (such as: Hilbert transform, wavelet transform and short-time Fourier transform), and for different time resolutions (per sample, windowed and entire file). === Process options === * Process '''Connectivity > Coherence NxN''':<<BR>><<BR>> {{attachment:gui_cohere1n.png}} <<BR>> {{attachment:gui_cohere1n_b.png}} * '''Time window:''' Segment of the time series used for the connectivity analysis. Select '''All file'''. * '''Connectivity metric '''shows variants of coherence measures. Select: '''Magnitude squared coherence'''. * '''Time-frequency decomposition '''selection of the time to time-frequency transformation. Select: (short-time) '''Fourier transform'''. * '''Options [Edit] '''shows the options of the selected time-frequency transformation. * '''Window length:''' Duration in seconds for the [[https://neuroimage.usc.edu/brainstorm/Tutorials/ArtifactsFilter#Evaluation_of_the_noise_level|spectrum estimation]]. Set to: '''1s'''. * '''Overlap:''' Percentage of overlap between consecutive sliding time windows. Set to: '''50%'''. * '''Highest frequency''': After the computation, removes all the frequencies above this threshold, mostly for visualization purposes. The value needs to be <= Fs/2. Set to: '''60 Hz'''. * '''Time resolution '''selection of the time resolution. Select: '''None'''. * '''Output options''': Select Estimate and save '''separately for each file'''. |
| Line 127: | Line 197: |
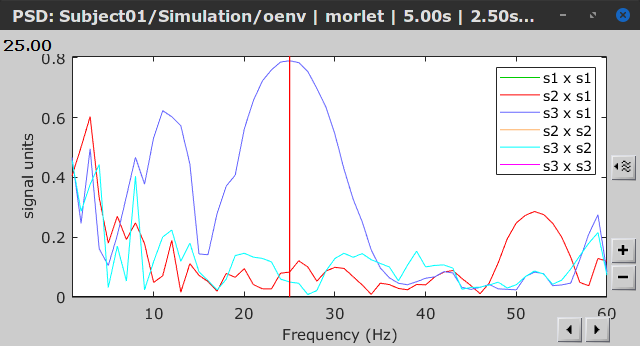
| Coherence is a function of frequency, as such, for each frequency point there is a connectivity graph and a connectivity matrix. Right-click on the coherence result file to see its display options: * '''Display as graph''': Plot the connectivity graph at a given frequency point. * '''Display as image''': Plot the connectivity matrix at a given frequency point. * '''Power spectrum''': Plot coherence as a function of frequency for all the possible node pairs. By clicking on the spectral representation of the coherence we change the frequency that is displayed in the connectivity graph and matrix. This frequency can be also changed in the Time window. {{attachment:res_cohere1n.png||width="700"}} <<BR>> In the same way, we can compute the other types of coherence. The figure below presents the spectra for the imaginary coherence (left) and the lagged coherence (right). {{attachment:res_cohere1n_b.png||width="700"}} <<BR>> We see the last two measures are similar but have different values in several frequencies. However, both imaginary and lagged coherence are more accurate than coherence. == Granger Causality == Granger causality (GC) is a method of directed functional connectivity, which is base on the Wiener-Granger causality methodology. GC is a measure of linear dependence, which tests whether the prediction of signal A (using a linear autoregressive model) is improved by adding signal B (also using a linear autoregressive model). If this is true, signal B has a Granger causal effect on the first signal A. In other words, independent information of the past of signal B improves the prediction of signal A obtained with the past of signal A alone. GC is nonnegative, and zero when there is no Granger causality. As only the past of the signals is considered, the GC metric is directional. The term independent is emphasized because it creates some interesting properties for GC, such as, that it is invariant under rescaling of A and B, as well as the addition of a multiple of A to B. See [[GrangerCausality|Granger causality - mathematical background]] for a complete formulation of the method. |
Coherence is frequency specific: a connectivity graph and a connectivity matrix are produced for each frequency bin of the spectrum. Right-click on the coherence result file to show display options: * '''Display as graph''': Plots a connectivity graph for each frequency bin. * '''Display as image''': Plot a connectivity matrix for each frequency bin. * '''Power spectrum''': Plot coherence as a function of frequency, between each time series. Open the 3 types of visualization: they are linked by clicking on the spectral representation of the coherence, which will change the current frequency bin and update the connectivity measures displayed in the graph and matrix. The value of the current frequency bin can also be changed in the Time panel. <<BR>><<BR>> {{attachment:res_cohere1n.png}} <<BR>><<BR>> Other variants of coherence can be derived following the above procedure. The figures below display the coherence spectra obtained from the imaginary coherence (left) and the lagged coherence (right) measures. || {{attachment:res_cohere1n_d.png||width="350"}} || || {{attachment:res_cohere1n_e.png||width="350"}} || <<BR>><<BR>> == Granger causality == Granger causality (GC) is a measure of '''directed functional connectivity''' based on the Wiener-Granger causality framework. GC measure linear dependencies between time series, and tests whether the prediction of the future of signal <<latex($$x(t)$$)>> (approximated by a linear autoregressive model) is improved by considering signal <<latex($$y(t)$$)>> (also approximated by a linear autoregressive model). If there is such improvement, one concludes that signal <<latex($$y(t)$$)>> has a Granger causal effect on the other signal. In sum, some '''independent information''' from the past of signal <<latex($$y(t)$$)>> improves the prediction of the future of signal <<latex($$x(t)$$)>>, with respect to only observing its past <<latex($$x(t)$$)>>. GC takes nonnegative values; its is zero when no Granger causality can be attributed. The term '''independent''' means that GC is invariant with the scale of the input signals <<latex($$x(t)$$)>> and <<latex($$y(t)$$)>>. <<BR>><<BR>> See [[GrangerCausality|Granger causality - mathematical background]] for a more complete background. |
| Line 147: | Line 215: |
| Despite the name, '''Granger causality indicates directionality but not true causality'''. <<BR>> For example, if a variable C is causing both A and B, but with a smaller delay for B than for A, then a GC measure between A and B would show a non-zero GC for B->A, even though B is not truly causing A (Bressler and Seth, 2011). }}} To compute the Granger causality values in Brainstorm, select the '''''Connectivity » Bivariate Granger causality NxN''''' process. {{attachment:gui_granger1n.png||width="400"}} <<BR>><<BR>> === Process options === * '''Time window:''' Segment of the signal used for the connectivity analysis. Check '''''All file'''''. * '''Sensor types or names:''' Leave it empty. * '''Include bad channels:''' Check it. * '''Removing evoked response''': Check this box to remove the averaged evoked. It is also recommended by some as it meets the zero-mean stationarity requirement (improves stationarity of the system). However, the problem with this approach is that it does not account for trial-to-trial variability (For a discussion see (Wang et al., 2008) '''''todo-> link to paper'''''). * '''Model order:''' The most common criteria used to define the order of the model are the [[Link|Akaike’s information]] criterion, the [[Bayesian-Schwartz’s criterion]], and the [[Hannan-Quinn criterion]]. Too low orders may lack the necessary details, while too big orders tend to create spurious values of connectivity. While our simulated signals were created with a model of 4, here we used as model order of 6 for a decent connectivity result. * '''Save individual results (one file per input file):''' option to save GC estimates on several files separately. * '''Concatenate input files before processing (one file):''' option to save GC estimates on several files as one concatenated matrix. |
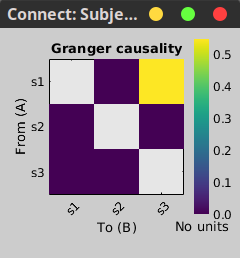
Despite the name, '''Granger causality indicates directionality but not true causality'''. <<BR>> For example, if a variable <<latex($$w$$)>> is causing both <<latex($$x$$)>> and <<latex($$y$$)>>, but with a smaller delay for <<latex($$y$$)>> than for <<latex($$x$$)>>, then the GC measure between <<latex($$x$$)>> and <<latex($$y$$)>> would show a non-zero GC for <<latex($$y$$)>> --> <<latex($$x$$)>>, even though <<latex($$y$$)>> is not truly causing <<latex($$x$$)>> ([[https://doi.org/10.1016/j.neuroimage.2010.02.059|Bressler and Seth, 2011]]). }}} === Process options === * Process '''Connectivity > Bivariate Granger causality NxN'''<<BR>><<BR>> {{attachment:gui_granger1n.png||width="400"}} * '''Time window:''' Time segment of the time series used for the connectivity analysis. Select '''All file'''. * '''Remove evoked response''': This option is recommended by some authors as it satisfies the zero-mean stationarity of the GC model, but does not account for trial-to-trial variability; see ([[https://doi.org/10.1016/j.neuroimage.2008.03.025|Wang et al., 2008]]). Leave it '''Unchecked'''. * '''Maximum Granger model order:''' The most common criteria used to define the order of the autoregressive models used by GC to approximate the input time series are the [[https://en.wikipedia.org/wiki/Akaike_information_criterion|Akaike’s information]] criterion, the [[https://en.wikipedia.org/wiki/Bayesian_information_criterion|Bayesian-Schwartz’s criterion]], and the [[https://en.wikipedia.org/wiki/Hannan–Quinn_information_criterion|Hannan-Quinn criterion]]. Low model orders will yield coarse approximations of the input time series. High model orders may yield spurious GC connectivity estimates. The simulated time series were created with an AR model of order 4; please use a maximum Granger model order of '''6'''. * '''Output options''': Select '''Save individual results'''. <<BR>> === Results visualization === The connectivity matrix (left panel below) is not symmetric because GC values are direction specific. The upper right elements of the matrix indicate there is a GC influence from signal 1 to signal 3. In the connectivity graph (right panel below) the directionality is shown with an arrowhead at the center for the arc connecting two nodes. || {{attachment:res_granger1n_a.png}} || || {{attachment:res_granger1n_b.png}} || <<BR>><<BR>> == Spectral Granger causality == The Spectral Granger causality is a measure of '''directed functional connectivity '''that was developed to indicate frequency specific influences between time series ([[https://doi.org/10.1103/PhysRevLett.100.018701|Dhamala et al., 2008]]). === Process options === * Process: '''Connectivity > Bivariate Granger causality NxN'''. <<BR>><<BR>> {{attachment:gui_spgranger1n.png||width="400"}} <<BR>><<BR>>. Here we used the same parameters as with [[#Granger_causality|GC]] plus two two extra parameters specific to spectral GC: * '''Maximum frequency resolution''': Width of frequency bins in PSD estimation. Set to '''1 Hz'''. * '''Highest frequency''': computes GC values under the specified frequency. Should be set <= Fs/2. Use: '''60 Hz'''. |
| Line 163: | Line 244: |
| The GC results with the simulates signals are below. As GC metric is not symmetric, the connectivity matrix (right) is not symmetric. The upper right element of this matrix shows there is a signal flow from channel 1 to channel 3. In the connectivity graph the directionality is shown as GRADIENT (TO BE UPDATED WITH THE NEW GRAPH LIBRARY). <<BR>><<BR>> {{attachment:res_granger1n.png||width="700"}} <<BR>><<BR>> == Spectral Granger causality == GC lacks of resolution in the frequency domain, as such, spectral Granger causality was introduced in [REF]. This metric is found in '''''Connectivity » Bivariate Granger causality NxN'''''. {{attachment:gui_spgranger1n.png||width="400"}} <<BR>><<BR>> === Process options === With respect to GC, spectral GC presents two extra parameters: * '''Maximum frequency resolution''': Width of frequency bins in PSD estimation. * '''Highest frequency of interest''': Highest frequency for the analysis, it should be <= Fs/2. === Result visualization === As with coherence, spectral GC can be plotted as a function of frequency. The plot below clearly shows a peak at 25 Hz, as expected. {{attachment:res_spgranger1n.png||width="325"}} <<BR>><<BR>> == Envelope Correlation (2020) == In the [[Tutorials/TimeFrequency|time-frequency tutorial]] the Morlet wavelets and Hilbert transform were introduced methods to decompose signals in the time-frequency (TF) domain. The result in this TF transformation can be seen as a set of [[linko|analytic signals]] associated with narrowband (defined by the TF transformation method) signals. The analytic signal is a complex temporal representation of a real signal that has been useful in signal processing due to its characteristics, more specifically, its module and phase correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the associated real signal. The instantaneous amplitude (or envelope) of these band analytic signals can be used to carry out the pairwise connectivity analysis with metrics such as correlation and coherence (including lagged coherence). In computing the envelope correlation, an optional step is to orthogonalize the envelopes by removing their real part of coherence before the correlation. This orthogonalization process alleviates the effect of volume conduction in MEG/EEG signals. These connectivity metrics can be computed with the '''''Connectivity » Envelope Correlation N×N [2020]''''' process. {{attachment:gui_henv1n.png||width="400"}} === Process options === * '''Time window:''' Segment of the signal used for the connectivity analysis. Check '''''All file'''''. * '''Sensor types or names:''' Leave it empty. * '''Include bad channels:''' Check it. * '''Removing evoked response''': Check this box to remove the averaged evoked * '''Time-frequency transformation method:''' Either Hilbert transform or Morlet wavelets. Each of this methods requires additional parameters that are found in an external panel that opens by clicking on '''''Edit'''''. See the [[Tutorials/TimeFrequency|time-frequency tutorial]] * '''Signal splitting:''' This process has the capability of splitting the input data into several blocks for performing time-frequency transformation, and then merging them to build a single file. This feature helps to save a huge amount of memory and, at the same time, avoid breaking a long-time recording to short-time signals, which makes inconsistency in dynamic network representation of spontaneous data. The maximum number of blocks which can be specified is 20. * '''Connectivity measure:''' This is the connectivity metric that will be used with the envelopes. * '''Parallel processing:''' Enables the use of the parallel processing toolbox in Matlab to accelerate the computational procedure. * '''Output configuration:''' Generally, the above calculation results in a 4-D matrix, where dimensions represent channels (1st and 2nd dimensions), time points (3rd dimension), and frequency (4th dimension). In the case that we analyze event-related data, we have also several files (trials). However, due to the poor signal-to-noise ratio of a single trial, an individual realization of connectivity matrices for each of them is not in our interests. Consequently, we need to average connectivity matrices among all trials of a specific event. The second option of this part performs this averaging. == Phase locking value == An alternative class of connectivity metrics considers only the relative instantaneous phase between the two signals, i.e., phase-locking or synchronization (Tass et al., 1998). Phase locking is a fundamental concept in dynamical systems that has been used in control systems (the phase-locked loop) and in the analysis of nonlinear, chaotic and non-stationary systems. Since the brain is a nonlinear dynamical system, phase locking is an appropriate approach to quantifying connectivity. A more pragmatic argument for its use in studies of LFPs, EEG, and MEG is that it is robust to fluctuations in amplitude that may contain less information about interactions than does the relative phase (Lachaux et al., 1999; Mormann et al., 2000). The most commonly used phase connectivity metric is the phase-locking value (PLV), which is defined as the length of the average vector of many unit vectors whose phase angle corresponds to the phase difference between two signals (Lachaux et al., 1999; Mormann et al., 2000). If the distribution of the phase difference between the two signals is uniform, the length of such an average vector will be zero. Conversely, if the phases of the two signals are strongly coupled, the length of the average vector will approach unity. For event-related studies, we would expect the marginal to be uniform across trials unless the phase is locked to a stimulus. In that case, we may have nonuniform marginals which could in principle lead to false indications of phase locking. between two signals. PHASE TIME SERIES AND ROSE PLOT Considering a pair of narrow-band analytic signals hats1(t) and hats2(t), obtained from the FT transformation using the Hilbert transform: |
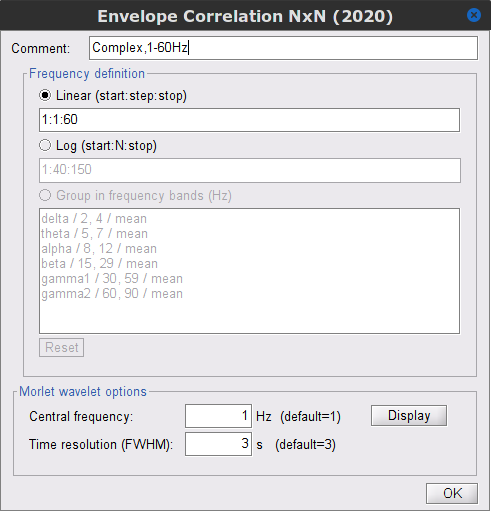
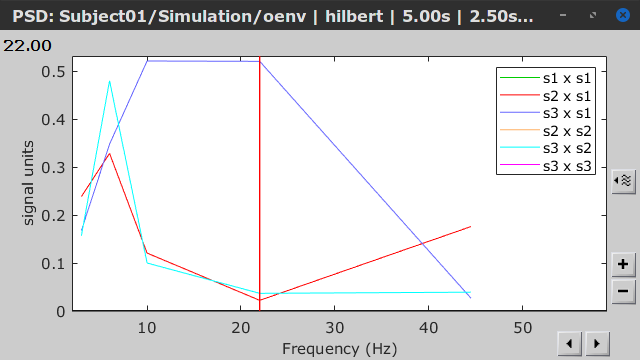
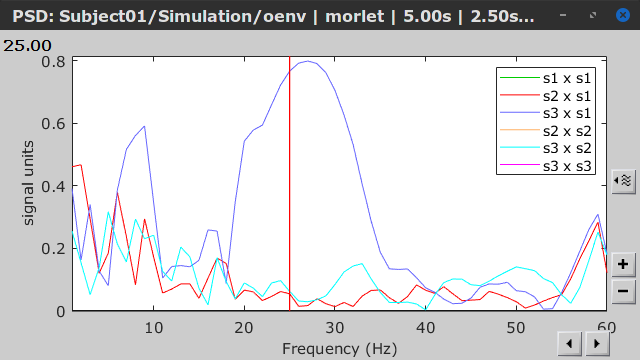
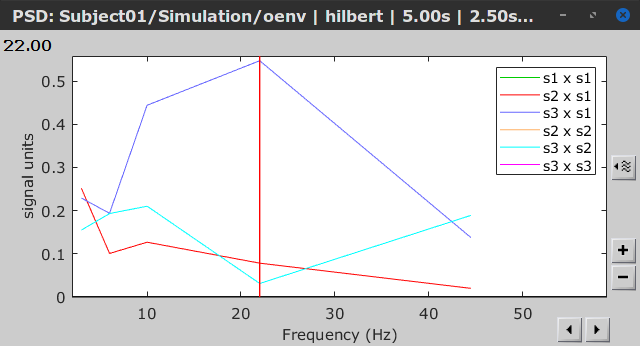
As with coherence, spectral GC can be plotted as a function of frequency. The display below shows a peak around 25 Hz that corresponds to the expected causal interaction of Signal 1 on Signal 3. {{attachment:res_spgranger1n.png}} <<BR>><<BR>> == Envelope correlation == In the [[Tutorials/TimeFrequency|time-frequency tutorial]], we have introduced '''Morlet wavelets''' and the '''Hilbert transform''' as methods to decompose time series in the time-frequency (TF) domain. The outcome of these two TF transformations is an [[https://en.wikipedia.org/wiki/Analytic_signal|analytic signal]], <<latex($$\tilde{x}(t)$$)>>, which is a complex time series uniquely associated to the original data time series, <<latex($$x(t)$$)>>, which '''module''' <<latex($$a_{\tilde{x}}(t)$$)>>, and '''phase''' <<latex($$\phi_{\tilde{x}}(t)$$)>>, correspond to the '''instantaneous amplitude''' (or envelope) and '''instantaneous phase''' of the original time series <<latex($$x(t)$$)>>, respectively. The real part of <<latex($$\tilde{x}(t)$$)>> is the original time series <<latex($$x(t)$$)>>, and the imaginary part is the Hilbert transform of that same time series <<latex($$x(t)$$)>>. . {{{#!latex \begin{eqnarray*} \tilde{x}(t)= x(t) + j\mathcal{H}\left\{ x(t) \right\} = a_{\tilde{x}}(t)e^{j\phi_{\tilde{x}}(t)} \\ \end{eqnarray*} }}} {{{#!wiki note The analytic signal of oscillatory or '''narrowband''' signals provide '''meaningful''' and '''interpretable''' estimations of instantaneous amplitude and phase. While it is technically feasible to derive these elements from broadband time series, they would not be interpretable (see [[https://mitpress.mit.edu/books/analyzing-neural-time-series-data|Cohen, 2014]]). }}} The instantaneous amplitude (or envelope) of the analytic signals can be used to carry out pairwise connectivity analysis with correlation. This is to say amplitude envelop correlation (AEC). An optional step consists in '''orthogonalizing''' the pairs of amplitude envelope time series before computing the correlation. Orthogonalization is performed by first removing the real part of their coherence to reduce volume conduction (at the sensor level) or cross-talk effects (at the source level) ([[https://psycnet.apa.org/doi/10.1038/nn.3101|Hipp et al., 2012]]). === Process options === * Process: '''Connectivity > Envelope Correlation N×N [2023]''' <<BR>><<BR>> {{attachment:gui_henv1n_ha.png||width="400"}} * '''Time window:''' Time segment of the signal used for the connectivity analysis. Select: '''All file'''. * '''Connectivity measure '''is the connectivity metric applied to the resulting signal amplitude envelopes. Select '''Envelope correlation (orthogonalized)'''. * '''Time-frequency decomposition:''' '''Hilbert transform''' or '''Morlet wavelets'''. Each method requires additional parameters that will be displayed in a separate panel after clicking on '''[Edit]'''. See the [[Tutorials/TimeFrequency|time-frequency tutorial]]. In the present example, we will use the '''Hilbert transform''' with the option '''Group in frequency bands''' to present the results for the canonical frequency bands. As the sampling frequency of the signals is 120Hz, thus, make sure you remove the '''"gamma2"''' band from the targeted frequency bands.<<BR>><<BR>> {{attachment:gui_henv1n_hb.png||height="276",width="227"}} * '''Time resolution:''' If '''Windowed''', connectivity is saved for each time window. If '''None''', the connectivity measures are averaged across all windows. Select '''Windowed'''. Set the additional parameters to define the windows: * '''Time window length''': Duration in milliseconds over which the connectivity measure is computed. Set to '''5s''' * '''Time window overlap:''' Percentage of overlap between consecutive time windows to compute the connectivity measure. Set to '''50%'''. * '''Use the parallel processing toolbox:''' If available, will call Matlab's parallel processing to accelerate computations. Leave it '''Unchecked'''. * '''Output options''': Select Estimate and save '''separately for each file'''. For sake of comparison, we will compute AEC again, but this time changing the TF decomposition method to '''Morlet wavelets''' with '''Linear = 1:1:60''' (frequencies from 1 to 60 Hz with 1 Hz step). . {{attachment:gui_henv1n_wb.png||height="276",width="227"}} === Results visualization === As with [[#Coherence|Coherence]] and [[#Spectral_Granger_causality|spectral Granger causality]], amplitude envelope correlations can be displayed as a function of frequency, and as a function of time if the '''Time resolution''' option was set to '''Windowed'''. Below are the AEC results obtained with the Hilbert transform (left panels) and with Morlet wavelets (right panels) for the first 5-s time window (top panels) and the 5-s last window (bottom panels). || {{attachment:res_henv1n_h.png||width="350"}} ||<style="text-align:center">First 5-s window || {{attachment:res_henv1n_w.png||width="350"}} || || {{attachment:res_henv1n_h2.png||width="350"}} ||<style="text-align:center">Last 5-s window || {{attachment:res_henv1n_w2.png||width="350"}} || == Phase-Locking Value == An alternative class of connectivity metrics considers the relative instantaneous phase between two time series as a marker of connectivity. Phase-locking or phase synchronization are two such measures ([[https://doi.org/10.1103/PhysRevLett.81.3291|Tass et al., 1998]]). In principle, phase-based measures are robust against fluctuations in signal amplitude, although low signal-to-noise conditions remain challenging for these measures ([[https://doi.org/10.1002/(SICI)1097-0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C|Lachaux et al., 1999]]; [[https://doi.org/10.1016/S0167-2789(00)00087-7|Mormann et al., 2000]]). The phase-locking value ('''PLV''') is a popular metric defined as the length of the average vector of many unit vectors whose phase angle corresponds to the phase difference between two time series ([[https://doi.org/10.1103/PhysRevLett.81.3291|Tass et al., 1998]]). If the distribution of the phase difference between the two signals is uniform, the length of such an average vector will be 0. If the phases of the two signals are strongly coupled, the length of the average vector will be close to 1. For event-related studies, we would expect phase differences across trials to be uniformly distributed, unless the phase of the brain signals is locked to the event onset, which would then indicate a form of phase locking between the two time series. Considering a pair of narrow-band analytic signals <<latex($$\tilde{x}(t)$$)>> and <<latex($$\tilde{y}(t)$$)>>, obtained from the Hilbert transform (see above): |
| Line 212: | Line 297: |
| PLV(t)= \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\ | \mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\ |
| Line 219: | Line 304: |
| \Delta \phi (t) = \phi_1 (t) - \phi_2 (t) = arg\left ( \frac{z_{1}(t)z_{2}^{*}(t)}{\left | z_{1}(t) \right |\left | z_{2}(t) \right |} \right ) \\ | \Delta \phi (t) = \phi_{\tilde{x}}(t) - \phi_{\tilde{y}}(t) = arg\left ( \frac{\tilde{x}(t)\tilde{y}^{*}(t)}{\left | \tilde{x}(t) \right |\left | \tilde{y}(t) \right |} \right ) \\ |
| Line 222: | Line 307: |
| {{attachment:gui_plv1n.png||width="400"}} === Process options === * '''Time window:''' Segment of the signal used for the connectivity analysis. Check '''''All file'''''. * '''Sensor types or names:''' Leave it empty. * '''Include bad channels:''' Check it. * '''Frequency bands for the Hilbert transform:''' Frequency bands used for the time-frequency transformation with the Hilbert tranform method. See the [[Tutorials/TimeFrequency|time-frequency tutorial]] * '''Keep time information:''' Computes PLV across trials, thus the result is a PLV time series for each frequency band. * '''Measure:''' How the resulting vector is reported. Select '''''Magnitude'''''. === Result visualization === IMAGE == Method selection and comparison == We can have a comparison between different connectivity functions. The following table briefly does this job. {{attachment:TableComparison.PNG||width="700",height="400"}} Comparing different approaches with the ground truth we find out that the HCorr function works slightly better than other coherence functions. {{attachment:Coh13_AR3.png||width="600",height="350"}} == Connectivity measure on real data : MEG/EEG data == As mentioned [[#General_considerations_in_connectivity_analysis|above]], the different connectivity metrics can be computed with '''sensor''' or '''source''' data. However, sensor-domain connectivity analyses present two important limitations: 1. '''They are not interpretable''', as the relation between the estimated connectivity and the underlying neuroanatomy is not straightforward. 1. Sensor data is severely corrupted by effects of '''field spread''' and '''volume conduction'''. Due to these effects the activity of a single brain area could cause a spurious connectivity between MEG/EEG sensors. Despite these limitations, sensor-domain connectivity analysis is commonly used. One approach to reduce the negative impact of field spread on connectivity analyses is to perform them in the source domain. In addition, source-domain connectivity analyses are '''interpretable''' as neuroanatomy is considered. As consequence, findings in this domain can be easily used in group studies using a normalization / registration. Regardless of the domain, it is highly recommended to '''have a clear hypothesis to test before starting the connectivity analysis'''. Although sensor- and source-domain connectivity analyses use different assumptions, the outcomes regarding the topology of the underlying networks should be consistent [Lai 2018]. Depending on the [[Tutorials/SourceEstimation#Source_estimation_options|source estimation method]] the number of obtained sources can be in the order of '''tens of thousands''', making the full connectivity analyses (N×N) impractical. As such, brain sources are often grouped in regions of intrests ROIs ([[Tutorials/Scouts|scouts]] in Brainstorm). The '''most critical step''' in performing a source-domain connectivity analysis is the definition of ROIs, this is not a trivial procedure as it depends on the source estimation method, experimental task, and data available [Schhoffen 2009]. Common approaches found in the literature to select the ROIs for connectivity analysis are: * '''A prior''': ROIs are selected based on a priori knowledge in a given experimental task * '''Coherence with a no-neuronal signal''': ROIs that present a strong coherence with an external no-neuronal signal are selected. * '''Power maps''': ROIs showing the strongest activity in an experimental task or ROIs that present the strongest differences of activity between experimental conditions are selected. * '''Full brain''': A set of ROIs covering the full brain ([[https://neuroimage.usc.edu/brainstorm/Tutorials/LabelFreeSurfer?highlight=(parcellation)#Cortical_parcellations|cortical parcellations]]) is selected. In this selection approach, there are not any a priori assumptions or hypotheses. Although it can be used for '''exploratory analyses''', it '''should not be taken as default for connectivity analyses'''. |
{{attachment:plv.png}} Several variants of PLV have been contritributed. Brainstorm features <<BR>>'''ciPLV''' ([[https://pubmed.ncbi.nlm.nih.gov/29952757/|Bruña 2018]]) and '''wPLI''' ([[https://pubmed.ncbi.nlm.nih.gov/21276857/|Vinck 2011]]) variants contributed to Brainstorm by Daniele Marinazzo. {{{#!wiki note PLV values tend to be overestimated when derived from few (<50) time samples. As a consequence, when comparing PLV values between conditions, please make sure that they are derived from about the same number of samples in each condition. }}} === Process options === * Process: '''Connectivity > Phase locking value NxN'''<<BR>><<BR>> {{attachment:gui_plv1n.gif}} * '''Time window:''' Time segment of the signal used for the connectivity analysis. Select '''All file'''. * '''Connectivity metric '''shows variants of phase locking measures. Select: '''Phase locking value'''. * '''Time-frequency decomposition ''' method for time-frequency transformation. Select: '''Hilbert transform'''. * '''Options [Edit] '''shows the options of the selected time-frequency transformation. * '''Frequency bands:''' Used for the time-frequency transformation with the Hilbert transform method. See the [[Tutorials/TimeFrequency|time-frequency tutorial]]. In this example, the sampling frequency of the signals being 120Hz, please remove the "gamma2" band. * '''Time resolution '''selection of the time resolution. Select: None. * '''Output options''': Select '''Save across combined files/epochs'''. <<BR>> === Results visualization === PLV is frequency resolved, and here was computed for the delta, theta, alpha, beta and gamma1 bands. With the simulated data, we expect a higher PLV value in the beta band (15 to 29 Hz), between Signal 1 and Signal 3. This is indeed our observation, with a peak at 22 Hz (center of beta band) in the PLV spectrum (left). The same is true for ciPLV (center) and wPLI (right). {{attachment:res_plv1n.png||width="650"}} == Phase-Transfer Entropy == Phase transfer entropy (PTE) is a '''directed connectivity''' metric that quantifies the [[https://en.wikipedia.org/wiki/Transfer_entropy|transfer entropy]] (TE) between two instantaneous phase time series ([[https://doi.org/10.1016/j.neuroimage.2013.08.056|Lobier et al., 2014]]). Similar to [[#Granger_Causality|GC]], TE estimates whether including the past of both source and target time series influences the ability to predict the future of the target time series. In PTE, if a phase signal <<latex($$\phi_{\tilde{x}}(t)$$)>> causes the signal <<latex($$\phi_{\tilde{y}}(t)$$)>>, the [[http://www.scholarpedia.org/article/Mutual_information|mutual information]], between <<latex($$\phi_{\tilde{y}}(t)$$)>> and the past of <<latex($$\phi_{\tilde{x}}(t)$$)>> i.e. <<latex($$\phi_{\tilde{x}}(t')$$)>> is larger than the mutual information of <<latex($$\phi_{\tilde{y}}(t)$$)>>, the past of <<latex($$\phi_{\tilde{y}}(t)$$)>> i.e. <<latex($$\phi_{\tilde{y}}(t')$$)>> and <<latex($$\phi_{\tilde{x}}(t')$$)>>. This relationship can be represented on the Venn diagram below, where <<latex($$\mathrm{I()}$$)>> and <<latex($$\mathrm{H()}$$)>>, indicate mutual information and the individual entropies, respectively. PTE values are positive and unbounded. {{attachment:pte.png}} === Process options === * Process: '''Connectivity > Phase Transfer Entropy NxN'''<<BR>><<BR>> {{attachment:gui_pte1n.png||width="400"}} * '''Time window:''' Time segment of the signal used for the connectivity analysis. Select '''All file'''. * '''Frequency bands:''' Used for the time-frequency transformation with the '''Hilbert transform''' method. See the [[Tutorials/TimeFrequency|time-frequency tutorial]]. In this example, as the sampling frequency of the signals is '''120 Hz''', make sure the "gamma2" band is removed from the option. * '''Return normalized phase transfer entropy:''' Divides each directional PTE value between two signals by the sum of both directional PTE values for those two signals. '''Uncheck this option''' * '''Output options''': Select '''Save individual results'''. <<BR>> === Results visualization === Here we computed PTE for the delta, theta, alpha, beta and gamma1 bands. From the synthetic data used here, we expect to observe a higher PTE value in the beta band, From Signal 1 To Signal 3. This is indeed shown with a peak at 22 Hz (center of beta band) in the PTE spectrum. {{attachment:res_pte1n.png||width="350"}} . == Summary: connectivity methods == The following table list the available connectivity metrics in Brainstorm and their description. ||<style="font-weight:bold;border-width:2px;">Metric ||<style="text-align:center;font-weight:bold;border-width:2px;">1×N ||<style="text-align:center;font-weight:bold;border-width:2px;">N×N ||<style="text-align:center;font-weight:bold;border-width:2px;">Directionality ||<style="text-align:center;font-weight:bold;border-width:2px;">Freq resolved ||<style="text-align:center;font-weight:bold;border-width:2px;">Time resolved ||<style="text-align:center;font-weight:bold;border-width:2px;">Function ||<style="text-align:center;font-weight:bold;border-width:2px;">Info || ||<style="border-width:2px;">Correlation ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_corrn.m` ||<style="text-align:center;border-width:2px;">[[#Correlation|Link]] || ||<style="border-width:2px;">Coherence ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_cohn.m` ||<style="text-align:center;border-width:2px;">[[#Coherence|Link]] || ||<style="border-width:2px;">Granger causality ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">`bst_granger.m` ||<style="text-align:center;border-width:2px;">[[#Granger_causality|Link]] || ||<style="border-width:2px;">Spectral Granger causality ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">`bst_granger_spectral.m` ||<style="text-align:center;border-width:2px;">[[#Spectral_Granger_causality|Link]] || ||<style="border-width:2px;">Envelope Correlation (2023) ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_henv.m` ||<style="text-align:center;border-width:2px;">[[#Envelope_Correlation_.282020.29|Link]] || ||<style="border-width:2px;">Phase locking value ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_connectivity.m` ||<style="text-align:center;border-width:2px;">[[#Phase_locking_value|Link]] || ||<style="border-width:2px;">Phase transfer entropy ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">`PhaseTE_MF.m` ||<style="text-align:center;border-width:2px;">[[#Phase_transfer_entropy|Link]] || <<HTML(<!-- )>> Real data: Auditory dataset [TODO] '''TODO''': Rewrite this section with '''coherence '''on '''scouts''', with '''single trials'''. -- In this section we will use the results obtained in the introduction tutorials. The goal here is only to illustrate the interface of these tools on real data, as the results are not particularly interesting. The [[Tutorials/CorticomuscularCoherence|corticomuscular coherence tutorial]] provides more complete and meaninful guidelines for computing connectivity measures on real MEG recordings. Let's go back to our [[DatasetIntroduction|auditory oddball dataset]], available in the protocol '''TutorialIntroduction''' if you have followed the introduction tutorials. As the stimulus is played on both ears, we expect to observe highly correlated activity in the '''primary auditory cortices''', in both experimental conditions (standard and deviant beeps), around '''0''' to '''150 ms''' after the stimulus due to auditory evoked responses at 50 and 100 ms (M50, M100). |
| Line 264: | Line 372: |
| Being an '''exploratory analysis''', the full-brain connectivity analysis can help to get a better understanding of the acquired data, and to develop hypothesis to test. However its outcomes should not be considered conclusive, as they may be the result of circular analysis. [Kriegeskorte 2009]. }}} The optimal selection of ROIs to perform souce-domain connectivity analysis is still an open question. == TODO : Connectivity measure on real data : MEG/EEG data == For all the brain imaging experiments, it is highly recommended to have a clear hypothesis to test before starting the analysis of the recordings. With this auditory oddball experiment, we would like to explore the temporal dynamics of the auditory network, the deviant detection, and the motor response. According to the literature, we expect to observe at least the following effects: * Bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). * Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. * Decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). * '''The''' first response peak (91ms), the sources with high amplitudes are located around the primary auditory cortex, bilaterally, which is what we are expecting for auditory stimulation. * For this experiment we will focus on the beta high and gamma frequency, as shown here https://brainworksneurotherapy.com/what-are-brainwaves, "Beta is a ‘fast’ activity, present when we are alert, attentive, engaged in problem-solving, judgment, decision making, or focused mental activity." * 1 dataset: * '''S01_AEF_20131218_02_600Hz.ds''': Run #2, 360s, 200 standard + 40 deviants For this data we select three main time windows to compute the connectivity: '''time 1 : 0-150 ms''' : we expect the bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). '''time 2 : 100-300 ms''': Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. '''time 3 : 300-550 ms''' : Frontal regions activation related to the decision making and '''motor'''preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. === Sources level === Connectivity is computed at the source points (dipole) or at a defined brain region also called scouts. The signal used art this level is obtained from the inverse problem process, in which each source-level node (dipole) is assigned with an activation value at each time point. Therefore, we can compute the connectivity matrix between all pairs of the node. This process is possible only of the inverse problem is computed '''(ref to tuto here). ''' To run this in brainstorm, you need to drag and drop the source files within the process1 tab, select the option 'source process' click on the Run button, then you can select the connectivity measure that you want to perform. As in the previous section, we can compute the source connectivity matrix for each trail, then average overall trial. However, this process is time and memory consuming. For each trial, a matrix of 15002x15002 elements is computed and saved in the hard disc (~0.9 Go per trial). In the case of the unconstrained source, the size is 45006x45006. {{attachment:connectivitySourceSpace.png||width="500",height="400"}} This is obviously a very large number and it does not really make sense. Therefore, the strategy is to reduce the dimensionality of the source space and adopt a parcellation scheme, in other terms we will use the scouts. Instead, to compute the connectivity value values between two dipoles, we will use a set of dipoles pairs that belong to a given area in the cortex. Although the choice of the optimal parcellation scheme for the source space is not easy. The optimal choice is to choose a parcellation based on anatomy, for example the Brodmann parcellation [[http://www.nature.com/nature/journal/v536/n7615/full/nature18933.html|here]]. In brainstorm these atlases are imported in Brainstorm as scouts (cortical regions of interest), and saved directly in the surface files as explained in this tutorial [[https://neuroimage.usc.edu/brainstorm/Tutorials/LabelFreeSurfer?highlight=(parcellation)#Cortical_parcellations|here]]. In this tutorial, we will use the scouts " Destrieux atlas'''" (following figure)''' {{attachment:destrieuxScouts.png||width="500",height="400"}} To select this atlas, from the connectivity menu, you have to check the box 'use scouts', select the scout function 'mean' and apply the function 'Before', save individual results. In this tutorial, we select the correlation as example, the same process is expected for the other methods. {{attachment:processConnectivityScouts.png||width="300",height="400"}} For more detail for these options please refer to this [[https://neuroimage.usc.edu/forums/t/choosing-scout-function-before-or-after/2454|thread]] The following matrix is the solution that we obtain with these scouts with the size of 148x148 for this atlas (~400 Ko) {{attachment:connectivityScoutDistrieux.png||width="500",height="400"}} For this data we select three main time windows to compute the connectivity: time 1 : 0-150 ms : we expect the bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). time 2 : 100-300 ms : Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. time 3 : 300-550 ms : Frontal regions activation related to the decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. ---- === Coherence === === Correlation === For this data we select three main time windows to compute the connectivity: time 1 : 0-150 ms : we expect the bilateral response in the '''primary auditory cortex''' (P50, N100), in both experimental conditions (standard and deviant beeps). time 2 : 100-300 ms : Bilateral activity in the '''inferior frontal gyrus''' and the auditory cortex corresponding to the detection of an abnormality (latency: 150-250ms) for the deviant beeps only. time 3 : 300-550 ms : Frontal regions activation related to the decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. ---- . '''For the time 1,''' We find high correlation value in both hemisphere on the temporal areas. This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas. Corresponding to the name of the areas here time 3 : 300-550 ms : Frontal regions activation related to the decision making and '''motor''' preparation, for the deviant beeps only (after 300ms). The computation are done here only for the second recording. ==== Coherence ==== ==== Correlation ==== '''For the time 1,''' We find high correlation value in both hemisphere on the temporal areas. This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas. Corresponding to: name of the areas here Similar results are observed either for the deviant and standard sounds. {{attachment:MatrixDeviantCorDestrieuxTime1.PNG||width="500",height="400"}} {{attachment:GraphDeviantCorDestrieuxTime1.PNG||width="600",height="400"}} '''For the time 3, ''' ---- === PLV === This connectivity is observed between the area 99 and 41 and between the 42 and 100 areas. Corresponding to: name of the areas here Similar results are observed either for the deviant and standard sounds. {{attachment:MatrixDeviantCorDestrieuxTime1.PNG||width="500",height="400"}} {{attachment:GraphDeviantCorDestrieuxTime1.PNG||width="600",height="400"}} '''For the time 3, ''' ==== PLV ==== ---- . {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} {{attachment:GraphDeviantPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} } {{attachment:GraphDevianPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} === TODO : Sensors level === Connectivity is computed at the sensors or the electrodes levels from the recorded time series. === PLV === {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} {{attachment:GraphDeviantPlvDestrieuxBandbetaHzTime3_all.PNG||width="345",height="300"}} Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. ---- . {{attachment:GraphStandardPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} } {{attachment:GraphDevianPlvDestrieuxBandbetaHzTime3_Max.PNG||width="345",height="300"}} === TODO : Sensors level === Connectivity is computed at the sensors or the electrodes levels from the recorded time series. === PLV === {{attachment:GraphStandardPlvMEGBandbetaHzTime3_All.PNG||width="345",height="300"}} {{attachment:GraphDevianPlvMEGBandbetaHzTime3_all.PNG||width="345",height="300"}} Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. ---- . {{attachment:GraphStandardPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} {{attachment:GraphDevianPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} '''<<TAG(Advanced)>> ''' ''TODO : discuss '' ''- Explain or give more information about the methods and how to choose the best parameters'' ex: plv better with 100 samples & narrow bands Using the option > right-click on figure> Graphic Options > Display Region max M or just use from the keyboard with M key. {{attachment:GraphStandardPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} {{attachment:GraphDevianPlvMEGBandbetaHzTime3_Max.PNG||width="345",height="300"}} ''TODO : discuss'' ''- Explain or give more information about the methods and how to choose the best parameters'' ex : plv better with 100 samples & narrow bands ''- Explain the choice either with ERP or without, and why (link to the cited paper, can't find it)'' ''- Show/add other relevant measures of statistics to separate the two conditions'' ''- Add the option : checkbox remove the erp for PLV and CORR and PTE'' ''- ...'' == Sections to add == * Discuss option concatenate vs. average for the estimation of coherence on single trials: https://neuroimage.usc.edu/forums/t/difference-between-averaging-coherence-and-concatenate/22726/4 * Discuss pValues computed for the various methods |
In the rest of this section, correlation is computed on the scouts time series of the average response for the standard and deviant conditions. On practice connectivity metrics are computed trial-wise and the results are aggregated. An example of this approach can be seen in the [[Tutorials/CorticomuscularCoherence|corticomuscular coherence tutorial]]. }}} In the [[Tutorials/Scouts#Other_regions_of_interest|Scouts tutorial]], we have created 4 scouts for these regions of interest: '''A1L''' and '''A1R''' for the left and right primary cortices respectively, '''IFGL''' for the left inferior frontal gyrus, and '''M1L''' for the left primary motor cortex. {{attachment:scouts_avg_rel.png}} Let's compute source-domain [[#Correlation|correlation]] for '''standard''' and '''deviant''' conditions for the Run #1: '''S01_AEF_20131218_01_600Hz_notch''' data. 1. Drag and drop the source files associated to the average standard response ('''Avg: standard (193 files)''') and the average deviant response ('''Avg: deviant (193 files)''') within the '''''Process1''''' tab, select the option 'source process' ( {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconResultList.gif}} ), and click on the '''''[Run]''''' button. 1. Add a the process, '''''Connectivity > Correlation NxN'''''. Set the time window from '''0 to 150 ms'''. Check the '''''Use scouts''''' option, and select '''User scouts''' as atlas in the drop menu. Set the '''''Scout function''''' to '''Mean''', for '''''When to apply the scout function''''' select '''Before'''. And select '''''Save individual results (one file per input)'''''. Finally click on '''''[Run]'''''. <<BR>><<BR>> 1. Display the connectivity matrices as '''Image''' (top) and as '''Graph''' (bottom). Adjust the colormaps to show signed values (no absolute), and set the a custom range from '''-0.8''' to '''0.8'''. Lastly, adjust the '''Intensity threshold''' for the graph to the maximum (around 0.7), so only the strongest correlations are kept, mainly, between scouts in the left and right auditory cortices. ||<style="text-align:center">Standard || ||<style="text-align:center">Deviant || || {{attachment:corr_0_150_std_intro.png||width="350"}} || || {{attachment:corr_0_150_dev_intro.png||width="350"}} || || {{attachment:corrg_0_150_std_intro.png||width="350"}} || || {{attachment:corrg_0_150_dev_intro.png||width="350"}} || In this early response period, we appreciate that the correlation matrices for the standard ann deviant response are quite similar, and the strongest correlation happens between the scouts on the primary auditory cortices; just as expected. <<HTML(--> )>> == Thresholding of connectivity estimates == === Interactive tools === Brainstorm provides tools to apply empirical thresholds to display the resulting connectivity estimates. Interactions can be filtered interactively based on their magnitudes, the distance between the nodes of the graph or their category. See the tutorial: [[https://neuroimage.usc.edu/brainstorm/Tutorials/ConnectivityGraph#Filtering_options|Connectivity graphs]]. {{attachment:display_panel.gif||height="195",width="192"}} === Threshold by percentile === The process '''Test > Threshold by percentile''' allows the selection of the top n% connectivity estimates in a single input file. {{attachment:percentile.png||width="300"}} All connectivity estimates (left panel below). The top-5% connectivity matrix (right panel below) only keeps the 5 percentile of all the connectivity estimates. || {{attachment:percentile_100.png||width="350"}} || || {{attachment:percentile_5.png||width="350"}} || === Statistical significance === Inference based threshold can be derived to assess the statistical significance of the connectivity estimates, for instance using non-parametric paired permutation tests. Connectivity outcomes can be computed for different experimental conditions, or between an active state and a baseline. '''Non-parametric paired permutation tests '''are available in Brainstorm to compare between two groups of repeated measures. More information in the [[https://neuroimage.usc.edu/brainstorm/Tutorials/Statistics#Nonparametric_permutation_tests|Statistics tutorial]]. {{attachment:stat_perm.gif||height="141",width="309"}} |
| Line 442: | Line 420: |
| '''TODO''': Document data storage. |
==== File name ==== The connectivity file structure is an extension of the time-frequency structure. The file names start with '''''timefreq_''''', followed by '''''connect1''''' (1xN) or '''''connectn''''' (NxN or AxB), the connectivity method and a time stamp. ''Example: timefreq_connectn_corr_220120_1350.mat''. ==== File structure ==== Right click on the first connectivity file computed > File > '''View file contents'''. . {{attachment:file_connect.gif}} The data structure is the same as for Brainstorm [[https://neuroimage.usc.edu/brainstorm/Tutorials/TimeFrequency#On_the_hard_drive|time-frequency files]]. Only the fields specific to connectivity analyses are documented below: * '''TF''': [Nr x Ntime x Nfreq] array containing all connectivity values. The connectivity matrix '''R''' computed in [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/connectivity/bst_connectivity.m#L292|bst_connectivity.m]] between two sets of signals A and B, is optimized and saved in the TF variable. The size of the R matrix is [Na x Nb x Ntime x Nfreq]. The relation between Na x Nb and Nr depends on the type of optimization in the file. See details below. * '''RefRowNames''': Cell-array of strings {Na x 1}. Labels of the rows of the connectivity matrix R (Y axis in the image display, with the label ''From''). In the case of a AxB process, these labels are the names of the signals extracted from the first list of files (FilesA). * '''RowNames''': Cell-array of strings {Nb x 1}. Labels of the columns of the connectivity matrix R (X axis in the image display, with the label ''To''). In the case of a AxB process, these labels are the names of the signals extracted from the second list of files (FilesB). * '''Freqs''': Double [1 x Nfreq] for a simple list of frequencies; or cell-array {Nfreq x 3} if using frequency bands, where each line represents a band {'band_name', 'frequency definition', 'function'} * '''Time''': [1,Ntime] for time-resolved files; [1,2] for files with no data dimension (e.g. correlation). When no time is available, this variable describes the time segment from which the connectivity measure was computed. * '''Options.isSymmetric''': Boolean indicating whether the matrix R saved in the TF field is symmetric (e.g. NxN correlation or coherence) or not (e.g. Granger causality). If the R matrix is symmetric, it is saved in a compressed format, with only the values from lower triangular matrix. ==== Connectivity matrix encoding ==== Let's consider the structure '''TfMat''', loaded from a connectivity file, for example by right-clicking on the file > File > Export to Matlab. The connectivity matrix '''R''' can be obtained with function [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/core/bst_memory.m#L1897|GetConnectMatrix]]. The size of R is '''[Na x Nb x Ntime x Nfreq]'''. {{{ R = bst_memory('GetConnectMatrix', TfMat); }}} If the matrix is not symmetrical (i.e., not compressed): for each time and frequency, the list of values from the first dimension of the TF variable is reshaped into a 2D matrix: [Na x Nb]. If the matrix is symmetrical and compressed: only the lower triangular matrix is saved in the TF variable. The full matrix is first reconstructed with function [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/process/functions/process_compress_sym.m#L118|process_compress_sym>Expand]], then reshaped into [Na x Nb]. Saving the connectivity matrix R back in the TF variable is possible by reshaping to [Nx1] ('''''R(:)''''') and then compressing again the matrix: {{{ TfMat.TF = process_compress_sym('Compress', R(:)); }}} |
| Line 445: | Line 454: |
| ==== References ==== <<Anchor(reference_x)>> 1. Reference #1 <<Anchor(reference_y)>> 2. Reference #2 <<Anchor(reference_z)>> 3. Reference #3 |
==== Related tutorials ==== * [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence|Corticomuscular coherence]] * [[https://neuroimage.usc.edu/brainstorm/Tutorials/ConnectivityGraph|Connectivity Graphs]] * [[https://neuroimage.usc.edu/brainstorm/Tutorials/FiberConnectivity|Virtual fibers for connectivity]] * [[https://neuroimage.usc.edu/brainstorm/GrangerCausality|Granger causality]] |
| Line 453: | Line 461: |
| * Lagged-Coherence: Pascual-Marqui RD. [[https://arxiv.org/pdf/0706.1776|Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions]], arXiv preprint arXiv:0706.1776. 2007 Jun 12. * Phase transfer entropy: Lobier M, Siebenhühner F, Palva S, Palva JM [[http://www.sciencedirect.com/science/article/pii/S1053811913009191|Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions]], NeuroImage 2014, 85:853-872 * Barzegaran E, Knyazeva MG. [[https://doi.org/10.1371/journal.pone.0181105|Functional connectivity analysis in EEG source space: The choice of method]] Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105. |
* Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M. <<BR>> [[https://doi.org/10.1016/j.clinph.2004.04.029|Identifying true brain interaction from EEG data using the imaginary part of coherency]]. <<BR>> Clinical Neurophysiology. 2004 Oct;115(10):2292–307. * Pascual-Marqui RD. <<BR>> [[https://arxiv.org/pdf/0706.1776|Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions.]] <<BR>> arXiv preprint arXiv:0706.1776. 2007 Jun 12. * Bressler SL, Seth AK. <<BR>> [[https://doi.org/10.1016/j.neuroimage.2010.02.059|Wiener–Granger causality: a well established methodology.]] <<BR>> Neuroimage. 2011 Sep 15;58(2):323-9. * Dhamala M, Rangarajan G, Ding M. <<BR>> [[https://doi.org/10.1103/PhysRevLett.100.018701|Estimating Granger causality from Fourier and wavelet transforms of time series data.]] <<BR>> Physical review letters. 2008 Jan 10;100(1):018701. * Hipp JF, Hawellek DJ, Corbetta M, Siegel M, Engel AK. <<BR>> [[https://doi.org/10.1038/nn.3101|Large-scale cortical correlation structure of spontaneous oscillatory activity.]] <<BR>> Nature neuroscience. 2012 Jun;15(6):884-90. * Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, et al. <<BR>> [[https://doi.org/10.1103/PhysRevLett.81.3291|Detection of n : m Phase Locking from Noisy Data: Application to Magnetoencephalography.]] <<BR>> Phys Rev Lett. 1998 Oct 12;81(15):3291–4. * Bruña R, Maestú F, Pereda E<<BR>>[[https://pubmed.ncbi.nlm.nih.gov/29952757|Phase locking value revisited: teaching new tricks to an old dog]]<<BR>>Journal of Neural Engineering, Jun 2018 * Vinck M, Oostenveld R, van Wingerden M, Battaglia F, Pennartz CM<<BR>>[[https://pubmed.ncbi.nlm.nih.gov/21276857|An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias]]<<BR>>Neuroimage, Apr 2011 * Lobier M, Siebenhühner F, Palva S, Palva JM. <<BR>> [[https://doi.org/10.1016/j.neuroimage.2013.08.056|Phase transfer entropy: a novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions.]] <<BR>> Neuroimage. 2014 Jan 15;85:853-72. * Barzegaran E, Knyazeva MG. <<BR>> [[https://doi.org/10.1371/journal.pone.0181105|Functional connectivity analysis in EEG source space: The choice of method]] <<BR>> Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105. * Lai M, Demuru M, Hillebrand A, Fraschini M. <<BR>> [[https://doi.org/10.1038/s41598-018-30869-w|A comparison between scalp- and source-reconstructed EEG networks.]] <<BR>> Sci Rep. 2018 Dec;8(1):12269. * Schoffelen J-M, Gross J. <<BR>> [[https://doi.org/10.1002/hbm.20745|Source connectivity analysis with MEG and EEG.]] <<BR>> Hum Brain Mapp. 2009 Jun;30(6):1857–65. * Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI. <<BR>> [[https://doi.org/10.1038/nn.2303|Circular analysis in systems neuroscience: the dangers of double dipping.]] <<BR>> Nat Neurosci. 2009 May;12(5):535–40. * Cohen MX. <<BR>> [[https://mitpress.mit.edu/books/analyzing-neural-time-series-data|Analyzing Neural Time Series Data: Theory and Practice]]. MIT Press; 2014. * Sadaghiani S, Brookes MJ, Baillet S.<<BR>>[[https://doi.org/10.1016/j.neuroimage.2021.118788|Connectomics of human electrophysiology]].<<BR>>NeuroImage. 2022 Feb;247:118788. * Sporns O. <<BR>> [[https://mitpress.mit.edu/9780262528986/networks-of-the-brain|Networks of the Brain]]. MIT Press; 2016. |
| Line 460: | Line 494: |
| * Connectivity matrix storage:[[http://neuroimage.usc.edu/forums/showthread.php?1796-How-the-Corr-matix-is-saved|http://neuroimage.usc.edu/forums/showthread.php?1796]] * Comparing coherence values: http://neuroimage.usc.edu/forums/showthread.php?1556 * Reading NxN PLV matrix: http://neuroimage.usc.edu/forums/t/pte-how-is-the-connectivity-matrix-stored/4618/2 * Export multiple PLV matrices: https://neuroimage.usc.edu/forums/t/export-multiple-plv-matrices/2014/4 * Scout function and connectivity: http://neuroimage.usc.edu/forums/showthread.php?2843 * Unconstrained sources and connectivity: http://neuroimage.usc.edu/forums/t/problem-with-surfaces-vs-volumes/3261 * Digonal values: http://neuroimage.usc.edu/forums/t/choosing-scout-function-before-or-after/2454/2 * Connectivity pipeline: https://neuroimage.usc.edu/forums/t/help-for-connectivity-pipeline/12558/4 * Ongoing developments: https://neuroimage.usc.edu/forums/t/connectivity-tutorial-and-methods-development-on-bst/12223/3 * Granger causality: https://neuroimage.usc.edu/forums/t/is-granger-causality-analysis-a-linear-operation/12506/12 * Amplitude Envelope Correlation: * https://neuroimage.usc.edu/forums/t/problem-with-time-dynamic-envelope-correlation/21542/9 * https://github.com/brainstorm-tools/brainstorm3/issues/142 |
* Granger causality: [[https://neuroimage.usc.edu/forums/t/is-granger-causality-analysis-a-linear-operation/12506/12|https://neuroimage.usc.edu/forums/t/12506]] * Coherence on single trials: [[https://neuroimage.usc.edu/forums/t/difference-between-averaging-coherence-and-concatenate/22726/4|https://neuroimage.usc.edu/forums/t/22726]] * ciPLV: https://neuroimage.usc.edu/forums/t/9751 * wPLI: https://neuroimage.usc.edu/forums/t/9434 * Coherence and PLV: https://neuroimage.usc.edu/forums/t/33379 * Removing ERP response for PLV: https://neuroimage.usc.edu/forums/t/32665 * Connectivity of subcortical ROIs: https://neuroimage.usc.edu/forums/t/33479 * Non-zero diagonals with unconstrained sources: https://neuroimage.usc.edu/forums/t/33700 * Coherence/Lagged coherence vs. Envelope correlation/Lagged coherence: https://neuroimage.usc.edu/forums/t/lagged-coherence/39440 |
| Line 476: | Line 514: |
| <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/GroupAnalysis&next=Tutorials/Scripting")>> | == Scripting == The following script from the Brainstorm distribution reproduces the analysis presented in this tutorial page: [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/script/tutorial_connectivity.m|brainstorm3/toolbox/script/tutorial_connectivity.m]] <<HTML(<div style="border:1px solid black; background-color:#EEEEFF; width:720px; height:500px; overflow:scroll; padding:10px; font-family: Consolas,Menlo,Monaco,Lucida Console,Liberation Mono,DejaVu Sans Mono,Bitstream Vera Sans Mono,Courier New,monospace,sans-serif; font-size: 13px; white-space: pre;">)>><<EmbedContent("https://neuroimage.usc.edu/bst/viewcode.php?f=tutorial_connectivity.m")>><<HTML(</div >)>> |
| Line 479: | Line 520: |
== TODO == '''Hossein, Richard''' * Granger Causality implementation: https://github.com/brainstorm-tools/brainstorm3/pull/433 '''Raymundo, Sylvain''' * Read data: Can we find something more meaningful than what we compute in the example in the dataset? A full connectome in a task vs. baseline maybe? |
Connectivity
Authors: Hossein Shahabi, Raymundo Cassani, Takfarinas Medani, François Tadel, Marc Lalancette, Sylvain Baillet
Brain functions (e.g., in cognition, behavior and perception) stem from the coordinated activity of multiple regions. Brain connectivity measures are designed to probe how brain regions (or nodes) interact as a network. A distinction is made between structural (fiber pathways), functional (non-directed statistical associations) and effective (causal interactions, or "directed functional connectivity") connectivity between regions. Here we explain how to compute various connectivity metrics for non-directed and directed functional connectivity analyses with Brainstorm, both with simulated (ground-truth) and empirical data.
We encourage the interested reader to learn more about the specific aspects of electrophysiology for studying human connectomics.
Contents
- Introduction
- Pre-requisites
- Simulated data
- Correlation
- Coherence
- Granger causality
- Spectral Granger causality
- Envelope correlation
- Phase-Locking Value
- Phase-Transfer Entropy
- Summary: connectivity methods
- Thresholding of connectivity estimates
- On the hard drive
- Additional documentation
- Scripting
- TODO
Introduction
Definitions
Connectivity analyses are commonly performed by computing a bivariate measure between pairs of regional time series of interest. The outcome (a.k.a a connectome) can be represented as a connectivity graph (left panel below), with each brain region as a node (x, y, z,...), and the connectivity measures shown above each edge of the graph. The connectome can also be represented by a connectivity array, a.k.a. an adjacency matrix (right panel below).
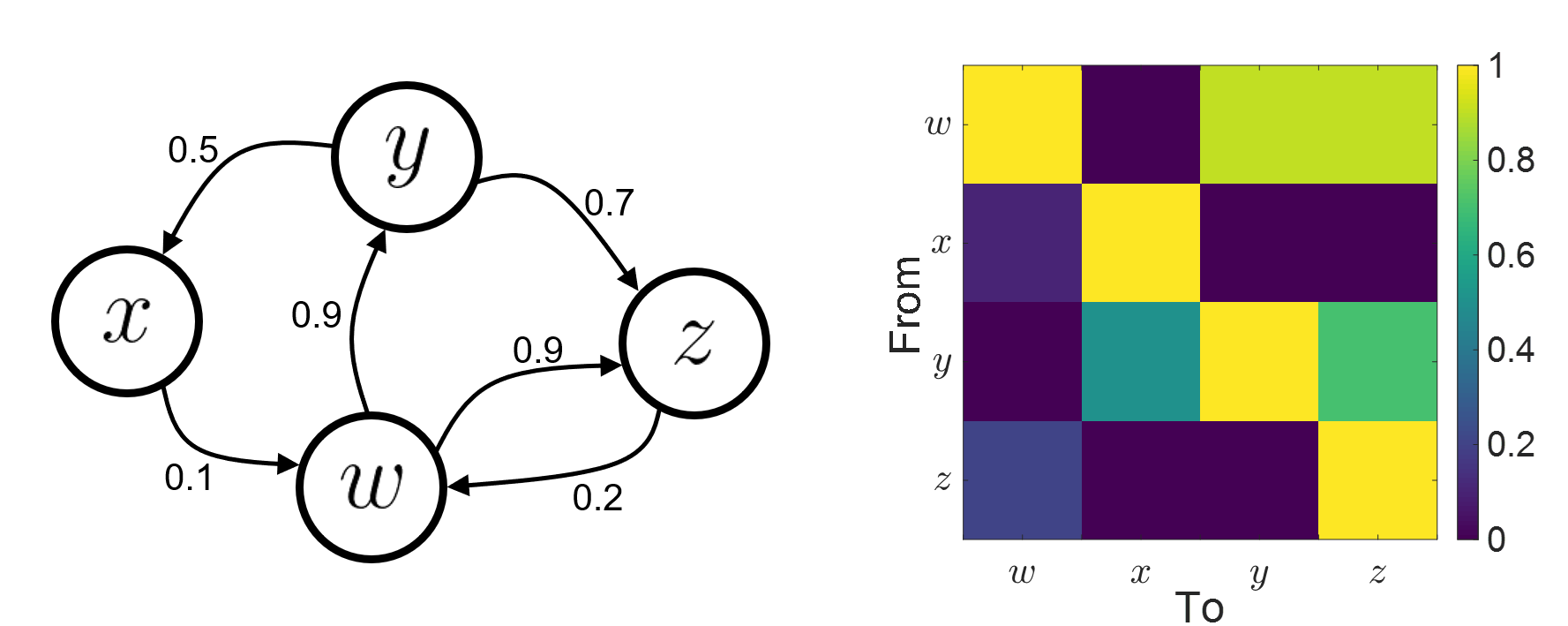
Sensors or sources: The time series used for connectivity analyses can be from sensor data (EEG/MEG signals) or from source time series (brain voxels or scouts).
Directed vs. non-directed: The direction of interactions between signals (as a measure of statistical causation) is estimated with directed metrics. Non-directed metrics produce symmetrical connectivity graphs/matrices: the connectivity measure "from Signal  to Signal
to Signal  " is identical to the connectivity measure "from Signal
" is identical to the connectivity measure "from Signal  to Signal
to Signal  ".
".
Experimental condition: Depending on the neuroscience question, connectivity analyses can be performed on resting-state or task (e.g., ongoing or trial-based) data.
Full (NxN) vs. seeded (1xN) connectivity: In a full connectivity analysis, the connectivity metric is computed for all the possible pairs of nodes between N time series (noted N×N here). Alternatively, seeded connectivity (noted 1×N) is measured between one time series of interest (a seed, e.g., one brain region or a behavioral marker) and N other regions/time series.
Time-frequency transformations: Some connectivity metrics rely on a time-frequency representation of the signals. These latter are obtained with approaches such as the short-time Fourier transform, Hilbert transform, or Morlet wavelets.
Just as in other areas of electrophysiology studies, connectivity analyses need to beguided by mechanistic hypotheses concerning the expected neurophysiological effects.
Sensor-level analyses
Their anatomical interpretation is limited and ambiguous.
Sensor data is affected by field spread and volume conduction of brain activity across the scalp/sensor array. Hence, activity from one single brain area is picked up at multiple, possibly distant sensor locations. Connectivity measures may show strong interactions between sensor time series, which may be wrongly interpreted as inter-regional brain connections.
Source-level analyses
Connectivity measures between source time series are neuroanatomically interpretable and can be derived across participants.
We recommended that the outcomes of sensor and source connectivity analyses are mutually compatible; see (Lai et al., 2018).
Full-brain connectomes
Whole-brain connectivity analyses at the typical resolution of cortical surfaces in Brainstorm involve thousands of source locations, making the N×N derivations impractical. For instance, 15000 cortical vertices would yield a connectivity matrix of 15000x15000x8 bytes = 1.6 GB. If unconstrained cortical sources are used and coherence is computed across 50 frequency bins, the memory allocation increases to 45000x45000x50x8 = 754 GB per participant/condition/trial/etc. Reducing the N (via e.g., cortical parcellations, ROIs) may be required for practical reasons, depending on computing resources.
Regions of interest
Grouping individual brain sources into ROIs, defined on the cortical surface or in the brain volume helps contain the computational resources required for connectivity analyses (see above). ROIs can be defined based on neuroscience priors and the purpose of the study (Schhoffen and Gross, 2009). You may consider:
Study priors from the literature in your field, specific working hypotheses in terms of neuro-anatomical brain structures expected to be involved.
Association with a non-neuronal signal (e.g., cortico-muscular coherence).
Signal strength, by defining ROIs from brain regions with strongest activity in current data.
Whole-brain cortical parcellation to reduce N.
The tutorial Corticomuscular coherence explains the computation of connectivity measures constrained and unconstrained brain maps for these cases:
One signal x full-brain source maps: link
One signal x scouts: link
ROI-based connectomes, i.e., scouts x scouts: link
Studies have reported similarities and differences between electrophysiological connectomes (from MEG/EEG) and fMRI connectomes. See how the electrophysiological connectomes provide unique insights on how functional communication is implemented in the brain in Sadaghiani et al., 2022.
On whole-brain connectivity analyses and the issue of circular analysis, please see Kriegeskorte et al., 2009.
Pre-requisites
Here we focus on the specifics on connectivity analyses with Brainstorm. Please make sure you are familiar with Brainstorm and go through all introduction tutorials first, before following the present tutorial.
We first use simulated, synthetic data to emphasize the theoretical aspects of each connectivity metric with respect to groundtruth outcomes. Real, empirical MEG data are featured later in the tutorial (same auditory oddball dataset as in the other tutorial sections).
Let's start by creating a new protocol in the Brainstorm database:
Select the menu File > Create new protocol > type in "TutorialConnectivity" and select the options:
Yes, use protocol's default anatomy,
No, use one channel file per condition.
Right-click on the TutorialConnectivity folder > New subject > Subject01
Simulated data
To compare connectivity metrics, let's use synthetic time series simulated with known ground truth interactions. We will use a multivariate autoregressive (MVAR) model that consists of the following three signals:
Signal 1: two oscillatory (rhythmic) components: One at 10 Hz (alpha band), and a stronger peak at 25 Hz (beta band).
Signal 2: Same as Signal 1, with the strongest peak at 10 Hz.
Signal 3: Same as above, with the two components (10 and 25 Hz) of same magnitude.
The 25-Hz component of Signal 3 will be driven in part by the 25-Hz component of Signal 1 (denoted Signal 1>>Signal 3).
Let's now generate the three time series:
In the Process1 tab, leave the file list empty and click on the button [Run]
Select process: Simulate > Simulate AR signals.
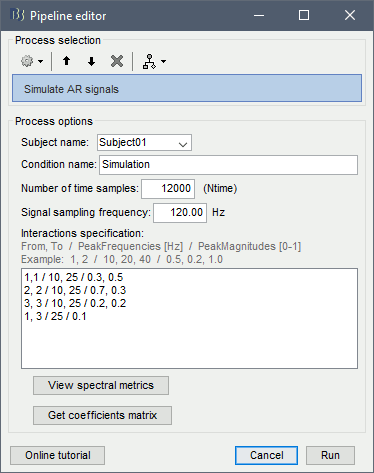
Process options:
Subject name: Target subject for the simulated signals: Select Subject01.
Condition name: Target folder where to store the simulated data in your database: Set to Simulation.
Number of time samples for each simulated time series: Set to 12,000.
Sampling frequency (Fs): Set to 120 Hz.
Interaction specifications: Spectral parameters for the signal components and their interactions in the MVAR model: From, To / Peak frequencies [Hz] / Peak relative magnitudes [0-1]
Set to:1, 1 / 10, 25 / 0.3, 0.5 2, 2 / 10, 25 / 0.7, 0.3 3, 3 / 10, 25 / 0.2, 0.2 1, 3 / 25 / 0.1
Display the groundtruth spectral metrics of the MVAR-generated time series: transfer function, cross-spectral power density, magnitude square coherence, directed transfer function (DTF) and partial directed coherence (PDC). The transfer function (
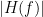 ) characterizes the relationships between signals in the frequency domain. It is a non-symmetric representation, which enables the identification of causal dependencies between signal components. The auto-transfer functions (shown in the graphs along the diagonal below) display the power spectra of each signal. The off-diagonal representations display the interactions between each pair of signals (see Signal 1 >> Signal 3 above). Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values.
) characterizes the relationships between signals in the frequency domain. It is a non-symmetric representation, which enables the identification of causal dependencies between signal components. The auto-transfer functions (shown in the graphs along the diagonal below) display the power spectra of each signal. The off-diagonal representations display the interactions between each pair of signals (see Signal 1 >> Signal 3 above). Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values.
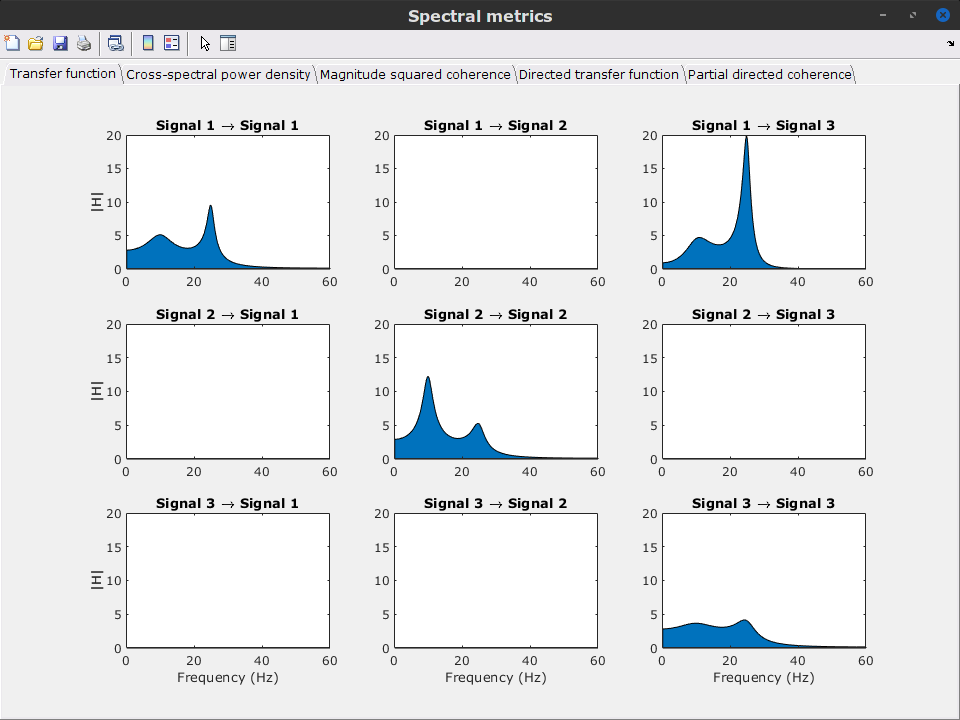
Get coefficients matrix: Shows the coefficients related to the MVAR model. These coefficients can be used in the process Simulate > Simulate AR signals (ARfit) to simulate the same model.
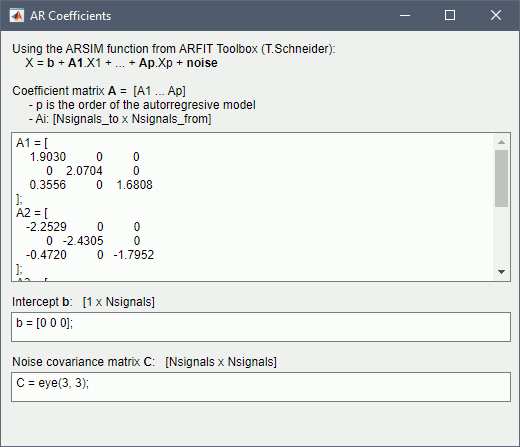
Execution:
Click Run to generate the time series with the MVAR model.
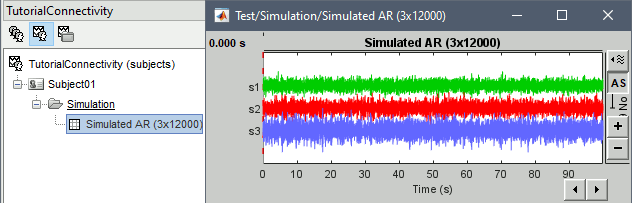
In the next sections, we will compute different connectivity metrics from these synthetic time series. Drag and drop the simulated data in the Process1 tab, click on [Run] (
 ) to open the Pipeline editor, and select the connectivity metric.
) to open the Pipeline editor, and select the connectivity metric.
This tutorial illustrates the computation of full connectivity graphs (Process 1: NxN). It is also possible to obtain connectivity measures between one of the time series of a given data file and the other time series in the same file (use Process1: 1xN), or between time series from two different data files (use Process2: AxB), as shown further below.
References used:
This process relies on the ARSIM function from the ARFit toolbox:
https://github.com/tapios/arfitNeumaier A, Schneider T
Estimation of parameters and eigenmodes of multivariate autoregressive models
ACM Transactions on Mathematical Software, 2001Schneider T, Neumaier A
Algorithm 808: ARfit – A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models
ACM Transactions on Mathematical Software, 2001
Correlation
Correlation is a relatively simple, non-directed connectivity metric of association between two time series. It is relatively limited without further preprocessing of the input time series: correlation is sensitive to volume conduction and is not frequency specific.
Process options
Process Connectivity > Correlation NxN:
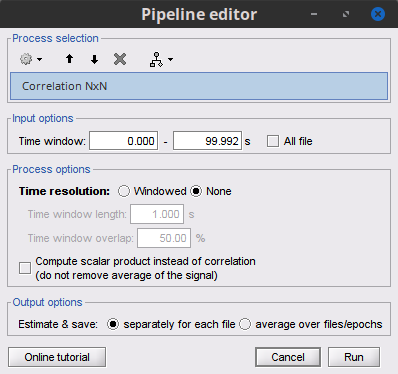
Time window: Time segment of the signals for connectivity analysis. Select: All file.
Time resolution: Select None
Windowed: correlation is computed in windows of a given length with a certain overlap percentage
None: correlation is computed using the entire time series
Compute scalar product: If left unchecked, the mean of the time series is subtracted before computing the correlation. Leave it unchecked.
Output options: Select Estimate and save separately for each file.
Result visualization
The results are stored as a N×N connectivity file, with a new icon
 . Right-click for display options:
. Right-click for display options:
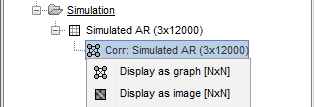
Display as graph: Plots the connectivity graph using a chord diagram where the color of the edges shows the value of the connectivity metric. See the connectivity graph tutorial for a detailed explanation of the options of this visualization.
Display as image: Plots the connectivity measures in an adjacency matrix.
Display fibers: Displays source connectivity edges as virtual white fiber tracts, as shown here.
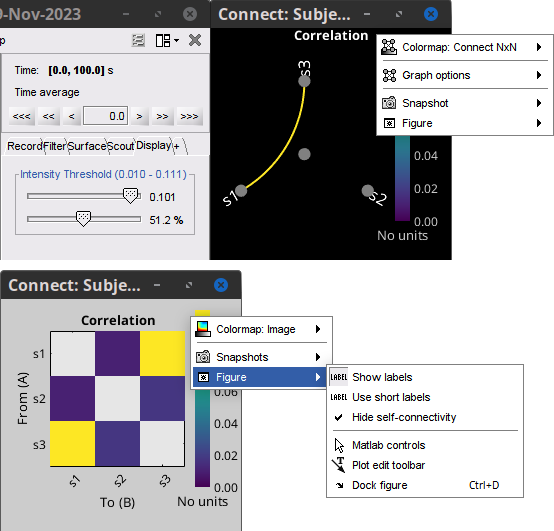
Display options:
Show labels: Click on the figure to display the names of the times series and the connectivity values in the figure legend. To display the labels corresponding to each column and row: right-click on the figure > Figure > Show labels. If the time series names are too long, use the option Use short labels.
Hide self-connectivity: In a square NxN connectivity matrix, the diagonal values correpond to the values of the connectivity metric between a time series and itself. These self-connectivity values are typically much higher than the other values of the matrix. When checked, these values are hidden so that to display the off-diagonal values more clearly.
Colormap: By default, the NxN colormap is configured to display the absolute values of the connectivity measures. Correlation values may be positive or negative. To display the negative values, make sure to change the colormap configuration: right-click on the figure > Colormap > Uncheck Absolute values.
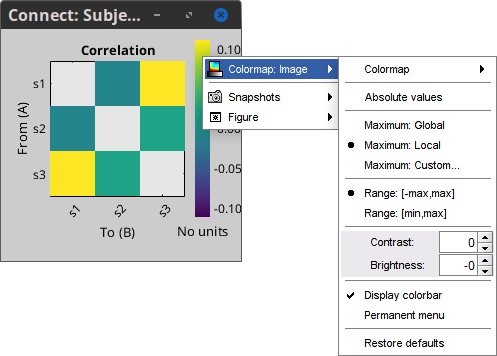
Coherence
Coherency or complex coherence, 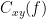 , is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Magnitude square coherence (MSC),
, is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Magnitude square coherence (MSC), 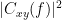 , or coherence, measures the covariance of two signals in the frequency domain. For a pair of time series
, or coherence, measures the covariance of two signals in the frequency domain. For a pair of time series 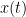 and
and 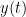 , with spectra
, with spectra 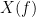 and
and 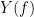 , the MSC is defined as:
, the MSC is defined as:
Two related measures, which address the problem of volume conduction, are imaginary coherence (Nolte et al., 2004), 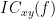 , and lagged coherence (Pascual-Maqui, 2007),
, and lagged coherence (Pascual-Maqui, 2007), 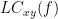 , which are defined as:
, which are defined as:
where 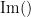 and
and 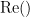 are the imaginary and real parts of a complex number, respectively.
are the imaginary and real parts of a complex number, respectively.
Note that the cross-spectrum (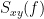 ) and the power spectral densities (
) and the power spectral densities (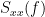 and
and 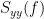 ), and as consequence also coherency (
), and as consequence also coherency (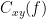 ) can be obtained through different time-frequency decomposition methods (such as: Hilbert transform, wavelet transform and short-time Fourier transform), and for different time resolutions (per sample, windowed and entire file).
) can be obtained through different time-frequency decomposition methods (such as: Hilbert transform, wavelet transform and short-time Fourier transform), and for different time resolutions (per sample, windowed and entire file).
Process options
Process Connectivity > Coherence NxN:
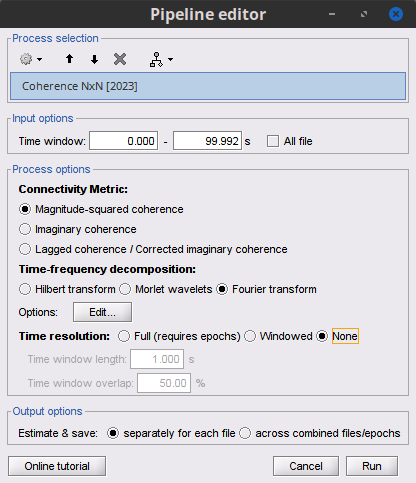
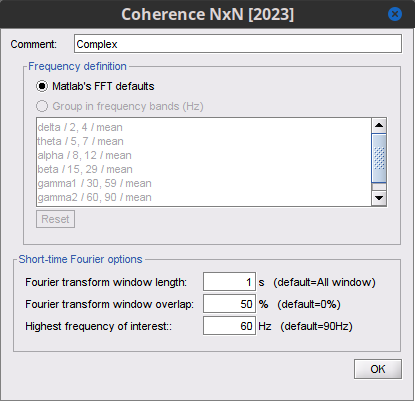
Time window: Segment of the time series used for the connectivity analysis. Select All file.
Connectivity metric shows variants of coherence measures. Select: Magnitude squared coherence.
Time-frequency decomposition selection of the time to time-frequency transformation. Select: (short-time) Fourier transform.
Options [Edit] shows the options of the selected time-frequency transformation.
Window length: Duration in seconds for the spectrum estimation. Set to: 1s.
Overlap: Percentage of overlap between consecutive sliding time windows. Set to: 50%.
Highest frequency: After the computation, removes all the frequencies above this threshold, mostly for visualization purposes. The value needs to be <= Fs/2. Set to: 60 Hz.
Time resolution selection of the time resolution. Select: None.
Output options: Select Estimate and save separately for each file.
Result visualization
Coherence is frequency specific: a connectivity graph and a connectivity matrix are produced for each frequency bin of the spectrum. Right-click on the coherence result file to show display options:
Display as graph: Plots a connectivity graph for each frequency bin.
Display as image: Plot a connectivity matrix for each frequency bin.
Power spectrum: Plot coherence as a function of frequency, between each time series.
Open the 3 types of visualization: they are linked by clicking on the spectral representation of the coherence, which will change the current frequency bin and update the connectivity measures displayed in the graph and matrix. The value of the current frequency bin can also be changed in the Time panel.
Other variants of coherence can be derived following the above procedure. The figures below display the coherence spectra obtained from the imaginary coherence (left) and the lagged coherence (right) measures.
|
|
|
Granger causality
Granger causality (GC) is a measure of directed functional connectivity based on the Wiener-Granger causality framework. GC measure linear dependencies between time series, and tests whether the prediction of the future of signal 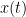 (approximated by a linear autoregressive model) is improved by considering signal
(approximated by a linear autoregressive model) is improved by considering signal 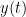 (also approximated by a linear autoregressive model). If there is such improvement, one concludes that signal
(also approximated by a linear autoregressive model). If there is such improvement, one concludes that signal 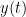 has a Granger causal effect on the other signal. In sum, some independent information from the past of signal
has a Granger causal effect on the other signal. In sum, some independent information from the past of signal 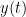 improves the prediction of the future of signal
improves the prediction of the future of signal 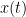 , with respect to only observing its past
, with respect to only observing its past 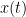 . GC takes nonnegative values; its is zero when no Granger causality can be attributed. The term independent means that GC is invariant with the scale of the input signals
. GC takes nonnegative values; its is zero when no Granger causality can be attributed. The term independent means that GC is invariant with the scale of the input signals 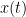 and
and 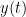 .
.
See Granger causality - mathematical background for a more complete background.
Despite the name, Granger causality indicates directionality but not true causality.
For example, if a variable 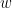 is causing both
is causing both  and
and 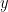 , but with a smaller delay for
, but with a smaller delay for 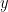 than for
than for  , then the GC measure between
, then the GC measure between  and
and 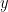 would show a non-zero GC for
would show a non-zero GC for  -->
-->  , even though
, even though  is not truly causing
is not truly causing  (Bressler and Seth, 2011).
(Bressler and Seth, 2011).
Process options
Process Connectivity > Bivariate Granger causality NxN
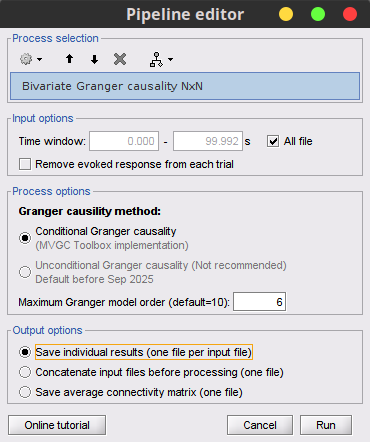
Time window: Time segment of the time series used for the connectivity analysis. Select All file.
Remove evoked response: This option is recommended by some authors as it satisfies the zero-mean stationarity of the GC model, but does not account for trial-to-trial variability; see (Wang et al., 2008). Leave it Unchecked.
Maximum Granger model order: The most common criteria used to define the order of the autoregressive models used by GC to approximate the input time series are the Akaike’s information criterion, the Bayesian-Schwartz’s criterion, and the Hannan-Quinn criterion. Low model orders will yield coarse approximations of the input time series. High model orders may yield spurious GC connectivity estimates. The simulated time series were created with an AR model of order 4; please use a maximum Granger model order of 6.
Output options: Select Save individual results.
Results visualization
The connectivity matrix (left panel below) is not symmetric because GC values are direction specific. The upper right elements of the matrix indicate there is a GC influence from signal 1 to signal 3. In the connectivity graph (right panel below) the directionality is shown with an arrowhead at the center for the arc connecting two nodes.
|
|
|
Spectral Granger causality
The Spectral Granger causality is a measure of directed functional connectivity that was developed to indicate frequency specific influences between time series (Dhamala et al., 2008).
Process options
Process: Connectivity > Bivariate Granger causality NxN.
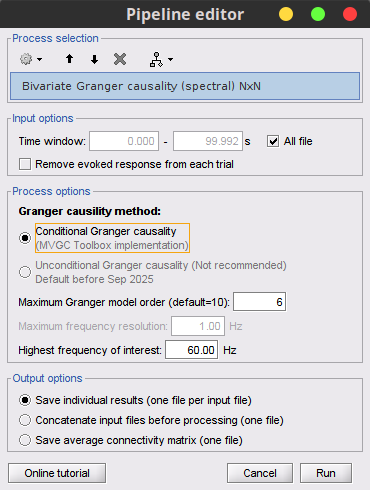
. Here we used the same parameters as with GC plus two two extra parameters specific to spectral GC:Maximum frequency resolution: Width of frequency bins in PSD estimation. Set to 1 Hz.
Highest frequency: computes GC values under the specified frequency. Should be set <= Fs/2. Use: 60 Hz.
Result visualization
As with coherence, spectral GC can be plotted as a function of frequency. The display below shows a peak around 25 Hz that corresponds to the expected causal interaction of Signal 1 on Signal 3.
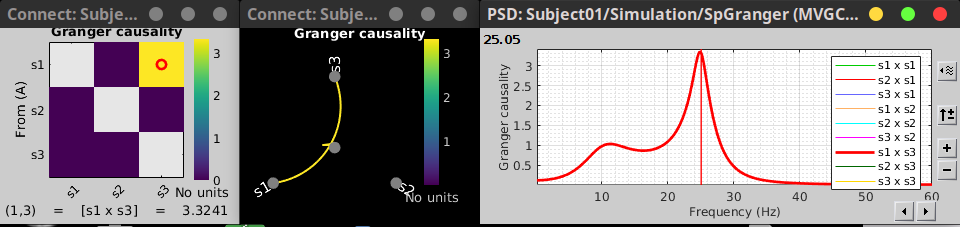
Envelope correlation
In the time-frequency tutorial, we have introduced Morlet wavelets and the Hilbert transform as methods to decompose time series in the time-frequency (TF) domain.
The outcome of these two TF transformations is an analytic signal, 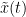 , which is a complex time series uniquely associated to the original data time series,
, which is a complex time series uniquely associated to the original data time series, 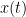 , which module
, which module 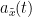 , and phase
, and phase 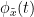 , correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the original time series
, correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the original time series 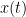 , respectively. The real part of
, respectively. The real part of 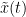 is the original time series
is the original time series 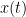 , and the imaginary part is the Hilbert transform of that same time series
, and the imaginary part is the Hilbert transform of that same time series 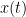 .
.
The analytic signal of oscillatory or narrowband signals provide meaningful and interpretable estimations of instantaneous amplitude and phase. While it is technically feasible to derive these elements from broadband time series, they would not be interpretable (see Cohen, 2014).
The instantaneous amplitude (or envelope) of the analytic signals can be used to carry out pairwise connectivity analysis with correlation. This is to say amplitude envelop correlation (AEC).
An optional step consists in orthogonalizing the pairs of amplitude envelope time series before computing the correlation. Orthogonalization is performed by first removing the real part of their coherence to reduce volume conduction (at the sensor level) or cross-talk effects (at the source level) (Hipp et al., 2012).
Process options
Process: Connectivity > Envelope Correlation N×N [2023]
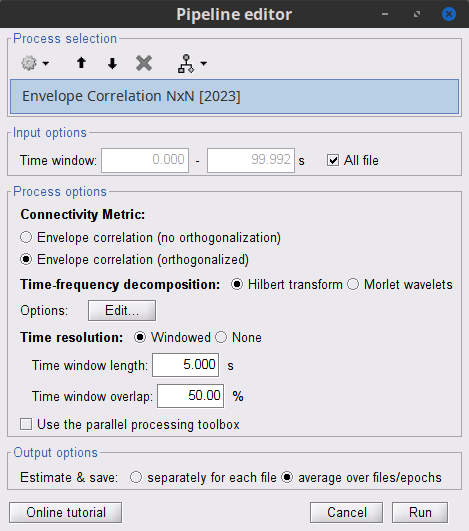
Time window: Time segment of the signal used for the connectivity analysis. Select: All file.
Connectivity measure is the connectivity metric applied to the resulting signal amplitude envelopes. Select Envelope correlation (orthogonalized).
Time-frequency decomposition: Hilbert transform or Morlet wavelets. Each method requires additional parameters that will be displayed in a separate panel after clicking on [Edit]. See the time-frequency tutorial. In the present example, we will use the Hilbert transform with the option Group in frequency bands to present the results for the canonical frequency bands. As the sampling frequency of the signals is 120Hz, thus, make sure you remove the "gamma2" band from the targeted frequency bands.
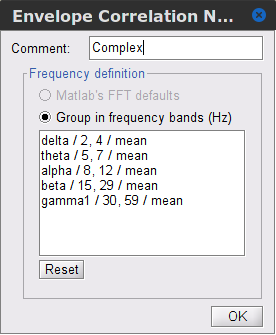
Time resolution: If Windowed, connectivity is saved for each time window. If None, the connectivity measures are averaged across all windows. Select Windowed. Set the additional parameters to define the windows:
Time window length: Duration in milliseconds over which the connectivity measure is computed. Set to 5s
Time window overlap: Percentage of overlap between consecutive time windows to compute the connectivity measure. Set to 50%.
Use the parallel processing toolbox: If available, will call Matlab's parallel processing to accelerate computations. Leave it Unchecked.
Output options: Select Estimate and save separately for each file.
For sake of comparison, we will compute AEC again, but this time changing the TF decomposition method to Morlet wavelets with Linear = 1:1:60 (frequencies from 1 to 60 Hz with 1 Hz step).
Results visualization
As with Coherence and spectral Granger causality, amplitude envelope correlations can be displayed as a function of frequency, and as a function of time if the Time resolution option was set to Windowed. Below are the AEC results obtained with the Hilbert transform (left panels) and with Morlet wavelets (right panels) for the first 5-s time window (top panels) and the 5-s last window (bottom panels).
|
First 5-s window |
|
|
Last 5-s window |
|
Phase-Locking Value
An alternative class of connectivity metrics considers the relative instantaneous phase between two time series as a marker of connectivity. Phase-locking or phase synchronization are two such measures (Tass et al., 1998). In principle, phase-based measures are robust against fluctuations in signal amplitude, although low signal-to-noise conditions remain challenging for these measures (Lachaux et al., 1999; Mormann et al., 2000).
The phase-locking value (PLV) is a popular metric defined as the length of the average vector of many unit vectors whose phase angle corresponds to the phase difference between two time series (Tass et al., 1998). If the distribution of the phase difference between the two signals is uniform, the length of such an average vector will be 0. If the phases of the two signals are strongly coupled, the length of the average vector will be close to 1. For event-related studies, we would expect phase differences across trials to be uniformly distributed, unless the phase of the brain signals is locked to the event onset, which would then indicate a form of phase locking between the two time series. Considering a pair of narrow-band analytic signals 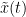 and
and  , obtained from the Hilbert transform (see above):
, obtained from the Hilbert transform (see above):
![\begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*} \begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_34340c3731fe7904b2885462bc74b6a893456cc5_p1.png)
with:
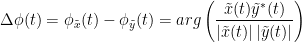
Several variants of PLV have been contritributed. Brainstorm features
ciPLV (Bruña 2018) and wPLI (Vinck 2011) variants contributed to Brainstorm by Daniele Marinazzo.
PLV values tend to be overestimated when derived from few (<50) time samples. As a consequence, when comparing PLV values between conditions, please make sure that they are derived from about the same number of samples in each condition.
Process options
Process: Connectivity > Phase locking value NxN
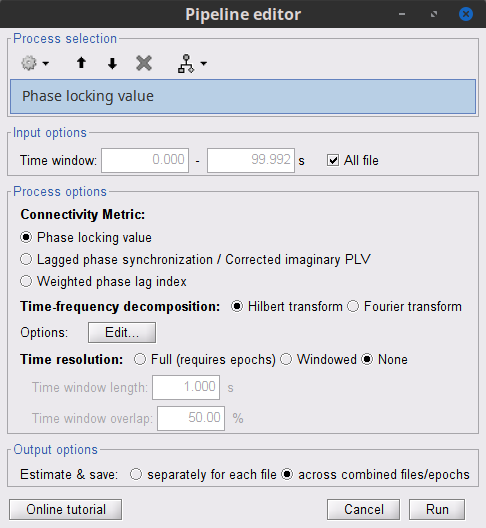
Time window: Time segment of the signal used for the connectivity analysis. Select All file.
Connectivity metric shows variants of phase locking measures. Select: Phase locking value.
Time-frequency decomposition method for time-frequency transformation. Select: Hilbert transform.
Options [Edit] shows the options of the selected time-frequency transformation.
Frequency bands: Used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial. In this example, the sampling frequency of the signals being 120Hz, please remove the "gamma2" band.
Time resolution selection of the time resolution. Select: None.
Output options: Select Save across combined files/epochs.
Results visualization
PLV is frequency resolved, and here was computed for the delta, theta, alpha, beta and gamma1 bands. With the simulated data, we expect a higher PLV value in the beta band (15 to 29 Hz), between Signal 1 and Signal 3. This is indeed our observation, with a peak at 22 Hz (center of beta band) in the PLV spectrum (left). The same is true for ciPLV (center) and wPLI (right).
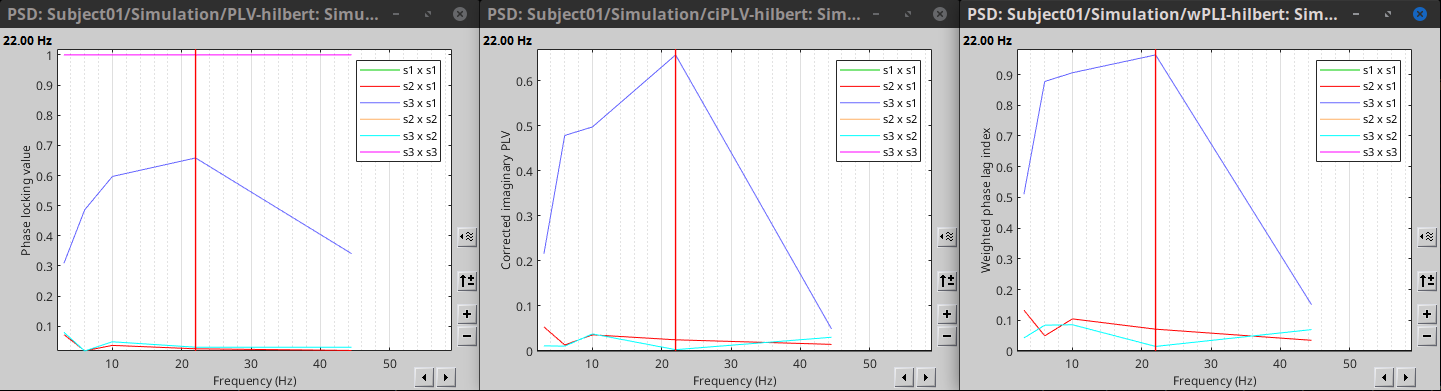
Phase-Transfer Entropy
Phase transfer entropy (PTE) is a directed connectivity metric that quantifies the transfer entropy (TE) between two instantaneous phase time series (Lobier et al., 2014). Similar to GC, TE estimates whether including the past of both source and target time series influences the ability to predict the future of the target time series. In PTE, if a phase signal 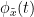 causes the signal
causes the signal 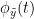 , the mutual information, between
, the mutual information, between 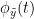 and the past of
and the past of 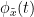 i.e.
i.e. 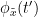 is larger than the mutual information of
is larger than the mutual information of 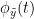 , the past of
, the past of 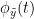 i.e.
i.e. 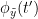 and
and 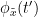 . This relationship can be represented on the Venn diagram below, where
. This relationship can be represented on the Venn diagram below, where 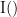 and
and 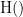 , indicate mutual information and the individual entropies, respectively. PTE values are positive and unbounded.
, indicate mutual information and the individual entropies, respectively. PTE values are positive and unbounded.
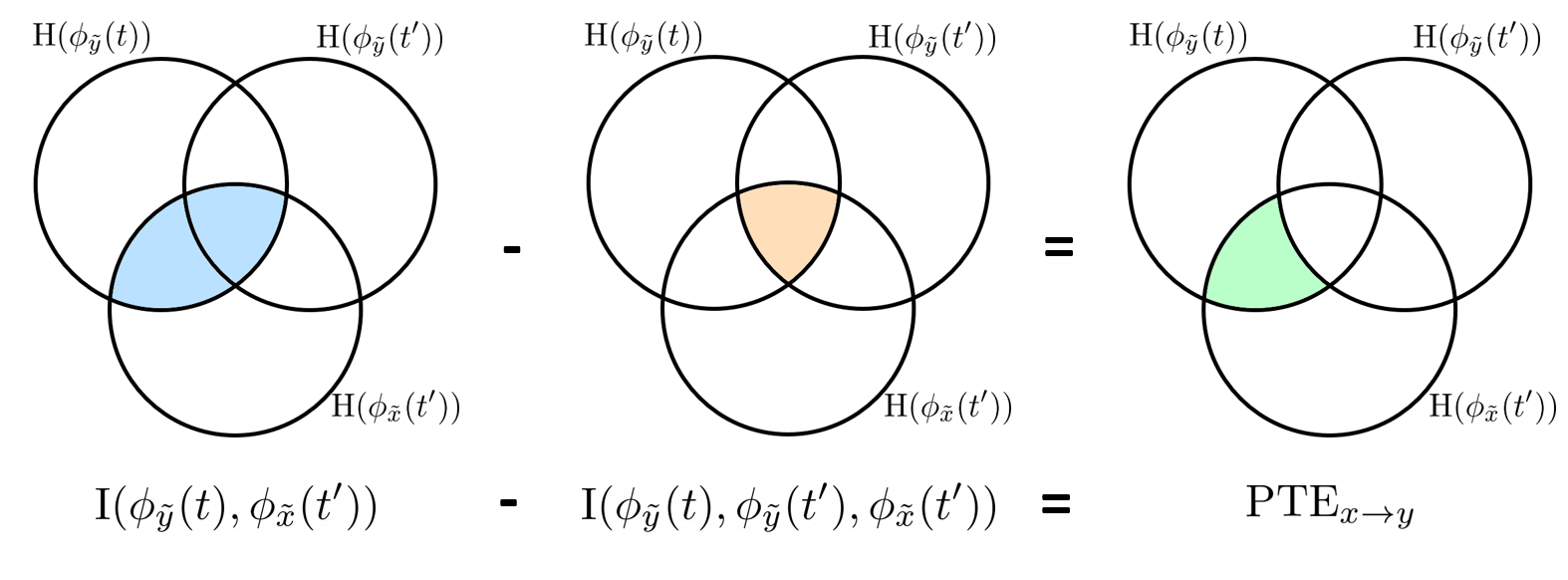
Process options
Process: Connectivity > Phase Transfer Entropy NxN
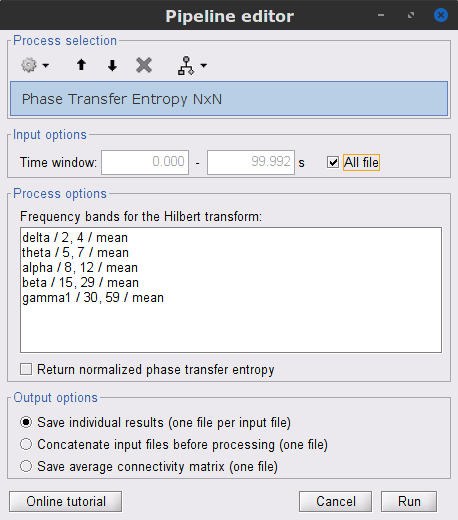
Time window: Time segment of the signal used for the connectivity analysis. Select All file.
Frequency bands: Used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial. In this example, as the sampling frequency of the signals is 120 Hz, make sure the "gamma2" band is removed from the option.
Return normalized phase transfer entropy: Divides each directional PTE value between two signals by the sum of both directional PTE values for those two signals. Uncheck this option
Output options: Select Save individual results.
Results visualization
Here we computed PTE for the delta, theta, alpha, beta and gamma1 bands. From the synthetic data used here, we expect to observe a higher PTE value in the beta band, From Signal 1 To Signal 3. This is indeed shown with a peak at 22 Hz (center of beta band) in the PTE spectrum.
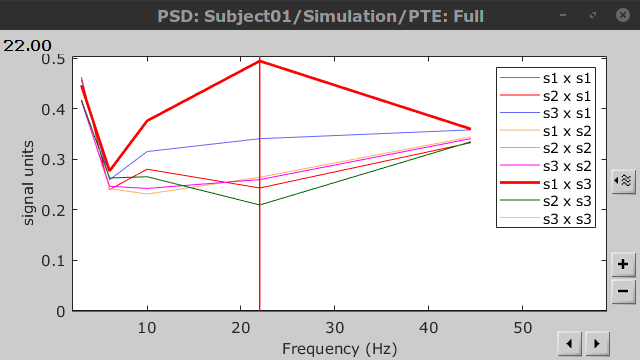 .
.
Summary: connectivity methods
The following table list the available connectivity metrics in Brainstorm and their description.
Metric |
1×N |
N×N |
Directionality |
Freq resolved |
Time resolved |
Function |
Info |
Correlation |
✅ |
✅ |
❌ |
❌ |
✅ |
bst_corrn.m |
|
Coherence |
✅ |
✅ |
❌ |
✅ |
✅ |
bst_cohn.m |
|
Granger causality |
✅ |
✅ |
✅ |
❌ |
❌ |
bst_granger.m |
|
Spectral Granger causality |
✅ |
✅ |
✅ |
✅ |
❌ |
bst_granger_spectral.m |
|
Envelope Correlation (2023) |
✅ |
✅ |
❌ |
✅ |
✅ |
bst_henv.m |
|
Phase locking value |
✅ |
✅ |
❌ |
✅ |
✅ |
bst_connectivity.m |
|
Phase transfer entropy |
❌ |
✅ |
✅ |
✅ |
❌ |
PhaseTE_MF.m |
Thresholding of connectivity estimates
Interactive tools
Brainstorm provides tools to apply empirical thresholds to display the resulting connectivity estimates. Interactions can be filtered interactively based on their magnitudes, the distance between the nodes of the graph or their category. See the tutorial: Connectivity graphs.
Threshold by percentile
The process Test > Threshold by percentile allows the selection of the top n% connectivity estimates in a single input file.
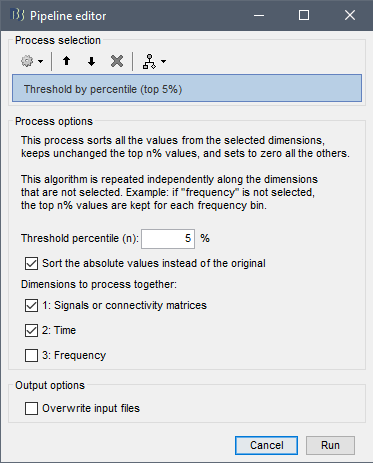
All connectivity estimates (left panel below). The top-5% connectivity matrix (right panel below) only keeps the 5 percentile of all the connectivity estimates.
|
|
|
Statistical significance
Inference based threshold can be derived to assess the statistical significance of the connectivity estimates, for instance using non-parametric paired permutation tests.
Connectivity outcomes can be computed for different experimental conditions, or between an active state and a baseline. Non-parametric paired permutation tests are available in Brainstorm to compare between two groups of repeated measures. More information in the Statistics tutorial.
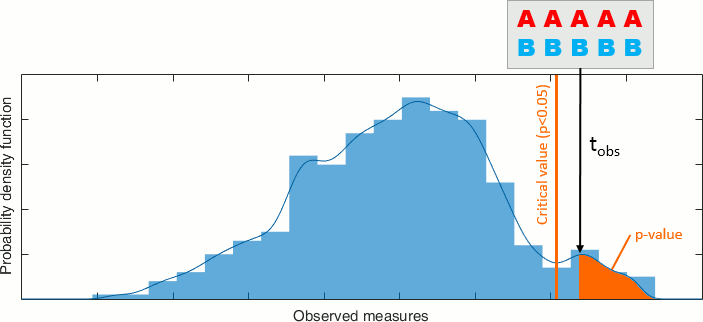
On the hard drive
File name
The connectivity file structure is an extension of the time-frequency structure. The file names start with timefreq_, followed by connect1 (1xN) or connectn (NxN or AxB), the connectivity method and a time stamp. Example: timefreq_connectn_corr_220120_1350.mat.
File structure
Right click on the first connectivity file computed > File > View file contents.
The data structure is the same as for Brainstorm time-frequency files. Only the fields specific to connectivity analyses are documented below:
TF: [Nr x Ntime x Nfreq] array containing all connectivity values. The connectivity matrix R computed in bst_connectivity.m between two sets of signals A and B, is optimized and saved in the TF variable. The size of the R matrix is [Na x Nb x Ntime x Nfreq]. The relation between Na x Nb and Nr depends on the type of optimization in the file. See details below.
RefRowNames: Cell-array of strings {Na x 1}. Labels of the rows of the connectivity matrix R (Y axis in the image display, with the label From). In the case of a AxB process, these labels are the names of the signals extracted from the first list of files (FilesA).
RowNames: Cell-array of strings {Nb x 1}. Labels of the columns of the connectivity matrix R (X axis in the image display, with the label To). In the case of a AxB process, these labels are the names of the signals extracted from the second list of files (FilesB).
Freqs: Double [1 x Nfreq] for a simple list of frequencies; or cell-array {Nfreq x 3} if using frequency bands, where each line represents a band {'band_name', 'frequency definition', 'function'}
Time: [1,Ntime] for time-resolved files; [1,2] for files with no data dimension (e.g. correlation). When no time is available, this variable describes the time segment from which the connectivity measure was computed.
Options.isSymmetric: Boolean indicating whether the matrix R saved in the TF field is symmetric (e.g. NxN correlation or coherence) or not (e.g. Granger causality). If the R matrix is symmetric, it is saved in a compressed format, with only the values from lower triangular matrix.
Connectivity matrix encoding
Let's consider the structure TfMat, loaded from a connectivity file, for example by right-clicking on the file > File > Export to Matlab. The connectivity matrix R can be obtained with function GetConnectMatrix. The size of R is [Na x Nb x Ntime x Nfreq].
R = bst_memory('GetConnectMatrix', TfMat);If the matrix is not symmetrical (i.e., not compressed): for each time and frequency, the list of values from the first dimension of the TF variable is reshaped into a 2D matrix: [Na x Nb].
If the matrix is symmetrical and compressed: only the lower triangular matrix is saved in the TF variable. The full matrix is first reconstructed with function process_compress_sym>Expand, then reshaped into [Na x Nb].
Saving the connectivity matrix R back in the TF variable is possible by reshaping to [Nx1] (R(:)) and then compressing again the matrix:
TfMat.TF = process_compress_sym('Compress', R(:));
Additional documentation
Related tutorials
Articles
Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M.
Identifying true brain interaction from EEG data using the imaginary part of coherency.
Clinical Neurophysiology. 2004 Oct;115(10):2292–307.Pascual-Marqui RD.
Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions.
arXiv preprint arXiv:0706.1776. 2007 Jun 12.Bressler SL, Seth AK.
Wiener–Granger causality: a well established methodology.
Neuroimage. 2011 Sep 15;58(2):323-9.Dhamala M, Rangarajan G, Ding M.
Estimating Granger causality from Fourier and wavelet transforms of time series data.
Physical review letters. 2008 Jan 10;100(1):018701.Hipp JF, Hawellek DJ, Corbetta M, Siegel M, Engel AK.
Large-scale cortical correlation structure of spontaneous oscillatory activity.
Nature neuroscience. 2012 Jun;15(6):884-90.Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, et al.
Detection of n : m Phase Locking from Noisy Data: Application to Magnetoencephalography.
Phys Rev Lett. 1998 Oct 12;81(15):3291–4.Bruña R, Maestú F, Pereda E
Phase locking value revisited: teaching new tricks to an old dog
Journal of Neural Engineering, Jun 2018Vinck M, Oostenveld R, van Wingerden M, Battaglia F, Pennartz CM
An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias
Neuroimage, Apr 2011Lobier M, Siebenhühner F, Palva S, Palva JM.
Phase transfer entropy: a novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions.
Neuroimage. 2014 Jan 15;85:853-72.Barzegaran E, Knyazeva MG.
Functional connectivity analysis in EEG source space: The choice of method
Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105.Lai M, Demuru M, Hillebrand A, Fraschini M.
A comparison between scalp- and source-reconstructed EEG networks.
Sci Rep. 2018 Dec;8(1):12269.Schoffelen J-M, Gross J.
Source connectivity analysis with MEG and EEG.
Hum Brain Mapp. 2009 Jun;30(6):1857–65.Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI.
Circular analysis in systems neuroscience: the dangers of double dipping.
Nat Neurosci. 2009 May;12(5):535–40.Cohen MX.
Analyzing Neural Time Series Data: Theory and Practice. MIT Press; 2014.Sadaghiani S, Brookes MJ, Baillet S.
Connectomics of human electrophysiology.
NeuroImage. 2022 Feb;247:118788.Sporns O.
Networks of the Brain. MIT Press; 2016.
Forum discussions
Granger causality: https://neuroimage.usc.edu/forums/t/12506
Coherence on single trials: https://neuroimage.usc.edu/forums/t/22726
Coherence and PLV: https://neuroimage.usc.edu/forums/t/33379
Removing ERP response for PLV: https://neuroimage.usc.edu/forums/t/32665
Connectivity of subcortical ROIs: https://neuroimage.usc.edu/forums/t/33479
Non-zero diagonals with unconstrained sources: https://neuroimage.usc.edu/forums/t/33700
Coherence/Lagged coherence vs. Envelope correlation/Lagged coherence: https://neuroimage.usc.edu/forums/t/lagged-coherence/39440
Scripting
The following script from the Brainstorm distribution reproduces the analysis presented in this tutorial page: brainstorm3/toolbox/script/tutorial_connectivity.m
TODO
Hossein, Richard
Granger Causality implementation: https://github.com/brainstorm-tools/brainstorm3/pull/433
Raymundo, Sylvain
- Read data: Can we find something more meaningful than what we compute in the example in the dataset? A full connectome in a task vs. baseline maybe?

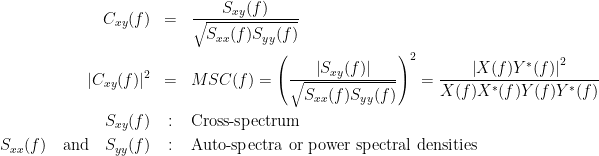
![\begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*} \begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_697a31e2ea80e1d7e07fbd14e43c910e44e14e3c_p1.png)