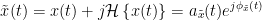|
Size: 24196
Comment:
|
← Revision 713 as of 2024-07-29 16:24:05 ⇥
Size: 55711
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| = Tutorial 28: Connectivity = '''[TUTORIAL UNDER DEVELOPMENT: NOT READY FOR PUBLIC USE] ''' ''Authors: Hossein Shahabi, Mansoureh Fahimi, Francois Tadel, Esther Florin, Sergul Aydore, Syed Ashrafulla, Elizabeth Bock, Sylvain Baillet'' |
<<HTML(<style>.backtick {font-size: 16px;}</style>)>><<HTML(<style>abbr {font-weight: bold;}</style>)>> <<HTML(<style>em strong {font-weight: normal; font-style: normal; padding: 2px; border-radius: 5px; background-color: #EEE; color: #111;}</style>)>> = Connectivity = ''Authors: Hossein Shahabi, Raymundo Cassani, Takfarinas Medani, François Tadel, Marc Lalancette, [[https://www.neurospeed-bailletlab.org/sylvain-baillet|Sylvain Baillet]]'' Brain functions (e.g., in cognition, behavior and perception) stem from the coordinated activity of multiple regions. [[http://www.scholarpedia.org/article/Brain_connectivity|Brain connectivity]] measures are designed to probe how brain regions (or nodes) interact as a network. A distinction is made between '''structural''' (fiber pathways), '''functional''' (non-directed statistical associations) and '''effective''' (causal interactions, or "directed functional connectivity") connectivity between regions. Here we explain how to compute various connectivity metrics for non-directed and directed functional connectivity analyses with Brainstorm, both with simulated (ground-truth) and empirical data. We encourage the interested reader to [[https://pubmed.ncbi.nlm.nih.gov/34906715/|learn more]] about the specific aspects of electrophysiology for studying human ''connectomics''. |
| Line 9: | Line 13: |
| During the past few years, the research focus in brain imaging moved from localizing functional regions to understanding how different regions interact together. It is now widely accepted that some of the brain functions are not supported by isolated regions but rather by a dense network of nodes interacting in various ways. Brain networks (connectivity) is a recently developed field of neuroscience which investigates interactions among regions of this vital organ. These networks can be identified using a wide range of connectivity measures applied on neurophysiological signals, either in time or frequency domain. The knowledge provides a comprehensive view of brain functions and mechanisms. This module of Brainstorm tries to facilitate the computation of brain networks and the representation of their corresponding graphs. Figure 1 illustrates a general framework to analyze brain networks. Preprocessing and source localization tasks for neural data are thoroughly described in previous sections of this tutorial. The connectivity module is designed to carry out remained steps, including the computation of connectivity measures, and statistical analysis and visualizations of networks. {{attachment:GeneralFlowConn.png||height="230",width="700"}} == General terms/considerations for a connectivity analysis == '''Sensors vs sources: '''The connectivity analysis can be performed either on sensor data (like EEG, MEG signals) or reconstructed sources (voxels/scouts). '''Nature of the signals: ''' The selection of connectivity method depends on the nature of the data. Some approaches are more suitable for spontaneous data (resting state) while others work better with task data (trials). '''Point-based connectivity vs. full network: '''Most of the connectivity functions in this toolbox have the option to either compute the connectivity between one point (channel) and the rest of the network (1 x N) or the entire network (N x N). While the later calculates the graph thoroughly, the first option enjoys a faster computation and it is more useful when you are interested in the connectivity of an ROI with the other regions of the brain. '''Temporal resolution: '''Connectivity networks can be computed in two ways; static and dynamic. Time-varying networks can present the dynamics of brain networks. In contrast, the static graphs illustrate a general perspective of brain connectivity which is helpful in specific conditions. Users need to decide which type of network is more informative for their study. '''Time-frequency transformation: ''' Many connectivity measures use a time-frequency transformation to transfer the data to the frequency domain. These approaches include short time Fourier transform, Hilbert transform, and Morlet wavelet. '''Output data structure:''' Consequently, computed connectivity matrices in this toolbox have up to four dimensions; channels x channels x frequency bands x time. Also, when dealing with trials and several files, each file has that 4-D structure. == Simulated data (AR model) == In order to compare different connectivity measures, we use simulated data with known ground truth. Three channels are |
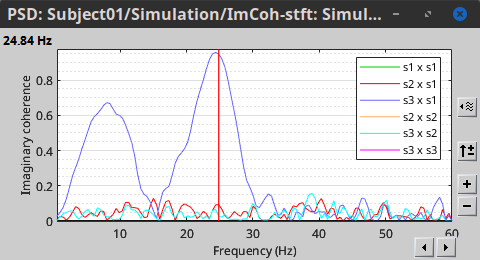
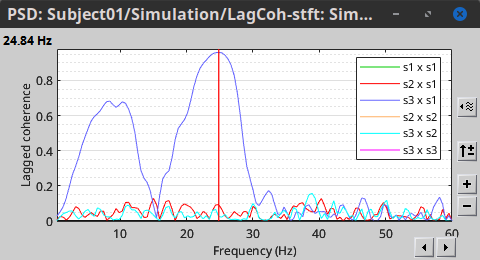
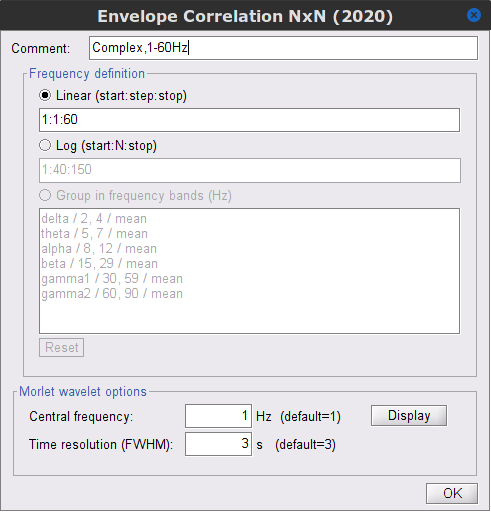
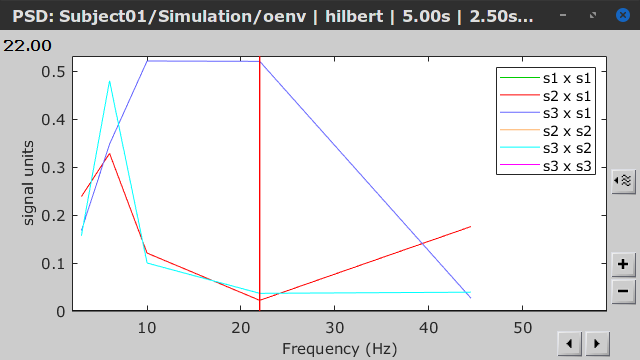
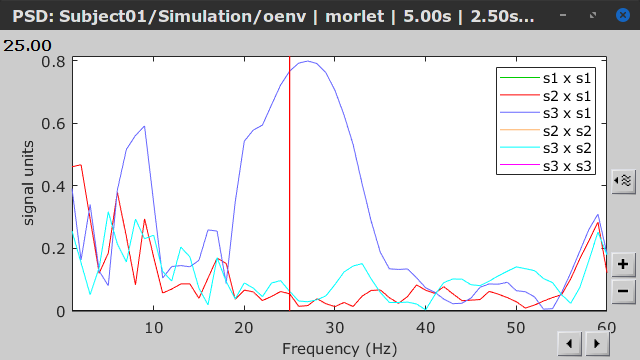
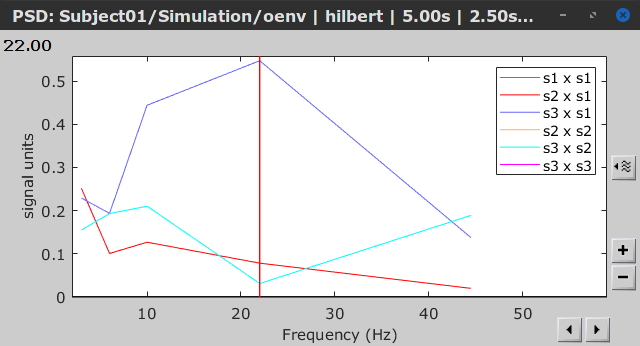
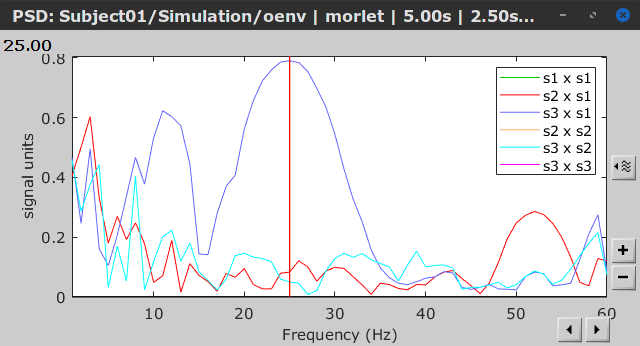
=== Definitions === Connectivity analyses are commonly performed by computing a bivariate measure between pairs of regional time series of interest. The outcome (a.k.a a ''connectome'') can be represented as a '''connectivity graph''' (left panel below), with each brain region as a node (x, y, z,...), and the connectivity measures shown above each edge of the graph. The ''connectome ''can also be represented by a '''connectivity array''', a.k.a. an adjacency matrix (right panel below). {{attachment:cnx_graph_matrix.png}} '''Sensors or sources:''' The time series used for connectivity analyses can be from '''sensor data''' (EEG/MEG signals) or from '''source time series''' (brain voxels or scouts). '''Directed vs. non-directed:''' The direction of interactions between signals (as a measure of statistical causation) is estimated with '''directed metrics'''. '''Non-directed metrics '''produce symmetrical connectivity graphs/matrices: the connectivity measure "from Signal <<latex($$x$$)>> to Signal <<latex($$y$$)>> " is identical to the connectivity measure "from Signal <<latex($$y$$)>> to Signal <<latex($$x$$)>>". '''Experimental condition:''' Depending on the neuroscience question, connectivity analyses can be performed on resting-state or task (e.g., ongoing or trial-based) data. '''Full (NxN) vs. seeded (1xN) connectivity:''' In a '''full connectivity analysis''', the connectivity metric is computed for all the possible pairs of nodes between N time series (noted N×N here). Alternatively, '''seeded connectivity''' (noted 1×N) is measured between one time series of interest (a ''seed, ''e.g., one brain region or a behavioral marker) and N other regions/time series. '''Time-frequency transformations:''' Some connectivity metrics rely on a [[Tutorials/TimeFrequency|time-frequency representation]] of the signals. These latter are obtained with approaches such as the short-time Fourier transform, Hilbert transform, or Morlet wavelets. Just as in other areas of electrophysiology studies, connectivity analyses need to be'''guided by mechanistic hypotheses concerning the expected neurophysiological effects'''. === Sensor-level analyses === 1. '''Their anatomical interpretation is limited and ambiguous'''. 1. Sensor data is affected by '''field spread''' and '''volume conduction of brain activity '''across the scalp/sensor array. Hence, activity from one single brain area is picked up at multiple, possibly distant sensor locations. Connectivity measures may show strong interactions between sensor time series, which may be wrongly interpreted as inter-regional brain connections. === Source-level analyses === Connectivity measures between source time series are '''neuroanatomically interpretable''' and can be derived across participants. We recommended that the outcomes of sensor and source connectivity analyses are mutually compatible; see ([[https://doi.org/10.1038/s41598-018-30869-w|Lai et al., 2018]]). '''Full-brain connectomes''' Whole-brain connectivity analyses at the typical resolution of cortical surfaces in Brainstorm involve '''thousands''' of source locations, making the N×N derivations impractical. For instance, 15000 cortical vertices would yield a connectivity matrix of 15000x15000x8 bytes = 1.6 GB. If unconstrained cortical sources are used and coherence is computed across 50 frequency bins, the memory allocation increases to 45000x45000x50x8 = 754 GB per participant/condition/trial/etc. Reducing the N (via e.g., cortical parcellations, ROIs) may be required for practical reasons, depending on computing resources. '''Regions of interest''' Grouping individual brain sources into ROIs, defined on the [[http://Tutorials/Scouts|cortical surface]] or in the brain [[https://neuroimage.usc.edu/brainstorm/Tutorials/TutVolSource#Volume_scouts|volume]] helps contain the computational resources required for connectivity analyses (see above). ROIs can be defined based on neuroscience priors and the purpose of the study ([[https://doi.org/10.1002/hbm.20745|Schhoffen and Gross, 2009]]). You may consider: * '''Study priors '''from the literature in your field, specific working hypotheses in terms of neuro-anatomical brain structures expected to be involved. * '''Association with a non-neuronal signal''' (e.g., cortico-muscular coherence). * '''Signal strength''', by defining ROIs from brain regions with strongest activity in current data. * '''Whole-brain '''[[https://neuroimage.usc.edu/brainstorm/Tutorials/LabelFreeSurfer#Cortical_parcellations|cortical parcellation]] to reduce N. The tutorial [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence|Corticomuscular coherence]] explains the computation of connectivity measures '''constrained''' and '''unconstrained''' brain maps for these cases: 1. '''One signal x full-brain source maps''': [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence#Method|link]] 2. '''One signal x scouts''': [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence#Coherence:_EMG_x_Scouts|link]] 3. ROI-based connectomes, i.e., '''scouts x scouts''': [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence#Coherence_Scouts_x_Scouts|link]] {{{#!wiki note Studies have reported similarities and differences between electrophysiological connectomes (from MEG/EEG) and fMRI connectomes. See how the '''electrophysiological connectomes provide unique insights on how functional communication is implemented in the brain''' in [[https://doi.org/10.1016/j.neuroimage.2021.118788|Sadaghiani et al., 2022]]. }}} {{{#!wiki caution On whole-brain connectivity analyses and the issue of circular analysis, please see [[https://doi.org/10.1038/nn.2303|Kriegeskorte et al., 2009]]. }}} == Pre-requisites == Here we focus on the specifics on connectivity analyses with Brainstorm. Please make sure you are familiar with Brainstorm and go through all [[http://neuroimage.usc.edu/brainstorm/Tutorials#Get_started|introduction tutorials]] first, before following the present tutorial. We first use simulated, synthetic data to emphasize the theoretical aspects of each connectivity metric with respect to groundtruth outcomes. Real, empirical MEG data are featured later in the tutorial (same auditory oddball dataset as in the other tutorial sections). Let's start by creating a new protocol in the Brainstorm database: * Select the menu File > Create new protocol > type in "'''TutorialConnectivity'''" and select the options: * '''Yes''', use protocol's default anatomy, * '''No''', use one channel file per condition. * Right-click on the TutorialConnectivity folder > New subject > Subject01<<BR>><<BR>> {{attachment:protocol_connect.gif}} == Simulated data == To compare connectivity metrics, let's use synthetic time series simulated with known ground truth interactions. We will use a [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Multivariate_Autoregressive_Model|multivariate autoregressive (MVAR)]] model that consists of the following three signals: * '''Signal 1''': two oscillatory (rhythmic) components: One at 10 Hz (alpha band), and a stronger peak at 25 Hz (beta band). * '''Signal 2''': Same as Signal 1, with the strongest peak at 10 Hz. * '''Signal 3''': Same as above, with the two components (10 and 25 Hz) of same magnitude. The 25-Hz component of''' '''Signal 3 will be driven in part by the 25-Hz component of Signal 1 (denoted '''Signal 1>>Signal 3'''). Let's now generate the three time series: * In the '''Process1''' tab, leave the file list empty and click on the button '''[Run]''' * Select process: '''Simulate > Simulate AR signals'''.<<BR>><<BR>> {{attachment:sim_process.gif}} Process options: * '''Subject name''': Target subject for the simulated signals: Select '''Subject01'''. * '''Condition name''': Target folder where to store the simulated data in your database: Set to '''Simulation'''. * '''Number of time samples''' for each simulated time series: Set to '''12,000'''. * '''Sampling frequency''' (Fs): Set to '''120 Hz'''. * '''Interaction specifications:''' Spectral parameters for the signal components and their interactions in the MVAR model: '''From, To / Peak frequencies [Hz] / Peak relative magnitudes [0-1]'''<<BR>> Set to: {{{ 1, 1 / 10, 25 / 0.3, 0.5 2, 2 / 10, 25 / 0.7, 0.3 3, 3 / 10, 25 / 0.2, 0.2 1, 3 / 25 / 0.1 }}} * '''Display the groundtruth spectral metrics''' of the MVAR-generated time series: transfer function, cross-spectral power density, [[#Coherence|magnitude square coherence]], [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Directed_Transfer_Function|directed transfer function (DTF)]] and [[https://en.wikipedia.org/wiki/Brain_connectivity_estimators#Partial_Directed_Coherence|partial directed coherence (PDC)]]. The '''transfer function '''(<<latex($$|H(f)|$$)>>) characterizes the relationships between signals in the frequency domain. It is a non-symmetric representation, which enables the identification of causal dependencies between signal components. The ''auto-transfer functions'' (shown in the graphs along the diagonal below) display the power spectra of each signal. The off-diagonal representations display the interactions between each pair of signals (see Signal 1 >> Signal 3 above). Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our '''ground truth for connectivity values'''.<<BR>><<BR>> {{attachment:sim_ar_spectra_metrics.png||width="100%"}} * '''Get coefficients matrix:''' Shows the coefficients related to the MVAR model. These coefficients can be used in the process '''Simulate > Simulate AR signals (ARfit)''' to simulate the same model.<<BR>><<BR>> {{attachment:sim_coef.gif}} Execution: * Click '''Run''' to generate the time series with the MVAR model. <<BR>><<BR>> {{attachment:sim_db.gif}} * In the next sections, we will compute different connectivity metrics from these synthetic time series. Drag and drop the simulated data in the '''Process1''' tab, click on '''[Run]''' ( {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconRun.gif}} ) to open the [[Tutorials/PipelineEditor#Selecting_processes|Pipeline editor]], and select the connectivity metric.<<BR>><<BR>> {{attachment:sim_select.gif}} * This tutorial illustrates the computation of full connectivity graphs ('''Process 1: NxN'''). It is also possible to obtain connectivity measures between one of the time series of a given data file and the other time series in the same file (use '''Process1: 1xN'''), or between time series from two different data files (use '''Process2: AxB'''), as shown further below. References used: * This process relies on the ARSIM function from the '''ARFit toolbox''': <<BR>>https://github.com/tapios/arfit * Neumaier A, Schneider T<<BR>>[[http://dx.doi.org/10.1145/382043.382304|Estimation of parameters and eigenmodes of multivariate autoregressive models]]<<BR>>ACM Transactions on Mathematical Software, 2001 * Schneider T, Neumaier A<<BR>>Algorithm 808: [[http://dx.doi.org/10.1145/382043.382316|ARfit – A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models]]<<BR>>ACM Transactions on Mathematical Software, 2001 <<BR>><<BR>> == Correlation == [[https://en.wikipedia.org/wiki/Correlation_and_dependence|Correlation]] is a relatively simple, non-directed connectivity metric of association between two time series. It is relatively limited without further preprocessing of the input time series: correlation is sensitive to volume conduction and is not frequency specific. === Process options === * Process '''Connectivity > Correlation NxN''':<<BR>><<BR>> {{attachment:gui_corr1n.png}} * '''Time window:''' Time segment of the signals for connectivity analysis. Select: '''All file'''. * '''Time resolution:''' Select '''None''' * '''Windowed:''' correlation is computed in windows of a given '''length''' with a certain '''overlap''' percentage * '''None:''' correlation is computed using the entire time series * '''Compute scalar product:''' If left unchecked, the mean of the time series is subtracted before computing the correlation. Leave it unchecked. * '''Output options''': Select Estimate and save '''separately for each file'''. === Result visualization === * The results are stored as a N×N connectivity file, with a new icon {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconConnectN.gif}} . Right-click for display options:<<BR>><<BR>> {{attachment:corr1n_file.gif}} * '''Display as graph''': Plots the connectivity graph using a [[https://en.wikipedia.org/wiki/Chord_diagram|chord diagram]] where the color of the edges shows the value of the connectivity metric. See the [[Tutorials/ConnectivityGraph|connectivity graph tutorial]] for a detailed explanation of the options of this visualization. * '''Display as image''': Plots the connectivity measures in an [[https://en.wikipedia.org/wiki/Adjacency_matrix|adjacency matrix]]. * '''Display fibers''': Displays source connectivity edges as virtual white fiber tracts, as shown [[#Tutorials.2FFiberConnectivity|here]]. <<BR>><<BR>> {{attachment:corr1n_graph_image.png}} Display options: * '''Show labels''': Click on the figure to display the names of the times series and the connectivity values in the figure legend. To display the labels corresponding to each column and row: right-click on the figure > Figure > '''Show labels'''. If the time series names are too long, use the option '''Use short labels'''. * '''Hide self-connectivity''': In a square NxN connectivity matrix, the diagonal values correpond to the values of the connectivity metric between a time series and itself. These self-connectivity values are typically much higher than the other values of the matrix. When checked, these values are hidden so that to display the off-diagonal values more clearly. * '''Colormap''': By default, the NxN colormap is configured to display the absolute values of the connectivity measures. Correlation values may be positive or negative. To display the '''negative values''', make sure to change the colormap configuration: right-click on the figure > Colormap > Uncheck '''Absolute values'''. <<BR>><<BR>> {{attachment:corr1n_image_relative.png}} <<BR>><<BR>> == Coherence == Coherency or complex coherence, <<latex($$C_{xy}(f)$$)>>, is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Magnitude square coherence (MSC), <<latex($$|C_{xy}(f)|^2$$)>>, or ''coherence'', measures the covariance of two signals in the frequency domain. For a pair of time series <<latex($$x(t)$$)>> and <<latex($$y(t)$$)>>, with spectra <<latex($$X(f)$$)>> and <<latex($$Y(f)$$)>>, the MSC is defined as: . {{{#!latex \begin{eqnarray*} C_{xy}(f) &=& \frac{S_{xy}(f)}{\sqrt{ S_{xx}(f)S_{yy}(f)}}\\ |C_{xy}(f)|^2 &=& MSC(f) = \left(\frac{\left |S_{xy}(f) \right |}{\sqrt{ S_{xx}(f)S_{yy}(f) }}\right)^2 = \frac{\left |X(f)Y^*(f) \right |^{2}}{X(f)X^*(f)Y(f)Y^*(f)} \\ S_{xy}(f) &:& \textrm{Cross-spectrum} \\ S_{xx}(f) \quad \textrm{and} \quad S_{yy}(f) &:& \textrm{Auto-spectra or power spectral densities} \\ \end{eqnarray*} }}} Two related measures, which address the problem of volume conduction, are '''imaginary coherence''' ([[https://doi.org/10.1016/j.clinph.2004.04.029|Nolte et al., 2004]]), <<latex($IC_{xy}(f)$)>>, and '''lagged coherence''' ([[https://arxiv.org/pdf/0706.1776|Pascual-Maqui, 2007]]), <<latex($LC_{xy}(f)$)>>, which are defined as: . {{{#!latex \begin{eqnarray*} IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\ LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\ \end{eqnarray*} }}} where <<latex($$\mathrm{Im()}$$)>> and <<latex($$\mathrm{Re()}$$)>> are the imaginary and real parts of a complex number, respectively. Note that the cross-spectrum (<<latex($$S_{xy}(f)$$)>>) and the power spectral densities (<<latex($$S_{xx}(f)$$)>> and <<latex($$S_{yy}(f)$$)>>), and as consequence also coherency (<<latex($$C_{xy}(f)$$)>>) can be obtained through different time-frequency decomposition methods (such as: Hilbert transform, wavelet transform and short-time Fourier transform), and for different time resolutions (per sample, windowed and entire file). === Process options === * Process '''Connectivity > Coherence NxN''':<<BR>><<BR>> {{attachment:gui_cohere1n.png}} <<BR>> {{attachment:gui_cohere1n_b.png}} * '''Time window:''' Segment of the time series used for the connectivity analysis. Select '''All file'''. * '''Connectivity metric '''shows variants of coherence measures. Select: '''Magnitude squared coherence'''. * '''Time-frequency decomposition '''selection of the time to time-frequency transformation. Select: (short-time) '''Fourier transform'''. * '''Options [Edit] '''shows the options of the selected time-frequency transformation. * '''Window length:''' Duration in seconds for the [[https://neuroimage.usc.edu/brainstorm/Tutorials/ArtifactsFilter#Evaluation_of_the_noise_level|spectrum estimation]]. Set to: '''1s'''. * '''Overlap:''' Percentage of overlap between consecutive sliding time windows. Set to: '''50%'''. * '''Highest frequency''': After the computation, removes all the frequencies above this threshold, mostly for visualization purposes. The value needs to be <= Fs/2. Set to: '''60 Hz'''. * '''Time resolution '''selection of the time resolution. Select: '''None'''. * '''Output options''': Select Estimate and save '''separately for each file'''. === Result visualization === Coherence is frequency specific: a connectivity graph and a connectivity matrix are produced for each frequency bin of the spectrum. Right-click on the coherence result file to show display options: * '''Display as graph''': Plots a connectivity graph for each frequency bin. * '''Display as image''': Plot a connectivity matrix for each frequency bin. * '''Power spectrum''': Plot coherence as a function of frequency, between each time series. Open the 3 types of visualization: they are linked by clicking on the spectral representation of the coherence, which will change the current frequency bin and update the connectivity measures displayed in the graph and matrix. The value of the current frequency bin can also be changed in the Time panel. <<BR>><<BR>> {{attachment:res_cohere1n.png}} <<BR>><<BR>> Other variants of coherence can be derived following the above procedure. The figures below display the coherence spectra obtained from the imaginary coherence (left) and the lagged coherence (right) measures. || {{attachment:res_cohere1n_d.png||width="350"}} || || {{attachment:res_cohere1n_e.png||width="350"}} || <<BR>><<BR>> == Granger causality == Granger causality (GC) is a measure of '''directed functional connectivity''' based on the Wiener-Granger causality framework. GC measure linear dependencies between time series, and tests whether the prediction of the future of signal <<latex($$x(t)$$)>> (approximated by a linear autoregressive model) is improved by considering signal <<latex($$y(t)$$)>> (also approximated by a linear autoregressive model). If there is such improvement, one concludes that signal <<latex($$y(t)$$)>> has a Granger causal effect on the other signal. In sum, some '''independent information''' from the past of signal <<latex($$y(t)$$)>> improves the prediction of the future of signal <<latex($$x(t)$$)>>, with respect to only observing its past <<latex($$x(t)$$)>>. GC takes nonnegative values; its is zero when no Granger causality can be attributed. The term '''independent''' means that GC is invariant with the scale of the input signals <<latex($$x(t)$$)>> and <<latex($$y(t)$$)>>. <<BR>><<BR>> See [[GrangerCausality|Granger causality - mathematical background]] for a more complete background. {{{#!wiki note Despite the name, '''Granger causality indicates directionality but not true causality'''. <<BR>> For example, if a variable <<latex($$w$$)>> is causing both <<latex($$x$$)>> and <<latex($$y$$)>>, but with a smaller delay for <<latex($$y$$)>> than for <<latex($$x$$)>>, then the GC measure between <<latex($$x$$)>> and <<latex($$y$$)>> would show a non-zero GC for <<latex($$y$$)>> --> <<latex($$x$$)>>, even though <<latex($$y$$)>> is not truly causing <<latex($$x$$)>> ([[https://doi.org/10.1016/j.neuroimage.2010.02.059|Bressler and Seth, 2011]]). }}} === Process options === * Process '''Connectivity > Bivariate Granger causality NxN'''<<BR>><<BR>> {{attachment:gui_granger1n.png||width="400"}} * '''Time window:''' Time segment of the time series used for the connectivity analysis. Select '''All file'''. * '''Remove evoked response''': This option is recommended by some authors as it satisfies the zero-mean stationarity of the GC model, but does not account for trial-to-trial variability; see ([[https://doi.org/10.1016/j.neuroimage.2008.03.025|Wang et al., 2008]]). Leave it '''Unchecked'''. * '''Maximum Granger model order:''' The most common criteria used to define the order of the autoregressive models used by GC to approximate the input time series are the [[https://en.wikipedia.org/wiki/Akaike_information_criterion|Akaike’s information]] criterion, the [[https://en.wikipedia.org/wiki/Bayesian_information_criterion|Bayesian-Schwartz’s criterion]], and the [[https://en.wikipedia.org/wiki/Hannan–Quinn_information_criterion|Hannan-Quinn criterion]]. Low model orders will yield coarse approximations of the input time series. High model orders may yield spurious GC connectivity estimates. The simulated time series were created with an AR model of order 4; please use a maximum Granger model order of '''6'''. * '''Output options''': Select '''Save individual results'''. <<BR>> === Results visualization === The connectivity matrix (left panel below) is not symmetric because GC values are direction specific. The upper right elements of the matrix indicate there is a GC influence from signal 1 to signal 3. In the connectivity graph (right panel below) the directionality is shown with an arrowhead at the center for the arc connecting two nodes. || {{attachment:res_granger1n_a.png}} || || {{attachment:res_granger1n_b.png}} || <<BR>><<BR>> == Spectral Granger causality == The Spectral Granger causality is a measure of '''directed functional connectivity '''that was developed to indicate frequency specific influences between time series ([[https://doi.org/10.1103/PhysRevLett.100.018701|Dhamala et al., 2008]]). === Process options === * Process: '''Connectivity > Bivariate Granger causality NxN'''. <<BR>><<BR>> {{attachment:gui_spgranger1n.png||width="400"}} <<BR>><<BR>>. Here we used the same parameters as with [[#Granger_causality|GC]] plus two two extra parameters specific to spectral GC: * '''Maximum frequency resolution''': Width of frequency bins in PSD estimation. Set to '''1 Hz'''. * '''Highest frequency''': computes GC values under the specified frequency. Should be set <= Fs/2. Use: '''60 Hz'''. === Result visualization === As with coherence, spectral GC can be plotted as a function of frequency. The display below shows a peak around 25 Hz that corresponds to the expected causal interaction of Signal 1 on Signal 3. {{attachment:res_spgranger1n.png}} <<BR>><<BR>> == Envelope correlation == In the [[Tutorials/TimeFrequency|time-frequency tutorial]], we have introduced '''Morlet wavelets''' and the '''Hilbert transform''' as methods to decompose time series in the time-frequency (TF) domain. The outcome of these two TF transformations is an [[https://en.wikipedia.org/wiki/Analytic_signal|analytic signal]], <<latex($$\tilde{x}(t)$$)>>, which is a complex time series uniquely associated to the original data time series, <<latex($$x(t)$$)>>, which '''module''' <<latex($$a_{\tilde{x}}(t)$$)>>, and '''phase''' <<latex($$\phi_{\tilde{x}}(t)$$)>>, correspond to the '''instantaneous amplitude''' (or envelope) and '''instantaneous phase''' of the original time series <<latex($$x(t)$$)>>, respectively. The real part of <<latex($$\tilde{x}(t)$$)>> is the original time series <<latex($$x(t)$$)>>, and the imaginary part is the Hilbert transform of that same time series <<latex($$x(t)$$)>>. . {{{#!latex \begin{eqnarray*} \tilde{x}(t)= x(t) + j\mathcal{H}\left\{ x(t) \right\} = a_{\tilde{x}}(t)e^{j\phi_{\tilde{x}}(t)} \\ \end{eqnarray*} }}} {{{#!wiki note The analytic signal of oscillatory or '''narrowband''' signals provide '''meaningful''' and '''interpretable''' estimations of instantaneous amplitude and phase. While it is technically feasible to derive these elements from broadband time series, they would not be interpretable (see [[https://mitpress.mit.edu/books/analyzing-neural-time-series-data|Cohen, 2014]]). }}} The instantaneous amplitude (or envelope) of the analytic signals can be used to carry out pairwise connectivity analysis with correlation. This is to say amplitude envelop correlation (AEC). An optional step consists in '''orthogonalizing''' the pairs of amplitude envelope time series before computing the correlation. Orthogonalization is performed by first removing the real part of their coherence to reduce volume conduction (at the sensor level) or cross-talk effects (at the source level) ([[https://psycnet.apa.org/doi/10.1038/nn.3101|Hipp et al., 2012]]). === Process options === * Process: '''Connectivity > Envelope Correlation N×N [2023]''' <<BR>><<BR>> {{attachment:gui_henv1n_ha.png||width="400"}} * '''Time window:''' Time segment of the signal used for the connectivity analysis. Select: '''All file'''. * '''Connectivity measure '''is the connectivity metric applied to the resulting signal amplitude envelopes. Select '''Envelope correlation (orthogonalized)'''. * '''Time-frequency decomposition:''' '''Hilbert transform''' or '''Morlet wavelets'''. Each method requires additional parameters that will be displayed in a separate panel after clicking on '''[Edit]'''. See the [[Tutorials/TimeFrequency|time-frequency tutorial]]. In the present example, we will use the '''Hilbert transform''' with the option '''Group in frequency bands''' to present the results for the canonical frequency bands. As the sampling frequency of the signals is 120Hz, thus, make sure you remove the '''"gamma2"''' band from the targeted frequency bands.<<BR>><<BR>> {{attachment:gui_henv1n_hb.png||height="276",width="227"}} * '''Time resolution:''' If '''Windowed''', connectivity is saved for each time window. If '''None''', the connectivity measures are averaged across all windows. Select '''Windowed'''. Set the additional parameters to define the windows: * '''Time window length''': Duration in milliseconds over which the connectivity measure is computed. Set to '''5s''' * '''Time window overlap:''' Percentage of overlap between consecutive time windows to compute the connectivity measure. Set to '''50%'''. * '''Use the parallel processing toolbox:''' If available, will call Matlab's parallel processing to accelerate computations. Leave it '''Unchecked'''. * '''Output options''': Select Estimate and save '''separately for each file'''. For sake of comparison, we will compute AEC again, but this time changing the TF decomposition method to '''Morlet wavelets''' with '''Linear = 1:1:60''' (frequencies from 1 to 60 Hz with 1 Hz step). . {{attachment:gui_henv1n_wb.png||height="276",width="227"}} === Results visualization === As with [[#Coherence|Coherence]] and [[#Spectral_Granger_causality|spectral Granger causality]], amplitude envelope correlations can be displayed as a function of frequency, and as a function of time if the '''Time resolution''' option was set to '''Windowed'''. Below are the AEC results obtained with the Hilbert transform (left panels) and with Morlet wavelets (right panels) for the first 5-s time window (top panels) and the 5-s last window (bottom panels). || {{attachment:res_henv1n_h.png||width="350"}} ||<style="text-align:center">First 5-s window || {{attachment:res_henv1n_w.png||width="350"}} || || {{attachment:res_henv1n_h2.png||width="350"}} ||<style="text-align:center">Last 5-s window || {{attachment:res_henv1n_w2.png||width="350"}} || == Phase-Locking Value == An alternative class of connectivity metrics considers the relative instantaneous phase between two time series as a marker of connectivity. Phase-locking or phase synchronization are two such measures ([[https://doi.org/10.1103/PhysRevLett.81.3291|Tass et al., 1998]]). In principle, phase-based measures are robust against fluctuations in signal amplitude, although low signal-to-noise conditions remain challenging for these measures ([[https://doi.org/10.1002/(SICI)1097-0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C|Lachaux et al., 1999]]; [[https://doi.org/10.1016/S0167-2789(00)00087-7|Mormann et al., 2000]]). The phase-locking value ('''PLV''') is a popular metric defined as the length of the average vector of many unit vectors whose phase angle corresponds to the phase difference between two time series ([[https://doi.org/10.1103/PhysRevLett.81.3291|Tass et al., 1998]]). If the distribution of the phase difference between the two signals is uniform, the length of such an average vector will be 0. If the phases of the two signals are strongly coupled, the length of the average vector will be close to 1. For event-related studies, we would expect phase differences across trials to be uniformly distributed, unless the phase of the brain signals is locked to the event onset, which would then indicate a form of phase locking between the two time series. Considering a pair of narrow-band analytic signals <<latex($$\tilde{x}(t)$$)>> and <<latex($$\tilde{y}(t)$$)>>, obtained from the Hilbert transform (see above): |
| Line 35: | Line 297: |
| x_{1}(n) & = & a_{1}x_{1}(n-1) + \cdots + a_{k}x_{1}(n-k) + e_{1}(n) \\ x_{2}(n) & = & a_{1}x_{2}(n-1) + \cdots + a_{k}x_{2}(n-k) + e_{2}(n) \\ x_{3}(n) & = & a_{1}x_{3}(n-1) + \cdots + a_{k}x_{3}(n-k) + b_{1}x_{2}(n-1) + \cdots + b_{r}x_{2}(n-r) + e_{3}(n) \\ |
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\ |
| Line 40: | Line 300: |
| where a1,...,an are coefficients of an all-pass filter and b1,...,bn are coefficients for a lowpass filter which describes the transfer function from channel 2 to channel 3. One can take the Fourier trnasform from these equations and rearrange them in a matrix form. Based on this model, we generated signals and tested the available connectivity measures. This dataset is available '''''here'''''. | with: |
| Line 44: | Line 304: |
| A(f)X(f) & = & E(f) \\ define \quad H(f) & = & A^{-1}(f) \quad Transfer \quad function\\ X(f) & = & H(f)E(f) \\ |
\Delta \phi (t) = \phi_{\tilde{x}}(t) - \phi_{\tilde{y}}(t) = arg\left ( \frac{\tilde{x}(t)\tilde{y}^{*}(t)}{\left | \tilde{x}(t) \right |\left | \tilde{y}(t) \right |} \right ) \\ |
| Line 49: | Line 307: |
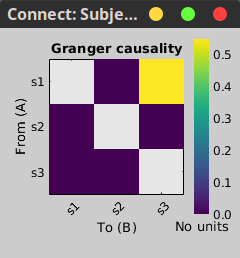
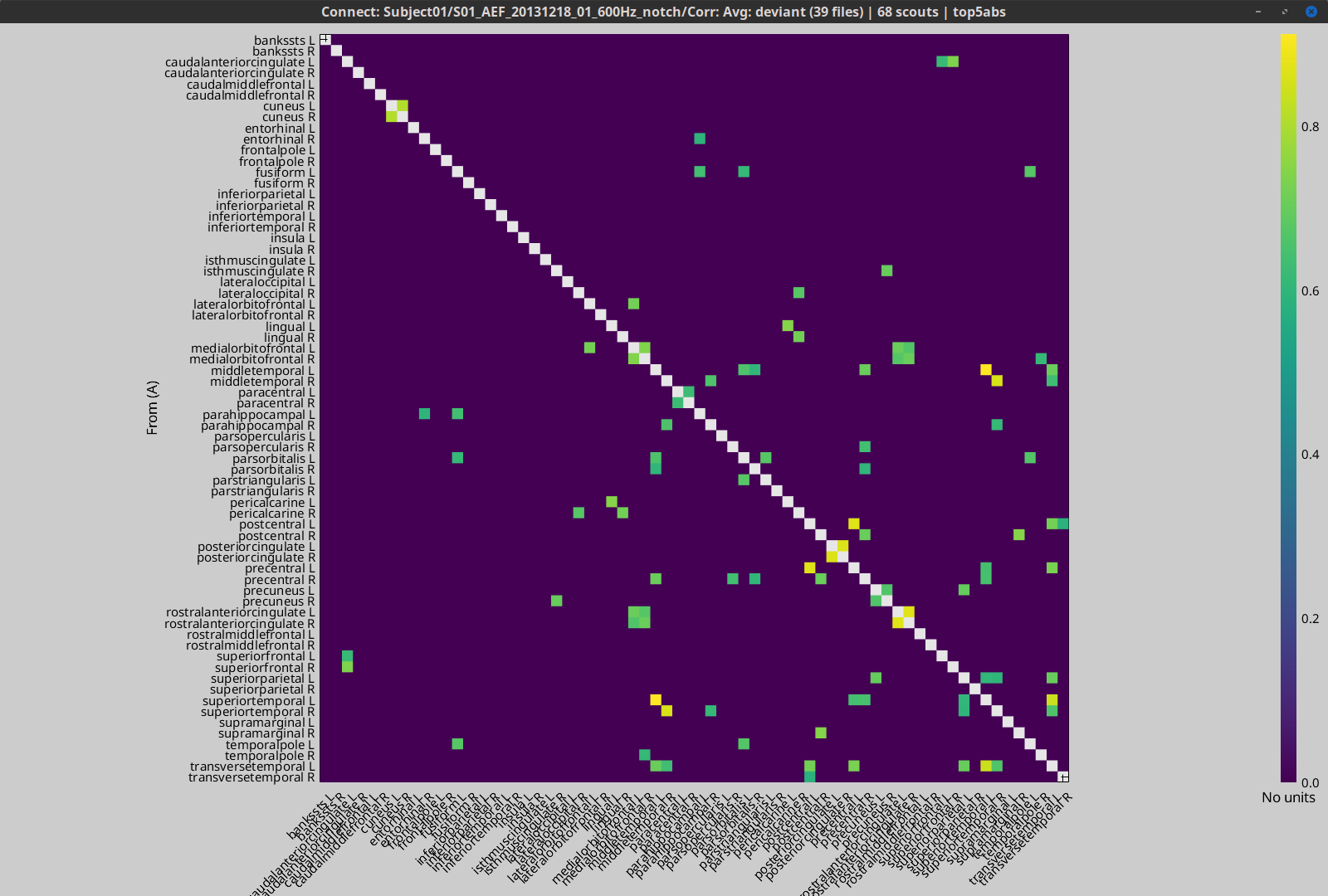
| {{attachment:TransferMatrix2_AR3.png||height="400",width="550"}} '''''TODO : explain the figure''''' == Coherence (FFT-based) == The coherence is a statistical measure which computes the relation between two signals, like x(t) and y(t), in the frequency domain. The magnitiude-squared coherence is, {{{#!latex \begin{eqnarray*} C_{xy}(f) &=& \frac{\left |S_{xy}(f) \right |^{2}}{S_{xx}(f)S_{yy}(f)} \\ S_{xy}(f) &:& Cross-spectral \quad density \\ S_{xx}(f) \quad and \quad S_{yy}(f) &:& Auto-spectral \quad density \\ \end{eqnarray*} }}} The coherence function uses the Fourier transform to compute the spectral densities. A related measure which alleviates the problem of volume conduction is the lagged-coherence '''''(ref)'''''. {{{#!latex \begin{eqnarray*} LC_{xy}(f) = \frac{Im \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ Re\left ( S_{xy}(f) \right ) \right ]^{2} }} \\ \end{eqnarray*} }}} '''''TODO : explain the elememts of the equation''''' * Put the Simulated data in the Process1 tab. * Click on [Run] to open the Pipeline editor. * Run the process: '''Connectivity > Coherence NxN ''' <<BR>><<BR>> {{attachment:StatCoherence_Process_ms1.PNG||height="400",width="350"}} * Set the options as follows: * '''Time window''': Select the entire signal. * '''Removing evoked response''': Check this box to remove the averaged evoked response from the individual trials. * '''Measure''': You can select either the "Magnitude-Squared" coherence or the "Imaginary" coherence. we first select the former one. * '''Maximum frequency resolution''': This value characterizes the distance between frequency bins. Smaller values give higher resolutions but probably noisier. * '''Highest frequency of interest''': It specifies the highest frequency which should be analyzed. Here, we selected Fs/2 = 125 Hz to have the coherence in all frequencies. * '''Output configuration''': Select one file per input file. In general, after running the connectivity processes, you can find a multi-dimensional matrix of connectivity in the database. In order to represent this matrix, there are several options. Right click on the file and select '''Power spectrum''' and '''Display as image''' These two figures are plotted here. The left figure shows the Coherence values in all analyzed frequencies. Another figure displays the Transfer matrix between channels for the selected frequency bin. {{attachment:rightMenuPlot.PNG||height="180",width="450"}} <<BR>><<BR>> {{attachment:StatCoherence-Results1.PNG||height="300",width="650"}} <<BR>><<BR>><<BR>> Similarly, we can run this process and select "imaginary coherence". which gives us the following representation, {{attachment:StatCoherence_Process_lc.PNG||height="400",width="350"}} <<BR>><<BR>> {{attachment:StatCoherence-Results_lc.PNG||height="300",width="650"}} <<BR>><<BR>> == Granger Causality == Granger Causality (GC) is a method of functional connectivity, adapted by Clive Granger in the 1960s, but later refined by John Geweke in the form that is used today. Granger Causality is originally formulated in economics but has caught the attention of the neuroscience community in recent years. Before this, neuroscience traditionally relied on stimulation or lesioning a part of the nervous system to study its effect on another part. However, Granger Causality made it possible to estimate the statistical influence without requiring direct intervention (ref: wiener-granger causality a well-established methodology). <<BR>><<BR>> Granger Causality is a measure of linear dependence, which tests whether the variance of error for a linear autoregressive model estimation of a signal (A) can be reduced when adding a linear model estimation of a second signal (B). If this is true, signal B has a Granger Causal effect on the first signal A, i.e., independent information of the past of B improves the prediction of A above and beyond the information contained in the past of A alone. The term independent is emphasized because it creates some interesting properties for GC, such as that it is invariant under rescaling of A and B, as well as the addition of a multiple of A to B. The measure of Granger Causality is nonnegative, and zero when there is no Granger causality(Geweke, 1982). <<BR>><<BR>> The main advantage of Granger Causality is that it is an asymmetrical measure, in that it can dissociate between A->B versus B->A. It is important to note however that though the directionality of Granger Causality is a step closer towards measuring effective connectivity compared to symmetrical measures, it should still not be confused with “true causality”. Effective connectivity estimates the effective mechanism generating the observed data (model-based approach), whereas GC is a measure of causal effect based on prediction, i.e., how well the model is improved when taking variables into account that are interacting (data-driven approach) (Barrett and Barnett, 2013). The difference with causality is best illustrated when there are more variables interacting in a system than those considered in the model. For example, if a variable C is causing both A and B, but with a smaller delay for B than for A, then a GC measure between A and B would show a non-zero GC for B->A, even though B is not truly causing A (Bressler and Seth, 2011). The complete formulation of this method is discussed in the advanced section. Here, we apply the Granger causality and its spectral version on the simulated data. * Put the Simulated data in the Process1 tab. * Click on [Run] to open the Pipeline editor. * Run the process: '''Connectivity > Bivariate Granger causality NxN ''' <<BR>><<BR>> {{attachment:StatGranger_Process.PNG||height="400",width="350"}} <<BR>><<BR>> '''Input options:''' * '''Time window:''' specifies the time window you want to use for your model. * '''Remove evoked response from each trial:''' this option refers to subtracting the average of phase-locked activity (ERP) from each individual trial. Presently some studies measure interdependency of ongoing brain activity by removing the average event-related potential from each trial. It is also recommended by some as it meets the zero-mean stationarity requirement (improves stationarity of the system). However, the problem with this approach is that it does not account for trial-to-trial variability (For a discussion see (Wang et al., 2008)). '''Estimator options:''' * '''Model order:''' Selection of model order is a critical issue and is typically evaluated from criteria derived from information theory. Several criteria have been proposed, of which the most used are Akaike’s information criterion, the Bayesian-Schwartz’s criterion, and the Hannan-Quinn criterion (Koichi and Antonio, 2014). Model fitting quality crucially depends on the proper model order selection. Too low orders may lack the necessary details, while too big orders tend to create spurious values of connectivity. Note that in our simulated example even though the simulation was created with an underlying model of 4, a Granger model order of 6 was selected with decent resulting connectivity. '''Output options:''' * '''Save individual results (one file per input file):''' option to save GC estimates on several files separately. * '''Concatenate input files before processing (one file):''' option to save GC estimates on several files as one concatenated matrix. {{attachment:StatGranger-Results_AR.PNG||height="350",width="350"}} <<BR>><<BR>> Spectral Granger causality {{attachment:StatGrangerSpect_Process.PNG||height="400",width="350"}} <<BR>><<BR>> {{attachment:StatGrangerSpect-Results_AR.PNG||height="350",width="350"}} <<BR>><<BR>> == Coherence and envelope (Hilbert/Morlet) == This process {{attachment:FlowChartHCorr.png||height="170",width="850"}} <<BR>><<BR>> * Put the Simulated data in the Process1 tab. * Click on [Run] to open the Pipeline editor. * Run the process: '''Connectivity > HCorr NxN ''' <<BR>><<BR>> {{attachment:DynHCorr_Process.PNG||height="550",width="400"}} * '''Input Options:''' The time range of the input signal can be specified here. Also, bad channels and the evoked response of trials can be discarded, if appropriate. * '''Time-frequency transformation method:''' The method for this transformation (Hilbert transform or Morlet Wavelet) should be selected. Additionally, this analysis needs further inputs, e.g. frequency ranges, number of bins, and Morlet parameters, which can be defined by an external panel as depicted in Figure 4 (By clicking on “Edit”). A complete description regarding time-frequency transformation can be found here. In the context of connectivity study, we must analyze complex output values of these functions, so two other options (power and magnitude) are disabled on the bottom of this panel. * '''Signal splitting:''' This process has the capability of splitting the input data into several blocks for performing time-frequency transformation, and then merging them to build a single file. This feature helps to save a huge amount of memory and, at the same time, avoid breaking a long-time recording to short-time signals, which makes inconsistency in dynamic network representation of spontaneous data. The maximum number of blocks which can be specified is 20. * '''Connectivity measure:''' Here, three major and widely used coherence based measures of brain connectivity can be computed. Next, desired parameters for windowing, i.e. window length and overlap, should be determined. Please note that these values are usually defined based on the nature of data, the purpose of the study, and the selected connectivity measure. * '''Parallel processing:''' This feature, which is only applicable for envelope correlation, employs the parallel processing toolbox in Matlab to fasten the computational procedure. As described in the advanced section of this tutorial, envelope correlation utilizes a pairwise orthogonalization approach to attenuate the cross-talk between signals. This process requires heavy computation, especially for a large number of channels, however, using Parallel Processing Toolbox, the software distributes calculations on several threats of CPU. The maximum number of pools varies on each computer and it is dependent on the CPU. * '''Output configuration:''' Generally, the above calculation results in a 4-D matrix, where dimensions represent channels (1st and 2nd dimensions), time points (3rd dimension), and frequency (4th dimension). In the case that we analyze event-related data, we have also several files (trials). However, due to poor signal to noise ratio of a single trial, an individual realization of connectivity matrices for each of them is not in our interests. Consequently, we need to average connectivity matrices among all trials of a specific event. The second option of this part performs this averaging. == Simulated data (phase synchrony) == == Correlation == The correlation is the basic approach to show the dependence or association among two random variables or MEG/EEG signals. While this method has been widely used in electrophysiology, it should not be considered as the best technique for finding the connectivity matrices. The correlation by its nature fails to alleviate the problem of volume conduction and cannot explain the association in different frequency bands. However, it still can provide valuable information in case we deal with a few narrow-banded signals. * Put the Simulated data in the Process1 tab. * Click on [Run] to open the Pipeline editor. * Run the process: '''Connectivity > Correlation NxN ''' <<BR>> {{attachment:StatCorrelation_Process.PNG||height="350",width="350"}} * Set the options as follows: * '''Time window''': Select the entire signal. * '''Estimator options''': leave the box unchecked so the means will be subtracted before computing the correlation. * '''Output configuration''': Select one file per input. == Phase locking value == <<BR>><<BR>> == Method selection and comparison == We can have a comparison between different connectivity functions. The following table briefly does this job. {{attachment:TableComparison.PNG||height="400",width="700"}} Comparing different approaches with the ground truth we find out that the HCorr function works slightly better than other coherence functions. {{attachment:Coh13_AR3.png||height="350",width="600"}} == Connectivity measures on real data == In this section we will show how to use the Brainstorm connectivity tools on real data. '''Experimental Setep and data recording:''' For this part we will use the LFP monkey data described in Bresslers et al (1993), these data are widely used over the last past years in many studies. The original data could be found in this link: http://www.ccs.fau.edu/~bressler/Data/Nakamura/LFP/Prepro/LFP.html These recordings were made using 51um diameter bipolar electrodes sepetated by 2.5mm in macaque monkeys. For our analysis we have selected the monkey 🙉 named GE. Voltage are recorded at 200Hz sampling rate. The signals are recorded from a total of 15 electrode pairs in the right hemisphere. The location of the electrodes are shown in this figure. Voltage are recorded at 200Hz sampling rate. '''<todo--> insert the figure with the electrodes position here.''' In these experiments the monkey was trained to depress a lever and wait for a visual stimulus (diagonal four dot with a shape of a line or a shape of diamond. The visual cue would inform the monkey to either let go of the lever (release) or keep the lever down (nogo, not release the lever). Defining the lever initial descent to be at time t = 0ms. Each trial last 600ms, the stimulus was given 100ms after the lever was depressed, and last for 100ms. On go trials, a water reward was provided 500 ms after stimulus onset if the hand was lifted within 500ms. On the nogo trials, the lever was depressed for 500ms. For more details about the experement please refer to Bresslers et al (1993). '''Importing and analysing data within brainstorm:''' For our case, we imported and adapted the data to the brainstorm format, you can download the data '''here ''''''todo--> ''''''(add the link here).''' Voltage are on recorded at 200Hz sampling rate. After pooling and ordering the dataset together, we select 480 trials for each condition. '''todo--> ''''''(add figure with the timeline)''' '''Phase Locking Value (PLV):''' Voltage are on recorded at 200Hz sampling rate. After pooling and ordering the dataset together, we select 480 trials for each condition. <<TAG(Advanced)>> == Granger Causality - Mathematical Background == {{attachment:GC_Math_Time2.PNG||height="450",width="700"}} <<BR>><<BR>> '''Practical issues about GC:''' '''Temporal resolution:''' the high time resolution offered by MEG/EEG and intracranial EEG allows for a very powerful application of GC and also offers the important advantage of spectral analysis. <<BR>><<BR>> '''Stationarity:''' the GC methods described so far are all based on AR models, and therefore assume stationarity of the signal (constant auto-correlation over time). However, neuroscience data, especially task-based data such as event-related potentials are mostly nonstationary. There are two possible approaches to solve this problem. The first is to apply methods such as differencing, filtering, and smoothing to make the data stationary (see a recommendation for time domain GC). Dynamical changes in the connectivity profile cannot be detected with the first approach. The second approach is to turn to versions of GC that have been adapted for nonstationary data, either by using a non-parametric estimation of GC or through measures of time-varying GC, which estimate dynamic parameters with adaptive or short-time window methods (Bressler and Seth, 2011). <<BR>><<BR>> '''Number of variables:''' Granger causality is very time-consuming in the multivariate case for many variables (O(m^2) where m represents the number of variables). Since each connection pair results in two values, there will also be a large number of statistical comparisons that need to be controlled for. When performing GC in the spectral domain, this number increases even more as statistical tests have to be performed per frequency. Therefore, it is usually recommended to select a limited number of ROIs or electrodes based on some hypothesis found in previous literature, or on some initial processing with a more simple and less computationally heavy measure of connectivity. <<BR>><<BR>> '''Pre-processing:''' The influence of pre-processing steps such as filtering and smoothing on GC estimates is a crucial issue. Studies have generally suggested to limit filtering only for artifact removal or to improve the stationarity of the data but cautioned against band-pass filtering to isolate causal influence within a specific frequency band (Barnett and Seth, 2011). <<BR>><<BR>> '''Volume Conduction:''' Granger causality can be performed both in the scalp domain or in the source domain. Though spectral domain GC generally does not incorporate present values of the signals in the model, it is still not immune from spurious connectivity measures due to volume conduction (for a discussion see (Steen et al., 2016)). Therefore, it is recommended to reduce the problem of signal mixing using additional processing steps such as performing source localization and doing connectivity in the source domain. <<BR>><<BR>> '''Data length:''' because of the extent of parameters that need to be estimated, the number of data points should be sufficient for a good fit of the model. This is especially true for windowing approaches, where data is cut into smaller epochs. A rule of thumb is that the number of estimated parameters should be at least (~10) several times smaller than the number of data points. <<BR>><<BR>> |
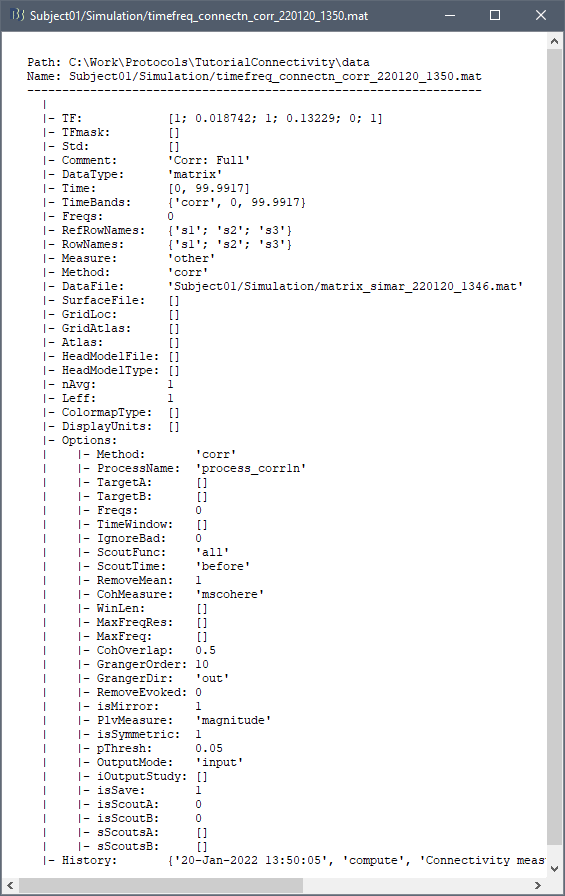
{{attachment:plv.png}} Several variants of PLV have been contritributed. Brainstorm features <<BR>>'''ciPLV''' ([[https://pubmed.ncbi.nlm.nih.gov/29952757/|Bruña 2018]]) and '''wPLI''' ([[https://pubmed.ncbi.nlm.nih.gov/21276857/|Vinck 2011]]) variants contributed to Brainstorm by Daniele Marinazzo. {{{#!wiki note PLV values tend to be overestimated when derived from few (<50) time samples. As a consequence, when comparing PLV values between conditions, please make sure that they are derived from about the same number of samples in each condition. }}} === Process options === * Process: '''Connectivity > Phase locking value NxN'''<<BR>><<BR>> {{attachment:gui_plv1n.gif}} * '''Time window:''' Time segment of the signal used for the connectivity analysis. Select '''All file'''. * '''Connectivity metric '''shows variants of phase locking measures. Select: '''Phase locking value'''. * '''Time-frequency decomposition ''' method for time-frequency transformation. Select: '''Hilbert transform'''. * '''Options [Edit] '''shows the options of the selected time-frequency transformation. * '''Frequency bands:''' Used for the time-frequency transformation with the Hilbert transform method. See the [[Tutorials/TimeFrequency|time-frequency tutorial]]. In this example, the sampling frequency of the signals being 120Hz, please remove the "gamma2" band. * '''Time resolution '''selection of the time resolution. Select: None. * '''Output options''': Select '''Save across combined files/epochs'''. <<BR>> === Results visualization === PLV is frequency resolved, and here was computed for the delta, theta, alpha, beta and gamma1 bands. With the simulated data, we expect a higher PLV value in the beta band (15 to 29 Hz), between Signal 1 and Signal 3. This is indeed our observation, with a peak at 22 Hz (center of beta band) in the PLV spectrum (left). The same is true for ciPLV (center) and wPLI (right). {{attachment:res_plv1n.png||width="650"}} == Phase-Transfer Entropy == Phase transfer entropy (PTE) is a '''directed connectivity''' metric that quantifies the [[https://en.wikipedia.org/wiki/Transfer_entropy|transfer entropy]] (TE) between two instantaneous phase time series ([[https://doi.org/10.1016/j.neuroimage.2013.08.056|Lobier et al., 2014]]). Similar to [[#Granger_Causality|GC]], TE estimates whether including the past of both source and target time series influences the ability to predict the future of the target time series. In PTE, if a phase signal <<latex($$\phi_{\tilde{x}}(t)$$)>> causes the signal <<latex($$\phi_{\tilde{y}}(t)$$)>>, the [[http://www.scholarpedia.org/article/Mutual_information|mutual information]], between <<latex($$\phi_{\tilde{y}}(t)$$)>> and the past of <<latex($$\phi_{\tilde{x}}(t)$$)>> i.e. <<latex($$\phi_{\tilde{x}}(t')$$)>> is larger than the mutual information of <<latex($$\phi_{\tilde{y}}(t)$$)>>, the past of <<latex($$\phi_{\tilde{y}}(t)$$)>> i.e. <<latex($$\phi_{\tilde{y}}(t')$$)>> and <<latex($$\phi_{\tilde{x}}(t')$$)>>. This relationship can be represented on the Venn diagram below, where <<latex($$\mathrm{I()}$$)>> and <<latex($$\mathrm{H()}$$)>>, indicate mutual information and the individual entropies, respectively. PTE values are positive and unbounded. {{attachment:pte.png}} === Process options === * Process: '''Connectivity > Phase Transfer Entropy NxN'''<<BR>><<BR>> {{attachment:gui_pte1n.png||width="400"}} * '''Time window:''' Time segment of the signal used for the connectivity analysis. Select '''All file'''. * '''Frequency bands:''' Used for the time-frequency transformation with the '''Hilbert transform''' method. See the [[Tutorials/TimeFrequency|time-frequency tutorial]]. In this example, as the sampling frequency of the signals is '''120 Hz''', make sure the "gamma2" band is removed from the option. * '''Return normalized phase transfer entropy:''' Divides each directional PTE value between two signals by the sum of both directional PTE values for those two signals. '''Uncheck this option''' * '''Output options''': Select '''Save individual results'''. <<BR>> === Results visualization === Here we computed PTE for the delta, theta, alpha, beta and gamma1 bands. From the synthetic data used here, we expect to observe a higher PTE value in the beta band, From Signal 1 To Signal 3. This is indeed shown with a peak at 22 Hz (center of beta band) in the PTE spectrum. {{attachment:res_pte1n.png||width="350"}} . == Summary: connectivity methods == The following table list the available connectivity metrics in Brainstorm and their description. ||<style="font-weight:bold;border-width:2px;">Metric ||<style="text-align:center;font-weight:bold;border-width:2px;">1×N ||<style="text-align:center;font-weight:bold;border-width:2px;">N×N ||<style="text-align:center;font-weight:bold;border-width:2px;">Directionality ||<style="text-align:center;font-weight:bold;border-width:2px;">Freq resolved ||<style="text-align:center;font-weight:bold;border-width:2px;">Time resolved ||<style="text-align:center;font-weight:bold;border-width:2px;">Function ||<style="text-align:center;font-weight:bold;border-width:2px;">Info || ||<style="border-width:2px;">Correlation ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_corrn.m` ||<style="text-align:center;border-width:2px;">[[#Correlation|Link]] || ||<style="border-width:2px;">Coherence ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_cohn.m` ||<style="text-align:center;border-width:2px;">[[#Coherence|Link]] || ||<style="border-width:2px;">Granger causality ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">`bst_granger.m` ||<style="text-align:center;border-width:2px;">[[#Granger_causality|Link]] || ||<style="border-width:2px;">Spectral Granger causality ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">`bst_granger_spectral.m` ||<style="text-align:center;border-width:2px;">[[#Spectral_Granger_causality|Link]] || ||<style="border-width:2px;">Envelope Correlation (2023) ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_henv.m` ||<style="text-align:center;border-width:2px;">[[#Envelope_Correlation_.282020.29|Link]] || ||<style="border-width:2px;">Phase locking value ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">`bst_connectivity.m` ||<style="text-align:center;border-width:2px;">[[#Phase_locking_value|Link]] || ||<style="border-width:2px;">Phase transfer entropy ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">✅ ||<style="text-align:center;border-width:2px;">❌ ||<style="text-align:center;border-width:2px;">`PhaseTE_MF.m` ||<style="text-align:center;border-width:2px;">[[#Phase_transfer_entropy|Link]] || <<HTML(<!-- )>> Real data: Auditory dataset [TODO] '''TODO''': Rewrite this section with '''coherence '''on '''scouts''', with '''single trials'''. -- In this section we will use the results obtained in the introduction tutorials. The goal here is only to illustrate the interface of these tools on real data, as the results are not particularly interesting. The [[Tutorials/CorticomuscularCoherence|corticomuscular coherence tutorial]] provides more complete and meaninful guidelines for computing connectivity measures on real MEG recordings. Let's go back to our [[DatasetIntroduction|auditory oddball dataset]], available in the protocol '''TutorialIntroduction''' if you have followed the introduction tutorials. As the stimulus is played on both ears, we expect to observe highly correlated activity in the '''primary auditory cortices''', in both experimental conditions (standard and deviant beeps), around '''0''' to '''150 ms''' after the stimulus due to auditory evoked responses at 50 and 100 ms (M50, M100). {{{#!wiki caution In the rest of this section, correlation is computed on the scouts time series of the average response for the standard and deviant conditions. On practice connectivity metrics are computed trial-wise and the results are aggregated. An example of this approach can be seen in the [[Tutorials/CorticomuscularCoherence|corticomuscular coherence tutorial]]. }}} In the [[Tutorials/Scouts#Other_regions_of_interest|Scouts tutorial]], we have created 4 scouts for these regions of interest: '''A1L''' and '''A1R''' for the left and right primary cortices respectively, '''IFGL''' for the left inferior frontal gyrus, and '''M1L''' for the left primary motor cortex. {{attachment:scouts_avg_rel.png}} Let's compute source-domain [[#Correlation|correlation]] for '''standard''' and '''deviant''' conditions for the Run #1: '''S01_AEF_20131218_01_600Hz_notch''' data. 1. Drag and drop the source files associated to the average standard response ('''Avg: standard (193 files)''') and the average deviant response ('''Avg: deviant (193 files)''') within the '''''Process1''''' tab, select the option 'source process' ( {{https://neuroimage.usc.edu/moin_static198/brainstorm1/img/iconResultList.gif}} ), and click on the '''''[Run]''''' button. 1. Add a the process, '''''Connectivity > Correlation NxN'''''. Set the time window from '''0 to 150 ms'''. Check the '''''Use scouts''''' option, and select '''User scouts''' as atlas in the drop menu. Set the '''''Scout function''''' to '''Mean''', for '''''When to apply the scout function''''' select '''Before'''. And select '''''Save individual results (one file per input)'''''. Finally click on '''''[Run]'''''. <<BR>><<BR>> 1. Display the connectivity matrices as '''Image''' (top) and as '''Graph''' (bottom). Adjust the colormaps to show signed values (no absolute), and set the a custom range from '''-0.8''' to '''0.8'''. Lastly, adjust the '''Intensity threshold''' for the graph to the maximum (around 0.7), so only the strongest correlations are kept, mainly, between scouts in the left and right auditory cortices. ||<style="text-align:center">Standard || ||<style="text-align:center">Deviant || || {{attachment:corr_0_150_std_intro.png||width="350"}} || || {{attachment:corr_0_150_dev_intro.png||width="350"}} || || {{attachment:corrg_0_150_std_intro.png||width="350"}} || || {{attachment:corrg_0_150_dev_intro.png||width="350"}} || In this early response period, we appreciate that the correlation matrices for the standard ann deviant response are quite similar, and the strongest correlation happens between the scouts on the primary auditory cortices; just as expected. <<HTML(--> )>> == Thresholding of connectivity estimates == === Interactive tools === Brainstorm provides tools to apply empirical thresholds to display the resulting connectivity estimates. Interactions can be filtered interactively based on their magnitudes, the distance between the nodes of the graph or their category. See the tutorial: [[https://neuroimage.usc.edu/brainstorm/Tutorials/ConnectivityGraph#Filtering_options|Connectivity graphs]]. {{attachment:display_panel.gif||height="195",width="192"}} === Threshold by percentile === The process '''Test > Threshold by percentile''' allows the selection of the top n% connectivity estimates in a single input file. {{attachment:percentile.png||width="300"}} All connectivity estimates (left panel below). The top-5% connectivity matrix (right panel below) only keeps the 5 percentile of all the connectivity estimates. || {{attachment:percentile_100.png||width="350"}} || || {{attachment:percentile_5.png||width="350"}} || === Statistical significance === Inference based threshold can be derived to assess the statistical significance of the connectivity estimates, for instance using non-parametric paired permutation tests. Connectivity outcomes can be computed for different experimental conditions, or between an active state and a baseline. '''Non-parametric paired permutation tests '''are available in Brainstorm to compare between two groups of repeated measures. More information in the [[https://neuroimage.usc.edu/brainstorm/Tutorials/Statistics#Nonparametric_permutation_tests|Statistics tutorial]]. {{attachment:stat_perm.gif||height="141",width="309"}} == On the hard drive == ==== File name ==== The connectivity file structure is an extension of the time-frequency structure. The file names start with '''''timefreq_''''', followed by '''''connect1''''' (1xN) or '''''connectn''''' (NxN or AxB), the connectivity method and a time stamp. ''Example: timefreq_connectn_corr_220120_1350.mat''. ==== File structure ==== Right click on the first connectivity file computed > File > '''View file contents'''. . {{attachment:file_connect.gif}} The data structure is the same as for Brainstorm [[https://neuroimage.usc.edu/brainstorm/Tutorials/TimeFrequency#On_the_hard_drive|time-frequency files]]. Only the fields specific to connectivity analyses are documented below: * '''TF''': [Nr x Ntime x Nfreq] array containing all connectivity values. The connectivity matrix '''R''' computed in [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/connectivity/bst_connectivity.m#L292|bst_connectivity.m]] between two sets of signals A and B, is optimized and saved in the TF variable. The size of the R matrix is [Na x Nb x Ntime x Nfreq]. The relation between Na x Nb and Nr depends on the type of optimization in the file. See details below. * '''RefRowNames''': Cell-array of strings {Na x 1}. Labels of the rows of the connectivity matrix R (Y axis in the image display, with the label ''From''). In the case of a AxB process, these labels are the names of the signals extracted from the first list of files (FilesA). * '''RowNames''': Cell-array of strings {Nb x 1}. Labels of the columns of the connectivity matrix R (X axis in the image display, with the label ''To''). In the case of a AxB process, these labels are the names of the signals extracted from the second list of files (FilesB). * '''Freqs''': Double [1 x Nfreq] for a simple list of frequencies; or cell-array {Nfreq x 3} if using frequency bands, where each line represents a band {'band_name', 'frequency definition', 'function'} * '''Time''': [1,Ntime] for time-resolved files; [1,2] for files with no data dimension (e.g. correlation). When no time is available, this variable describes the time segment from which the connectivity measure was computed. * '''Options.isSymmetric''': Boolean indicating whether the matrix R saved in the TF field is symmetric (e.g. NxN correlation or coherence) or not (e.g. Granger causality). If the R matrix is symmetric, it is saved in a compressed format, with only the values from lower triangular matrix. ==== Connectivity matrix encoding ==== Let's consider the structure '''TfMat''', loaded from a connectivity file, for example by right-clicking on the file > File > Export to Matlab. The connectivity matrix '''R''' can be obtained with function [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/core/bst_memory.m#L1897|GetConnectMatrix]]. The size of R is '''[Na x Nb x Ntime x Nfreq]'''. {{{ R = bst_memory('GetConnectMatrix', TfMat); }}} If the matrix is not symmetrical (i.e., not compressed): for each time and frequency, the list of values from the first dimension of the TF variable is reshaped into a 2D matrix: [Na x Nb]. If the matrix is symmetrical and compressed: only the lower triangular matrix is saved in the TF variable. The full matrix is first reconstructed with function [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/process/functions/process_compress_sym.m#L118|process_compress_sym>Expand]], then reshaped into [Na x Nb]. Saving the connectivity matrix R back in the TF variable is possible by reshaping to [Nx1] ('''''R(:)''''') and then compressing again the matrix: {{{ TfMat.TF = process_compress_sym('Compress', R(:)); }}} |
| Line 227: | Line 454: |
| ==== References ==== | ==== Related tutorials ==== * [[https://neuroimage.usc.edu/brainstorm/Tutorials/CorticomuscularCoherence|Corticomuscular coherence]] * [[https://neuroimage.usc.edu/brainstorm/Tutorials/ConnectivityGraph|Connectivity Graphs]] * [[https://neuroimage.usc.edu/brainstorm/Tutorials/FiberConnectivity|Virtual fibers for connectivity]] * [[https://neuroimage.usc.edu/brainstorm/GrangerCausality|Granger causality]] |
| Line 229: | Line 461: |
| * '''Phase transfer entropy''': Lobier M, Siebenhühner F, Palva S, Palva JM [[http://www.sciencedirect.com/science/article/pii/S1053811913009191|Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions]], NeuroImage 2014, 85:853-872 | * Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M. <<BR>> [[https://doi.org/10.1016/j.clinph.2004.04.029|Identifying true brain interaction from EEG data using the imaginary part of coherency]]. <<BR>> Clinical Neurophysiology. 2004 Oct;115(10):2292–307. * Pascual-Marqui RD. <<BR>> [[https://arxiv.org/pdf/0706.1776|Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions.]] <<BR>> arXiv preprint arXiv:0706.1776. 2007 Jun 12. * Bressler SL, Seth AK. <<BR>> [[https://doi.org/10.1016/j.neuroimage.2010.02.059|Wiener–Granger causality: a well established methodology.]] <<BR>> Neuroimage. 2011 Sep 15;58(2):323-9. * Dhamala M, Rangarajan G, Ding M. <<BR>> [[https://doi.org/10.1103/PhysRevLett.100.018701|Estimating Granger causality from Fourier and wavelet transforms of time series data.]] <<BR>> Physical review letters. 2008 Jan 10;100(1):018701. * Hipp JF, Hawellek DJ, Corbetta M, Siegel M, Engel AK. <<BR>> [[https://doi.org/10.1038/nn.3101|Large-scale cortical correlation structure of spontaneous oscillatory activity.]] <<BR>> Nature neuroscience. 2012 Jun;15(6):884-90. * Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, et al. <<BR>> [[https://doi.org/10.1103/PhysRevLett.81.3291|Detection of n : m Phase Locking from Noisy Data: Application to Magnetoencephalography.]] <<BR>> Phys Rev Lett. 1998 Oct 12;81(15):3291–4. * Bruña R, Maestú F, Pereda E<<BR>>[[https://pubmed.ncbi.nlm.nih.gov/29952757|Phase locking value revisited: teaching new tricks to an old dog]]<<BR>>Journal of Neural Engineering, Jun 2018 * Vinck M, Oostenveld R, van Wingerden M, Battaglia F, Pennartz CM<<BR>>[[https://pubmed.ncbi.nlm.nih.gov/21276857|An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias]]<<BR>>Neuroimage, Apr 2011 * Lobier M, Siebenhühner F, Palva S, Palva JM. <<BR>> [[https://doi.org/10.1016/j.neuroimage.2013.08.056|Phase transfer entropy: a novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions.]] <<BR>> Neuroimage. 2014 Jan 15;85:853-72. * Barzegaran E, Knyazeva MG. <<BR>> [[https://doi.org/10.1371/journal.pone.0181105|Functional connectivity analysis in EEG source space: The choice of method]] <<BR>> Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105. * Lai M, Demuru M, Hillebrand A, Fraschini M. <<BR>> [[https://doi.org/10.1038/s41598-018-30869-w|A comparison between scalp- and source-reconstructed EEG networks.]] <<BR>> Sci Rep. 2018 Dec;8(1):12269. * Schoffelen J-M, Gross J. <<BR>> [[https://doi.org/10.1002/hbm.20745|Source connectivity analysis with MEG and EEG.]] <<BR>> Hum Brain Mapp. 2009 Jun;30(6):1857–65. * Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI. <<BR>> [[https://doi.org/10.1038/nn.2303|Circular analysis in systems neuroscience: the dangers of double dipping.]] <<BR>> Nat Neurosci. 2009 May;12(5):535–40. * Cohen MX. <<BR>> [[https://mitpress.mit.edu/books/analyzing-neural-time-series-data|Analyzing Neural Time Series Data: Theory and Practice]]. MIT Press; 2014. * Sadaghiani S, Brookes MJ, Baillet S.<<BR>>[[https://doi.org/10.1016/j.neuroimage.2021.118788|Connectomics of human electrophysiology]].<<BR>>NeuroImage. 2022 Feb;247:118788. * Sporns O. <<BR>> [[https://mitpress.mit.edu/9780262528986/networks-of-the-brain|Networks of the Brain]]. MIT Press; 2016. |
| Line 232: | Line 494: |
| * Connectivity matrix storage:[[http://neuroimage.usc.edu/forums/showthread.php?1796-How-the-Corr-matix-is-saved|http://neuroimage.usc.edu/forums/showthread.php?1796]] * Comparing coherence values: http://neuroimage.usc.edu/forums/showthread.php?1556 * Reading NxN PLV matrix: http://neuroimage.usc.edu/forums/t/pte-how-is-the-connectivity-matrix-stored/4618/2 * Scout function and connectivity: http://neuroimage.usc.edu/forums/showthread.php?2843 * Unconstrained sources and connectivity: http://neuroimage.usc.edu/forums/t/problem-with-surfaces-vs-volumes/3261 * Digonal values: http://neuroimage.usc.edu/forums/t/choosing-scout-function-before-or-after/2454/2 * Connectivity pipeline: https://neuroimage.usc.edu/forums/t/help-for-connectivity-pipeline/12558/4 * Ongoing developments: https://neuroimage.usc.edu/forums/t/connectivity-tutorial-and-methods-development-on-bst/12223/3 * Granger causality: https://neuroimage.usc.edu/forums/t/is-granger-causality-analysis-a-linear-operation/12506/12 |
* Granger causality: [[https://neuroimage.usc.edu/forums/t/is-granger-causality-analysis-a-linear-operation/12506/12|https://neuroimage.usc.edu/forums/t/12506]] * Coherence on single trials: [[https://neuroimage.usc.edu/forums/t/difference-between-averaging-coherence-and-concatenate/22726/4|https://neuroimage.usc.edu/forums/t/22726]] * ciPLV: https://neuroimage.usc.edu/forums/t/9751 * wPLI: https://neuroimage.usc.edu/forums/t/9434 * Coherence and PLV: https://neuroimage.usc.edu/forums/t/33379 * Removing ERP response for PLV: https://neuroimage.usc.edu/forums/t/32665 * Connectivity of subcortical ROIs: https://neuroimage.usc.edu/forums/t/33479 * Non-zero diagonals with unconstrained sources: https://neuroimage.usc.edu/forums/t/33700 * Coherence/Lagged coherence vs. Envelope correlation/Lagged coherence: https://neuroimage.usc.edu/forums/t/lagged-coherence/39440 |
| Line 252: | Line 514: |
| <<EmbedContent("http://neuroimage.usc.edu/bst/get_prevnext.php?prev=Tutorials/GroupAnalysis&next=Tutorials/Scripting")>> | == Scripting == The following script from the Brainstorm distribution reproduces the analysis presented in this tutorial page: [[https://github.com/brainstorm-tools/brainstorm3/blob/master/toolbox/script/tutorial_connectivity.m|brainstorm3/toolbox/script/tutorial_connectivity.m]] <<HTML(<div style="border:1px solid black; background-color:#EEEEFF; width:720px; height:500px; overflow:scroll; padding:10px; font-family: Consolas,Menlo,Monaco,Lucida Console,Liberation Mono,DejaVu Sans Mono,Bitstream Vera Sans Mono,Courier New,monospace,sans-serif; font-size: 13px; white-space: pre;">)>><<EmbedContent("https://neuroimage.usc.edu/bst/viewcode.php?f=tutorial_connectivity.m")>><<HTML(</div >)>> |
| Line 255: | Line 520: |
== TODO == '''Hossein, Richard''' * Granger Causality implementation: https://github.com/brainstorm-tools/brainstorm3/pull/433 '''Raymundo, Sylvain''' * Read data: Can we find something more meaningful than what we compute in the example in the dataset? A full connectome in a task vs. baseline maybe? |
Connectivity
Authors: Hossein Shahabi, Raymundo Cassani, Takfarinas Medani, François Tadel, Marc Lalancette, Sylvain Baillet
Brain functions (e.g., in cognition, behavior and perception) stem from the coordinated activity of multiple regions. Brain connectivity measures are designed to probe how brain regions (or nodes) interact as a network. A distinction is made between structural (fiber pathways), functional (non-directed statistical associations) and effective (causal interactions, or "directed functional connectivity") connectivity between regions. Here we explain how to compute various connectivity metrics for non-directed and directed functional connectivity analyses with Brainstorm, both with simulated (ground-truth) and empirical data.
We encourage the interested reader to learn more about the specific aspects of electrophysiology for studying human connectomics.
Contents
- Introduction
- Pre-requisites
- Simulated data
- Correlation
- Coherence
- Granger causality
- Spectral Granger causality
- Envelope correlation
- Phase-Locking Value
- Phase-Transfer Entropy
- Summary: connectivity methods
- Thresholding of connectivity estimates
- On the hard drive
- Additional documentation
- Scripting
- TODO
Introduction
Definitions
Connectivity analyses are commonly performed by computing a bivariate measure between pairs of regional time series of interest. The outcome (a.k.a a connectome) can be represented as a connectivity graph (left panel below), with each brain region as a node (x, y, z,...), and the connectivity measures shown above each edge of the graph. The connectome can also be represented by a connectivity array, a.k.a. an adjacency matrix (right panel below).
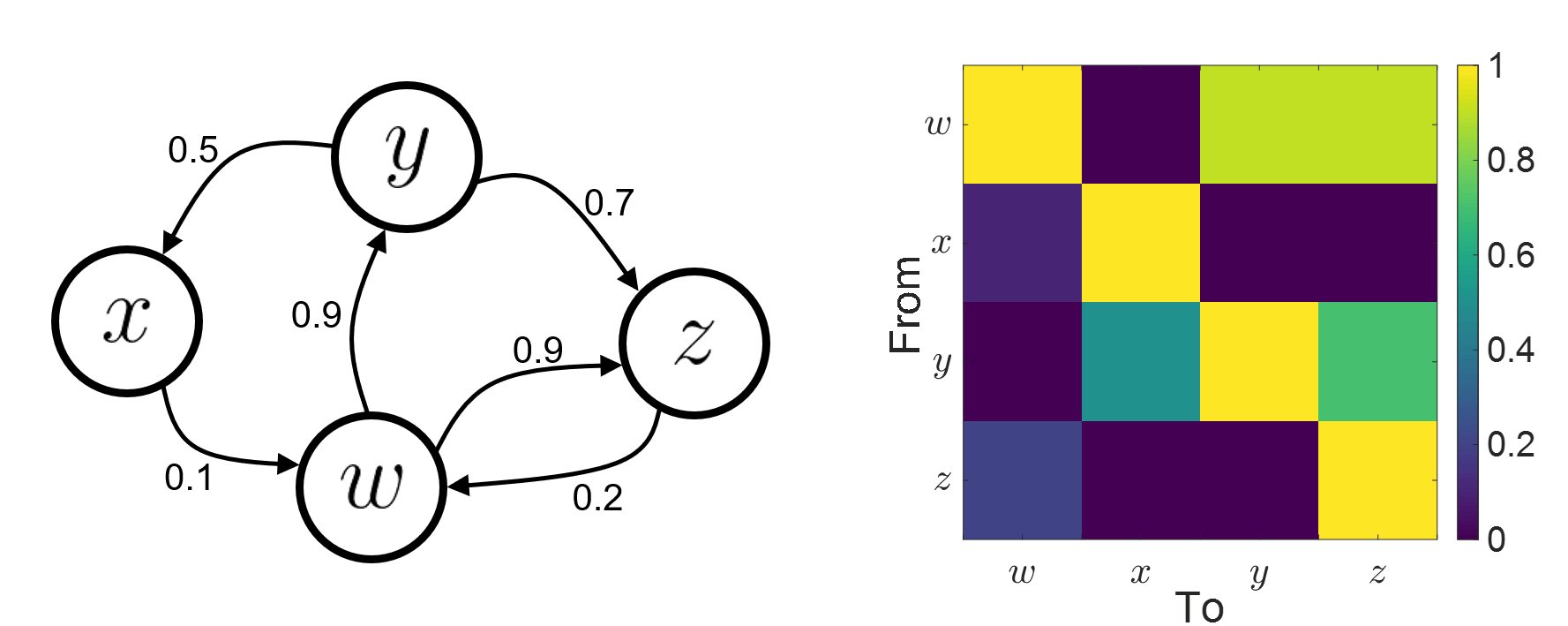
Sensors or sources: The time series used for connectivity analyses can be from sensor data (EEG/MEG signals) or from source time series (brain voxels or scouts).
Directed vs. non-directed: The direction of interactions between signals (as a measure of statistical causation) is estimated with directed metrics. Non-directed metrics produce symmetrical connectivity graphs/matrices: the connectivity measure "from Signal  to Signal
to Signal  " is identical to the connectivity measure "from Signal
" is identical to the connectivity measure "from Signal  to Signal
to Signal  ".
".
Experimental condition: Depending on the neuroscience question, connectivity analyses can be performed on resting-state or task (e.g., ongoing or trial-based) data.
Full (NxN) vs. seeded (1xN) connectivity: In a full connectivity analysis, the connectivity metric is computed for all the possible pairs of nodes between N time series (noted N×N here). Alternatively, seeded connectivity (noted 1×N) is measured between one time series of interest (a seed, e.g., one brain region or a behavioral marker) and N other regions/time series.
Time-frequency transformations: Some connectivity metrics rely on a time-frequency representation of the signals. These latter are obtained with approaches such as the short-time Fourier transform, Hilbert transform, or Morlet wavelets.
Just as in other areas of electrophysiology studies, connectivity analyses need to beguided by mechanistic hypotheses concerning the expected neurophysiological effects.
Sensor-level analyses
Their anatomical interpretation is limited and ambiguous.
Sensor data is affected by field spread and volume conduction of brain activity across the scalp/sensor array. Hence, activity from one single brain area is picked up at multiple, possibly distant sensor locations. Connectivity measures may show strong interactions between sensor time series, which may be wrongly interpreted as inter-regional brain connections.
Source-level analyses
Connectivity measures between source time series are neuroanatomically interpretable and can be derived across participants.
We recommended that the outcomes of sensor and source connectivity analyses are mutually compatible; see (Lai et al., 2018).
Full-brain connectomes
Whole-brain connectivity analyses at the typical resolution of cortical surfaces in Brainstorm involve thousands of source locations, making the N×N derivations impractical. For instance, 15000 cortical vertices would yield a connectivity matrix of 15000x15000x8 bytes = 1.6 GB. If unconstrained cortical sources are used and coherence is computed across 50 frequency bins, the memory allocation increases to 45000x45000x50x8 = 754 GB per participant/condition/trial/etc. Reducing the N (via e.g., cortical parcellations, ROIs) may be required for practical reasons, depending on computing resources.
Regions of interest
Grouping individual brain sources into ROIs, defined on the cortical surface or in the brain volume helps contain the computational resources required for connectivity analyses (see above). ROIs can be defined based on neuroscience priors and the purpose of the study (Schhoffen and Gross, 2009). You may consider:
Study priors from the literature in your field, specific working hypotheses in terms of neuro-anatomical brain structures expected to be involved.
Association with a non-neuronal signal (e.g., cortico-muscular coherence).
Signal strength, by defining ROIs from brain regions with strongest activity in current data.
Whole-brain cortical parcellation to reduce N.
The tutorial Corticomuscular coherence explains the computation of connectivity measures constrained and unconstrained brain maps for these cases:
One signal x full-brain source maps: link
One signal x scouts: link
ROI-based connectomes, i.e., scouts x scouts: link
Studies have reported similarities and differences between electrophysiological connectomes (from MEG/EEG) and fMRI connectomes. See how the electrophysiological connectomes provide unique insights on how functional communication is implemented in the brain in Sadaghiani et al., 2022.
On whole-brain connectivity analyses and the issue of circular analysis, please see Kriegeskorte et al., 2009.
Pre-requisites
Here we focus on the specifics on connectivity analyses with Brainstorm. Please make sure you are familiar with Brainstorm and go through all introduction tutorials first, before following the present tutorial.
We first use simulated, synthetic data to emphasize the theoretical aspects of each connectivity metric with respect to groundtruth outcomes. Real, empirical MEG data are featured later in the tutorial (same auditory oddball dataset as in the other tutorial sections).
Let's start by creating a new protocol in the Brainstorm database:
Select the menu File > Create new protocol > type in "TutorialConnectivity" and select the options:
Yes, use protocol's default anatomy,
No, use one channel file per condition.
Right-click on the TutorialConnectivity folder > New subject > Subject01
Simulated data
To compare connectivity metrics, let's use synthetic time series simulated with known ground truth interactions. We will use a multivariate autoregressive (MVAR) model that consists of the following three signals:
Signal 1: two oscillatory (rhythmic) components: One at 10 Hz (alpha band), and a stronger peak at 25 Hz (beta band).
Signal 2: Same as Signal 1, with the strongest peak at 10 Hz.
Signal 3: Same as above, with the two components (10 and 25 Hz) of same magnitude.
The 25-Hz component of Signal 3 will be driven in part by the 25-Hz component of Signal 1 (denoted Signal 1>>Signal 3).
Let's now generate the three time series:
In the Process1 tab, leave the file list empty and click on the button [Run]
Select process: Simulate > Simulate AR signals.
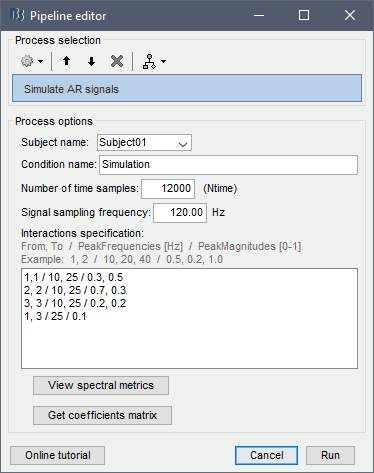
Process options:
Subject name: Target subject for the simulated signals: Select Subject01.
Condition name: Target folder where to store the simulated data in your database: Set to Simulation.
Number of time samples for each simulated time series: Set to 12,000.
Sampling frequency (Fs): Set to 120 Hz.
Interaction specifications: Spectral parameters for the signal components and their interactions in the MVAR model: From, To / Peak frequencies [Hz] / Peak relative magnitudes [0-1]
Set to:1, 1 / 10, 25 / 0.3, 0.5 2, 2 / 10, 25 / 0.7, 0.3 3, 3 / 10, 25 / 0.2, 0.2 1, 3 / 25 / 0.1
Display the groundtruth spectral metrics of the MVAR-generated time series: transfer function, cross-spectral power density, magnitude square coherence, directed transfer function (DTF) and partial directed coherence (PDC). The transfer function (
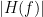 ) characterizes the relationships between signals in the frequency domain. It is a non-symmetric representation, which enables the identification of causal dependencies between signal components. The auto-transfer functions (shown in the graphs along the diagonal below) display the power spectra of each signal. The off-diagonal representations display the interactions between each pair of signals (see Signal 1 >> Signal 3 above). Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values.
) characterizes the relationships between signals in the frequency domain. It is a non-symmetric representation, which enables the identification of causal dependencies between signal components. The auto-transfer functions (shown in the graphs along the diagonal below) display the power spectra of each signal. The off-diagonal representations display the interactions between each pair of signals (see Signal 1 >> Signal 3 above). Here, we see the transfer function from signal 1 to signal 3. These transfer functions are our ground truth for connectivity values.
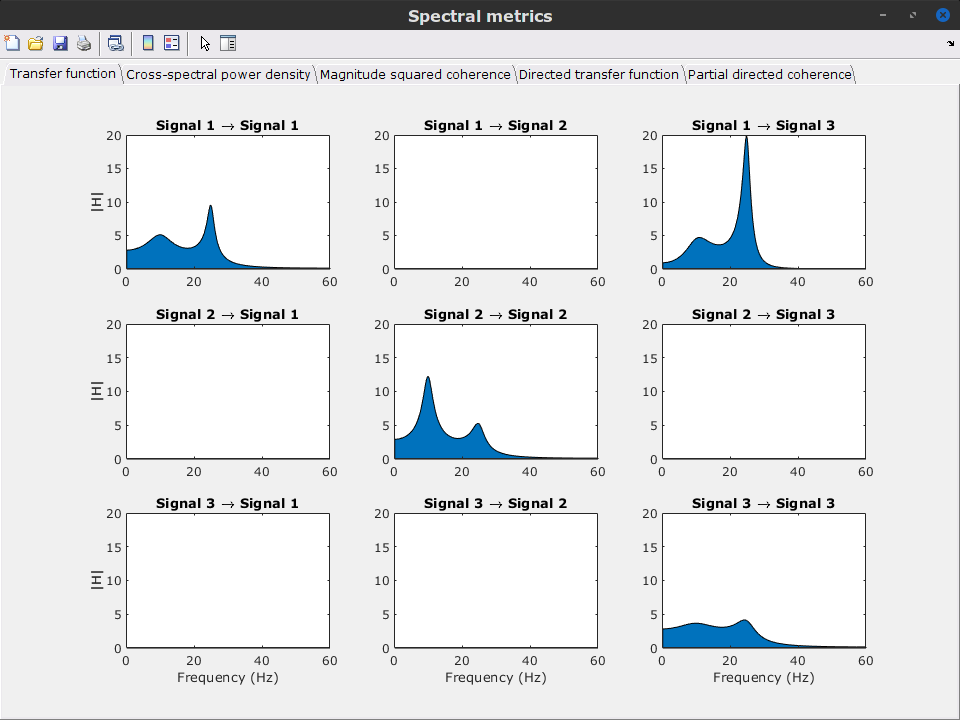
Get coefficients matrix: Shows the coefficients related to the MVAR model. These coefficients can be used in the process Simulate > Simulate AR signals (ARfit) to simulate the same model.
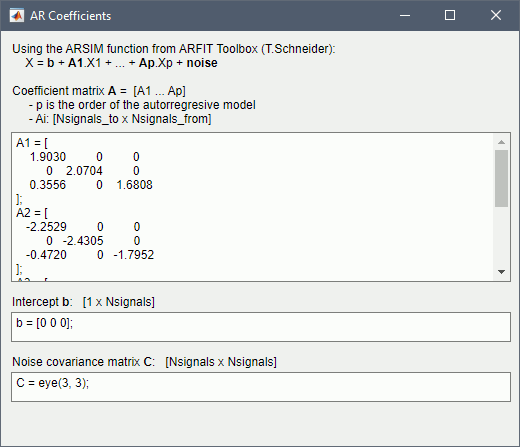
Execution:
Click Run to generate the time series with the MVAR model.
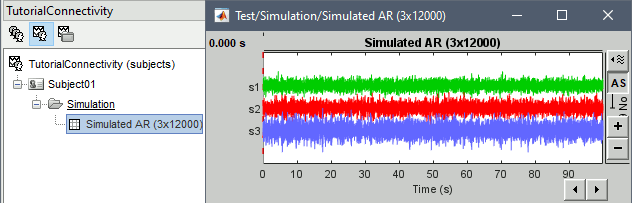
In the next sections, we will compute different connectivity metrics from these synthetic time series. Drag and drop the simulated data in the Process1 tab, click on [Run] (
 ) to open the Pipeline editor, and select the connectivity metric.
) to open the Pipeline editor, and select the connectivity metric.
This tutorial illustrates the computation of full connectivity graphs (Process 1: NxN). It is also possible to obtain connectivity measures between one of the time series of a given data file and the other time series in the same file (use Process1: 1xN), or between time series from two different data files (use Process2: AxB), as shown further below.
References used:
This process relies on the ARSIM function from the ARFit toolbox:
https://github.com/tapios/arfitNeumaier A, Schneider T
Estimation of parameters and eigenmodes of multivariate autoregressive models
ACM Transactions on Mathematical Software, 2001Schneider T, Neumaier A
Algorithm 808: ARfit – A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models
ACM Transactions on Mathematical Software, 2001
Correlation
Correlation is a relatively simple, non-directed connectivity metric of association between two time series. It is relatively limited without further preprocessing of the input time series: correlation is sensitive to volume conduction and is not frequency specific.
Process options
Process Connectivity > Correlation NxN:
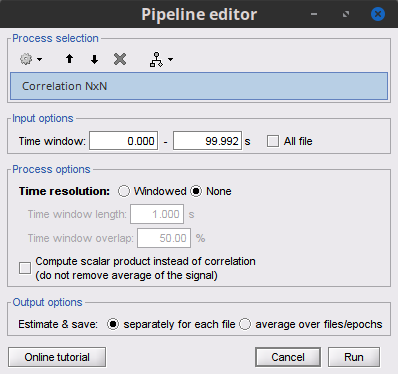
Time window: Time segment of the signals for connectivity analysis. Select: All file.
Time resolution: Select None
Windowed: correlation is computed in windows of a given length with a certain overlap percentage
None: correlation is computed using the entire time series
Compute scalar product: If left unchecked, the mean of the time series is subtracted before computing the correlation. Leave it unchecked.
Output options: Select Estimate and save separately for each file.
Result visualization
The results are stored as a N×N connectivity file, with a new icon
 . Right-click for display options:
. Right-click for display options:
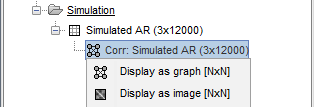
Display as graph: Plots the connectivity graph using a chord diagram where the color of the edges shows the value of the connectivity metric. See the connectivity graph tutorial for a detailed explanation of the options of this visualization.
Display as image: Plots the connectivity measures in an adjacency matrix.
Display fibers: Displays source connectivity edges as virtual white fiber tracts, as shown here.
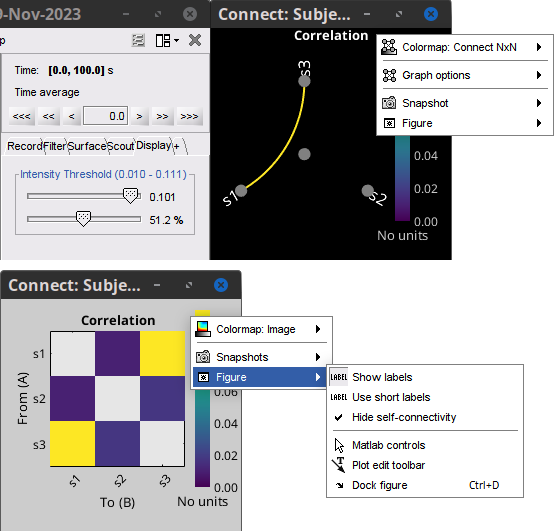
Display options:
Show labels: Click on the figure to display the names of the times series and the connectivity values in the figure legend. To display the labels corresponding to each column and row: right-click on the figure > Figure > Show labels. If the time series names are too long, use the option Use short labels.
Hide self-connectivity: In a square NxN connectivity matrix, the diagonal values correpond to the values of the connectivity metric between a time series and itself. These self-connectivity values are typically much higher than the other values of the matrix. When checked, these values are hidden so that to display the off-diagonal values more clearly.
Colormap: By default, the NxN colormap is configured to display the absolute values of the connectivity measures. Correlation values may be positive or negative. To display the negative values, make sure to change the colormap configuration: right-click on the figure > Colormap > Uncheck Absolute values.
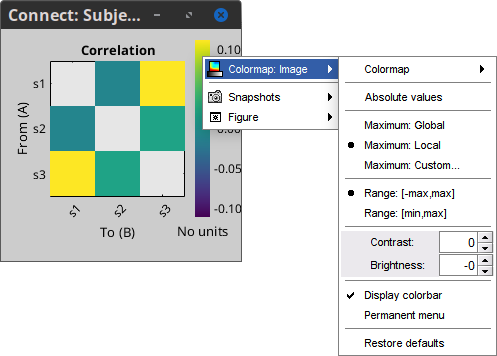
Coherence
Coherency or complex coherence, 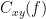 , is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Magnitude square coherence (MSC),
, is a complex-valued metric that measures the linear relationship of two signals in the frequency domain. Magnitude square coherence (MSC), 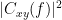 , or coherence, measures the covariance of two signals in the frequency domain. For a pair of time series
, or coherence, measures the covariance of two signals in the frequency domain. For a pair of time series 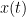 and
and 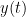 , with spectra
, with spectra 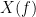 and
and 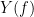 , the MSC is defined as:
, the MSC is defined as:
Two related measures, which address the problem of volume conduction, are imaginary coherence (Nolte et al., 2004), 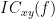 , and lagged coherence (Pascual-Maqui, 2007),
, and lagged coherence (Pascual-Maqui, 2007), 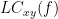 , which are defined as:
, which are defined as:
where 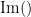 and
and 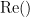 are the imaginary and real parts of a complex number, respectively.
are the imaginary and real parts of a complex number, respectively.
Note that the cross-spectrum (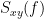 ) and the power spectral densities (
) and the power spectral densities (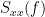 and
and 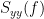 ), and as consequence also coherency (
), and as consequence also coherency (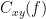 ) can be obtained through different time-frequency decomposition methods (such as: Hilbert transform, wavelet transform and short-time Fourier transform), and for different time resolutions (per sample, windowed and entire file).
) can be obtained through different time-frequency decomposition methods (such as: Hilbert transform, wavelet transform and short-time Fourier transform), and for different time resolutions (per sample, windowed and entire file).
Process options
Process Connectivity > Coherence NxN:
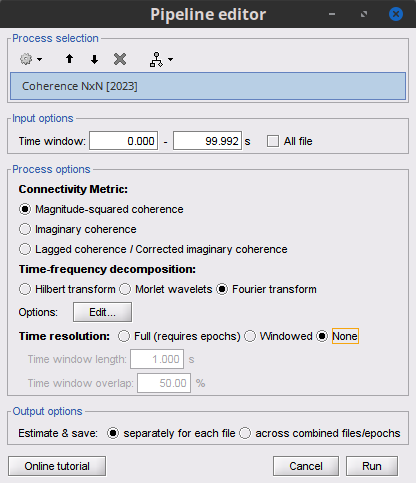
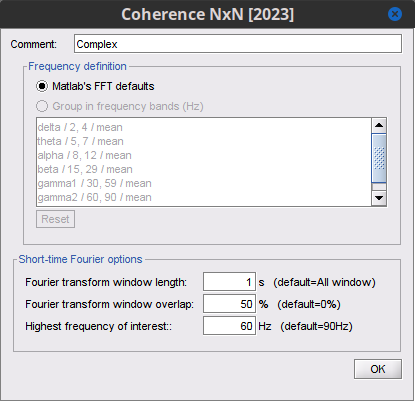
Time window: Segment of the time series used for the connectivity analysis. Select All file.
Connectivity metric shows variants of coherence measures. Select: Magnitude squared coherence.
Time-frequency decomposition selection of the time to time-frequency transformation. Select: (short-time) Fourier transform.
Options [Edit] shows the options of the selected time-frequency transformation.
Window length: Duration in seconds for the spectrum estimation. Set to: 1s.
Overlap: Percentage of overlap between consecutive sliding time windows. Set to: 50%.
Highest frequency: After the computation, removes all the frequencies above this threshold, mostly for visualization purposes. The value needs to be <= Fs/2. Set to: 60 Hz.
Time resolution selection of the time resolution. Select: None.
Output options: Select Estimate and save separately for each file.
Result visualization
Coherence is frequency specific: a connectivity graph and a connectivity matrix are produced for each frequency bin of the spectrum. Right-click on the coherence result file to show display options:
Display as graph: Plots a connectivity graph for each frequency bin.
Display as image: Plot a connectivity matrix for each frequency bin.
Power spectrum: Plot coherence as a function of frequency, between each time series.
Open the 3 types of visualization: they are linked by clicking on the spectral representation of the coherence, which will change the current frequency bin and update the connectivity measures displayed in the graph and matrix. The value of the current frequency bin can also be changed in the Time panel.
Other variants of coherence can be derived following the above procedure. The figures below display the coherence spectra obtained from the imaginary coherence (left) and the lagged coherence (right) measures.
|
|
|
Granger causality
Granger causality (GC) is a measure of directed functional connectivity based on the Wiener-Granger causality framework. GC measure linear dependencies between time series, and tests whether the prediction of the future of signal 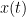 (approximated by a linear autoregressive model) is improved by considering signal
(approximated by a linear autoregressive model) is improved by considering signal 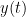 (also approximated by a linear autoregressive model). If there is such improvement, one concludes that signal
(also approximated by a linear autoregressive model). If there is such improvement, one concludes that signal 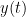 has a Granger causal effect on the other signal. In sum, some independent information from the past of signal
has a Granger causal effect on the other signal. In sum, some independent information from the past of signal 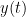 improves the prediction of the future of signal
improves the prediction of the future of signal 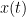 , with respect to only observing its past
, with respect to only observing its past 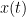 . GC takes nonnegative values; its is zero when no Granger causality can be attributed. The term independent means that GC is invariant with the scale of the input signals
. GC takes nonnegative values; its is zero when no Granger causality can be attributed. The term independent means that GC is invariant with the scale of the input signals 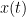 and
and 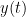 .
.
See Granger causality - mathematical background for a more complete background.
Despite the name, Granger causality indicates directionality but not true causality.
For example, if a variable 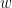 is causing both
is causing both  and
and 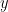 , but with a smaller delay for
, but with a smaller delay for 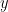 than for
than for  , then the GC measure between
, then the GC measure between  and
and 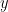 would show a non-zero GC for
would show a non-zero GC for  -->
-->  , even though
, even though  is not truly causing
is not truly causing  (Bressler and Seth, 2011).
(Bressler and Seth, 2011).
Process options
Process Connectivity > Bivariate Granger causality NxN
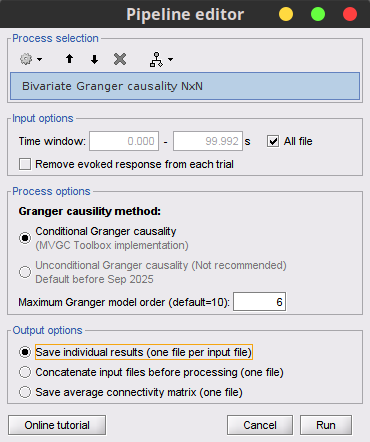
Time window: Time segment of the time series used for the connectivity analysis. Select All file.
Remove evoked response: This option is recommended by some authors as it satisfies the zero-mean stationarity of the GC model, but does not account for trial-to-trial variability; see (Wang et al., 2008). Leave it Unchecked.
Maximum Granger model order: The most common criteria used to define the order of the autoregressive models used by GC to approximate the input time series are the Akaike’s information criterion, the Bayesian-Schwartz’s criterion, and the Hannan-Quinn criterion. Low model orders will yield coarse approximations of the input time series. High model orders may yield spurious GC connectivity estimates. The simulated time series were created with an AR model of order 4; please use a maximum Granger model order of 6.
Output options: Select Save individual results.
Results visualization
The connectivity matrix (left panel below) is not symmetric because GC values are direction specific. The upper right elements of the matrix indicate there is a GC influence from signal 1 to signal 3. In the connectivity graph (right panel below) the directionality is shown with an arrowhead at the center for the arc connecting two nodes.
|
|
|
Spectral Granger causality
The Spectral Granger causality is a measure of directed functional connectivity that was developed to indicate frequency specific influences between time series (Dhamala et al., 2008).
Process options
Process: Connectivity > Bivariate Granger causality NxN.
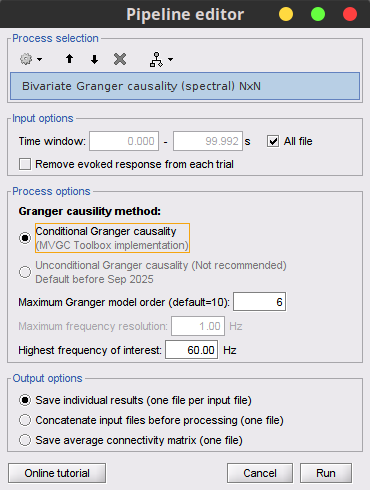
. Here we used the same parameters as with GC plus two two extra parameters specific to spectral GC:Maximum frequency resolution: Width of frequency bins in PSD estimation. Set to 1 Hz.
Highest frequency: computes GC values under the specified frequency. Should be set <= Fs/2. Use: 60 Hz.
Result visualization
As with coherence, spectral GC can be plotted as a function of frequency. The display below shows a peak around 25 Hz that corresponds to the expected causal interaction of Signal 1 on Signal 3.
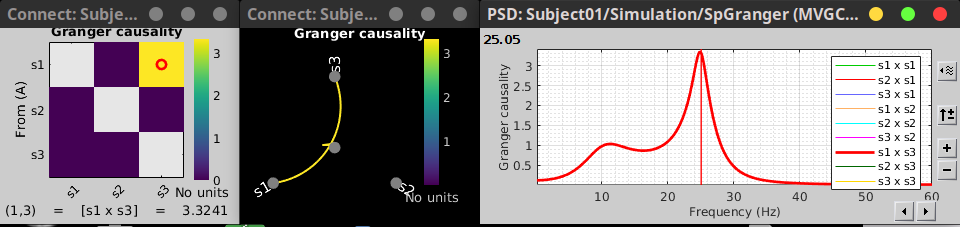
Envelope correlation
In the time-frequency tutorial, we have introduced Morlet wavelets and the Hilbert transform as methods to decompose time series in the time-frequency (TF) domain.
The outcome of these two TF transformations is an analytic signal, 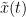 , which is a complex time series uniquely associated to the original data time series,
, which is a complex time series uniquely associated to the original data time series, 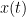 , which module
, which module 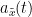 , and phase
, and phase 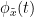 , correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the original time series
, correspond to the instantaneous amplitude (or envelope) and instantaneous phase of the original time series 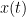 , respectively. The real part of
, respectively. The real part of 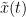 is the original time series
is the original time series 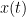 , and the imaginary part is the Hilbert transform of that same time series
, and the imaginary part is the Hilbert transform of that same time series 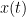 .
.
The analytic signal of oscillatory or narrowband signals provide meaningful and interpretable estimations of instantaneous amplitude and phase. While it is technically feasible to derive these elements from broadband time series, they would not be interpretable (see Cohen, 2014).
The instantaneous amplitude (or envelope) of the analytic signals can be used to carry out pairwise connectivity analysis with correlation. This is to say amplitude envelop correlation (AEC).
An optional step consists in orthogonalizing the pairs of amplitude envelope time series before computing the correlation. Orthogonalization is performed by first removing the real part of their coherence to reduce volume conduction (at the sensor level) or cross-talk effects (at the source level) (Hipp et al., 2012).
Process options
Process: Connectivity > Envelope Correlation N×N [2023]
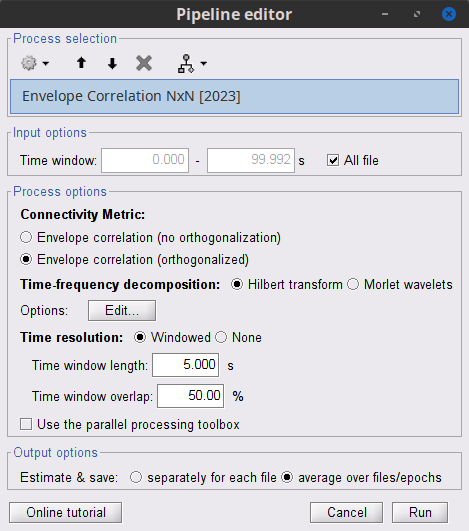
Time window: Time segment of the signal used for the connectivity analysis. Select: All file.
Connectivity measure is the connectivity metric applied to the resulting signal amplitude envelopes. Select Envelope correlation (orthogonalized).
Time-frequency decomposition: Hilbert transform or Morlet wavelets. Each method requires additional parameters that will be displayed in a separate panel after clicking on [Edit]. See the time-frequency tutorial. In the present example, we will use the Hilbert transform with the option Group in frequency bands to present the results for the canonical frequency bands. As the sampling frequency of the signals is 120Hz, thus, make sure you remove the "gamma2" band from the targeted frequency bands.
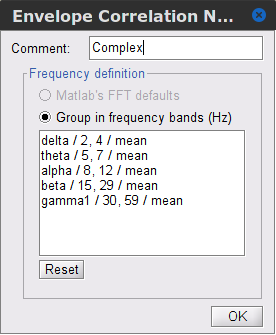
Time resolution: If Windowed, connectivity is saved for each time window. If None, the connectivity measures are averaged across all windows. Select Windowed. Set the additional parameters to define the windows:
Time window length: Duration in milliseconds over which the connectivity measure is computed. Set to 5s
Time window overlap: Percentage of overlap between consecutive time windows to compute the connectivity measure. Set to 50%.
Use the parallel processing toolbox: If available, will call Matlab's parallel processing to accelerate computations. Leave it Unchecked.
Output options: Select Estimate and save separately for each file.
For sake of comparison, we will compute AEC again, but this time changing the TF decomposition method to Morlet wavelets with Linear = 1:1:60 (frequencies from 1 to 60 Hz with 1 Hz step).
Results visualization
As with Coherence and spectral Granger causality, amplitude envelope correlations can be displayed as a function of frequency, and as a function of time if the Time resolution option was set to Windowed. Below are the AEC results obtained with the Hilbert transform (left panels) and with Morlet wavelets (right panels) for the first 5-s time window (top panels) and the 5-s last window (bottom panels).
|
First 5-s window |
|
|
Last 5-s window |
|
Phase-Locking Value
An alternative class of connectivity metrics considers the relative instantaneous phase between two time series as a marker of connectivity. Phase-locking or phase synchronization are two such measures (Tass et al., 1998). In principle, phase-based measures are robust against fluctuations in signal amplitude, although low signal-to-noise conditions remain challenging for these measures (Lachaux et al., 1999; Mormann et al., 2000).
The phase-locking value (PLV) is a popular metric defined as the length of the average vector of many unit vectors whose phase angle corresponds to the phase difference between two time series (Tass et al., 1998). If the distribution of the phase difference between the two signals is uniform, the length of such an average vector will be 0. If the phases of the two signals are strongly coupled, the length of the average vector will be close to 1. For event-related studies, we would expect phase differences across trials to be uniformly distributed, unless the phase of the brain signals is locked to the event onset, which would then indicate a form of phase locking between the two time series. Considering a pair of narrow-band analytic signals 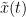 and
and 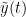 , obtained from the Hilbert transform (see above):
, obtained from the Hilbert transform (see above):
![\begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*} \begin{eqnarray*}
\mathrm{PLV} = \left | E\left [ e^{j\Delta \phi (t)} \right ] \right | \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_34340c3731fe7904b2885462bc74b6a893456cc5_p1.png)
with:
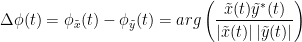
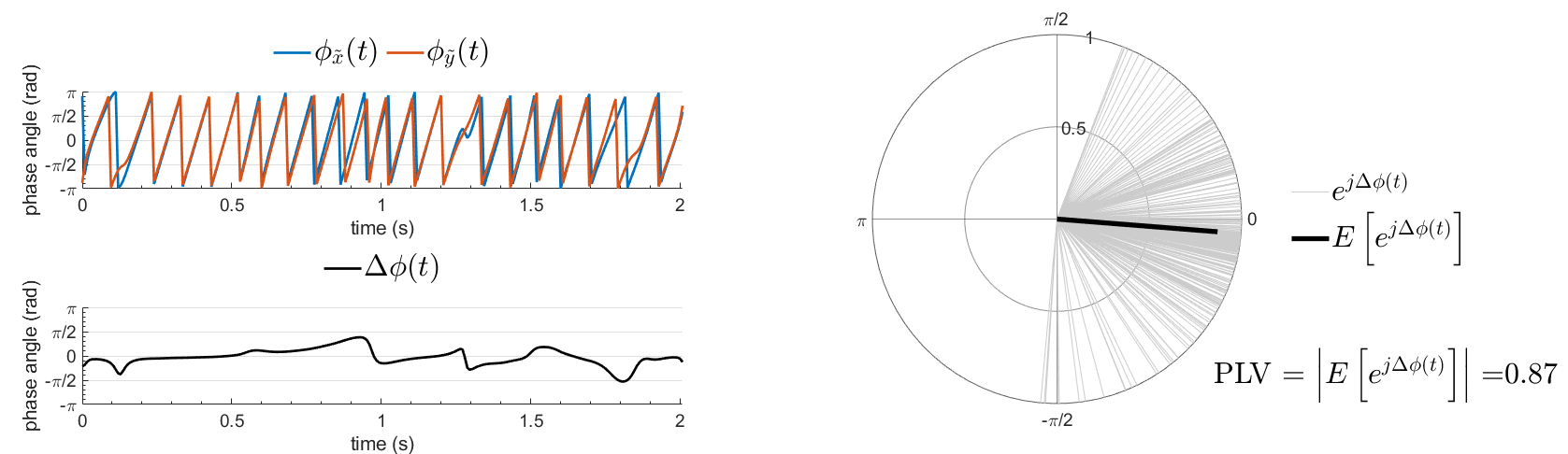
Several variants of PLV have been contritributed. Brainstorm features
ciPLV (Bruña 2018) and wPLI (Vinck 2011) variants contributed to Brainstorm by Daniele Marinazzo.
PLV values tend to be overestimated when derived from few (<50) time samples. As a consequence, when comparing PLV values between conditions, please make sure that they are derived from about the same number of samples in each condition.
Process options
Process: Connectivity > Phase locking value NxN
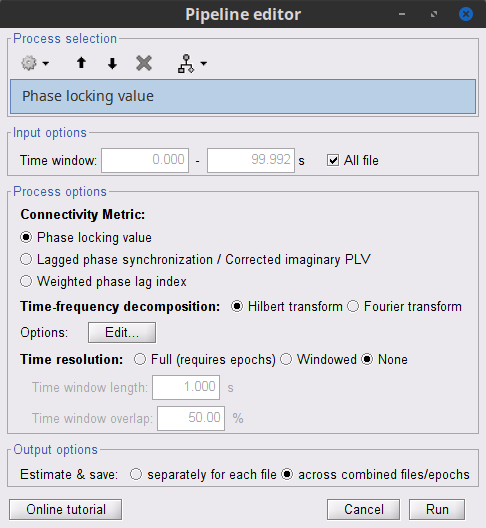
Time window: Time segment of the signal used for the connectivity analysis. Select All file.
Connectivity metric shows variants of phase locking measures. Select: Phase locking value.
Time-frequency decomposition method for time-frequency transformation. Select: Hilbert transform.
Options [Edit] shows the options of the selected time-frequency transformation.
Frequency bands: Used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial. In this example, the sampling frequency of the signals being 120Hz, please remove the "gamma2" band.
Time resolution selection of the time resolution. Select: None.
Output options: Select Save across combined files/epochs.
Results visualization
PLV is frequency resolved, and here was computed for the delta, theta, alpha, beta and gamma1 bands. With the simulated data, we expect a higher PLV value in the beta band (15 to 29 Hz), between Signal 1 and Signal 3. This is indeed our observation, with a peak at 22 Hz (center of beta band) in the PLV spectrum (left). The same is true for ciPLV (center) and wPLI (right).
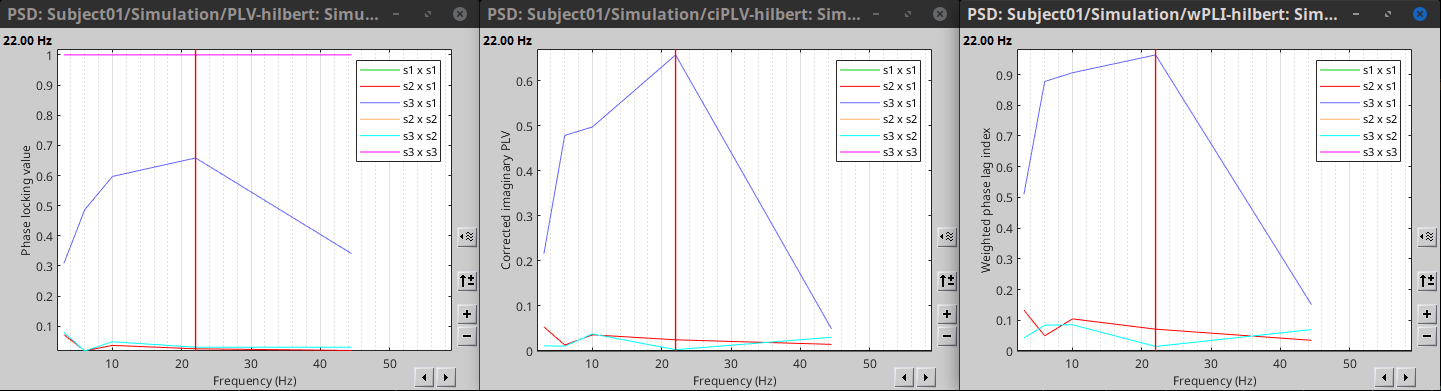
Phase-Transfer Entropy
Phase transfer entropy (PTE) is a directed connectivity metric that quantifies the transfer entropy (TE) between two instantaneous phase time series (Lobier et al., 2014). Similar to GC, TE estimates whether including the past of both source and target time series influences the ability to predict the future of the target time series. In PTE, if a phase signal  causes the signal
causes the signal  , the mutual information, between
, the mutual information, between  and the past of
and the past of 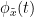 i.e.
i.e. 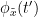 is larger than the mutual information of
is larger than the mutual information of 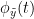 , the past of
, the past of 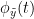 i.e.
i.e. 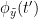 and
and 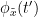 . This relationship can be represented on the Venn diagram below, where
. This relationship can be represented on the Venn diagram below, where 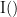 and
and 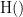 , indicate mutual information and the individual entropies, respectively. PTE values are positive and unbounded.
, indicate mutual information and the individual entropies, respectively. PTE values are positive and unbounded.
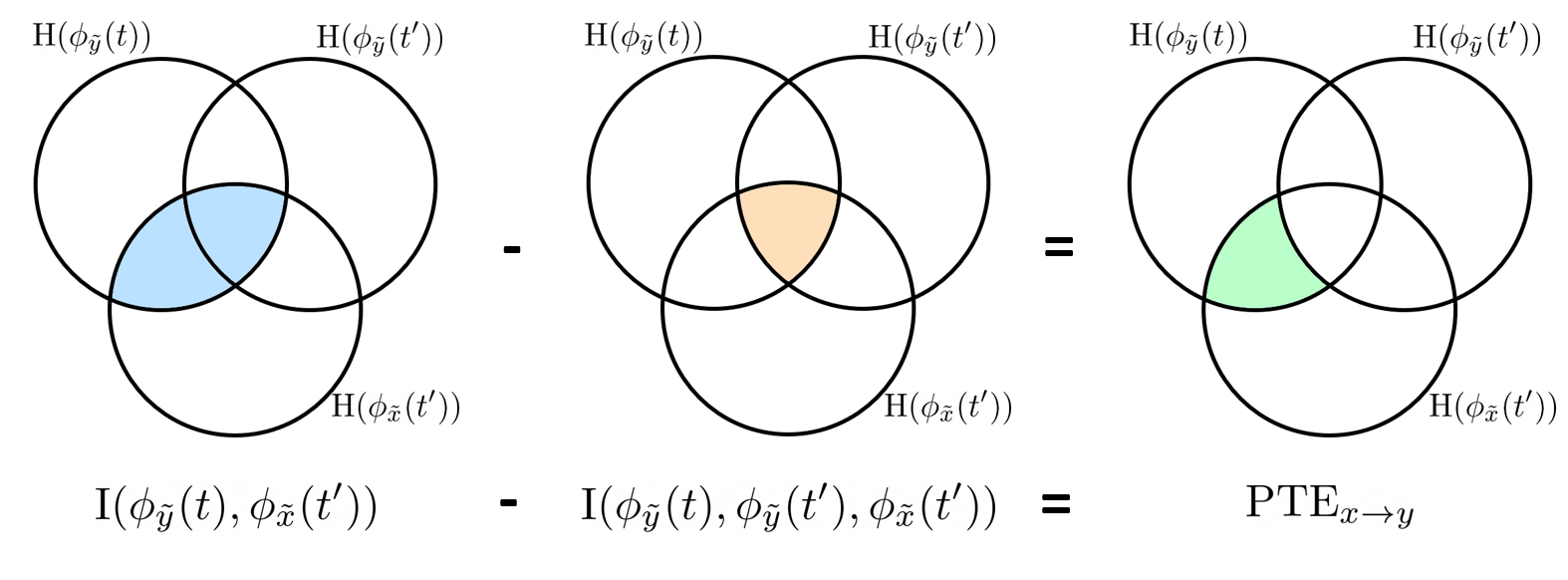
Process options
Process: Connectivity > Phase Transfer Entropy NxN
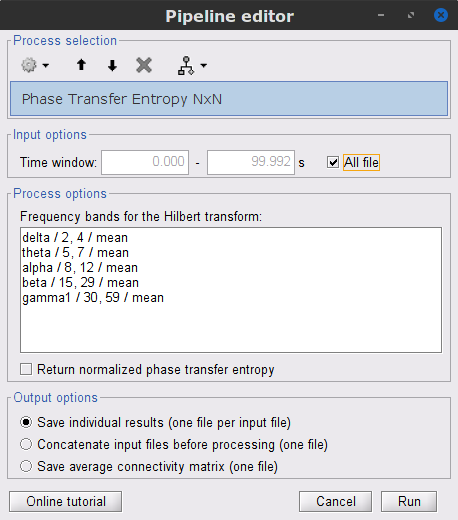
Time window: Time segment of the signal used for the connectivity analysis. Select All file.
Frequency bands: Used for the time-frequency transformation with the Hilbert transform method. See the time-frequency tutorial. In this example, as the sampling frequency of the signals is 120 Hz, make sure the "gamma2" band is removed from the option.
Return normalized phase transfer entropy: Divides each directional PTE value between two signals by the sum of both directional PTE values for those two signals. Uncheck this option
Output options: Select Save individual results.
Results visualization
Here we computed PTE for the delta, theta, alpha, beta and gamma1 bands. From the synthetic data used here, we expect to observe a higher PTE value in the beta band, From Signal 1 To Signal 3. This is indeed shown with a peak at 22 Hz (center of beta band) in the PTE spectrum.
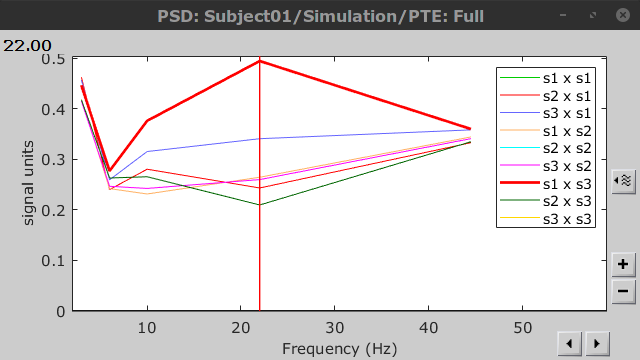 .
.
Summary: connectivity methods
The following table list the available connectivity metrics in Brainstorm and their description.
Metric |
1×N |
N×N |
Directionality |
Freq resolved |
Time resolved |
Function |
Info |
Correlation |
✅ |
✅ |
❌ |
❌ |
✅ |
bst_corrn.m |
|
Coherence |
✅ |
✅ |
❌ |
✅ |
✅ |
bst_cohn.m |
|
Granger causality |
✅ |
✅ |
✅ |
❌ |
❌ |
bst_granger.m |
|
Spectral Granger causality |
✅ |
✅ |
✅ |
✅ |
❌ |
bst_granger_spectral.m |
|
Envelope Correlation (2023) |
✅ |
✅ |
❌ |
✅ |
✅ |
bst_henv.m |
|
Phase locking value |
✅ |
✅ |
❌ |
✅ |
✅ |
bst_connectivity.m |
|
Phase transfer entropy |
❌ |
✅ |
✅ |
✅ |
❌ |
PhaseTE_MF.m |
Thresholding of connectivity estimates
Interactive tools
Brainstorm provides tools to apply empirical thresholds to display the resulting connectivity estimates. Interactions can be filtered interactively based on their magnitudes, the distance between the nodes of the graph or their category. See the tutorial: Connectivity graphs.
Threshold by percentile
The process Test > Threshold by percentile allows the selection of the top n% connectivity estimates in a single input file.
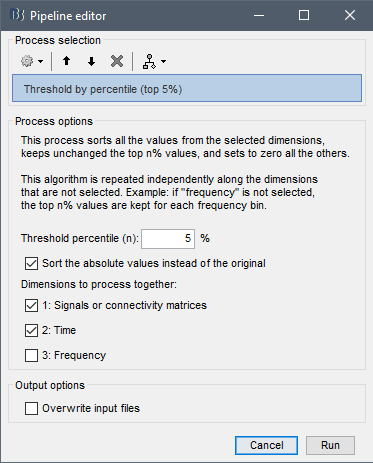
All connectivity estimates (left panel below). The top-5% connectivity matrix (right panel below) only keeps the 5 percentile of all the connectivity estimates.
|
|
|
Statistical significance
Inference based threshold can be derived to assess the statistical significance of the connectivity estimates, for instance using non-parametric paired permutation tests.
Connectivity outcomes can be computed for different experimental conditions, or between an active state and a baseline. Non-parametric paired permutation tests are available in Brainstorm to compare between two groups of repeated measures. More information in the Statistics tutorial.
On the hard drive
File name
The connectivity file structure is an extension of the time-frequency structure. The file names start with timefreq_, followed by connect1 (1xN) or connectn (NxN or AxB), the connectivity method and a time stamp. Example: timefreq_connectn_corr_220120_1350.mat.
File structure
Right click on the first connectivity file computed > File > View file contents.
The data structure is the same as for Brainstorm time-frequency files. Only the fields specific to connectivity analyses are documented below:
TF: [Nr x Ntime x Nfreq] array containing all connectivity values. The connectivity matrix R computed in bst_connectivity.m between two sets of signals A and B, is optimized and saved in the TF variable. The size of the R matrix is [Na x Nb x Ntime x Nfreq]. The relation between Na x Nb and Nr depends on the type of optimization in the file. See details below.
RefRowNames: Cell-array of strings {Na x 1}. Labels of the rows of the connectivity matrix R (Y axis in the image display, with the label From). In the case of a AxB process, these labels are the names of the signals extracted from the first list of files (FilesA).
RowNames: Cell-array of strings {Nb x 1}. Labels of the columns of the connectivity matrix R (X axis in the image display, with the label To). In the case of a AxB process, these labels are the names of the signals extracted from the second list of files (FilesB).
Freqs: Double [1 x Nfreq] for a simple list of frequencies; or cell-array {Nfreq x 3} if using frequency bands, where each line represents a band {'band_name', 'frequency definition', 'function'}
Time: [1,Ntime] for time-resolved files; [1,2] for files with no data dimension (e.g. correlation). When no time is available, this variable describes the time segment from which the connectivity measure was computed.
Options.isSymmetric: Boolean indicating whether the matrix R saved in the TF field is symmetric (e.g. NxN correlation or coherence) or not (e.g. Granger causality). If the R matrix is symmetric, it is saved in a compressed format, with only the values from lower triangular matrix.
Connectivity matrix encoding
Let's consider the structure TfMat, loaded from a connectivity file, for example by right-clicking on the file > File > Export to Matlab. The connectivity matrix R can be obtained with function GetConnectMatrix. The size of R is [Na x Nb x Ntime x Nfreq].
R = bst_memory('GetConnectMatrix', TfMat);If the matrix is not symmetrical (i.e., not compressed): for each time and frequency, the list of values from the first dimension of the TF variable is reshaped into a 2D matrix: [Na x Nb].
If the matrix is symmetrical and compressed: only the lower triangular matrix is saved in the TF variable. The full matrix is first reconstructed with function process_compress_sym>Expand, then reshaped into [Na x Nb].
Saving the connectivity matrix R back in the TF variable is possible by reshaping to [Nx1] (R(:)) and then compressing again the matrix:
TfMat.TF = process_compress_sym('Compress', R(:));
Additional documentation
Related tutorials
Articles
Nolte G, Bai O, Wheaton L, Mari Z, Vorbach S, Hallett M.
Identifying true brain interaction from EEG data using the imaginary part of coherency.
Clinical Neurophysiology. 2004 Oct;115(10):2292–307.Pascual-Marqui RD.
Coherence and phase synchronization: generalization to pairs of multivariate time series, and removal of zero-lag contributions.
arXiv preprint arXiv:0706.1776. 2007 Jun 12.Bressler SL, Seth AK.
Wiener–Granger causality: a well established methodology.
Neuroimage. 2011 Sep 15;58(2):323-9.Dhamala M, Rangarajan G, Ding M.
Estimating Granger causality from Fourier and wavelet transforms of time series data.
Physical review letters. 2008 Jan 10;100(1):018701.Hipp JF, Hawellek DJ, Corbetta M, Siegel M, Engel AK.
Large-scale cortical correlation structure of spontaneous oscillatory activity.
Nature neuroscience. 2012 Jun;15(6):884-90.Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, et al.
Detection of n : m Phase Locking from Noisy Data: Application to Magnetoencephalography.
Phys Rev Lett. 1998 Oct 12;81(15):3291–4.Bruña R, Maestú F, Pereda E
Phase locking value revisited: teaching new tricks to an old dog
Journal of Neural Engineering, Jun 2018Vinck M, Oostenveld R, van Wingerden M, Battaglia F, Pennartz CM
An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias
Neuroimage, Apr 2011Lobier M, Siebenhühner F, Palva S, Palva JM.
Phase transfer entropy: a novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions.
Neuroimage. 2014 Jan 15;85:853-72.Barzegaran E, Knyazeva MG.
Functional connectivity analysis in EEG source space: The choice of method
Ward LM, editor. PLOS ONE. 2017 Jul 20;12(7):e0181105.Lai M, Demuru M, Hillebrand A, Fraschini M.
A comparison between scalp- and source-reconstructed EEG networks.
Sci Rep. 2018 Dec;8(1):12269.Schoffelen J-M, Gross J.
Source connectivity analysis with MEG and EEG.
Hum Brain Mapp. 2009 Jun;30(6):1857–65.Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI.
Circular analysis in systems neuroscience: the dangers of double dipping.
Nat Neurosci. 2009 May;12(5):535–40.Cohen MX.
Analyzing Neural Time Series Data: Theory and Practice. MIT Press; 2014.Sadaghiani S, Brookes MJ, Baillet S.
Connectomics of human electrophysiology.
NeuroImage. 2022 Feb;247:118788.Sporns O.
Networks of the Brain. MIT Press; 2016.
Forum discussions
Granger causality: https://neuroimage.usc.edu/forums/t/12506
Coherence on single trials: https://neuroimage.usc.edu/forums/t/22726
Coherence and PLV: https://neuroimage.usc.edu/forums/t/33379
Removing ERP response for PLV: https://neuroimage.usc.edu/forums/t/32665
Connectivity of subcortical ROIs: https://neuroimage.usc.edu/forums/t/33479
Non-zero diagonals with unconstrained sources: https://neuroimage.usc.edu/forums/t/33700
Coherence/Lagged coherence vs. Envelope correlation/Lagged coherence: https://neuroimage.usc.edu/forums/t/lagged-coherence/39440
Scripting
The following script from the Brainstorm distribution reproduces the analysis presented in this tutorial page: brainstorm3/toolbox/script/tutorial_connectivity.m
TODO
Hossein, Richard
Granger Causality implementation: https://github.com/brainstorm-tools/brainstorm3/pull/433
Raymundo, Sylvain
- Read data: Can we find something more meaningful than what we compute in the example in the dataset? A full connectome in a task vs. baseline maybe?

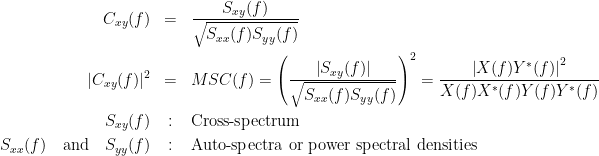
![\begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*} \begin{eqnarray*}
IC_{xy}(f) &=& \mathrm{Im} \left (C_{xy}(f) \right ) = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) }} \\
LC_{xy}(f) &=& \frac{\mathrm{Im} \left (C_{xy}(f) \right )}{\sqrt{ 1 - \left [ \mathrm{Re}\left ( C_{xy}(f) \right ) \right ]^{2} }} = \frac{\mathrm{Im} \left (S_{xy}(f) \right )}{\sqrt{ S_{xx}(f)S_{yy}(f) - \left [ \mathrm{Re}\left ( S_{xy}(f) \right ) \right ]^{2} }} \\
\end{eqnarray*}](/brainstorm/Tutorials/Connectivity?action=AttachFile&do=get&target=latex_697a31e2ea80e1d7e07fbd14e43c910e44e14e3c_p1.png)